ABSTRAK
Tugas akhir ini membahas tentang penyelesaian numeris masalah nilai awal dengan menggunakan metode Runge-Kutta dan metode blok rasional. Metode Runge-Kutta yang digunakan yaitu, Runge-Kutta tingkat satu (metode Euler) dan Runge-Kutta tingkat dua (metode Heun). Kedua metode numeris Runge-Kutta tersebut sering digunakan untuk menyelesaikan masalah nilai awal.
ABSTRACT
This final assignment discusses about numerical solutions to initial value problems using Runge-Kutta and rational block methods. The Runge-Kutta methods cosidered in this final assignment are the first order Runge-Kutta (Euler’s method) and the second order Runge-Kutta (Heun’s method). Both these Runge-Kutta numerical methods are often used to solve initial value problems.
i
METODE RUNGE-KUTTA DAN BLOK RASIONAL UNTUK
MENYELESAIKAN MASALAH NILAI AWAL
Tugas Akhir
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains
Program Studi Matematika
Oleh : Agung Christian NIM: 133114019
PROGRAM STUDI MATEMATIKA, JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
ii
RUNGE-KUTTA AND RATIONAL BLOCK METHODS FOR
SOLVING INITIAL VALUE PROBLEM
FINAL ASSIGNMENT
Presented as Partial Fulfillment of the
Requirements to Obtain the Degree of Sarjana Sains Mathematics Study Program
Written by: Agung Christian Student Number: 133114019
MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY YOGYAKARTA
v MOTTO
“Hal yang paling penting dalam hidup bukanlah kemenangan
namun perjuangan. Hal yang perlu bukanlah menaklukan, tapi
telah berjuang dengan baik”
~Eddie the eagle~
vi
HALAMAN PERSEMBAHAN
Karya ini aku persembahkan kepada:
Tuhan Yesus Kristus yang selalu membuatku kuat dan bertahan pada pilihan yang aku buat.
vii
PERNYATAAN KEASLIAN
Saya menyatakan dengan sesungguhnya, bahwa tugas akhir yang saya tulis ini
tidak memuat karya atau bagian karya orang lain kecuali yang disebutkan dalam
daftar pustaka, sebagaimana layaknya karya ilmiah.
Yogyakarta, 20 Februari 2017
viii
LEMBAR PERNYATAAN PERSETUJUAN
PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS
Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma:
Nama : Agung Christian
NIM : 133114019
Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan
Universitas Sanata Dharma karya ilmiah saya yang berjudul:
METODE RUNGE-KUTTA DAN BLOK RASIONAL UNTUK MENYELESAIKAN MASALAH NILAI AWAL
beserta perangkat yang diperlukan (bila ada). Dengan demikian saya memberikan
kepada Perpustakaan Universitas Sanata Dharma untuk menyimpan, mengalihkan
ke dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data,
mendistribusikan secara terbatas dan mempublikasikannya di internet atau media
lain untuk kepentingan akademis tanpa perlu meminta ijin dari saya maupun
memberikan royalti kepada saya selama tetap menyantumkan nama saya sebagai
penulis.
Demikian pernyataan ini saya buat dengan sebenarnya,
Dibuat di Yogyakarta
Pada tanggal: 20 Februari 2017
Yang menyatakan
ix ABSTRAK
Tugas akhir ini membahas tentang penyelesaian numeris masalah nilai
awal dengan menggunakan metode Runge-Kutta dan metode blok rasional.
Metode Runge-Kutta yang digunakan yaitu, Runge-Kutta tingkat satu (metode
Euler) dan Runge-Kutta tingkat dua (metode Heun). Kedua metode numeris
Runge-Kutta tersebut sering digunakan untuk menyelesaikan masalah nilai awal.
Metode blok rasional diperkenalkan oleh Teh Yuan Ying dan
kawan-kawan pada tahun 2014. Metode ini merupakan metode yang tidak banyak dikenal
umum, sehingga metode ini jarang digunakan. Metode blok rasional merupakan
gabungan dari metode satu langkah dan dua langkah yang dalam penghitungannya
metode blok rasional membentuk suatu blok yang di dalamnya terdapat tiga buah
titik. Jadi metode blok rasional mampu menghitung nilai hampiran dua buah titik
secara bersamaan dalam satu iterasi. Selain itu metode blok rasional juga
mempunyai penyelesaian yang lebih akurat dibandingkan dengan metode Euler
dan metode Heun. Hal ini dapat dilihat melalui simulasi dengan komputer.
Kesalahan dari metode blok rasional relatif lebih kecil dibandingkan metode Euler
x ABSTRACT
This final assignment discusses about numerical solutions to initial value
problems using Runge-Kutta and rational block methods. The Runge-Kutta
methods cosidered in this final assignment are the first order Runge-Kutta
(Euler’s method) and the second order Runge-Kutta (Heun’s method). Both these
Runge-Kutta numerical methods are often used to solve initial value problems.
Rational block method was introduced by Teh Yuan Ying and colleagues
in 2014. This method is not widely known in general, so this method is rarely
used. Rational block method is a combination of one-step and two-step methods
where in the calculations, rational block method forms a block in which there are
three points. Therefore, rational block method is able to calculate the
approximation values of two points simultaniously in one iteration. Furthermore,
rational block method also has more accurate solution than Euler’s and Heun’s
methods. This can be seen in computer simulation. The error of rational block
xi
KATA PENGANTAR
Puji dan syukur penulis panjatkan kepada Tuhan Yesus Kristus atas berkat
dan rahmat melimpah yang selalu diberikan kepada penulis sehingga penulis
dapat menyelesaikan tugas akhir ini. Tugas akhir ini merupakan salah satu syarat
yang harus dipenuhi oleh penulis agar penulis dapat memperoleh gelar Sarjana
Sains (S.Si.). Pada kesempatan kali ini, penulis ingin mengucapkan terimakasih
kepada seluruh pihak yang telah membantu penulis dalam menyelesaikan tugas
akhir ini.
Penulis ingin mengucapkan terima kasih yang sebesar-besarnya kepada:
1. Bapak Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D. selaku dosen pembimbing
dan Dekan Fakultas Sains dan Teknologi, Universitas Sanata Dharma.
2. Bapak Hartono, S.Si., M.Sc., Ph.D. selaku Ketua Program Studi
Matematika, Fakultas Sains dan Teknologi, Universitas Sanata Dharma.
3. Romo Prof. Dr. Frans Susilo, S.J., Ibu Any Herawati, S.Si., M.Si., Bapak
Ig. Aris Dwiatmoko, M.Sc., Bapak Dr. rer. nat. Herry P. Suryawan, M.Si.,
dan Ibu Lusia Krismiyati Budiasih, S.Si., M.Si., selaku dosen-dosen
Program Studi Matematika yang sangat membantu penulis selama proses
menimba ilmu di Program Studi Matematika, Universitas Sanata Dharma.
4. Bapak/Ibu dosen dan karyawan yang selalu membantu dan memberikan
masukan dan dukungannya kepada penulis.
5. Kedua orang tuaku yang selalu mengingatkan dan memberi semangat
xii
6. Keluarga besar F. B. Soeharto atas dukungan, semangat, dan motivasi
yang selalu diberikan kepada penulis.
7. Teman-teman seperjuangan, mahasiswa/i Program Studi Matematika
angkatan 2013 atas suka duka dan pahit manisnya pengalaman yang
pernah kita jalani bersama.
8. Kakak tingkat dan adik tingkat mahasiswa/i Program Studi Matematika
karena boleh mengenal, bercanda, berbagi suka duka bersama kalian.
9. Teman-teman OMK Gereja St. F. X. Kidul Loji Yogyakarta atas bantuan
dan dukungannya selama ini. Terima kasih karena selalu ada saat susah
maupun senang.
10.Semua pihak yang tidak dapat disebutkan satu per satu.
Penulis menyadari bahwa masih banyak kekurangan dalam penulisan tugas
akhir ini. Oleh karena itu, penulis mohon kritik dan saran kepada pembaca supaya
penulis dapat menyempurnakan karya ini. Semoga tugas akhir ini dapat
bermanfaat bagi pembaca dan bagi kemajuan ilmu pengetahuan.
Yogyakarta, 20 Februari 2017
Penulis
xiii DAFTAR ISI
Halaman
HALAMAN JUDUL ……..……..……..……..……..……..……..…... i
HALAMAN PERSETUJUAN PEMBIMBING ………. iii
HALAMAN PENGESAHAN ……….……. iv
MOTTO ……… v
HALAMAN PERSEMBAHAN ……….. vi
PERNYATAAN KEASLIAN KARYA ………... vii
PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH ..… viii
ABSTRAK ……….. ix
ABSTRACT ………. x
KATA PENGANTAR ……… xi
DAFTAR ISI ……… xiii
BAB I: PENDAHULUAN ……….. 1
A. Latar Belakang ………
B. Rumusan Masalah ……….………
C. Batasan Masalah ……….……
D. Tujuan Penulisan ………
E. Manfaat Penulisan ………
F. Metode Penulisan ………
G. Sistematika Penulisan ………
1
xiv
A. Persamaan Diferensial ………
1. Definisi Persamaan Diferensial ………..………
2. Klasifikasi Persamaan Diferensial ………..…….
3. Masalah Nilai Awal ……….
4. Teorema Eksistensi dan Ketunggalan ………..
B. Metode Pendekatan atas Nilai Fungsi ………
1. Deret Taylor ………
2. Metode Euler ………..………
3. Metode Heun ………..………
C. Penyelesaian Analitis Masalah Nilai Awal ………
1. Persamaan Diferensial Biasa Tingkat Satu ……….………
2. Persamaan Diferensial Biasa Tingkat Dua ……….………
3. Penyelesaian Analitis Persamaan Diferensial Biasa ……… 7
BAB III: METODE BLOK RASIONAL ………. 30
A. Metode Blok Rasional ………..
B. Penyelesaian Numeris Masalah Nilai Awal …………..………… 30
42
BAB IV: KEKONVERGENAN METODE NUMERIS ……… 53
A. Definisi dan Teorema untuk Kekonvergenan ………
B. Kekonvergenan Metode Euler ………
C. Kekonvergenan Metode Heun ………
xv
B. Saran ………..…. 63
DAFTAR PUSTAKA ……… 64
LAMPIRAN 1……….. 66
1
BAB I
PENDAHULUAN
A. Latar Belakang
Dalam dunia sains dan teknik, model matematika sangat berguna
untuk menyelesaikan berbagai macam persoalan yang ada. Ada berbagai
macam model matematika yang bisa diterapkan, salah satunya model
per-samaan matematika yang terdiri atas beberapa turunan fungsi yang tidak
diketahui. Persamaan tersebut biasa disebut persamaan diferensial.
Ber-dasarkan banyaknya variabel bebas, persamaan diferensial dibedakan
men-jadi dua jenis, yaitu persamaan diferensial biasa dan persamaan diferensial
parsial.
Pada tugas akhir ini akan dibahas mengenai penyelesaian masalah
nilai awal dari suatu persamaan diferensial biasa. Persamaan diferensial
biasa adalah persamaan yang memuat beberapa turunan dari fungsi yang
tidak diketahui dan memuat satu variabel bebas. Untuk menyelesaikan
suatu persamaan diferensial biasa diperlukan nilai awal. Persamaan
diferensial yang disajikan bersama nilai awalnya disebut masalah nilai
awal. Masalah nilai awal yang melibatkan turunan pertama dapat ditulis
dalam bentuk:
′ = �( , ), = �
dengan merupakan variabel bebas, merupakan titik awal, dan �
Ada dua cara yang bisa dilakukan untuk menyelesaikan masalah
nilai awal, yaitu secara analitis dan numeris. Penyelesaian masalah nilai
awal secara analitis tidak selalu mudah didapatkan. Ada beberapa bentuk
persamaan diferensial yang sulit diselesaikan secara analitis. Jika masalah
nilai awal sulit diselesaikan secara analitis, maka masalah nilai awal
terse-but dapat dicoba diselesaikan secara numeris. Dalam tugas akhir ini akan
dibahas penyelesaian masalah nilai awal suatu persamaan diferensial biasa
secara numeris dengan menggunakan metode Euler, metode Heun, dan
metode blok rasional.
Metode Euler dan metode Heun merupakan metode numeris yang
sering digunakan untuk menyelesaikan masalah nilai awal, sedangkan
metode blok rasional merupakan metode yang tidak terlalu populer dan
oleh karena itu metode ini jarang digunakan. Akan tetapi, metode blok
ra-sional mempunyai penghitungan yang lebih cepat dibandingkan dengan
metode Euler dan metode Heun. Hal ini karena dalam satu iterasi, metode
blok rasional mampu menghitung nilai pendekatan dua titik secara
bersamaan. Penghitungan masalah nilai awal dengan metode blok rasional
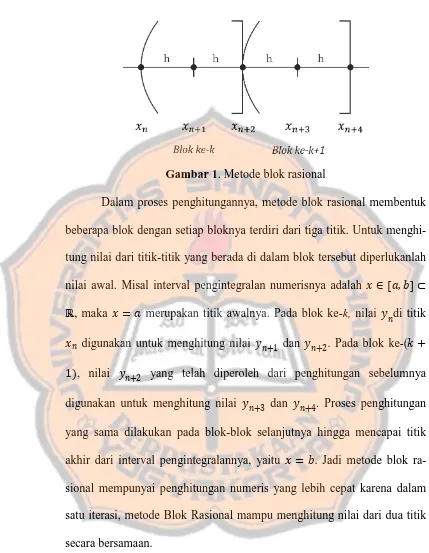
Gambar 1. Metode blok rasional
Dalam proses penghitungannya, metode blok rasional membentuk
beberapa blok dengan setiap bloknya terdiri dari tiga titik. Untuk
menghi-tung nilai dari titik-titik yang berada di dalam blok tersebut diperlukanlah
nilai awal. Misal interval pengintegralan numerisnya adalah ∈ [ , ] ⊂
ℝ, maka = merupakan titik awalnya. Pada blok ke-k, nilai �di titik
� digunakan untuk menghitung nilai �+ dan �+ . Pada blok ke-(� +
, nilai �+ yang telah diperoleh dari penghitungan sebelumnya
digunakan untuk menghitung nilai �+ dan �+ . Proses penghitungan
yang sama dilakukan pada blok-blok selanjutnya hingga mencapai titik
akhir dari interval pengintegralannya, yaitu = . Jadi metode blok
ra-sional mempunyai penghitungan numeris yang lebih cepat karena dalam
satu iterasi, metode Blok Rasional mampu menghitung nilai dari dua titik
secara bersamaan.
B. Rumusan Masalah
1. Bagaimana menyelesaikan masalah nilai awal dari suatu
persa-maan diferensial biasa dengan menggunakan metode Euler, metode
Heun, dan metode blok rasional?
2. Bagaimana kekonvergenan metode Euler, metode Heun, dan
metode blok rasional?
C. Batasan Masalah
Masalah yang dibahas dalam tugas akhir ini terbatas pada penyelesaian
masalah nilai awal dari suatu persamaan diferensial biasa tingkat satu dan
tingkat dua.
D. Tujuan Penulisan
Tujuan penulisan tugas akhir ini:
1. Menyelesaikan masalah nilai awal dari suatu persamaan diferensial
biasa secara numeris dengan menggunakan metode Euler, metode
Heun, dan metode blok rasional.
2. Menganalisis kekonvergenan metode Euler, metode Heun, dan
metode blok rasional dengan analisis numeris dan simulasi
komput-er.
E. Manfaat penulisan
Manfaat penulisan dari tugas akhir ini yaitu kita dapat menyelesaikan
F. Metode Penulisan
Metode penulisan yang digunakan dalam tugas akhir ini yaitu studi
pustaka dengan mempelajari buku-buku dan jurnal-jurnal yang berkaitan
dengan persamaan diferensial dan metode numeris serta dengan simulasi
komputer.
BAB II: PERSAMAAN DIFERENSIAL DAN METODE NUMERIS
A. Persamaan Diferensial
1. Definisi Persamaan Diferensial
2. Klasifikasi Persamaan Diferensial
3. Masalah Nilai Awal
4. Teorema Eksistensi dan Ketunggalan
1. Deret Taylor
2. Metode Euler
3. Metode Heun
C. Penyelesaian Analitis Masalah Nilai Awal
1. Persamaan Diferensial Biasa Tingkat Satu
2. Persamaan Diferensial Biasa Tingkat Dua
3. Penyelesaian Analitis Persamaan Diferensial Biasa
BAB III: METODE BLOK RASIONAL
A. Metode Blok Rasional
B. Penyelesaian Numeris Masalah Nilai Awal
BAB IV: KEKONVERGENAN METODE NUMERIS
A. Definisi dan Teorema untuk Kekonvergenan
B. Kekonvergenan Metode Euler
C. Kekonvergenan Metode Heun
D. Kekonvergenan Metode Blok Rasional
BAB V: PENUTUP
A. Kesimpulan
7
BAB II
PERSAMAAN DIFERENSIAL DAN METODE NUMERIS
Pada bab II ini akan dipaparkan beberapa pokok bahasan penting dalam
persa-maan diferensial dan metode numeris.
A. Persamaan Diferensial
Pada bagian ini akan dibahas pengertian, klasifikasi dan contoh-contoh
persamaan diferensial.
1. Definisi 2.1. (Persamaan Diferensial)
Persamaan Diferensial adalah suatu persamaan yang terdiri dari beberapa
turunan fungsi yang tidak diketahui, yang menyatakan hubungan fungsi
ter-sebut dengan turunan-turunannya. (Boyce, W. E. and R. C. DiPrima)
2. Klasifikasi Persamaan Diferensial
Berdasarkan beberapa kriteria, persamaan diferensial
diklasifikasikan ke dalam beberapa jenis.
a.Persamaan Diferensial Biasa dan Parsial.
Salah satu klasifikasi penting dalam persamaan diferensial yaitu
banyaknya variabel bebas yang terdapat dalam persamaan diferensial
tersebut. Banyaknya variabel bebas dalam suatu persamaan diferensial
akan menentukan jenis persamaan diferensial. Berdasarkan banyaknya
variabel bebas, persamaan diferensial dibedakan menjadi dua jenis,
Definisi 2.2. (Persamaan Diferensial Biasa)
Persamaan Diferensial Biasa (PDB) adalah suatu persamaan
diferensial yang hanya melibatkan turunan biasa dan mempunyai satu
variabel bebas. (Boyce, W. E. and R. C. DiPrima)
Contoh persamaan diferensial biasa:
+ = (1)
+ − = (2)
+ 55 = (3)
+ = sin (4)
dengan merupakan variabel tak bebas dan merupakan variabel
bebas. Persamaan (1) – (4) dapat ditulis dalam bentuk lain, yaitu:
′ + = (5)
′′ + ′ − = (6)
+ 5 = (7)
′+ = sin (8)
Definisi 2.3. (Persamaan Diferensial Parsial)
Persamaan Diferensial parsial (PDP) adalah suatu persamaan
diferensial yang melibatkan turunan parsial dan mempunyai lebih dari
satu variabel bebas. (Boyce, W. E. and R. C. DiPrima)
Contoh persamaan diferensial parsial:
� ,
� +
� ,
� =
dengan , merupakan variabel tak bebas dan , merupakan
varia-bel bebas.
b.Tingkat Persamaan Diferensial
Tingkat (orde) dari suatu persamaan diferensial adalah tingkat
turunan tertinggi pada persamaan diferensial tersebut. Jika turunan
tertinggi suatu persamaan diferensial adalah n, maka persamaan
diferensial tersebut merupakan persamaan diferensial tingkat n. Contoh
persamaan (1) merupakan persamaan diferensial tingkat satu,
persa-maan (2) merupakan persapersa-maan diferensial tingkat dua dan persapersa-maan
(3) merupakan persamaan diferensial tingkat sepuluh. Jadi, jika turunan
tertinggi dari suatu persamaan diferensial adalah �, maka persamaan
tersebut merupakan persamaan diferensial tingkat �. Berikut merupakan
bentuk umum persamaan diferensial biasa berdasar tingkatannya.
′′ = , , ′ persamaan diferensial tingkat dua
= ( , , ′, … , ) persamaan diferensial tingkat sepuluh
� = ( , , ′, … , �− ) persamaan diferensial tingkat �
c.Linier dan Non-Linier.
Salah satu klasifikasi penting pada persamaan diferensial adalah
ketika persamaan diferensial tersebut bersifat linier atau non-linier.
Definisi 2.4. (Persamaan Diferensial Biasa Linier)
Persamaan diferensial biasa disebut linier jika
( , , ′, ′′, … . , � ) = memuat semua suku fungsi linier dari
var-iabel , ′, ′′, … . , � . (Boyce, W. E. and R. C. DiPrima)
Secara umum, persamaan diferensial biasa linier ditulis dalam bentuk:
� + �− + + � = (9)
dengan , , , … , � merupakan fungsi dari dan
merupakan variabel tak bebas. Contoh dari persamaan diferensial biasa
linier adalah persamaan (1) dan (2) karena kedua persamaan tersebut
Definisi 2.5. (Persamaan Diferensial Biasa Non-linier)
Persamaan diferensial biasa disebut non-linier jika persamaan
diferensial tersebut tidak memenuhi persamaan (9). (Boyce, W. E. and
R. C. DiPrima)
Contoh dari persamaan diferensial biasa non-linier adalah persamaan
(4) karena pada persamaan tersebut terdapat fungsi y dan sin y.
3. Masalah Nilai Awal
Pada bagian ini akan dijelaskan pengertian masalah nilai awal dan
contoh-contohnya.
Definisi 2.6. Masalah nilai awal
Masalah nilai awal adalah persamaan diferensial yang disajikan
bersama dengan nilai awalnya. Misalkan masalah nilai awal untuk
persamaan diferensial tingkat ke-� diberikan oleh:
( , , ′, … , � ) = .
Hal ini berarti mencari penyelesaian persamaan diferensial pada interval I
yang memenuhi kondisi awal,
= ,
′ = ,
�− =
dengan ∈ � dan , , … , �− merupakan suatu konstanta.
Contoh masalah nilai awal, yaitu:
′ = − , = (10)
′′ + ′ + = , = . , ′ = − (11)
′ = + , = . (12)
4. Teorema Eksistensi dan Ketunggalan
Teorema eksistensi dapat membantu untuk mencari tahu apakah
penyelesaian masalah nilai awal tersebut ada atau tidak. Jika adalah
fungsi kontinu yang melewati , , maka masalah nilai awal tersebut
mempunyai penyelesaian. Selanjutnya, jika masalah nilai awal tersebut
mempunyai penyelesaian, dapat diperiksa apakah penyelesaiannya
tung-gal atau tidak. Oleh karena itu, untuk memeriksa ketungtung-galan dari
penyelesaian masalah nilai awal tersebut dapat digunakan teorema
ke-tunggalan. Jika , kontinu dan �� juga kontinu, maka masalah nilai
awal tersebut mempunyai penyelesaian yang tunggal. Lebih lanjut,
diberikan teorema eksistensi dan ketunggalan sebagai berikut.
Teorema.
Diberikan masalah nilai awal:
Jika dan �� adalah fungsi yang kontinu pada daerah
� = { , : < < , < < }
yang memuat , , maka masalah nilai awal mempunyai
penyelesaian tunggal pada interval − � ≤ ≤ + �, dengan
� > .
Bukti: Dapat dilihat dalam buku referensi Fundamentals of Differential
Equations and Boundary Value Problem. (6th edition). Chapter 13.
B. Metode Pendekatan atas Nilai Fungsi
Pada bagian ini akan dibahas beberapa metode pendekatan antara lain
deret Taylor, metode Euler dan metode Heun.
1. Deret Taylor
Jika − = ℎ, maka deret Taylor dapat ditulis sebagai berikut:
= + ℎ! ′ + +ℎ�
�! � + ,
atau dapat ditulis dalam notasi sigma sebagai berikut:
= ∑ℎ�! � � ∞
�=
2. Metode Euler
Metode Euler merupakan metode numeris yang sering digunakan dalam
menyelesaikan masalah nilai awal. Metode Euler diperoleh dengan
men-guraikan suatu fungsi ke dalam deret Taylor sampai dua suku awal. Metode
ini mempunyai tingkat keakuratan satu.
Berikut ini rumusan dari metode Euler.
Diberikan masalah nilai awal:
′ = , , = .
Misalkan � = � adalah hampiran nilai di titik � dengan � = +
� ℎ untuk � = , , , … , . Metode Euler diturunkan dengan cara
menguraikan �+ di sekitar � ke dalam deret Taylor, sehingga diperoleh:
�+ = �+ �+ −! � �′ + �+ −! � �′′ + .
Jika persamaan di atas dipotong sampai suku kedua, maka diperoleh:
�+ = �+ �+ −! � �′ + � ℎ ,
dengan � ℎ adalah suku sisa atau kesalahan pemotongan lokal dari metode
Euler. Diketahui bahwa ′ = , dan ℎ = �+ − �, maka persamaan
tersebut menjadi:
3. Metode Heun
Metode Heun merupakan perbaikan dari metode Euler. Metode Euler
mempunyai penghitungan yang lebih sederhana dibandingkan dengan metode
Heun. Metode Heun merupakan metode Runge-Kutta tingkat dua. Bentuk
umum penyelesaian persamaan diferensial biasa dengan menggunakan
metode Runge-Kutta tingkat dua, yaitu:
�+ = �+ � + � ,
dengan � = ℎ �, � dan � = ℎ �+ ℎ, �+ � .
Dari persamaan Runge-Kutta tingkat dua tersebut diketahui bahwa
, , � , � adalah koefisien-koefisien yang tidak diketahui nilainya. Oleh
karena itu akan dicari nilai dari koefisien-koefisien tersebut.
Misalkan,
= �, � ,
=� ��, � ,
=� �, �
� .
Dengan menguraikan � ke dalam deret Taylor di sekitar , sampai suku
tingkat satu, diperoleh:
� = ℎ � + ℎ, �+ �
= ℎ ( + ℎ� ��, � + � � ��, � )
= ℎ ( + ℎ + ℎ )
= ℎ + ℎ ( + ).
Agar persamaan (*) sama dengan persamaan (**) haruslah,
+ = ,
= ,
= .
= − = − ,
= = ,
= = .
Jadi metode Runge-Kutta tingkat dua mempunyai tak hingga banyak
penyelesaian. Salah satu contoh metode Runge-Kutta tingkat dua yaitu
metode Heun. Metode Heun merupakan penyelesaian khusus dari metode
Runge-Kutta dengan mengambil
= , = , = = ,
sehingga diperoleh rumus metode Heun, yaitu:
�+ = �+ ℎ [ �, � + �+ , �+∗ ],
dimana �+∗ = �+ ℎ �, � .
C. Penyelesaian Analitis Masalah Nilai Awal
Sebelum masuk ke contoh penyelesaian persamaan diferensial biasa,
terlebih dahulu akan dipaparkan beberapa metode penyelesaian persamaan
diferensial biasa.
1. Persamaan Diferensial Biasa Tingkat Satu
Pada bagian ini akan dijelaskan teknik penyelesaian persamaan diferensial
biasa tingkat satu, yaitu (a) persamaan diferensial biasa yang langsung
diintegralkan, (b) persamaan diferensial biasa dengan variabel terpisah, (c)
a. Persamaan diferensial biasa yang bisa langsung diintegralkan.
Akan dicari penyelesaian umum untuk persamaan diferensial biasa
berikut:
= .
Dengan pengintegralan, diperoleh sebagai berikut:
=
≡ =
≡ ∫ =∫
≡ = ∫ + �.
Jadi, diperoleh penyelesaian umum dari suatu persamaan diferensial
biasa, yaitu:
= ∫ + �.
b. Persamaan diferensial biasa dengan variabel terpisah.
Akan dicari penyelesaian umum untuk persamaan diferensial biasa
berikut:
= , .
Penyelesaian persamaan diferensial tersebut dapat dicari sebagai
beri-kut.
Misalkan , = dengan fungsi dalam dan
=
≡ = .
Dengan pegintegralan, diperoleh:
∫ =∫
≡ ∫ =∫ + �.
Jadi, diperoleh penyelesaian umum dari suatu persamaan diferensial
biasa, yaitu:
∫ =∫ + �,
dengan � suatu konstanta.
c. Persamaan diferensial biasa linier
Akan dicari penyelesaian untuk persamaan diferensial biasa berikut:
+ = .
Persamaan diferensial biasa linier tingkat satu dapat diselesaikan
dengan metode faktor integral. Berikut langkah-langkah mencari
faktor integral.
Diberikan persamaan diferensial biasa linier tingkat satu.
Persa-maan tersebut dikalikan dengan suatu fungsi � > dengan �
adalah fungsi dalam yang tidak diketahui nilainya. Sehingga
� + � = � .
Persamaan tersebut dapat diubah menjadi,
[� ]= �
≡ � + � = � ,
sehingga diperoleh
�= �
≡ � � =
Dengan pengintegralan diperoleh:
∫� � =∫
≡ ln|� |=∫
≡ � = ∫ � � .
Diperoleh faktor integral, yaitu:
� = ∫ � � .
Karena faktor integral diketahui, maka dapat dicari penyelesaian dari
persamaan diferensial biasa linier tingkat satu.
+ =
≡ � + � = �
≡ [� ] = � .
∫ [� ] = ∫ �
≡ � = ∫ � + �
≡ = � [∫� + �],
dengan � adalah suatu konstanta. Jadi, diperoleh penyelesaian
persa-maan diferensial biasa linier tingkat satu, yaitu:
= � [∫� + �].
2. Persamaan Diferensial Biasa Tingkat Dua
Pada bagian ini akan dijelaskan teknik penyelesaian persamaan diferensial
biasa tingkat dua, yaitu (a) persamaan diferensial biasa koefisien konstan
homogen, (b) persamaan diferensial biasa koefisien konstan non homogen.
a. Persamaan diferensial biasa koefisien konstan homogen
Diberikan persamaan diferensial biasa tingkat dua koefisien konstan
homogen:
+ + =
dengan , , adalah konstanta. Misalkan penyelesaian umum
persamaan diferensial biasa koefisien konstan homogen yaitu
= � . Maka dapat dicari turunan pertama dan kedua dari
penyelesaian tersebut, yaitu:
′ = ,
dengan adalah konstanta. Dengan mensubstitusikan ′ dan ′′ ,
maan karakteristik diatas terdapat tiga kemungkinan dalam
menen-tukan akar-akarnya.
1) Terdapat dua akar real berbeda, yaitu dan .
2) Terdapat satu akar real yang sama, yaitu =
3) Terdapat dua akar kompleks
Diasumsikan akar-akar dari persamaan karakteristik real berbeda.
Dengan demikian diperoleh dua penyelesaian, yaitu:
= ,
= .
Jadi, penyelesaian umum persamaan diferensial biasa homogen
ting-kat dua menjadi:
= + ,
atau
= � + � ,
b. Persamaan diferensial biasa koefisien konstan non-homogen.
Diberikan persamaan diferensial biasa tingkat dua koefisien konstan
non-homogen:
+ + = ,
dengan , , adalah konstanta dan ≠ adalah fungsi dalam x.
Penyelesaian persamaan diferensial biasa tingkat dua koefisien
konstan non-homogen dapat diselesaikan dengan metode koefisien tak
tentu. Misalkan � dan � adalah penyelesaian persamaan diferensial
biasa tingkat dua koefisien konstan non-homogen, maka:
�′′+ �′+ � = ,
dan
�′′+ �′+ � = .
Dengan mengeliminasi kedua persamaan diferensial tersebut,
di-peroleh:
�′′− �′′ + �′− �′ + � − � = .
Dengan kata lain, � − � adalah penyelesaian persamaan diferensial
biasa tingkat dua koefisien konstan homogen. Diketahui bahwa
per-samaan diferensial biasa tingkat dua koefisien konstan homogen
mempunyai penyelesaian umum:
= + .
Hal ini berakibat,
� − � = � + � ,
� = � + � + � .
Dengan mengambil = � dan � = � diperoleh:
= + + �,
dengan adalah penyelesaian umum persamaan diferensial biasa
tingkat dua koefisien konstan homogen dan � adalah salah satu
penyelesaian persamaan diferensial biasa tingkat dua koefisien
kon-stan non-homogen.
3. Penyelesaian Analitis Persamaan Diferensial Biasa
Pada bagian ini diberikan tiga contoh masalah nilai awal yang akan
diselesaikan secara analitis.
a. Contoh 1.
Diberikan masalah nilai awal
′ = − ,
dengan nilai awal = .
Penyelesaian:
Persamaan ini merupakan persamaan diferensial biasa tingkat satu
dengan variabel terpisah.
Dari
= − ,
dengan mengalikan − disetiap ruasnya diperoleh:
Penyelesaian persamaan (i.1), yaitu:
dari penyelesaian umumnya. Oleh karena itu, dengan
mensubsti-tusikan = , diperoleh:
Jadi, diperoleh penyelesaian khususnya, yaitu:
= − .
b. Contoh 2.
′′ + ′ + = ,
dengan nilai awal = . , ′ = − .
Penyelesaian:
Masalah nilai awal tersebut merupakan persamaan diferensial biasa
tingkat dua dengan koefisien konstan homogen. Dari masalah nilai
awal diketahui
′′ + ′ + = .
Misalkan penyelesaian umum persamaan diferensial biasa koefisien
konstan homogen yaitu = � . Maka dapat dicari turunan pertama
dan kedua dari penyelesaian umum tersebut, yaitu:
′= ,
′′= ,
dengan ≠ . Dengan mensubstitusikan ′ dan ′′ ke dalam
masa-lah nilai awal, maka diperoleh:
+ + =
≡ ( + + ) =
≡ + + = .
Diperoleh persamaan karakteristik:
+ + .
Dari persamaan karakteristik tersebut dapat dicari akar-akarnya, yaitu:
= − ,
Persamaan karakteristik tersebut mempunyai dua akar real berbeda.
Dengan mensubstitusikan dan ke dalam penyelesaian umumnya,
maka diperoleh:
= − ,
= − .
Sehingga penyelesaian umumnya menjadi:
= +
= − + − .
Diketahui nilai awalnya = . , ′ = − . Akan dicari
penyelesaian khusus dari penyelesaian umumnya.
❖ Untuk = . .
Dengan mensubstitusikan = diperoleh
= − + − =
Dengan mensubstitusikan = diperoleh
≡ − − . − − = −
≡ − − = −
Dengan mengeliminasi dan diperoleh:
= . , = .
Sehingga diperoleh penyelesaian khususnya, yaitu:
= . − + − .
c. Contoh 3.
Diberikan masalah nilai awal
′ = + ,
dengan nilai awal = .
Penyelesaian:
Masalah nilai awal tersebut merupakan persamaan diferensial biasa
dengan variabel terpisah.
Penyelesaian umum persamaan (iii.1) diperoleh sebagai berikut:
dengan pengintegralan diperoleh
dari penyelesaian umumnya. Oleh karena itu, dengan
mensubsti-tusikan = , diperoleh:
Pada bab II ini, telah dipaparkan pengertian dan penyelesaian persamaan
diferensial biasa secara analitis. Selain itu, disajikan pula metode numeris untuk
masalah nilai awal dengan metode Euler dan metode Heun. Kedua metode
terakhir ini (metode Euler dan metode Heun) akan dijadikan pembanding bagi
30 BAB III
METODE BLOK RASIONAL
A. Rumusan Metode Blok Rasional
Metode blok rasional merupakan suatu metode yang digunakan untuk
me-nyelesaikan masalah nilai awal dari suatu persamaan diferensial biasa. Metode
ini merupakan gabungan dari metode satu langkah dan metode dua langkah.
Untuk menghitung nilai hampiran , metode blok rasional membentuk sebuah
barisan blok dimana dalam satu blok terdiri dari tiga titik.
Diberikan masalah nilai awal sebagai berikut:
′ = , , = � (3.1.1)
dengan , : ℝ → ℝ dan , diasumsikan memenuhi semua
syarat-syarat pada masalah nilai awal tersebut, sehingga masalah nilai awal
mempunyai penyelesaian yang tunggal. Jika semua kondisi terpenuhi maka
masalah nilai awal (3.1.1) mempunyai penyelesaian yang tunggal. Lebih
lanjut, akan dipaparkan proses penghitungan metode blok rasional.
Misal akan dicari penyelesaian numeris dalam suatu interval atas
variabel . Oleh karena itu, dibentuk interval pengintegralan numerisnya yaitu
∈ [ , ] ⊂ ℝ dengan adalah titik awal dan adalah titik akhir interval
atas variabel . Metode blok rasional mempunyai proses penghitungan yang
sederhana, yaitu menghitung penyelesaian numeris dari suatu blok ke blok
lainnya. Oleh karena itu, interval ∈ [ , ] ⊂ ℝ didiskretkan menjadi
{ , , … �, �+ , … , }⊂ ℝ
Setelah interval tersebut didiskretkan menjadi sebuah barisan titik-titik,
kemudian barisan tersebut dibagi menjadi beberapa bagian ke dalam sebuah
barisan blok dengan setiap blok terdiri dari tiga titik yang diilustrasikan seperti
pada Gambar 1.
Gambar 1. Metode blok rasional.
Pada Gambar 1, dapat dilihat bahwa blok ke-� terdiri dari tiga titik yaitu
�, �+ dan �+ . Pada blok ke-�, setiap titik di dalam blok tersebut
dipisahkan oleh ukuran langkah ℎ yang konstan. Pada blok ke- � + , blok
ini juga terdiri dari tiga titik, yaitu �+ , �+ dan �+ dengan setiap titik di
dalam blok tersebut juga dipisahkan oleh ukuran langkah ℎ yang konstan.
Lebih umum, setiap titik dalam interval atas variabel dipisahkan oleh suatu
ukuran langkah ℎ yang konstan.
Untuk menghitung nilai hampiran pada setiap titik, maka terlebih
da-hulu harus diketahui nilai awalnya. Jika nilai awal diketahui, maka nilai
ham-piran pada setiap titik dapat dihitung. Dari Gambar 1 dapat dilihat,
misalkan pada blok ke-� nilai hampiran � diketahui. Disini nilai hampiran �
diketahui maka untuk menghitung nilai hampiran �+ diperlukan informasi
pada titik sebelumnya, yaitu �, � . Dengan menggunakan metode rasional
satu langkah, maka nilai hampiran �+ dapat dihitung. Selanjutnya, untuk
menghitung nilai hampiran �+ diperlukan informasi pada titik sebelumnya,
yaitu �, � dan �+ , �+ . Dengan menggunakan metode rasional dua
langkah, maka nilai hampiran �+ dapat dihitung. Jadi, nilai hampiran � di
titik � digunakan untuk menghitung nilai hampiran �+ dan �+ secara
ber-samaan dalam satu iterasi.
Dengan proses yang sama, nilai hampiran �+ yang telah diperoleh dari
penghitungan sebelumnya, digunakan untuk menghitung nilai hampiran �+
dengan metode rasional satu langkah dan menghitung nilai hampiran �+
dengan metode rasional dua langkah. Secara keseluruhan, proses
penghi-tungan yang sama diulang sebanyak berhingga kali sampai mendapatkan nilai
hampiran di titik akhir, yaitu .
Berikut ini merupakan analisis metode blok rasional. Pada sumbu- , dapat
didefinisikan bahwa titik �, �+ dan �+ diberikan oleh:
� = + � ℎ, (3.1.2)
�+ = + � + ℎ = �+ ℎ, (3.1.3)
�+ = + � + ℎ = �+ ℎ. (3.1.4)
Di sini adalah titik awal interval atas variabel x dan ℎ merupakan ukuran
langkah yang konstan atau ℎ merupakan jarak antar titik yang saling
berdeka-tan. Nilai h diperoleh dengan rumus ℎ =�� − �0
langkah pengintegralan. Untuk menghitung nilai hampiran di dalam interval
tersebut, terlebih dahulu harus diasumsikan bahwa penyelesaian hampiran dari
masalah nilai awal (3.1.1) direpresentasikan secara lokal pada interval
[ � , �+ ] dengan hampiran rasional:
≈ � = + + (3.1.5)
dengan , dan adalah koefisien-koefiisen yang tidak diketahui nilainya.
Hampiran rasional pada persamaan (3.1.5) harus melalui titik �, � dan
�+ , �+ . Selain itu, harus diasumsikan pada titik tersebut turunannya
diberikan oleh ′ = , dan " = ′ , . Untuk menghitung turunan dari
hampiran rasional � dapat menggunakan rumus aturan rantai. Diberikan
persamaan:
≈ � = + + .
Misalkan = + dan = + , maka rumus turunan aturan rantai
dapat ditulis:
�′ = ′ − ′,
sehingga diperoleh,
�′ = + −+ +
= + −+ −
�′ merupakan turunan pertama dari hampiran rasional (3.1.5). Dengan
menggunakan rumus yang sama, dapat dihitung turunan keduanya, yaitu
�" . Diberikan:
yang harus dipenuhi, yaitu:
� � = � = + + �
dapat dilihat bahwa keempat persamaan tersebut mengandung koefisien ,
dan yang tidak diketahui nilainya. Oleh karena itu, untuk menghitung nilai
supaya dalam penyelesaiannya tidak terdapat koefisien , dan . Berikut
adalah langkah-langkah mengeliminasi koefisien , dan .
�+ − � =
Dari persamaan (3.1.8) dan (3.1.3) diketahui
:
� + � = −+ � dan �+ = �+ ℎ.
Dengan mensubstitusikan � + � dan �+ ℎ ke persamaan (3.1.10)
Hasil dari eliminasi ketiga koefisien ini merupakan metode rasional orde dua
satu langkah. Metode ini merupakan rumus metode rasional III yang dapat
dilihat pada karangan Lambert (1974):
�+ = �+
ℎ ( �)
�− ℎ �′
(3.1.12)
Persamaan (3.1.12) adalah rumus yang akan digunakan untuk mencari nilai
hampiran �+ dengan menggunakan informasi pada titik sebelumnya, yaitu
�, � .
Selanjutnya, untuk mencari nilai hampiran �+ , harus diasumsikan bahwa
penyelesaian hampiran dari masalah nilai awal (3.1.1) direpresentasikan
secara lokal pada interval [ �, �+ ] dengan hampiran rasional yang sama
pa-da persamaan (3.1.5). Karena nilai hampirannya berapa-da papa-da interval
[ �, �+ ], maka hampiran rasional (3.1.5) harus melalui titik
�, � , �+ , �+ dan �+ , �+ . Selain itu, harus diasumsikan pada
ti-tik tersebut turunannya diberikan oleh ′= , . Metode yang digunakan
untuk menghitung nilai hampiran �+ adalah metode dua langkah. Oleh
ka-rena itu, untuk menghitung nilai hampiran �+ diperlukan
informasi-informasi di titik �, � dan �+ , �+ sehingga diperoleh lima persamaan
yang harus dipenuhi, yaitu:
� � = � = + + �
� , (3.1.13)
� �+ = �+ = + + �+
� �+ = �+ = + + �+
(3.1.17) dapat dilihat bahwa kelima persamaan tersebut mengandung koefisien
, , dan � yang tidak diketahui nilainya, maka untuk menghitung nilai
�+ terlebih dahulu harus mengeliminasi , , dan �. Berikut adalah
langkah-langkah mengeliminasi koefisien , , dan �.
= + −ℎ + ℎ
�+ + �+
= +ℎ −
�+ + �+ .
(3.1.18)
Dari (3.1.17) dan (3.1.4) diketahui:
�+ + �+ = −+
Dengan mensubstitusikan persamaan (3.1.20) ke persamaan (3.1.21)
�+ + �+ = �+ − � + �
Dengan mensubstitusi �+ ℎ
�+ − � ke persamaan (3.1.19), diperoleh:
(3.1.22), maka harus dibuktikan:
≡ + �+ = ℎ �+ − �
�+ − � − ℎ �+ .
Dengan mensubstitusikan + �+ ke persamaan (3.1.22), diperoleh:
�+ − �+ =
Hasil dari eliminasi keempat koefisien tersebut merupakan metode rasional
orde tiga dua langkah. Metode ini merupakan rumus metode II yang dapat
dilihat pada karangan Lambert (1974):
�+ = �+ +
ℎ �+ �+ − �
( �+ − �)− ℎ �+ . (3.1.23)
Persamaan (3.1.23) adalah rumus yang akan digunakan untuk mencari nilai
hampiran �+ dengan menggunakan informasi pada titik sebelumnya, yaitu
�, � dan �+ , �+ .
Jadi, metode blok rasional didasarkan pada hampiran rasional (3.1.5) yang
dari metode blok rasional agak sederhana. Jika nilai � diketahui, maka dapat
dihitung nilai hampiran �+ dengan menggunakan rumus (3.1.12), setelah itu
dihitung nilai hampiran �+ dengan menggunakan rumus (3.1.23).
B. Penyelesaian Numeris Masalah Nilai Awal
Pada bagian ini akan diselesaikan contoh-contoh masalah nilai awal pada
bab II dengan menggunakan metode Euler, metode Heun dan metode blok
ra-sional. Selain mencari penyelesaiannya, akan dicari pula kesalahan (error)
maksimum dari setiap metode numeris (metode Euler, metode Heun dan
metode blok rasional) yang digunakan untuk menyelesaikan masalah nilai
awal tersebut. Oleh karena itu, perlu didefinisikan kesalahan maksimum
se-bagai berikut:
� = max� �| n− � |
dengan N adalah banyaknya langkah pengintegralan, n adalah penyelesaian
numeris pada langkah ke-� dan � adalah penyelesaian eksak pada langkah
ke-�. Untuk mempermudah penghitungan dan menggambar penyelesaiannya,
maka digunakan software MATLAB. Berikut diberikan tiga contoh masalah
nilai awal seperti yang sudah dikerjakan secara analitis pada bab II.
1. Contoh 1
Diberikan masalah nilai awal sebagai berikut:
Masalah nilai awal tersebut merupakan persamaan diferensial biasa
tingkat satu dengan variabel terpisah. Berdasarkan penyelesaian analitis
masalah nilai awal pada bab II, diperoleh penyelesaian eksaknya, yaitu:
= − �. (3.2.1)
Persamaan (3.2.1) merupakan penyelesaian khusus (penyelesaian
eksak) dari Contoh 1. Karena penyelesaian eksak diketahui, maka dapat
dihitung kesalahan maksimum dari setiap metode numeris.
Tabel 1. Kesalahan maksimum untuk Contoh 1
� Euler Heun Blok Rasional
32 0.066654 0.007616 0.003021
64 0.030792 0.001683 0.000749
128 0.014851 0.000397 0.000187
256 0.007304 0.000096 0.000047
Dari Tabel 1 dapat dilihat bahwa kesalahan maksimum dari metode
blok rasional lebih kecil dibandingkan dengan kedua metode numeris
lainnya (metode Euler dan metode Heun). Hal ini berarti metode blok
rasional mempunyai penyelesaian numeris yang lebih akurat
dibandingkan dengan metode Euler dan metode Heun. Hal tersebut juga
diperlihatkan pada Gambar 2 dan Gambar 3, untuk � = metode
blok rasional mempunyai kesalahan maksimum yang lebih kecil dari
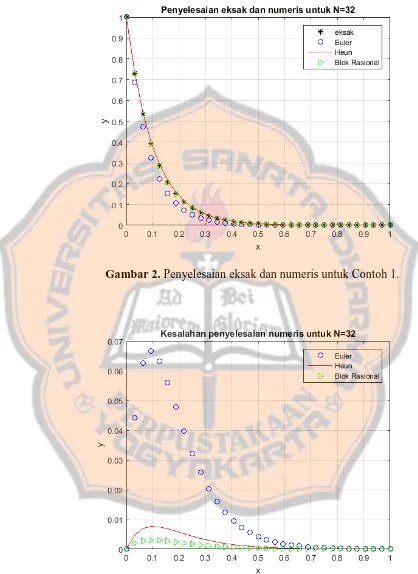
Gambar 2. Penyelesaian eksak dan numeris untuk Contoh 1.
Dari Gambar 2 dapat dilihat bahwa penyelesaian ketiga metode numeris
tersebut selalu mendekati penyelesaian eksaknya. Hal ini berarti ketiga
metode numeris tersebut cukup baik sebagai pendekatan penyelesaian
eksaknya. Selain itu, ketiga metode numeris tersebut dapat
menyelesaikan masalah nilai awal tersebut dengan baik. Hal ini dapat
dilihat pada Gambar 3 dengan kesalahan maksimum dari metode
numeris tersebut kurang dari sama dengan 0.066654. Jadi dapat
disim-pulkan bahwa dengan nilai kesalahan maksimum yang kecil
. , maka ketiga metode numeris tersebut dapat menyelesaikan
masalah nilai awal pada Contoh 1 dengan baik.
2. Contoh 2
Diberikan masalah nilai awal sebagai berikut:
′′ + ′ + = ,
= . , ′ = − , ∈ [ , ].
Masalah nilai awal tersebut merupakan persamaan diferensial biasa
tingkat dua dengan koefisien konstan homogen. Karena ketiga metode
numeris tersebut tidak dapat menyelesaikan persamaan diferensial biasa
tingkat dua, maka persamaaan diferensial tersebut harus diubah ke
ben-tuk persamaan diferensial biasa tingkat satu.
Misal:
′ = , dengan = .
′ = − − , dengan = − .
Berdasarkan penyelesaian analitis masalah nilai awal pada bab II,
di-peroleh penyelesaian eksaknya, yaitu:
= . − + − .
Karena diketahui, maka dapat dihitung ′ = . Sehingga
di-peroleh:
= − − − − .
Dari penyelesaian eksak tersebut, dapat dicari kesalahan maksimum dari
penyelesaian numerisnya.
Table 2. Kesalahan maksimum untuk Contoh 2
� Euler Heun Blok Rasional
32 298872461.45 1.253348 x
10^12
0.017842
64 0.007843 0.004487 0.003982
128 0.002421 0.000661 0.000940
256 0.000880 0.000126 0.000233
Dari Tabel 2 dapat dilihat bahwa untuk � yang berukuran kecil (pada masalah
ini yaitu � = ) metode Euler dan metode Heun mempunyai kesalahan
maksimum yang sangat besar. Hal ini terjadi karena ketidakstabilan metode
Euler dan metode Heun untuk nilai � yang berukuran kecil. Namun demikian,
hal tersebut tidak berlaku untuk metode blok rasional. Metode ini mampu
menyelesaikan masalah nilai awal dengan baik, dengan kesalahan maksimum
0.017842. Jika diambil nilai � yang lebih besar, metode Euler dan metode
dapat dilihat untuk � = , metode Euler dan metode Heun mempunyai
kesalahan maksimum yang sangat kecil . . Dengan mengambil
nilai � yang semakin besar, maka kesalahan maksimum dari ketiga metode
numeris tersebut akan semakin kecil. Berikut ini adalah gambar penyelesaian
numeris dan kesalahan maksimum dari ketiga metode numeris untuk � =
.
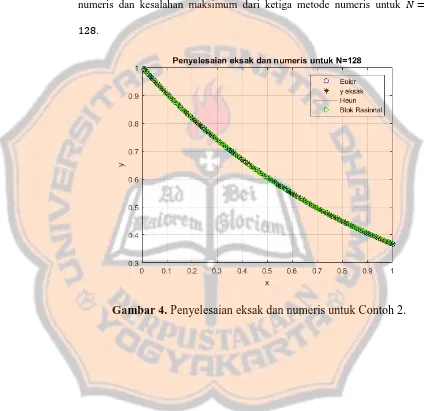
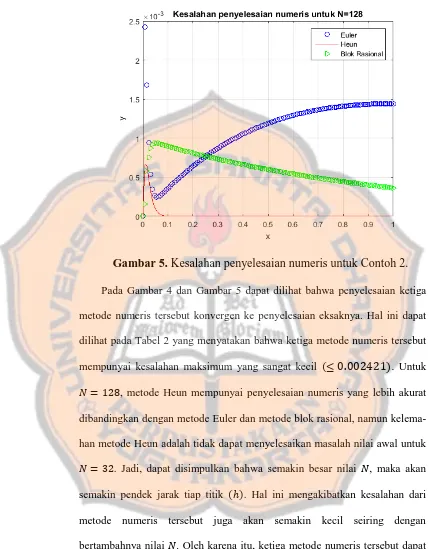
Gambar 5. Kesalahan penyelesaian numeris untuk Contoh 2. Pada Gambar 4 dan Gambar 5 dapat dilihat bahwa penyelesaian ketiga
metode numeris tersebut konvergen ke penyelesaian eksaknya. Hal ini dapat
dilihat pada Tabel 2 yang menyatakan bahwa ketiga metode numeris tersebut
mempunyai kesalahan maksimum yang sangat kecil . . Untuk
� = , metode Heun mempunyai penyelesaian numeris yang lebih akurat
dibandingkan dengan metode Euler dan metode blok rasional, namun
kelema-han metode Heun adalah tidak dapat menyelesaikan masalah nilai awal untuk
� = . Jadi, dapat disimpulkan bahwa semakin besar nilai �, maka akan
semakin pendek jarak tiap titik ℎ . Hal ini mengakibatkan kesalahan dari
metode numeris tersebut juga akan semakin kecil seiring dengan
bertambahnya nilai �. Oleh karena itu, ketiga metode numeris tersebut dapat
3. Contoh 3
Diberikan masalah nilai awal sebagai berikut:
′ = + , = , ∈ [ , ].
Masalah nilai awal tersebut merupakan persamaan diferensial biasa
tingkat satu dengan variable terpisah. Berdasarkan penyelesaian analitis
masalah nilai awal pada bab II, diperoleh penyelesaian eksaknya, yaitu:
= tan +� .
Penyelesaian eksak tersebut mempunyai titik singular yaitu = �. Jika
=� maka nilai = tan � akan menuju tak hingga (infinity).
Dari penyelesaian khusus tersebut, dapat dicari kesalahan maksimum dari
penyelesaian numeris.
Tabel 3. Kesalahan maksimum untuk contoh 3. Disini inf adalah infinity.
� Euler Heun Rational Block
32 186471279.48 inf 13.92
64 Inf inf 3.64
128 Inf inf 1.20
256 Inf inf 67.13
Pada Tabel 3 dapat dilihat bahwa untuk � berukuran kecil maupun
be-sar, metode Euler dan metode Heun tidak dapat menyelesaikan masalah
nilai awal tersebut. Hal ini terjadi karena saat = ð metode Euler dan
metode Heun mempunyai penyelesaian numeris yang divergen. Jadi
hingga (inf). Namun hal ini tidak berlaku untuk metode blok rasional,
metode ini mampu menyelesaikan masalah nilai awal dengan cukup
baik. Walaupun metode blok rasional mampu menyelesaikan masalah
nilai awal ini dengan cukup baik, metode ini mempunyai kesalahan. Hal
ini dapat dilihat pada Tabel 3, kesalahan maksimum dari metode blok
rasional . . Secara khusus untuk � = , metode ini mempunyai
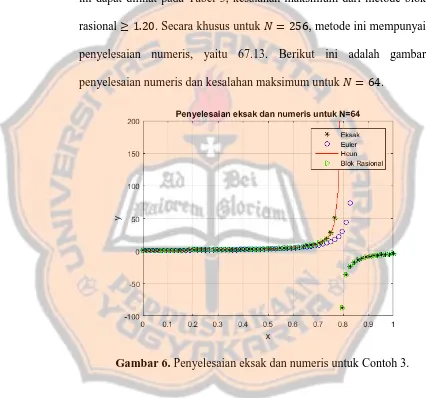
penyelesaian numeris, yaitu 67.13. Berikut ini adalah gambar
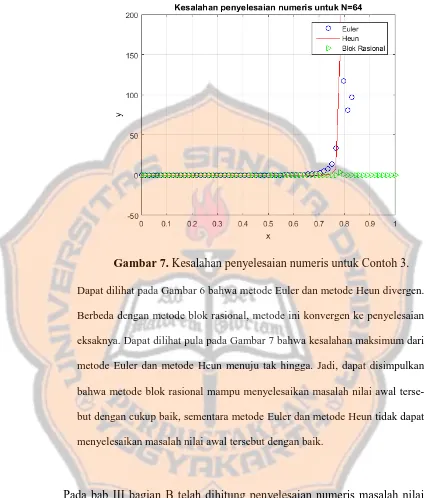
penyelesaian numeris dan kesalahan maksimum untuk � = .
Gambar 7. Kesalahan penyelesaian numeris untuk Contoh 3. Dapat dilihat pada Gambar 6 bahwa metode Euler dan metode Heun divergen.
Berbeda dengan metode blok rasional, metode ini konvergen ke penyelesaian
eksaknya. Dapat dilihat pula pada Gambar 7 bahwa kesalahan maksimum dari
metode Euler dan metode Heun menuju tak hingga. Jadi, dapat disimpulkan
bahwa metode blok rasional mampu menyelesaikan masalah nilai awal
terse-but dengan cukup baik, sementara metode Euler dan metode Heun tidak dapat
menyelesaikan masalah nilai awal tersebut dengan baik.
Pada bab III bagian B telah dihitung penyelesaian numeris masalah nilai
awal untuk contoh 1, contoh 2 dan contoh 3 dengan menggunakan metode
Euler, metode Heun dan metode blok rasional. Dari penghitungan numeris ini
diperoleh hasil bahwa metode blok rasional mempunyai hampiran penyelesaian
Selanjutnya, diberikan tiga contoh masalah nilai awal (contoh 4, contoh 5
dan contoh 6) yang berbeda dengan contoh masalah nilai awal pada bab III.
Ketiga contoh masalah nilai awal ini (contoh 4, contoh 5 dan contoh 6)
dihitung dan diselesaikan dengan menggunakan metode Euler, metode Heun
dan metode blok rasional. Penghitungan ini dilakukan untuk melihat apakah
metode blok rasional juga mempunyai penyelesaian yang lebih baik
dibandingkan dengan metode Euler dan metode Heun. Hasil dari penghitungan
numeris ini yaitu metode blok rasional juga mempunyai penyelesaian yang
lebih baik dibandingkan dengan metode Euler dan metode Heun. Contoh
53 BAB IV
KEKONVERGENAN METODE NUMERIS
Pada bab ini akan dibahas kekonvergenan metode Euler, metode Heun dan
metode blok rasional.
A. Definisi dan Teorema untuk Kekonvergenan Definisi 4.1. Kesalahan pemotongan lokal
Diberikan metode satu langkah sebagai berikut:
= �
+ = + ℎ ,
untuk setiap = , , , … , − . Metode satu langkah tersebut mempunyai
kesalahan pemotongan lokal sebagai berikut:
� + ℎ = + −( + ℎ ℎ , )= +ℎ− − ,
untuk setiap = , , , … , − , dimana dan + adalah penyelesaian
pada titik dan + .
Definisi 4.2. Kekonsistenan
Metode satu langkah dikatakan konsisten jika,
lim
ℎ→ max|� ℎ |=
dengan � ℎ adalah kesalahan pemotongan lokal pada langkah ke-n.
Definisi 4.3. Kekonvergenan
lim
ℎ→ max | − | =
dengan adalah penyelesaian numeris pada langkah ke- dan adalah
penyelesaian eksak. Pada bab III telah didefinisikan kesalahan maksimum
pemotongan global, yaitu:
= max | − |
Dengan kata lain suatu metode satu langkah dikatakan konvergen ke
penyelesaian eksanya jika = ketika ℎ → .
Definisi 4.4. Syarat Lipschitz
|| | − | ||
dengan demikian , memenuhi syarat Lipschitz di D dengan konstanta
Lipschitz = .
Lemma 4.6.
Untuk setiap − dan > , berlaku + �.
Bukti:
Dengan menerapkan Teorema Taylor untuk = �, = dan = ,
diperoleh:
= + −! + −! �,
= + − + − �,
= + + �,
dengan < � < . Dari persamaan di atas diperoleh:
+ + + � = �.
Karena + , maka
+ �. ∎
Teorema 4.7.
Misalkan syarat Lipschitz dengan konstanta Lipschitz dan kesalahan
pemotongan lokal terbatas oleh � ℎ � ℎ = max|� ℎ |, maka kesalahan
| − | � ℎ [ x−x − ].
Bukti:
Dari definisi kekonvergenan diketahui bahwa adalah kesalahan
pemotongan global dan � ℎ adalah kesalahan pemotongan lokal. Diketahui
bahwa = , oleh karena itu dapat dicari:
+ = | + − + |
= | + ℎ , − + |
= | − − ℎ [ + ℎ− − , ]|
= | − − ℎ [ + ℎ− − , ]
+ ℎ[ , − , ]|
| − | − ℎ | + ℎ− − , |
+ ℎ| , − , |.
Dengan menerapkan definisi kesalahan pemotongan lokal dan syarat
Lipschitz, maka diperoleh:
+ | | − ℎ|� ℎ | + ℎ | − |
| | − ℎ|� ℎ | + ℎ | |
| | + ℎ − ℎ|� ℎ |.
Dari hasil di atas dapat dicari nilai dari | |, yaitu:
| | = 0,
| | | | + ℎ + ℎ|� ℎ |
deret geometri tersebut dapat ditulis menjadi:
+ ℎ −
+ ℎ − = + ℎ ℎ − .
Sehingga diperoleh,
| | ℎ|� ℎ | + ℎ −
ℎ � ℎ [ + ℎ − ].
Berdasarkan Lemma 4.6, diperoleh,
B. Kekonvergenan Metode Euler
Diketahui bahwa metode Euler mempunyai persamaan:
+ = + ℎ ( , ).
Jika persamaan Euler diuraikan ke dalam deret Taylor maka diperoleh:
+ = + + −! ′ + + −! ′′ �
dengan � + . Metode Euler diperoleh dengan memotong dua suku
awal, oleh karena itu diperoleh:
+ = + ℎ ′ + ℎ ′′ �
Berdasarkan definisi kekonvergenan, maka:
lim
ℎ→ max |
ℎ
[ x−x − ]|= .
Karena | |= , maka metode Euler konvergen.
C. Kekonvergenan Metode Heun
Misalkan � + adalah penyelesaian eksak di titik + dan +
adalah penyelesaian numeris di titik + . Jika � + diuraikankan ke
� + = + + −
Diketahui bahwa metode Heun mempunyai persamaan sebagai berikut:
+ = + ℎ [ , + + , + ∗ ]
dengan + ∗= + ℎ ( , ). Jika + , + ∗ diuraikankan ke dalam
deret Taylor di sekitar , maka diperoleh:
+ , + ∗ = + , +
= + ℎ ′+ℎ ′′ � .
Sehingga metode Heun dapat ditulis sebagai berikut:
+ = + ℎ [ , + + , + ∗ ]
= + ℎ [ + + ℎ ′+ℎ ′′ � ]
= + ℎ + ℎ ′+ℎ ′′ � ,
+ = + ℎ +ℎ ′+ℎ ′′ � . (**)
+ − + = + ℎ +ℎ ′+ℎ6 ′′ �
Jadi, diperoleh kesalahan pemotongan lokal metode Heun yaitu −ℎ3 ′′ � =
−ℎ3 ′′′ � . Karena metode Heun memotong deret Taylor + di sekitar
sampai tingkat kedua, maka metode Heun memiliki tingkat keakuratan yang
lebih tinggi dibandingkan dengan metode Euler. Misalkan | ′′′ � | , maka
dapat dicari kesalahan pemotongan global dari metode Heun, yaitu:
| | � ℎ [ x−x0 �− ]
−ℎ [ x−x0 �− ].
Berdasarkan definisi kekonvergenan, maka:
lim
ℎ→ max | −
ℎ
[ x−x − ]|= .
Karena | |= , maka metode Heun konvergen.
D. Kekonvergenan Metode Blok Rasional
Berdasarkan simulasi pada bab III, Contoh 1, Contoh 2, Contoh 3 dapat
baik dibandingkan dengan metode Euler dan metode Heun. Hal tersebut dapat
dilihat pada Tabel 1, Tabel 2, Tabel 3 dan Gambar 2, Gambar 4, Gambar 6
dimana penyelesaian metode blok rasional selalu konvergen ke penyelesaian
eksaknya. Teori kekonvergenan metode blok rasional dapat dilihat dalam
62 BAB V PENUTUP
A. Kesimpulan
Ada dua cara yang dapat digunakan untuk menyelesaikan masalah
nilai awal, yaitu dengan cara analitis atau dengan cara numeris.
Penyelesaian masalah nilai awal secara numeris dapat dilakukan dengan
berbagai macam metode. Dalam tugas akhir ini digunakan tiga macam
metode numeris, yaitu metode Euler, metode Heun, dan metode blok
rasional. Dari analisis numeris dan simulasi-simulasi yang telah dilakukan
pada bab III, diperoleh hasil bahwa metode blok rasional mempunyai
penyelesaian yang lebih baik dibandingkan dengan metode Euler dan
metode Heun. Secara umum, metode blok rasional dapat menyelesaikan
masalah nilai awal dengan cukup baik. Maksud dari cukup baik di sini
yaitu bahwa metode blok rasional mempunyai penyelesaian yang selalu
mendekati penyelesaian eksaknya. Hal ini berbeda dengan metode Euler
dan metode Heun. Metode Euler dan metode Heun dapat dengan baik
menyelesaikan masalah nilai awal tertentu, namun metode Euler dan
metode Heun tidak dapat menyelesaikan masalah nilai awal untuk masalah
tertentu yang lain. Kelemahan metode Euler dan metode Heun yaitu kedua
metode tersebut tidak dapat menyelesaikan masalah nilai awal yang
B. Saran
Tugas akhir ini membahas tentang penyelesaian masalah nilai awal
dengan menggunakan metode Euler, metode Heun dan metode blok
rasional. Tentu masih banyak kekurangan dalam tugas akhir ini. Dalam
tugas akhir ini hanya dibahas masalah nilai awal persamaan diferensial
biasa linier koefisien konstan homogen tingkat satu dan dua. Saran dari
penulis, tugas akhir ini bisa dikembangkan untuk menyelesaikan masalah
nilai awal persamaan diferensial biasa non linier koefisien konstan non
homogen tingkat tiga, empat, atau tingkat yang lebih tinggi dan dapat
ditambahkan pula syarat bagaimana menentukan bahwa kesalahan
64
Daftar Pustaka
Boyce, W. E. and R. C. DiPrima. (2012). Elementary Differential Equation and
Boundary Value Problem. (10th Edition). New York: John Wiley & Sons,
Inc.
Burden, R. L. and J. D. Faires. (2011). Numerical Analysis. (9th edition). Boston: PWS Publishing Company.
Hackbusch, W. (2014). The Concept of Stability in Numerical Mathematics. Berlin: Springer-Verlag.
https://mtaufiknt.files.wordpress.com/2009/10/bab5-metnum-untuk-mna.pdf. Diakses tanggal 15 Januari 2017.
Lambert, J. D. (1974). Two unconventional classes of methods for stiff systems,
Stiff Differential Equations, edited by Willoughby R. A. New York:
Plenum Press. 171-186.
Mungkasi, S. (2014). Metode rasional eksplisit untuk masalah nilai awal.
Prosiding Seminar Nasional Sains dan Pendidikan Sains IX, 21 Juni 2014,
UKSW, Salatiga, Indonesia, 629-635.
Mungkasi, S. dan A. Christian. (2017). Runge-Kutta and rational block methods for solving initial value problems, Journal of Physics: Conference Series 795(1):012040.
Munir, L. (2007). Metode Numerik: Revisi kedua. Bandung: Informatika.
Nagle, R. K., E. B. Saff, and A. D. Snider. (2012). Fundamentals of Differential
Equations and Boundary Value Problem. (6th edition). Boston: Pearson.
Nagle, R. K., E. B. Saff, and A. D. Snider. (2012). Fundamentals of Differential
Equations. (8th edition). Boston: Pearson.
Teh, Y. Y., Z. Omar, and K. H. Mansor. (2014). An A-stable explicit rational block method for the numerical solution of initial value problem.
Proceedings of the International Conference on the Analysis and Mathematical Applications in Engineering and Science, 19-22 January
2014, CSRI, Curtin University, Sarawak, Malaysia, pp 233-241.