Regresi Logistik Page 1
REGRESI LOGISTIK BINER
Metode regresi merupakan analisis data yang mendeskripsikan hubungan kausalitas antara variabel respon dan prediktor (Hosmer dan Lemeshow, 2000). Perbedaan mendasar antara regresi linier dan regresi logistik adalah type dari variabel respon. Regresi logistik merupakan salah satu metode yang dapat digunakan untuk mendapatkan hubungan antara variabel respon yang bersifat kategorik dengan variabel prediktor (Agresti, 1990). Berdasarkan jenis skala data, regresi logistik dibedakan atas 3 macam, yaitu regresi logistik biner, multinomial, dan regresi logistik ordinal.
1. Regresi Logistik Biner (Binary Logistic Regression)
Regresi Logistik Biner ialah regresi dengan variabel respon yang mempunyai dua kategori / dua kejadian, yakni sukses atau gagal. Dengan demikian sering disebut dengan regresi logistik biner. Sedangkan jenis data pada variabel prediktor dapat berupa nominal, ordinal, interval maupun ratio.
2. Regresi Logistik Multinomial (Multinomial Logistic Regression)
Pada regresi logistik multinomial, data variabel respon yang digunakan adalah data berskala nominal dengan lebih dari 2 kategori. Sedangkan jenis data pada variabel prediktor dapat berupa nominal, ordinal, interval maupun ratio.
3. Regresi Logistik Ordinal (Ordinal Logistic Regression)
Pada regresi logistik ordinal, data variabel respon yang digunakan adalah data berskala ordinal dengan lebih dari 2 kategori. Sedangkan jenis data pada variabel prediktor dapat berupa nominal, ordinal, interval maupun ratio.
Pengantar Regresi Logistik Biner
Regresi logistik merupakan suatu metode analisis data yang digunakan untuk mencari hubungan antara variabel respon (y) yang bersifat biner atau dikotomus dengan variabel prediktor (x) yang bersifat polikotomus (Hosmer dan Lemeshow, 1989). Outcome dari variabel respon y terdiri dari 2 kategori yaitu “sukses” dan “gagal” yang dinotasikan dengan y=1 (sukses) dan y=0 (gagal). Dalam keadaan demikian, variabel y mengikuti distribusi Bernoulli untuk setiap observasi tunggal. Fungsi Probabilitas untuk setiap observasi adalah diberikan sebagai berikut,
Regresi Logistik Page 2
y y
y
f( )=π (1−π )1− ; y = 0, 1 (1)
Dimana jika y = 0 maka f(y) = 1 – π dan jika y = 1 maka f(y) = π. Fungsi regresi logistiknya dapat dituliskan sebagai berikut
z e z f − + = 1 1 ) ( ekuivalen z z e e z f + = 1 ) ( (2) Dengan z=β0 +β1x1 +...+βpxp
Nilai z antara − dan ∞ +∞ sehingga nilai f(z) terletak antara 0 dan 1 untuk setiap nilai z yang diberikan. Hal tersebut menunjukkan bahwa model logistik sebenarnya menggambarkan probabilitas atau risiko dari suatu objek. Model regresi logistiknya adalah sebagai berikut ) ... ( ) ... ( 1 1 0 1 1 0 e 1 e ) ( p p p p x x x x x β β β β β β π ++ +++ + + = (3)
Dimana p = banyaknya variabel prediktor
Untuk mempermudah pendugaan parameter regresi maka model regresi logistik pada persamaan (3) dapat diuraikan dengan menggunakan transformasi logit dari π(x).
{
}
{
( 0 11 ... )}
1 ) ( x pxp e x β β β π + + + + = ( 0 1x1 ... pxp) eβ +β + +β{
}
{
( 0 11 ... )}
) ( ) ( x pxp e x x π β β β π + + + + = ( 0 1x1 ... pxp) e β +β + +β π(x) = ( 0 1x1 ... pxp) e β +β + +β – ( 0 11 ... ) ) ( x pxp e x β β β π + + + π(x) ={
}
( 0 11 ... ) ) ( 1 x pxp e x β β β π + + + − ) ( 1 ) ( x x π π − = ) ... ( 0 1x1 pxp eβ +β + +β − ( ) 1 ) ( ln x x π π = ln ( 0 1x1 ... pxp) eβ +β + +β − ( ) 1 ) ( ln x x π π = p px x β β β0 + 1 1+...+ Sehingga diperoleh persamaan berikutp px x x x x g β β β π π = + + + − = ... ) ( 1 ) ( ln ) ( 0 1 1 (4)
Regresi Logistik Page 3 Model tersebut merupakan fungsi linier dari parameter-parameternya. Dalam model regresi linier, diasumsikan bahwa amatan dari variabel respon diekspresikan sebagai y = E(Y|x) + ε dimana
(
|)
0 1 1 p pE Y x =β β+ x + + β x (5)
merupakan rataan dari populasi dan ε merupakan komponen acak yang menunjukkan penyimpangan amatan dari rataannya dan ε diasumsikan mengikuti sebaran normal dengan rataan nol dan varians konstan.
Estimasi Parameter
Estimasi parameter dalam regresi logistik dilakukan dengan metode Maximum Likelihood. Metode tersebut mengestimasi parameter β dengan cara memaksimumkan fungsi likelihood dan mensyaratkan bahwa data harus mengikuti suatu distribusi tertentu. Pada regresi logistik, setiap pengamatan mengikuti distribusi bernoulli sehingga dapat ditentukan fungsi likelihoodnya.
Jika xi dan yi adalah pasangan variabel bebas dan terikat pada pengamatan ke-i dan
diasumsikan bahwa setiap pasangan pengamatan saling independen dengan pasangan pengamatan lainnya, i = 1, 2, ..., n maka fungsi probabilitas untuk setiap pasangan adalah sebagai berikut
(
)
yi i i i x x x f( )=π( )yi 1−π( )1− ; y i = 0, 1 (6) dengan,( )
∑ + ∑ = = = p j j j p j j j x x i e e x 0 0 1 β β π (7)dimana ketika j = 0 maka nilai xij = xi0 = 1.
Setiap pasangan pengamatan diasumsikan independen sehingga fungsi likelihoodnya merupakan gabungan dari fungsi distribusi masing-masing pasangan yaitu sebagai berikut
( )
∏
∏
= − = − = = n i y i i n i i i x x x f l 1 1 y 1 ) ( 1 ) ( ) ( ) (β π i πFungsi likelihood tersebut lebih mudah dimaksimumkan dalam bentuk log l(β) dan dinyatakan dengan L(β).
Regresi Logistik Page 4 L(β) = ln l(β)
{
[
]
[
]
}
1 ln ( ) (1 ) ln 1 ( ) n i i i i i y π x y π x = =∑
+ − − =( )
0 0 1 1 ln 1 p j ij j x n p n i ij j j i i y x e β β = = = = ∑ − + ∑ ∑ ∑
Nilai β maksimum didapatkan melalui turunan L(β) terhadapβdan hasilnya adalah sama dengan nol.
∑
∑
= = ∑ ∑ + − = ∂ ∂ = = n i n i x x ij ij i j p j j ij p j ij j e e x x y L 1 1 0 0 1 ) ( β β β β sehingga, ˆ( ) 0 1 1 = −∑
∑
= = n i n i i ij ij ix x x y π dengan j = 0, 1, ..., p (8)Estimasi varians dan kovarians dikembangkan melalui teori MLE (Maximum Likelihood Estimation) dari koefisien parameternya (Rao, 1973 dalam Hosmer dan Lemeshow, 1989). Teori tersebut menyatakan bahwa estimasi varians kovarians didapatkan melalui turunan kedua L(β).
(
)
∑
= − = ∂ ∂ n i i i iu ij u j x x x x L 1 ) ( 1 ) ( ) ( π π β β β ; dengan j, u = 0, 1, ..., pMatriks varians kovarians berdasarkan estimasi parameter diperoleh melalui invers matriks dan diberikan sebagai berikut
( )
{
[
( )
(
( )
)
]
}
1 x π 1 x π ov C = x i − i x − T ˆ ˆ Diag βˆ ˆ dan xT diberikan oleh, = k 21 k 1 k 21 11 x ... x x ... ... ... x ... x x 1 ... 1 1 n n T xDiag
[
πˆ( )
xi(
1−πˆ( )
xi)
]
adalah merupakan matriks diagonal (n x n) dengan diagonal utamanya adalah[
πˆ( )
xi(
1−πˆ( )
xi)
]
. Penaksir SE(βˆ) diberikan oleh akar kuadrat diagonal utama. Untuk mendapatkan nilai taksiranβdari turunan pertama fungsi L(β) yang non linier maka digunakan metode iterasi Newton Raphson. Persamaan yang digunakan adalahRegresi Logistik Page 5 ( )t ( )t
( )
( )t ( )t q H 1 1 − + =β − β ; t = 1, 2, … sampai konvergen (9) dengan,( )
( )
( )
0 1 K β β β , , ... , T L L L β β β ∂ ∂ ∂ = ∂ ∂ ∂ qdan H merupakan matriks Hessian. Elemen-elemennya adalah
( )
u j ju L h β β ∂ ∂ ∂ = 2 β , sehingga = kk k2 k1 2k 22 21 1k 12 11 h h h h h h h h h
H , dan pada setiap iterasi berlaku, (10)
dari persamaan (10) diperoleh,
( ) ( )
{
(
)
}
1(
)
1 ( ) ( ) ( ) βt βt T Diag π (x ) 1 π (x )t t T t i i − + = + − − x x x y m (11)dengan m(t)= π(xi) (t). Langkah-langkah iterasi Newton Raphson diberikan sebagai berikut,
a. Menentukan nilai dugaan awal β (0) kemudian dengan menggunakan persamaan (10) maka didapatkan π (x )i (0).
b. Dari π (x )i (0) pada langkah a. diperoleh matriks Hessian H (0) dan vektor q (0).
c. Proses selanjutnya untuk t > 0 digunakan persamaan (10) dan (11) hingga π (x )i ( )t dan β( )t konvergen.
Pengujian Estimasi Parameter
Setelah parameter hasil estimasi diperoleh, maka kemudian dilakukan pengujian keberartian terhadap koefisien β secara univariat terhadap variabel respon yaitu dengan membandingkan parameter hasil maksimum likelihood, dugaan β dengan standard error parameter tersebut. Hipotesis pengujian parsial adalah sebagai berikut,
H0 : βi =0 H1 : βi ≠0 ; i = 1, 2, ..., p Statistik uji: ) ˆ ( ˆ i i SE W β β = (12)
Regresi Logistik Page 6 Statistik uji W tersebut, yang juga disebut sebagai Statistik uji Wald, mengikuti distribusi normal sehingga H0 ditolak jika W >Zα/2 dan dapat diperoleh melalui persamaan
berikut, 2 2 2 ) ˆ ( ˆ i i SE W β β = (13)
Statistik uji tersebut mengikuti distribusi Chi-Squred sehingga H0 ditolak jika
) , ( 2 2 α χ v
W > dengan v degrees of freedom banyaknya prediktor.
Setelah diperoleh variabel prediktor yang signifikan berpengaruh terhadap variabel respon pada pengujian univariat, langkah selanjutnya adalah menentukan variabel manakah hasil pengujian univariat yang signifikan mempengaruhi variabel respon secara bersama-sama. Pengujian ini dilakukan untuk memeriksa keberartian koefisien β secara serentak (multivariat) / overall terhadap variabel respon. Hipotesis yang digunakan diberikan sebagai berikut.
H0 : β1 =β2 =...=βi =0
H1 : Paling tidak terdapat satu βi ≠0; i = 1, 2, ..., p
Statistik uji:
(
)
( )∑
= − − − = n i y i y i n n i i i n n n n G 1 1 0 1 ˆ 1 ˆ ln 2 0 π π (14) dimana:∑
= = n i i y n 1 1∑
(
)
= − = n i i y n 1 0 1 n=n1+n0Statistik uji G adalah merupakan Likelihood Ratio Test dimana nilai G mengikuti distribusi Chi-Squred sehingga H0 ditolak jika G>χ2(v,α)dengan v derajat bebas adalah
banyaknya parameter dalam model tanpa β . 0
Intepretasi Koefisien Parameter
Intepretasi terhadap koefisien parameter ini dilakukan untuk menentukan kecenderungan/hubungan fungsional antara variabel prediktor dengan variabel respon serta menunjukkan pengaruh perubahan nilai pada variabel yang bersangkutan. Dalam hal ini digunakan besaran Odds ratio atau eβ dan dinyatakan dengan ψ . Odds ratio diartikan
Regresi Logistik Page 7 dibandingkan pada x=0. Keputusan tidak terdapat hubungan antara variabel prediktor dengan variabel respon diambil jika nilai Odds ratio (ψ ) = 1.
Jika nilai Odds ratio (ψ ) < 1, maka antara variabel prediktor dan variabel respon terdapat hubungan negatif setiap kali perubahan nilai variabel bebas (x) dan jika Odds ratio (ψ ) > 1 maka antara variabel prediktor dengan variabel respon terdapat hubungan positif setiap kali perubahan nilai variabel bebas (x).
LATIHAN SOAL
1. Suatu tes psikologi diberikan kepada beberapa orang tua untuk menentukan apakah ada gejala – gejala yang menunjukkan melemahnya tubuh karena faktor usia.yang terjadi pada orang tua. Salah satu variabel yang digunakan adalah score yang diperoleh dari subtest Wechler Adult Inteligence Scale.
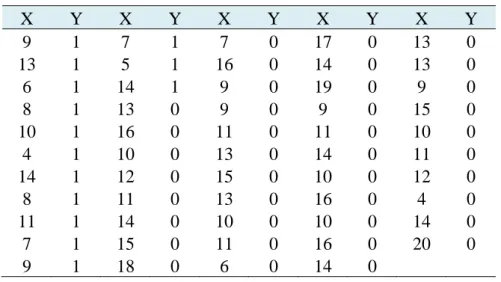
Tabel 1 X Y X Y X Y X Y X Y 9 1 7 1 7 0 17 0 13 0 13 1 5 1 16 0 14 0 13 0 6 1 14 1 9 0 19 0 9 0 8 1 13 0 9 0 9 0 15 0 10 1 16 0 11 0 11 0 10 0 4 1 10 0 13 0 14 0 11 0 14 1 12 0 15 0 10 0 12 0 8 1 11 0 13 0 16 0 4 0 11 1 14 0 10 0 10 0 14 0 7 1 15 0 11 0 16 0 20 0 9 1 18 0 6 0 14 0 X : Score WAIS
Y : Keadaan lemah karena usia (1=ada gejala) a. Tentukan modelnya
b. Interpretasikan keterikatan antara ketidakseimbangan gejala pada WAIS dan tes signifikansi pada efek yang ditimbulkan.
Solusi:
Binary Logistic Regression: y versus x
Link Function: Logit
Regresi Logistik Page 8
Variable Value Count
y 1 14 (Event) 0 40
Total 54
Logistic Regression Table
Odds 95% CI Predictor Coef SE Coef Z P Ratio Lower Upper Constant 2,40404 1,19184 2,02 0,044
x -0,323530 0,113980 -2,84 0,005 0,72 0,58 0,90
Log-Likelihood = -25,509
Test that all slopes are zero: G = 10,789, DF = 1, P-Value = 0,001
Goodness-of-Fit Tests
Method Chi-Square DF P Pearson 8,08303 15 0,920 Deviance 9,41897 15 0,855 Hosmer-Lemeshow 4,53347 6 0,605
Table of Observed and Expected Frequencies:
(See Hosmer-Lemeshow Test for the Pearson Chi-Square Statistic) Group Value 1 2 3 4 5 6 7 8 Total 1 Obs 0 2 1 1 1 2 4 3 14 Exp 0,4 1,0 0,8 1,8 1,8 2,3 2,5 3,4 0 Obs 8 8 5 7 5 4 1 2 40 Exp 7,6 9,0 5,2 6,2 4,2 3,7 2,5 1,6 Total 8 10 6 8 6 6 5 5 54 Measures of Association:
(Between the Response Variable and Predicted Probabilities) Pairs Number Percent Summary Measures
Concordant 419 74,8 Somers' D 0,56 Discordant 104 18,6 Goodman-Kruskal Gamma 0,60 Ties 37 6,6 Kendall's Tau-a 0,22 Total 560 100,0 Tabulated statistics: y; C4 Rows: y Columns: C4 0 1 All 0 37 3 40 68,52 5,56 74,07 1 9 5 14 16,67 9,26 25,93 All 46 8 54 85,19 14,81 100,00 Cell Contents: Count % of Total
Regresi Logistik Page 9
MTB > let c5=2,404-0,32*c1 MTB > let c6=exp(c5)/(1+exp(c5))