2.1
Masalah Transportasi
Masalah transportasi pertama kali digunakan pada awal perang dunia kedua un-tuk menenun-tukan bagaimana mengirimkan pasukan yang terletak disuatu tempat
latihan Amerika Serikat ke medan perang di Eropa dan Asia, kemudian dikem-bangkan oleh F. L. Hitchcock sejak 1941 sebagai persoalan distribusi atau
trans-portasi produk dari gudang ke pelanggan. Ilustrasinya adalah sebagai berikut:
Gambar 1. Jaringan Masalah Transportasi
Sebuah perusahaan memiliki sejumlah gudang penyedia suatu produk yang
tersebar di beberapa daerah. Pada daerah tersebut, juga tersebar pelanggan yang masing-masing membutuhkan sejumlah produk pada saat yang sama.
Masing-masing pelanggan membutuhkan produk dengan jumlah yang berbeda-beda. Dalam distribusi produk dari gudang ke suatu pelanggan, perusahaan
memer-lukan biaya tertentu. Biaya distribusi bergantung pada jumlah produk yang didistribusikan. Oleh karena itu, Manajer harus mengatur distribusi dari setiap
gudang agar biaya transportasi minimal dan seluruh permintaan pelanggan ter-penuhi. Nunkeaw et al (2009) menyatakan model masalah transportasi dalam
Model 2.1
Persamaan (2.1) adalah fungsi tujuan model transportasi untuk
memini-mumkan total biaya transportasi. Total jumlah barang yang diangkut dari suatu gudang untuk didistribusikan tidak lebih dari kapasitas gudang tersebut, seperti
yang dinyatakan oleh persamaan (2.2). Persamaan (2.3) adalah persamaan yang menunjukkan bahwa total jumlah barang yang diangkut dari setiap gudang ke
suatu pelanggan tepat memenuhi jumlah barang kebutuhan setiap pelanggan. Persamaan (2.4) menunjukkan bahwa total jumlah produk yang tersedia di
selu-ruh gudang harus sama dengan total jumlah permintaan seluselu-ruh pelanggan, dan persamaan (2.5) menunjukkan bahwa persamaan (2.2), persamaan (2.3), dan
persamaan (2.4) adalah kendala yang tak negatif.
Nunkeawet al (2009) juga menilai bahwa penggunaan hanya satu fungsi tu-juan dalam masalah transportasi tidak cukup karena itu akan kurang mendekati
solusi optimal di dunia nyata. Oleh karena itu, perusahaan perlu mempertim-bangkan beberapa fungsi tujuan lain. Fungsi-fungsi tersebut dapat berkaitan
2.2
Program Tujuan Ganda dan Solusi Pareto-Optimal
Dalam Caramiaet al, sebuah persoalan optimisasi dengan fungsi tujuan tunggal
dapat diformulasikan sebagai berikut:
minf(x)
x∈S
di manaf adalah sebuah fungsi skalar dan S adalah daerah fisibel yang didefin-isikan sebagai
S ={x∈Rm :
Ax
= 0}.di mana
A
adalah matriks koefisienx
pada kendala. Program Tujuan Ganda dapat dimodelkan secara matematis sebagai berikut:min [f1(x), f2(x), . . . , fn(x)]
x∈S,
di mana n > 1. Definisikan Ruang Objektif adalah ruang yang mengandung seluruh fungsi tujuan, dan definisikan
C ={y∈R:y=f(x), x∈S}.
Konsep skalar dari ”optimalitas” tidak dapat langsung diaplikasikan pada Program Tujuan Ganda. Di sini, notasi optimalitas Pareto akan diperkenalkan
sebagai berikut:
• Sebuah titikx∗
dikatakan Pareto optimum lemah atau sebuah solusi efisien lemah untuk masalah Program Tujuan Ganda jika dan hanya jika tidak
terdapat x∈S sehingga fi(x)< fi(x∗
) untuk setiap i∈ {1, . . . , n}.
• Sebuah titik x∗
dikatakan Pareto optimum kuat atau sebuah solusi efisien
yang tepat untuk masalah Program Tujuan Ganda jika dan hanya jika tidak terdapat x∈S sehingga fi(x)≤fi(x∗) untuk setiap i∈ {1, . . . , n}.
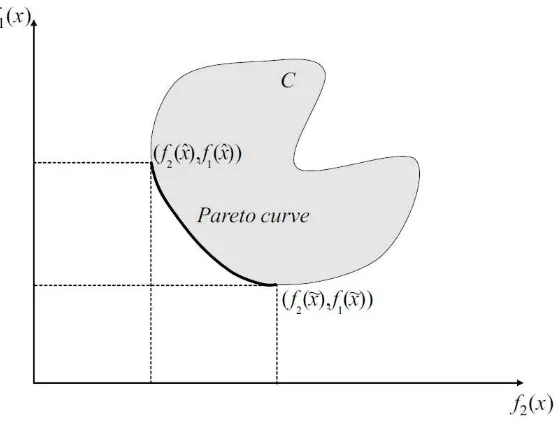
disebut Pareto front atau Kurva Pareto. Bentuk dari permukaan Pareto meng-indikasikan hubungan antara setiap fungsi tujuan. Sebuah contoh kurva Pareto
ditampilkan pada Gambar 2, di mana setiap titik di antara (f2(ˆx), f1(ˆx)) dan
(f2(˜x), f1(˜x)) disebut Pareto front. Titik-titik tersebut disebut titik non-inferior
atau titik tak-terdominasi.
Gambar 2. Contoh Kurva Pareto
Contoh Pareto optimum lemah dan kuat ditunjukkan pada Gambar 3: titikp1 dan p5 adalah Pareto optimum lemah; titik p2, p3, danp4 adalah Pareto
optimum kuat.
2.3
Metode
LexicographicMathias Ehrgott mengemukakan bahwa dalam optimisasi lexicographic, setiap
fungsi tujuan akan dipertimbangkan berdasarkan tingkat kepentingan atau pri-oritas. Sebuah solusi optimal ˆxdari suatu masalah disebut optimallexicographic dan ˆy = f(ˆx) adalah sebuah vector minimal lexicographicdalam Y = f(X), di manaX adalah himpunan vektorxyang memenuhi kendala (fisibel). Optimisasi lexicographicjuga dapat ditulis dengan notasi “lexmin” sebagai berikut:
lexmin
x∈X (f1(x), f2(x), . . . , fp(x)) 2.6
Notasi “lexmin” pada persamaan (3.4) di atas menunjukkan proses
meminimum-kan setiap fungsi tujuan secaralexicographi atau berurutan, yaitu dari fungsi tu-juan 1 hingga fungsi tutu-juanp. Algoritma optimisasilexicographicakan dijelaskan lebih rinci pada Bab 3. Berikut diberikan definisi solusi dari sebuah optimisasi lexicographic.
Definisi 2.1.
Sebuah solusi fisibel xˆ∈ X adalah solusi lexicographic, jika tidak terdapat x∈ X sehinggaf(x)<lex f(ˆx).fungsi tujuan telah diurutkan secara lexicographic. Pada definisi di atas, dapat
dinyatakan bahwa ˆx∈ X adalah optimal lexicographic, jika
f(ˆx)≤lexf(x),∀x∈ X.
Dalam tulisannya, Isermann menggunakan notasi%untuk menggambarkan ketidaksamaanlexicographicseperti notasi≥lexpada Mathias Ehrgott. Ia
menje-laskan optimisasilexicographic dengan memisalkanRadalah himpunan bilangan real, R0 adalah himpunan bilangan real non-negatif, Rm adalah ruang vektor
bilangan real dengan dimensi m, dan Rm0 adalah Rm dengan unsur non-negatif.
diaplikasikan: untuka, b∈Rm, ketidaksamaan lexicographic kuat (the strict lex-icographic inequality)a≻bdipenuhi, jika dan hanya jika,ai ≻bi dipenuhi untuk
i = min{1, . . . , m | ak 6= bk}; dan ketidaksamaan lexicographic lemah (the weak lexicographic inequality) a %b dipenuhi, jika dan hanya jika, a ≻ b atau a =b. Untuk setiap dua matriks berorde (m×n),A = (a1, . . . , an), B = (b1, . . . , bn).
A ≻ B dipenuhi jika dan hanya jika aj ≻ bj untuk setiap j = 1, . . . , n.