Pertemuan Ke 2 s d 4

Pertemuan Ke 2 s/d 4

MATA KULIAH : METODE NUMERIK

JURUSAN : TEKNIK MESIN S-1

FAKULTAS : TEKNIK INDUSTRI

DOSEN :

Error , Nilai Fungsi Dan Pendeferensialan Numerik

2.1. Galat (

Error

)

Angka bena digunakan untuk menangani hampiran (aprogsimasi) yang berkaitan dengan manipulasi bilangan. Angka bena atau digit dikembangkan secara formal menandakan keadalan suatu nilai numerik. Angka bena( significant digits) angka yang dapat digunakan dengan pasti.

Galat (Error)

Galat numerik timbul karena penggunaan hampiran(aprogsimasi) untuk menya-takan operasi atau besaran matematis yang eksak.Hubungan nilai eksak(sejati / sebenar-nya) dengan nilai pendekatannya (aprogsimasi) dapat dirumuskan sebagai berikut.

Nilai sejati (true value) = aprogsimasi + galat (2.4)

atau

Et = Nilai sejati – Aprogsimasi (2.5)

Dimana Et , menunjukkan nilai eksak dari galat dan t menyatakan galat sejati

( true error).

Kelemahan rumus (2.5) tingkat besaran nilai yang diperiksa tidak diperhatikan, oleh karenanya perlu menormalkan galat terhadap nilai sejatinya.

Menormalkan galat terhadap nilai sejati :

Galat relatif pecahan = galat/ nilai sejati, atau Galat relatif dikalikan 100 persen yaitu :



t = [( galat sejati)/ nilai sejati] x 100% (2.6)



t menunjukkan prosentase galat relatif yang sejati

Dalam masalah rekayasa nilai eksak(true value) tidak diketahui oleh karenanya perlu adanya alternatif lain untuk menentukan galat yaitu perlunya penormalan galat dengan nilai pendekatannya.

Menormalkan galat terhadap nilai pendekatan (aprogsimasi)

a= [( galat pendekatan)/ nilai pendekatan] x 100% (2.7)

dilakukan secara berulang atau secara iterasi. Sedangkan prosentase galat relatif dirumuskan rumus sbb :

nilai pendekatan sekarang - nilai pendekatan sebelumnya

a =  x 100% ( 2.8)

nilai pendekatan sekarang

nilai galat pada persamaan ( 2.4) sampai ( 2.8) dapat positif atau negatif,

penghitu-ngan dihentikan apabila dipenuhi |

_

a | <



s dimana



s =( 0,5 x 102-n )% , n

adalah angka bena (digit) yang diperhatikan.

Contoh 1 :

lanjutkan sampai suku ke lima dari deret diatas. Dan tentukan error relatifnya.

Jawab :

Untuk

3

x  , tentukan nilai cos(₃

)

1. iterasi pertama : Perhitungan diawali dengan menentukan nilai

diperoleh

dan error relatifnya

%

dan seterusnya

Jika diperhatikan dari keempat iterasi (hitungan), tampak pada iterasi yang ke empat nilai error (galat) relatifnya semakin kecil. Hal ini diartikan bahwa pada

iterasi keempat nilai ) 3

cos( _{semakin mendekati nilai sebenarnya (sejati).}

3.

Nilai fungsi dengan deret Taylor.

Deret Taylor menyediakan sarana untuk menetukan nilai fungsi pada suatu titik

dalam bentuk nilai fungsi dan turunannya pada titik yang lain. Sebelum memulai

dengan penggunaan deret Taylor untuk menentukan nilai fungsi diingatkan kembali

dengan Teorema Taylor yaitu

Jika fungsi f dan n +1 turunannya kontinu pada selang yang memuat a dan

3.1. Nilai fungsi

disebut dengan pendekatan orde pertama dan seterusnya. Untuk menentukan nilai fungsi f(xi+1) disekitar x = xi adalah sebagai berikut.

Pendekatan orde-nol

f(x_i₁) f(x_i) ( 3.4)

Persamaan 3.2 menunjukkan bahwa nilai f pada titik baru sama dengan nilai

f pada titik lama.

Pendekatan orde-pertama

)

Pendekatan orde-kedua

2

Pendekatan orde-ketiga

3

dan seterusnya.

Dengan menuliskan h =xI+1 –xI maka rumus deret Taylor 3.1 dapat di sederhanaan

sebagai berikut

n

3.2. Pendeferensialan Numerik

Penulisan deret Taylor untuk meramal kecepatan suatu fungsi waktu yaitu

dipero leh

Persamaan 3.11 dapat dinyatakan sebagai berikut

)

3.1.1. Selisih Terbagi Berhingga (finit divided difference) Turunan Pertama

Dengan menggunakan rumus 3.12 dapat diturunkan selisih maju (forward diference) dan selisih mundur(backward diference) dari turunan pertama yaitu:

)

dapat ditulis

) sebelumnya berdasarkan suatu nilai sekarang adalah sebagai berikut :

...

dengan hanya memperhatikan dua suku pertama didapat rumus berikut

h

Dengan mengingat uraian deret Taylor maju yaitu :

... 2

) ( " )

( ' )

( )

( 2

1    

 h

x f

h x f

x f x

f i

i i

i

( 3.17)

dengan mengurangkan uraian deret Taylor 3.15 ke uraian deret taylor 3.17 didapat rumus selisih terpusat dari turunan pertama adalah sebagai berikut

( ) 2

) ( ) ( ) (

' 1 1 _{O h}2

h x f x f x

f i i

i 



   _(3.16)

3.1.4. Selisih Berhingga Dari Turunan Yang Lebih Tinggi

1. Selisih terbagi berhingga maju kedua ( second forward finite divided

difference)

) (

) (

) (

2 )

( )

(

" 2

2

1

2 _{O h}

h

x f

x f

x f

x

f i i i

i      

(3.17)

2. Selisih terbagi berhingga mundur kedua ( second backward finite divided difference)

) (

) (

) (

2 )

( )

(

" 2

2

2

1 _{O h}

h

x f

x f

x f

x

f i i i

i      

( 3.11)

Rumus derivatif maju(forward difference) dan derivatif mundur ( backward difference) dapat ditulis dalam bentuk table.

Koefisien diperoleh dengan cara menguraikan rumus binomium newton ( a-b)n _:

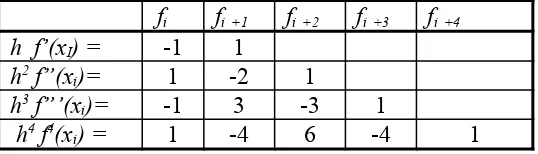
1. Tabel rumus-rumus derivatif maju( forward difference) dari turunan-turunan pertama hingga yang ke empat untuk tingkat kesalahan O(h).

fi fi+1 fi+2 fi+3 fi+4

h f’(xI) = -1 1

h2 _f”(x

i)= 1 -2 1

h3 _f”’(x

i)= -1 3 -3 1

h4 _f4_(x

i) = 1 -4 6 -4 1

Tabel 3.1 Forward difference dari O( h)

2. Derivatif mundur (backward difference) dari turunan-turunan pertama hingga yang

fi -4 fi -3 fi -2 fi-1 fi

h f’(xI) = -1 1

h2 _f”(x

i)= 1 2 1

h3 _f”’(x

i)= 1 3 -3 1

h4 _f4_(x

i) = 1 -4 6 -4 1

Tabel 3.2. Backrward difference dari O( h)

Dimana

fi = f( x) , fi+1 = f( x + h), fi+2 = f( x + 2h), fi+3 = f( x + 3h)

dan fi+4 = f( x + 4h),

fi = f( x) , fi-1 = f( x - h), fi-2 = f( x - 2h), fi-3 = f( x - 3h)

dan fi-4 = f( x - 4h),

2 fi = ( fi ) , 2 fi =  (fi) dan seterusnya

Cara membaca tabel

Untuk membaca tabel 3.1, pandang baris pertama tabel 3.1 forward difference dari O(h), dari tabel tersebut dapat dibaca bahwa

) ( ) ( ) ( ) ( '

h O h

i x f i x f

i f i f i x hf

    

  

1 1

3. Derivatif maju( forward difference) dan derivatif mundur (backward difference) untuk tingkat kesalahan O(h)2_{. Yaitu}

fi fi+1 fi+2 fi+3 fi+4 fi+5

2h f’(xi) = -3 4 - 1

h2 _f’’(x

i)= 2 - 5 4 -1

2h3 _{f”’ (x}

i )= -5 18 - 24 14 -3

h4 _f4_(x

i) = 3 - 14 26 - 24 11 -2

Tabel 3.3 Forward difference O( h)2

fi - 5 fi - 4 fi -3 fi -2 fi-1 fi

2h f’(xI) = 1 - 4 3

h2 _f”(x

i)= - 1 4 - 5 2

2h3 _f”’(x

i)= 3 - 14 24 - 18 5

h4 _f4_(x

i) = -2 11 - 24 26 - 14 3

Tabel 3.4. Backrward difference dari O( h)2

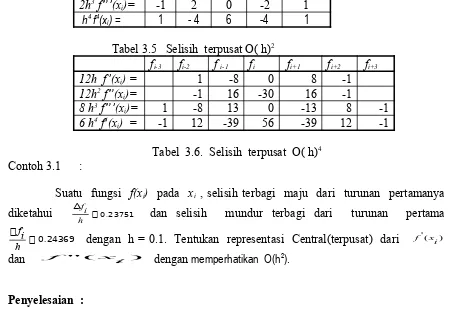
3. Tabel Selisih Terpusat (central ) .

fi-2 fi-1 fi fi+1 fi+2

2h f’(xi) = -1 0 1

h2 _f”(x

2h3 _f”’(x

Penyelesaian :

Dengan menggunakan rumus selisih maju terbagi maka dapat dinyatakan

Sedangkan dari rumus Central (terpusat) untuk turunan pertama dan kedua dengan memperhatikan O(h2_{) dapat diturunkan}

...

Buat algoritma pemrogramannya untuk menentukan turunan pertama dari y = x3 _{, untuk h kecil yang bervariasi mulai dari 1 sampai 10}-10 _{gunakan forward}

diffe-rence pada x = 10 .

Secara Umum soal diatas dapat dibuat algoritmanya sebagai berikut Langkah 1. Masuk nilai x. (input).

Langkah 2. Definisikan A : 1-10.

Langkah 3. Hitung H ₁₀A

1



Langkah 4. Hitung S = f(x+H) – f(x)

Langkah 5. Tentukan Derivatif= DER ( DER= S/H) Langkah 6. Cetak H, S, DER

Langkah 7. Ulang perhitungan sampai batas toleransi dipenuhi. Langkah 8. Stop ( jika batas toleransi telah di penuhi)

Dengan menggunakan bahasa pemrograman pascal silakan dibuat programnya.

LATIHAN

1. Diberikan data sebagai berikut

x 0 1 2 3 4

f(x) 30 33 28 12 -22

Tentukan f ’(0), f ’(2), f ”(4) dan f”(0) dengan menggunakan selisih maju , mundur dan terpusat ( central) yang memperhatikan O(h) dan O( h)2

.

2. Berikut representasi fungsi data fisik dalam bentuk interval

x 0 0.5 1.0 1.5 2.0 2.5 3.0 f( x) 1.00 0.80 0.20 0.25 0.31 0.38 0.44

Tentukan f ‘( 1.5) dengan memperhatikan O(h)2 _{, dengan h = 0.5.}

3. Dengan memperhatikan fungsi f(x) = sin 10x. tentukan f’(0) dengan

menggunakan selisih maju dari O(h) dan O(h)2 _{dengan h =0.2. Ulangi}

perhitungan dengan memperhatikan h = 0.01 bandingkan hasilnya dan nyatakan gambarnya.

3.1.5 Perambatan galat (Error)

Hal ini bertujuan mengkaji bagaimana error dalam bilangan dapat merambat melalui fungsi matematis. Contohnya , apabila kita ingin mengalikan dua bilangan yang mempunyai error maka bagaimana menaksir error dalam hasil kali ini.

Seandainya dipunyai fungsi f(x), dengan x sebai perubah bebas. Dan x

merupakan pendekatan dari x. Untuk mengetahui pengaruh penyimpangan x dan x

pada nilai fungsi tersebut dapat di perhatikan rumus berikut ,

) ( ) ( )

(x~ f x f x~

f  

 ( 3.12)

~ ~ ~

) ( ' )

(x f x x

f  

 ( 3.13)

dimana f(x) menyatakan suatu taksiran error dari fungsi dan

x menyatakan taksiran error dari x.

Contoh 3.3 :

Tentukan defleksi Y dari puncak tiang perahu layar yang dirumuskan

EI FL Y

8 4 

Dimana F adalah beban samping ( pon/kaki), L adalah tinggi (kaki), E modulus kekenyalan( pon/kaki2_{) dan I momen inersi ( kaki}4_{). Taksirlah eror dalam Y jika}

F = 50 pon/kaki , L = 30 pon /kaki , E = 1.5 X 108 _{pon/ kaki}4 _{dan I = 0.06 kaki}4

F = 2 pon/kaki ,  L = 0.1 pon /kaki , E = 0.01 X 108 pon/ kaki4 dan

 I = 0.0006 kaki2

Daftar Pustaka

- Chapra S.C& Canale R.P ( 1988) ‘ Metode Numerik’ Mc Graw-Hill, Inc.