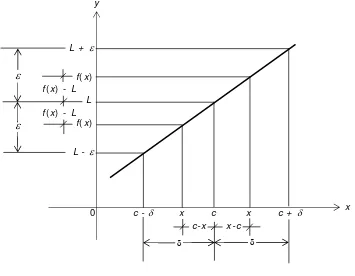
Sebelum mendefinisikan limit, terlebih dahulu perhatikan gambar berikut !
Dari gambar 1 di atas, perhatikan bahwa
Untuk x < c , maka : 0 < c – x < δ atau 0 > x – c > -δ
Untuk x > c , maka : 0 < c – x < δ
Dari kedua persamaan diatas didapat : 0< x−c <
δ
Untuk f(x) < L, maka L – f(x) < ε atau f(x) – L > -ε Untuk f(x) > L, maka f(x) – L < ε.
Sehingga didapat : f(x)−L <ε
c - δ x c x c + δ L + ε
f(x) L f(x) L - ε
ε
ε
f(x) - L f(x) - L
0 y
x
Gambar 3.1
c- x x - c
Dari Ilustrasi di atas didapat definisi sebagai berikut :
Pernyataan : f x L
c
x→ =
) (
lim , berarti untuk setiap ε > 0 terdapat δ > 0
sedemikian rupa sehingga jika 0< x-c <δ maka f(x)-L <ε
Dengan demikian :
1. Jika sebuah fungsi terdefinisi pada suatu selang terbuka yang memuat
bilangan riil c tertentu, kecuali mungkin di titik c itu sendiri, dan 2. Jika f(x) mendekati bilangan riil L tertentu pada saat x mendekati c, Maka
dapat ditulis :
L x f c
x→ ( )=
lim
dibaca “ limit f(x) adalah L bila x mendekati c” atau “f(x) mendekati L bila x
mendekati c”
B. Sifat-sifat Limit fungsi
Untuk menyederhanakan permasalahan, berikut diberikan rumus-rumus
penyelesaian limit yang didapat dengan bantuan definisi limit. Pada rumus-rumus ini
b, c, k dan L adalah bilangan-bilangan riil, a bilangan ril positif, sedangkan m dan n
adalah bilangan riil positif.
Sifat-sifat limit :
1. x c
c
x→ =
lim
Contoh 3.1
a) lim 5
5 =
→ x
x
b) lim 7
7 =−
− → x
x
2. k k
c
x→ =
Contoh 3.7
a) x e
e e
x
9 9
lim = =
→ → 9x xlim
b) lim 3 (4 ) 3(4 π)
π
π = → − = −
→ x
x 3(4-x) xlim
8. lim
n
c
x ⎥⎦
⎤ ⎢⎣
⎡ =
→ →[ ( )] ( )
lim f x n f x
c x
Contoh 3.8
1 ) 1 ( ) 3 (
lim 7
7
2
2 ⎥⎦ = − =−
⎤ ⎢⎣
⎡ −
=
→
→ x
x x
7
lim 3)
-(x
9. Teorema Sandwich ( teorema apit )
Misal terdapat f(x) ≤ h(x) ≤ g(x) untuk setiap harga x pada suatu selang terbuka yang mengandung c, kecuali mungkin di titik c itu sendiri.
Jika = =
→c f(x) L
xlim xlim→c g (x), maka : limx→c h(x)=L
Contoh 3.9
Selesaikan
x 1 cos x lim 2
0 x→
Penyelesaian :
1 1 cos
1≤ ≤
−
x , x ≠ 0
2 2
2 cos1 x
x x
x ≤ ≤
− (kalikan semua suku dengan x2)
lim 2 0
0 =
→ -x
x
lim 2 0
0 =
→ x
x
Karena : =
→
2 0
lim-x
x lim 0
2
0 =
→ x
x , maka x x x
1 cos lim 2
0
10. Limit sepihak
Contoh 3.10
Jika f(x) =
Penyelesaian :
5
Soal-soal
C. Limit fungsi trigonometri dan siklometri
Beberapa limit fungsi trigonometri :
1. lim sin 1
0 =
→ x x
x
Untuk menunjukkan , perhatikan gambar berikut !
Luas ∆OPQ < Sektor OPQ < ∆OPT (*)
Luas ∆OPQ = θ= r sinθ
2 1 sin r 2 1 .
r 2 (**)
Luas sektor OPQ = r2
2 1θ
(***)
Luas ∆OPT = r. r t anθ
2 1
= r t anθ
2
1 2 (****)
Substitusi persamaan (**) s/d (****) ke persamaan (*) didapat :
θ <
θ <
θ r t an 2 1 r 2 1 sin r 2
1 2 2 2 ( # )
Jika pers. (#) dibagi r sinθ
2
1 2 didapat :
θ < θ θ <
cos 1 sin
1 atau > θ
θ θ >sin cos 1
Gunakan teorema apit !
1 1 lim
0 =
→
θ dan θlim→0cosθ=1, maka :
1 sin lim
0 θ =
θ
→
θ atau x 1
x sin lim
0
x→ =
θ 0
r
T Q
P x y
Gambar 3.2
0 < θ < 2
2. lim cosx 1
0
x→ =
3. lim sinx 0
0
x→ =
4. lim t an x 0
0
x→ =
5. 1
x x t an lim
0
x→ =
6. 1
x t an
x lim
0
x→ =
7. 0
x 1 -x cos lim
0
x→ =
Beberapa limit fungsi siklometri (invers trigonometri)
1. 1
x x arcsin lim
0
x→ =
Bukti : y =arcsin x ⇔ x=sin y untuk -1 ≤ x ≤ 1 dan -π/2 ≤ y ≤ π/2
Jadi : =
→ x x
x
arcsin lim
0 → y=
y
y sin
lim
0 sin 1
1 lim
0
=
→
y y
y ( terbukti )
2. lim arctan 1
0 =
→ x x
x
3. limarcsin 0
0 =
→ x
x
4.
2 arccos lim
0
π
x
x→ =
5. limarctan 0
0 =
→ x
x
6. lim cot 0
0 =
→ arc x
Soal-soal
Hitung limit berikut, jika ada !
1.
D. Limit tak hingga
Jika kita lakukan pengamatan terhadap limx→c− f(x) dan → + c x
lim f(x) mungkin akan didapat bahwa f(x) membesar atau mengecil tanpa batas.
Untuk memecahkan limit tak hingga perhatikan teorema berikut !
Contoh 3.11
Tentukan
∞ →
xlim x x-4
x x x
+ − + +
4 3 4
5
7 3
2
Penyelesaian :
am = 2 ; bn = 5 ; m = 4 ; n = 4
Karena m = n , maka
∞ →
x
lim
4
-x x
x x x
+ − + +
4 3 4
5
7 3
2
= n m b a
= 5 2
E. Kekontinuan fungsi
Suatu fungsi dikatakan kontinu disuatu titik a jika tiga syarat berikut terpenuhi. i) lim f(x)
a
x→ ada
ii) f(a) terdefinisi
iii) lim f(x)
a
x→ = f(a)
Contoh 3.15
Jelaskan apakah fungsi-fungsi berikut kontinu di titik a
1. f(x) = 2 3 +
x ; a = -2
2. f(x) = ⎪⎩ ⎪ ⎨ ⎧
= ≠ −
−
3 6
3 3
9 2
x
x x x
jika jika
; a = 3
Penyelesaian :
1. =∞
+
−
→ 2
3 lim
2x
x .
Karena syarat i) tidak terpenuhi maka f(x) tak kontinu di titik a = -2
2. 6
3 9 lim
2
3 − =
−
→ x x
Karenalim ( ) (3)
3
f x f
x→ = maka f(x) kontinu di titik a =3.
Telah disebutkan diatas bahwa bila ketiga syarat kekontinuan terpenuhi maka
suatu fungsi dikatakan kontinu di suatu titik a. Akan tetapi bila salah satu syarat tidak terpenuhi maka fungsi tersebut tak kontinu di titik a. Jika syarat kekontinuan tidak terpenuhi, tetapi lim f(x)
a
x→ ada, maka dikatakan bahwa ketakkontinuan f(x) di titik a dapat dihapuskan dengan jalan mendefinisikan f(a) = lim f(x)
a
x→ maka f(x) menjadi kontinu di titik a. Jika syarat kekontinuan tidak terpenuhi danlim f(x)
a
x→ tidak ada
maka ketakkontinuan f(x) di titik a tidak dapat dihapuskan.
Contoh 3.16
Diketahui f(x) =
2 4 2
+ − x x
. Tentukan ketakkontinuan fungsi tersebut.
Penyelesaian :
=
+ −
−
→ 2
4 lim
2
2 x
x
x lim→−2( −2)=−4
x
x , f(-2) tak terdefinisi
Jadi f(x) tak kontinu di titik a = -2. Akan tetapi ketakkontinuan tersebut dapat dihapuskan karena lim ( )
2 x f
x→− ada.
Selanjutnya lakukan definisi ulang lim( 2) ( 2) 4
2 − = − =−
−
→ x f
x . Sehingga f(x)
dapat ditulis menjadi :
f(x) = ⎪⎩ ⎪ ⎨ ⎧
= ≠ +
−
2 x jika 4
--2 x jika
2 4 2
x x
Contoh 3.17
Diketahui f(x) =
9 1
−
x . Tentukan ketakkontinuan fungsi tersebut.
= dapat dihapuskan.
Soal-soal
Tentukan apakah fungsi-fungsi berikut kontinu di titik a
1. f(x) =
Tentukan apakah fungsi-fungsi berikut kontinu atau tak kontinu di titik a. Jika tak kontinu tentukan apakah ketak kontinuan tersebut dapat dihapuskan atau tidak.