MASALAH PEMODELAN JARINGAN LOGISTIK BANYAK PRODUK MUHAMAD YANDRIE AZIS

(1)

MASALAH PEMODELAN JARINGAN LOGISTIK

BANYAK PRODUK

MUHAMAD YANDRIE AZIS

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2008

(2)

MUHAMAD YANDRIE AZIS. Logistics Network Problem For Many Products. Supervised by PRAPTO TRI SUPRIYO and SISWANDI.

The logistics network problem especially in the distribution part has attracted intensive attention of the researches and practitioners. Planning logistics network is needed to comprehend the market circumstance and customer demand, so that one can maximize profit and win the competition in the economic globalitation. Planning this logistics network problem can be modeled as a problem of MIP (mixed integer programming). MIP is the optimization problems with linear objective function and constraints as well as some certain integer variables.

This paper presents how to optimize the logistics network for many products using MIP to satisfy its objective function and constraints. Model was build based on the request of some products which had to be delivered from some factories to some groceries, and then from a grocery, the products would be delivered to some retailers. There was an example given in this paper about how to solve the problem by using software lingo 8.0.

(3)

ABSTRAK

MUHAMAD YANDRIE AZIS. Masalah Pemodelan Jaringan Logistik Banyak Produk. Dibimbing oleh PRAPTO TRI SUPRIYO dan SISWANDI.

Masalah jaringan logistik di bagian distribusi telah menarik perhatian peneliti dan praktisi. Perencanaan jaringan logistik diperlukan untuk memahami keadan pasar dan permintaan konsumen, sehingga dapat digunakan untuk merencanakan proses produksi dan mengorganisir penyimpanan, sehingga dapat memaksimalkan laba dan memenangkan kompetisi dalam globalisasi ekonomi. Permasalahan perencanaan jaringan logistik ini dapat dimodelkan sebagai masalah MIP (mixed integer programming). MIP adalah masalah optimisasi dengan fungsi objektif dan kendala yang linear serta variabel-variabel tertentu yang bernilai integer.

Tulisan ini akan membahas bagaimana mengoptimalkan jaringan logistik banyak produk menggunakan model MIP sedemikian sehingga memenuhi fungsi objektif dan kendalanya. Model dibangun berdasarkan adanya permintaan beberapa produk yang harus dikirimkan dari beberapa pabrik ke beberapa grosir, kemudian dari grosir, produk tersebut dikirimkan ke beberapa pengecer. Selanjutnya diberikan contoh kasus yang diselesaikan menggunakan software Lingo 8.0.

(4)

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

MUHAMAD YANDRIE AZIS

G54103015

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2008

(5)

Judul

:

Masalah Pemodelan Jaringan Logistik Banyak Produk

Nama

:

Muhamad Yandrie Azis

NRP :

G54103015

Menyetujui :

Pembimbing I,

Drs. Prapto Tri Supriyo, M.Kom.

NIP 131878952

Pembimbing II,

Drs. Siswandi, M.Si.

NIP 131957320

Mengetahui :

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Dr. drh. Hasim, DEA

NIP 131578806

(6)

KATA PENGANTAR

Assalamualaikum, Wr. Wb.,

Alhamdulillahi Rabbil Alamin, Segala puji dan syukur penulis panjatkan kehadirat Allah SWT

atas rahmat serta nikmat sehat jasmani maupun rohani sehingga penulis mampu menyelesaikan karya ilmiah ini. Shalawat serta salam tercurah kepada junjungan kita nabi besar Muhammad SAW yang telah memberikan suri tauladan kepada umatnya hingga akhir jaman.

Berbagai permasalahan muncul selama penulisan karya ilmiah ini. Oleh karena itu, dalam kesempatan ini penulis mengucapkan terima kasih kepada :

1. Bpk. Drs. Prapto Tri Supriyo , M.Kom selaku Pembimbing I yang telah meluangkan waktu dan pikirannya membimbing, memberikan dorongan dan pengarahan kepada penulis hingga penulisan karya ilmiah ini selesai, Bpk. Drs. Siswandi, M.Si. selaku Pembimbing II atas bimbingan dan saran yang telah bapak berikan, Bpk. Ir. N. Kutha Ardhana, M.Sc selaku dosen penguji atas saran dan masukan yang telah Bapak berikan.

2. Bapak (H. Muhammad Sugiono) dan Mamah (Hj. Miskiah) yang telah memberikan kasih sayang yang tak terkira, perhatian, bantuan dan dorongan serta doa yang tak henti sehingga penulis bisa menjalankan tugas sebagai mahasiswa sampai pada tahap akhir ini.

3. Kakakku, A Arifin beserta istrinya Teh Eva juga keponakanku Zahra dan Adik-adikku, Hanif juga Latifah yang selalu memberikan semangat dan doanya.

4. Dosen-dosen di departemen matematika, terima kasih atas ilmu yang telah Bapak dan Ibu berikan, serta staff departemen matematika : Mas Deny, Mas Yono, Mas Bono, Bu Ade, Bu Susi, Bu Marisi, terima kasih atas bantuan selama di Departemen Matematika.

5. Teman-teman Matematika 40 : Elis, Nchie, Uve, Sri, Marlin, Yuda, Uli, Walidah, Dwi, Sawa, Mufti, Komeng, Demi, Amie, Mika, Gatha, Indah, Ifni, Iwit, Mita, Icha, Vina, Meta, Achie, Herni, Nisa, Prima (Teman seperjuangan selama menulis skripsi), Aam, Lili, Manto, Mukafi, Ari, Abdilah, Jayadin, Rusli (Terima kasih sudah membantu pemograman), Berri, Rama (Terima kasih telah membantu konsumsi seminar dan sebagai pembahas), Anton, Dimas, Ali, Rahmat, Febrian, Yusuf, Putra. Kalian semua mewarnai kisah bahagia, sedih, susah, senang bersama selama 4 tahun di Departemen Matematika.

6. Adik-adik kelasku Matematika angkatan 41: Niken dan Diah yang telah bersedia menjadi pembahas.

7. Seorang wanita yang telah memberikan warna dalam hidup saya. Terima kasih atas perhatian, semangat dan doanya.

8. Semua pihak yang ikut membantu dan penulis tidak dapat menyebutkan satu persatu.

Penulisan karya ilmiah ini tidak mungkin luput dari kekurangan, oleh karena itu kririk dan saran dari semua pihak akan sangat membantu demi kesempurnaan penulisan ini. Harapan penulis adalah semoga penulisan karya ilmiah ini akan memberikan manfaat bagi para pembacanya.

Wassalamualaikum Wr. Wb.

Bogor, Januari 2008

(7)

RIWAYAT HIDUP

Muhamad Yandrie Azis dilahirkan di Garut pada tanggal 8 November 1984. Penulis merupakan anak kedua dari pasangan H. Muhammad Sugiono dan Hj. Miskiyah yang bertempat tinggal di Perum Cijati Asri tahap 2 Blok B-12 RT 02/16 Desa Jayawaras Kecamatan Tarogong Kidul Garut 44151.

Pada tahun 1991 penulis mulai bersekolah di SDN kartika III-2. Dan tahun 1997 penulis melanjutkan sekolah ke SLTPN 1 Garut. Pada tahun 2003 penulis lulus dari SMUN 1 Garut dan berhasil menjadi mahasiswa Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor melalui jalur USMI (Undangan Seleksi Masuk IPB).

Selama mengikuti kegiatan perkuliahan penulis Pernah aktif dalam keanggotaan himpunan profesi matematika yang dikenal dengan nama GUMATIKA dan menjabat sebagai anggota Departemen Sosial Masyarakat pada periode 2004/2005. Penulis juga aktif dalam olahraga Fitness dari tahun 2005 sampai sekarang.

(8)

DAFTAR ISI

Halaman

Daftar Tabel ……… viii

Daftar Gambar ……… viii

Daftar Lampiran ……… viii

I PENDAHULUAN 1.1 Latar Belakang ……… 1

1.2 Tujuan ……… 1

II LANDASAN TEORI 2.1 Linear Programming ……… 1

2.1.1 Solusi suatu Linear Programming ………. 1

2.2 Integer Linear Programming ………. 2

2.3 Metode Branch and Bound untuk menyelesaikan masalah Integer Programming ………. 3

III PEMODELAN……… 4

IV STUDI KASUS MASALAH PEMODELAN JARINGAN LOGISTIK ……..………… 6

V SIMPULAN DAN SARAN 5.1 Simpulan……… 11

5.2 Saran ……….. 11

DAFTAR PUSTAKA ……….. 12

(9)

DAFTAR TABEL

Halaman

1 Kapasitas produksi produk i pada pabrik j (dalam satuan)... 6

2 Kapasitas penyimpanan produk i pada grosir m (dalam satuan)... 6

3 Permintaan untuk produk i pada pengecer n (dalam satuan)... 6

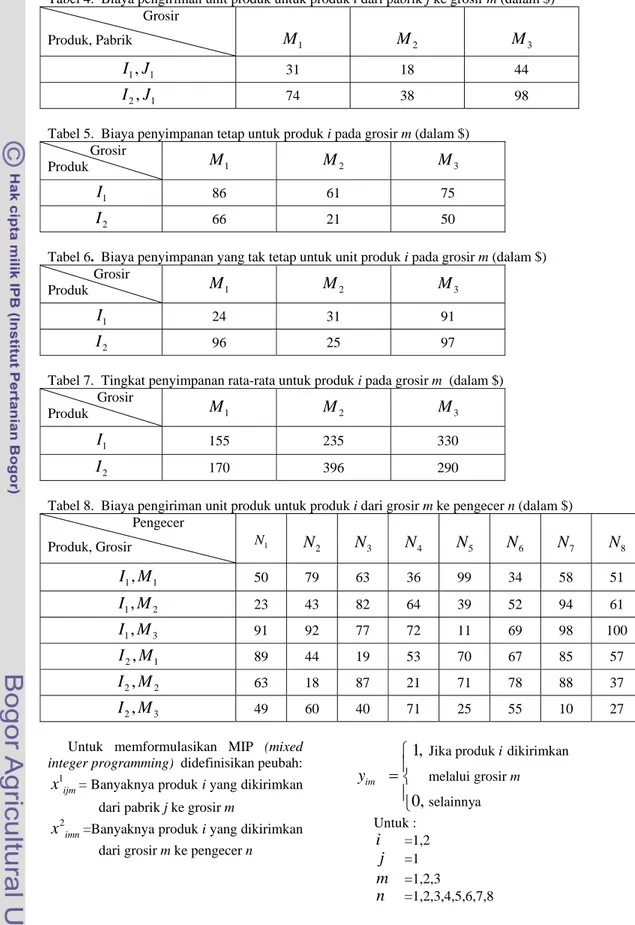
4 Biaya pengiriman unit produk untuk produk i dari pabrik j ke grosir m (dalam $)... 7

5 Biaya pemyimpanan tetap untuk produk i ke grosir m (dalam $)... 7

6 Biaya pemyimpanan yang tak tetap untuk unit produk i pada grosir m (dalam $)... 7

7 Tingkat pemyimpanan rata-rata untuk produk i pada grosir m (dalam $)... 7

8 Biaya pengiriman unit produk untuk produk i dari grosir m ke pengecer n (dalam $). 7

9 Banyaknya produk i yang dikirimkan dari pabrik j ke grosir m... 9

10 Banyaknya produk i yang dikirimkan dari grosir m ke pengecer n... 10

DAFTAR GAMBAR

Halaman 1 Daerah Fisibel IP ……… 3

2 Daerah Fisibel untuk Subproblem 2 dan Subproblem 3 ... 4

3 Metode Branch and Bound untuk menentukan solusi IP ... 4

4 Daerah Fisibel IP ……… 14

DAFTAR LAMPIRAN

Halaman 1 Contoh penyelesaian suatu LP dengan metode Branch and Bound……… 14

2 Program untuk menyelesaikan masalah MIP (mixed integer programming) dengan menggunakan Lingo 8.0... 16

(10)

I. PENDAHULUAN

1.1 Latar Belakang

Dalam sepuluh tahun terakhir, masalah jaringan logistik di bagian distribusi telah menarik perhatian peneliti dan praktisi. Perencanaan jaringan logistik diperlukan untuk meneliti keadaan pasar dan memahami pemintaan konsumen, sehingga dapat memulai merencanakan proses produksi dan mengorganisir penyimpanan dengan sungguh-sungguh. Hal ini dilakukan supaya dapat memaksimalkan laba dan memenangkan kompetisi dalam globalisasi ekonomi.

Ada beberapa jenis model perencanaan jaringan logistik yang dikembangkan oleh para peneliti, seperti distribusi produksi jaringan logistik produk tunggal dengan menggunakan metode pemograman matematika untuk menemukan penempatan fasilitas dengan meminimumkan biaya atau memaksimalkan laba (Chohen dan Lee, 1985; Geotschalkx et al, 1995). Sedangkan Model stokhastik dengan mengambil permintaan konsumen sebagai variabel acak dan menggunakan bilangan bulat stokhastik untuk

memprogram perencanaan distribusi produksi jaringan logistik (logistics network), (Escudero dan Galindo, 1999; MirHassani et

al., 2000).

Tulisan ini akan membahas bagaimana mengoptimalkan jaringan logistik banyak produk menggunakan model MIP (mixed

integer programming) sedemikian sehingga

memenuhi fungsi objektif dan kendalanya. Proses perencanaan jaringan logistik tersebut dilakukan dengan cara mengirimkan produk yang dihasilkan oleh pabrik ke grosir, kemudian dari grosir produk tersebut akan dikirimkan ke masing-masing pengecer yang berbeda.

1.2 Tujuan

Tujuan penulisan ini adalah membahas model jaringan logistik banyak produk dengan menggunakan MIP (mixed integer

programming) guna memenuhi permintaan

konsumen dan sekaligus meminimumkan total biaya pengiriman.

II. LANDASAN TEORI

Untuk membuat model perencanaan jaringan logistik, diperlukan beberapa pemahaman teori seperti linear

programming (LP), integer linear

programming (ILP), dan metode branch and bound. Berikut ini akan dibahas satu persatu.

2.1 Linear Programming

LP merupakan tindakan untuk memperoleh hasil yang optimal dari tujuan yang diinginkan terhadap kendala yang ada. Model LP meliputi pengoptimuman suatu fungsi linear terhadap kendala linear.

Pada tulisan ini, suatu LP mempunyai bentuk standar seperti berikut :

Minimumkan fungsi objektif z = cTx

Terhadap kendala Ax = b

x≥ 0

dengan b≥ ....(1) 0 dengan x dan c berupa vektor berukuran n,

vektor b berukuran m, sedangkan A berupa matriks berukuran m x n yang disebut juga matriks kendala.

[Nash & Sofer, 1996]

2.1.1 Solusi suatu Linear Programming Untuk menyelesaikan suatu masalah LP, metode simpleks merupakan salah satu metode yang dapat menghasilkan solusi optimum. Metode ini dikembangkan oleh Dantzig pada tahun 1947. Dalam perkembangannya, metode ini adalah metode yang paling umum digunakan untuk menyelesaikan masalah LP, yaitu berupa metode iteratif untuk menyelesaikan masalah LP dalam bentuk standar.

Pada LP (1), vektor x yang memenuhi kendala Ax= disebut solusi dari LP (1). b

Definisi 1 (Solusi Fisibel)

Suatu solusi dikatakan fisibel jika memenuhi semua kendala pada LP.

[Nash & Sofer, 1996] Definisi 2 (Daerah Fisibel/Himpunan Fisibel)

Daerah fisibel atau himpunan fisibel adalah himpunan dari semua solusi fisibel.

(11)

2

Misalkan matriks A dapat dinyatakan

sebagai A = ( B N ), dengan B adalah

matriks yang elemennya berupa koefisien variabel basis dan N merupakan matriks

yang elemennya berupa koefisien variabel nonbasis pada matriks kendala. Matriks B

disebut matriks basis untuk LP (1). Berikut definisi matriks Basis :

Definisi 3 (Matriks Basis)

Matriks B disebut matriks basis untuk LP

(1) jika B adalah matriks tak singular, yaitu

matriks yang determinannya tidak sama dengan nol.

[Garfinkel & Nemhauser, 1972] Jika vektor x dapat dinyatakan sebagai vektor x xB

xN

⎛ ⎞ = ⎜ ⎟

⎝ ⎠ dengan xB adalah vektor variabel basis dan xN adalah vektor variabel nonbasis, maka Ax=b dapat dinyatakan

sebagai

(

)

xB Ax B N xN Bx_B Nx_N b ⎛ ⎞ = _⎜ _⎟ ⎝ ⎠ = + = …(2)

Karena B adalah matriks tak singular,

maka B memiliki invers, sehingga dari (2) xB dapat dinyatakan sebagai

1 1

x_b=B− b−B− _NxN

…(3) Definisi 4 (Solusi Basis)

Vektor x disebut solusi basis jika : i. x memenuhi kendala persamaan (Ax=b)

dari LP.

ii. Kolom-kolom dari matriks koefisien yang berpadanan dengan komponen tak nol dari x adalah bebas linear.

[Nash & Sofer, 1996] Definisi 5 (Solusi Fisibel Basis)

Vektor x disebut solusi fisibel basis jika x merupakan solusi basis dan

x

≥

0

.

[Nash & Sofer, 1996] Ilustrasi solusi basis dan solusi fisibel basis dapat dilihat dalam contoh berikut :

Contoh 1

Misalkan diberikan LP berikut: Minimumkan 2z= − x₁−3x₂ terhadap : 2− x₁+x₂+x₃= 4 − +x₁ 2x₂+x₄=11 x₁+x₅= 5 , , , , ₅ 0 1 2 3 4 x x x x x ≥ …(4) Dari LP tersebut didapatkan :

2 1 1 0 0 4 1 2 0 1 0 , 11 1 0 0 0 1 5 A b − ⎛ ⎞ ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ = −_⎜ _⎟ =_{⎜ ⎟} ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ Misalkan dipilih

(

₃ ₄ ₅

)

T dan

(

₁ ₂

)

T x_B= x x x x_N = x x

maka matriks basisnya adalah 1 0 0 0 1 0 0 0 1 B ⎛ ⎞ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠

Dengan menggunakan matriks basis tersebut, diperoleh

(

)

(

)

0 0 , 1 _{4 11 5} T xN T x_B B b = − = = …(5)

Solusi (5) merupakan solusi basis, karena solusi tersebut memenuhi kendala pada LP (4) dan kolom-kolom pada matriks kendala yang berpadanan dengan komponen taknol dari (5) yaitu B adalah bebas linear (kolom yang satu bukan merupakan kelipatan dari kolom yang lain). Solusi (5) juga merupakan solusi fisibel basis, karena nilai-nilai variabelnya lebih dari atau sama dengan nol.

2.2 Integer Linear Programming (ILP) Model ILP atau disingkat Integer

Programming (IP), adalah suatu model LP yang

menggunakan bilangan bulat (integer) sebagai variabel keputusanya. Jika model mengharapkan semua variabel bernilai integer, maka masalah tersebut dinamakan pure integer

programming. Jika model hanya mengharapkan

variabel-variabel tertentu bernilai integer, maka masalah tersebut dinamakan mixed integer

programming. Jika model hanya mengharapkan

nilai 0 dan 1 untuk variabelnya, maka masalah tersebut dinamakan zero one integer

programming.

[Garfinkel & Nemhauser, 1972] Definisi 5(Linear Programming Relaksasi)

LP-Relaksasi dari suatu IP merupakan LP yang diperoleh dari IP tersebut dengan menghilangkan kendala integer atau kendala 0-1 pada variabelnya.

(12)

2.3 Metode Branch and Bound untuk menyelesaikan masalah Integer

Programming

Dalam penulisan karya ilmiah ini, untuk memperoleh solusi optimal dari masalah IP digunakan software Lingo 8.0 yaitu sebuah program yang didesain untuk menentukan solusi model linear, nonlinear, dan optimisasi integer menjadi lebih cepat, mudah, dan lebih efisien.

Software Lingo 8.0 ini menggunakan

metode branch and bound untuk

menyelesaikan masalah ILP.

Prinsip dasar metode branch and bound adalah memecah daerah fisibel dari masalah LP-relaksasi dengan membuat

subproblem-subproblem.

Ö Branch

Membuat partisi daerah solusi ke dalam

subproblem. Tujuannya untuk menghapus

daerah solusi yang tidak fisibel. Hal ini dicapai dengan menentukan kendala yang penting untuk menghasilkan solusi IP, secara tidak langsung titik integer yang tidak fisibel terhapus. Dengan kata lain, hasil pengumpulan dari subproblem-subproblem yang lengkap menunjukkan setiap titik

integer yang fisibel dari masalah asli.

Karena sifat alami partisi itu, maka proses tersebut dinamakan branching.

Ö Bound

Misalkan masalahnya diasumsikan merupakan tipe maksimisasi, nilai objektif yang optimal untuk setiap subproblem dibuat dengan membatasi pencabangan dengan batas atas dari nilai objektif yang dihubungkan dengan sembarang nilai integer yang fisibel. Hal ini sangat penting untuk mengatur dan menempatkan solusi optimum. Operasi ini yang menjadi alasan dinamakan

bounding.

[Taha, 1975] Aspek kunci dari metode branch and

bound adalah sebagai berikut:

Langkah 1 : Periksa apakah IP memenuhi kondisi berikut :

1) Subproblem tidak fisibel.

2) Subproblem menghasilkan solusi optimal dengan semua variabel bernilai integer. 3) Nilai optimal untuk subproblem lebih

kecil dari (dalam masalah

memaksimumkan) batas bawah (lower

bound/LB).

Jika ketiga kondisi tersebut tidak terpenuhi maka cabang subproblem tidak diperlukan. Langkah 2 : Sebuah subproblem mungkin dapat dihapuskan dari pertimbangan dengan kondisi sebagai berikut :

1) Subproblem tidak fisibel.

2) Batas bawah (yang menunjukkan nilai optimal dari kandidat terbaik) setidaknya lebih besar dari nilai optimal subproblem.

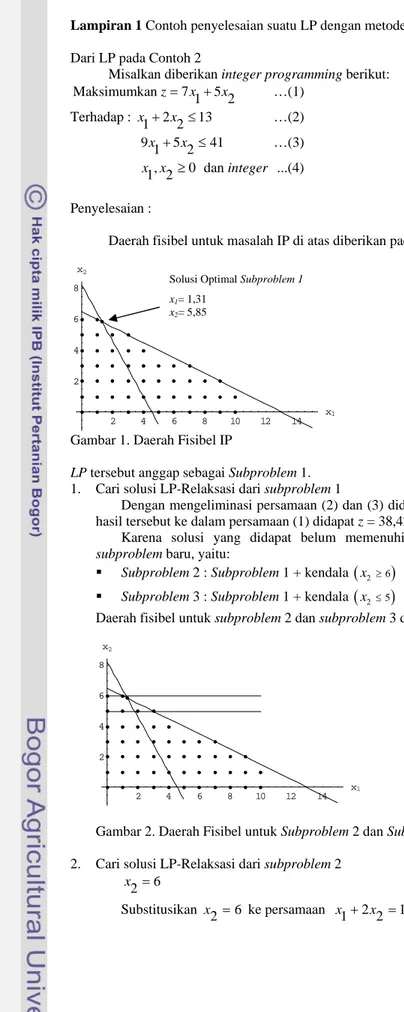
[Winston, 1995] Contoh 2

Misalkan diberikan IP berikut: Maksimumkan 7z= x₁+5x₂ Terhadap : 2 13 1 2 x + x ≤ 9x₁+5x₂≤41 x x_{1 2}, ≥0 dan integer

Daerah fisibel untuk masalah IP di atas diberikan pada gambar berikut :

2 4 6 8 10 12 14 x1 2 4 6 8 x2

Gambar 1. Daerah Fisibel IP Metode branch and bound dimulai dengan menentukan solusi LP-relaksasi (subproblem 1). Solusi LP-relaksasi untuk masalah di atas adalah x1 = 1,31, x2 = 5,85, dan z = 38,42. Solusi tersebut tidak memenuhi kendala integer. Oleh karena itu, harus dibuat subproblem yang baru dengan memilih variabel yang tidak memenuhi kendala integer. Dengan memilih x2 = 5,85 secara sembarang, diketahui bahwa daerah (5<x2<6) dari daerah fisibel subproblem 1 tidak akan memuat solusi IP yang fisibel karena tidak memenuhi kendala integer.

Subproblem yang baru adalah sebagai berikut :

 Subproblem 2 : Subproblem 1 + kendala

(

x2 ≥6

)

(

x2 ≤5

)

Daerah fisibel untuk subproblem 2 dan

subproblem 3 diberikan pada gambar berikut:

x1= 1,31

x2= 5,85

(13)

4

2 4 6 8 10 12 14 x1 2 4 6 8 x2

Gambar 2. Daerah Fisibel untuk

Subproblem 2 dan Subproblem 3

Subproblem 2 dan subproblem 3 tidak dapat

diselesaikan secara bersamaan, sehingga harus diselesaikan dengan dua masalah linear

programming yang berbeda. Pada subproblem 2

diperoleh solusi x1 = 1, x2 = 6, dan z = 37. Karena semua variabel bernilai integer (solusinya memenuhi kendala integer), maka tidak perlu membuat subproblem baru. Pada

subproblem 3 diperoleh solusi x1 = 1,7778, x2 = 5, dan z = 37,4446 Karena variabelnya tidak memenuhi kendala integer, maka harus dibuat

subproblem baru. Subproblem untuk masalah IP

di atas diberikan pada gambar berikut:

Gambar 3. Metode branch and bound untuk menentukan solusi IP Pada Gambar 3, subproblem 2 dan

subproblem 5 merupakan kandidat terbaik

karena semua variabelnya bernilai integer.

Subproblem 2 dan subproblem 5 merupakan

solusi optimal untuk masalah IP di atas karena mempunyai nilai z sama besar. Solusi lengkapnya dapat dilihat pada lampiran 1.

III PEMODELAN

Langkah awal membangun model perencanaan jaringan logistik adalah mendeskripsikan masalah tersebut secara jelas dan lengkap. Selanjutnya masalah tersebut diformulasikan dalam bentuk MIP

(mixed integer programming) yang siap

diselesaikan dengan metode yang sesuai. Model perencanaan jaringan logistik dapat dilihat dalam gambar 4. Model ini menunjukan alur pengiriman produk dari

pabrik sampai ke pengecer N. Produk I yang dihasilkan dari produksi pabrik J akan dikirimkan ke pengecer N lewat grosir M. Beberapa hal yang akan diselesaikan guna memenuhi permintaan konsumen dan sekaligus meminimumkan total biaya pengiriman produk adalah menentukan berapa banyak produk yang akan dikirimkan melewati masing-masing rute pengiriman produk dan melalui grosir mana saja.

x1 = 1,31, x2= 5,85 dan z = 38,42

x1 = 1, x2 = 6 dan z = 37 x1= 1,7778, x2= 5 dan z = 37,4446

Solusi tak fisibel x1= 2, x2= 4,6 dan z = 37

Subproblem 1 Subproblem 2∗ Subproblem 3 Subproblem 4 Subproblem 5∗ 6 2 x ≥ x₂≤5 2 1 x ≥ 1 1 x ≤

(14)

Gambar 4. Gambar perencanaan jaringan logistik Fungsi objektif model MIP (mixed

integer programming) bertujuan untuk

memperkecil total biaya yang meliputi komponen berikut :

1. Biaya pengiriman poduk dari pabrik ke grosir

2. Biaya penyimpanan tak tetap yang disepakati oleh grosir

3. Biaya pengiriman produk dari grosir ke pengecer

Sedangkan kendala tambahan yaitu:

1. Jumlah produk yang dikirim dari pabrik ke grosir tidak boleh melebihi kapasitas produksi pada pabrik tersebut.

2. Jumlah produk yang dikirimkan dari grosir ke pengecer tidak boleh melebihi kapasitas penyimpanan produk pada grosir.

3. Jumlah produk yang dikirimkan grosir harus lebih kecil dari jumlah produk yang diterima grosir.

Misalkan: Indeks: i = Indeks produk j = Indeks pabrik m = Indeks grosir n = Indeks pengecer Parameter: I = Banyaknya produk J = Banyaknya pabrik M = Banyaknya grosir N = Banyaknya pengecer ij

P = Kapasitas produksi untuk produk i

pada pabrik j

im

K = Kapasitas penyimpanan untuk produk i

pada grosir m

in

D = Permintaan untuk produk i pada

pengecer n 1

ijm

C = Biaya pengiriman unit produk untuk produk i dari pabrik j ke grosir m im

F = Biaya penyimpanan tetap untuk produk i pada grosir m

im

C = Biaya penyimpanan yang tak tetap

untuk unit produk i pada grosir m

im

I = Tingkat penyimpanan rata-rata untuk produk i pada grosir m

2

imn

C

= Biaya pengiriman unit produk untuk produk i dari grosir m ke pengecer n.

Variabel keputusan:

1

ijm

x

= Banyaknya produk i yang dikirimkan

dari pabrik j ke grosir m

2

imn

x

dari grosir m ke pengecer n Jika produk dikirimkan melalui grosir selainnya

1,

0,

⎧

⎪

= ⎨

⎪

⎩

im i m

y

Model di atas dapat diformulasikan sebagai berikut:

(

)

1 1 2 2 1 1 1 + 1 1 + + 1 1 1 ∑ ∑ ∑ ∑ ∑ ∑ ∑ ∑ = = = = = = = = M J I M I N M I

Minimum C_{ijm ijm}x y_im F_im C_{im im}I C _imnx _imn

m j i m i n m i 1 M J J 2 M M M 2 J 1 J N1 2 N N N Permintaan konsumen

(

Produk ,P P1 2,...,P l

)

(15)

6

dengan kendala sebagai berikut:

1. Jumlah produk yang dikirimkan dari pabrik tidak boleh melebihi kapasitas poduksi pada pabrik tersebut.

1 _, _, 1 ≥ ∑ ∀ = M P_ij x_ijm i j m

2. Jumlah produk yang dikirimkan keluar dari grosir tidak boleh melebihi kapasitas penyimpanannya. 2 _, _, 1 ≥ ∑ ∀ = N K_im x _imn i m n

3. Karena grosir tidak memproduksi produk, maka jumlah produk yang dikirimkan keluar dari grosir tidak boleh melebihi jumlah produk yang dikirimkan ke grosir tersebut. 1 2 _, _, 1 ≥ 1 ∀ ∑ ∑ = = J N x_ijm x _imn i m j n

4. Memastikan bahwa semua permintaan konsumen pada pengecer sudah dipenuhi.

2 , , 1 = ∑ ∀ = M D_in x _imn i n m

5. Memastikan semua variabel keputusan

2

x imn adalah tak negatif. 2

0 , ,

≥ ∀

x _imn i m n

1

x ijm adalah tak negatif. 1 _≥₀ _∀_{, ,} x_ijm i j m

7. Memastikan variabel keputusan _{yim adalah} biner.

{ }

0,1 ,

y_{im ∈} ∀i m

IV. STUDI KASUS MASALAH PEMODELAN JARINGAN LOGISTIK

Suatu pabrik menghasilkan dua macam produk. Produk tersebut akan dikirimkan ke tiga grosir yang berbeda, kemudian dari grosir produk tersebut akan dikirimkan ke delapan pengecer yang berbeda.

Asumsi yang digunakan dalam memodelkan jaringan logistik ini terdiri dari: satu pabrik

( )

J1 , dua produk

(

I1 2,I

)

, tiga

grosir

(

M₁,M₂,M₃

)

dan delapan pengecer

(N N₁, ₂,N₃,N₄,N₅,N₆,N₇,N₈).

Data hipotetik yang dibangkitkan secara acak untuk memodelkan jaringan logistik dengan model MIP (mixed integer programming) diberikan sebagai berikut :

Tabel 1. Kapasitas produksi produk i pada pabrik j (dalam satuan) Pabrik Produk

J

1 1

I

705 2

I

811

Tabel 2. Kapasitas penyimpanan produk i pada grosir m (dalam satuan)

Grosir Produk

M

1

M

2

M

3 1

I

246 389 422 2

I

253 494 312

Tabel 3. Permintaan untuk produk i pada pengecer n (dalam satuan)

Pengecer Produk

N

1

N

2

N

3

N

4

N

5

N

6

N

7

N

8 1

I

72 25 44 89 40 12 52 65 2

I

52 10 100 79 32 93 60 32

(16)

Tabel 4. Biaya pengiriman unit produk untuk produk i dari pabrik j ke grosir m (dalam $) Grosir Produk, Pabrik

M

1

M

2

M

3 1

,

1

I J

31 18 44 2

,

1

I J

74 38 98

Tabel 5. Biaya penyimpanan tetap untuk produk i pada grosir m (dalam $)

Grosir Produk

M

1

M

2

M

3 1

I

86 61 75 2

I

66 21 50

Tabel 6. Biaya penyimpanan yang tak tetap untuk unit produk i pada grosir m (dalam $)

Grosir Produk

M

1

M

2

M

3 1

I

24 31 91 2

I

96 25 97

Tabel 7. Tingkat penyimpanan rata-rata untuk produk i pada grosir m (dalam $)

Grosir Produk

M

1

M

2

M

3 1

I

155 235 330 2

I

170 396 290

Tabel 8. Biaya pengiriman unit produk untuk produk i dari grosir m ke pengecer n (dalam $)

Pengecer Produk, Grosir N1

N

₂

N

₃

N

₄

N

₅

N

₆

N

₇

N

₈ 1

,

1

I M

50 79 63 36 99 34 58 51 1

,

2

I M

23 43 82 64 39 52 94 61 1

,

3

I M

91 92 77 72 11 69 98 100 2

,

1

I M

89 44 19 53 70 67 85 57 2

,

2

I M

63 18 87 21 71 78 88 37 2

,

3

I M

49 60 40 71 25 55 10 27

Untuk memformulasikan MIP (mixed integer programming) didefinisikan peubah:

1

ijm

x

dari pabrik j ke grosir m 2

imn

x

=Banyaknya produk i yang dikirimkan

dari grosir m ke pengecer n

Jika produk dikirimkan melalui grosir selainnya

1,

0,

⎧

⎪

= ⎨

⎪

⎩

im i m

y

Untuk :

i

=1,2

j

=1

m

=1,2,3

n

=1,2,3,4,5,6,7,8

(17)

8

Sehingga masalahnya dapat diformulasikan sebagai berikut :

(

)

1 1 2 2 1 1 1 + 1 1 + + 1 1 1 ∑ ∑ ∑ ∑ ∑ ∑ ∑ ∑ = = = = = = = = M J I M I N M I

Minimum C_{ijm ijm}x y_im F_im C_{im im}I C _imnx _imn

m j i m i n m i

Dengan kendala sebagai berikut:

1. Jumlah produk yang dikirimkan dari pabrik tidak boleh melebihi kapasitas poduksi pada pabrik tersebut.

1 3 , ; 1 ≥ ∑ ∀ = P_ij x_ijm i j m 1 1 1 1 1 1 , ; 11 111 112 113 , ; 21 211 212 213 ≥ + + ∀ ≥ + + ∀ P x x x i j P x x x i j i= 1,2 j= 1

2. Jumlah produk yang dikirimkan dari grosir tidak boleh melebihi kapasitas penyimpanannya. 2 8 , , 1 ≥ ∑ ∀ = K_im x_imn i m n 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 ... , 11 111 112 118 ... , 12 121 122 128 ... , 13 131 132 138 ... , 21 211 212 218 ... , 22 221 222 228 ... , 23 231 232 238 ≥ + + + ∀ ≥ + + + ∀ ≥ + + + ∀ ≥ + + + ∀ ≥ + + + ∀ ≥ + + + ∀ K x x x i m K x x x i m K x x x i m K x x x i m K x x x i m K x x x i m

i

=

1,2

m

=

1,2,3

3. Karena grosir tidak memproduksi produk, maka jumlah produk yang dikirimkan keluar dari grosir tidak boleh melebihi jumlah produk yang dikirimkan ke grosir tersebut

1 1 8 2 _, _, 1 ≥ 1 ∀ ∑ ∑ = xijm = ximn i m j n 1 2 2 2 1 2 2 2 ... , 111 111 112 118 ... , 112 121 122 128 ≥ + + + ∀ ≥ + + + ∀ x x x x i m x x x x i m 1 2 2 2 1 2 2 2 1 2 2 2 ... , 113 131 132 138 ... , 211 211 212 218 ... , 212 221 222 228 ≥ + + + ∀ ≥ + + + ∀ ≥ + + + ∀ x x x x i m x x x x i m x x x x i m 1 2 2 _... 2 _, 213≥ 231+ 232+ + 238∀ x x x x i m

i

=

1,2

m

=

1,2,3

4. Memastikan bahwa semua permintaan konsumen pada pengecer sudah dipenuhi. 2 2 2 2 3 , , 1 11 111 121 131 = ∑ ∀ = = + + D_in x _imn i n m D x x x 2 2 2 2 2 2 12 112 122 132 .. 18 118 128 138 = + + = + + D x x x D x x x 2 2 2 2 2 2 2 2 2 21 211 221 231 22 212 222 232 .. 28 218 228 238 = + + = + + = + + D x x x D x x x D x x x

i

=

1,2

n

=

1,2,3,4,5,6,7,8

2

imn

x

adalah tak negatif

2 _≥₀ _∀_{, ,} x _imn i m n

i

=

1,2

m

=

1,2,3

n

=

1,2,3,4,5,6,7,

1

ijm

x

adalah tak negatif

1 _≥₀ _∀_{, ,} x_ijm i j m

i

=

1,2

j

=

1

m

=

1,2,3

7. Memastikan variabel keputusan

y

_im

adalah biner

{ }

0,1 ,

y_{im ∈} ∀i m

i

=

1,2

(18)

Jika masalah di atas diuraikan secara manual sebagai berikut :

(

)

(

)

(

)

1 1 2 2 1 1 2 2 1 1 2 2 1 1 ... ... Minimum C_{1,1,1 1,1,1}+ _1,1 _1,1 _{1,1 1,1} C_{1,1,1 1,1,1} C_{1,1,1 1,1,1}+ _1,1 1,1 1,1 1,1 C_{1,1,1 1,1,8} +C_{1,1,2 1,1,2}+ C_1,2 1,2 1,2 1,2 _{1,2,1 1,2,1} C_{1,1,2 1,1,2}+ _1,2 + + + + + + + + + + x y F C I x x y F C I x x y F C I x x y

(

F

)

(

)

(

)

(

)

2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 ... ... C 1,2 1,2 1,2 _{1,2,1 1,2,8} +C_{1,1,3 1,1,3}+ C_1,3 _1,3 _{1,3 1,3} _{1,3,1 1,3,1} C_{1,1,3 1,1,3}+ _1,3 _1,3 _{1,3 1,3} C_{1,3,1 1,3,8} +C_{2,1,1 2,1,1}+ C_2,1 _2,1 _{2,1 2,1} _2,1,1 _2,1,1 C 2 + + + + + + + + + + + + C I x x y F C I x x y F C I x x y F C I x

(

)

(

)

(

)

(

)

1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 ... + C2,1 2,1 2,1 ,1,1 2,1,1 2,1 2,1,1 2,1,8 +C_{2,1,2 2,1,2}+ C_2,2 2,2 2,2 2,2 _2,2,1 _2,2,1 C_{2,1,2 2,1,2}+ _2,2 2,2 2,2 2,2 C _2,2,1 _2,2,8 +C_{2,1,3 2,1,3}+ C_2,3 _2,3 _{2,3 2,3} _2,3,1 _2, + + + + + + + + + + x y F C I x x y F C I x x y F C I x x y F C I x

(

)

1 1 2 2 ... 3,1 C_{2,1,3 2,1,3}+ _2,3 _2,3 _{2,3 2,3} C _2,3,1 _2,3,8 + + x y F +C I + x

Dengan kendala:

Misalkan diuraikan kendala 6

1 111 1 112 1 113 0 1, 2; 1; 1, 2, 3 0 1, 2; 1; 1, 2, 3 0 1, 2; 1; 1, 2, 3 ≥ ∀ = = = ≥ ∀ = = = ≥ ∀ = = = x i j m x i j m x i j m 1 211 1 212 1 213 0 1, 2; 1; 1, 2, 3 0 1, 2; 1; 1, 2, 3 0 1, 2; 1; 1, 2, 3 ≥ ∀ = = = ≥ ∀ = = = ≥ ∀ = = = x i j m x i j m x i j m

Pada uraian tersebut, terlihat bahwa banyak sekali persamaan maupun pertidaksamaan yang harus diselesaikan. Sangat melelahkan jika digunakan metode

branch and bound secara manual.

Masalah di atas selanjutnya diselesaikan menggunakan Lingo 8.0 (Lihat lampiran 2).

Nilai fungsi objektif yang didapat adalah 70248, diperoleh pada iterasi ke 9. Hal ini memperlihatkan bahwa semua pengiriman produk dari pabrik sudah sampai di pengecer. Diuraikan sebagai berikut:

Tabel 9. Banyaknya produk i yang dikirimkan dari pabrik j ke grosir m Grosir Produk, Pabrik

M

1

M

2

M

3 1

,

1

I J

197 162 40 2

,

1

I J

100 298 60

(19)

10

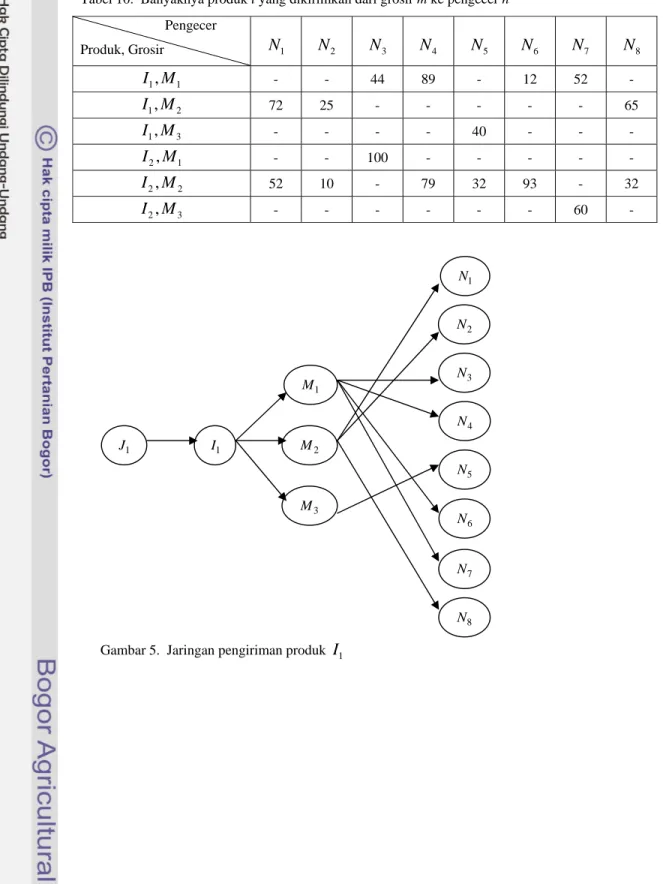
Tabel 10. Banyaknya produk i yang dikirimkan dari grosir m ke pengecer n

Gambar 5. Jaringan pengiriman produk

I

₁

Pengecer Produk, Grosir

N

1

N

2

N

3

N

4

N

5

N

6

N

7

N

8 1

,

1

I M

- - 44 89 - 12 52 - 1

,

2

I M

72 25 - - - 65 1

,

3

I M

- - - - 40 - - - 2

,

1

I M

- - 100 - - - 2

,

2

I M

52 10 - 79 32 93 - 32 2

,

3

I M

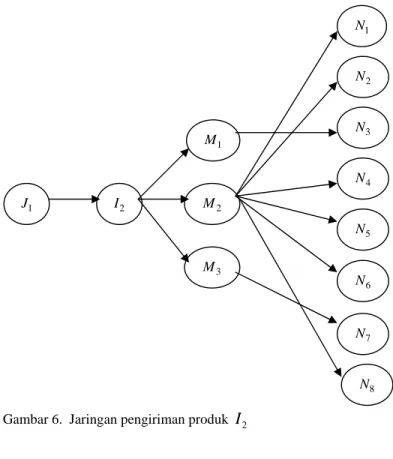
- - - 60 - 3 M 2 M 1 N 2 N 3 N 4 N 5 N 6 N 7 N 8 N 1 J 1 M 1 I

(20)

Gambar 6. Jaringan pengiriman produk

I

₂

Dari solusi optimal yang diperoleh dapat diketahui terdapat banyak kemungkinan pilihan bagi suatu produk dapat dikirimkan ke pengecer melewati grosir. Hal ini dipengaruhi oleh tingkat penyimpanan rata-rata produk i pada grosir m dan biaya

pengiriman unit produk untuk produk i dari

grosir m ke pengecer n.

Pengiriman produk tersebut akan meminimimumkan total biaya pengiriman dengan memilih salah satu alur pengiriman produk ke pengecer melewati grosir.

V. SIMPULAN DAN SARAN

5.1 Simpulan

Masalah perencanaan jaringan logistik sangat diperlukan perusahaan untuk mempelajari keadaan pasar, memahami permintaan konsumen, dan memaksimalkan laba yang didapat. Telah diperlihatkan bahwa masalah jaringan logistik dapat dipandang sebagai masalah MIP (mixed

integer programming).

Untuk mempermudah pembahasan telah dicantumkan contoh kasus yang berkaitan dengan permasalahan jaringan logistik. Adapun data yang digunakan berupa data hipotetik.

Penyelesaian masalah ini menggunakan

software Lingo 8.0 dengan metode Branch and Bound, sehingga dapat memenuhi permintaan

konsumen dan sekaligus meminimumkan total biaya pengiriman.

5.2 Saran

Pada tulisan ini telah dibahas bagaimana memodelkan jaringan logistik dengan model MIP (mixed integer programming). Akan lebih baik lagi jika ada yang menindaklanjuti penelitian ini dengan mengambil data secara real. 3 M 2 M 1 N 2 N 3 N 4 N 5 N 6 N 7 N 8 N 1 J 1 M 2 I

(21)

12 DAFTAR PUSTAKA

Garfinkel, R.S & G.L. Nemhauser. 1972. Integer Programming. John

Willey & Sons, New York.

Ma, Hongze & Suo. Chenxia. 2006. A Model for Designing Multiple Products Logistics Networks. Itnernational Journal of Physical Distribution & Logsctics Management. ABI/INFORM Global pg. 127.

Nash, S.G. & A. Sofer. 1996. Linear and Nonlinear Programming McGraw-Hill,

New York.

Taha, H.A. 1975. Integer Programming.

Academic Press, New York.

Winston, W.L. 1995. Introduction to Mathematical Programming 2nded.

(22)

(23)

14

x1

Lampiran 1 Contoh penyelesaian suatu LP dengan metode branch and bound

Dari LP pada Contoh 2

Misalkan diberikan integer programming berikut:

Maksimumkan 7z= x₁+5x₂ …(1) Terhadap : x₁+2x₂≤13 …(2) 9x₁+5x₂≤41 …(3) , 0 1 2 x x ≥ dan integer ...(4) Penyelesaian :

Daerah fisibel untuk masalah IP di atas diberikan pada gambar berikut :

2 4 6 8 10 12 14 x1 2 4 6 8 x2

Gambar 1. Daerah Fisibel IP

LP tersebut anggap sebagai Subproblem 1.

1. Cari solusi LP-Relaksasi dari subproblem 1

Dengan mengeliminasi persamaan (2) dan (3) didapat x1 = 1,31, x2 = 5,85. Substitusikan hasil tersebut ke dalam persamaan (1) didapat z = 38,42.

Karena solusi yang didapat belum memenuhi kendala integer maka harus dibuat

subproblem baru, yaitu:

(

x2≥6

)

(

x2≤5

)

Daerah fisibel untuk subproblem 2 dan subproblem 3 diberikan pada gambar berikut :

2 4 6 8 10 12 14 x1 2 4 6 8 x2

Gambar 2. Daerah Fisibel untuk Subproblem 2 dan Subproblem 3 2. Cari solusi LP-Relaksasi dari subproblem 2

6 2

x =

Substitusikan x₂ = ke persamaan 6 x₁+2x₂ =13 …(5)

Solusi Optimal Subproblem 1

x1= 1,31

(24)

x1

Sehingga didapatkan x₁= . Substitusikan nilai x1 dan x2 1 yang didapat ke persamaan (1) sehingga diperoleh z = 37.

3. Cari solusi LP-Relaksasi dari subproblem 3 5

2

x =

Substitusikan 5x₂ = ke persamaan (3)

Sehingga didapatkan x1=1, 7778. Substitusikan nilai x1 dan x2 yang didapat ke persamaan (1)

sehingga diperoleh z = 37,4446.

Karena solusi yang didapat belum memenuhi kendala integer maka harus dibuat

subproblem baru, yaitu:

(

x₁≤1

)

(

x₁≥2

)

Daerah fisibel untuk subproblem 4 dan subproblem 5 diberikan pada gambar berikut :

2 4 6 8 10 12 14 x1 2 4 6 8 x2

Gambar 4. Daerah Fisibel untuk subproblem 4 dan subproblem 5 4. Cari solusi LP-Relaksasi dari subproblem 4

1 1 x =

Substitusikan x₁= ke persamaan (5) 1

Sehingga didapatkan x₂ = . Substitusikan nilai x1 dan 6 x2 yang didapat ke persamaan (1) sehingga diperoleh z =37. Karena titik (1,31;5,85) tidak berada di daerah fisibel subproblem 4, maka subproblem 4 tidak memiliki solusi fisibel.

5. Cari solusi LP-Relaksasi dari subproblem 5

1 2 x =

Substitusikan x₁ =2 ke persamaan 9x₁+5x₂=41 …(6)

Sehingga didapatkan x₂ =4, 6. Substitusikan nilai x1 dan x2 yang didapat ke persamaan (1) sehingga diperoleh z = 37.

Dari subproblem-subproblem di atas terlihat bahwa subproblem 2 dan subproblem 5 yang memenuhi kendala integer. Karena nilai fungsi objektik dari kedua subproblem tersebut sama, maka solusi optimal dari LP tersebut terdapat pada titik x₁= dan 1 x₂= serta 6 x₁ =2 dan

4, 6 2

x = dengan nilai fungsi objektif 37. Subproblem 4 Subproblem 5

(25)

16

Lampiran 2 Program untuk menyelesaikan masalah MIP (mixed integer programming) dengan menggunakan Lingo 8.0. MODEL: SETS: PRODUKi/PROD1,PROD2/; PABRIKj/PAB1/; GROSIRm/GROS1,GROS2,GROS3/; PENGECERn/ECER1,ECER2,ECER3,ECER4,ECER5,ECER6,ECER7,ECER8/; PRODUKPABRIK(PRODUKi,PABRIKj):P; PRODUKPENGECER(PRODUKi,PENGECERn):D; PRODUKPABRIKGROSIR(PRODUKPABRIK,GROSIRm):C1,X1; PRODUKGROSIR(PRODUKi,GROSIRm):F,II,Y,C2,K; PRODUKGROSIRPENGECER(PRODUKGROSIR,PENGECERn):C3,X2; ENDSETS

MIN = @SUM(PRODUKPABRIKGROSIR(I,J,M):C1(I,J,M)*X1(I,J,M))+

@SUM(PRODUKGROSIR(I,M):Y(I,M)*(F(I,M)+C2(I,M)*II(I,M)))+

@SUM(PRODUKGROSIRPENGECER(I,M,N):C3(I,M,N)*X2(I,M,N));

!KENDALA;

@FOR(PRODUKPABRIK(I,J):P(I,J)>=@SUM(GROSIRm(M):X1(I,J,M)));

@FOR(PRODUKGROSIR(I,M):K(I,M)>=@SUM(PENGECERn(N):X2(I,M,N)));

@FOR(PRODUKGROSIR(I,M):@SUM(PABRIKj(J):X1(I,J,M))>=@SUM(PENGECERn( N):X2(I,M,N)));

@FOR(PRODUKPENGECER(I,N):D(I,N)=@SUM(GROSIRm(M):X2(I,M,N)));

@FOR(PRODUKGROSIRPENGECER(I,M,N):X2(I,M,N)>=0);

@FOR(PRODUKPABRIKGROSIR(I,J,M):X1(I,J,M)>=0);

@FOR(PRODUKGROSIR(I,M):@BIN(Y(I,M)));

DATA: P = 705 811; D = 72 25 44 89 40 12 52 65 52 10 100 79 32 93 60 32; C1 = 31 18 44 74 38 98; F = 86 61 75 66 21 50; II = 155 235 330 170 396 290; C2 = 73 82 12 53 57 91; K = 246 389 422 253 494 312; C3 =50 79 63 36 99 34 58 51 23 43 82 64 39 52 94 61 91 92 77 72 11 69 98 100 89 44 19 53 70 67 85 57 63 18 87 21 71 78 88 37 49 60 40 71 25 55 10 27; ENDDATA

Global optimal solution found at iteration: 9 Objective value: 70248.00

Variable Value Reduced Cost P( PROD1, PAB1) 705.0000 0.000000 P( PROD2, PAB1) 811.0000 0.000000 D( PROD1, ECER1) 72.00000 0.000000 D( PROD1, ECER2) 25.00000 0.000000 D( PROD1, ECER3) 44.00000 0.000000 D( PROD1, ECER4) 89.00000 0.000000 D( PROD1, ECER5) 40.00000 0.000000

(26)

D( PROD1, ECER6) 12.00000 0.000000 D( PROD1, ECER7) 52.00000 0.000000 D( PROD1, ECER8) 65.00000 0.000000 D( PROD2, ECER1) 52.00000 0.000000 D( PROD2, ECER2) 10.00000 0.000000 D( PROD2, ECER3) 100.0000 0.000000 D( PROD2, ECER4) 79.00000 0.000000 D( PROD2, ECER5) 32.00000 0.000000 D( PROD2, ECER6) 93.00000 0.000000 D( PROD2, ECER7) 60.00000 0.000000 D( PROD2, ECER8) 32.00000 0.000000 C1( PROD1, PAB1, GROS1) 31.00000 0.000000 C1( PROD1, PAB1, GROS2) 18.00000 0.000000 C1( PROD1, PAB1, GROS3) 44.00000 0.000000 C1( PROD2, PAB1, GROS1) 74.00000 0.000000 C1( PROD2, PAB1, GROS2) 38.00000 0.000000 C1( PROD2, PAB1, GROS3) 98.00000 0.000000 X1( PROD1, PAB1, GROS1) 197.0000 0.000000 X1( PROD1, PAB1, GROS2) 162.0000 0.000000 X1( PROD1, PAB1, GROS3) 40.00000 0.000000 X1( PROD2, PAB1, GROS1) 100.0000 0.000000 X1( PROD2, PAB1, GROS2) 298.0000 0.000000 X1( PROD2, PAB1, GROS3) 60.00000 0.000000 F( PROD1, GROS1) 86.00000 0.000000 F( PROD1, GROS2) 61.00000 0.000000 F( PROD1, GROS3) 75.00000 0.000000 F( PROD2, GROS1) 66.00000 0.000000 F( PROD2, GROS2) 21.00000 0.000000 F( PROD2, GROS3) 50.00000 0.000000 II( PROD1, GROS1) 24.00000 0.000000 II( PROD1, GROS2) 31.00000 0.000000 II( PROD1, GROS3) 91.00000 0.000000 II( PROD2, GROS1) 96.00000 0.000000 II( PROD2, GROS2) 25.00000 0.000000 II( PROD2, GROS3) 97.00000 0.000000 Y( PROD1, GROS1) 0.000000 1838.000 Y( PROD1, GROS2) 0.000000 2603.000 Y( PROD1, GROS3) 0.000000 1167.000 Y( PROD2, GROS1) 0.000000 5154.000 Y( PROD2, GROS2) 0.000000 1446.000 Y( PROD2, GROS3) 0.000000 8877.000 C2( PROD1, GROS1) 73.00000 0.000000 C2( PROD1, GROS2) 82.00000 0.000000 C2( PROD1, GROS3) 12.00000 0.000000 C2( PROD2, GROS1) 53.00000 0.000000 C2( PROD2, GROS2) 57.00000 0.000000 C2( PROD2, GROS3) 91.00000 0.000000 K( PROD1, GROS1) 246.0000 0.000000 K( PROD1, GROS2) 389.0000 0.000000 K( PROD1, GROS3) 422.0000 0.000000 K( PROD2, GROS1) 253.0000 0.000000 K( PROD2, GROS2) 494.0000 0.000000 K( PROD2, GROS3) 312.0000 0.000000 C3( PROD1, GROS1, ECER1) 50.00000 0.000000 C3( PROD1, GROS1, ECER2) 79.00000 0.000000 C3( PROD1, GROS1, ECER3) 63.00000 0.000000 C3( PROD1, GROS1, ECER4) 36.00000 0.000000 C3( PROD1, GROS1, ECER5) 99.00000 0.000000 C3( PROD1, GROS1, ECER6) 34.00000 0.000000

(27)

18

C3( PROD1, GROS1, ECER7) 58.00000 0.000000 C3( PROD1, GROS1, ECER8) 51.00000 0.000000 C3( PROD1, GROS2, ECER1) 23.00000 0.000000 C3( PROD1, GROS2, ECER2) 43.00000 0.000000 C3( PROD1, GROS2, ECER3) 82.00000 0.000000 C3( PROD1, GROS2, ECER4) 64.00000 0.000000 C3( PROD1, GROS2, ECER5) 39.00000 0.000000 C3( PROD1, GROS2, ECER6) 52.00000 0.000000 C3( PROD1, GROS2, ECER7) 94.00000 0.000000 C3( PROD1, GROS2, ECER8) 61.00000 0.000000 C3( PROD1, GROS3, ECER1) 91.00000 0.000000 C3( PROD1, GROS3, ECER2) 92.00000 0.000000 C3( PROD1, GROS3, ECER3) 77.00000 0.000000 C3( PROD1, GROS3, ECER4) 72.00000 0.000000 C3( PROD1, GROS3, ECER5) 11.00000 0.000000 C3( PROD1, GROS3, ECER6) 69.00000 0.000000 C3( PROD1, GROS3, ECER7) 98.00000 0.000000 C3( PROD1, GROS3, ECER8) 100.0000 0.000000 C3( PROD2, GROS1, ECER1) 89.00000 0.000000 C3( PROD2, GROS1, ECER2) 44.00000 0.000000 C3( PROD2, GROS1, ECER3) 19.00000 0.000000 C3( PROD2, GROS1, ECER4) 53.00000 0.000000 C3( PROD2, GROS1, ECER5) 70.00000 0.000000 C3( PROD2, GROS1, ECER6) 67.00000 0.000000 C3( PROD2, GROS1, ECER7) 85.00000 0.000000 C3( PROD2, GROS1, ECER8) 57.00000 0.000000 C3( PROD2, GROS2, ECER1) 63.00000 0.000000 C3( PROD2, GROS2, ECER2) 18.00000 0.000000 C3( PROD2, GROS2, ECER3) 87.00000 0.000000 C3( PROD2, GROS2, ECER4) 21.00000 0.000000 C3( PROD2, GROS2, ECER5) 71.00000 0.000000 C3( PROD2, GROS2, ECER6) 78.00000 0.000000 C3( PROD2, GROS2, ECER7) 88.00000 0.000000 C3( PROD2, GROS2, ECER8) 37.00000 0.000000 C3( PROD2, GROS3, ECER1) 49.00000 0.000000 C3( PROD2, GROS3, ECER2) 60.00000 0.000000 C3( PROD2, GROS3, ECER3) 40.00000 0.000000 C3( PROD2, GROS3, ECER4) 71.00000 0.000000 C3( PROD2, GROS3, ECER5) 25.00000 0.000000 C3( PROD2, GROS3, ECER6) 55.00000 0.000000 C3( PROD2, GROS3, ECER7) 10.00000 0.000000 C3( PROD2, GROS3, ECER8) 27.00000 0.000000 X2( PROD1, GROS1, ECER1) 0.000000 40.00000 X2( PROD1, GROS1, ECER2) 0.000000 49.00000 X2( PROD1, GROS1, ECER3) 44.00000 0.000000 X2( PROD1, GROS1, ECER4) 89.00000 0.000000 X2( PROD1, GROS1, ECER5) 0.000000 75.00000 X2( PROD1, GROS1, ECER6) 12.00000 0.000000 X2( PROD1, GROS1, ECER7) 52.00000 0.000000 X2( PROD1, GROS1, ECER8) 0.000000 3.000000 X2( PROD1, GROS2, ECER1) 72.00000 0.000000 X2( PROD1, GROS2, ECER2) 25.00000 0.000000 X2( PROD1, GROS2, ECER3) 0.000000 6.000000 X2( PROD1, GROS2, ECER4) 0.000000 15.00000 X2( PROD1, GROS2, ECER5) 0.000000 2.000000 X2( PROD1, GROS2, ECER6) 0.000000 5.000000 X2( PROD1, GROS2, ECER7) 0.000000 23.00000 X2( PROD1, GROS2, ECER8) 65.00000 0.000000 X2( PROD1, GROS3, ECER1) 0.000000 94.00000

(28)

X2( PROD1, GROS3, ECER2) 0.000000 75.00000 X2( PROD1, GROS3, ECER3) 0.000000 27.00000 X2( PROD1, GROS3, ECER4) 0.000000 49.00000 X2( PROD1, GROS3, ECER5) 40.00000 0.000000 X2( PROD1, GROS3, ECER6) 0.000000 48.00000 X2( PROD1, GROS3, ECER7) 0.000000 53.00000 X2( PROD1, GROS3, ECER8) 0.000000 65.00000 X2( PROD2, GROS1, ECER1) 0.000000 62.00000 X2( PROD2, GROS1, ECER2) 0.000000 62.00000 X2( PROD2, GROS1, ECER3) 100.0000 0.000000 X2( PROD2, GROS1, ECER4) 0.000000 68.00000 X2( PROD2, GROS1, ECER5) 0.000000 35.00000 X2( PROD2, GROS1, ECER6) 0.000000 25.00000 X2( PROD2, GROS1, ECER7) 0.000000 51.00000 X2( PROD2, GROS1, ECER8) 0.000000 56.00000 X2( PROD2, GROS2, ECER1) 52.00000 0.000000 X2( PROD2, GROS2, ECER2) 10.00000 0.000000 X2( PROD2, GROS2, ECER3) 0.000000 32.00000 X2( PROD2, GROS2, ECER4) 79.00000 0.000000 X2( PROD2, GROS2, ECER5) 32.00000 0.000000 X2( PROD2, GROS2, ECER6) 93.00000 0.000000 X2( PROD2, GROS2, ECER7) 0.000000 18.00000 X2( PROD2, GROS2, ECER8) 32.00000 0.000000 X2( PROD2, GROS3, ECER1) 0.000000 46.00000 X2( PROD2, GROS3, ECER2) 0.000000 102.0000 X2( PROD2, GROS3, ECER3) 0.000000 45.00000 X2( PROD2, GROS3, ECER4) 0.000000 110.0000 X2( PROD2, GROS3, ECER5) 0.000000 14.00000 X2( PROD2, GROS3, ECER6) 0.000000 37.00000 X2( PROD2, GROS3, ECER7) 60.00000 0.000000 X2( PROD2, GROS3, ECER8) 0.000000 50.00000

Row Slack or Surplus Dual Price 1 70248.00 -1.000000 2 306.0000 0.000000 3 353.0000 0.000000 4 49.00000 0.000000 5 227.0000 0.000000 6 382.0000 0.000000 7 153.0000 0.000000 8 196.0000 0.000000 9 252.0000 0.000000 10 0.000000 -31.00000 11 0.000000 -18.00000 12 0.000000 -44.00000 13 0.000000 -74.00000 14 0.000000 -38.00000 15 0.000000 -98.00000 16 0.000000 41.00000 17 0.000000 61.00000 18 0.000000 94.00000 19 0.000000 67.00000 20 0.000000 55.00000 21 0.000000 65.00000 22 0.000000 89.00000 23 0.000000 79.00000 24 0.000000 101.0000 25 0.000000 56.00000 26 0.000000 93.00000

(29)

20

27 0.000000 59.00000 28 0.000000 109.0000 29 0.000000 116.0000 30 0.000000 108.0000 31 0.000000 75.00000 32 0.000000 0.000000 33 0.000000 0.000000 34 44.00000 0.000000 35 89.00000 0.000000 36 0.000000 0.000000 37 12.00000 0.000000 38 52.00000 0.000000 39 0.000000 0.000000 40 72.00000 0.000000 41 25.00000 0.000000 42 0.000000 0.000000 43 0.000000 0.000000 44 0.000000 0.000000 45 0.000000 0.000000 46 0.000000 0.000000 47 65.00000 0.000000 48 0.000000 0.000000 49 0.000000 0.000000 50 0.000000 0.000000 51 0.000000 0.000000 52 40.00000 0.000000 53 0.000000 0.000000 54 0.000000 0.000000 55 0.000000 0.000000 56 0.000000 0.000000 57 0.000000 0.000000 58 100.0000 0.000000 59 0.000000 0.000000 60 0.000000 0.000000 61 0.000000 0.000000 62 0.000000 0.000000 63 0.000000 0.000000 64 52.00000 0.000000 65 10.00000 0.000000 66 0.000000 0.000000 67 79.00000 0.000000 68 32.00000 0.000000 69 93.00000 0.000000 70 0.000000 0.000000 71 32.00000 0.000000 72 0.000000 0.000000 73 0.000000 0.000000 74 0.000000 0.000000 75 0.000000 0.000000 76 0.000000 0.000000 77 0.000000 0.000000 78 60.00000 0.000000 79 0.000000 0.000000 80 197.0000 0.000000 81 162.0000 0.000000 82 40.00000 0.000000 83 100.0000 0.000000 84 298.0000 0.000000 85 60.00000 0.000000