Aplikasi Wavelet Haar dan Wavelet DAUB4 dalam kompresi citra - USD Repository

BAB I

PENDAHULUAN

A. Latar Belakang Masalah

Dalam penelitian yang dilakukan oleh para matematikawan, insinyur, dan fisikawan, sering ditemui beberapa masalah mengenai pemrosesan sinyal secara sederhana. Sinyal dapat dianggap sebagai suatu fungsi. Masalah-masalah pemrosesan sinyal yang sering muncul antara lain mengenai cara untuk menjernihkan suara (denoising sinyal suara), bagaimana menjernihkan citra yang blur (denoising sinyal citra), memperkecil ukuran citra (kompresi citra), dan masih banyak lagi.

Penghapusan sinyal suara merupakan salah satu pengolahan sinyal yang penting dalam analisis sinyal suara. Penghapusan sinyal suara merupakan teknik penghapusan derau (noise) yang sering muncul dalam suara. Contoh adanya derau dalam suara adalah munculnya suara derau yang mengganggu dalam penyampaian pesan suara, misalnya komunikasi jarak jauh melalui telepon. Adanya intensitas derau yang tinggi maupun rendah bisa menurunkan kualitas suara dan menyebabkan hilangnya beberapa detail informasi dari suara tersebut.

alat sensor lain.” Dari definisi citra di atas, dapat disimpulkan bahwa citra adalah rekaman dari suatu objek dalam bentuk gambar.

Citra digital atau yang sering disebut citra diskrit dapat dianggap sebagai representasi data diskrit yang memiliki informasi tata letak dan intensitas warna (Chris Solomon-Toby Breckon : 2011). Secara matematis, citra dapat didefinisikan sebagai matriks berukuran M baris dan N kolom yang merepresentasikan fungsi f(x,y), dengan x dan y adalah koordinat spasial, dan amplitudo f di titik koordinat (x,y) dinamakan intensitas atau tingkat keabuan dari citra pada titik tersebut. Apabila nilai x, y, dan nilai amplitudo f secara keseluruhan berhingga dan bernilai diskrit maka dapat dikatakan bahwa citra tersebut merupakan citra digital. Contoh dari citra digital adalah foto digital.

Berikut ini merupakan salah satu contoh citra digital:

Gambar 1.1 Citra wajah seekor kucing

Sumber gambar :http://www.google.com/imgres

Masalah yang sering muncul pada citra adalah adanya noise atau bercak-bercak pada citra. Untuk mengatasi masalah bercak-bercak pada citra maka dilakukan metode penjernihan citra. Penjernihan citra merupakan pengolahan citra yang bertujuan untuk memperjelas citra yang blur karena adanya noise / bercak-bercak dalam citra tersebut. Bercak-bercak adalah gambar atau piksel yang mengganggu kualitas citra. Adanya intensitas bercak yang tinggi maupun rendah bisa menurunkan kualitas suatu citra dan menyebabkan hilangnya beberapa detail informasi dari citra tersebut. Contoh dari adanya bercak dalam suatu citra adalah bintik hitam atau putih yang muncul secara acak yang tidak diinginkan dalam citra.

Di zaman modern seperti sekarang ini, tentu diperlukan segala sesuatu yang praktis dan efisien. Hal ini juga muncul dalam pengolahan suatu data multimedia seperti citra digital. Citra digital memiliki ukuran yang beragam, ada yang berukuran kecil, sedang, besar atau sangat besar. Ukuran yang dimilki suatu citra sangat berperan dalam efisiensi pengolahannya. Misalkan dalam penyimpanan, citra yang berukuran kecil, lebih praktis karena kapasitas penyimpanan yang dibutuhkan juga lebih kecil. Begitu pula dalam hal pengiriman citra, tentu citra yang berukuran kecil akan lebih efisien karena pengirimannya pun menjadi lebih cepat. Oleh karena itu diperlukan solusi yang tepat untuk memperkecil ukuran citra.

multimedia seperti memperkecil ukuran citra digital. Ada 2 jenis kompresi yang dapat digunakan, yaitu lossy compression dan lossless compression. 1. Lossy compression merupakan teknik kompresi yang mengakibatkan data

yang telah melalui proses pemampatan dan pemekaran akan kehilangan sebagian data, sehingga data tersebut tidak dapat direkonstruksi kembali karena telah terjadi penghilangan data. Metode ini cocok digunakan untuk kompresi pada penyimpanan data citra digital atau data suara digital.

2. Lossless compression merupakan teknik kompresi yang tidak menyebabkan kehilangan data, sehingga data yang telah melalui proses pemampatan dapat kembali seperti seperti data sebelum proses pemampatan (kompresi tanpa kehilangan). Metode kompresi ini cocok digunakan untuk kompresi berkas database. Kompresi citra cukup penting dalam pengolahan citra karena kompresi citra dapat memperkecil ukuran citra sehingga dapat memperkecil kapasitas yang dibutuhkan untuk penyimpanan dan mempercepat pengiriman citra.

Berikut ini merupakan contoh hasil dari kompresi citra :

Citra asli Citra hasil kompresi

Diberikan pula contoh hasil kompresi seperti berikut ini :

Citra hasil kompresi Cita asli

Gambar 1.4 Gambar 1.5

Sumber gambar : http://lunalightsworld.wordpress.com/

Dari contoh hasil citra yang telah melalui proses kompresi seperti di atas, terdapat perbedaan yang terlihat secara kasat mata antara citra yang asli/ citra yang belum melalui proses kompresi dengan citra yang sudah melalui proses kompresi. Selain penyimpanannya membutuhkan kapasitas yang lebih kecil, juga dapat mempercepat pengiriman citra.

Kompresi citra yang merupakan suatu metode pengolahan citra, tidak lepas dari tinjauan Matematika. Sebuah citra diskrit dapat ditulis dalam bentuk matriks seperti berikut:

    

 

    

 



1 , 1

, 2 1 , 1

2 , 2

, 2 2 , 1

, ,

2 , 1

N N M N M

M

f f

f

f f

f

f f

f

 

   



Indeks baris pada setiap kolom bertambah besar dari bawah ke atas ( notasi ini biasa digunakan dalam pemrosesan citra).

Secara umum terdapat banyak teknik untuk kompresi citra, seperti teknik kompresi BMP (Bit Map Picture), teknik kompresi JPEG (Joint Picture Experts Group), teknik kompresi JPEG 2000 yang merupakan pengembangan dari teknik kompresi JPEG, teknik kompresi GIF (Graphic Interchange Format), PNG (Portable Network Graphics) dan masih banyak lagi.

Masalah-masalah yang berhubungan dengan sinyal seperti di atas, tentu membutuhkan teknik penyelesaian yang tepat untuk mengatasinya. Dari sini, munculah Wavelet sebagai teori yang dapat diaplikasikan dalam pemrosesan sinyal. Pemrosesan sinyal seperti penghapusan derau suara, penjernihan citra, dan kompresi sinyal (kompresi citra, kompresi audio) dapat diproses menggunakan metode Wavelet.

Gambar 1.6 Dasar algoritma kompresi citra digital metode Wavelet

Metode Wavelet menjadi sarana yang tepat dalam pemrosesan sinyal baik sinyal suara maupun citra. Dalam skripsi ini, penulis hanya akan membahas mengenai aplikasi metode Wavelet Haar dan Wavelet Daub4 dalam kompresi citra keabu-abuan.

Untuk melakukan kompresi citra dengan metode Wavelet, hal pertama yang dilakukan adalah transformasi sinyal citra, selanjutnya menginverskan kembali hasil transformasi sinyal citra tersebut seperti sudah dipaparkan secara sekilas dalam dasar algoritma kompresi di atas, namun untuk lebih jelasnya akan di bahas dalam bab III dan IV.

Rekonstruksi (Invers)

Pemfilteran Transformasi

Kolom Transformasi

Baris

B. RUMUSAN MASALAH

Permasalahan yang akan dibahas dalam tulisan ini akan dirumuskan sebagai berikut :

1. Apa itu Wavelet Haar dan Wavelet Daub4?

2. Bagaimana aplikasi Wavelet Haar dan Wavelet Daub4 dalam kompresi citra?

C. BATASAN MASALAH

Penulis akan membatasi beberapa hal untuk uraian masalah yang akan dibahas, yaitu :

1. Tulisan ini dibatasi pada proses kompresi citra menggunakan metode Wavelet Haar dan Wavelet Daub4.

2. Citra yang digunakan adalah citra keabu-abuan (gray-scale)

3. Sinyal yang di olah dalam kompresi citra hanya terbatas pada sinyal 2-Dimensi.

D. TUJUAN PENULISAN

E. METODE PENULISAN

Metode yang digunakan penulis adalah metode studi pustaka, yaitu dengan mempelajari buku-buku yang berkaitan dengan Wavelet dalam aplikasinya untuk pemrosesan sinyal.

F. MANFAAT PENULISAN

Memperoleh pengetahuan mengenai terapan matematika dalam bidang pemrosesan sinyal khusunya sinyal 2-dimensi dalam kompresi citra menggunakan metode Wavelet.

G. SISTEMATIKA PENULISAN

BAB I PENDAHULUAN

A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penulisan G. Sistematika Penulisan

BAB II LANDASAN TEORI

BAB III WAVELET HAAR

A. Transformasi Haar

B. Konservasi dan Pemampatan Energi C. Wavelet Haar

D. Analisis Multiresolusi E. Kompresi Sinyal

BAB IV WAVELET DAUB4

BAB V APLIKASI WAVELET HAAR dan WAVELET DAUB4

BAB VI PENUTUP

A.Kesimpulan B.Saran

BAB II

LANDASAN TEORI

Dalam bab ini, akan dibahas mengenai dasar-dasar aljabar linear seperti ruang vektor, perkalian skalar/hasil kali dalam, dan matriks yang akan digunakan sebagai landasan untuk pokok bahasan pada bab-bab berikutnya.

A. Ruang Vektor

Operasi-operasi penjumlahan dan perkalian dengan skalar digunakan dalam konteks yang beraneka ragam dalam matematika. Operasi-operasi ini biasanya memenuhi aturan-aturan ilmu hitung yang sama. Sehingga teori umum mengenai sistem-sistem matematika yang melibatkan penjumlahan dan perkalian dengan skalar akan dapat diterapkan dalam berbagai bidang matematika. Sistem-sistem matematika dengan bentuk ini disebut ruang vektor. Berikut definisi dari ruang vektor.

Definisi 2.1.1

Misalkan V adalah suatu himpunan di mana didefinisikan operasi-operasi penjumlahan dan perkalian dengan skalar. Sehingga dapat diartikan bahwa untuk setiap pasang elemen-elemen x dan y di dalam V dapat diasosiasikan dengan elemen x + y yang tunggal yang juga berada di V, dan dengan setiap elemen x di V dan setiap skala  dapat diasosiasikan dengan elemen x

operasi-operasi penjumlahan dan perkalian dengan skalar dikatakan membentuk suatu ruang vektor jika memenuhi aksioma-aksioma berikut:

A1. Komutatif terhadap penjumlahan

x y y

x   , untuk setiap x,yV. A2. Asosiatif terhadap penjumlahan

) ( )

(xy xx yz , untuk setiap x,y,zV. A3. Elemen identitas terhadap penjumlahan

Terdapat elemen 0V sehingga x0x, untuk setiap xV. A4. Elemen invers terhadap penjumlahan

Untuk setiap xVterdapat elemen xdi V sehingga x(x)0. A5. Sifat distribusi pertama

y x y

x ) . . (

.  

    , untuk setiap skalar dan setiap x,yV.

A6. Sifat distribusi kedua

x x

x . .

. )

(   , untuk setiap skalar dan setiap xV. A7. Asosiatif terhadap perkalian dengan skalar

) . ( . )

( x  x , untuk setiap skalar dan  dan setiapxV. A8. Sifat identitas perkalian dengan skalar

V 

x x

x untuk setiap .

1 .

A9. Tertutup terhadap penjumlahan

A10. Tertutup terhadap perkalian dengan skalar

Untuk setiap skalar  dan xV, maka  .x terdefinisi dan merupakan elemen dalam V .

Contoh 2.1.2

Misalkan n

n

Selanjutnya, misalkan diketahui

Definisi 2.1.3 (Definisi Ruang Bagian)

Jika S adalah subhimpunan tak kosong dari suatu ruang vektor V, dan S memenuhi syarat-syarat berikut

(i)



xSjika xS untuk sembarang skalar  . (ii) xyS jika xS dan yS.

Maka S disebut ruang bagian (subspace) dari V.

Contoh 2.1.4

Misalkan S=

Akan dibuktikan bahwa S adalah ruang bagian dari V.

1) Diketahui S

Sehingga

2) Diketahui S

Jadi terbukti bahwa S adalah ruang bagian dari .

Definisi 2.1.5

Definisi 2.1.6

Vektor-vektor v1,v2,,v_n dalam ruang vektor V disebut bebas linear

(linearly independent) jika,

0 v v

v

v1c 2  cn n cn n 

c_{1 2}  _{1 1}

mengakibatkan semua skalar-skalar c1,,c_nharus sama dengan 0.

Definisi 2.1.7

Vektor-vektor v1,v2,,v_n dalam ruang vektor V disebut bergantung

linear (linearly dependent) jika terdapat skalar-skalar c1,c2,,c_n yang tidak semuanya nol sehingga

0 v v

v

v1c 2 cn n cn n 

c_{1 2}  _{1 1}

Definisi 2.1.8

Vektor-vektor v1,v2,,v_n membentuk basis untuk ruang vektor V jika dan

hanya jika :

(i) v₁,,v_n bebas linear

Definisi 2.1.9

Misalkan V adalah ruang vektor. Jika V memiliki basis yang terdiri dari n vektor, maka V memiliki dimensi n.

Ruang bagian {0} dari V dikatakan memiliki dimensi 0. V dikatakan memiliki dimensi hingga jika terdapat himpunan berhingga vektor yang menjadi basis V, jika tidak demikian, maka dikatakan bahwa V memiliki dimensi tak hingga.

B. Hasil Kali Dalam

Pada sub-bab ini akan dibahas mengenai konsep-konsep dari hasil kali dalam dari ruang vektor. Khususnya akan dibahas mengenai hasil kali dalam pada ruang vektor yang elemen-elemennya adalah suatu fungsi dengan variabel bebas t .

Definisi 2.2.1 ( Hasil Kali Dalam )

Hasil kali dalam pada ruang vektor V adalah sebuah operasi pada V yang memetakan setiap pasang vektor-vektor x dan y di dalam V dengan sebuah bilangan Real x,y yang memenuhi syarat berikut :

(i) Aksioma Positif 0 ,x 

x dan x,x 0x0.

(ii) Aksioma Simetri

x y y

(iii)Aksioma Penjumlahan

z y z x z y

x ,  ,  , untuk semua x, y, z di dalam V.

(iv) Aksioma Homogenitas

y x y

x,  ,

  untuk semua x, y di dalam V semua skalar.

Definisi 2.2.2 (Hasil Kali Dalam Kompleks)

Hasil kali dalam suatu ruang vektor kompleks V adalah suatu fungsi R

V

V 



, : yang memenuhi sifat-sifat berikut ini,

(i) Aksioma Positif 0 ,v 

v dan v,v 0v0.

(ii) Simetri Konjugat

v w w

v,  , untuk setiap vektor v,wV. (iii) Aksioma Penjumlahan

w v w u w v

u ,  ,  , untuk setiap vektor u,v,wV . (iv) Aksioma Homogenitas

w v w

v, c ,

c  untuk setiap vektor v,wV dan skalar cC.

Contoh 2.2.3 ( Hasil Kali Dalam Ruang Vektor )

Jika diberikan n

n

didefinisikan sebuah hasil kali dalam x,y dengan





Definisi 2.2.4a

Sebuah ruang vektor V dikatakan ruang linear bernorma jika untuk setiap vektor v V dikaitkan dengan sebuah bilangan real v yang disebut norma

i. v 0 dengan kesamaan berlaku jika dan hanya jika v = 0.

ii. v   v untuk setiap skalar .

iii. vw  v  w untuk semua v,wV.

Definisi 2.2.4b

Misalkan Vmerupakan sebuah ruanghasil kali dalam, maka



 v v v

v , untuk semua V

mendefinisikan sebuah norma pada V. Sehingga berlaku

V 

 v v v

v 2 , untuk semua .

Teorema 2.2.5

Andaikan V, dengan hasil kali dalam , adalah suatu ruang hasil kali 

dalam (real maupun kompleks). Maka untuk setiap X,Y V berlaku, (i) Ketaksamaan Cauchy-Schwarz : X,Y  X Y

(ii) Ketaksamaan Segitiga : XY  X  Y

Persamaan ini terpenuhi jika dan hanya jika X atau Y , salah satunya adalah kelipatan tak negatif dari yang lain.

Bukti :

1. Bukti untuk ruang hasil kali dalam real

Andaikan bahwa salah satu dari kedua vektor tersebut, misalkan Y, adalah suatu vektor taknol. Misalkan t adalah suatu variabel real, maka :

(2.2) ,

2

(2.1) ,

0

2 2 2

2

Y t Y X t X

tY X tY X tY

X

 



 

  

Ruas kanan dalam persamaan di atas merupakan suatu polinomial kuadrat dalam t dengan _X 2 _2_{t X},_{Y t}2 _Y 2 _0_{, yang}

menyebabkan persamaan tersebut tidak memiliki akar-akar real yang berbeda. Oleh karena itu, diskriminan-nya harus tidak positif. Dalam kasus ini berarti,

Diskriminan 4 X,Y 24 X 2 Y 2 0

Sehingga dari persamaan di atas diperoleh ,

Y X Y

X, 

2. Bukti untuk ruang hasil kali dalam kompleks

Misalkan  adalah suatu argumen (arg) dari X,Y , sehingga



i

e Y

X,  X,Y





pernyataan yang sama seperti pada pembuktian sebelumnya yaitu pembuktian dalam kasus hasil kali dalam real.

(ii) Bukti untuk ketaksamaan segitiga

Dengan mengikuti bukti seperti dalam ketaksamaan Cauchy-Schwarz diperoleh :





Definisi 2.2.6

Andaikan V adalah suatu ruang hasil kali dalam.

(i) Vektor X dan Y dalam V dikatakan ortogonal jika X,Y 0.

(ii) Himpunan dari vektor-vektor e_i, i1,,N, dikatakan ortonormal jika

setiap e_i memiliki panjang e_i 1, dan e_i dan ej ortogonal untuk i j.

(iii)Ruang bagian V₁ dan V₂ dari V dikatakan ortogonal jika setiap vektor dalam V₁ adalah ortogonal terhadap setiap vektor dalam V₂.

Suatu basis ortonormal atau sistem ortonormal pada V adalah suatu basis dari V yang terdiri dari vektor-vektor ortonormal.

Teorema 2.2.7

Jika u dan v adalah vektor-vektor di dalam sebuah ruang hasil kali dalam V dan v0, maka

(i) proyeksi skalar dari u pada v diberikan oleh

v v u,





dan

(ii) proyeksi vektor dari u pada v diberikan oleh

v v v

v u v v v

v u v v p

, , 1

,

1 _

        

        

(ii) u = p jika dan hanya jika u sebuah perkalian skalar dari v.

Ini mengakibatkan

Jadi terbukti jika u v( sebuah perkalian skalar dari v), maka

p u

Definisi 2.2.8

Andaikan V adalah suatu ruang hasil kali dalam dan adalah suatu ruang bagian berdimensi-N dengan basis ortonormal



e1,e2,,eN



. Proyeksi

ortogonal dari suatu vektor v V ke , diberikan oleh persamaan berikut,

j

Contoh 2.2.9

Diketahui bidang 



2xy3z0



. Himpunan vektor-vektor sehingga vektor







2,1, 1



adalah proyeksi ortogonal dari v ke bidang .

Teorema 2.2.10 (Ortogonal Gram-Schmidt)

terdapat suatu basis ortonormal



e1,,eN



untuk , sedemikian sehingga

setiap adalah suatu kombinasi linear dari v₁,,v_N.

Bukti :

Didefinisikan e1v1/v1 . Jelas bahwa, e1 memiliki panjang 1. Misalkan

adalah proyeksi ortogonal dari ke rentang garis e₁. Menurut definisi 2.2.8

1 1 2

0 v ,e e

v 

Gambar 2.2.1 Ortogonal Gram-Schmidt

Pada gambar di atas, ditunjukkan bahwa vektor dari ke adalah ortogonal terhadap . Sehingga





1 1 2 2

2 0 0

2 2

,

ke dari vektor

e e v v

v v v

v E

 

 

dan bahwa

0

, , ,

, ,

, 1 2 2 1 1 1 2 1 2 1 1 1

2



 



 v v e e e v e v e e e e

Untuk memperoleh panjang vektor 1, didefinisikan e2 E2/ E2 . dan ,

keduanya adalah saling ortogonal satu sama lain, dan karena adalah kelipatan dari , vektor adalah kombinasi linear dari dan .

Jika N > 2, maka proses ini akan dilanjutkan. Proyeksi ortogonal dari ke terhadap ruang vektor yang direntang oleh dan

2 2 3 1 1 3

0 , ,

ortogonal

Proyeksi v  v e e  v e e

Sehingga,



3 1 1 3 2 2



3 0 3

3 v v v v ,e e v ,e e

E     

dan himpunan E3/ E3 . Pernyataan yang sama untuk menunjukkan

bahwa adalah ortogonal terhadap dan . Jadi,



e1,e2,e3



adalah suatu

himpunan ortonormal dari vektor-vektor. Demikian seterusnya sehingga didapat himpunan ortonormal



e₁,e₂,,e_N



yang merupakan kombinasi

linear dari



v1,v2,,vN



Definisi 2.2.11 ( Matriks Ortogonal )

Andaikan U adalah matriks berukuran n n . U dikatakan ortogonal jika

I UUT 

Sehingga berlaku,

1



U

UT _(2.10)

Contoh 2.2.12

Diberikan suatu matriks U berikut ini,



Sehingga,



Teorema 2.2.13 ( Matriks Ortogonal Mempertahankan Jarak )

Andaikan U adalah suatu matriks ortogonal n n dan x adalah suatu vektor-n. Maka

x

x 

U

Bukti :

 

x x

x x x

x x

x x

x x

x x

x x x

       



U

I U U

U U

U U

U U U

T n T T

T T

T T

T

Jadi

dalam) kali

hasil (definisi menurut

identitas) matriks

(sifat menurut

(2.2.11) menurut

BAB III

WAVELET HAAR

Wavelet Haar merupakan tipe wavelet yang paling sederhana. Dalam bentuk diskrit, Wavelet Haar dinyatakan ke dalam suatu operasi matematis yang disebut dengan transformasi Haar. Transformasi Haar berperan penting dalam transformasi Wavelet Daubechies yang akan dibahas pada bab IV. Dalam bab ini akan dibahas tentang transformasi Wavelet Haar.

A. Transformasi Haar

Misalkan diketahui suatu sinyal yang merupakan suatu fungsi dengan variabel bebas t, dengan t menyatakan waktu. Suatu sinyal diskrit merupakan suatu fungsi dari waktu dengan nilai-nilai secara diskrit. Secara umum sinyal diskrit dapat dituliskan dalam bentuk

) , , ,

(f1 f2  fN



f

dengan N adalah suatu bilangan bulat positif genap yang merupakan panjang dari f. Nilai-nilai dari f adalah N bilangan real f1,f2,, fN.

Nilai-nilai ini menggambarkan Nilai-nilai ukuran dari suatu sinyal analog g, yang diukur dalam nilai-nilai waktu t t1,t2,,tN. Sehingga nilai-nilai dari f

adalah :

 

t f g

 

t fN g

 

tN

g

Transformasi Wavelet Haar diperoleh dengan memecah suatu sinyal diskrit menjadi 2 subsinyal yang masing-masing panjangnya setengah panjang sinyal aslinya. Transformasi ini diawali dengan menentukan subsinyal tren (trend) dan subsinyal fluktuasi (fluctuation). Untuk memperoleh subsinyal tren pertama yang dinotasikan dengan

) untuk mempertahankan energi dari sinyal (yang akan dijelaskan lebih lanjut

dalam bagian B). Sehingga diperoleh 

a , lalu dilanjutkan sampai diperoleh



Selain subsinyal tren, terdapat juga subsinyal fluktuasi. Subsinyal fluktuasi pertama dari f dinotasikan dengan ( 1, 2, , /2)

memperoleh subsinyal fluktuasi adalah dengan menghitung rata-rata selisih

dari setiap pasang nilai f dan kemudian dikalikan dengan 2 . Dengan kata

lain 

sampai diperoleh



Misalkan f didefinisikan dengan 8 nilai yaitu : f= (4,6,10,12,8,6,5,5) maka subsinyal tren pertama ( dari f adalah

yang diperoleh dari perhitungan rumus (3.2). Subsinyal fluktuasi yang pertama ( dari f adalah

yang diperoleh dari perhitungan rumus (3.3).

3.1.2 Transformasi Haar, Level-1

Transformasi Wavelet Haar ditunjukkan dengan beberapa level. Level-1 adalah pemetaan yang didefinisikan dengan _f H1 (a1 |d1)_{, yaitu} pemetaan dari suatu sinyal diskrit f ke subsinyal tren pertama dan subsinyal fluktuasi pertama . Dari contoh di atas diperoleh :

(4,6,10,12,8,6,5,5)

Pemetaan memiliki invers. Inversnya memetakan transformasi sinyal ( kembali ke sinyal f, dengan rumus seperti berikut:



  



    



2 ,

2 ,

, 2 , 2

2 / 2 / 2 / 2 / 1

1 1

1 d a d aN dN aN dN

a



dengan kata lain,

,

,

,

dan

seterusnya.

Berikut ini akan ditunjukkan diagram invers transformasi dari contoh di atas:

5 11 7 5

- - 0

f : 4 6 10 12 8 6 5 5

diperoleh sinyal asli f= (4,6,10,12,8,6,5,5).

B. Konservasi dan Pemampatan Energi

Dalam sub-bab ini akan dibahas mengenai pentingnya konservasi dan pemampatan energi dari sinyal.

Definisi 3.2.1

Konservasi energi dari sinyal adalah suatu sifat mempertahankan energi pada sinyal.

Definisi 3.2.3

Energi dari suatu sinyal f dapat diartikan sebagai jumlahan kuadrat dari nilai-nilai sinyalnya. Sehingga energi f dari suatu sinyal f dapat

2

Secara matematis, energi suatu sinyal dapat diartikan sebagai panjang dari suatu vektor.

Contoh 3.2.4

Andaikan f= (4,6,10,12,8,6,5,5), maka f dapat dihitung sebagai berikut

446

Dengan menggunakan nilai-nilai dari transformasi Haar level-1 ( = diperoleh,

dijumlahkan maka berdasarkan (3.1.2) dan (3.1.3)

2 dengan menjumlahkan 2 2

dan m

m d

2 2

1 2

2 / 2

1 2

2 / 2

1 aN d dN f fN

a     

Jadi dengan kata lain,



 

_a1_|d1





f.

Konservasi energi merupakan sifat penting dalam tranformasi Haar yang berguna dalam proses pemampatan sinyal. Sebagai contohnya,

f= (4,6,10,12,8,6,5,5)

memiliki subsinyal tren pertama ( dari f, yaitu

Sehingga energi dari adalah

_a1 2521212492252440

Sedangkan subsinyal fluktuasi yang pertama ( dari f adalah

Sehingga energi dari adalah

6 0 2 2

2   



1

d 

Jadi, energi dari subsinyal tren pertama ( adalah 98.7% 446

440_

dari total

energi sinyal. Dengan kata lain, transformasi Haar telah mendistribusi energi sinyal f sehingga 98 % dari total energi dipadatkan ke dalam subsinyal yang merupakan setengah panjangnya dari sinyal f . Pemadatan energi seperti ini dinamakan pemampatan energi.

. Pemampatan energi akan terjadi ketika nilai-nilai subsinyal fluktuasi lebih kecil dari subsinyal tren.

3.2.7 Transformasi Haar Multi-level

Transformasi Haar level-1 dalam transformasinya diperoleh subsinyal tren pertama dan subsinyal fluktuasi pertama . Dalam transformasi Haar level-2 akan ditunjukkan dengan menghitung suatu subsinyal tren kedua dan subsinyal fluktuasi kedua hanya untuk subsinyal tren .

Contoh 3.2.8

Diberikan f= (4,6,10,12,8,6,5,5) dan .

Untuk memperoleh tren kedua digunakan rumus (3.2) yaitu dengan menghitung rata-rata dari setiap pasang nilai dan kemudian dikalikan dengan 2 yang dapat ditunjukkan dengan diagram penghitungan seperti berikut :

: 5 11 7 5

16 12

Untuk memperoleh fluktuasi kedua digunakan rumus (3.3) yaitu dengan menghitung rata-rata selisih dari setiap pasang nilai dan kemudian dikalikan dengan 2 yang dapat ditunjukkan dengan diagram penghitungan seperti berikut :

-6 2

Sehingga transformasi Haar level-2 dari f= (4,6,10,12,8,6,5,5) adalah sinyal

(

Untuk sinyal f= (4,6,10,12,8,6,5,5) transformasi Haar level-3 juga dapat didapatkan dengan cara yang sama seperti pada tramsformasi Haar level-2, yaitu dengan menentukan subsinyal tren ketiga digunakan rumus (3.2) yaitu dengan menghitung rata-rata dari setiap pasang nilai dan kemudian dikalikan dengan 2 yang dapat ditunjukkan dengan diagram penghitungan seperti berikut :

16 12

14

Dan untuk memperoleh fluktuasi ketiga digunakan rumus (3.3) yaitu dengan menghitung rata-rata selisih dari setiap pasang nilai dan kemudian dikalikan dengan 2 yang dapat ditunjukkan dengan diagram penghitungan seperti berikut :

16 12

Sehingga hasil dari transformasi Haar level-3 sinyal f= (4,6,10,12,8,6,5,5) adalah

(

Perhitungan yang menarik dalam pemampatan energi terjadi dalam level-2 dan level-3 transformasi Haar seperti yang telah dihitung di atas.

Pertama, diketahui bahwa

_a2_|d2_|d12561443642220446

 hal ini terjadi karena

konservasi energi.

Kedua, dapat dihitung bahwa

400 144

256 



2

a 

Sehingga dari sini, dapat diketahui bahwa transformasi sinyal Haar level-2 mempunyai hampir 90 % dari total energi f yang termuat dalam subsinyal tren kedua yang mana merupakan dari panjang sinyal f. Sekarang akan dicari,

_a3_|d3_|d2_|d11962423642220446

 (karena konservasi

energi), dan

392 2 196

3   

a

 , jadi memuat dari total energi sinyal f.

Hal ini menunjukkan bahwa pemampatan dari transformasi Haar level-3 hampir 88 % dari

total energi f yang termuat dalam subsinyal tren yang merupakan dari

Contoh 3.2.9

Diberikan suatu sinyal yang dihasilkan dari 1024 sampel nilai dari fungsi

 

x x



x



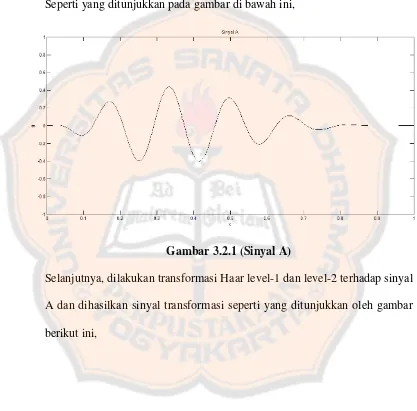
x g _20 2 1_ 4 cos12

Seperti yang ditunjukkan pada gambar di bawah ini,

Gambar 3.2.1 (Sinyal A)

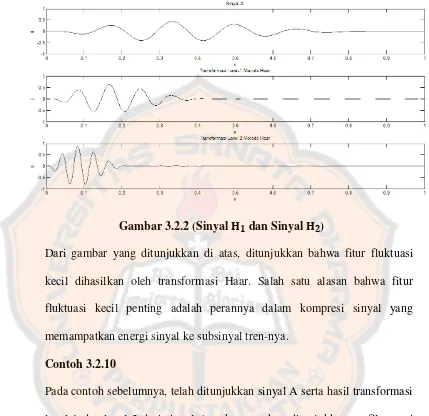
Selanjutnya, dilakukan transformasi Haar level-1 dan level-2 terhadap sinyal A dan dihasilkan sinyal transformasi seperti yang ditunjukkan oleh gambar berikut ini,

Gambar 3.2.2 (Sinyal dan Sinyal )

Dari gambar yang ditunjukkan di atas, ditunjukkan bahwa fitur fluktuasi kecil dihasilkan oleh transformasi Haar. Salah satu alasan bahwa fitur fluktuasi kecil penting adalah perannya dalam kompresi sinyal yang memampatkan energi sinyal ke subsinyal tren-nya.

Contoh 3.2.10

Pada contoh sebelumnya, telah ditunjukkan sinyal A serta hasil transformasi level-1 dan level-2 dari sinyal A, sekarang akan ditunjukkan profil energi komulatif dari sinyal A dan energi komulatif dari transformasi level-1 nya yang didefinisikan dengan

    

 

   

1 , , ,

,

2 3 2 2 2 1 2 2 2 1 2

1 _

f f

f

f f f f f f

 



Gambar 3.2.3 (Gambar Energi Komulatif Sinyal)

Dari ilustrasi gambar di atas, terlihat bahwa hasil dari energi komulatif transformasi level-1 lebih cepat mendekati 1 daripada energi komulatif pada sinyal asli, dan energi komulatif transformasi level-2 lebih cepat mendekati 1 daripada energi komulatif transformasi sinyal level-1. Pada sinyal yang sudah mengalami proses transformasi terjadi pemampatan energi, di mana energi tersebut dimampatkan pada nilai-nilai tren sub-sinyal. Di sinilah peran penting dari nilai fluktuasi yang kecil.

C. Wavelet Haar

Secara umum Wavelet Haar level-1, didefinisikan dengan

Wavelet Haar level-1 memiliki sejumlah sifat yang menarik yaitu : Pertama, setiap Wavelet-nya memiliki energi 1 karena

1 2 1 2 1 0 0

2 1 2

1 2 2

2 2

           _       

 

W



Kedua, setiap Wavelet-nya memiliki nilai-nilai fluktuasi taknol

dengan nilai rata-rata 0. Hal-hal ini lah yang menjadikan fungsi-fungsi ini disebut Wavelet, yaitu memiliki nilai-nilai fluktuasi yang kecil. Tujuan pengenalan Wavelet Haar level-1 ini adalah untuk memperoleh subsinyal fluktuasi dengan lebih mudah, yaitu merupakan hasil perkalian skalar f

Definisi 3.3.1

Perkalian skalar fg dari sinyal f (f1,f2,,fN) dan g(g1,g2,,gN)

didefinisikan dengan

fg f1g1 f2g2 fNgN. (3.5)

Menggunakan Wavelet Haar level-1, dapat ditentukan nilai-nilai subsinyal fluktuasi sebagai perkalian skalar.

Contoh 3.3.2

Subsinyal fluktuasi level-1 Wavelet Haar,

Dengan cara yang sama, dan seterusnya. Rumus dalam (3.3),

   



 

 

2

2 1

2m m

m

f f

d , untuk m1,2,3,,N/2dapat dituliskan dalam bentuk

perkalian skalar Wavelet Haar level-1 sebagai berikut,

, untuk m1,2,3,,N/2 (3.6)

elementer ini disebut sebagai sinyal skala (scaling signal) Haar level-1, yang didefinisikan sebagai berikut :

Dengan menggunakan sinyal skala Haar nilai-nilai dari

2 2

1,a , ,aN

a  untuk

subsinyal tren pertama dapat didefinisikan sebagai perkalian skalar :

, untuk m1,2,3,,N/2 (3.7)

sinyal skala Haar secara umum sama dengan Wavelet Haar. Sinyal-sinyal skala nya memiliki energi 1. Tidak seperti Wavelet Haar, nilai rata-rata sinyal skala Haar taknol yaitu

.

Sinyal-sinyal skala tersebut memiliki energi 1 dan nilai rata-rata .

Nilai dari subsinyal tren level-2 adalah perkalian skalar dari sinyal-sinyal skala dengan sinyal f . Sehingga memenuhi,



2



4 / 2

2 2

1 ,f V , ,f VN

V f

a2    

 (3.8)

Sehingga Wavelet Haar level-2 didefinisikan dengan

Wavelet-wavelet ini merupakan kelipatan 4 dari wavelet pertama .

Wavelet-wavelet ini semuanya juga memiliki energi 1 dan nilai rata-rata 0. Menggunakan perkalian skalar, fluktuasi level-2 memenuhi



2



4 / 2

2 2

1 ,f W , ,f WN

W f

d2      (3.9)

D. Analisis Multiresolusi

Dalam sub-bab sebelumnya telah dibahas bahwa transformasi Wavelet Haar dapat dideskripsikan menggunakan perkalian dalam dengan sinyal-sinyal skala dan wavelet. Dalam sub-bab ini akan dibahas mengenai invers transformasi Haar juga dapat dideskripsikan dalam sinyal-sinyal elementer. Hal ini disebut dengan analisis multiresolusi (multiresolution analysis/ MRA). MRA merupakan bagian pokok dari analisis wavelet.

Definisi 3.4.1 (Definisi Resolusi Citra)

Resolusi citra adalah representasi ukuran dari suatu citra.

Berikut ini merupakan operasi-operasi dasar yang akan digunakan dalam pemrosesan sinyal. Diberikan dua sinyal f (f₁,f₂,,f_N) dan

) , , ,

(g₁ g₂  g_N 

g , akan ditunjukkan operasi-operasi aljabar sebagai

berikut :

1) Penjumlahan dan pengurangan

Penjumlahan f + g dari sinyal f dan g didefinisikan dengan menjumlahkan nilai-nilainya, yaitu



f g f g fN gN





g _{1 1}, _{2 2},,

f (3.10) Penjumalahan f - g dari sinyal f dan g didefinisikan dengan mengurangkan nilai-nilainya, yaitu



f g f g fN gN





g _{1 1}, _{2 2},,

f (3.11)

2) Perkalian dengan konstanta

Suatu sinyal f dikalikan dengan suatu konstanta c adalah dengan mengalikan setiap nilainya dengan c, yaitu



cf cf cfN



cf  ₁, ₂,, (3.12)

Jika didefinisikan suatu sinyal-sinyal elementer N

N R

0 0

2 0

1 ,V , ,V

V 





Maka dapat dituliskan dengan,

0

Rumus (3.14) disebut ekspansi natural dari suatu sinyal f dalam suku-suku dari basis natural dari sinyal-sinyal 0 0

2 0

1,V , ,VN

V  .

Berikut ini akan ditunjukkan bahwa MRA Haar mengekspresikan f sebagai suatu jumlahan dari perkalian skalar dari suatu himpunan basis yang berbeda dari sinyal-sinyal elementer. Dalam sub-bab sebelumnya sudah dibahas mengenai bagaimana mengekspresikan transformasi Haar level-1 dalam suku-suku wavelet dan sinyal-sinyal skala. Oleh karena itu invers dari transformasi Haar level-1 dapat diekspresikan dalam suku-suku sinyal elementer yang sama. Untuk mendefinsikan MRA Haar level-1 digunakan (3.4) untuk mengekspresikan sinyal f, yaitu sebagai berikut

Rumus di atas menunjukkan bahwa sinyal f dapat diekspresikan sebagai jumlahan dari dua sinyal yang disebut sinyal rata-rata pertama dan sinyal detail pertama. Sehingga,

1 dengan



D disebut sinyal detail pertama dan didefinisikan dengan



Menggunakan sinyal-sinyal skala dan wavelet dan menggunakan operasi dasar aljabar dengan sinyal, sinyal rata-rata dan sinyal detail dapat diekspresikan sebagai berikut,

Aplikasi rumus perkalian skalar untuk koefisien dalam (3.7) yaitu adalah





1



1



1



1



1

1 1 1 1

V V f V

V f V V f

A     2 2   N/2 N/2

dan aplikasi rumus perkalian skalar untuk koefisien dalam (3.6) yaitu adalah





1



1



1



1



1

1 1 1 1

W W f W

W f W W f

D     2 2   N/2 N/2

Kedua rumus di atas menunjukkan bahwa sinyal rata-rata adalah suatu kombinasi dari sinyal-sinyal skala Haar dengan nilai-nilai dari subsinyal pertama sebagai koefisien, dan juga bahwa sinyal detail adalah suatu kombinasi dari Wavelet Haar dengan nilai-nilai dari subsinyal fluktuasi pertama sebagai koefisien-koefisiennya.

Berdasarkan persamaan (3.17)

1 1

D A

f  

Di mana, sinyal disebut sinyal rata-rata pertama dan sinyal 1

D disebut sinyal detail pertama. Menggunakan sinyal-sinyal skala dan wavelet Haar dan menggunakan operasi dasar aljabar dengan sinyal, sinyal rata-rata dan sinyal detail dapat diekspresikan seperti pada persamaan (3.20a) dan (3.20b),

N N

N R

a a

a    

 1 1 1

1 1

V V

V

A _{1 2 2}  _{/2 /2}

N N

N R

d d

d    

 1 1 1

1 1

W W

W

D 1 2 2  /2 /2

Selanjutnya, akan ditunjukkan bahwa sinyal skala dan Wavelet dari Wavelet Haar adalah bebas linear.

1

Sehingga diperoleh

0

Jordan, sehingga diperoleh matriks eselon baris tereduksi sebagai berikut,

0

8 2

1l  l 

l 

Jadi sinyal skala dan Wavelet pada Metode Haar adalah bebas linear.

Contoh 3.4.1

Diberikan sinyal f= (4,6,10,12,8,6,5,5) dan .

Aplikasi dari (3.17) maka diperoleh sinyal rata-rata pertama,



5,5,11,11,7,7,5,5





1

A

Menggunakan rumus (3.20a), sinyal rata-rata pertama juga juga dapat diekspresikan dalam suku-suku sinyal skala Haar sebagai berikut,

1 1

1 1

1 1

V V

V V

A 5 2 11 2 ₂ 7 2 ₃ 5 2 ₄

Diketahui pula bahwa subsinyal fluktuasi pertama dari



4,6,10,12,8,6,5,5





f adalah , dengan cara yang

sama seperti pada , menggunakan aplikasi (4.19) maka diperoleh sinyal detail pertama,



1,1,1,1,1,1,0,0





1

D

Jadi dengan menggunakan penyelesaian dari diperoleh,



5,5,11,11,7,7,5,5

 

 1,1,1,1,1,1,0,0





f

Fluktuasi-fluktuasi diperluas dengan menjumlahkan detail-detail untuk menghasilkan resolusi sinyal f.

Menggunakan rumus (4.20b), sinyal detail pertama juga bisa diekspresikan dalam suku-suku Wavelet Haar, yaitu

1 1

3 1

1 1 1

W W

W W

D  2  2 ₂  2 0 ₄

Rumus tersebut menunjukkan bahwa nilai 1

D terbentuk dari nilai-nilai fluktuasi yang dipasangkan dengan Wavelet Haar.

3.4.2 Analisis Multiresolusi, Multi-level

Dalam bahasan sebelumnya, telah dibahas mengenai MRA Haar level-1 dari suatu sinyal. Hal ini dapat diperluas ke dalam level yang lebih besar, banyaknya level sejumlah k, dengan adalah panjangnya sinyal.

Level-2 dari MRA suatu sinyal f yaitu diekspresikan f sebagai

1 2

2 _{D D}

A

f    (3.21)

Dari sini adalah sinyal rata-rata kedua dan adalah sinyal detail kedua. Berdasarkan rumus (3.17) dan (3.21), dapat dilihat bahwa

2 D A

A1 2 (3.22)

Sehingga sinyal rata-rata level-2 memenuhi,













2

4 / 2

4 / 2

2 2 2 2

2 2

N

N V

V f V

V f V V f

A   1 1     (3.23a)













2

Contoh 3.4.3

Jika f= (4,6,10,12,8,6,5,5) dan diketahui bahwa , maka berdasarkan (3.23a) diperoleh,



8,8,8,8,6,6,6,6



A maka sinyal rata-rata

terbentuk menjadi dua kali lebih banyak dari sinyal rata-rata yang dibentuk .

Sehingga berdasarkan (3.21) diperoleh



8,8,8,8,6,6,6,6

 

3, 3,3,3,1,1, 1, 1

 

1,1, 1,1,1, 1,0,0





5,5,11,11,7,7,5,5





1

A , dan penjumlahan kedua dengan detail sudah cukup untuk menghasilkan resolusi keseluruhan sinyal f.

Secara umum, sejumlah N nilai-nilai sinyal yang terbagi sebanyak , maka MRA level-k adalah sebagai berikut

1

D D D

A

f  k  k 2

E. Kompresi Sinyal

Metode kompresi transformasi Wavelet :

1) Menentukan transformasi Wavelet sinyal yang akan dikompresi

2) Menentukan nilai-nilai yang mendekati nol dalam transformasi yang dihasilkan (nilai threshold)

3) Mengirimkan nilai-nilai taknol yang diperoleh dari transformasi pada langkah sebelumnya, di mana himpunan nilai-nilai sinyal yang didapatkan lebih kecil dari nilai-nilai sinyal asli.

4) Menentukan invers pada transformasi Wavelet yang sudah didapatkan untuk menghasilkan hasil kompresi sinyal.

Dalam sub-bab ini akan dibahas mengenai salah satu aspek penting dalam pemrosesan sinyal, yaitu penghapusan derau (noise) dalam sinyal. Ketika suatu sinyal menerima transmisi dari suatu jarak tertentu akan berpotensi terjadi kerusakan pada sinyal tersebut seperti munculnya derau-derau yang merusak sinyal suara yang dikirim. Biasanya, derau-derau tersebut mengubah nilai-nilai sinyal asli. Model sederhana untuk mendeskripsikan hal ini adalah sebagai berikut,

(sinyal yang terkontaminasi) = (sinyal asli) + (derau) (3.24) Persamaan di atas akan diwakilkan dengan persamaan

f = s + n (3.25) di mana f adalah sinyal yang terkontaminasi, s adalah sinyal asli, dan n

adalah derau yang merusak sinyal. Terdapat beberapa jenis derau, secara umum jenis-jenis tersebut adalah sebagai berikut :

1. Derau acak (random noise)

Derau sinyal ini sangat mengombang-ambingkan sinyal, nilai-nilainya beralih dengan cepat antara nilai atas, dan nilai rata-rata. Untuk mudahnya, harus diuji derau acak dengan suatu nilai rata-rata nol.

Gambar 3.4.1 (Gambar Sinyal Terkontaminasi Derau Acak)

2. Derau pop (pop noise)

Jenis derau ini terdengar pada rekaman analog. Derau suara ini dianggap terjadi secara acak, terpencil “pops”. Sebagai suatu model untuk jenis derau ini ditambahkan beberapa nilai tak nol ke dalam sinyal asli pada lokasi-lokasi terpencil.

Berikut ini merupakan contoh dari derau acak yang muncul pada suatu sinyal suara,

3. Derau acak lokal (localized random noise)

Pada derau jenis ini, terkadang derau muncul seperti pada tipe 1, tetapi hanya pada segmen-segmen sinyal. Hal ini terjadi jika ada gangguan singkat pada lingkungan selama transmisi sinyal.

Gambar 3.4.3 (Gambar Sinyal Terkontaminasi Derau Acak

Lokal)

Selain jenis-jenis derau di atas, tentu dapat juga terjadi gangguan pada sinyal yang merupakan kombinasi dari ketiga tipe derau tersebut.

Berikut ini metode dasar untuk penghapusan derau suara.

Metode Pemfilteran /Transformasi Nilai Ambang Batas

Andaikan bahwa sinyal f adalah suatu sinyal terkontaminasi yang tidak lain adalah sinyal asli s ditambah dengan sinyal derau n. Juga dapat diandaikan dua kondisi berikut ini :

2. Semua nilai transformasi derau sinyal memiliki nilai-nilai yang berada di bawah suatu threshold derau yang memenuhi .

Kemudian derau yang ada pada f dapat dihapus/dihilangkan dengan transformasi threshold-nya : semua nilai-nilai transformasinya yang memiliki nilai dibawah threshold derau adalah suatu himpunan yang menuju 0 dan suatu invers transformasi yang ditunjukkan, diharapkan memberikan pendekatan yang baik. Pada sub-bab selanjutnya akan dijelaskan tentang galat.

3.5.1 Galat

Galat dari sinyal f dibandingkan dengan sinyal asli s yang didefinisikan seperti berikut ini



 



2





2

2 2 2 1 1

Galat f s  f s  f_N s_N (3.26)



f s f s fN sN



maks   

 , , ,

maks

Galat 1 1 2 2  (3.27)

Hasil dari denoising dengan transformasi Haar tidak selalu efektif. Seperti pada contoh berikut ini.

Definisi 3.5.2

Contoh 3.5.3

Diberikan sinyal asli yaitu sinyal A yang merupakan sinyal yang diberikan oleh suatu fungsi,

 

x x



x



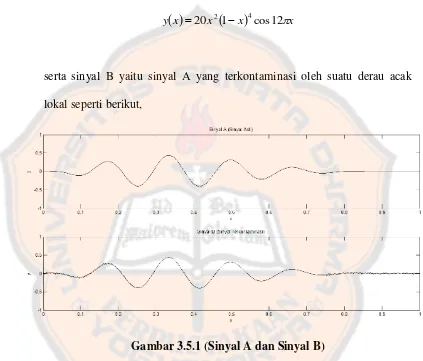
x y _20 2 1_ 4cos12

serta sinyal B yaitu sinyal A yang terkontaminasi oleh suatu derau acak lokal seperti berikut,

Gambar 3.5.1 (Sinyal A dan Sinyal B)

Gambar 3.5.2 (Transformasi Level-1 Sinyal B)

Berikut ini transformasi level-2 sinyal B

Berikut ini transformasi level-3 sinyal B

Gambar 3.5.4 (Transformasi Level-3 Sinyal B)

Selanjutnya pada transformasi level-3 dari sinyal B dilakukan thresholding (menge-nolkan nilai-nilai ambang batas) yang bertujuan untuk menghapus derau pada sinyal. Hal ini ditunjukkan seperti dalam ilustrasi pada gambar berikut ini,

Selanjutnya, dilakukan invers terhadap sinyal yang sudah ditransformasi untuk memperoleh hasil denoising dari sinyal B. Berikut ini ilustrasi gambar dari hasil penghapusan derau.

Gambar 3.5.6 (Sinyal C/ Sinyal Hasil Penghapusan Derau)

Gambar 3.5.7 (Sinyal A dan Sinyal C)

Dari ilustrasi pada gambar 3.5.7 di atas, terlihat jelas bahwa sinyal hasil penghapusan derau tidak menghasilkan pendekatan yang baik terhadap sinyal asli A. Menghitung galat berfungsi untuk meyakinkan penilaian ini. Galat antara sinyal A dan sinyal B adalah 7.374561e-003 atau sekitar 0.0073 sementara galat antara sinyal A dan sinyal C adalah 1.0764e-002 atau sekitar 0.0107. Hal ini menunjukkan bahwa galat setelah dilakukan penghapusan derau pada sinyal lebih besar dari galat sebelum dilakukan penghapusan derau.

BAB IV

WAVELET DAUB4

Wavelet Daubechies diperkenalkan oleh Ingrid Daubechies yang bertujuan untuk lebih menyempurnakan Wavelet Haar. Salah satu aplikasi Wavelet Daubechies adalah kompresi citra digital. Transformasi Wavelet Daubechies didefinisikan sama seperti Wavelet Haar yaitu dengan menghitung rata-rata dan selisih rata-rata melalui hasil kali dalam sinyal dengan sinyal skala(V) dan Wavelet (W).

A. Wavelet Daub4

Transformasi Wavelet Daub4 merupakan transformasi Daubechies yang paling sederhana. Transformasi Wavelet Daub4 didefinisikan sama seperti transformasi Wavelet Haar. Jika suatu sinyal f mempunyai panjang sejumlah N dengan N adalah bilangan genap, maka transformasi Daub4 level-1 adalah pemetaan _f D1 (_a1|_d1) _{dari sinyal f ke subsinyal tren}

pertama dan subsinyal fluktuasi . Setiap nilai am dari tren



a1,,aN/2





1

a adalah sama dengan hasil kali dalam berikut ini

1

. m m

dengan 1

m

V adalah sinyal skala level-1 dari f. Begitu juga, setiap nilai dm

dari fluktuasi 



d1,,dN/2



1

d adalah sama dengan hasil kali dalam berikut ini,

1

. m m

d f W (4.2)

dengan Wm1 adalah Wavelet level-1 dari f.

Seperti transformasi Haar, transformasi Wavelet Daub4 juga dapat diperluas menjadi multi-level sebanyak k, dengan adalah panjangnya sinyal. Perluasan transformasi ini sama seperti perluasan transformasi Haar yaitu dengan mengaplikasikan transformasi Daub4 level-2 dalam subsinyal tren pertama . Pengaplikasian tersebut menghasilkan pemetaan

) | ( 2 2

2 _{a d}

Wavelet Daubechies, sinyal-sinyal skala dan Wavelet-nya menggunakan beberapa nilai yang lebih banyak. Sinyal skala berikut ini merupakan sinyal skala dalam Wavelet Daub4 yang merupakan salah satu transformasi dari metode Daubechies, yaitu :

2 4

3 1

,

2 4

3 3

,

2 4

3 3

,

2 4

3 1

(4.3)

Menggunakan bilangan-bilangan skala di atas, sinyal skala level-1 Daub4 didefinisikan dengan :

Sinyal-sinyal skala di atas mempunyai pola yang sama. Sebagai contohnya, untuk setiap sinyal skala mempunyai suatu pendukung 4 unit. Sinyal skala kedua adalah suatu pergeseran 2 unit dari sinyal skala pertama . Dengan demikian, sinyal skala ketiga adalah suatu pergeseran 4 unit dari sinyal skala pertama , dan setiap deret subsinyal skala adalah suatu pergeseran dengan suatu kelipatan dari 2 unit dari . Untuk akan

memiliki N-2 unit pergeseran , tetapi karena



1,2,3,4



memiliki

panjang 4, ini mengakibatkan 3dan 4 ke luar dari panjangnya sinyal f

yaitu N. Untuk menghindari masalah ini, maka dilakukan sistem melingkar yaitu dengan . Sinyal-sinyal skala Haar juga

memiliki sifat ini dalam pergeseran dua atau lebih (multiples) unit dari sinyal skala pertama. Tetapi karena sinyal skala pertama Haar hanya memiliki dua nilai pendukung taknol, maka tidak terdapat pengaruh sistem melingkardalam kasus Haar.

Sinyal-sinyal skala Daub4 level-2 dihasilkan dengan mengulang operasi-operasi yang digunakan dalam basis natural dalam V ,V , ,VN0

0 2 0

1 

untuk memperluas sinyal-sinyal skala level-1. Menggunakan basis natural, sinyal-sinyal skala Daub4 level-1 memenuhi

0 2 2 4 0

1 2 3 0 2 2 0

1 2 1 1

 

   

 m m m m

m V V V V

V     (4.5a)

Dengan cara yang sama seperti sinyal skala Daub4 level-1, sinyal skala Daub4 level-2 didefinisikan oleh

1

Sinyal-sinyal skala Daub4 level-k didefinisikan sama oleh rumus-rumus dalam (4.5a) dan (4.5b), tetapi diaplikasikan ke dalam sinyal-sinyal skala yang sebelumnya.

Suatu sifat penting dari sinyal-sinyal skala adalah memiliki energi 1. Hal ini dipenuhi karena sifat identitas oleh bilangan-bilangan skala ;

1 memiliki energi 1. Sifat identitas lain yang dipenuhi oleh bilangan-bilangan skala adalah

2

Akan dicari , sehingga

Misal (r) adalah rata-rata dari 4 nilai f yaitu

Selanjutnya rata-rata dari empat nilai f dikalikan dengan 2 ,

1

Jadi, setiap nilai tren level-1 fV₁1 adalah rata-rata dari empat nilai dalam f

yang dikalikan dengan .

Selain sinyal skala, Wavelet Daubechies juga memiliki bentuk Wavelet (W) yang berbeda dengan Wavelet Haar. Bilangan-bilangan Wavelet

dalam Wavelet Daub4 didefinisikan dengan :

Bilangan-bilangan Wavelet ini berelasi dengan bilangan-bilangan skala dengan persamaan :

(4.9)

Wavelet-wavelet di atas merupakan terjemahan dari , dengan suatu sistem melingkar untuk pola Wavelet yang terakhir. Wavelet Daub4 level-1 memenuhi persamaan berikut

0 2 2 4 0

1 2 3 0 2 2 0

1 2 1 1

 

   

 m m m m

m V V V V

W    

Dengan cara yang sama, Wavelet Daub4 level-2 didefinisikan dengan,

1 2 2 4 1

1 2 3 1 2 2 1

1 2 1 2

 

   

 m m m m

m V V V V

W    

Level-level selanjutnya Wavelet Daub4 didefinisikan dengan cara yang sama.

Semua Wavelet Daub4 memiliki energi 1. Untuk Daub4 level-1 hal ini jelas, karena

1

2 4 2 3 2 2 2

1    

Dan Wavelet Daub4 level-k juga memiliki energi 1. Setiap nilai fluktuasi

1

m m

d f W dapat ditunjukkan sebagai suatu selisih dalam nilai-nilai f

karena,

0 fluktuasi 1

m W

f akan nol jika sinyal f bernilai konstan.

Selain persamaan (4.11) juga berlaku persamaan sebagai berikut, 0

3 2 1

01 2 3 4  (4.12)

Contoh 4.1.1

Misal diketahui f 



k,k,,k



dan Sehingga





0

(4.11) persamaan dari

Selanjutnya akan diberikan suatu contoh ilustrasi hasil transformasi beberapa level dari suatu fungsi sinyal dengan menggunakan metode Wavelet Daub4.

Contoh 4.1.2

Diberikan suatu sinyal yang dihasilkan dari 1024 sampel nilai dari fungsi

 

x x



x



x

g 20 2 1 4cos12

Seperti yang ditunjukkan pada gambar di bawah ini,

Gambar 4.1.1 (Sinyal Asli)

Selanjutnya, dilakukan transformasi Daub4 level-2 , level-3, dan level-5 terhadap sinyal A dan dihasilkan sinyal transformasi seperti yang ditunjukkan oleh gambar di bawah ini,

Gambar 4.1.3 (Sinyal )

Gambar 4.1.4 (Sinyal )

Setiap level transformasi Daub4 memiliki invers. Invers untuk transfromasi Daub4 level-1 memetakan transformasi



a1|d1



kembali ke sinyal f yang dihitung secara eksplisit sebagai berikut ini,

1 1

D A

f   (4.13a) Dengan sinyal rata-rata pertama didefinisikan oleh,













N

Dan sinyal detail pertama didefinisikan oleh,













N diekspresikan sebagai jumlahan dari suatu sinyal rata-rata ditambah sinyal detail . Sedangkan dalam rumus (4.13b),

adalah suatu kombinasi dari sinyal-sinyal skala elementer. Jadi adalah suatu jumlahan dari komponen-komponen yang merupakan kelipatan dari sinyal-sinyal skala 1

m

V . Demikian juga sinyal detail adalah kombinasi

Berdasarkan persamaan (4.13a) sinyal detail pertama. Berdasarkan persamaan (4.13b) dan persamaan (4.13c), sinyal rata-rata dan sinyal detail dapat diekspresikan sebagai berikut,

N

Dan sinyal detail pertama didefinisikan oleh,

N

Selanjutnya, akan ditunjukkan bahwa sinyal skala dan Wavelet dari Wavelet Daub4 adalah bebas linear.

