BAB II
LANDASAN TEORI
2.1 Steganografi
Istilah steganografi berasal dari bahasa Yunani, yaitu steganos yang berarti penyamaran atau penyembunyian dan graphein yang berarti tulisan. Jadi, steganography bisa diartikan sebagai seni menyamarkan/menyembunyikan pesan tertulis ke dalam pesan lainnya.
Steganography dan cryptography adalah saudara sepupu dalam keluarga spycraft. Cryptography adalah pengacakan suatu pesan sehingga artinya tidak mudah dimengerti, sedangkan steganography berarti menghilangkan pesan sehingga pesan tersebut tidak dapat dilihat[2]. Terdapat beberapa istilah yang berkaitan dengan
steganografi, antara lain: hiddentext atau embedded message merupakan pesan yang disembunyikan, covertext atau cover-object merupakan pesan yang digunakan untuk menyembunyikan embedded message, stegotext atau stego-object merupakan pesan yang sudah berisi embedded message. Steganografi membutuhkan dua properti, yaitu wadah penampung dan data rahasia yang akan disembunyikan. Steganografi digital
menggunakan media digital sebagai wadah penampung, misalnya citra, audio, teks
dan video, dan data yang disembunyikan juga dapat berupa citra, audio, teks, atau
video.
+ =
Gambar 2.1 Skema Proses Steganografi
2.1.1 Kriteria Steganografi yang Baik
Wadah Penampung
Penyembunyian data rahasia kedalam citra digital akan mengubah kualitas citra
tersebut. Hal ini tergantung pada ukuran file media penyimpan dan ukuran file pesan yang disisipkan. Untuk itu ada beberapa hal atau kriteria yang harus diperhatikan
dalam penyembunyian data, yaitu :
1. Fidelity
Mutu citra penampung data tidak jauh berubah, setelah terjadi penambahan
pesan rahasia, stego-data masih terlihat dengan baik. Pengamat tidak mengetahui kalau di dalam stego-data tersebut terdapat pesan rahasia. 2. Robustness
Pesan yang disembunyikan harus tahan (robust) terhadap berbagai operasi manipulasi yang dilakukan pada stego-data, seperti pengubahan kontras, penajaman, pemampatan, rotasi, perbesaran gambar, pemotongan
(cropping), enkripsi, dan sebagainya. Bila pada citra penampung dilakukan operasi-operasi pengolahan citra tersebut, maka pesan yag disembunyikan
seharusnya tidak rusak (tetap valid jika diekstraksi kembali).
3. Recovery
Data yang disembunyikan harus dapat diungkapkan kembali (recovery). Karena tujuan steganografi adalah penyembunyian informasi, maka
sewaktu-waktu pesan rahasia di dalam stego-data harus dapat diambil kembali untuk digunakan lebih lanjut[16].
Steganography menyembunyikan pesan dalam data lain tanpa mengubah data yang ditumpanginya tersebut sehingga data yang ditumpanginya sebelum dan setelah
proses penyembunyian hampir terlihat sama[2].
Ekstraksi
Hidden text
Stegomedium * Stegoimage
Key Embedding Hidden text
Stegomedium
Gambar 2.2 Skema Embedding dan Ekstraksi
2.1.2 Steganografi Teknik End Of File (EOF)
Metode end of file (EOF) merupakan metode yang melakukan penyisipan (penambahan) diakhir file. Untuk teknik ini dapat menambahkan data atau file yang akan disembunyikan lebih dari ukuran file image. Data yang disembunyikan tersebut akan disisipkan pada akhir file sehingga file image akan terlihat sedikit berbeda dengan aslinya[1]. Karena metode EOF tidak mensyaratkan maksimal panjang pesan
yang dapat disisipkan. Hal ini akan menyebabkan ukuran citra menjadi semakin besar.
Agar tidak menimbulkan kecurigaan, tetap harus dipertimbangkan agar pesan yang
disisipkan tidak terlalu mengubah ukuran dan bentuk fisik citra pada saat
ditampilkan[5]. Dalam teknik EOF, data yang disisipkan pada akhir file diberi tanda khusus sebagai pengenal awaldan pengenal akhir dari data tersebut[15].
Gambar 2.3.a Citra Asli Gambar 2.3.b Stego-image
Citra gambar 2.3.a diatas merupakan citra asli sebelum disisipi teks, dan citra
gambar 2.3.b stego-image adalah citra asli yang telah disisipi teks “ales sanro sotardodo” dengan teknik end of file (EOF), perbedaan antara kedua foto sekilas tidak tampak, tetapi jika lebih diamati lagi maka ada perbedaan antara kedua foto, yaitu
gambar 2.3.b ada sedikit goresan dibawah foto, dan dari segi ukuran juga akan ada
perbedaan, yaitu gambar 2.3.a berukuran 300x200 piksel dan gambar 2.3.b 301x200
piksel.
2.2 Kriptografi
Kriptografi adalah ilmu yang mempelajari bagaimana supaya pesan atau dokumen kita
aman, tidak bisa dibaca oleh pihak yang tidak berhak. Dalam perkembangannya,
kriptografi juga digunakan untuk identifikasi pengiriman pesan dengan tanda tangan
digital dan keaslian pesan dengan sidik jari digital (fingerprint). Kriptografi mempunyai sejarah yang sangat panjang. Sejak jaman Romawi, Yulius Caesar telah menggunakan teknik kriptografi yang sekarang dianggap kuno dan sangat mudah
dibobol untuk keperluan militernya.
Seni dan ilmu untuk menjaga keamanan pesan disebut sebagai kriptografi. Dan
ciphertext. Proses yang merupakan kebalikan dari enkripsi disebut sebagai dekripsi, dan pesan asli tersebut disebut plaintext. Jadi dekripsi akan membuat ciphertext menjadi plaintext[6]. Pengirim (sender) adalah entitas yang mengirim pesan kepada entitas lainnya, penerima (receiver) adalah entitas yang menerima pesan, entitas ini dapat berupa orang, mesin (komputer), dan lain sebagainya. Kriptografi membentuk
sebuah sistem yang dinamakan sistem kriptografi. Sistem kriptografi (cryptosystem) adalah kumpulan yang terdiri dari algoritma kriptografi, semua plainteks dan
cipherteks yang mungkin, dan kunci [SCH96]. Penyadap (eavesdropper) adalah orang yang mencoba menangkap pesan selama ditransmisikan, tujuan penyadap adalah
untuk mendapatkan informasi sebanyak-banyaknya mengenai sistem kriptografi yang
digunakan untuk berkomunikasi dengan maksud untuk memecahkan cipherteks, nama
lain penyadap antara lain: enemy, adversary, intruder, interceptor, bad guy. Kriptanalisis (cryptanalysis) adalah ilmu dan seni untuk memecahkan cipherteks menjadi plainteks tanpa mengetahui kunci yang digunakan, dan pelakunya disebut
kriptanalis. Kriptologi (cryptology) adalah studi mengenai kriptografi dan kriptanalisis, baik kriptografi maupun kriptanalis keduanya saling berkaitan[8].
2.2.1 Tujuan Kriptografi
Tujuan kriptografi adalah :
1. Kerahasiaan (confidentiality) adalah layanan yang ditujukan untuk menjaga agar pesan tidak dapat dibaca oleh pihak-pihak yang tidak berhak. Di dalam
kriptografi, layanan ini direalisasikan dengan menyandikan pesan menjadi
cipherteks.
2. Integritas (integrity) adalah layanan yang menjamin bahwa pesan masih asli/utuh atau belum pernah dimanipulasi selama pengiriman. Untuk menjaga
integritas data, sistem harus memiliki kemampuan untuk mendeteksi
manipulasi pesan oleh pihak-pihak yang tidak berhak, antara lain penyisipan,
pengahapusan, dan pensubtitusian data lain kedalam pesan yang sebenarnya.
3. Otentikasi (authentication), adalah layanan yang berhubungan dengan identifikasi, baik mengidentifikasi kebenaran pihak-pihak yang berkomunikasi
berkomunikasi harus dapat mengotentikasi satu sama lain sehingga ia dapat
memastikan sumber pesan.
4. Nirpenyangkalan (Non-repidiation) adalah layanan untuk mencegah entitas yang berkomunikasi melakukan penyangkalan, yaitu pengirim pesan
menyangkal melakukan pengiriman atau penerima pesan memberi otoritas
kepada penerima pesan untuk melakukan pembelian, namun kemudian ia
menyangkal telah melakukan pembelian.
2.2.2 Kriptografi Simetri dan Asimetri
Selain berdasarkan sejarah yang membagi kriptografi menjadi kriptografi klasik dan
kriptografi modern, maka berdasarkan kunci yang digunakan untuk enkripsi dan
dekripsi, kriprografi dapat dibedakan menjadi kriptografi kunci-simetri (symmetric-key cryptography) dan kriptografi kunci-nirsimetri (asymmetric-key cryptography)[8].
2.2.2.1Kriptografi Simetri
Algoritma simetri disebut juga sebagai algoritma konvensional adalah algoritma yang
menggunakan kunci enkripsi yang sama dengan kunci dekripsinya[6]. Istilah lain
untuk kriptografi kunci-simetri adalah kriptografi kunci-privat (private-key cryptography) atau kriptografi kunci rahasia (secret-key cryptography). Sistem kriptografi kunci-simetri (disingkat menjadi “kriptografi simetri” saja),
mengasumsikan pengirim dan penerima pesan sudah berbagi pada kerahasiaan
kuncinya. Kriptografi simetri satu-satunya jenis kriptografi yang dikenal dalam
catatan sejarah hingga tahun 1976. Ada puluhan algoritma kriptografi modern yang
termasuk ke dalam sistem kriptografi simetri, diantaranya adalah DES (data encryption standard), blowfish, twofish, triple-DES, IDEA, serpent, dan yang terbaru adalah AES (advanced encryption standard).
Aplikasi kriptografi simetri yang utama adalah melindungi kerahasisaan data
yang dikirim melalui saluran yang tidak aman dan melindungi kerahasisaan data yang
disimpan pada media yang tidak aman. Kelemahan dari sistem ini adalah baik
pengirim pesan harus mencari cara yang aman untuk memberitahukan kunci kepada
penerima pesan[8].
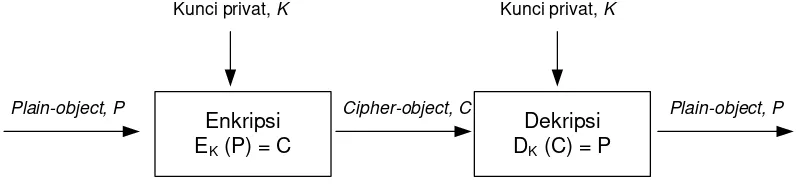
Enkripsi EK (P) = C
Dekripsi DK (C) = P
Kunci privat, K Kunci privat, K
Cipher-object, C
Plain-object, P Plain-object, P
Gambar 2.4 Skema Kriptografi Simetri
Keterangan :
K : kunci privat
P : plaintext
C : ciphertext
EK(P) : rumus enkripsi
DK(C) : rumus dekripsi
2.2.2.2Kriptografi Asimetri
Algoritma asimetri (disebut juga algoritma kunci publik) didesain sedemikian
sehingga kunci yang digunakan untuk enkripsi berbeda dari kunci yang digunakan
untuk dekripsi[6]. Pada kriptografi jenis ini, setiap orang yag berkomunikasi
mempunyai sepasang kunci yaitu kunci privat dan kunci publik. Pengirim
mengenkripsi pesan dengan menggunakan kunci publik sipenerima pesan (receiver). Hanya penerima pesan yang dapat mendekripsi pesan karna hanya dia yang
mengetahui kunci privatnya sendiri[8]. Penemuan sistem kriptografi kunci publik pada
akhir tahun 1970, dan membawa perubahan yang cepat pada penelitian kriptografi.
Solusi untuk masalah pendistribusian kunci telah ditemukan(disarankan) oleh Diffie dan Hellman pada tahun 1976. Kriptografi asimetris dengan menggunakan dua kunci telah disarankan, dimana salah satu kunci merupakan kunci publik dan salah satu
kunci merupakan kunci privat (rahasia) [11]. Contoh algoritma kriptogafi kunci-publik
Enkripsi EK1 (P) = C
Dekripsi DK2 (C) = P
Kunci publik, K1 Kunci privat, K2
Cipher-object, C
Plain-object, P Plain-object, P
Gambar 2.5 Skema Kriptografi Asimetri
Keterangan :
K1 : kunci publik
K2 : kunci privat
P : plaintext
C : ciphertext
EK1(P) : rumus enkripsi
DK2(C) : rumus dekripsi
Kunci enkripsi tidak sama dengan kunci dekripsi, kunci enkripsi bersifat publik
(tidak rahasia) dan dapat diketahui oleh orang lain, sedangkan kunci dekripsi bersifat
privat (rahasia) dan tidak dapat diketahui oleh orang lain yang tidak diinginkan.
2.2.3 Landasan Matematika
Teori bilangan (number theory) adalah teori yang mendasar dalam memahami kriptografi, khususnya sistem kriptografi kunci-publik. Bilangan yang dimaksud disini
hanyalah bilangan bulat (integer).
2.2.3.1 Sifat Pembagian Pada Bilangan Bulat
2.2.3.2 Teorema Euclidian
Misalkan m dan n adalah dua buah bilangan bulat dengan syarat n>0. Jika m dibagi dengan n maka terdapat dua buah bilangan bulat unik q (quotient) dan r (remainder), sedemikian sehingga :
m = nq + r ... (2.1) dengan0≤ r ≤ n
Contoh :
(i) 1987 dibagi dengan 97 memberikan hasil bagi 20 dan sisa 47, atau ditulis
sebagai : 1987 = 97 . 20 + 47
2.2.3.3 Bilangan Prima
Kriptografi kunci asimetri menggunakan bilangan prima yang besar. Sebuah bilangan
bulat positif adalah bilangan prima jika dan hanya jika bilangan tersebut hanya
mempunyai 2 buah bilangan yang dapat membagi bilangan tersebut[3].
Contoh :
(i) Apakah 2 bilangan prima?. Bilangan 2 dapat dibagi oleh bilangan 2 dan 1, maka
2 termasuk bilangan prima.
(ii) Apakah 4 bilangan prima?. Bilangan 4 dapat dibagi oleh bilangan 4, 2, dan 1,
maka 4 tidak termasuk bilangan prima.
(iii) Apakah 7 bilangan prima?. Bilangan 7 dapat dibagi oleh bilangan 7, dan 1,
maka 7 termasuk bilangan prima.
(iv) Apakah 9 bilangan prima?. Bilangan 9 dapat dibagi oleh bilangan 9, 3, dan 1,
maka bilangan 9 tidak termasuk bilangan prima.
2.2.3.4 Relatif Prima
Dua buah bilangan bulat a dan b dikatakan relatif prima jika PBB(a,b) = 1. Jika a dan b relatif prima, maka terdapat bilangan bulat m dan n sedemikian sehingga
(i) 20 dan 3 relatif prima sebab PBB(20,3) = 1. Begitu juga 7 dan 11 relatif prima
karena PBB(7,11) = 1. Tetapi 20 dan 5 tidak relative prima sebab PBB(20,5) = 5
≠ 1
(ii) Bilangan 20 dan 3 adalah relatif prima karena PBB(20,3) = 1, atau dapat ditulis
2 . 20 + (-13).3 = 1
2.2.4 Kriptografi Algoritma ElGamal
Algoritma ElGamal pada mulanya digunakan untuk pengamanan tanda tangan digital, dan keamanan dari skema ini terletak pada susahnya menghitung logaritma
diskrit[11]. Algoritma ElGamal dibuat oleh Taher ElGamal pada tahun 1984. Algoritma ini pada mulanya digunakan untuk digital signature, kemudian dimodifikasi sehingga juga bisa digunakan untuk enkripsi dan dekripsi. ElGamal digunakan di dalam perangkat lunak sekuriti yang dikembangkan oleh GNU, program PGP, dan pada system sekuriti lainnya.
Algoritma membangkitkan pasangan kunci
1. Pilih sembarang bilangan prima p ( p dapat di-share di antara kelompok ) 2. Pilih dua buah bilangan acak, g dan x, dengan syarat g < p dan 1≤ x≤ p-2 3. Hitung
y = gx mod p ... (2.3) Hasil dari algoritma ini :
Kunci publik : tripel (y,g,p) Kunci pivat : pasangan (x,p)
Catatan : g dan p tidak rahasia, sebab mereka diperlukan pada perhitungan enkripsi/dekripsi[8].
Tanda tangan digital – ElGamal
Untuk menandai pesan, M, pilih bilangan acak, k, dimana k relatif prima dengan p-1. Kemudian hitung
dan gunakan algoritma euclidian extended untuk mengatasi b dengan persamaan berikut :
M = (xa+xb) mod (p-1) ... (2.5) pasangan kunci tanda tangan : a dan b. nilai random, k, harus dirahasiakan.
Untuk membutikan tanda tangan, periksa bahwa
ya abmod p= gMmod p ... (2.6) setiap tanda tangan ElGamal atau enkripsi membutuhkan nilai baru (k), dan nilai harus dipilih secara acak. Jika Eve menemukan nilai k yang pernah digunakan Alice, dia dapat mengetahui kunci privat (x) Alice. Dan jika Eve memperoleh dua pesan yang tertandatangan atau terenkripsi dengan kunci k yang sama, bahkan dia tidak mengetahuinya, dia bisa menemukan nilai x [12].
Algoritma Enkripsi/Dekripsi Enkripsi:
1. Susun plaintext menjadi blok-blok m1, m1, ..., sedemikian sehingga setiap blok
merepresentasikan nilai di dalam selang [0, p-1]. 2. Pilih bilangan acak k, yang dalam hal ini 1≤ k≤ p-2. 3. Setiap blok m di enkripsi dengan rumus
a = gkmod p
b = ykm mod p ... (2.7) pasangan a dan b adalah cipherteks untuk blok pesan m. Jadi, ukuran cipherteks dua kali ukuran plainteksnya.
Dekripsi
1. Gunakan kunci privat x untuk mendekripsi a dan b menjadi plainteks m dengan persamaan :
m= b/ax mod p ... (2.8) (ax)-1 = ap-1-x mod p ... (2.9) Keterangan :
x : bilangan acak (x<p) y : kunci publik
m : plainteks a,b : cipherteks[8]
Contoh algoritma ElGamal dengan file citra grayscale 5x5 piksel
17 34 98 112 34
8 45 22 221 12
19 12 123 243 8
45 78 145 123 67
99 124 167 231 54
34 42 176 56 92
Matriks citra asli 5x5 piksel
• Membangkitkan Kunci
o Bangkitkan bilangan acak prima (p=257)
o Pilih dua buah bilangan acak g dan x, g < p (g=2) dan 1≤x≤p-2 ( x=35) o Hitung y=gx mod p ( y = 235 mod 257 = 8 )
o Kunci publik y=8, g=2, p=257 o Kunci privat x=35, p=257
• Enkripsi Citra
o Anggap setiap matriks citra telah disusun dengan sederetan m1, m2, .... o Pilih bilangan acak 1≤k≤p-2 (k= 7)
o Hitung nilai a = gk mod p (a = 27 mod 257 = 128) o Hitung b = ykm mod p (sebanyak m)
30 60 52 243 60
256 155 190 133 127
94 127 81 66 256
155 183 14 81 88
84 113 204 196 186
60 59 235 250 117
Matriks cipher citra 5x5 piksel
o Yang akan di kirimkan adalah cipher a dan cipher-image
• Dekripsi
o Hitung nilai (ax)-1 ((ax)-1 = ap-1-x mod p = 128257-1-35 mod 257 = 249) o Hitung m = b/ax mod p (sebanyak cipher citra)
o Sehingga didapat plain citra
17 34 98 112 34
8 45 22 221 12
19 12 123 243 8
45 78 145 123 67
99 124 167 231 54
Matriks citra hasil 5x5 piksel
2.3 Citra
Citra adalah suatu representasi (gambaran), kemiripan, atau imitasi dari suatu objek.
Citra analog adalah citra yang bersifat kontinu, seperti pada gambar pada monitor
televisi, foto sinar-X, foto yang tercetak di kertas foto, lukisan, pemandangan alam,
hasil CT-Scan, gambar-gambar yang terekam pada pita kaset, dan lain sebagainya. Citra analog tidak dapat dipresentasikan dalam komputer sehingga tidak bisa diproses
di komputer secara langsung. Oleh sebab itu, agar citra ini dapat diproses di komputer,
Namun yang disimpan dalam memori hanyalah angka-angka yang menunjukkan besar
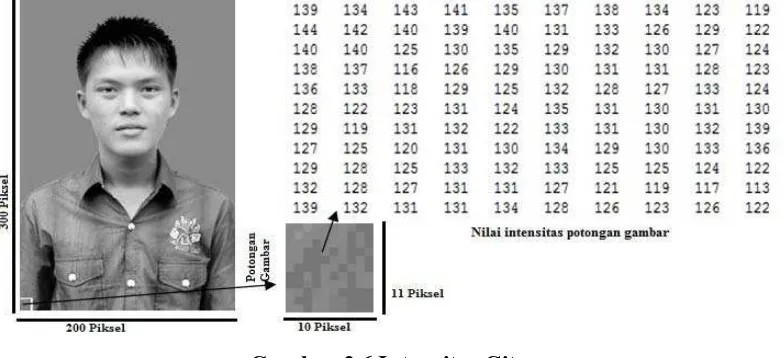
intensitas pada masing-masing pixel tersebut[16]. Berikut contoh citra grayscale 200x300 piksel dengan skala keabuan 256, diambil sebagian dari sudut kiri bawah
sebesar 11x10 piksel
Gambar 2.6 Intensitas Citra
Pada gambar 2.6 terlihat angka-angka yang menunjukkan besar intensitas dari
potongan gambar, dan gambar tersebut mempunyai besar intensitas warna dengan
skala keabuan 8–bit.
2.3.1 Citra Bitmap (*.bmp)
Citra bitmap sering juga disebut sebagai citra raster. Citra yang menyimpan data kode citra secara digital dan lengkap (cara penyimpanannya adalah per piksel). Citra bitmap
dipresentasikan dalam bentuk matriks atau dipetakan dengan menggunakan bilangan
biner atau sistem bilangan lain. Bitmap merupakan media elektronik yang paling tepat
untuk gambar-gambar dengan perpaduan gradiasi warna yang rumit, seperti foto dan
lukisan digital. Citra bitmap biasanya diperoleh dengan cara scanner, camera digital, video capture, dan lain-lain. BMP merupakan format umum untuk menyimpan citra bitmap dikembangkan oleh microsoft [16].
2.3.2 Citra JPEG (*.jpg)
atau layanan online yang lain. Format JPEG mendukung pewarnaan CMYK, RGB, dan grayscale. JPEG menggunakan format 24-bit dan oleh sebab itu informasi semua warna dalam gambar RGB dipertahankan tetapi kompresi ukuran dengan secara selektif menghilangkan data awal warna persepsi manusia. Jika suatu kompresi
dilakukan dengan level tinggi, maka kualitas gambar akan kurang baik, sebaliknya
jika kompresi dilakukan dengan level rendah, maka kualitas gambar akan semakin
tinggi [10]. Suatu jenis kompresi gambar, yaitu JPEG, telah dikembangkan untuk digunakan sebagai alat kompresi yang efisien dan fleksibel. Kompresi gambar JPEG
memiliki empat mode operasi yang dirancang untuk mendukung berbagai aplikasi
gambar diam dan kontinu. Kebanyakan aplikasi menggunakan baseline coder/decoder sekuensial yang sangat efektif dan cukup untuk berbagai aplikasi.
2.4 Mean Squared Error (MSE)
Perbaikan citra pada dasarya merupakan proses yang bersifat subjektif sehingga
parameter keberhasilannya bersifat subjektif pula. Untuk itu perlu adanya alat ukur
kuantitatif yang bisa digunakan untuk mengukur kinerja prosedur perbaikan citra. Alat
ukur ini disebut mean squared error (MSE) yang dinyatakan dengan persamaan sebagai berikut.
��� = ���1 ∑ ∑� (��(�,�)− ��(�,�))2
�=1
�
�=1 ... (2.10)
Keterangan :
M : panjang citra N : lebar citra
��(�,�) : intensitas citra di titik (i,j) sebelum terkena noise (sebelum citra berubah) ��(�,�) : intensitas citra di titik (i,j) setelah noise dihilangkan.
Semakin kecil nilai MSE, semakin bagus prosedur perbaikan citra yang