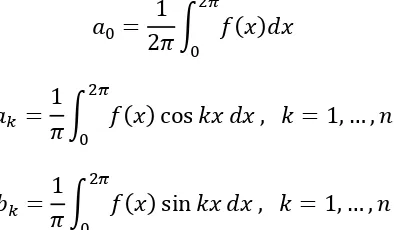Pertemuan 13
Barisan dan Deret Tak Hingga
13.1 Pendahuluan
Kita semua telah mengetahui cara untuk menjumlahkan dua atau beberapa buah bilangan, namun bagaimana cara untuk menjumlahkan sejumlah bilangan tak terhingga belumlah jelas. Pada pertemuan kali ini, kita akan mempelajari teori deret tak hingga. Deret tak hingga terkadang memiliki suatu jumlahan berhingga, terkadang tidak. Terdapat suatu metode penting yang menyatakan suatu fungsi terdiferensiasi ( ) sebagai suatu jumlahan tak hingga atas pangkat dari . Selain itu, kita juga akan memeriksa suatu metode yang dapat merepresentasikan suatu fungsi sebagai jumlahan tak hingga atas fungsi sinus dan cosinus, yang sangat berguna dalam mempelajari fungsi.
13.2 Barisan Tak Hingga Definisi 13.1 Barisan tak hingga
Suatu barisan bilangan tak hingga adalah suatu fungsi yang domainnya merupakan himpunan bilangan bulat positif.
Definisi 13.2 Konvergen, Divergen, Limit
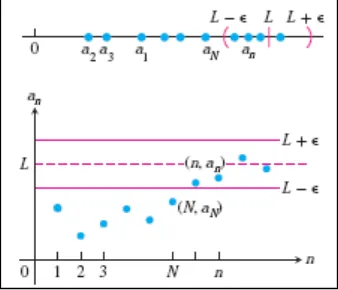
Barisan { } konvergen ke bilangan jika untuk setiap bilangan positif terdapat suatu bilangan bulat sedemikian sehingga untuk seluruh ,
| |
Jika tidak ada bilangan yang memenuhi, maka kita katakan bahwa { } divergen.
Jika { } konvergen ke , kita tulis , atau cukup , dan kita sebut sebagai limit dari barisan (Gambar 13.1).
(Thomas’s Calculus, 11th
ed, p.749) Contoh 13.1 Menerapkan definisi
Tunjukkan bahwa a. b. Jawaban
a. Misal diberikan . Akan ditunjukkan bahwa terdapat suatu bilangan bulat sedemikian sehingga untuk seluruh ,
| |
Hasil ini akan berlaku jika ( ⁄ ) atau ⁄ . Jika merupakan sembarang bilangan bulat lebih besar dari ⁄ , maka hasilnya akan berlaku untuk seluruh . Terbukti.□
b. Misal diberikan . Akan ditunjukkan bahwa terdapat suatu bilangan bulat sedemikian sehingga untuk seluruh ,
| |
Karena , kita dapat menggunakan sembarang bilangan bulat positif dan hasilnya akan berlaku. Terbukti.□
Definisi 13.3 Divergen menuju tak hingga
Barisan { } divergen menuju tak hingga jika untuk setiap bilangan terdapat suatu bilangan bulat sedemikian sehingga untuk seluruh lebih besar dari , . Jika kondisi ini berlaku kita tulis
Demikian pula jika untuk setiap bilangan terdapat suatu bilangan bulat sedemikian sehingga untuk seluruh , , kita katakan { } divergen menuju negatif tak hingga dan ditulis
Suatu barisan juga bisa divergen tanpa menuju tak hingga atau negatif hingga. Misalnya barisan { } { } dan { } juga merupakan contoh barisan yang divergen.
Teorema 13.1 Menghitung limit barisan
1. Aturan Penjumlahan: ( ) 2. Aturan Selisih: ( ) 3. Aturan Perkalian: ( )
4. Aturan Perkalian Konstan: ( ) (sembarang nilai )
5. Aturan Pembagian: jika
Contoh 13.2 Menerapkan teorema 13.1
Dengan mengombinasikan Teorema 13.1 dan limit pada Contoh 13.1, diperoleh: a. ( )
b. ( ) ( ) c.
d.
( ⁄ ) ( ⁄ )
Teorema 13.2 Teorema Sandwich untuk barisan
Misal { } { }, dan { } adalah barisan-barisan bilangan real. Jika berlaku untuk seluruh di bawah suatu indeks , dan jika , maka
.
Teorema 13.3 Teorema fungsi kontinu untuk barisan
Misal { } adalah barisan bilangan real. Jika dan jika adalah suatu fungsi yang kontinu pada dan terdefinisi pada seluruh , maka ( ) ( ).
Teorema 13.4 Menggunakan aturan L’Hopital
Anggap bahwa ( ) adalah sebuah fungsi yang terdefinisi pada seluruh dan bahwa
{ } adalah suatu barisan bilangan real sedemikian sehingga ( ) untuk . Maka
( )
Contoh 13.3 Menerapkan aturan L’Hopital Tunjukkan bahwa
Fungsi terdefinisi untuk seluruh dan berlaku dengan barisan yang diberikan pada bilangan bulat positif. Oleh karenanya, dengan Teorema 13.4, akan sama dengan
jika ada. Dengan menggunakan aturan L’Hopital diperoleh
⁄
Maka dapat disimpulkan bahwa . Terbukti.□
Contoh 13.4 Menerapkan aturan L’Hopital untuk menentukan kekonvergenan Apakah barisan yang suku ke- adalah
( )
konvergen? Jika iya, tentukan . Jawaban
Limitnya mengarah pada bentuk tak tentu . Kita dapat menerapkan aturan L’Hopital jika pertama kita ubah bentuknya menjadi dengan mengambil logaritma natural dari :
( )
( )
Maka,
( )
( ) ⁄
( ⁄ ⁄ ) aturan L’Hopital
Karena dan ( ) kontinu, Teorema 13.4 memberikan
Barisan { } konvergen ke .□
Keenam barisan berikut konvergen ke limitnya masing-masing:
1.
2. √
3. ⁄ ( ) 4. (| | )
5. ( ) ( )
6.
( ) Dalam rumus (3) – (6), tetap saat .
Contoh 13.5 Menerapkan teorema 13.5 a. ( )
b. √ ⁄ ( ⁄ ) ( ) c. √ ⁄ ( ⁄ ) d. ( )
e. ( ) ( ) f.
.□
Definisi 13.4 Barisan tak turun
Sebuah barisan { } dengan sifat bahwa untuk seluruh disebut sebagai barisan tak turun.
Contoh 13.6 Barisan tak turun
a. Barisan dari bilangan asli b. Barisan
c. Barisan konstanta { }.□
Definisi 13.5 Terbatas, batas atas, batas atas terkecil
Sebuah barisan { } terbatas dari atas jika terdapat sebuah bilangan sedemikian sehingga untuk seluruh . Bilangan adalah batas atas untuk { }. Jika adalah batas atas dari { }, tapi tidak ada bilangan kurang dari yang merupakan batas atas untuk { }, maka merupakan batas atas terkecil untuk { }.
Contoh 13.7 Menerapkan definisi
a. Barisan tidak memiliki batas atas. b. Barisan
Tidak ada bilangan kurang dari yang merupakan batas atas dari barisan tersebut, jadi adalah batas atas terkecil barisan tersebut.□
Teorema 13.6 Teorema barisan tak turun
Suatu barisan tak turun dari bilangan real konvergen jika dan hanya jika barisan tersebut terbatas dari atas. Jika suatu barisan tak turun konvergen, barisan tersebut konvergen ke batas atas terkecilnya.
13.3 Deret Tak Hingga
Definisi 13.6 Deret tak hingga, suku ke- , jumlahan parsial, konvergen, jumlahan Untuk suatu barisan bilangan { }, suatu ekspresi dari bentuk
adalah suatu deret tak hingga. Bilangan adalah suku ke- dari deret tersebut. Deret { } didefinisikan oleh
∑
adalah barisan jumlahan parsial dari deret tersebut, bilangan adalah jumlahan parsial ke-. Jika barisan jumlahan parsial tersebut konvergen ke suatu limit , kita katakan bahwa deret tersebut konvergen dan jumlahannya adalah . Dalam kasus ini, kita juga tuliskan
∑
Jika barisan jumlahan parsial dari deret tersebut tidak konvergen, kita katakan deret tersebut divergen.
Deret Geometri
Deret geometri adalah deret dengan bentuk
dimana dan adalah bilangan real tetap dan .
Jika | | , deret geometri konvergen ke ( )⁄ :
∑
| |
Jika | | , deret tersebut divergen.
Contoh 13.8 Indeks mulai dari
Deret geometri dengan ⁄ dan ⁄ adalah
∑ ( )
⁄
( ⁄ )
Contoh 13.9 Bola yang memantul
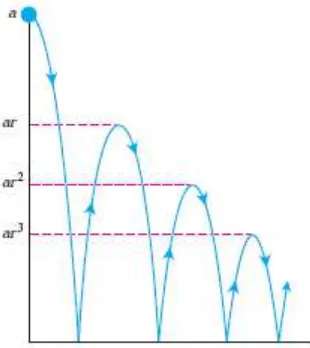
Anda menjatuhkan sebuah bola dari ketinggian meter ke atas permukaan datar. Setiap kali bola menyentuh permukaan tersebut setelah jatuh dengan jarak , bola tersebut memantul sejauh , dimana positif namun kurang dari . Temukan jarak total yang dilalui bola tersebut naik dan turun (Gambar 13.2).
Gambar 13.2 Contoh 13.9 memperlihatkan cara menggunakan deret geometri untuk menghitung total jarak yang ditempuh bola yang memantul jika tinggi tiap pantulan
berkurang sebanyak faktor (Thomas’s Calculus, 11th
ed, p.765) Jawaban
Jarak total yang ditempuh adalah
Jika m dan ⁄ , maka jaraknya adalah
( ( ⁄ )⁄ ) ( ⁄⁄ )
Contoh 13.10 Deret nongeometri namun telescoping Temukan jumlahan dari deret ∑
( )
Jawaban
Kita cari pola dari barisan jumlahan parsial yang mungkin mengarah pada rumus untuk . Perhatikan
( )
jadi
∑
( )
∑ (
)
dan
Sekarang kita melihat bahwa saat . Deret tersebut konvergen, dan jumlahannya adalah :
∑
( )
Deret Divergen
Salah satu alasan bahwa suatu deret tidak konvergen adalah karena sukunya tidak menjadi kecil.
Contoh 13.11 Jumlahan parsial melebihi sembarang bilangan a. Deret
∑
divergen karena jumlahan parsial naik melebihi sembarang bilangan . Setelah , jumlahan parsial lebih besar dari .□
∑
divergen karena jumlahan parsial terus naik untuk setiap bilangan yang ditetapkan. Setiap suku lebih besar dari , sehingga suku lebih besar dari .□
Teorema 13.7
Jika ∑ konvergen, maka .
Uji divergen untuk suku
ke-∑ divergen jika tidak ada atau berbeda dari nol.
Contoh 13.12 Menerapkan uji suku ke-a. ∑ divergen karena b. ∑ divergen karena
c. ∑ ( ) divergen karena ( ) tidak ada d. ∑
divergen karena .□ Teorema 13.8
Jika ∑ dan ∑ merupakan deret konvergen, maka
1. Aturan Penjumlahan: ∑( ) ∑ ∑ 2. Aturan Selisih: ∑( ) ∑ ∑
3. Aturan Perkalian Konstan: ∑ ∑ ( )
Contoh 13.13 Temukan jumlahan deret berikut a. ∑ ∑ ( )
∑ ∑
( ⁄ ) ( ⁄ )
b. ∑ ∑
( ( ⁄ ))
13.4 Uji Integral, Uji Perbandingan, Uji Rasio dan Akar Akibat 13.1 Akibat dari Teorema 13.6
Suatu barisan ∑ dari suku-suku nonnegative konvergen jika dan hanya jika jumlahan parsialnya terbatas dari atas.
Deret
∑
disebut sebagai deret harmonis. Deret ini divergen, namun tidak sesuai dengan uji suku ke-. Suku ke- deret tersebut, , menuju ke nol, tapi deret tersebut tetaplah divergen. Alasannya karena tidak ada batas atas untuk jumlahan parsialnya. Untuk melihat alasannya, kelompokkan suku-suku deret tersebut dengan cara:
( ) ( ) ( )
Jumlahan dua suku pertama adalah . Jumlahan dua suku selanjutnya adalah , lebih besar dari . Jumlahan empat suku selanjutnya adalah yang lebih besar dari . Demikian seterusnya. Jadi umumnya, jumlahan dari suku yang diakhiri dengan ⁄ lebih besar dari ⁄ ⁄ . Barisan jumlahan parsial deret tersebut tidak terbatas dari atas: Jika , jumlahan parsialnya lebih besar dari ⁄ . Dengan demikian, deret harmonis divergen.□
Teorema 13.9 Uji Integral
Misal { } adalah barisan suku-suku positif. Anggap bahwa ( ), dimana adalah fungsi kontinu, positif, dan turun atas untuk seluruh ( suatu bilangan bulat
positif). Maka deret ∑ dan integral ∫ ( ) keduanya konvergen atau keduanya
divergen.
Contoh 13.15 Deret-Tunjukkan bahwa
deret-∑
( suatu konstanta real) konvergen jika dan divergen jika . Jawaban
Jika , maka ( ) ⁄ adalah suatu fungsi turun positif atas . Karena
∫ ∫ [
]
( )
deret tersebut konvergen oleh Uji Integral. Kita tekankan bahwa jumlahan dari deret-bukanlah ( )⁄ . Deret tersebut konvergen, tapi kita tidak tahu nilai deret tersebut konvergen.
Jika , maka dan
∫ ( )
Deret tersebut divergen oleh Uji Integral.
Jika , kita peroleh deret harmonis (divergen)
Deret tersebut konvergen untuk , namun divergen untuk tiap nilai lainnya.□ Contoh 13.16 Deret konvergen
Deret
∑
konvergen oleh Uji Integral. Fungsi ( ) ( ⁄ ) positif, kontinu, dan turun untuk
, dan
∫ [ ]
[ ]
Kembali kita tekankan bahwa ⁄ bukanlah jumlahan dari deret tersebut. Deret tersebut konvergen, namun kita tidak tahu nilai dari jumlahannya.□
Teorema 13.10 Uji Perbandingan
Misal ∑ adalah suatu deret tanpa suku-suku negatif.
a. ∑ konvergen jika terdapat suatu deret konvergen ∑ dengan untuk seluruh
b. ∑ divergen jika terdapat suatu deret divergen atas suku-suku nonnegative ∑ dengan untuk seluruh , untuk suatu bilangan bulat .
Contoh 13.17 Menerapkan Uji Perbandingan a. Deret
∑
divergen karena suku
lebih besar dari suku ke- dari deret harmonis divergen tersebut.□ b. Deret
∑
konvergen karena suku-sukunya semuanya positif dan kurang dari sama dengan suku bersesuaian dari
∑
Deret geometri pada ruas kiri konvergen dan kita peroleh
∑
( ⁄ )
Fakta bahwa adalah batas atas dari jumlahan parsial dari ∑
tidak berarti bahwa deret tersebut konvergen ke .□
Teorema 13.11 Uji Perbandingan Limit
Misalkan bahwa dan untuk seluruh ( suatu bilangan bulat).
1. Jika , maka ∑ dan ∑ keduanya konvergen atau keduanya divergen.
2. Jika
Contoh 13.18 Menerapkan Uji Perbandingan Limit
Manakah diantara deret berikut yang konvergen, dan mana yang divergen? a.
∑ konvergen oleh bagian 1 dari Uji Perbandingan Limit.□
Teorema 13.12 Uji Rasio
Misal ∑ adalah suatu deret dengan suku-suku positif dan anggap bahwa
a. ∑
13.5 Deret Berubah, Absolut dan Kondisional Konvergen Teorema 13.14 Uji Deret Berubah (Teorema Leibniz) Deret
∑( )
konvergen jika ketiga kondisi berikut terpenuhi:
1. Seluruh positif.
2. untuk seluruh , untuk suatu bilangan bulat . 3. .
Contoh 13.21
Deret harmonis berubah
∑( )
memenuhi ketiga syarat dari Teorema 13.14 dengan . Oleh karenanya deret tersebut konvergen.□
Teorema 13.15 Teorema Perkiraan Deret Berubah
Jika deret berubah ∑ ( ) memenuhi ketiga kondisi dari Teorema 13.14, maka untuk ,
( )
memperkirakan jumlahan dari deret tersebut dengan suatu error dimana nilai absolutnya kurang dari , nilai numeris dari suku pertama berikutnya yang tidak digunakan. Lebih lanjut, sisanya, , memiliki tanda yang sama dengan suku pertama berikutnya yang tidak digunakan.
Contoh 13.22
Kita coba terapkan Teorema 13.15 pada suatu deret yang jumlahannya telah kita ketahui:
∑( )
|
Jumlahan dari delapan suku pertama adalah . Jumlahan dari deret tersebut adalah
( ⁄ ) ⁄
Selisihnya, ( ⁄ ) , bernilai positif dan kurang dari
( ⁄ ) .□
Definisi 13.7 Konvergen absolut dan konvergen bersyarat
Suatu deret ∑ konvergen absolut jika deret atas nilai-nilai absolut yang bersesuaian,
Deret aslinya juga konvergen karena deret tersebut konvergen secara absolut.
b. Untuk ∑ , deret nilai absolut yang bersesuaian adalah . Deret aslinya konvergen secara absolut; oleh karenanya deret tersebut konvergen.□ Teorema 13.17 Teorema Pengaturan Ulang untuk Deret Konvergen Absolut
Jika ∑ konvergen absolut, dan merupakan suatu pengaturan dari
Seperti yang kita lihat dalam Contoh 13.23, deret
konvergen secara absolut. Pengaturan kembali yang mungkin untuk suku-suku dari deret tersebut dapat dimulai dengan suatu suku positif, kemudian dua suku negatif, lalu tiga suku positif, empat suku negatif, dan seterusnya: setelah suku ke- dengan salah satu tanda, ambil suku dengan tanda lainnya. Sepuluh suku pertama deret tersebut bisa jadi seperti ini:
Teorema pengaturan kembali menyatakan bahwa kedua deret di atas konvergen ke nilai yang sama. Dalam contoh ini, jika kita mulai dari deret kedua, mungkin kita bisa menukarnya dengan deret pertama jika memang diketahui nilainya. Bahkan kita dapat melakukan yang lebih baik: Jumlahan tiap deret sama dengan
∑( )
∑( )
13.6 Deret Pangkat (Power)
Definisi 13.8 Deret pangkat, center, coefficients
Suatu deret pangkat sekitar adalah suatu deret dengan bentuk
∑
Suatu deret pangkat sekitar adalah suatu deret dengan bentuk
∑ ( )
( ) ( ) ( )
dimana pusat dan koefisien merupakan konstanta.
Contoh 13.25 Suatu deret geometri
Dengan mengambil seluruh koefisien dalam persamaan deret pangkat sekitar di atas, diperoleh deret pangkat geometri
∑
Ini merupakan deret geometri dengan suku pertama dan rasio . Deret ini konvergen ke
( )⁄ untuk | | . Kita ekspresikan dengan menulis
Contoh 13.26 Menguji kekonvergenan menggunakan uji rasio Untuk nilai-nilai apakah deret pangkat berikut konvergen? a. ∑ ( ) Deret ini konvergen absolut untuk seluruh .
c. | | |( ) ( )
| ( )| | kecuali . Deret ini divergen untuk seluruh nilai kecuali .
Teorema 13.18 Teorema Kekonvergenan untuk Deret Pangkat
Jika deret pangkat ∑ konvergen untuk , maka
( ) ∑ ( )
( ) ∑ ( ) ( )
dan seterusnya. Setiap deret turunan ini konvergen ke setiap titik interior dari interval kekonvergenan dari deret aslinya.
Contoh 13.27 Menerapkan turunan suku-per-suku Temukan deret untuk ( ) dan ( ) jika
( )
∑
Jawaban
( ) ( )
∑
( ) ( ) ( )
∑ ( )
Teorema 13.20 Teorema Integral Suku-per-Suku Misalkan bahwa
( ) ∑ ( )
konvergen untuk ( ). Maka
∑ ( )
∫ ( ) ∑ ( )
untuk .
Contoh 13.28 Deret untuk Identifikasi fungsi
( )
Jawaban
Kita turunkan deret asli suku-per-suku dan peroleh
( )
Ini merupakan deret geometri dengan suku pertama dan rasio , jadi
( ) ( )
Sekarang kita dapat mengintegrasikan ( ) ( ⁄ ) untuk memperoleh
∫ ( ) ∫
Deret untuk ( ) adalah nol saat , jadi . Dengan demikian,
( )
Teorema 13.21 Teorema Perkalian Deret untuk Deret Pangkat
Jika ( ) ∑ dan ( ) ∑ konvergen absolut untuk | | , dan
∑
maka ∑ konvergen absolut ke ( ) ( ) untuk | | :
(∑
) (∑
) ∑
Contoh 13.29
∑
untuk | |
dengan dirinya sendiri untuk memperoleh suatu deret pangkat untuk ( )⁄ , untuk
| | . Jawaban Misalkan
( ) ∑
( )⁄
( ) ∑
( )⁄
dan
Maka, dengan Teorema Perkalian Deret
( ) ( ) ∑
∑( )
( )
adalah deret untuk ( )⁄ . Deret tersebut seluruhnya konvergen absolut untuk | | .
Perhatikan bahwa Contoh 13.27 memberikan jawaban yang sama karena
( ) ( )
13.7 Deret Taylor dan Maclaurin
Definisi 13.9 Deret Taylor, Deret Maclaurin
∑ ( ) ( )( )
( ) ( )( ) ( )( ) ( ) ( )( )
Deret Maclaurin dibangun oleh adalah
∑ ( ) ( )
( ) ( ) ( ) ( ) ( )
deret Taylor yang dibangun dengan pada .
Contoh 13.30 Mencari deret Taylor
Temukan deret Taylor yang dibangun oleh ( ) ⁄ pada . Dimana, jika ada, deret tersebut konvergen ke ⁄ ?
Jawaban
Kita harus menemukan ( ) ( ) ( ) Dengan mengambil turunan kita peroleh
( ) ( )
( ) ( ) ( ) ( )
( ) ( )
( )( ) ( ) ( ) ( )( )
( )
Deret Taylor-nya adalah
( ) ( )( ) ( )( ) ( ) ( )( )
( ) ( )
( ) ( )
Ini merupakan deret geometri dengan suku pertama ⁄ dan rasio ( ) ⁄ . Deret ini konvergen absolut untuk | | dan jumlahannya adalah
⁄
Dalam contoh ini deret Taylor dibangun oleh ( ) ⁄ pada konvergen ke ⁄ untuk | | atau .□
Definisi 13.10 Polinomial Taylor dengan order
Misalkan adalah suatu fungsi dengan turunan tingkat untuk dalam beberapa interval yang mengandung sebagai suatu titik interior. Maka untuk sembarang bilangan bulat dari hingga , polinomial Taylor order dibangun oleh pada adalah polinomial
( ) ( ) ( )( ) ( )( ) ( ) ( )( )
( )( )
( )
Contoh 13.31 Mencari polinomial Taylor untuk
Temukan deret Taylor dan polinomial Taylor yang dibangun oleh ( ) pada . Jawaban
Cosinus dan turunannya adalah
( ) ( )
( ) ( )( )
( )( ) ( ) ( )( ) ( ) Pada , cosinus adalah dan sinus adalah , jadi
( )( ) ( ) ( )( ) . Deret Taylor dibangun oleh pada adalah
( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ∑ ( )( )
Ini juga merupakan deret Maclaurin untuk .
Karena ( )( ) , polinomial Taylor dari order dan sama:
( ) ( ) ( )
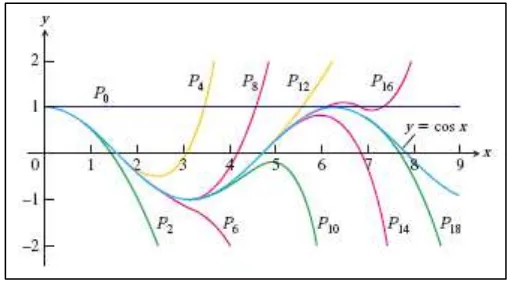
Gambar 13.3 memperlihatkan seberapa baik polinomial ini memperkirakan ( ) di dekat . Hanya bagian tangan kanan dari grafik ditampilkan karena grafik tersebut simetri terhadap sumbu- .□
Gambar 13.3 Polinomial ( ) ∑ ( ) ( )
konvergen ke sebagai . (Thomas’s Calculus, 11th
ed, p.809) Teorema 13.22 Teorema Taylor
Jika dan turunan pertamanya ( ) kontinu pada interval tertutup antara
dan , dan ( ) terdiferensiabel pada interval terbuka diantara dan , maka terdapat suatu bilangan antara dan sedemikian sehingga
( ) ( ) ( )( ) ( )( ) ( ) ( )( )
( )( )
( ) ( )
Rumus Taylor
Jika memiliki turunan untuk seluruh tingkat dalam suatu interval terbuka yang mengandung , maka untuk setiap bilangan bulat positif dan untuk setiap dalam ,
( ) ( ) ( )( ) ( )( ) ( )( )
( ) ( )
dimana
( ) ( ) ( )( )( )
Teorema 13.23 Teorema Perkiraan Sisa
| ( )| | |( )
Jika kondisi ini berlaku untuk setiap dan kondisi lainnya dari Teorema Taylor dipenuhi oleh , maka deret tersebut konvergen ke ( ).
Contoh 13.32 Deret Taylor untuk pada
Tunjukkan bahwa deret Taylor untuk pada konvergen ke untuk setiap nilai dari .
Jawaban
Kita tambahkan suku sisanya ke polinomial Taylor untuk (Contoh 13.31) untuk memperoleh rumus Taylor untuk dengan :
( ) ( ) ( )
Karena turunan dari cosinus memiliki nilai absolut kurang dari sama dengan , Teorema Perkiraan Sisa dengan memberikan
| ( )| | |
( )
Untuk setiap nilai dari , saat . Oleh karenanya, deret tersebut konvergen ke
untuk setiap nilai dari . Jadi,
∑( )( )
Contoh 13.33 Menemukan deret Taylor dengan substitusi Temukan deret Taylor untuk pada .
Jawaban
Kita dapat menemukan deret Taylor untuk dengan substitusi untuk dalam deret Taylor untuk :
∑( )( ) ( )
( ) ( ) ( )
Persamaan dari Contoh 13.32 sebelumnya berlaku untuk , menyiratkan bahwa juga berlaku untuk , jadi deret yang baru dibentuk di atas konvergen untuk seluruh .□
Contoh 13.34 Menemukan deret Taylor dengan perkalian Temukan deret Taylor untuk pada .
Jawaban
Kita dapat menemukan deret Taylor untuk dengan mengalikan deret Taylor untuk
(Contoh 13.32) dengan :
( )
Deret yang baru konvergen untuk seluruh karena deret untuk konvergen untuk seluruh .□
Definisi 13.11 Identitas Euler
Untuk setiap bilangan real , .
Deret Binomial Untuk ,
( ) ∑ ( )
dimana kita definisikan
( ) ( ) ( )
dan
( ) ( )( ) ( )
Contoh 13.35 Menggunakan deret Binomial Jika ,
dan
( ) ( )( ) ( ) ( ) ( ) ( )
Dengan nilai-nilai koefisien ini dan dengan diganti oleh , rumus deret Binomial menghasilkan deret geometri
( ) ∑( )
( )
Gambar 13.4 Beberapa deret Taylor yang umum dijumpai (Thomas’s Calculus, 11th
ed, p.831) 13.8 Deret Fourier
Diperkenalkan oleh Joseph Fourier, metode ini memperkirakan fungsi dengan jumlahan dari fungsi-fungsi sinus dan cosinus.
Beberapa persamaan yang perlu dicari adalah nilai-nilai koefisien deret Fourier sebagai berikut:
∫ ( )
∫ ( )
∫ ( )
Kondisi yang perlu dipenuhi untuk menemukan koefisien-koefisien di atas hanyalah bahwa integralnya harus ada. Jika kita anggap dan gunakan aturan ini untuk memperoleh koefisien-koefisien dari suatu deret tak hingga, maka hasil jumlahannya disebut sebagai deret Fourier untuk ( ),
∑( )
Contoh 13.36 Menemukan perluasan deret Fourier
Deret Fourier dapat digunakan untuk merepresentasikan beberapa fungsi yang tidak dapat direpresentasikan oleh deret Taylor, seperti fungsi tangga yang diperlihatkan pada Gambar 13.5 berikut.
( ) {
Gambar 13.5 (a) Fungsi tangga Contoh 13.36, (b) Grafik dari deret Fourier untuk adalah periodik dan memiliki nilai ⁄ pada tiap titik diskontinu
(Thomas’s Calculus, 11th
Koefisien dari deret Fourier dapat dihitung menggunakan persamaan-persamaan deret Fourier:
∫ ( )
(∫ ∫
)
∫ ( )
(∫ ∫ )
([ ] [ ] )
∫ ( )
(∫ ∫ )
([ ] [ ] )
( )
Jadi
dan
Deret Fourier-nya adalah
(
)
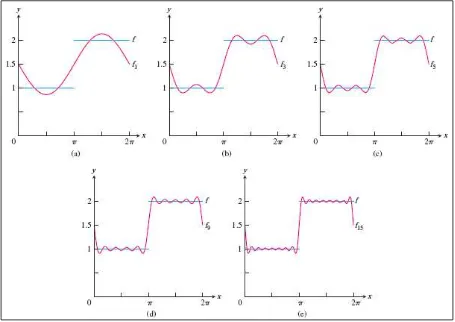
tiap titik ini memiliki nilai ⁄ , nilai rata-rata dari limit satu-sisi dari tiap sisi. Kekonvergenan dari deret Fourier dari dapat dilihat pada Gambar 13.6 berikut.□
Gambar 13.6 Perkiraan fungsi Fourier , dan dari fungsi
( ) {
(Thomas’s Calculus, 11th