PERBANDINGAN CAPITAL ASSET PRICING MODEL (CAPM) DAN THREE FACT ORS MODEL FAMA AND FRENCH (T FMFF) DALAM MENGEST IMASI RET URN SAHAM.

(1)

OPEN JOURNAL SYSTEMS Journal Help

USER Username Password

Remember me

Log In

NOTIFICATIONS

View

Subscribe / Unsubscribe

JOURNAL CONTENT Search

All

Search

Browse

By Issue By Author

E - J u r n a l M a t e m a t i k a

E-Jurnal Matematika http://ojs.unud.ac.id/index.php/mtk/index

(2)

By Title

Other Journals

FONT SIZE

INFORMATION For Readers For Authors For Librarians

HOME ABOUT LOG IN REGISTER SEARCH CURRENT ARCHIVES EDITORIAL

TEAM CONTACT

Home

>

Vol 4, No 4 (2015)

E-Jurnal Matematika merupakan salah satu jurnal elektronik yang ada di Universitas Udayana, sebagai media komunikasi

antar peminat di bidang ilmu matematika dan terapannya, seperti statistika, matematika finansial, pengajaran matematika dan terapan matematika dibidang ilmu lainnya. Jurnal ini lahir sebagai salah satu bentuk nyata peran serta jurusan

Matematika FMIPA UNUD guna mendukung percepatan tercapainya target mutu UNUD, selain itu jurnal ini terbit didorong oleh surat edaran Dirjen DIKTI tentang syarat publikasi karya ilmiah bagi program Sarjana di Jurnal Ilmiah. E-jurnal Matematika

juga menerima hasil-hasil penelitian yang tidak secara langsung berkaitan dengan tugas akhir mahasiswa meliputi penelitian

(3)

atau artikel yang merupakan kajian keilmuan.

(4)

KLASIFIKASI KARAKTERISTIK KECELAKAAN LALU LINTAS DI KOTA DENPASAR DENGAN PENDEKATAN

CLASSIFICATION AND REGRESSION TREES (CART)

PDF

I GEDE AGUS JIWADIANA, I KOMANG GDE SUKARSA, I GUSTI AYU MADE SRINADI 146-151

MENENTUKAN FORMULA PREMI TAHUNAN TIDAK KONSTAN PADA ASURANSI JOINT LIFE PDF

I GEDE BAGUS PASEK SUBADRA, I NYOMAN WIDANA, DESAK PUTU EKA

NILAKUSMAWATI

152-157

OPTIMALISASI PENJUALAN KAIN ENDEK DENGAN METODE KARUSH-KUHN-TUCKER (KKT) PDF

I GEDE ARIS JANOVA PUTRA, NI MADE ASIH, I NYOMAN WIDANA 158-162

METODE QUEST DAN CHAID PADA KLASIFIKASI KARAKTERISTIK NASABAH KREDIT PDF

NUR FAIZA, I WAYAN SUMARJAYA, I GUSTI AYU MADE SRINADI 163-168

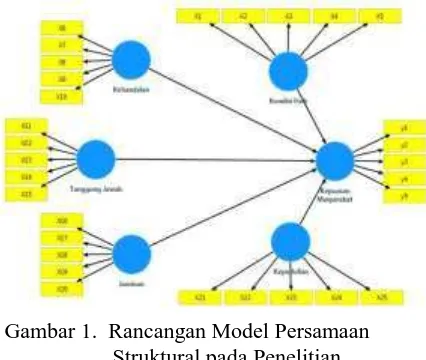
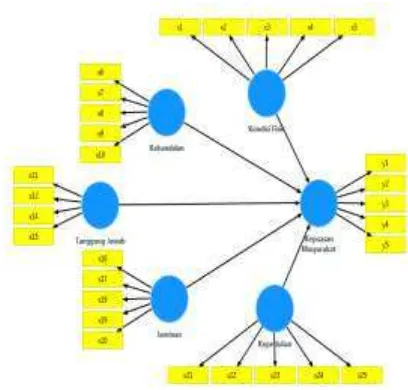
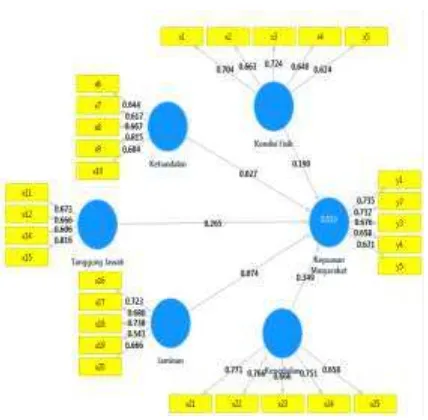
MODEL PERSAMAAN STRUKTURAL TINGKAT KEPUASAN MASYARAKAT TERHADAP KUALITAS PELAYANAN

JALAN TOL BALI MANDARA

PDF

I PUTU AGUS WIDHIANTARA, I KOMANG GDE SUKARSA, I PUTU EKA N. KENCANA 169-175

ESTIMASI MODEL REGRESI SEMIPARAMETRIK MENGGUNAKAN ESTIMATOR KERNEL UNIFORM (Studi

Kasus: Pasien DBD di RS Puri Raharja)

PDF

ANNA FITRIANI, I GUSTI AYU MADE SRINADI, MADE SUSILAWATI 176-180

(5)

PERBANDINGAN CAPITAL ASSET PRICING MODEL (CAPM) DAN THREE FACTORS MODEL FAMA AND

FRENCH (TFMFF) DALAM MENGESTIMASI RETURN SAHAM

PDF

KADEK MIRA PITRIYANTI, KOMANG DHARMAWAN, G.K. GANDHIADI 181-187

ESTIMASI NILAI CONDITIONAL VALUE AT RISK MENGGUNAKAN FUNGSI GAUSSIAN COPULA PDF

HERLINA HIDAYATI, KOMANG DHARMAWAN, I WAYAN SUMARJAYA 188-194

MENENTUKAN PREMI TAHUNAN UNTUK TIGA ORANG PADA ASURANSI JIWA HIDUP GABUNGAN (JOINT

LIFE)

PDF

TRI YANA BHUANA, I NYOMAN WIDANA, LUH PUTU IDA HARINI 195-200

OPTIMALISASI PERENCANAAN PRODUKSI DENGAN PREEMPTIVE GOAL PROGRAMMING (STUDI KASUS: UD.

DODOL MADE MERTA TEJAKULA, SINGARAJA)

PDF

NI PUTU DEVIYANTI, NI KETUT TARI TASTRAWATI, I WAYAN SUMARJAYA 201-207

This work is licensed under a Creative Commons Attribution 4.0 International License. ISSN: 2303-1751

(6)

OPEN JOURNAL SYSTEMS

Journal Help

USER

Username Password

Remember me

Log In

NOTIFICATIONS

View

Subscribe / Unsubscribe

JOURNAL CONTENT

Search

All

Search

Browse

By Issue By Author By Title Other Journals

E - J u r n a l M a t e m a t i k a

(7)

FONT SIZE

INFORMATION

For Readers For Authors For Librarians

HOME ABOUT LOG IN REGISTER SEARCH CURRENT ARCHIVES EDITORIAL

TEAM CONTACT

Home > About the Journal > Editorial Team

Desak Putu Eka Nilakusumawati, Jurusan Matematika, Fakultas MIPA, Universitas Udayana, Indonesia

I Made Eka Dwipayana, Jurusan Matematika, Fakultas MIPA, Universitas Udayana, Bali-Indonesia

Dr. Tjokorda Bagus Oka, Jurusan Matematika, Fakultas MIPA, Universitas Udayana, Bali-Indonesia

Dr. Komang Dharmawan, Jurusan Matematika, Fakultas MIPA, Universitas Udayana, Bali-Indonesia

Drs. GK Gandhiadi, Jurusan Matematika, Fakultas MIPA, Universitas Udayana, Bali-Indonesia

Ir. I Komang Gde Sukarsa, Jurusan Matematika, Fakultas MIPA, Universitas Udayana, Bali-Indonesia

Editorial Team http://ojs.unud.ac.id/index.php/mtk/about/editorialTeam

(8)

Ir. I Putu Eka Nila Kencana, Jurusan Matematika, Fakultas MIPA, Universitas Udayana, Bali-Indonesia

I Gusti Ayu Made Srinadi, Jurusan Matematika, Fakultas MIPA, Universitas Udayana, Bali-Indonesia

Made Susilawati, Jurusan Matematika, Fakultas MIPA, Universitas Udayana, Bali-Indonesia

This work is licensed under a Creative Commons Attribution 4.0 International License. ISSN: 2303-1751

(9)

E-Jurnal Matematika Vol. 4 (4), November 2015, pp. 146-151 ISSN: 2303-1751

146

KLASIFIKASI KARAKTERISTIK KECELAKAAN LALU LINTAS DI

KOTA DENPASAR DENGAN PENDEKATAN

CLASSIFICATION AND

REGRESSION TREES

(CART)

I Gede Agus Jiwadiana§1,IKomang Gde Sukarsa2, I Gusti Ayu Made Srinadi3

1

Jurusan Matematika, Fakultas MIPA - Universitas Udayana [Email: [email protected]]

2_{Jurusan Matematika, Fakultas MIPA - Universitas Udayana [Email: [email protected]]}

3_{Jurusan Matematika, Fakultas MIPA - Universitas Udayana [Email: [email protected]]}

§

Corresponding Author

ABSTRACT

The aim of this research is to determine the classification characteristics of traffic accidents in Denpasar city in January-July 2014 by using Classification And Regression Trees (CART). Then, for determine the explanatory variables into the main classifier of CART. The result showed that optimum CART generate three terminal node. First terminal node, there are 12 people were classified as heavy traffic accident characteritics with single accident, and second terminal nodes, there are 68 people were classified as minor traffic accident characteristics by type of traffic accident rear, front-front, front-side, pedestrians, side-side and location of traffic accident in district road and sub-district road. For third terminal node, there are 291 people were classified as medium traffic accident characteristics by type of traffic accident front-rear, front-front, front-side, pedestrians, side-side and location of traffic accident in municipality road and explanatory variables into the main splitter to make of CART is type of traffic accident with maximum homogeneity measure of 0.03252.

Keywords: CART, traffic accident, terminal node

1. PENDAHULUAN

Umumnya masalah klasifikasi diselesaikan dengan menggunakan metode regresi logistik dan analisis diskriminan (Lusyanti [1]). Analisis diskriminan memerlukan asumsi multivariate normal dan varians kovarians sama, sedangkan metode regresi logistik tidak memerlukan kedua asumsi tersebut. Metode ini memerlukan data yang lengkap, dan sensitif terhadap outlier.

Salah satu metode alternatif masalah klasifikasi yang lebih longgar atau tidak terikat oleh asumsi-asumsi dan tidak berbentuk

probabilitas adalah metode klasifikasi

berstruktur pohon yang diperkenalkan oleh Breimen, L., Friedmen, J., Olshen, R., dan

Stone, C. pada tahun 1984 yaitu Classification

and Regression Trees (CART). Metode CART

merupakan alat yang digunakan dalam

eksplorasi data nonparametrik yang dapat

digunakan untuk melihat hubungan antara variabel terikat dengan variabel bebas yang berukuran besar dan kompleks (Pratiwi dan Zain [2]). Variabel bersifat kompleks dapat berupa dimensinya yang besar atau jenis variabel bebasnya campuran, misalnya kontinu dan kategorik, baik nominal maupun ordinal. Jika variabel terikatnyanya berupa variabel kontinu maka akan diperoleh model pohon regresi, jika variabel terikatnyanya kategorik maka akan diperoleh model pohon klasifikasi.

Model CART dikenal karena kesederhanaan dan efisiensi ketika berhadapan dengan kasus yang jumlah datanya besar. CART diperoleh menggunakan pembagian cepat yang secara rekursif mempartisi data menjadi sub yang lebih kecil.

(10)

Jiwadiana, I G.A., Sukarsa, I K.G., Srinadi, I G.A.M. Klasifikasi Karakteristik Kecelakaan Lalu Lintas…

menerapkan metode CART dalam bidang kesehatan yaitu memprediksi berat badan bayi lahir. Penelitian ini menghasilkan model pohon regresi karena variabel terikatnyanya bersifat kontinu. Pratiwi dan Zain [2] meneliti tentang klasifikasi pengangguran terbuka menggunakan CART di Provinsi Sulawesi Utara.

Salah satu kasus yang terkait dengan metode CART adalah karakteristik kecelakaan lalu lintas. Pihak kepolisian telah mengumpulkan data kecelakaan lalu lintas setiap harinya sehingga menghasilkan data dalam jumlah yang besar untuk setiap bulannya. Data tersebut berupa data bertipe kategorik. Penelitian tentang kecelakaan lalu lintas pernah dilakukan oleh Afidah [3]. Masalah yang muncul dalam

kecelakaan lalu lintas ini adalah pada

karakteristik kecelakaan lalu lintas. Karakteristik kecelakaan lalu lintas ini dibagi menjadi tiga kelompok yaitu ringan, sedang, dan berat. Ketiga kelompok tersebut dipengaruhi oleh empat faktor yaitu faktor manusia, kendaraan, jalan, dan alam (lingkungan) (Afidah [3]). Perlu cara untuk mengetahui faktor-faktor apakah

yang dapat memengaruhi karakteristik

kecelakaan lalu lintas tersebut, sehingga pihak kepolisian dapat mengambil tindakan yang dapat mengurangi kondisi korban. Penelitian tentang kecelakaan lalu lintas pernah dilakukan oleh Afidah [3], meneliti pola tingkat keparahan korban lalu lintas dengan menggunakan regresi logistik multinomial.

Permasalahan dalam penelitian adalah bagaimana klasifikasi karakteristik dan variabel apa yang mejadi pemilah utama dalam penentuan klasifikasi karakteristik kecelakaan lalu lintas di Kota Denpasar dari bulan Januari sampai Juli 2014?

Tujuan penelitian adalah untuk mengetahui klasifikasi karakteristik dan variabel yang

mejadi pemilah utama dalam penentuan

klasifikasi karakteristik kecelakaan lalu lintas di Kota Denpasar dari bulan Januari sampai Juli 2014.

2. METODE PENELITIAN

Penelitian ini menggunakan data sekunder yang diperoleh dari POLRESTA (Kepolisian Resor Kota) tentang data Kecelakaan Lalu Lintas di Kota Denpasar dari bulan Januari sampai bulan Juli 2014.

Gambaran umum variabel terikat dan variabel bebas dalam penelitian dapat dilihat pada Tabel 1.

Tabel 1. Gambaran Umum Variabel Terikat dan Variabel Bebas

Penelitian ini dilaksanakan dengan metode studi kasus, yaitu dilakukan dengan menerapkan

teori untuk menganalisis data dengan

menggunakan program CART Pro EX V6.0.

No Peubah Jenis Kategori

1 Karakteristik

kecelakaan lalu lintas

(variabel terikat)

Diskrit 1. Ringan

2. Sedang

3. Berat

2 Jenis

kecelakaan lalu lintas

(variabel bebas)

Diskrit 1. Tunggal

2.

Samping-samping

3. Depan-samping

4. Depan-depan

5. Depan-belakang

6. Pejalan kaki

3 Waktu

(variabel bebas)

Diskrit 1. Lalu lintas padat (antara pukul

06.00 WITA –

08.00 WITA, antara pukul

12.00 WITA –

13.30 WITA, antara pukul

16.00 WITA –

18.00 WITA) 2. Lalu lintas sepi

(selain waktu padat)

4 Lokasi Status

jalan (variabel bebas)

Diskrit 1. Nasional

2. Provinsi

3. Kabupaten

4. Kodya

5. Kecamatan

5 Jenis kelamin

(variabel bebas)

Diskrit 1. Laki-laki

2. Perempuan

6 Umur(variabel

bebas)

(11)

148

Langkah-langkah yang dilakukan dalam

penelitian ini adalah:

1) Penentuan pemilah dan pemilahan secara

rekursif pada simpul dengan menggunakan pemilah Indeks Gini yaitu:

 



   





i j t | i p t | j p t i

dengan i

 

t adalah nilai indeks gini,

 

j|t

p adalah proporsi kelas j pada simpul

t, dan p

 

i|t adalah proporsi kelas i pada

simpul t (Timofeev [4]). Penetapan sebuah

simpul sebagai simpul terminal, jika banyak data pada simpul tersebut kurang atau sama dengan 5.

2) Penandaan label kelas simpul yang

ditentukan berdasarkan jumlah kelas

terbanyak pada simpul.

3) Pemangkasan CART yang dilakukan untuk

mendapatkan pohon yang minimum dengan menggunakan persamaan berikut:

   

T RT T

R_







dengan R

 

T adalah Resubtitution Estimate

(Proporsi kesalahan pada sub pohon T,



adalah kompleksitas parameter, dan T

adalah jumlah simpul terminal pada pohon T (Breimen [5]).

4) Pemilihan CART optimal dengan

menggunakan Cross Validation V-Fold

Estimate.Amatan dalam L dibagi menjadi V bagian yang saling lepas dengan ukuran kurang lebih sama besar ditiap kelasnya. Learning sample ke-v dengan v= 1,2,...,V

digunakan untuk membentuk pohon

T

_k v .

Misal d v

 

x adalah hasil

pengklasifikasian, maka penduga sampel uji untuk

R

ts

 

T

_k v adalah:

 



 















v n n,j L x n n v v v k ts j x d X N 1 T R

Dengan menggunakan amatan induk L untuk

membentuk deretan pohon

 

T_k , maka

penduga validasi silang lipat V untuk

T

_k v

adalah:

 



 

    V 1 v v k ts k cv T R V 1 T R

Pohon klasifikasi optimum dipilih T_k*

dengan

 

cv

 

_k

k k cv

T

R

min

*

T

R



.

3 HASIL DAN PEMBAHASAN

Objek orang pada penelitian ini adalah data kecelakaan lalu lintas di Kota Denpasar dari Bulan Januari sampai Bulan Juli 2014. Variabel terikat pada penelitian ini adalah karakteristik kecelakaan lalu lintas, sedangkan variabel bebasnya adalah jenis laka (kecelakaan lalu lintas), waktu, lokasi laka, jenis kelamin, dan umur. Dari 371 data kecelakaan lalu lintas di Kota Denpasar selama tahun 2014, diperoleh gambaran karakteristik kecelakaan lalu lintas yaitu kecelakaan ringan 24% atau 87 orang, kecelakaan sedang sebesar 53% atau 198 orang, dan kecelakaan berat sebesar 23% atau 86 orang.

3.1 Pembentukan CART Awal

CART awal dibentuk dengan menggunakan metode pemilahan Indeks Gini. Metode ini memisahkan kelas yang anggota kelasnya terbesar lebih dahulu atau yang merupakan kelas terpenting dalam simpul tersebut. Berikut ini, diberikan kemungkinan pemilah pada masing-masing variabel bebas:

1) Jenis laka

 

x dengan 6 kategori nominal, ₁

kemungkinan pemilah 261131

2) Waktu

 

x dengan 2 kategori nominal, ₂

mempunyai kemungkinan pemilah

1

2

21





3) Lokasi status jalan

 

x₃ dengan 5 kategori nominal, mempunyai kemungkinan pemilah

15 1 251 

4) Jenis kelamin

 

x4 dengan 2 kategori

nominal, mempunyai kemungkinan pemilah

1

2

21





Umur

 

x₅ merupakan data kontinu. Dari 371

orang, terdapat n nilai amatan berbeda, maka

terdapat n-1 kemungkinan pemilah.

(12)

sebagai pemilah pertama dalam pembentukan pohon. Dari lima variabel bebas, pemilahan

pertama kali dilakukan terhadap simpul

akar/utama yang didasarkan pada jenis laka dengan nilai indeks gini 0,03252. Nilai indeks gini masing-masing variabel ditampilkan dalam Tabel 2.

Tabel 2. Nilai Indeks Gini

Peubah jenis laka terpilih sebagai pemilah utama karena memberikan nilai indeks gini tertinggi dari variabel lain. Dengan kata lain bahwa, variabel bebas jenis laka merupakan peubah utama yang berperan penting dalam pembentukan CART.

Pemilahan ini memisahkan simpul utama menjadi kelompok jenis kecelakaan depan-belakang, depan-depan, depan-samping, pejalan-kaki, samping-samping, dan kelompok jenis kecelakaan tunggal. Hasil pemilahan pada simpul ini, jumlah objek sebelah kiri sebanyak 359 orang dan sebelah kanan sebanyak 12 orang. Dari 359 orang tersebut, terdapat karakteristik kecelakaan berat sebesar 74 orang, kecelakaan ringan 87 orang, dan kecelakaan sedang 198

orang. Sedangkan dari 12 orang pada simpul kanan tersebut hanya terdapat 12 orang dengan karakteristik kecelakaan berat. Selanjutnya simpul dua dipilah berdasarkan lokasi laka, dan seterusnya muncul variabel-variabel bebas jenis kelamin, umur, dan waktu laka. Secara umum semua variabel bebas muncul sebagai pemilah.

Penghentian pembentukan CART dilakukan ketika banyaknya amatan pada simpul kurang dari 5 atau dalam simpul terdapat amatan yang homogen. Maka didapatkan CART awal dengan 42 simpul terminal.

3.2 Pemangkasan Pohon

Hasil dari pembentukan CART dengan metode pemilahan Indeks Gini berukuran sangat besar yaitu 42 simpul. Ukuran pohon yang besar

ini dapat menimbulkan overfitting. Untuk

mengatasinya maka dicari pohon dugaan yang yang layak dengan memangkas pohon tersebut.

Pemangkasan CART merupakan suatu upaya untuk menentukan ukuran CART yang terbaik bagi CART yang terbentuk. Proses

pemangkasan pohon dilakukan apabila

memenuhi persamaanR

 

t R

   

t_left Rt_{r ight} , maka t_{r ig h t} dan t_left dipangkas. Berdasarkan perhitungan program yang digunakan diperoleh 18 sub pohon yang dihasilkan dari proses pemangkasan.

Setelah CART dipangkas, ditentukan CART

optimum menggunakan penduga silang lipat V

(Cross Validation V-Fold Estimate). CART

optimum didapatkan berdasarkan nilai Rcv

minimum yaitu 0,83540+/-0,03440 atau

0,80100≤ cv

R ≤0,86980 dengan parameter

kompleksitas





0,020682. Berdasarkan

kriteria ini, didapatkan CART optimum dengan tiga simpul akhir. Letak pemangkasan CART tersebut dapat dilihat pada Tabel 3.

Variabel

bebas Pemisah

Indeks gini

N kiri

N kanan

1 Jenis Laka

depan-belakang, 0,03252 359 12

depan-depan,

depan-samping,

pejalan kaki,

samping-samping

2 Lokasi Laka

Jalan

Kabupaten, 0,02304 277 94

Jalan

Kecamatan,

Jalan Kodya

3 Jenis

Kelamin Perempuan 0,01267 123 248

4 Umur 39.50000 0,00566 270 101

(13)

150

Tabel 3. Letak Pemangkasan CART

Pohon Jumlah simpul

terminal

Cross-Validated Relative Cost (biaya kesalahan)

Resubtitution Relative Cost (penduga pengganti)

komplesitas parameter

1 42 0,91886 +/- 0,04079 0,48357 0,000000

11 15 0,87560 +/- 0,04126 0,59757 0,005648

12 14 0,89038 +/- 0,04101 0,60893 0,007584

13 13 0,89474 +/- 0,04107 0,62069 0,007851

14 9 0,85753 +/- 0,04151 0,67477 0,009023

15 8 0,85646 +/- 0,04143 0,68998 0,010150

16 7 0,85240 +/- 0,04070 0,71065 0,013791

17 6 0,85310 +/- 0,04058 0,73220 0,014379

18 5 0,84997 +/- 0,03953 0,75824 0,017367

19** 3 0,83540 +/- 0,03440 0,82025 0,020682

20 1 1,00000 +/- 0,00003 1,00000 0,059926

Berdasarkan Rcv minimum sebesar

0,83540+/-0,03440 diperoleh CART optimum dari proses pemangkasan dengan simpul-simpul terminal yang dihasilkan dan digambarkan pada Gambar 1.

Gambar 1. CART Optimum dengan Tiga Simpul Terminal

Dalam proses pemangkasan berdasarkan

cv

R minimum, didapatkan CART dengan tiga

simpul terminal. Dengan peubah yang masuk dalam CART tersebut adalah jenis laka dan lokasi laka. Jenis laka menjadi pemilah utama dalam pembentukan CART. Ketiga simpul terminal yang dihasilkan dapat diuraikan sebagai berikut:

1. Simpul terminal pertama, terdiri dari 12

orang yang dikelompokkan sebagai

karakteristik kecelakaan lalu lintas berat dengan jenis laka tunggal.

2. Simpul terminal kedua, terdiri dari 68

karakteristik kecelakaan lalu lintas ringan dengan jenis laka belakang, depan-depan, depan-samping, pejalan kaki, samping-samping dan lokasi laka jalan Kabupaten, jalan Kecamatan.

3. Simpul terminal ketiga, terdiri dari 291

karakteristik kecelakaan lalu lintas sedang dengan jenis laka belakang, depan-depan, depan-samping, pejalan kaki, samping-samping dan lokasi laka jalan Kodya.

4. KESIMPULAN

Berdasarkan hasil dan pembahasan dapat disimpulkan bahwa CART optimum yang terbentuk menghasilkan tiga simpul terminal yaitu simpul terminal pertama, terdiri dari 12 orang yang dikelompokkan sebagai karakteristik kecelakaan lalu lintas berat dengan jenis laka tunggal, simpul terminal kedua, terdiri dari 68 orang yang dikelompokkan sebagai karakteristik kecelakaan lalu lintas ringan dengan jenis laka depan-belakang, depan-depan, depan-samping, pejalan kaki, samping-samping dan lokasi laka jalan Kabupaten, jalan Kecamatan, serta Simpul

Node 1 Kelas = sedang

N = 371

N = 359 Node 3

Kelas = berat N = 12

Node 1 Kelas = ringan

N = 68

(14)

terminal ketiga, terdiri dari 291 orang yang dikelompokkan sebagai karakteristik kecelakaan lalu lintas sedang dengan jenis laka depan-belakang, depan-depan, depan-samping, pejalan kaki, samping-samping dan lokasi laka jalan kodya dan variabel bebas yang menjadi pemilah utama dalam pembentukan CART adalah jenis laka dengan nilai indeks gini 0,03252.

Daftar Pustaka

[1] Lusyanti, Merlina. 2010. Perbandingan Metode Regresi Logistik Dengan Metode Pohon Klasifikasi Pada Data Polikotomus

(Studi Kasus Pada Faktor Yang

Berpengaruh Terhadap Keberhasilan

Pengobatan Akupuntur Pada Penderita

Obesitas Di LP3A Surabaya). Skripsi.

Surabaya: Institut Teknologi Sepuluh Nopember (tidak dipublikasikan).

[2] Pratiwi, F. E., dan Zain, I. 2014. Klasifikasi

Pengangguran Terbuka Menggunakan

CART (Classification and Regression Tree) di Provinsi Sulawesi Utara. Sains dan Seni Pomit, Jurusan Statistika, FMIPA, Institut Teknologi Sepuluh Nopember.

[3] Afidah, L. N. 2011. Pola Tingkat Keparahan Korban Kecelakaan Lalu Lintas dengan Menggunakan Regresi Logistik Multinomial (Studi Kasus Kecelakaan Lalu

Lintas di Surabaya). Skripsi. Surabaya:

Institut Teknologi Sepuluh Nopember (tidak dipublikasikan).

[4] Timofeev, R. 2004. Classification and

Regression Trees (CART) Theory and Applications. Berlin: Center of Applied

Statistics and Economics Humboldt

University.

[5] Breimen, L. F. 1984. Classification and

(15)

152

MENENTUKAN FORMULA PREMI TAHUNAN TIDAK KONSTAN

PADA ASURANSI

JOINT LIFE

I Gede Bagus Pasek Subadra§1,I Nyoman Widana2, Desak Putu Eka Nilakusmawati3

1

Jurusan Matematika Fakultas MIPA – Universitas Udayana [Email: [email protected]]

2_{Jurusan Matematika Fakultas MIPA}_–_{Universitas Udayana [Email: [email protected]]}

3_{Jurusan Matematika Fakultas MIPA}_–_{Universitas Udayana [Email: [email protected]]}

§

ABSTRACT

The aim of this research was to determine the annual premium formula that turns on the joint life insurance. This formula uses the reference insurance contracts of the previous research Insurance Models for Joint Life and Last Survivor Benefits. The first step is to determine the value of mortality tables by using the Table Helligman-pollard. Furthermore, determining the value of a life annuity and

single premium. The results of this research was formula to be affected by the changing premium ( )

with the increase and decrease in constant interest.

Keywords: The Annual Premium, The Annual Premium Turned, Joint Life Insurance, α.

1. PENDAHULUAN

Pada kebutuhan hidup berkeluarga tentunya sebagai seorang kepala keluarga ingin sekali

berusaha untuk menjamin kesejahteraan

keluarganya. Kesejahteraan tersebut akan

terganggu apabila kepala keluarga jatuh sakit, cacat ataupun meninggal dunia. Sebagian dari jaminan kesejahteraan dapat diperoleh apabila kepala keluarga mengasuransikan dirinya agar kesejahteraan hidup keluarga dapat terpenuhi (Sembiring [5]). Kesejahteraan tersebut dapat terpenuhi apabila kepala keluarga tersebut mengikuti asuransi. Sampai saat ini ada berbagai jenis kontrak asuransi, yaitu asuransi individu atau asuransi untuk satu orang dan asuransi bersama atau asuransi minimal dua orang.

Asuransi jiwa merupakan salah satu

instrumen yang dapat digunakan untuk

memindahkan resiko, dimana apabila terjadi resiko kematian pada seseorang maka ahli warisnya akan memperoleh sejumlah dana yang disebut uang pertanggungan atau santunan.

Sebagai konsekuensinya peserta asuransi

diwajibkan untuk membayar sejumlah uang

kepada perusahaan asuransi jiwa setiap jangka waktu tertentu, yang biasa disebut premi.

Perusahaan asuransi jiwa merupakan

perusahaan yang memberikan jasa dalam penanggulangan risiko yang dikaitkan dengan hidup atau meninggalnya seseorang yang dipertanggungkan. Suatu perusahaan asuransi

jiwa tidak menutup kemungkinan untuk

menawarkan produk asuransi kepada peserta yang ingin melakukan asuransi jiwa secara bersama atau asuransi joint life. Asuransi joint life adalah suatu keadaan di mana aturan hidup dan matinya merupakan gabungan dari dua faktor atau lebih, misalnya suami-istri, orangtua-anak, suami-istri-orangtua-anak, dan lain sebagainya (Futami [3]). Peserta yang mengikuti asuransi joint life wajib membayar suatu kewajiban (premi) setiap tahunnya sesuai dengan kontrak.

Dilihat dari besarnya pembayaran premi, ada dua jenis pembayaran premi, yaitu pembayaran premi standar/konstan dan pembayaran premi yang berubah atau premi tidak konstan. Untuk pembayaran premi standar/konstan setiap tahun besar pembayarannya selalu sama sedangkan jika setiap tahun besar pembayaran preminya

(16)

Subadra, I G.B.P., Widana, I N., Nilakusmawati, D.P.E. Menentukan Formula Premi Tahunan Tidak Konstan pada…

pembayaran premi yang berubah atau premi tidak konstan. Hal ini juga perlu dilakukan mengingat besarnya penghasilan masyarakat tidak selalu tetap.

Pada penelitian ini akan dilakukan

bagaimana menentukan formula premi tahunan tidak konstan pada asuransi joint life.

2. METODE PENELITIAN

Pada penelitian ini digunakan kontrak asuransi yang terdiri dari pasangan suami-istri, apabila peserta berusia x tahun dan y tahun tetap hidup mencapai kontrak asuransi berakhir atau

dengan kata lain peserta mencapai usia

dan , maka peserta mendapatkan uang pertanggungan sebesar Q. Apabila salah satu dari peserta meninggal dunia sebelum masa kontrak misalnya apabila y meninggal dunia sebelum masa kontrak berakhir maka x mulai tahun ke-n selama seumur hidup setiap tahunnya mendapatkan uang pertanggungan (benefit)

sebesar , demikian juga sebaliknya apabila x

meninggal dunia maka y akan mendapat uang

pertanggungan (benefit) sebesar . Apabila

kematian dari pasangan juga terjadi (x dan y meninggal) sebelum kontrak berakhir maka ahli waris akan mendapatkan uang pertanggungan sejumlah premi yang telah dibayarkan, pada akhir tahun kematiannya (Futami [2]).

Perbandingan antara peluang meninggalnya

peserta x tahun sebelum mencapai usia

tahun dengan peluang peserta x tahun tetap bertahan hidup selama 1 tahun (Matvejevs & Matvejevs [4]) dapat dirumuskan sebagai

dengan merupakan nilai

kostanta dari Tabel 2.1.

Peluang orang berusia x tahun akan tetap hidup selama n tahun dan y tahun akan tetap hidup

selama n tahun dinotasikan dengan

(Futami, [3]) dirumuskan sebagai

Anuitas yang pembayarannya dijanjikan akan dilakukan selang beberapa waktu kemudian disebut anuitas tunda. Anuitas yang ditunda

pembayarannya ada yang dilakukan di awal tahun (Futami [2]) dapat dirumuskan sebagai

| ̈

Tabel 2.1. Nilai Konstan dari Formula Helligman-Pollard

Konstan Pria Wanita

A 0.00194 0.00115

B 0.05093 0.03310

C 0.14249 0.12811

D 0.00607 0.00029

E 1.61992 23.44606

F 57.83349 21.11713

G 0.00005 0.00006

H 1.10715 1.09116

.

Nilai sekarang anuitas awal dari anuitas hidup berjangka joint life apabila x dan y tetap

hidup

(Matvejevs

&

Matvejevs

[4])

dirumuskan sebagai

̈ ⌉

Besar premi ditentukan dengan prinsip ekuivalensi dan mempunyai persamaan

dengan L menyatakan besarnya kerugian pihak penanggung yang didefinisikan sebagai variabel random dari nilai tunai benefit yang dibayarkan pihak penanggung.

Premi tunggal adalah pembayaran premi asuransi yang dilakukan pada waktu kontrak

asuransi disetujui, selanjutnya tidak ada

pembayaran lagi. Premi tunggal pure

endowment adalah pembayaran premi pada suatu

kontrak asuransi jiwa yang dibayarkan

pemegang polis, mulai dari saat kontrak dimulai sampai dengan jangka waktu tertentu (Eric V. Slud [1]). Premi tunggal pure endowment joint life untuk peserta yang berusia x tahun dan y tahun, dengan jangka waktu tertanggung n tahun (Futami [3]) dirumuskan sebagai

|̅̅̅

Asuransi berjangka adalah suatu asuransi apabila pemegang polis mulai disetujuinya kontrak asuransi sampai dengan jangka waktu tertentu (meninggal) sebelum masa kontrak

(17)

154

pertanggungannya (Matvejevs & Matvejevs [4]). Premi tunggal asuransi berjangka joint life dirumuskan sebagai

⌉ ∑

Usia tertanggung x tahun dan y tahun, meninggal pada tahun polis pertama besarnya uang pertanggungan dikalikan 1, meninggal tahun polis kedua besarnya uang pertanggungan dikalikan 2, dan seterusnya. Setiap tahun apabila meninggal besarnya uang pertanggungan selalu bertambah 1. Asuransi yang demikian ini disebut juga asuransi berjangka menaik. Untuk masa

pertanggungan selama n tahun, uang

pertanggungan dibayarkan pada akhir masa pertanggungan, single preminya dinotasikan

dengan _⌉ (Futami [3]) dan dirumuskan

sebagai

⌉ ∑

( )

Sehubungan dengan asuransi tersebut maka nilai tunai dari pendapatan premi dan nilai tunai dari benefit yang dibayarkan oleh pihak penanggung dapat (Matvejevs & Matvejevs [4]) dirumuskan sebagai

1. Nilai tunai dari pendapatan premi tahunan

konstan pada joint life dapat dinyatakan sebagai

( )

2. Nilai tunai dari benefit yang dibayarkan oleh

pihak penanggung dapat dinyatakan sebagai

∑ ∑ |

⌉

|̅̅̅ | ̈ | ̈

⌉

3. Dengan menggunakan prinsip ekuivalensi,

besar preminya adalah

̈ ⌉ |̅̅̅ | ̈ | ̈ ⌉

Sehingga besarnya premi tahunan yang harus dibayarkan oleh peserta asuransi adalah

|̅̅̅

_{| ̈}

| ̈

̈ ⌉ ⌉

3. HASIL PENELITIAN DAN DISKUSI

3.1 Premi Konstan

Nilai premi tahunan konstan pada asuransi

joint life sudah dicari dengan menggunakan

rumus persamaan (2.3). dengan menggunakan

Sehingga diperoleh

3.2 Formula Premi Tahunan Tidak Konstan

Kontrak asuransi melibatkan pasangan suami-istri dengan usia berturut-turut x tahun dan y tahun. Pembayaran premi dilakukan n tahun selama keduanya masih hidup. Besarnya pembayaran premi selalu berubah setiap tahunnya tergantung tingkat bunga menurun atau

menaik yang digunakan ( ). Misalkan P

pembayaran yang dilakukan di tahun pertama,

merupakan pembayaran di tahun kedua, dan seterusnya sampai tahun ke-n yang

pembayarannya adalah .

Rincian dari uang pertanggungan (benefit) adalah

1. Setelah n tahun apabila kedua peserta (x dan

y) masih tetap hidup mereka akan

mendapatkan uang pertanggungan sebesar Q rupiah. Dengan demikian kontrak asuransi ini berakhir.

2. Jika salah satu dari pasangan ini meninggal

dunia, misalkan y meninggal dunia, maka ada dua kemungkinan untuk pembayaran benefitnya, yaitu :

a. Di akhir tahun dari kematian

(18)

premi yang telah dibayarkan akan dikembalikan.

b. Setelah berakhirnya masa pembayaran

premi yaitu setelah pasangannya

mencapai usia tahun. Maka setiap

tahunnya peserta x memperoleh uang

pertanggungannya sebesar rupiah

selama seumur hidup (selama x masih tetap hidup) demikian juga sebaliknya jika peserta x yang meninggal dunia maka peserta y akan memperoleh

sebesar rupiah.

3. Jika pasangan yang keduanya meninggal

dunia sebelum kontrak selesai dengan kata lain x dan y meninggal maka kontrak berakhir dan tidak ada lagi pembayaran.

Sehubungan dengan kontrak asuransi

tersebut maka nilai tunai dari pendapatan premi dan nilai tunai dari benefit yang dibayarkan oleh pihak penanggung dapat dirumuskan sebagai

1. Nilai tunai dari pendapatan premi tahunan

tidak konstan pada joint life dapat dinyatakan sebagai

(

)

̈ ⌉ ∑

2. Nilai tunai dari pengembalian premi yang

dibayarkan oleh pihak penanggung

dinyatakan sebagai

∑

( )

∑

₍

)

Sehingga nilai tunai yang diharapkan dari benefit yang dibayarkan oleh pihak penanggung adalah

∑ ∑

∑

( )

∑

₍

)

|̅̅̅ | ̈ | ̈

∑

( )

∑

₍

)

3. Dengan menggunakan prinsip ekivalensi,

besar preminya adalah

( ̈ ⌉) ∑

|̅̅̅ | ̈ | ̈

∑

( )

∑

₍

)

Dengan demikian dapat ditentukan formula premi tahunan tidak konstan yang harus dibayarkan peserta asuransi joint life, yaitu:

̈ ⌉ ∑ ( )

[ |̅̅̅ | ̈ | ̈

∑

₍

)

∑

]

Berikut diberikan contoh perhitungan

(ilustrasi kasus) perhitungan premi tahunan tidak konstan.

1. Usia mulai asuransi

(19)

156

usia suami (x) adalah 50 tahun dan usia istri (y) adalah 45 tahun.

2. Masa pertanggungan asuransi

Masa pertanggungan asuransi adalah

lamanya peserta melakukan kontrak

asuransi. Dalam kasus ini, ditetapkan untuk

masa pertanggungan asuransi .

3. Tingkat bunga

Besarnya tingkat bunga yang digunakan

adalah konstan yaitu

4. Santunan

Besarnya santunan setelah masa

pertanggungan berakhir apabila kedua peserta masih hidup, maka mereka akan

diberikan uang sejumlah 1 rupiah (

rupiah) demikian juga apabila (y) meninggal dan (x) tetap hidup diakhir kontrak, maka (x)

akan memperoleh 1 rupiah ( rupiah)

setiap tahunnya selama seumur hidup. Hal yang sama juga berlaku apabila (x) meninggal dan (y) tetap hidup, maka akan

dibayar sebesar 1 rupiah ( rupiah).

Tetapi apabila (x) dan (y) meninggal dunia sebelum kontrak berakhir, maka semua pembayaran premi yang telah dibayarkan akan dikembalikan.

Berdasarkan rumus yang diperoleh,

besarnya pembayaran premi tahunan tidak konstan sangat dipengaruhi oleh besarnya nilai

yang digunakan. Misalkan dipilih bernilai

negatif maka ini berarti besar pembayaran

preminya selalu menurun setiap tahun.

Demikian pula sebaliknya jika dipilih bernilai

positif maka preminya selalu meningkat sebesar setiap tahun. Pada penelitian ini mula-mula

besarnya nilai yang digunakan adalah

dari premi konstan atau dengan kata lain premi

menurun sebesar dan premi

meningkat sebesar Sedangkan

konstanta- konstanta yang lain nilainya sama dengan konstanta pada perhitungan premi konstan.

Jika diperoleh besar premi

tahun pertamanya adalah

Akibatnya besar premi pada tahun ke-t untuk t=1,2,3,…10 adalah

Sedangkan jika besar premi tahun

pertamanya adalah

Dan premi pada pada tahun ke-t adalah

Setelah mendapatkan hasil dari premi tahunan tidak konstan maka dapat dibandingkan hasilnya dengan premi tahunan konstan, dapat dilihat pada Tabel 3.1.

Tabel 3.1. Premi Kostan dan Premi Tidak Konstan

Tahun Premi

Konstan

Premi menurun

Premi meningkat

1 0.34753 0.46914 0.22592

2 0.34753 0.43439 0.26067

3 0.34753 0.39964 0.29542

4 0.34753 0.36489 0.33017

5 0.34753 0.33014 0.36492

6 0.34753 0.29539 0.39967

7 0.34753 0.26064 0.43442

8 0.34753 0.22589 0.46917

9 0.34753 0.19114 0.50392

10 0.34753 0.15639 0.53867

Jumlah

Premi 3.4753 3.12765 3.82295

Perbandingan antara premi menurun

dengan premi meningkat terlihat pada Tabel

3.1.

Pada pembayaran tahun pertama premi

menurun dengan premi meningkat adalah 2 : 1

dan setelah pembayaran di akhir tahun terlihat bahwa perbandingannya adalah 1 : 3. Tetapi untuk besarnya uang pertanggungan yang didapatkan jauh berbeda antara premi

menurun dengan meningkat. Pada premi

menurun sebesar 3.12765 sedangkan premi meningkat sebesar 3.82295.

(20)

Gambar 3.1. Premi Konstan dan Premi Menurun

Sedangkan grafik untuk premi konstan dan premi meningkat dapat dilihat pada Gambar 3.2.

Gambar 3.2 Premi Konstan dan Premi Meningkat

Untuk pembayaran premi yang menurun (PT) , dari Gambar 3.1 terlihat bahwa

Selain itu, perlu dicatat bahwa mulai di tahun ke-5 peserta asuransi joint life akan membayar premi yang lebih kecil daripada peserta dengan model pembayaran premi konstan. Hal yang sebaliknya berlaku untuk pembayaran premi yang selalu meningkat.

dan ditahun ke-5 peserta asuransi joint life ini akan membayar premi yang lebih besar daripada dengan model pembayaran premi konstan.

4. KESIMPULAN DAN SARAN

Berdasarkan pembahasan dan hasil

penelitian yang diperoleh, maka dapat

disimpulkan, bahwa:

Rumusan/formula penentuan premi tahunan tidak konstan pada asuransi joint life adalah

̈ ⌉ ⌉ |̅̅̅ _{| ̈}

| ̈ ∑

₍

)

∑

untuk masa pertanggungan n tahun.

Beberapa saran untuk penelitian selanjutnya, yaitu: (1) Peneliti dapat melanjutkan penelitian tentang bagaimana menentukan formula premi

tahunan pada asuransi joint life untuk

tertanggung lebih dari 2 orang dan (2) Peneliti dapat juga melanjutkan penelitian dalam menentukan formula dari cadangan premi pada asuransi joint life.

DAFTAR PUSTAKA

[1] Eric V. Slud, 2001. Actuarial Mathematics. College Park.

[2] Futami, T., 1993. Matematika Asuransi Jiwa Bagian I. Tokyo: Oriental Life Insurance Cultural Development Center. [3] _________. 1994. Matematika Asuransi

Jiwa Bagian II. Tokyo: Oriental Life Insurance Cultural Development Center [4] Matvejevs, A. & Matvejevs, A., 2001.

Insurance Models for Joint Life and Last Survivor Benefit, Informatica, 12(4), pp. 547-58.

[5] Sembiring, R.K., 1986. Asuransi I. Jakarta: Universitas Terbuka, Depdikbud.

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

1 2 3 4 5 6 7 8 9 10

0 0.1 0.2 0.3 0.4 0.5 0.6

(21)

158

OPTIMALISASI PENJUALAN KAIN ENDEK DENGAN

METODE KARUSH-KUHN-TUCKER (KKT)

I Gede Aris Janova Putra§1,Ni Made Asih2, I Nyoman Widana3

1

Jurusan Matematika, FMIPA – Universitas Udayana [Email: [email protected]]

2_{Jurusan Matematika, FMIPA}_–_{Universitas Udayana [Email: [email protected]]}

3_{Jurusan Matematika, FMIPA}_–_{Universitas Udayana [Email: [email protected]]}

§

ABSTRACT

This study is conducted to determine the optimal sales value of endek mastuli, endek rangrang, endek saraswati, endek gradasi, and endek alam in Novala Busana Shop and Trans Collection Shop in order to reache maximum advantage by using Karush-Kuhn-Tucker (KKT) method. Karush-Khun-Tucker method can be used to find the optimum solution of the function regardless of whether linear or nonlinear. In the workmanship is KKT method essentially involves the same steps as Lagrange method, from a Lagrangean to be able to calculate the critical points, finding all solutions , and calculate of the value . In this study, most of quarterly show that which must be sold are kind of endek mastuli in reaching the maximum benefit. For other kinds of endek is constantly provided but it is not as much as before. Suggested to the next research could involve more variated variable with more interesting cases.

Keywords: Karush-Khun-Tucker (KKT) method, Lagrangean, Optimization, Constraint, Endek

1. PENDAHULUAN

Setiap suatu usaha dagang, tentu hal yang ingin dicapai adalah memperoleh keuntungan

yang maksimum. Pencapaian keuntungan

maksimum dapat dicapai dengan suatu strategi

penjualan. Salah satunya dalam ilmu

matematika dapat diselesaikan dengan metode optimasi. Contoh kasus optimasi berkendala yaitu mengetahui jenis kain endek yang akan dijual untuk mencapai keuntungan yang maksimum.

Penelitian ini merupakan studi kasus penjualan kain endek pada dua toko yaitu toko Novala Busana dan toko Trans Collection. Adapun tujuan penelitian adalah mengetahui bentuk fungsi tujuan dan fungsi kendala yang diperoleh dari penjualan kain endek pada masing-masing toko, dan menentukan nilai optimal penjualan (proporsi suatu item yang dijual untuk mencapai keuntungan yang maksimum) yang diperoleh dengan metode Karush-Kuhn-Tucker (KKT).

Karush-Kuhn-Tucker pada tahun 1951 mengemukakan teknik optimasi yang dapat digunakan dalam pencarian titik optimum dari suatu fungsi yang berkendala tanpa memandang linier maupun nonlinier. Misalkan menghadapi masalah optimasi dalam bentuk:

Maksimumkan/Minimumkan:

) dengan (1) dengan kendala

atau 0 dengan

(banyak kendala lebih kecil atau sama dengan banyak variabel)

Pertama tuliskan kembali persyaratan yang tak

negatif menjadi

sehingga himpunan kendalanya adalah

persyaratan ketidaksamaan yang masing-masing dengan tanda lebih kecil dari pada atau sama dengan. Kemudian tambahkan variabel-variabel

,…, berturut-turut pada ruas

(22)

Putra, I G.A.J., Asih, N.M., Widana, I N. Optimalisasi Penjualan Kain Endek dengan Metode Karush-Kuhn-Tucker

demikian merubah setiap ketidaksamaan

menjadi suatu kesamaan. Variabel slack yang

ditambahkan berbentuk suku-suku kuadrat untuk menjamin bahwa mereka tak negatif [1]. Kemudian bentuk fungsi Lagrange:

∑ [ ]

∑ [ ] (2)

Fungsi Lagrange yang dibentuk adalah fungsi

tujuan ditambahkan dengan total kendala.

Untuk adalah pengali-pengali

Lagrange [2].

Langkah terakhir selesaikan sistem persamaan:

(3)

(4)

(5)

Persamaan-persamaan (3), (4), dan (5)

membentuk persyaratan Karush-Kuhn-Tucker

(KKT) untuk maksimasi/minimasi program linier dan nonlinier [3]. Sehingga syarat Karush-Kuhn-Tucker (KKT) untuk kasus: Minimumkan:

) dengan (6) dengan kendala

dengan

dapat dinyatakan dalam satu set pernyataan sebagai berikut: (7)

∑ Catatan:

(i) Jika permasalahannya adalah

memaksimumkan, maka .

(ii) Jika kendalanya adalah , maka

.

(iii)Jika permasalahannya adalah

memaksimumkan dan jika kendalanya

adalah , maka .

Nilai optimum (nilai maksimum atau nilai minimum) suatu fungsi multi variabel dengan

kendala (constrains) berupa suatu persamaan

adalah suatu kasus optimasi yang sering

ditemukan dalam teori maksimum dan minimum yang terdapat dalam kalkulus. Adapun metode matematika yang dapat digunakan untuk kasus

tersebut adalah metode pengali Lagrange [4].

Sedangkan untuk menentukan nilai optimum suatu fungsi matematika multi variabel dengan kendala berupa suatu pertidaksamaan adalah suatu hal yang perlu dipelajari lebih lanjut dalam

teori optimasi. Metode Karush-Kuhn-Tucker

(KKT) adalah suatu metode untuk menentukan nilai optimum suatu fungsi dengan kendala berupa pertidaksamaan [5].

Prosedur menggunakan metode

Karush-Kuhn-Tucker (KKT) dalam memecahkan suatu masalah optimasi dengan kendala berupa pertidaksamaan, langkahnya sama halnya dengan

menggunakan metode Lagrange untuk

memecahkan masalah optimasi dengan kendala berupa suatu persamaan yaitu:

1. Membentuk suatu fungsi ‘Lagrangian’ L, maka dapat menghitung titik-titik kritisnya dan menguji nilai fungsi objektif pada setiap titik kritis yang memuat fungsi objektif optimal. Jadi dalam hal ini dibentuk suatu fungsi

Lagrange yang didefinisikan dengan:

∑

2. Mencari semua solusi dalam himpunan

persamaan berikut:

dengan

Penyelesaian dari setiap sistem persamaan ini,

selanjutnya disebut titik kritis dari L.

Selanjutnya misalkan M menotasikan

himpunan titik-titik kritis yaitu

M ={(x, λ)|(x, λ) adalah titik kritis dari L}.

3. Langkah terakhir yaitu menghitung nilai dari f

(23)

160

2. METODE PENELITIAN

Sumber data dalam penelitian ini diperoleh dari data sekunder, yaitu melalui dokumen-dokumen yang terdapat pada toko Novala Busana dan toko Trans Collection periode 1

tahun (1 April 2014 – 31 Maret 2015). Dalam

penelitian ini, variabel yang digunakan adalah jenis kain endek dan harga kain endek. Untuk

variabel jenis kain endek yaitu kain endek

mastuli ( ), kain endek rangrang kain

endek saraswati ( ), kain endek gradasi ( ),

dan kain endek alam ( ). Sedangkan untuk

variabel harga kain endek yaitu harga modal kain endek dan harga jual kepada konsumen. Langkah-langkah yang digunakan dalam metode penelitian ini adalah:

1. Penyajian data penjualan masing-masing

toko.

2. Menentukan variabel keputusan

3. Menentukan fungsi tujuan

4. Menentukan fungsi batasan

5. Mempartisi menjadi 4 bagian (Triwulan)

6. Optimalisasi KKT dengan bantuan

software Matlab

3. HASIL DAN PEMBAHASAN

Berdasarkan jenis-jenis kain endek yang diteliti penjualannya pada toko Novala Busana dan toko Trans Collection, dapat ditentukan variabel keputusan, yaitu:

= Jumlah penjualan kain endek mastuli (pcs)

= Jumlah penjualan kain endek rangrang (pcs)

= Jumlah penjualan kain endek saraswati (pcs)

= Jumlah penjualan kain endek gradasi (pcs)

= Jumlah penjualan kain endek alam (pcs)

Tujuan yang ingin dicapai dalam

penelitian ini adalah untuk mencapai

keuntungan maksimum pada setiap jenis kain endek. Keuntungan diperoleh dari selisih antara harga modal dan harga jual kepada konsumen. Koefisien dari masing-masing variabel keputusan menunjukan keuntungan dari setiap jenis kain endek.

Fungsi tujuan Toko Novala Busana

Fungsi tujuan Toko Trans Collection

Selanjutnya adalah menentukan fungsi batasan. Fungsi batasan dibentuk berdasarkan peluang masing-masing produk yang terjual terhadap total produk yang disediakan pada masing-masing toko. Periode waktu yang digunakan selama 1 tahun yang dipartisi menjadi 4 bagian, setiap bagian terdiri dari 3

bulan (triwulan). Bentuk baku fungsi

batasannya yaitu:

Fungsi Batasan Toko Novala Busana Triwulan I (April, Mei, Juni)

Triwulan II (Juli, Agustus, September)

Triwulan III (Oktober,November,Desember)

Triwulan IV (Januari, Februari, Maret)

Fungsi Batasan Toko Trans Collection Triwulan I (April, Mei, Juni)

Triwulan II (Juli, Agustus, September)

Triwulan III (Oktober,November,Desember)

(24)

Putra, I G.A.J., Asih, N.M., Widana, I N. Optimalisasi Penjualan Kain Endek dengan Metode Karush-Kuhn-Tucker

Triwulan IV (Januari, Februari, Maret)

Setelah menentukan variabel keputusan, memodelkan fungsi tujuan dan fungsi batasan

maka membetuk Lagrangian untuk

menghitung titik-titik kritisnya, dan langkah

selanjutnya memaksimumkan dengan

syarat: ∑

Untuk mempermudah perhitungan dalam

mencari masing-masing nilai digunakan

software Matlab, diperoleh nilai

455.6098, 0.0000,

384.3902, 0.0000, 0.0000. Hasil

tersebut menunjukan bahwa toko Novala Busana dalam triwulan I akan mencapai keuntungan maksimum apabila terjual kain

endek mastuli sebanyak 456 pcs dan

endek saraswati sebanyak 384 pcs,

dengan mencapai keuntungan maksimum yaitu sebesar Rp 59.156.000. Dengan langkah yang sama seperti pada triwulan 1, maka hasil yang diperoleh untuk triwulan 2,3,4 apabila dibentuk tabel maka hasilnya:

Tabel 1. Keuntungan Maksimum Triwulan Toko Novala Busana Tri Wulan x 1 (pcs) x 2 (pcs) x 3 (pcs) x 4 (pcs) x 5 (pcs) Keuntungan (Rp)

I 456 0 384 0 0 59.156.000

II 580 0 260 0 0 60.396.000

III 840 0 0 0 0 63.000.000

IV 840 0 0 0 0 63.000.000

Hasil tersebut menunjukan bahwa triwulan I dan triwulan II sebaiknya sebagian besar

menjual kain endek mastuli dan kain

endek saraswati ( ). Pada triwulan III dan

triwulan IV toko Novala Busana cukup dengan memaksimalkan penjualan kain endek

mastuli maka toko telah memperoleh

keuntungan maksimum.

Menentukan nilai optimum pada triwulan I toko Trans Collection, untuk mencari

masing-masing nilai digunakan software

Matlab untuk mempermudah perhitungan,

sehingga diperoleh nilai 392.6316,

0.000, 447.3684, 0.0000,

0.0000.

Sehingga Toko Trans Collection dalam triwulan I akan mencapai keuntungan maksimum apabila terjual kain endek mastuli

sebanyak 393 pcs dan endek

saraswati sebanyak 447 pcs dengan

keuntungan maksimum yaitu sebesar Rp 62.179.000. Dengan langkah yang sama seperti pada triwulan I, maka hasil yang diperoleh untuk triwulan II, III, IV apabila dibentuk tabel maka hasilnya:

Tabel 2. Keuntungan Maksimum Triwulan Toko Trans Collection

Toko Trans Collection pada keempat triwulan periode 1 April 2014 sampai dengan

31 Maret 2015, hasil yang diperoleh

menunjukkan bahwa triwulan I, triwulan II dan triwulan III sebaiknya sebagian besar menjual

kain endek mastuli ( ) dan kain endek

saraswati ( ). Sedangkan pada triwulan IV

toko Trans Collection cukup dengan

memaksimalkan penjualan kain endek

mastuli maka toko telah memperoleh

keuntungan maksimum.

4. KESIMPULAN DAN SARAN

Pada penelitian ini diperoleh kesimpulan yaitu, toko Novala Busana berdasarkan triwulan I dan II jenis kain endek yang dijual sebagian

Tri wulan x 1 (pcs) x 2 (pcs) x 3 (pcs) x 4 (pcs) x 5 (pcs) Keuntungan (Rp)

I 393 0 477 0 0 62.179.000

II 499 0 390 0 0 63,871.000

III 837 0 3 0 0 75.516.000

(25)

162

besar adalah endek mastuli dan endek

saraswati untuk mencapai keuntungan yang

maksimum. Sedangkan pada triwulan III dan IV yang dijual sebagian besar adalah kain endek

mastuli Keuntungan terbesar, terlihat pada

triwulan III dan IV yaitu sebesar Rp. 63.000.000.

Pada toko Trans Collection berdasarkan triwulan I, II, dan III jenis kain endek yang

dijual sebagian besar adalah endek mastuli

dan endek saraswati ( ). Sedangkan pada

triwulan IV produk yang dijual sebagian besar adalah kain endek mastuli. Keuntungan terbesar, terlihat pada triwulan IV yaitu sebesar Rp. 75.600.000.

Hasil penelitian menunjukan sebagian besar yang harus dijual adalah jenis kain endek mastuli untuk mencapai keuntungan yang maksimum, akan tetapi pada kasus kehidupan dunia nyata, setiap individu belum tentu menyukai satu jenis kain endek yang sama. Dengan demikian disarankan untuk masing-masing toko, bukan berarti jenis kain endek lain tidak mesti dijual melainkan tetap tersediakan walaupun tidak sebanyak sebelumnya. Pada

penelitian selanjutnya diharapkan dapat

melibatkan variabel yang lebih bervariasi dengan kasus yang lebih menarik.

DAFTAR PUSTAKA

[1] A. Taha, H. 1996. Riset Operasi. Terjemahan Daniel Wirajaya. Jakarta: Penerbit Binarupa Aksara.

[2] Amalia. 2010. Peranan Persyaratan Karush-Kuhn-Tucker dalam

Menyelesaikan Pemrograman Kuadratis. Skripsi. Universitas Sumatra Utara. http://repository.usu.ac.id/bitstream/12345 6789/14099/1/10E00011.pdf. Diakses tanggal 3 Februari 2015.

[3] Luknanto, D. 2000. Pengantar Optimasi Non Linier. Yogyakarta: UGM.

hhtp://luk.Staff.Ugm.ac.id/Optimasi/pdf/no nlinier2003/.pdf. (Diunduh 2 Februari 2015).

[4] Purcell, E. J., Varberg, D., & Rigdon, S. E. 2004. Kalkulus. Edisi Kedelapan

Terjemahan Julian Gressando. Jakarta: Penerbit Erlangga.

(26)

METODE QUEST DAN CHAID PADA KLASIFIKASI

KARAKTERISTIK NASABAH KREDIT

Nur Faiza§1,I Wayan Sumarjaya2, I Gusti Ayu Made Srinadi3

1

Jurusan Matematika, FMIPA, Universitas Udayana [Email: [email protected]]

2_{Jurusan Matematika, FMIPA, Universitas Udayana [Email: [email protected]]}

3_{Jurusan Matematika, FMIPA, Universitas Udayana [Email: [email protected]]}

§

ABSTRACT

This aim of this research is to find out the classification results and to compare the magnitude of misclassification of QUEST and CHAID methods on the classification of customer of Adira Kredit Elektronik branch Denpasar. QUEST (Quick, Unbiased, Efficient Statistical Trees) and CHAID (Chi-squared Automatic Interaction Detection) are nonparametric methods that produce tree diagram which is easy to interpret. The QUEST and CHAID classification methods conclude that: 1) QUEST method produces three groups which predict customers into the current category, whereas CHAID method produces four groups which also predict customer into the current category; 2) both methods

generate the biggest classification accuracy for customers that current categorywhich share similar

characteristics; 3) both methods also have the same degree of accuracy in classifying customer data Adira Kredit Elektronik branch Denpasar.

Keywords: Classification, QUEST, CHAID, customer credit status.

1. PENDAHULUAN

Klasifikasi merupakan pengelompokan secara sistematis suatu objek atau benda ke dalam golongan atau pola-pola tertentu berdasarkan

kesamaan ciri. Masalah klasifikasi sering

dijumpai dalam kehidupan sehari-hari, baik pada bidang industri, sosial, kesehatan maupun pendidikan.

Penelitian

ini

membahas

metode

klasifikasi pohon menggunakan metode

QUEST dan CHAID dengan variabel

berskala kategorik, dengan tujuan untuk

mengetahui

hasil

klasifikasi

dan

membandingkan

besarnya

kesalahan

klasifikasi dari metode QUEST dan CHAID

pada klasifikasi data nasabah Adira Kredit

Elektronik Cabang Denpasar.

Metode QUEST merupakan algoritma

yang diperkenalkan oleh Loh dan Shih [3],

sebagai salah satu bentuk metode pohon

klasifikasi yang menghasilkan pohon biner.

QUEST diterapkan pada data dengan variabel

respon kategorik dan variabel prediktor

berupa variabel kategorik maupun numerik.

QUEST merupakan modifikasi dari analisis

diskriminan kuadratik. Analisis diskriminan

kuadratik diterapkan pada proses penentuan

simpul penyekat.

Algoritma QUEST dibagi menjadi tiga bagian yaitu, algoritma pemilihan variabel penyekat, algoritma penentuan simpul penyekat, dan algoritma penghentian pembentukan pohon [3].

Langkah-langkah algoritma pemilihan

variabel penyekat dengan variabel kategorik

adalah sebagai berikut: pertama, untuk setiap

variabel prediktor kategorik, lakukan uji

khi-kuadrat dan hitung

p-value

. Kedua, pilih

(27)

p-Faiza, N., Sumarjaya, I W., Srinadi, I G.A.M. Metode Quest dan Chaid pada Klasifikasi Karakteristik Nasabah Kredit

164

value

terkecil atau yang paling signifikan

sebagai variabel penyekat (Loh dan Shih [3]).

Setelah terpilih variabel penyekat, langkah selanjutnya adalah menentukan simpul penyekat.

Apabila variabel penyekat yang terpilih berupa

variabel kategorik dan terdiri lebih dari dua kategori, maka dilakukan transformasi ke variabel numerik dan selanjutnya diterapkan analisis diskriminan kudratik untuk mencari akar

dari persamaan kuadrat ,

dengan:

̅ ̅

̅ ̅ | _| .

dengan ̅ dan adalah rata-rata dan ragam

variabel penyekat dari pengamatan variabel

respon pertama, sedangkan ̅ dan adalah

rata-rata dan ragam variabel penyekat dari pengamatan variabel respon kedua[3]. Jika akar yang dihasilkan adalah akar tunggal, maka akar tersebut dipilih sebagai simpul penyekat. Tetapi jika akar yang dihasilkan terdiri dari 2 akar, maka akan dipilih akar yang mendekati rata-rata dari variabel respon pertama sebagai simpul penyekat.

Proses pemilihan simpul secara rekursif akan

terhenti apabila salah satu dari aturan

penghentian tercapai. Ada empat aturan

penghentian pembentukan pohon yaitu: pertama, jika simpul penyekat menjadi murni yaitu apabila semua kasus masuk ke dalam salah satu kategori variabel respon. Kedua, jika semua kasus yang terdapat di dalam simpul memiliki nilai-nilai identik untuk tiap variabel prediktor. Kedua, jika kedalaman pohon sudah mencapai kedalaman pohon maksimum yang ditetapkan. Keempat, jika banyaknya kasus yang masuk ke dalam simpul sudah mencapai jumlah minimum yang ditetapkan.

Hasil analisis dari metode QUEST akan dibandingkan dengan metode pendahulunya, yaitu metode CHAID. CHAID merupakan algoritma yang diperkenalkan oleh Kass (1980), metode klasifikasi yang lebih dulu diterapkan dan menghasilkan pohon nonbiner (Kass [2]).

CHAID diterapkan pada data dengan variabel respon dan variabel prediktor berupa variabel kategorik.

CHAID membedakan variabel prediktor kategorik menjadi tiga bentuk yang berbeda, yaitu: monotonik, bebas, dan mengambang (Gallagher [1]).

Algoritma CHAID secara lengkap yaitu sebagai berikut (Kass [2]): Pertama, untuk setiap variabel prediktor, buat tabulasi silang kategori variabel prediktor dengan kategori-kategori variabel respon. Kedua, untuk setiap tabulasi silang yang diperoleh (susun subtabel

yang berukuran yang mungkin, adalah

banyaknya kategori variabel respon) cari pasangan kategori variabel prediktor yang memiliki angka uji paling kecil. Jika angka uji tidak mencapai nilai kritis, gabungkan kedua

kategori tersebut menjadi satu kategori

campuran. Ulangi langkah ini sampai angka uji kategori campuran melampaui nilai kritis. Ketiga, untuk setiap kategori gabungan yang terbentuk dari 3 atau lebih kategori asal, temukan pemisahan biner yang memiliki angka uji yang paling besar (pemisahan berdasarkan tipe variabel prediktor). Jika angka uji ini lebih besar dari nilai kritis, buatlah pemisahan tersebut dan kembali ke langkah 2 di atas. Keempat, untuk setiap tabulasi silang variabel prediktor yang telah digabungkan secara optimal, pilih yang memiliki angka uji paling besar. Jika angka uji ini lebih besar dari nilai kritis, bagilah data

menurut kategori–kategori yang telah

digabungkan dari variabel prediktor yang telah

dipilih. Pada tahap ini apabila terjadi

pengurangan tabel kontingensi dari tabel asal maka gunakan uji koreksi Bonferoni dan jika tidak maka lakukan uji khi-kuadrat untuk uji signifikansi. Kelima, untuk setiap pembagian data yang belum dianalisis, kembali ke langkah 1.

(28)

macet. Kelompok-kelompok yang terbentuk tersebut akan digunakan oleh Adira Kredit Elektronik Cabang Denpasar sebagai acuan untuk menentukan sasaran utama pemasaran dengan mempertimbangkan status kredit. Dengan penentuan kelompok sasaran kredit yang tepat,

diharapkan risiko kredit macet bisa

diminimalkan.

Adanya kesamaan karakteristik dari metode QUEST dan CHAID yaitu dapat diterapkan pada data variabel kategorik dan dalam pemilihan variabel penyekat menggunakan uji khi-kuadrat. Sehingga penulis tertarik untuk melakukan penelitian dengan metode QUEST dan CHAID yang akan diterapkan pada data nasabah Adira Kredit Elektronik Cabang Denpasar. Penelitian ini membandingkan hasil klasifikasi dari kedua metode tersebut untuk dapat dijadikan bahan analisis perusahaan dalam menentukan calon nasabah pada masa yang akan datang.

2. METODE PENELITIAN

Penelitian ini mengambil data nasabah Adira Kredit Elektronik Cabang Denpasar sebagai study kasus. Data diperoleh dari hasil pengisian formulir aplikasi permohonan kredit nasabah Adira Kredit Elektronik Cabang Denpasar yang sebelumnya sudah pernah mengajukan kredit dan melakukan pengajuan kembali pada bulan September sampai dengan Oktober 2014.

Adapun Variabel yang digunakan dalam penelitian ini berupa variabel kategori yaitu

meliputi status kredit ( ), jenis kelamin ( ),

status pernikahan ( ), jenis pekerjaan ( ), dan

status tempat tinggal ( ), pendidikan terakhir

( ), jabatan nasabah ( ), lama angsuran ( ),

dan pendapatan per bulan ( ).

Langkah-langkah yang dilakukan dalam metode penelitian ini adalah:

1. Mengumpulkan dan menyeleksi data.

2. Meringkas dan menyajikan data.

3. Pembentukan pohon klasifikasi.

4. Menginterpretasi hasil klasifikasi.

5. Perbandingan persentase kesalahan klasifikasi.

3. HASIL DAN PEMBAHASAN

3.1. Klasifikasi dengan Metode QUEST

Gambar 1 menunjukkan bahwa dari 626 sampel yang diteliti, hasil yang didapatkan adalah nasabah dengan status lancar sebanyak 550 orang (87,9%) dan nasabah dengan status macet sebanyak 76 orang (12,1%). Variabel pendapatan

per bulan ( ) adalah variabel prediktor yang

paling signifikan, sehingga variabel tersebut

dipilih sebagai variabel penyekat. Variabel

pendapatan per bulan ( ) disekat menjadi 2

simpul, yaitu simpul ke-1 dengan kategori

nasabah yang memiliki pendapatan per bulan <Rp2.000.000 dan Rp2.000.000-Rp5.000.000 menjadi satu simpul, dan simpul ke-2 dengan

kategori nasabah yang memiliki pendapatan per

bulan >Rp5.000.000 menjadi satu simpul. Pada simpul ke-1 proses penyekatan dilanjutkan dan menjadi simpul dalam, karena variabel status

tempat tinggal ( ) merupakan variabel prediktor

kedua yang signifikan untuk membagi kategori pada simpul ke-1. Sementara pada simpul ke-2 proses penyekatan dihentikan karena semua kasus yang terdapat di dalam simpul memiliki nilai-nilai identik untuk tiap variabel prediktor, sehingga simpul ke-2 menjadi simpul akhir.

Variabel status tempat tinggal ( ) disekat

menjadi 2 simpul, yaitu simpul ke-3 dengan

kategori nasabah yang status tempat tinggal milik

mertua, kontrak, dan kos menjadi satu kelompok,

dan simpul ke-4 dengan kategori nasabah yang

(29)

Faiza, N., Sumarjaya, I W., Srinadi, I G.A.M. Metode Quest dan Chaid pada Klasifikasi Karakteristik Nasabah Kredit

166

Gambar 1. Diagram Pohon Klasifikasi QUEST untuk Data Nasabah

Hasil metode QUEST berdasarkan Gambar 1 mendapatkan 3 kelompok, yang diringkas dalam Tabel 1 dan Tabel 2 berikut:

Tabel 1. Hasil Klasifikasi Dari Diagram Pohon QUEST

Kelompok 1 Nasabah yang memiliki