BAB II
TINJAUAN PUSTAKA
2.1 UMUM
Aliran air dalam suatu aliran dapat berupa aliran saluran terbuka (open chanel flow) maupun aliran pipa (pipe flow). Kedua jenis aliran tersebut sama dalam banyak hal namun berbeda dalam satu hal yaitu aliran terbuka harus memiliki permukaan bebas (free surface) sedangkan aliran pipa/tertutup tidak demikian, karena air harus mengisi seluruh aliran. Permukaan bebas dipengaruhi oleh tekanan udara. Aliran pipa yang terkurung dalam saluran tertutup tidak terpengaruh langsung oleh tekanan
udara kecuali oleh tekanan hidrolik. Saluran terbuka adalah saluran yang mengalirkan air dengan suatu permukaan bebas. Menurut asalnya saluran ini dapat digolongkan menjadi saluran alam (natural) dan saluran buatan (artificial).
Saluran tertutup/pipa adalah saluran tertutup yang biasanya berpenampang lingkaran dan digunakan untuk mengalirkan fluida dengan
tampang aliran penuh. Fluida yang dialirkan melalui pipa biasa berupa zat cair/gas dan tekanan bisa lebih besar/lebih kecil dari tekanan atmosfer. Apabila zat cair di dalam pipa tidak penuh maka aliran termasuk dalam aliran saluran terbuka
(Bambang Triatmojo, 1993).
Transisi saluran perubahan penampang setempat (dipandang dari segi
hulu dan hilir. Tikungan, ekspansi dan penyempitan adalah contoh khas dari transisis saluran.
Dalam pendistribusian air diperlukan cara untuk mengalirkan air agar dapat mengalir dari sumber air ke semua pemakai air. Ada beberapa metode pendistribusian air yang terdiri dari tiga sistem metode yaitu sistem gravitasi,
sistem pemompaan dan sistem gabungan. • Sistem Gravitasi
Metode pendistribusian ini menggunakan gravitasi untuk pendistribusianna dengan bergantung pada topograi sumber daya air dan
daerah distribusinya. Biasanya ditempatkan pada daerah yang lebih tinggi dari daerah distribusiny, agar air yang didistribusikan dapat mengalir dengan sendirinya tanpa menggunakan pompa.
• Sistem Pemompaan
Metode ini menggunakan suatu pompa untuk mendistribusikan air menuju lokasi pemakaian air. Pompa terebut dihubungkan langsung dengan pipa yang menangani pendistribusian.
• Sistem Gabungan
Metode ini merupakan penggabungan antara gravitasi dan
2.2 Kebutuhan Konsumsi Air Bersih 2.2.1 Kebutuhan Air Domestik
Pemenuhan kebutuhan air untuk domestik memiliki bagian terbesar dalam
kebutuhan dasar perencanaan unit pengolahan. Faktor kebiasaan, pola dan tingkat kehidupan yang didukung oleh adanya perkembangan sosial ekonomi
memberikan pengaruh terhadap peningkatan kebutuhan dasar air. Dikenal ada 2 (dua) kategori fasilitas penyediaan air bersih/minum, yaitu :
a. Fasilitas Perpipaan, terdiri dari : Sambungan Rumah (SR), SambunganHalaman,
dan Sambungan Umum.
b. Fasilitas Non Perpipaan, terdiri dari : Sumur Umum, Hidran Umum/Kran.
Perlu diketahui pula adalah jumlah kebutuhan rata-rata air bersih per orang
per hari, dimana dibedakan atas kategori kota dan perdesaan. Tingkat pemakaian air bersih secara umum ditentukan berdasarkan kebutuhan manusia untuk kehidupan
sehari-hari. Kebutuhan air menurut jenis kota berdasarkan standar kebutuhan air bersih (Departemen PU, 2007) pada tabel 2.1:
Tabel 2.1 Standar Kebutuhan Air Bersih (Dep. PU, 2007
Kecil 20.000 – 500.000 130 30 20
IKK <20.000 100 30 20
Sumber : Kebijaksanaan operasional program air bersih, Direktorat Jendral Cipta Karya , DPU
2.2.2 Kebutuhan Non Domestik
Kebutuhan air non domestik merupakan tahap berikutnya dalam perhitungan kebutuhan air bersih, besaran pemakaiannya ditentukan oleh jumlah
konsumen non domestik yang terdiri dari fasilitas-fasilitas yang telah disebutkan. Sebagaimana penjelasan sebelumnya bahwa ada beberapa faktor yang dapat
menentukan perkembangan jumlah fasilitas tersebut, yaitu pertambahan penduduk, jenis dan perluasan fasilitas serta perkembangan sosial ekonomi. Perhitungan proyeksi fasilitas dapat dilakukan dengan pendekatan perbandingan
jumlah penduduk.
2.3 DEFINISI ALIRAN FLUIDA
Dalam konsep mekanika fluida semua bahan nampak berada dalam dua keadaan, yaitu sebagai zat padat dan cair (fluida). Perbedaan kedua keadaan tersebut secara teknis terletak pada reaksi kedua zat tersebut terhadap tegangan
geser atau tegangan singgung yang dialaminya.
Fluida dapat didefinisikan sebagai suatu zat mampu alir dan dapat
menyesuaikan bentuk dengan bentuk wadah yang ditempatinya, serta apabila diberikan tegangan geser, betapapun kecilnya akan menyebabkan fluida tersebut bergerak dan berubah bentuk secara terus-menerus selama tegangan tersebut
Dengan pengertian diatas maka fluida dapat dibedakan atas zat cair dan gas. Dimana kedua zat ini pun berbeda secara teknis akibat gaya kohesif. Zat cair
cenderung mempertahankan volumenya dan akan membutuhkan permukaan bebas dalam medan gravitasi. Aliran muka bebas sangat dipenuhi efek gravitasi sedangkan zat gas akan memuai dengan bebas sampai tertahan oleh dinding yang
membatasinya. Gas tersebut akan membentuk atmosfir yang pada hakekatnya akan bersifat hidrostatik.
Definisi yang lebih tepat untuk membedakan zat padat dengan fluida ialah dari karateristik deformasi bahan tersebut. Zat padat dianggap sebagai bahan yang menunjukkan reaksi deformasi yang terbatas ketika menerima suatu gaya geser.
2.4 ALIRAN FLUIDA DALAM PIPA
1. Aliran Laminer dan Turbulen
Beberapa tahun yang lalu, Osborne Reynolds telah melakukan beberapa percobaan untuk menentukan kriteria aliran laminar dan turbulen.Reynolds menemukan bahwa aliran selalu menjadi laminar, jika
kecepatan alirannya diturunkan sedemikian rupa sehingga bilangan Reynolds lebih kecil dari 2000 (Re < 2300). Begitupula dikatakan alirannya
turbulen, pada saat bilangan Reynolds lebih besar dari 4000 (Re > 4000). Dan jika bilangan Reynolds berada diantara 2300 dan 4000 (2300 < Re >4000) maka lairan tersebut adalah aliran yang berada pada daerah transisi.
Sedangkan aliran turbulen di tandai dengan adanya ketidak beraturan atau fluktuasi di dalam aliran fluida (bergejolak). Karena aliran fluida pada aliran
laminar bergerak dalam lintasan yang sama / tetap maka aliran laminar dapat diamati. Pada aliran turbulen partikel fluida tidak membuat frekuensi tertentu dan tidak memperlihatkan pola gerakan yang dapat diamati.Aliran
turbulen hampir dapat dijumpai pada setiap praktek hidrolika dan diantara laminar dengan turbulen terdapat daerah yang dikenal dengan daerah
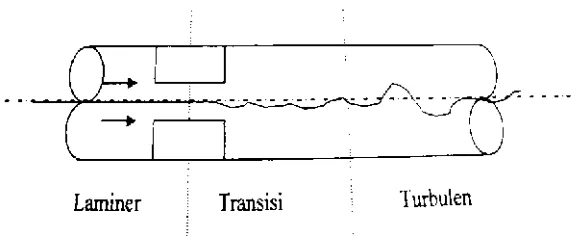
transisi. Pada gambar 2.1 berikut terlihat skema mengenai jenis aliran fluida.
Gambar 2.1: Skema aliran dalam pipa
Untuk menganalisis kedua jenis aliran ini diberikan parameter tak
berdimensi yang dikenal dengan nama bilangan Reynolds (white. 1986)
sebagai berikut:
��
=
�.� �dimana : Re = Bilangan Reynolds
D = Diameter pipa
v = Kecepatan aliran air
� = viskositas kinematis air
Daerah transisi dari aliran laminer dan turbulen terbentuk karena adanya bilangan Reynolds tertentu pada aliran laminer menjadi tidak stabil, jika
suatu gangguan kecil diberikan pada aliran,pengaruh aliran ini semakin besar. Suatu aliran dikatakan stabil bila gangguan – gangguan diredam. Ternyata pada waktu bilangan Reynold tertentu aliran pipa yang lamier
bersifat stabil untuk tiap gangguan kecil.
Karena transisi tergantung pada gangguan-gangguan yang dapat
berasal dari luar atau karena kekasaran permukaan pipa, transisi tersebut dapat terjadi dalam selang bilangan Reynolds. Dan telah diketahui bahwa aliran laminar pada kondisi dimana bilangan Reynolds lebih kecil dari 2300
( Re < 2300 ) dan turbulen jika bilangan Reynolds lebih besar dari 4000 ( Re> 4000). Dan jika bilangan Reynolds berada diantara 2300 dan 4000 (
2300 <Re> 4000) adalah merupakan daerah transisi.
2. Aliran seragam dan tak seragam
Aliran boleh dianggap seragam atau tidak seragam, tergantung pada
variasi luas potongan melintang dan kecepatan aliran dalam arah aliran.Aliran dikatakan seragam jika kecepatannya tidak bervariasi sepanjang aliran.
3. Aliran Steady dan tidak steady
Aliran disebut steady (tenang) apabila aliran disemua tempat sepanjang
lintasan tidak berubah menurut waktu, dan apabila bervariasi dikatakan tidak steady. Aliran air yang konstan di dalam pipa bersifat steady, namun pada saat katup alirannya sedang dibuka atau ditutup, maka itu tidak steady.
2.5 KECEPATAN DAN KAPASITAS ALIRAN FLUIDA
Penentuan kecepatan di beberapa titik pada suatu penampang
memungkinkan untuk membantu dalam menentukan besarnya kapasitas aliran fluida sehingga pengukuran kecepatan merupakan fase yang sangat penting dalam menganalisa suatu aliran fluida. Kecepatan dapat diperoleh dengan
melakukan pengukuran terhadap waktu yang dibutuhkan suatu partikel untuk bergerak sepanjang jarak yang telah ditentukan.
Kapasitas aliran (Q) untuk fluida yang inkompresibel, yaitu:
Q = A.V
dimana:
Q = Kapasitas aliran (m3/s)
A = Luas penampang aliran (m2)
V = Kecepatan aliran fluida (m/s)
Untuk nilai kecepatan searah gaya gravitasi, maka kecepatan dihitung
berdasarkan tinggi jatuh air atau √(2�ℎ), maka diperoleh persamaan:
Q = �2�ℎx 0,25 π D2
... ( 2.2 )
2.6 PERSAMAAN KONTINUITAS
Persamaan kontinuitas dihasilkan dari prinsip kekekalan massa.
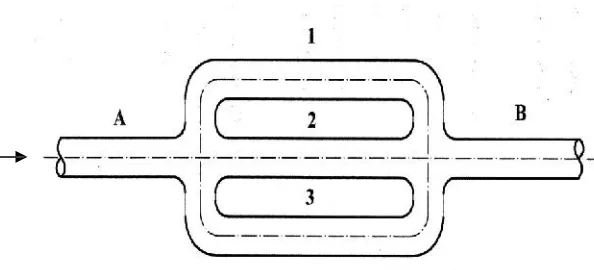
Untuk aliran mantap massa fluida yang melalui semua bagian dalam arus fluida per satuan waktu adalah sama. Untuk pipa bercabang, berdasarkan persamaan kontinuitas debit aliran yang menuju titik cabang harus sama
dengan debit yang meninggalkan titik tersebut terlihat pada gambar 2.2.
Gambar 2.2: Persamaan kontinuitas pipa bercabang
Persamaan kontinuitas untuk pipa bercabang:
V1 A1 = V2 A2 = V3 A3 =… = Vn.An
dimana:
A = luas penampang (m2)
V = kecepatan rata-rata arus aliran (m/s)
2.7 BILANGAN REYNOLDS
Ada tiga faktor yang mempengaruhi keadaan aliran yaitu kekentalan (µ), rapat massa zat cair (p), dan diameter pipa (D). Pada aliran tak
disebabkan adanya efek gesekan sebagai fungsi bilangan Reynolds. .Angka Reynolds mempunyai bentuk seperti:
Re = D.v.p /µ
dimana:
v = kecepatan rata-rata aliran (m/s)
µ = viskositas absolute (Pa/ detik)
p = kerapatan fluida (kg/m3)
Untuk angka Reynolds di bawah 2000, aliran pada kondisi tersebut adalah laminer. Aliran akan turbulen apabila angka Reynolds lebih besar 4000. Apabila angka Reynolds berada di antara kedua nilai tersebut adalah transisi.
Angka Reynolds pada kedua nilai di atas (Re = 2000 dan Re = 4000) disebut dengan batas kritik bawah dan atas (Triatmodjo, 1993).
2.8 SISTEM PERPIPAAN
Sistem perpipaan dapat ditemukan pada hampir semua jenis industri, dari sistem pipa tunggal yang sederhana sampai sistem pipa bercabang yang sangat
kompleks.
1. Sistem perpipaan tunggal
perubahan ketinggian dan total head loss merupakan fungsi dari factor gesekan, perubahan penampang.
Untuk aliran tak mampu mampat, sifat fluida diasumsikan tetap.Pada saat sistem telah ditentukan, maka konfigurasi sistem, kekasaran permukaan pipa, perubahan elevasi, dan kekentalan fluida bukan lagi
merupakan variabel bebas.
2. Sistem pipa majemuk
Pada kenyataannya kebanyakan sistem perpipaan adalah sistem pipa majemuk, yaitu rangkaian pipa seri, paralel maupun berupa jaringan perpipaan.Untuk rangkaian pipa seri maupun paralel, penyelesaiaannya
adalah serupa dengan perhitungan tegangan dan tahanan pada hukum ohm.Penurunan tekanan dan laju aliran identik dengan tegangan dan arus
pada listrik.Namun persamaannya tidak identik dengan hukum ohm, karena penurunan tekanan sebanding dengan kuadrat dari laju aliran.Semua sistem pipa majemuk lebih mudah diselesaikan dengan persamaan empiris.
Ada beberapa contoh sistem pipa majemuk, dengan memenuhi kaidah-kaidah tertentu sebagai berikut:
a. Sistem Pipa yang disusun secara seri
Gambar 2.3: Sistem pipa yang disusun secara seri
Q0 = Q1 = Q2 = ...= Qn Atau
Qn = A1 V1 = A2 V2 = A3 V3 =...=An Vn
Dan jika hL adalah rugi head untuk perlengkapan pipa dan katup, maka :
∑hL = hL1 + hL2 + hL3 +...+ hLn
b. Sistem perpipaan disusun secara paralel
Jika dua buah pipa atau lebih dipasang secara paralel,
total laju aliran sama dengan jumlah laju aliran yang melalui setiap cabang dan kerugian head, terlihat pada gambar 2.4.
Pada sebuah cabang sama dengan kerugian head pada cabang yang lain. Ini diekspresikan (Olson R.,1993) sebagai :
Gambar 2.4: Sistem pipa yang disusun secara paralel ... ( 2.6 )
... ( 2.7 )
Q0 = Q1 + Q2 + Q3+ ... +Qn
atau
Qn = A1 V1 + A2 V2 + A3 V3 +...+ An Vn atau
hL1 = hL2 = hL3 =...= hLn
Kerugian head pada setiap cabang boleh dianggap
sepenuhnya terjadi akibat gesekan, atau rugi akibat katup dan perlengkapan pipa. Kalau kerugian head totalnya (total head losses) diketahui, relatif cukup mudah untuk mencari masing-masing Q1dan menjumlahkannya. Soal sebaliknya, jika laju aliran totalnya Q yang diketahui, diperlukan
pengulangan yang lumayan jumlahnya untuk menentukan bagaimana aliran total ini terbagi kedalam ketiga cabang pipa itu. Prosedur yang biasa ialah dengan menebak Q1 = Q/3
misalnya, lalu menghitung kerugian headnya dan dari nilainya itu kita peroleh Q1 dan Q3 dan dengan menggunakan
persamaan hn= hL1 = hL2= ... = hLn.
Kemudian, kalau jumlahnya tidak betul, turunkan
tebakan yang pertama dari Q1 dan Q3, lalu kita uji lagi jumlahnya.Kalau perlu naikkan atau turunkan lagi Q1.
... ( 2.9 )
.... ( 2.10 )
c. Jaringan pipa
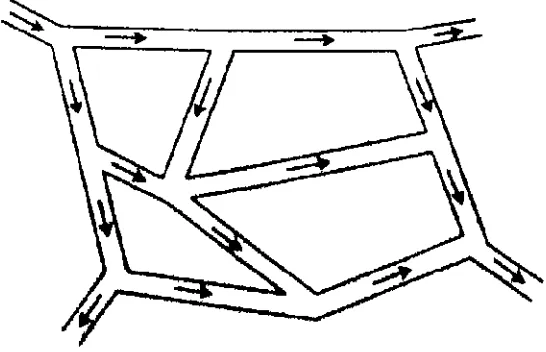
Jaringan ini merupakan saluran air yang digunakan
untuk sebuah rumah tangga, komplek perumahan maupun kota, terihat pada gambar 2.5 berikut:
Gambar 2.5: Rangkaian jaringan pipa
Dalam sistem ini tidak dapat diselesaikan dengan kaidah –
kaidah diatas karena persamaannya tidak linier , maka penyelesaiaannya diperoleh dengan iterasi numeric yang
pertama kali ditemukan oleh Hardy – Cross pada tahun 1936
2.9 KERUGIAN TINGGI TEKAN (HEAD LOSS)
Kerugian tinggi tekan (head loss) terdiri dari kerugian tinggi tekan mayor
dan kerugian tinggi tekan minor. Head losses mayor terjadi karena kerugian gesekan terjadi didalam pipa, dan kerugian head losses minor terjadi karena
Head loss merupakan hilangnya energi mekanik persatuan massa fluida. Sehingga satuan head loss adalah satuan panjang yang setara dengan satu satuan
energi yang dibutuhkan untuk memindahkan satu satuan massa fluida setinggi satu satuan panjang yang bersesuaian.
2.9.1 Mayor Head Loss
Dalam kajian ini digunakan persamaan Hazen – Williams dan
Darcy – Weisbach.
2.9.1.1. Persamaan Hazen – Williams
hf = S.L, jadi dapat diturunkan sebagai berikut:
dengan :
Q = debit aliran pada pipa (m3/s)
0,849 = konstanta
Chw = koefisien kekasaran Hazen – Williams
A = Luas penampang aliran (m2)
hf = Kehilangan tinggi tekan mayor (m)
D = Diameter pipa (m)
L = Panjang pipa (m)
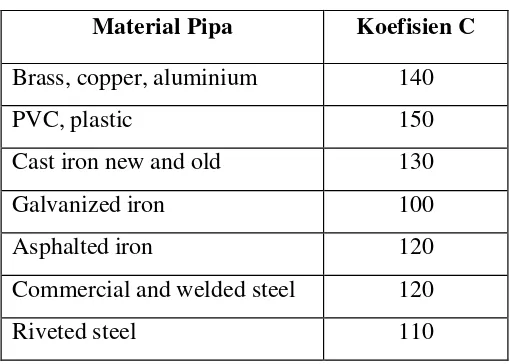
Koefisien kekasaran pipa untuk formula Hazen-Williams dapat dilihat pada tabel 2.2 berikut:
Tabel 2.2: koefisien kekasaran Hazen – Wiliam, C
Material Pipa Koefisien C
Brass, copper, aluminium 140
PVC, plastic 150
Cast iron new and old 130
Galvanized iron 100
Asphalted iron 120
Commercial and welded steel 120
Concrete 130
Wood stave 120
Sumber: Ram Gupta. S, “Hydrology & Hydraulic Engineering Systems.
Pearson. NewJersey. 1989. Hal. 550.
2.9.1.2. Persamaan Darcy – Weisbach
Persamaan Darcy – Weisbach berlaku untuk aliran laminer dan turbulen. Faktor gesekan untuk laminer dapat dihitung secara analisis,
sedangkan untuk aliran turbulen harus ditentukan secara empiris.
ℎ
�=
�.�.� 2 �.2�dimana:
hf = kerugian head karena gesekan (m)
f = faktor gesekan (diperoleh dari diagram Moody) D = diameter pipa (m)
L = panjang pipa (m)
V = kecepatan aliran fluida dalam pipa (m/s)
g = percepatan gravitasi = 9,81 m/s2
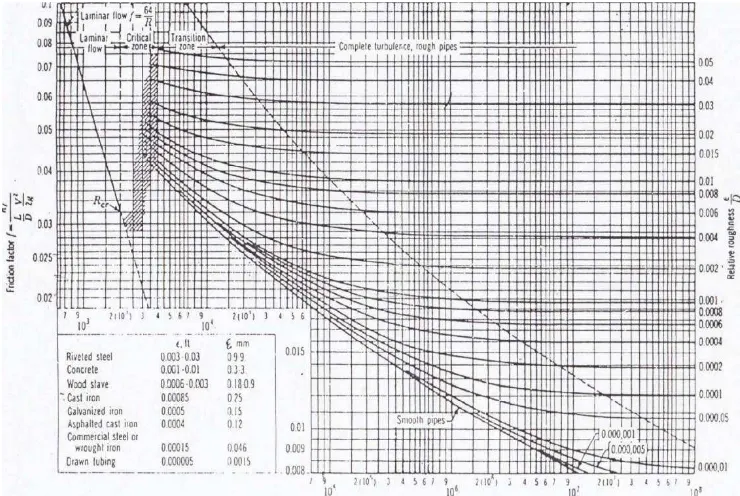
Diagram Moody (gambar 2.6) memberikan faktor gesekan pipa. Faktor ini dapat ditentukan oleh bilangan Reynold dan kekasaran relatif
dari pipa. Bila pipa semakin kasar, maka kemungkinan turbulent akan semakin besar. Kekasaran relatif dapat didefenisikan sebagai :
e/D
dengan , e = absolute roughness atau kekasaran relatif ( tergantung oleh jenis bahan material pipa)
... ( 2.15 )
D = diameter pipa
Sedangkan bilangn Reynold diidentifikasikan sebagai:
� = �.�
V = kinematic viscosity of fluid
Untuk aliran laminer nilai f dapat dicari dengan rumur sebagai berikut:
�
=
64 ��Untuk aliran turbulen dapat digunakan persamaan Swamee – Jain yang dikembangkan untuk memperoleh faktor gesekan, f selain menggunakan
diagram Moody dimana nilai Re dan e/d sudah diketahui:
Gambar 2.6: Diagram Moody
Nilai kekasaran untuk beberapa jenis pipa dapat disajikan pada tabel 2.3 berikut:
Tabel 2.3: Nilai kekerasan dinding untuk berbagai pipa komersil
Bahan
Kekasaran (ε)
mm ft
Brass 0.0015 0.000005
Concrete
-Steel forms, smooth 0.18 0.0006
Copper 0.0015 0.000005
Iron
“Fundamental of Hydraulic Engineering Systems Fourth Edition”.
Pearson. New Jersey. 2010. Hal. 83.
2.9.2 Minor Head Loss
Merupakan kehilangan tinggi energi yang terjadi karena adanya fitting dan
valve yang terdapat disepanjang sistem perpipaan. Dapat dicari dengan rumus:
n = jumlah fitting/valve untuk diameter sama
k = koefisien gesekan
V = kecepatan rata – rata aliran (m/s)
g = kecepatan gravitasi (m2/s)
2.10 METODE HARDY – CROSS
Metode Hardy – Cross adalah salah satu metode yang digunakan untuk
menyelesaikan persoalan jaringan pipa yang terdiri multi loop. Metode ini merupakan metode numerik untuk menentukan harga distribusi laju aliran dan jatuh tekanan pada loop jaringan pipa.
Metode Hardy – Cross adalah metode yang berdasarkan pada hubungan antara persamaan dasar kontinuitas dan kehilangan tinggi tekan aliran dalam pipa.
Maka dapat dijabarkan kerugian tinggi tekan (hf) pada loop:
ℎ
� = �.��Dimana n adalah konstanta, berdasarkan Darcy – weisbach n = 2, dan Hazen – Williams n = 1,85. Sementara konstanta kosreksi pipa, berdasarkan persamaan Darcy – weisbach,
�
=
8 ℎ�.� �2��5Dan berdasarkan Hazen – Williams (satuan – SI),
�
=
10,704 .� �1,85 .�4,871Dimana C adalah koefisien Hazen – Williams berdasarkan jenis pipa, L = panjang
pipa dan d = diameter pipa.
Karena metode Hardy – Cross berdasarkan persamaan kontinuitas dan
kerugian tinggi tekan aliran, maka harus memenuhi persyaratan:
... ( 2.21 )
... ( 2.22 )
1. Jumlah air yang masuk sama dengan keluar pada setiap titik percabangan.
∑ ��� = ∑ ����
2. Jumlah kerugian tinggi tekan pada tiap loop adalah sama dengan nol.
∑.���� �ℎ��= ∑������� ��� = 0
Metode Hardy – Cross adalah metode dengan menggunakan penyelesaian iterasi matematik, maka untuk persoalan jaringan pipa tersebut, langkah prosedur penyelesaiannya adalah:
1. Perkiraan secara sembarang laju aliran dan arah aliran pada masing – masing pipa pada setiap loop.
2. hitung nilai K.
3. Hitung nilai ∑���� �(±)�� ��� = 0, dimana n = 2 ( karena dalam kasus ini
menggunakan persamaan Darcy – Weisbach), dan ± adalah arah aliran pada loop
tertutup mengikuti arah jarum jam. Tanda (+) untuk arah aliran searah jarum jam dan (-) untuk arah berlawanan jarum jam.
4. Jika hasil perhitungan nomor 3 tidak sama dengan nol, maka hitung koreksi
sesatan untuk laju aliran, dengan persamaan:
∆� = ∑∑���� �(±)������
������� −1�
���� �
5. Hitung laju aliran volume perkiraan baru untuk iterasi berikutnya dengan
6. Iterasi akan dihentikan jika ∆� = 0 atau sampai batas toleransi yang ditentukan.
2.11 POMPA
Pompa adalah salah satu mesin fluida yang berfungsi untuk memberikan
energy kepada suatu fluida, dimana fluida adalah zat cair, sehingga zat cair tersebut dapat dipindahkan dari suatu tempat ke tempat lain.Dalam operasinya
pompa digerakkan oleh suatu penggerak mula, dalam hal ini dapat digunakan motor listrik maupun motor torak.
2.11.1 Pompa Sentrifugal
Merupakan suatu jenis pompa dimana headnya dibentuk oleh gaya sentrifugal maupun lift yang ditimbulkan oeh sudu – sudu yang berputar.
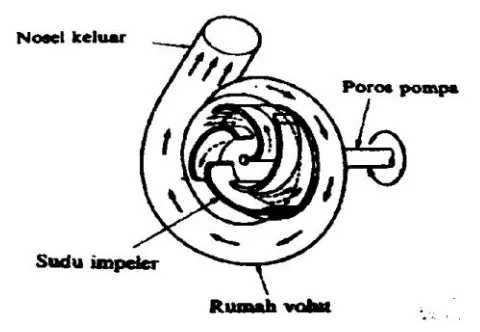
Pompa ini dapat diperlihatkan oleh gambar 2.7 dibawah ini, yang mempunyai impeler (baling – baling) untuk mengangkat air dari suatu tempat ke tempat lainnya.
Gambar 2.7: Pompa sentrifugal
sudu ikut berputar. Karena timbul gaya sentrifugal maka zat cair mengalir dari tengah impeller keluar melalui saluran diantara sudu-sudu. Disinilah
head tekanan zat cair menjadi lebih lebih tinggi demikian pula head kecepatannya bertambah besar karena zat cair mengalami percepatan. Zat cair yang keluar dari impeller ditampung oleh saluran berbentuk volut
(spiral) dikelilingi impeller dan disalurkan ke luar pompa melalui nossel.Di dalam nosel ini sebagian head kecepatan aliran diubah menjadi head tekan.
Jadi impeller pompa berfungsi untuk memberikan kerja kepada zat cair sehingga energi yang dikandungnya menjadi bertambah besar. Selisih energy satuan berat atau head total zat cair antara flens isap dan
flens keluar pompa disebut head total pompa.
Dari uaraian di atas jelas bahwa pompa sentrifugal dapat mengubah
energy mekanik dalam bentuk kerja poros menjadi energy fluida. Energi inilah yang mengakibatkan pertambahan head tekan, head kecepatan, head potensial pada zat cair yang mengalir secara kontinyu. Pada prinsipnya
pompa sentrifugal mempunyai dua komponen utama yaitu:
a. Elemen berputar yang terdiri atas : impeller dan poros
b. Elemen Stasioner (diam) yaitu rumah pompa (casing) yang
mengalirkan fluida ke impeller dengan tekanan dan kecepatan yang tinggi.
Bila head pompa hanya ditimbulkan oleh satu impeller saja, maka jenis pompa ini disebut pompa bertingkat satu (single state), tetapi
digabungkan di dalam satu urmah, dimana sisi isapnya diambil dari sisi pengeluaran impeller sebelumnya maka jenis ini disebut pompa
bertingkat ganda ( multy – stage pump) dan jenis ini digunakan jika ingin memperoleh head pompa yang besar.
2.11.2 Head Pompa
Head pompa adalah energi per satuan berat yang harus disediakan untuk
mengalirkan sejumlah zat cair yang direncanakan sesuai dengan kondisi instalasi pompa, atau tekanan untuk mengalirkan sejumlah zat cair, yang umumnya dinyatakan dalam satuan panjang. Menurut persamaan Bernoulli yang berbunyi “bila fluida inkompresibel mengalir sepanjang pipa yang penampangnya mempunyai beda ketinggian, perbedaan tekanan tidak hanya tergantung pada perbedaan ketinggian tetapi juga pada perbedaan antara kecepatan dimasing - masing titik tersebut”. Dalam persamaan Bernoulli, ada tiga macam head (energy) fluida dari sistem instalasi aliran, yaitu energi tekanan, energi kinetik dan energi
potensial.
Head dapat bervariasi pada penampang yang berbeda, tetapi pada kenyataannya selalu ada rugi energi. Head total pompa yang harus disediakan
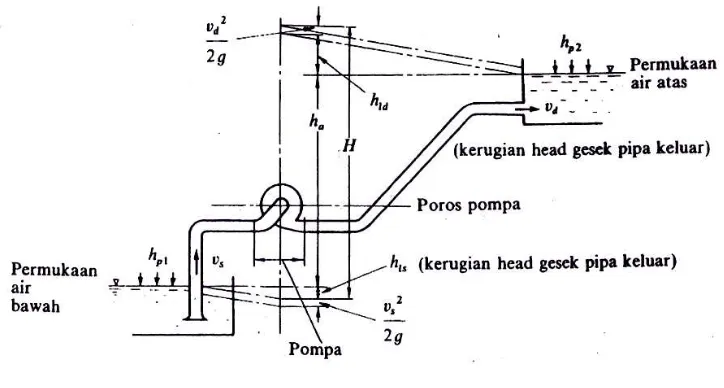
Gambar 2.8: Head Pompa
Dari gambar 2.8 kita dapat menentukan head total pompa dengan persamaan dibawah ini:
Hsis = ha + Δhp + hl +
dimana:
Hsis = head sistem pompa (m)
ha = head statis total (m)
Δhp = perbedaan head tekanan yang bekerja pada kedua permukaan (m),
∆hp = hp2 – hp1
hl = berbagai kerugian di pipa, katup , belokan, sambungan dll (m)
vd2/2g = he a d k e c e p a t a n k e l u a r ( m)
g = k e c e p a t a n g r a v i t a s i ( m/ s2)
Head total pompa salah satunya dipengaruhi oleh berbagai kerugian pada sistem perpipaan yaitu gesekan dalam pipa, katup, belokan, sambungan, reduser
dll. Untuk menentukan head total yang harus disediakan pompa, perlu menghitung terlebih dahulu kerugaian-kerugaian pada instalasi. Dimana kerugian-kerugian tersebut akan dijumlahkan untuk mengetahui kerugian head
yang terjadi dalam instalasi. Berikut akan dihitung kerugian head pemipaan dan instalasi pengujian pompa.
2.11.3 Kerugian Head
Berikut ini adalah macam – macam kerugian dalam instalasi pompa antara lain:
1. Head kerugian gesek dalam pipa lurus, dirumuskan sebagai berikut:
ℎ
�=
10,666.�2. Kerugian belokan � , dirumuskan sebagai berikut:
ℎ
�=
�.� 22�
... ( 2.29 )
dimana:
Hf = kerugian head (m)
V = kecepatan aliran (m/s)
g = kecepatan gravitasi (m/s2)
R = jari – jari lengkung belokan (m)
� = sudut belokan (%)
f = koesfisien kerugian
3. Kerugian katup isap dengan saringan
dimana:
hf = kerugian head (m)
v = kecepatan aliran (m/s) g = gaya gravitasi (m/s2)
f = koefisien kerugian katup isap 4. Kerugian akibat pengecilan penampang secara mendadak
dimana:
hf = kerugian head (m)
v2 = kecepatan aliran sisi keluar (m/s)
... ( 2.31 )
... ( 2.32 )
g = gaya gravitasi (m/s2)
f = koefisien kerugian katup isap
5. Kerugian karena pembesaran penampang secara mendadak
dimana:
hf = kerugian head (m)
v1 = kecepatan aliran sisi masuk (m/s)
v2 = kecepatan aliran sisi keluar (m/s) g = gaya gravitasi (m/s2)
f = koefisien kerugian katup isap 2.11.4 Kecepatan Spesifik
Kecepatan spesifik merupakan indeks jenis pompa yang memakai
kapasitas, putaran pompa dan tinggi tekan yang diperoleh pada titik efesiensi maksimum pompa. Kecepatan spesifik digunakan untuk menentukan bentuk umum impeller. Kecepatan spesifik dapat didefenisikan seperti persamaan
berikut:
dimana: ns = putaran spesifik
N = putaran pompa (rpm)
Q = debit aliran (m3/s)
H = head pompa (m)
... ( 2.34 )
dalam persamaan diatas digunakan untuk pompa-pompa yang sebangun bentuk impelernya, meskipun ukuran dan putarannya berbeda. Dengan kata lain harga nS dapat dipakai sebagai parameter untuk menyatakan jenis pompa. Dalam menghitung nS untuk pompa sentrifugal jenis isapan ganda (double suction) nilai Q dari persamaan adalah Q/2. Karena kapasitas aliran melalui sebelah impeler adalah setengah dari kapasitas aliran keseluruhan.
2.11.5 Penentuan Daya
Dari instalasi pengujian pompa ini dapat diketahui besarnya daya hidrolis yang dibangkitkan dan daya motor penggerak yang diperlukan untuk menggerakkannya, sehingga besarnya efesiensi dari pompa dan efesiensi dari sistem instalasi pengujian pompa dapat diketahui. Besarnya daya dan besarnya efesiensi tersebut dapat dihitung dengan rumus berikut :
2.11.5.1 Daya Hidrolis
Daya hidrolis (daya pompa teoritis) adalah daya yang diperlukan untuk mengalirkan sejumlah zat cair. Daya hidrolis dapat dihitung dengan persamaan berikut.
Ph = γ . htot . Q dimana:
Ph = daya hidrolis (Kw)
Y = berat jenis air (KN/m3)
htot = Head total (m) Q = debit aliran (m3/s)
2.11.5.2 Daya Poros
Daya poros yang diperlukan untuk menggerakan sebuah pompa adalah sama
dengan daya hidrolis ditambah kerugian daya didalam pompa. Daya ini dapat dinyatakan sebagai berikut.
dimana:
Ps = daya poros (Kw)
Ph = daya hidrolis (Kw)
�� = efisiensi pompa
2.11.5.3 Daya Motor
Daya motor dapat dihitung dengan cara menggunakan data voltase dan arus listrik dengan rumus berikut ini:
Pi = V . I . Cosθ
dimana:
Pi = Daya motor (Kw)
V = tegangan listrik (volt)
I = arus listrik (amper)
Cosθ = faktor daya
... ( 2.37 )
2.11.5.4 Efisensi pompa
Efisiensi pompa merupakan perbandingan antara output dan input atau
antara daya hidrolis pompa dengan daya poros pompa. Harga efisiensi yang tertinggi sama dengan satu harga efisiensi pompa yang didapat dari pabrik pembuatnya. Rumus efisiensi dapat dilihat seperti berikut ini.
��
=
�ℎ��
�
100%
Ps = daya poros (Kw)
Ph = daya hidrolis (Kw)
�� = efisiensi pompa
2.11.6 Karakteristik Pompa
Karakteristik dari pompa sentrifugal merupakan hubungan antara tekanan yang dibangkitkan (head) dan kecepatan aliran volum (kapasitas). Karakteristik dapat juga menyertakan kurva efisiensi dan harga brake horse power-
nya. Karakteristik pompa sentrifugal dapat digambarkan dalam kurva karakteristik yang melukiskan jalannya lintasan dan besaran-besaran tertentu
terhadap besaran kapasitas, besaran-besaran itu adalah:
• Head pompa (H) • Daya pompa (P) • Efisiensi pompa (n)
Karakteristik pompa berbeda-beda berdasarkan pada jenis pompa, putaran spesifik dan pabrik pembuatnya. Contoh karakteristik sebuah pompa
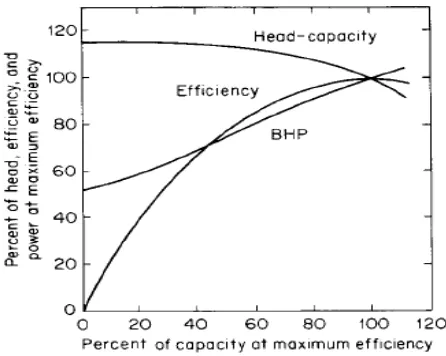
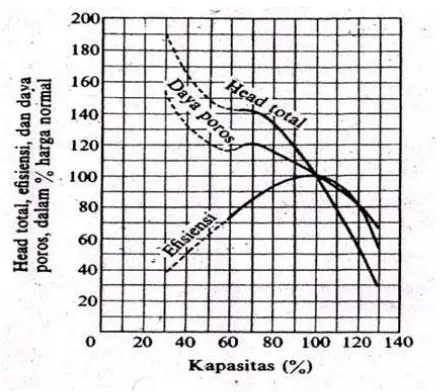
dapat digambarkan dalam gambar 2.9. Kurva-kurva karakteristik, yang menyatakan besarnya head total pompa, daya poros, dan efesiensi pompa, terhadap kapasitas. Kurva performansi tersebut, pada umumnya digambarkan
pada putaran yang tetap. Kurva efesiensi terhadap kapasitas dari pompa sentrifugal umumnya berbentuk lengkung seperti kurva berikut ini:
Gambar 2.9: kurva head, efisiensi dan daya
Dari grafik tersebut terlihat bahwa kurva head – kapasitas menjadi semakin curam pada pompa dengan harga ns yang semakin besar. Disini head pada kapasitas nol (shut of head) semakin tinggi pada ns yang semakin besar.
Kurva daya terhadap kapasitas mempunyai harga minimum apabila kapasitas aliran sama dengan nol pada pompa sentrifugal dengan ns kecil. Kurva efisiensi
Dalam memilih pompa yang tepat bagi keperluan tertentu, karakteristik pompa sangat penting untuk diperhatikan dan dipertimbangkan. Pompa sangat penting untuk diperhatikan dan dipertimbangkan. Seperti gambar 2.10 kurva karateristik pompa volut, gambar 2.11 karakteristik pompa aliran campur, gambar 2.12 kurva karakteristik aliran aksial.
Gambar 2.10: kurva karakteristik pompa volut
Gambar 2.12: kurva karakteristik aliran aksial 2.12 OPERASI SERI DAN OPERASI PARALEL POMPA 2.12.1 Operasi seri dan paralel dengan karakteristik pompa sama
Jika head atau kapasitas yang diperlukan tidak dapat dicapai dengan satu
pompa saja, maka dapat digunakan dua pompa atau lebih yang disusun secara seri atau paralel.
2.12.1.1 Susunan Seri
Bila head yang diperlukan besar dan tidak dapat dilayani oleh satu pompa, maka dapat digunakan lebih dari satu pompa yang disusun secara seri.
Penyusunan pompa secara seri dapat digambarkan pada gambar 2.13 berikut.
2.12.1.2 Susunan Paralel
Susunan paralel dapat digunakan bila diperlukan kapasitas yang besar
yang tidak dapat dihandle oleh satu pompa saja, atau bila diperlukan pompa cadangan yang akan dipergunakan bila pompa utama rusak/diperbaiki. Penyusunan pompa secara paralel dapat digambarkan pada gambar 2.14 berikut.
Gambar 2.14: Susunan Paralel
Pada gambar 2.15, digambarkan grafik operasi seri dan paralel dari pompa-
pompa dengan karakteristik yang sama.
Gambar 2.15: Operasi seri dan paralel dari pompa-pompa dengan
Gambar 2.15. menunjukan kurva head – kapasitas dari pompa-pompa yang mempunyai karakteristik yang sama yang di pasang secara paralel atau
seri. Dalam gambar ini kurva untuk pompa tunggal diberi tanda (1) dan untuk susunan seri yang terdiri dari dua buah pompa diberi tanda (2). Harga head kurva (2) diperoleh dari harga head kurva (1) dikalikan (2) untuk
kapasitas (Q) yang sama. Kurva untuk susunan paralel yang terdiri dari dua buah pompa, diberi tanda (3). Harga kapasitas (Q) kurva (3) ini diperoleh
dari harga kapasitas pada kurva (1) dikalikan (2) untuk head yang sama.
Dalam gambar ditunjukkan tiga buah kurva head-kapasitas sistem, yaitu R1, R2, dan R3. Kurva R3 menujukkan tahanan yang lebih tinggi dibanding
dengan R2 dan R1.
Jika sistem mempunyai kurva kapasitas head R3, maka titik kerja pompa 1 akan terletak di (D). Jika pompa ini disusun seri sehingga menghasilkan kurva (2) maka titik kerja akan pindah ke (E). Disini terlihat bahwa head titik (E)
tidak sama dengan dua kali lipat head (D), karena ada perubahan (berupa kenaikan) kapasitas.
Sekarang jika sistem mempunyai kurva head-kapasitas R1 maka titik
kerja pompa (1) akan terletak di (A). Jika pompa ini disusun paralel
sehingga menghasilkan kurva (3) maka titik kerjanya akan berpindah ke (B). Disini terlihat bahwa kapasitas dititik (B) tidak sama dengan dua kali lipat kapasitas dititik (A), karena ada perubahan (kenaikan) head system.
Jika sistem mempunyai kurva karakteristik seperti R2 maka laju aliran
adalah seperti R1 dan R3 maka akan diperlukan pompa dalam susunan
paralel atau seri. Susunan paralel pada umumnya untuk laju aliran besar, dan
susunan seri untuk head yang tinggi pada operasi. Untuk susunan seri, karena pompa kedua menghisap zat cair bertekanan dari pertama, maka perlu perhatian
khusus dalam hal kekuatan konstruksi dan kerapatan terhadap kebocoran dari rumah pompa.
2.12.2 Operasi paralel dengan karakterisktik pompa berbeda
Pompa-pompa yang berbeda karakteristiknya dapat pula bekerjasama secara paralel. Hal ini ditunjukkan dalam gambar 2.16. Dimana pompa (1)
mempunyai kapasitas kecil dan pompa (2) mempunyai kapasitas besar.
Gambar 2.16: operasi paralel dari pompa – pompa dengan karakteristik berbeda
Jika keduanya dipasang secara paralel maka akan menghasilkan kurva karakteristik (3). Disini, untuk kurva head-kapasitas sistem R1 akan dicapai titik
(1) beroperasi dititk (D) dengan kapasitas Q1 dan pompa (2) beroperasi dititik (E) dengan kapasitas Q2. Laju aliran total Q = Q1 + Q2.
Apabila kurva head-kapasitas sistem naik lebih curam dari pada R2, maka pompa (1) tidak dapat lagi menghasilkan aliran keluar karena head yang dimiliki tidak tinggi untuk melawan head sistem. Bahkan jika head sistem
lebih tinggi dari pada head ini pompa, aliran akan membalik masuk kedalam pompa (1). Untuk mencegah aliran balik ini pompa perlu dilengkapi dengan katup cegah (check valve) pada pipa keluarnya. Kondisi operasi seperti ini pada
umumnya tidak dikehendaki. Jadi untuk operasi paralel sebaiknya dipakai pompa-pompa dengan head tertutup (shut-off head) yang tidak terlalu berbeda.
2.12.3 Operasi Seri dengan Karakteristik Pompa Berbeda
Pada gambar 2.17. memperlihatkan karakteristik susunan seri dari dua
buah pompa yang mempunyai karakteristik berbeda. Kurva (1) adalah dari pompa kapasitas kecil, kurva (2) dari pompa kapasitas besar, dan kurva (3) merupakan karakteristik operasi kedua pompa dalam susunan seri.
Jika sistem pipa mempunyai kurva karakteristik R1 maka titik