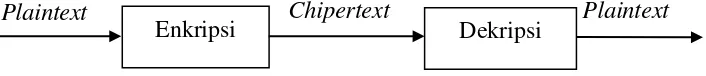BAB II
LANDASAN TEORI
2.1. Kompresi
2.1.1. Definisi Kompresi
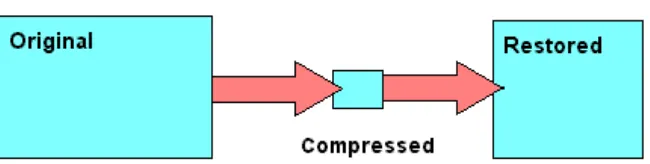
Kompresi data adalah ilmu atau seni yang merepresentasikan informasi dalam bentuk yang lebih compact (Shanmugasundaram, 2011). Istilah kompresi tersebut diterjemahkan dari kata bahasa Inggris “compression” yang berarti pemampatan. Dalam bidang teknik, kompresi berarti proses memampatkan sesuatu yang berukuran besar sehingga menjadi kecil. Dengan demikian, kompresi data berarti teknik untuk mengurangi ukuran data agar penyimpanannya jauh lebih padat dan juga untuk mengurangi waktu pengiriman data tersebut (Budiman & Rachmawati, 2017). Kompresi data bertujuan untuk mengurangi jumlah bit yang digunakan untuk menyimpan atau mengirimkan informasi (Gailly, 1995).
Tujuan daripada kompresi data tidak lain adalah untuk mengurangi data yang berlebihan (Redundancy Data) sehingga ukuran data menjadi lebih kecil dan lebih ringan sehingga mengurangi biaya untuk penyimpanan (Rani, 2016).
Gambar 2.1 Diagram Blok Proses Kompresi dan Dekompresi Data (Pu, 2006)
2.1.2. Penggolongan Kompresi
Secara garis besar terdapat 2 buah penggolongan algoritma kompresi data yaitu kompresi lossy dan kompresi lossless (Merdiyan, M. 2005).
1. Kompresi Lossless merupakan metoda kompresi data yang memungkinkan data asli dapat disusun kembali dari data hasil kompresi maka rasio kompresi pun tidak dapat terlalu besar untuk memastikan semua data dapat dikembalikan ke bentuk semula (Sidhu et al, 2014). Contoh metode ini adalah Levenstein Code, Elias
Gamma Code, Shannon-Fano Coding, Huffman Coding, Arithmetic Coding, Run
Length Encoding dan lain-lain.Konsep dasar kompresi lossless dapat dilihat pada Gambar 2.2.
Gambar 2.2. Ilustrasi Kompresi Lossless (Sayood, 2006)
2. Kompresi Lossy adalah suatu metode untuk mengkompresi dan mendekompresi data yang dimana data setelah didekompresi mungkin berbeda dari data aslinya, tetapi perbedaan itu cukup dekat (Sidhu et al, 2014). Metode ini paling sering digunakan untuk kompres data multimedia (Audio file dan gambar). Format kompresi Lossy mengalami generation loss yaitu jika mengalami proses kompresi-dekompresi berulang kali maka akan menyebabkan kehilangan kualitas secara progresif. Contoh metode ini adalah Transform Coding, Wavelet, dan lain-lain.Konsep dasar kompresi lossy dapat dilihat pada Gambar 2.3.
Uncompressed Data Kompresi Compressed Data
Gambar 2.3. Ilustrasi Kompresi Lossy (Sayood, 2006)
2.1.3. Pengukuran Kinerja Kompresi Data
Ada beberapa faktor pembanding yang digunakan dalam penelitian ini, yaitu Ratio of Compression (RC), Compression Ratio (CR), Redundancy (Rd).
1. Ratio of Compression (Rc)
Ratio of Compression (Rc) adalah perbandingan antara ukuran data sebelum dikompresi dengan ukuran data setelah dikompresi (Salomon, 2007).
2. Compression Ratio (Cr)
Compression Ratio (Cr) adalah persentasi besar data yang telah dikompresi yang didapat dari hasil perbandingan antara ukuran data setelah dikompresi dengan ukuran data sebelum dikompresi (Salomon, 2007).
3. Saving Percentages / Space Saving (SS)
Saving Percentages menghitung persentasi penyusutan dari data sebelum dilakukan kompresi (Rani, 2016).
2.1.4. Konsep Kompresi Data
yang lebih pendek dibandingkan oleh bit-bit data sebelum dikompresi. Bit-bit data yang lebih pendek tersebut biasanya tidak akan bisa dibaca oleh komputer sebelum dilakukan proses encoding. Didalam komputer satu karakter direpresentasikan oleh bilangan ASCII (American Standard Code For Information Interchange) sebanyak delapan bit dalam bilangan biner. Jika ternyata jumlah bit-bit data tersebut bukan merupakan kelipatan delapan. Maka dibentuk variabel baru sebagai penambahan ke bit-bit data itu agar bit-bit data tersebut habis dibagi delapan. Variabel ini adalah padding dan flag bits.
1. Flag Bits
Flag bits adalah penambahan bilangan biner sepanjang delapan bit setelah padding dimana flag bits ini adalah sejumlah bilangan yang memberikan sebuah tanda bahwa terdapat n buah padding di dalam bit-bit data hasil dari kompresi. Penambahan flag bits ini dimaksudkan untuk mempermudah dalam membaca bit-bit data hasil kompresi pada saat proses dekompresi. Contoh misalkan bit-bit data yang telah diberikan padding adalah 10010110. Karena terdapat 1 bit penambahan padding maka flag bitsnya adalah bilangan biner dari 1 dengan panjang 8 bit yaitu 00000001. Sehingga bit-bit datanya menjadi 1001011000000001 setelah diberikan flag bits.
2. Padding
Padding adalah penambahan bit 0 sebanyak kekurangan jumlah bit-bit data pada hasil proses kompresi sehingga jumlah keseluruhan bit-bit data tersebut merupakan kelipatan delapan (habis dibagi delapan). Contoh misalkan dihasilkan bit-bit data hasil kompresi yaitu 1001011. Terdapat 7 bit data dalam bilangan biner. Maka dilakukan penambahan bit 0 sebanyak 1 kali agar jumlah bit-bit data tersebut habis dibagi delapan. Sehingga bit bit data itu menjadi 10010110 setelah diberikan padding.
2.1.5. Algoritma Levenstein Code
Pada tahun 1968 Vladimir Levenstein mengembangkan kode Levenstein yang dapat digunakan untuk bilangan bulat non-negatif. Proses encoding dan decoding dilakukan dibeberapa tahap (Antoni et al, 2014).
1. Set angka pertama dari C dengan 1. Letakkan kode-sejauh-ini pada string kosong. 2. Ambil nilai biner dari n tanpa angka 1 (buang indeks ke-0 dari nilai biner) di awal dan tambahkan pada kode-sejauh-ini.
3. Nyatakan M sebagai jumlah bit yang ditambahkan pada tahap 2.
4. Jika M ≠ 0, tambahkan C dengan 1 dan lakukan langkah 2 kembali, tetapi dengan nilai M, bukan n.
5. Jika M = 0, tambahkan 1 sejumlah diikuti dengan 0 ke kode-sejauh-ini dan berhenti.
Untuk contoh kasus, kita anggap . Nilai biner dari 4 adalah “100”, kita ambil “00” dan didapatkan dan � maka kode sejauh ini adalah “00”. Kemudian hitung nilai biner dari yaitu “10”, kita ambil “0” dan didapatkan dan � maka kode sejauh ini adalah “000”. Kemudian hitung nilai biner yaitu “1”, kita ambil ” ” dan didapatkan maka kode sejauh ini adalah “000”. Karena maka kode adalah tambahkan “1” sejumlah � yaitu 3 diikuti “0” dan digabungkan dengan kode sejauh ini sehingga menjadi 1110000. Sehingga 4 pada kode Levenstein adalah 1110|0|00.
Tabel 2.1 Tabel Kode Levenstein (Salomon, 2007) n Kode Levenstein N Kode Levenstein
0 0 9 11100 1 001
1 10 10 11100 1 010
2 110 0 11 11100 1 011 3 110 1 12 11100 1 100 4 1110 0 00 13 11100 1 101 5 1110 0 01 14 11100 1 110 6 1110 0 10 15 11100 1 111 7 1110 0 11 16 111100 0 00 0000 8 11100 1 000 17 111100 0 00 0001
Decoding dilakukan dengan Brute Force Decoding sebagai berikut: 1. Baca flag bits (8 bit paling akhir) untuk mengetahui jumlah padding bits. 2. Periksa mulai dari bit pertama (paling kiri),
4. Bila bit ke- tidak terdapat dalam tabel, baca string di depannya, bit sampai kumpulan bit tersebut terdapat dalam tabel.
5. Lakukan langkah 3 dan 4 sampai batas sebelum padding.
2.2. Kriptografi
2.2.1. Definisi Kriptografi
Kriptografi berasal dari Bahasa Yunani : “cryptos” artinya rahasia, sedangkan
“graphein” artinya tulisan. Kriptografi adalah ilmu mengenai teknik enkripsi dimana data diacak menggunakan suatu kunci enkripsi menjadi sesuatu yang sulit dibaca oleh seseorang yang tidak memiliki kunci dekripsi (Kromodimoeljo, 2009). Kriptografi adalah suatu ilmu dan seni untuk menjaga kerahasiaan pesan dengan cara menyandikan ke dalam bentuk yang tidak dapat dimengerti maknanya.
Fungsi-fungsi mendasar dalam kriptografi adalah enkripsi dan dekripsi. Enkripsi adalah proses mengubah suatu pesan asli (plaintext) menjadi suatu pesan dalam bahasa sandi (ciphertext). Enkripsi bisa diartikan dengan cipher atau kode, dimana pesan asli (plaintext) diubah menjadi kode-kode tersendiri sesuai metode yang disepakati kedua belah pihak, baik pengirim maupun penerima (Prerna et al, 2014). Sedangkan dekripsi adalah proses mengubah pesan dalam suatu bahasa sandi (ciphertext) menjadi pesan asli (plaintext) kembali. Urutan proses kriptografi dapat dilihat pada Gambar 2.4 berikut :
Gambar 2.4 Urutan proses kriptografi (Widyartono, A. 2011). 2.2.2. Tujuan Kriptografi
Kriptografi bertujuan untuk memberikan layanan keamanan (Kurniawan, Y. 2004) sebagai berikut:
1. Kerahasiaan (Confidentiality)
Layanan yang ditujukan untuk menjaga pesan tidak dapat dibaca oleh pihak-pihakyang tidak berhak.
2. Keutuhan Data (Integrity)
Penerima harus dapat memeriksa apakah pesan telah dimodifikasi ditengah jalanatau tidak. Seorang penyusup seharusnya tidak dapat memasukkan tambahan
kedalam pesan, mengurangi atau mengubah pesan selama data berada diperjalanan.
3. Autentikasi (Message Authentication)
Penerima pesan dapat memastikan keaslian pengirimnya. Penyerang tidak dapat berpura- pura sebagai orang lain.
4. Menolak Penyangkalan (Nonrepudiation)
Pengirim seharusnya tidak dapat mengelak bahwa dialah pengirim pesan yang sesungguhnya. Tanpa kriptografi, seseorang dapat mengelak bahwa dialah pengirim email yang sesungguhnya.
2.2.3. Sistem Kriptografi
Sistem kriptografi adalah algoritma, seluruh kemungkinan plaintext, ciphertext dan kunci. P adalah notasi yang digunakan untuk plaintext, C adalah ciphertext, E adalah fungsi enkripsi dan D adalah fungsi dekripsi (Schneier, 1996). Sedangkan untuk kunci dapat dinotasikan sebagai K.
Berdasarkan kunci yang dipakai, algoritma kriptografi dibagi menjadi tiga, yaitu algoritma simetri (menggunakan satu kunci untuk enkripsi dan dekripsi), algoritma asimetri (menggunakan kunci yang berbeda untuk enkripsi dan dekripsi) dan fungsi hash (Ariyus, 2008).
Selain berdasarkan kunci yang dipakai, karakteristik kriptografi juga dibagi berdasarkan tipe operasi yang dipakai untuk enkripsi dan dekripsi serta berdasarkan tipe pengolahan pesan (Sadikin, 2012).
2.2.4. Jenis Kriptografi
Algoritma Kriptografi dibagi tiga berdasarkan kunci yang dipakai, yaitu algoritmasimetri (menggunakan satu kunci untuk proses enkripsi dan dekripsi), algoritmaasimetri (menggunakan kunci yang berbeda untuk proses enkripsi dan dekripsi), dan fungsi hash (Ariyus, 2008).
1. Kriptografi Simetri
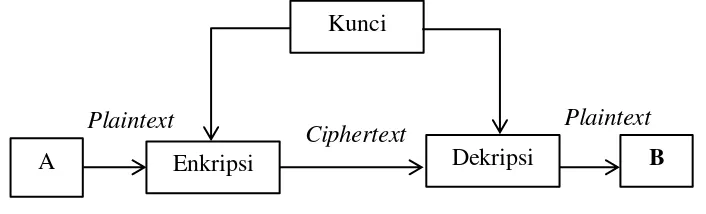
konvensional (conventional cryptography). Skema Algoritma Simetri dapat dilihat pada Gambar2.5.
Gambar 2.5 Skema Algoritma Simetris (Halim, A. 2013)
Sebelum melakukan pengiriman pesan, pengirim dan penerima harus memilih suatu kunci tertentu yang sama untuk dipakai bersama, dan kunci ini haruslah rahasia bagi pihak yang tidak berkepentingan sehingga algoritma ini disebut juga algoritma kunci rahasia (secret-key algorithm) (Ayushi, 2010). Jika kunci tersebut diketahui oleh orang lain maka orang tersebut dapat melakukan enkripsi dan dekripsi pada pesan. Yang termasuk algoritma kunci simetris adalah Hill Cipher, Affine Cipher, OTP, DES, RC2, RC4, RC5, IDEA, Twofish, Magenta, FEAL, dan lain-lainnya.
2. Kriptografi Asimetri
Algoritma asimetris disebut juga dengan kriptografi kunci publik karena algortima ini memiliki kunci yang berbeda untuk enkripsi dan dekripsi, dimana enkripsi menggunakan public key dan untuk dekripsinya menggunakan private key. Public key dan private key harus saling berpasangan secara matematis. Dengan memberikan publickey, pembuat kunci berhak memberikan dan mendapatkan public key agar pesan aman dan hanya bisa dibaca oleh si pembuat kunci. Dalam kriptografi kunci asimetri, hampirsemua algoritma kriptografinya menggunakan konsep kunci publik, seperti
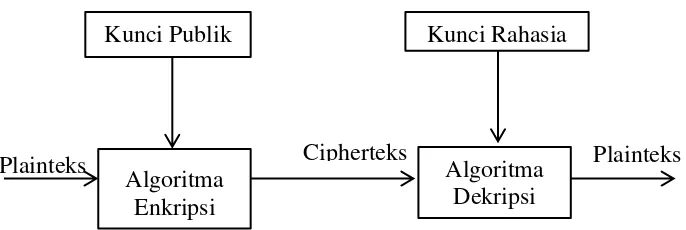
Rivest Shamir-Adleman (RSA), El-Gamal, Rabin dan sebagainya (Harahap, 2014). Skema kriptografi asimetris ditunjukkan secara umum pada Gambar 2.6.
Kunci
Enkripsi Dekripsi B
A
Plaintext
Gambar 2.6 Skema Algoritma Asimetris ( Halim, A. 2013)
Kriptografi asimetri ini dapat dianalogikan seperti kotak surat yang terkunci dan memiliki lubang untuk memasukan surat. Setiap orang dapat memasukkan surat ke dalam kotak surat tersebut, tetapi hanya pemilik surat yang memiliki kunci dan yang dapat membuka kotak surat. Kunci publik dapat dikirim ke penerima melalui saluran yang sama dengan saluran yang digunakan untuk mengirim pesan, tidak perlu takut, karena pihak yang tidak berkepentingan tidak akan dapat mendekripsi pesan tersebut, karena tidak memiliki kunci privat.
3. Fungsi Hash
Fungsi hash adalah sebuah fungsi yang masukannya adalah sebuah pesan dan keluarannya adalah sebuah sidik pesan (message fingerprint) (Ariyus, 2008).
Fungsi hash sering disebut dengan fungsi hash satu arah (one-way function), message digest, fingerprint, fungsi kompresi dan message authentication code (MAC) yang merupakan suatu fungsi matematika yang mengambil masukan panjang variabel dan mengubahnya ke dalam urutan biner dengan panjang yang tetap. Fungsi hash biasanya diperlukan bila ingin membuat sidik jari dari suatu pesan. Sidik jari pada pesan merupakan suatu tanda bahwa pesan tersebut benar-benar berasal dari orang yang diinginkan (Ariyus, 2008). Beberapa fungsi hash yang banyak dipakai adalah MD5 dan SHA.
2.2.5. Algoritma Hill Cipher
Hill Cipher termasuk dalam salah satu kriptosistem polialfabetik, artinya setiap karakter alfabet bisa dipetakan ke lebih dari satu macam karakter alfabet. Lester S.Hill yang menemukan Hill Cipher pada tahun 1929.Teknik Hill Cipher dikembangkan oleh Lester S.Hill pada Hunter Collage. Hill Cipher menggunakan matriks untuk
Kunci Publik
Algoritma Enkripsi
Algoritma Dekripsi
Plainteks Cipherteks Plainteks
mentransformasi string berupa blok huruf (Simamora,2015).
Misalkan m adalah bilangan bulat positif, dan � � 26 � misalkan K ={� � merupakan matriks yang nilai elemennya terdiri dari 26}, maka untuk suatu kunci K, dapat didefenisikan � ��� dan �
��� dimana semua operasi dilakukan dalam matriks 26.
Cara kerja Hill Cipher dapat disederhanakan dengan cara perkalian dengan matriks kunci (K). K merupakan sebuah matriks kunci � � yang invertible, yaitu memiliki multiplicative inverse sehingga ∙ . Kunci harus memiliki invers karena matriks tersebut adalah kunci yang digunakan untuk melakukan dekripsi. Cara mencari matriks kunci itu sendiri adalah dengan mencari GCD (Greatest Common Divisor) dari matriks K tersebut. Cara kerja Hill Cipher dapat diuraikan sebagai berikut. Pertama tentukan matriks kunci secara acak. Misal matriks kuncinya:
( )
Lalu buktikan matriks kunci tersebut apakah mempunyai invers atau tidak. Syarat matriks punya invers yaitu determinan matriks . Jika sudah memenuhi syarat, maka selanjutnya buktikan � � .Sebagai contoh, buktikan apakah matriks kunci ini mempunyai invers apabila diketahui :
( ) Determinan matriks :
( )
Setelah didapat determinan maka dilakukan pembuktian selanjutnya : � �
��� ���
Maka terbukti matriks diatas merupakan matriks kunci karena memenuhi syarat yaitu � � . Setelah mendapatkan matriks kunci, maka rumus enkripsi dan dekripsi sebagai berikut:
Dimana :
� � � �
� � � �
� �
�
Langkah-langkah untuk proses enkripsi plaintext dengan Hill Cipher adalah sebagai berikut (Ramadhani, 2016) :
1. Pilih suatu matriks kunci yang berupa matriks bujur sangkar yang dipakai sebagai kunci.
2. Transformasikan tiap huruf dalam teks ke bilangan bulat yang sesuai .
3. Kelompokkan barisan angka yang didapat ke dalam beberapa blok vektor � yang panjangnya sama dengan ukuran matriks .
4. Hitung � ∙ � ��� untuk tiap vektor �.
5. Kembalikan tiap angka dalam vektor sandi � ke huruf yang sesuai untuk mendapatkan teks sandi. Skema kerja enkripsi Hill Cipher dapat dilihat pada Gambar 2.7.
Gambar 2.7 Illustrasi Enkripsi Hill Cipher
Untuk mentransformasikan plaintext maka pertama sekali semua alphanumerik dinyatakan dalam Tabel 2.2 seperti berikut:
Tabel 2.2 Transformasi Alphanumerik
Algoritma proses pendekripsian Hill Cipher dapat diuraikan dalam bentuk langkah-langkah sebagai berikut (Ramadhani, 2016) :
1. Hitung matriks ��� sebagai kunci pembuka. ada jika � � .
2. Transformasikan tiap huruf dalam teks ke bilangan bulat yang sesuai .
3. Kelompokkan barisan angka yang didapat ke dalam beberapa blok vektor � yang panjangnya sama dengan ukuran matriks .
4. Hitung � ∙ � ��� untuk tiap vector �.
5. Kembalikan tiap angka dalam vektor sandi � ke huruf yang sesuai untuk mendapatkan teks sandi. Gambar 2.8 berikut adalah ilustrasi dekripsi Hill Cipher
Gambar 2.8 Illustrasi Dekripsi Hill Cipher
Contoh : Kode Hill dengan mengunakan matriks 3×3 dengan kunci matriks :
( )
Ciphertext adalah “MAWQYC”.
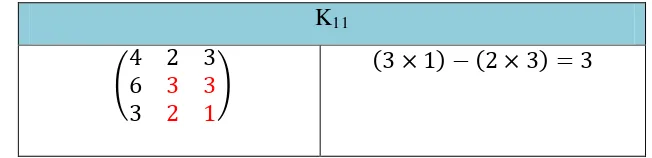
a. Cari Adjoint yaitu transpose matriks kofaktor dari matriks K yang ditunjukkan pada Tabel 2.4.
Tabel 2.4 Adjoint dari Matriks K K11
(
)
Hitung
Plaintext
Ciphertext
Tranformasi ke Bentuk Nilai
Tranformasi ke Bentuk Huruf
Susun Matriks Dalam Bentuk
Matriks C
K12
( )
K13
(
)
K21
(
)
K22
( )
K23
(
)
K31
(
)
K32
(
)
K33
( )
Maka didapatkan adjoint dari matriks K adalah :
� ( 2 2 22 2
2
)
� ( )
b. Cari determinan matriks K :
( )
c. Cari invers determinan K
�
��� ��� ���
��� Kemudian cari nilai X seperti pada tabel 2.5.
Tabel 2.5 Proses Pencarian Invers determinan X ���
1 3
2 6
3 9
4 12
9 1
d. Kemudian cari .
( f. Proses dekripsi dapat dilihat pada tabel 2.6.
Tabel 2.6 Dekripsi Hill Cipher
Jadi, Dekripsi dari “MAWQYC” adalah “SEMOGA” .
2.3. File Teks
Masukan dan keluaran data teks direpresentasikan sebagai set karakter atau sistem kode yang dikenal oleh sistem komputer. Ada tiga macam set karakter yang umum digunakan untuk masukan dan keluaran pada komputer, yaitu ASCII, Unicode, dan EBCDIC, ASCII (American Standard Code for Information Interchange) merupakan suatu standar internasional dalam kode huruf dan simbol seperti Hex, dan Unicode tetapi ASCII bersifat lebih universal. ASCII digunakan oleh komputer dan alat komunikasi lain untuk menunjukkan teks. Kode ASCII memiliki komposisi bilangan biner sebanyak 8 bit, dimulai dari 00000000 dan 11111111. Total kombinasi yang dihasilkan sebanyak 256, dimulai dari kode 0 hingga 255 dalam sistem bilangan desimal. Unicode adalah suatu standar industri yang dirancang untuk mengizinkan teks dan simbol dari semua sistem tulisan di dunia untuk ditampilkan dan dimanipulasi secara konsisten oleh komputer. EBCDIC (Extended Binary Code Decimal Interchange Code) merupakan set karakter yang diciptakan oleh komputer merk IBM. EBCDIC terdiri dari 256 karakter yang masing-masing berukuran 8 bit (Sudewa, 2003). Kode ASCII dapat dilihat pada tabel 2.7 berikut:
Tabel 2.7 Kode ASCII
Dec Char Dec Char Dec Char Dec Char Dec Char Dec Char
0 NUL 43 + 86 V 129 HOP 172 ¬ 215 ×
1 SOH 44 , 87 W 130 BPH 173 - 216 Ø
2 STX 45 - 88 X 131 NBH 174 ® 217 Ù
3 ETX 46 . 89 Y 132 IND 175 ¯ 217 Ú
4 EOT 47 / 90 Z 133 NEL 176 ° 218 Û
5 ENQ 48 0 91 [ 134 SSA 177 ± 219 Ü
6 ACK 49 1 92 \ 135 ESA 178 ² 220 Ü
7 BEL 50 2 93 ] 136 HTS 179 ³ 221 Ý
8 BS 51 3 94 ^ 137 HTJ 180 ´ 222 Þ
9 TAB 52 4 95 _ 138 VTS 181 µ 223 ß
10 LF 53 5 96 ` 139 PLD 182 ¶ 224 à
11 VT 54 6 97 A 140 PLU 183 · 225 á
12 FF 55 7 98 B 141 RI 184 ¸ 226 â
14 SO 57 9 100 D 143 SS3 186 º 228 ä
15 SI 58 : 101 E 144 DCS 187 » 229 å
16 DLE 59 ; 102 F 145 PU1 188 ¼ 230 æ
17 DC1 60 < 103 G 146 PU2 189 ½ 231 ç
18 DC2 61 = 104 H 147 STS 190 ¾ 232 è
19 DC3 62 > 105 I 148 CCH 191 ¿ 233 é
20 DC4 63 ? 106 J 149 MW 192 À 234 ê
21 NAK 64 @ 107 K 150 SPA 193 Á 235 ë
22 SYN 65 A 108 L 151 EPA 194 Â 236 ì
23 ETB 66 B 109 M 152 SOS 195 Ã 237 í
24 CAN 67 C 110 N 153 SGCI 196 Ä 238 î
24 EM 68 D 111 O 154 SCI 197 Å 239 ï
26 SUB 69 E 112 P 155 CSI 198 Æ 240 ð
27 ESC 70 F 113 Q 156 ST 199 Ç 241 ñ
28 FS 71 G 114 R 157 OSC 200 È 242 ò
29 GS 72 H 115 S 158 PM 201 É 243 ó
30 RS 73 I 116 T 159 APC 202 Ê 244 ô
31 US 74 J 117 U 160 Space 203 Ë 245 õ
32 (space) 75 K 118 V 161 ¡ 204 Ì 246 ö
33 ! 76 L 119 W 162 ¢ 205 Í 247 ÷
34 " 77 M 120 X 163 £ 206 Î 248 ø
35 # 78 N 121 Y 164 ¤ 207 Ï 249 ù
36 $ 79 O 122 Z 165 ¥ 208 Ð 250 ú
37 % 80 P 123 { 166 ¦ 209 Ñ 251 û
38 & 81 Q 124 | 167 § 210 Ò 252 ü
39 ' 82 R 125 } 168 ¨ 211 Ó 253 ý
40 ( 83 S 126 ~ 169 © 212 Ô 254 Þ
41 ) 84 T 127 • 170 ª 213 Õ 255 ÿ
2.4. Penelitian yang Relevan
Berikut ini beberapa penelitian yang terkait dengan algoritma RSA dan Levenstein: a. Erdiansyah, Umri (2014) dalam skripsi yang berjudul Perbandingan Algoritma
Elias Delta Code Dengan Levenstein Untuk Kompresi File Teks. Dalam skripsi ini, dapat disimpulkan bahwa, penelitian menunjukkan dalam kinerja metode Elias Delta Code lebih baik dibandingkan dengan metode Levenstein dengan rasio kompresi rata-rata sebesar 114.69% pada kompresi String Homogen, dan rasio kompresi rata-rata sebesar 252.03% pada kompresi String Heterogen.
b. Yulandari, Zulaiha (2016) dalam skripsi yang berjudul Perbandingan Algoritma Ternary Comma Code (Tcc) dan Levenstein Code dalam Kompresi File Text. Dalam skripsi ini disimpulkan bahwa Hasil pengujian kompresi file teks *.txt dengan karakter yang sama (homogen) dan berbeda (heterogen) menunjukkan bahwa metode Ternary Comma Code lebih baik dibandingkan dengan metode Levenstein Code.
c. Antoni (2014) dalam tesis yang berjudul Analisis Hasil Kompresi Data Teks pada Algoritma Elias Gamma Code, Elias Delta Code dan Levenstein Code. Dalam tesis ini disimpulkan bahwa Algoritma Levenstein Code baik digunakan jika nilai terbesar yang akan dikodekan tidak diketahui sebelumnya, atau untuk kompres data yang nilai kecil jauh lebih sering daripada nilai besar namun waktu yang diperlukan untuk melakukan kompresi tidak secepat bila dibandingkan dengan algoritma Elias Gamma Code dan Elias Delta Code.
d. Sihombing, Marlina (2014) dalam skripsi yang berjudul Sistem Kriptografi
Hybrid (Hill Cipher dan Knapsack) pada Pengamanan File. Dalam skripsi ini disimpulkan bahwa pada enkripsi file dengan Algoritma Hill Cipher terdapat perbedaan ukuran file asli dengan file yang terenkripsi, dimana file yang terenkripsi akan lebih besar ukuran file-nya dibandingkan dengan ukuran file aslinya.
e. Ramadhani,Fitri (2016) dalam skripsi yang berjudul Implementasi Algoritma Hill
Cipher 3x3 dan Rabin Public Key pada Pengirimam Short Message Service