Teori Efektif Energi Rendah dan Kosmologi Braneworld

Bab V Teori Efektif Energi Rendah dan Kosmologi Braneworld

V.1 Pendahuluan

Di dalam Bab IV telah dipelajari bahwa persamaan-persamaan induksi pada brane mengandung sebuah tensor Weyl terproyeksi yang membawa informasi medan-medan gravitasional pada bulk. Agar persamaan gravitasional pada brane menjadi tertutup, maka persamaan Einstein 5-dimensi pada bulk harus diselesaikan melalui informasi yang ada pada bulk. Secara prinsip, bagi pengamat yang terlokalisasi pada brane sangat sulit untuk mengetahui geometri bulk. Zen, dkk., (2006) telah mengkaji bahwa jika solusi vakum brane telah diketahui maka perturbasi terhadap solusi vakum dapat dipandang sebagai penambahan materi pada brane dan persamaan tensor Weyl terproyeksi dapat diselesaikan melalui pendekatan perturbatif. Bab ini bertujuan untuk mencari teori efektif energi rendah untuk sistem satu dan dua buah brane dengan menggunakan skema gradien ekspansi serta meninjau aspek kosmologi brane. Tanpa mengetahui geometri dari bulk, keberadaan tensor Weyl dapat diselesaikan secara aljabar melalui eleminasi langsung sehingga persamaan Einstein pada brane secara utuh ditentukan oleh besaran-besaran pada brane. Sehingga efek dari dimensi ekstra dalam teori efektif 4-dimensi dapat diamati secara langsung melalui persamaan-persamaan gravitasional pada brane yang diselesaikan untuk masing-masing orde ekspansi.

Sistematika pembahasan pada bab ini adalah sebagai berikut: Sub Bab V.2 membahas model untuk sistem satu buah brane dan persamaan persamaan pada

bulk diturunkan dari aksi melalui variasi terhadap metrik. Sub Bab V.3 diturunkan

persamaan-persamaan efektif pada brane serta aplikasi kosmologi braneworld dalam model kosmologi FRW. Persamaan Friedmann termodifikasi diturunkan untuk orde-2 dan mengkonfirmasi hasilnya dengan solusi eksak yang diperoleh oleh Charmousis dan Dufaux (2002) serta Maeda, dkk., (2004). Sub Bab V.4 persamaan efektif 4-dimensi diperoleh untuk sistem dua buah brane. Dengan asumsi bahwa metrik pada masing-masing brane dihubungan secara konformal, penurunan persamaan medan gravitasional dapat diperoleh secara serempak.

Implikasi kosmologi dan dinamika radion dibahas pada Sub Bab V.5. Sub Bab V.6 merangkum hasil-hasil yang diperoleh.

V.2 Sistem Satu Buah 3-brane V.2.1 Model

Model satu buah 3-brane dengan tegangan σ dan dimasukan dalam ruang-waktu

AdS5 yang memiliki sebuah skala kurvatur bulk l, dapat digambarkan melalui aksi berikut

(

)

5 4 2 2 1 12 2 mat S d x g R d x h L l σ κ ⎛ ⎞ = − _⎜ + _⎟+ − ⎝ ⎠

∫

∫

− , (V.1)

di mana R dan berturut-turut adalah skalar Ricci dan konstanta gravitasional dalam 5-dimensi. Diasumsikan pula ada simetri Z2 dalam ruang-waktu AdS5 dan

brane ditempakan di y = 0 dalam sistem koordinat yang diberikan oleh persamaan

(V.2). Medan-medan materi, Lmat, adalah terlokalisasi pada brane. Metrik induksi pada brane dinyatakan oleh h

2

κ

μν. Aksi 5-dimensi (V.1) selanjutnya diselesaikan

melalui metode ekspansi gradien untuk memperoleh aksi efektif braneworld energi rendah. Dengan memilih sistem koordinat Gaussian sebagai latar belakang solusinya,

( )

2 2

,

ds =dy +g_μν y x dx dxμ ν, (V.2)

maka persamaan-persamaan medan pada bulk diberikan oleh

(4) 1 (4) 4 y K R ν ν ν ν μ μ ⎡ μ δμ R⎤ ∂ ∑ − ∑ = −_⎢ − _⎥ ⎣ ⎦ , (V.3) 2 2 1 4 yK K l μν μν ∂ − ∑ ∑ − = − 4 , (V.4) 2 (4) 2 3 4K l μν μν ⎡ R⎤ 12 − ∑ ∑ =_{⎣ ⎦}+ , (V.5) 3 0 4 K ν ν μ μ ∇ ∑ − ∇ = . (V.6)

Di dalam persamaan di atas, kurvatur ekstrinsik didekomposisikan menjadi bagian

traceless dan bagian trace sebagai berikut

1 4 Kν_μ= ∑ +ν_μ δ_μν K , K log y g ∂ = − − ∂ . (V.7)

Dekomposisi ini bertujuan untuk menyederhanakan persamaan-persamaan dan memudahkan dalam perhitungan. Syarat junction untuk sistem satu buah 3-brane diberikan oleh

(

2 5 0 2 y Kν_μ δ_μνK ₌ κ σδν_μ T_μν

)

⎡ − ⎤ = − + ⎣ ⎦ . (V.8)

Persamaan (V.3) adalah sebuah persamaan tensor yang menggambarkan bagaimana materi-materi pada brane dapat menyebabkan kelengkungan pada

brane, sesuai dengan prinsip relativitas umum. Persamaan tensor ini menentukan

evolusi dari kurvatur ekstrinsik. Persamaan (V.4) dan (V.5) adalah persamaan-persamaan skalar, bagaimana kelengkungan pada bulk dapat memberikan tekanan pada brane sebagaimana telah dijelaskan pada bab IV. Hal ini juga mengakibatkan brane melengkung. Persamaan (V.6) adalah sebuah persamaan vektor yang memberikan kendala bagi evolusi kurvatur ekstrinsik. Persamaan-persamaan (V.3) – (V-6) bersama-sama dengan Persamaan-persamaan (V.8) menggambarkan dinamika evolusi untuk sistem satu buah brane. Aksi efektif 4-dimensi dapat diperoleh dengan mensubstitusikan solusi dari persamaan (V.3) – (V-6) ke persamaan aksi (V.1) dan mengintegrasikan terhadap koordinat dimensi ekstra, y.

V.2.2 Ekspansi Energi Rendah

Dalam metode iterasi energi rendah atau dinamakan dengan metode ekspansi gradien, parameter ekspansi didefinisikan pada daerah energi rendah, yaitu rapat energi pada brane jauh lebih kecil dari tegangan brane,

(V.9) Ini berarti bahwa rapat energi pada brane dapat diabaikan terhadap tegangan

brane. Kondisi ini berhubungan dengan orde ke-0 dalam perturbasi dan

merupakan solusi vakum. Untuk orde yang lebih tinggi, kondisi vakum ini harus diganggu dengan menambahkan materi pada brane. Syarat yang diberikan oleh persamaan (V.9) dapat diterjemahkan sebagai berikut:

(V.10) Kemudian melalui analisis dimensi persamaan (V.10) menghasilkan

(V.11) di mana adalah skala kurvatur brane. Parameter ekspansi kemudian didefinisikan oleh

(V.12) Parameter ekspansi ini dapat diartikan bahwa kurvatur pada brane dapat diabaikan dibandingkan dengan kurvatur ekstrinsik pada energi rendah. Iterasi kemudian dilakukan dengan menuliskan metrik sebagai jumlah dari tensor-tensor lokal yang dibangun oleh metrik induksi pada brane. Metrik sebagai sebuah deret perturbatif diberikan oleh

2 2 2 (1) (2)

( ) ( ) ( , ) ( , )

ds =dy +a y _⎣⎡h_μν xμ +g_μν y xμ +g_μν y xμ + _⎦⎤dx dxμ ν

)

. (V.13) Metrik induksi pada brane diberikan oleh hμν =gμν(y=0,x . Dalam perumusan

kurvatur kovarian (Shiromizu dan Koyama, 2003), ekspansi secara langsung dilakukan pada kurvatur ekstrinsik dan tensor Weyl, kemudian persamaan gerak diselesaikan pada bulk.

Kuantitas-kuantitas lain yang diekspansi adalah tensor kurvatur ekstrinsik K_μν ,

(0) (1) 2 (2)

K_μν =K_μ ν +εK_μ ν +ε K_μ ν + . (V.14) Solusi masing-masing orde dari ekspansi kemudian dilakukan sebagai berikut: untuk orde ke-0, suku kurvatur pada brane diabaikan. Dengan kata lain tidak ada materi pada brane dan hanya ada tegangan brane. Berikut diselesaikan masing-masing orde perturbasi.

V.3 Persamaan-Persamaan Efektif pada Brane V.3.1 Solusi Orde-0

Tanpa keberadaan materi pada brane, solusi orde-0 terkait dengan solusi vakum dan solusinya diberikan oleh

(0) 1 (0) , K l l ν ν μ δμ 4 K = = . (V.15)

(0) 1 (0) , 2 K yg μν μν ∂ = − ∂ (V.16)

diperoleh metrik bulk orde-0 sebagai berikut

2 2 2

( ) ( )

ds =dy +a y h_μν x dx dxμ μ ν. (V.17)

di mana a(y) menyatakan factor kelengkungan yang diberikan oleh

1 ( ) exp a y y l ⎛ = _⎜− ⎝ ⎠ ⎞ ⎟. (V.18)

Tensor h_μν adalah konstanta integrasi yang hanya bergantung pada koordinat

brane xμ dan menyatakan metrik induksi pada brane. Tanpa keberadaan materi pada brane, solusi orde ke-0 menghasilkan sebuah kendala antara tegangan brane dan konstanta kosmologi pada bulk. Dari syarat junction, hubungan antara parameter-parameter tersebut diberikan oleh

2 6 l σ κ = . (V.19)

Sebagaimana diharapkan, persamaan yang diperoleh adalah syarat ketertalaan untuk model satu buah brane yang memberikan implikasi fisis bahwa konstanta kosmologi brane menjadi lenyap yaitu berkaitan dengan brane Minkowski.

V.3.2 Solusi Orde-1

Solusi orde-1 diperoleh dengan mengambil perhitungan dari suku-suku yang diabaikan pada orde-0. Pada orde ini, keberadaan materi pada brane menjadi relevan dalam persamaan dinamika. Untuk orde-1, persamaan (V-3) – (V-6) menjadi (1) (1) 4 (1) (4) _{( )} 1 (4) _{( )} 4 y R g R g l ν ν ν ν μ μ ⎡ μ δμ ⎤ ∂ ∑ − ∑ = −_⎢ − _⎥ ⎣ ⎦ , (V.20) (1) 2 (1) 0 yK K l ∂ − = , (V.21) (1) (1) (4) 6 ( ) K R g l = ⎣⎡ ⎤⎦ , (V.22) (1) 3 (1) 0 4 D_ν ∑ _μν − D K_μ = , (V.23)

di mana D_μ adalah turunan kovarian terhadap metrik induksi h_μν . Kemudian menyatakan ekspansi orde-1 dengan tensor Ricci diambil untuk komponen metrik (1) (4) ( ) R gνμ ⎡⎣ ⎤⎦ 2 ( )

a y h_μν , sehingga tensor Ricci pada brane terhadap metrik induksi dapat dituliskan sebagai (4)R hν_μ( ).

Substitusi metrik orde-0 pada skalar Ricci R(g), maka persamaan (V.22) menghasilkan bagian trace kurvatur ekstrinsik,

(1) (4) 2 ( ) 6 l K a = R h . (V.24)

Dapat dilihat bahwa persamaan (V.21) secara trivial dipenuhi. Selanjutnya, bagian

traceless kurvatur ekstrinsik diperoleh dengan mengintegrasikan persamaan

(V.20). Hasilnya adalah (1) (1) (4) (4) 2 1 ( ) ( ) 2 4 l R h R h a a4 ν μ ν ν ν μ μ μ χ δ ⎛ ∑ = _⎜ − + ⎝ ⎠ ⎞ ⎟ . (V.25)

Disini χ(1)νμ adalah sebuah konstanta integrasi yang memenuhi . Dengan

menggabungkan persamaan (V.25) dan bagian trace kurvatur ekstrinsik (V.24), solusi tensor kurvatur ekstrinsik orde-1 adalah

(1) 0 μ μ χ = (1) (1) (4) (4) 2 1 ( ) ( ) 2 6 l K R h R h a a4 ν μ ν ν ν μ μ μ χ δ ⎛ = _⎜ − ⎝ ⎠⎞ +⎟ , (V.26)

Tensor kurvatur ektrinsik (V.26) terkait dengan tensor energi-momentum pada

brane melalui syarat junction dan menentukan persamaan dinamika gravitasional

pada brane. Syarat junction pada orde-1 menjadi

2 (1) (1) (4) (4) (1) 0 1 ( ) 2 2 2 y l Kν_μ δ_μνK ₌ ⎛ Rν_μ δ_μν R⎞ χ _μν xμ κ Tν ⎡ − ⎤ = _⎜ − _⎟+ = ⎣ ⎦ _{⎝ ⎠} μ . (V.27)

Persamaan evolusi tensor Weyl dengan metrik (V.17) diberikan oleh

2 3 y y E K K K K K K l ν ν ν νλ ν αβ ν μ = ∂ μ − ∂δμ − μλ +δμ αβ − δμ. (V.28) Dengan menggunakan ungkapan tensor kurvatur ekstrinsik serta trace-nya yang dinyatakan oleh persamaan (V.28), maka solusi tensor Weyl untuk orde-1 adalah

(1) 2 (1) ( ) ( ) E x x l ν μ ν μ = χ μ μ . (V.29)

Persamaan (V.27) bersama-sama dengan persamaan (V.29) menghasilkan persamaan gravitasional pada brane pada orde-1:

2 (4) 1 (4) (1) 2 R R T E l ν ν ν ν μ μ μ μ κ δ − = − . (V.30)

Konstanta integrasi χ(1)_μν terkendala oleh persamaan Codacci (V.23),

(1) (1) (1) (4) (4) (4) 2 4 3 1 4 2 4 8 D l l 2 D D K D R R D R a a ν ν μ ν ν ν ν μ μ ν μ μ μ χ δ ⎛ ⎞ ∑ − = _⎜ − _⎟+ − ⎝ ⎠ a ₂ (4) 1 (4) ₄( ) 2 2 D x l D R R a a ν μ ν μ ν ν ν μ μ χ δ ⎡ ⎤ = _⎢ − _⎥+ ⎣ ⎦ (4) 2 4 ( ) 2 D x l D G a a ν μ ν μ ν ν μ χ = + =0 Sehingga diperoleh (1) (1) 0, 0 D_νχ _μν = χ _μμ = . (V.31) Jadi konstanta integrasi memiliki sifat transversal dan traceless terhadap geometri

brane. Dapat dilihat bahwa persamaan Einstein dalam relativitas umum diperoleh

pada solusi orde ke-1 dengan suku tambahan yaitu tensor Weyl terproyeksi pada brane. Pada bab IV telah dibahas bahwa proyeksi tensor Weyl memberikan efek non-lokal yang mengakibatkan persamaan pada brane menjadi tidak tertutup. Namun pada penurunan di atas

(1)

2 /

E μν = χνμ l

(1)ν

μ

χ adalah konstanta integrasi yang hanya bergantung pada koordinat brane, yang berarti pula . Efek dari bulk dibawa oleh proyeksi tensor Weyl melalui kuantitas skala kurvatur

bulk, l, diberikan oleh persamaan (V.29). Dalam kosmologi

Friedmann-Robertson-Walker, suku ini berhubungan dengan radiasi gelap karena berbanding terbalik dengan faktor skala pangkat empat.

(1) (1)

( )

E μν =E μν x

V.3.3 Solusi Orde-2

Untuk melihat koreksi lain dari relativitas umum dalam teori efektif 4-dimensi selain konstanta integrasi (1)ν

μ

berikut ini kontanta integrasi diambil χ(1)_μν =0. Untuk solusi orde-2, persamaan (V.3) – (V.6) menjadi (2) (2) 4 (2) (4) 1 (4) (1) (1) ( ) ( ) 4 y R g R g K l ν ν ν ν ν μ μ ⎡ μ δμ ⎤ ∂ ∑ − ∑ = −_⎢ − _⎥ + ∑ ⎣ ⎦ μ , (V.32) 2 (2) 2 (2) 1 (1) (1) (1) 4 yK K K l α β β α ∂ − = + ∑ ∑ , (V.33) (2) (2) (1)2 (1) (1) (4) 6 3 ( ) 4 K K R g l α β β α ⎡ ⎤ =− + ∑ ∑ _{+ ⎣ ⎦ ,} (V.34) (2) 3 (2) (1) (1) (1) (1) 0 4 D_ν ∑ _μν − D K_μ + Γ_ναα∑ _μν −Γ ∑_αμν _να = μ ₊ , (V.35)

Tensor Ricci dan skalar Ricci orde-2 dihitung dengan menggunakan metrik bulk sampai pada orde-1, yaitu

2 (1) ( , ) ( ) ( ) ( , g_μν y xμ =a y ⎡_⎣h_μν xμ +g_μν y x ⎤_⎦

(

)

2 (4) 2 2 (4) ( ) ( ) 1 ( ) ( ) 2 6 l l a y h_μν xμ a ⎛ R_μν h h_μν R h ⎞ = + − _⎜ − _⎟ ⎝ ⎠. (V.36) Sehingga diperoleh

(

)

(

)

(2) ₂ (4) 1 (4) 4 2 1 (4) (4) 4 2 2 l Rν_μ δ_μν R a− a− D Dσ _μ R_σν D Dσ ν R ⎡ ₋ ⎤ _{= −} ⎡_{− +} ⎢ ⎥ ⎢ ⎣ ⎦ ⎣ μσ 1 (4) 1 (4) 1 (4) 3D D R 2D D R 12 D D R ν σ ν ν σ μ σ μ δμ + + − _σ (4) (4) 1(4) (4) 1 (4) (4) 1(4) 2 6 4 6 Rνα R_μα R_μν R δ_μν⎛ Rαβ R_αβ R ⎞⎤ + − − _⎜ − _⎟⎥ ⎝ ⎠⎦

(

) ( )

2 4 2 1 (4) 1 (4) 2 6 4 l a− a− ⎡Sν_μ xμ R⎛ Rν_μ δν_μ R⎞⎤ ≡ − _⎢ + _⎜ − _⎟⎥ ⎝ ⎠ ⎣ ⎦, (V.37) di mana

( )

2 (4) (4) 1(4) (4) 1 (4) (4) 1 (4) 3 4 12 Sν_μ = R_νβ R_μβ − R Rν_μ − δ_μν Rαβ R_αβ + δ_μν R 1 (4) (4) 2

( )

(4) 2 D D R D D R 3D D R σν ν σ ν μ σ σ μ μ ⎡ ⎤ − _⎢ + − _⎥ ⎣ ⎦ (4) (4) 1 1 2 D D R 6 D D R σ ν ν α σ μ δμ α ⎡ − _⎢⎣− − ⎦ ⎤ ⎥. (V.38)

Sifa-sifat dari tensor ini dapat dilihat dari persamaan (V.37) dan memenuhi hubungan

0, 0

S_μμ = D_{ν μ}Sν = . (V.39)

Dengan menggunakan persamaan (V.37) dan hasil dari orde-1 dapat diperoleh

2 (1) (1) (4) (4) (4) 4 1 1 12 4 l K R R a ν ν μ ⎛ μ δ ∑ = _⎜ − ⎝ R⎠ ν μ ⎞⎟ , (V.40)

dan integrasi persamaan evolusi (V.32) menghasilkan

(2) 2 3 (2) (4) (4) (4) 4 2 2 4 1 2 2 24 4 l y l l S R R R a a a a ν μ ν ν ν ν μ μ μ μ χ δ ⎛ ⎞ ⎛ ⎞ ∑ = − _⎜ + _⎟ − _⎜ − _⎟+ ⎝ ⎠ ⎝ ⎠ , (V.41)

di mana χ( 2)ν_μ adalah konstanta integrasi yang hanya bergantung pada koordinat

brane xμ. Untuk memahami arti fisis dari konstanta integrasi ini, didefinisikan 3 (2) (2) 4 l S ν ν ν μ μ μ χ =χ + 3 (4) (4) 1(4) (4) 1 (4) (4) 1(4) 2 8 3 4 3 l R_μα R_αν R R_μν δν_μ R_βα R_αβ R ⎡ ⎛ ⎤ + _⎢ − − _⎜ − ⎞_⎟⎥ ⎝ ⎠ ⎣ ⎦. (V.42)

Sehingga persamaan tensor Weyl terproyeksi orde-2 pada brane dapat ditulis serupa dengan persamaan (V.29),

(2) (2) 2 ( ) E x l ν μ ν μ μ χ = , (V.43)

Dalam ungkapanχ( 2)ν_μ , kurvatur ekstrisik pada brane adalah

3 (2) (4) (4) (4) (4) (4) 2 (4) (4) 0 5 1 2 3 24 12 2 y l K _μν R Rν_μ R_μα R_αν δ_μν R δ_μν Rα R = ⎛ ⎞ = _⎜ − − + _⎟ ⎝ ⎠ β β α ( 2)ν μ χ + . (V.44)

Dengan mengambil trace persamaan ini, dapat disusun sebuah persamaan

3 (2) (2) (2) 2 l K _μν −δ_μνK = P_μν +χ _μν , (V.45) dengan (4) (4) (4) 2 (4) (4) (4) (4) 1 1 1 1 8 2 6 4 Pμν = δμν ⎜⎛ Rαβ Rαβ − R ⎞⎟+ R Rνμ− Rαμ Rν ⎝ ⎠ α Z . (V.46) Secara formal persamaan Codacci dapat diintegrasi untuk memperoleh

(2) (2)

1 2

Di sini τν_μ adalah tensor yang tidak dapat dinyatakan dalam ungkapan kuantitas-kuantitas lokal, Kuantitas-kuantitas-kuantitas dan adalah koefisien-koefisien konstan. Sedangkan bagian lokal

1

c c2

Zν_μ adalah tensor bebas divergensi yang didefinisikan oleh

(4) (4) 1 (4) 2 (4) (4)

4

Zν_μ = R Rν_μ − δν_μ R −D D_μ ν R+δ_μνD D_α α R. (V.48) Tensor Sν_μ dan Zν_μ adalah bebas linear, sehingga kombinasinya menghasilkan sebuah tensor bebas divergensi,

1 3

Hν_μ =Sν_μ + Zν_μ. (V.49) Masing-masing dari tensor ini dapat diperoleh melalui variasi terhadap metrik dari aksi-aksi berikut ini

4 1 2 4 2 3 d x Rαβ R_αβ R d x S_μν g δ ⎛_⎜ − ⎞_⎟= ⎝ ⎠

∫

∫

_δ μν , (V.50) 4 2 4 2 d x R d x Z_μν gμν δ

_∫

=

_∫

δ , (V.51)

(

)

4 4 2 d x Rαβ R_αβ d x H_μν g δ

_∫

=

_∫

_δ μν . (V.52)

Dengan mensubstitusikan persamaan (V.47) ke persamaan (V.45) maka diperoleh

3 (2) 1 2 2 l P c S c Z ν ν ν ν ν μ μ μ μ μ τ = +χ − − , (V.53)

Persamaan ini menghubungan konstanta integrasi χ( 2)_μν dengan bagian tensor non lokal τνμ dan parameter-parameter bebas dan c1 c2. Syarat traceless

(2) 0 μ μ χ = menghasilkan 3 (4) (4) (4) (4) 2 2 1 3 8 3 l R R R c D D μ αβ α μ αβ τ = − ⎛_⎜ − ⎞_⎟− ⎝ ⎠ α R. (V.54)

Jadi τ_μμ menyatakan anomali trace dalam konteks korespondensi AdS/CFT (Maldacena, 1998) serta dalam braneworld (Gidding, dkk., 2000, Hawking, dkk., 2000, Gubser, 2001, Shiromizu dan Ida, 2001; Koyama dan Soda, 2001, Padilla, 2006). Sifat non lokal tensorτ menunjukan bahwa tensor ini berhubungan _μν dengan energi-momentum dari CFT holografik pada brane.

Dengan memasukkan solusi-solusi orde-2 ke dalam syarat junction maka dapat diperoleh persamaan efektif pada brane yang meliputi koreksi untuk persamaan gravitasional 4-dimensi relativitas umum. Syarat junction kemudian menjadi

2

(1) (1) (2) (2)

2

K _μν −δν_μK +K _μν −δν_μK =κ T_μν. (V.55) Substitusi hasil-hasil perhitungan sebelumnya ke persamaan (V.55) maka diperoleh

(

2 (4) 1 2 2 G T c S c Z l l

)

ν ν ν ν ν μ μ μ μ μ κ _τ = − + + . (V.56) Atau 2 (4) 2 2 (2) G T l P l l ν ν ν ν μ μ μ μ κ _χ = + − . (V.57)

Tensor Pμν dapat ditentukan secara lokal dan mengandung suku kuadratik

energi-momentum tensor sehingga persamaan (V.57) menjadi tertutup.

Untuk memperoleh orde ke-n dapat digunakan formula rekursif berikut ini,

( ) ₁ ( ) 4 (4) (4) ( ) ( 1) 4 1 1 1 4 n _n n p p dy a R R K a p ν ν ν ν μ μ δμ μ − − = ⎛_{⎡ ⎤} ⎞ ∑ = − ⎜_⎜⎢ − _⎥ − ∑ ⎟_⎟ ⎣ ⎦ ⎝

∑

⎠

∫

, (V.58a) 1 _{( )} ( ) ( ) ( ) ( ) ( ) (4) 1 3 6 4 n _n n p n p p n p p l K K K α_{β α}β − − − = ⎛ ⎞ R ⎡ ⎤ = _⎜− + ∑ ∑ +_{⎣ ⎦ ⎟} ⎝ ⎠

∑

, (V.58b) 1 ( ) ( ) ( ) ( ) ( ) ( ) 1 2 1 4 n n n p n p p n p y p K K K K l α β β α − − − = ⎛ ⎞ ∂ − = _⎜ + ∑ ∑ _⎟ ⎝ ⎠

∑

, (V.59a)

(

)

1 ( ) ( ) ( ) ( ) ( ) ( ) 1 3 4 n n n p n p p n p D_{ν μ}ν D K_{μ να}α _μν _αμν p_ν − − − = ∑ − +

∑

Γ ∑ −Γ ∑ α oleh . (V.59b)

Bagian traceless dan trace kurvatur ekstrinsik didefinisikan oleh persamaan (V.7).

V.3.4 Implikasi Kosmologi Sistem Satu Buah Brane

Sebagai aplikasi kosmologi1 ), tinjau kosmologi homogen dan isotropik pada

brane dengan metrik induksi diberikan

1)

Aplikasi kosmologi untuk orde-1 dapat dilihat pada paper Zen, dkk., (2006) di mana persamaan Friedmann dengan koreksi radiasi gelap diberikan oleh 2 4

4 8 3 G C H a π _ρ = + .

2 2

( ) ij i

h dx dx_μν μ ν = −dt +a t γ dx dxj. (V.60) Disini adalah sebuah faktor skala. Komponen yang tidak lenyap dari tensor ( ) a t P_μν adalah 4 4 3 3 , 4 4 t j t i P = − H P = −⎛_⎜ H +H H2 δ_ij ⎝ ⎠ ⎞ ⎟ , (V.61)

Perhitungan secara langsung menghasilkan bahwa tensor Pμν memenuhi

0

D P_{ν μ}ν = . (V.62)

Sehingga dari persamaan (V.57) diperoleh

(2)

0

D_νχ _μν = . (V.63)

Jadi χ( 2)ν_μ adalah komponen pada kosmologi brane yang berperilaku sebagai suku radiasi gelap. Komponen-(tt) dari persamaan (V.57), dengan mengabaikan suku radiasi, menghasilkan persamaan Friedmann termodifikasi

2 2 2 3 4 l H l κ ρ = + 4 H . (V.64)

Charmousis dan Dufaux (2002) serta Maeda dan Torii (2004) telah memperoleh bentuk solusi eksak dari persamaan Friedmaan termodifikasi dalam braneworld Gauss-Bonnet tanpa suku radiasi gelap, hasil ringkasnya dapat ditulis sebagai berikut

(

)

(

2 2 2 2 4 2 H l 3 1 2l H l α κ ρ σ_{+ = +} − ⎛ _{− +} ⎜ ⎝

)

⎠ 2 2 ⎞ ⎟. (V.65)

Disini α adalan parameter konstan, kontribusi dari suku Gauss-Bonnet. Dalam kasus yang diturunkan di atas maka untuk α = 0,

(

)

2

6 H l

κ ρ σ+ = 2 + −2

. (V.66)

Jika ruas kanan persamaan (66) diekspansi untuk parameter ekspansi yang kecil , 2 2 l H ε = 2 2 1 2 2 1 4 4 1 1 2 8 l H + = + l H − l H + , (V.67) maka diperoleh persamaan yang sama seperti persamaan (V.64). Jadi dapat dikonfirmasi validitas dari ekspansi gradien. Sehingga menarik juga untuk dikaji jika aksi (V.1) ditambahkan suku Gauss-Bonnet dalam skema ini.

V.4 Sistem Dua Buah Brane

Pada pasal sebelumnya, model dengan satu buah brane dapat digambarkan oleh sebuah teori efektif 4-dimensi dalam energi rendah. Berikut ini dikaji sebuah sistem dengan dua buah brane pada limit energi rendah. Dinamika untuk sistem dua buah brane sedikit lebih rumit dari sistem dengan satu buah brane. Jarak antara kedua brane dapat mempengaruhi dinamika kedua brane dan dinamika dari sistem secara keseluruhan. Sebagaimana diperlihatkan di bawah ini, jika ada dua buah brane dimasukan dalam ruang-waktu bulk, teori 4-dimensi efektif berperilaku seperti teori Brans-Dicke (secara umum adalah teori skalar-tensor) dan medan skalar Brans-Dicke bekerja sebagai sebuah radion. Asumsi yang sama seperti pasal sebelumnya bahwa tegangan-tegangan brane σ( )+ dan σ( )− jauh lebih besar dari rapat energi ρ( )+ dan ρ( )− . Untuk sistem dua buah brane, ada satu buah derajat kebebasan tambahan yaitu radion yang juga harus diambil dalam perhitungan dan memodifikasi skema ekspansi.

V.4.1 Model

Aksi untuk sistem dengan dua buah brane diberikan oleh 1₂ 5 1₂ 2 S d x g R l κ ⎛ ⎞ = − _⎜ + _⎟ ⎝ ⎠

∫

2

(

)

(

)

4 ( ) ( ) ( ) 4 ( ) ( ) ( ) d x h+ L+ σ + d x h− L− σ − +

_∫

− − +

_∫

− − . (V.68)

Metrik 5-dimensi dapat dipilih dalam suatu bentuk di mana radion secara eksplisit ada dalam metrik,

2 ( , ) 2

( , )

y x

ds =eφ μ dy +g_μν y x dx dxμ μ ν . (V.69)

Brane yang memiliki tegangan positif ditempatkan di y = 0 sedangkan brane

yang memiliki tegangan negatif di y = l. Dalam kasus ini ( ,φ y xμ) menentukan jarak wajar antara kedua brane (Lihat Gambar V.1),

( ', ) 0 ( ) ' l y x d x =

∫

eφ dy . (V.70)

Dalam sistem koordinat (V.69), persamaan-persamaan medan bulk dapat diperoleh melalui variasi aksi (V.68):

(4) 1 (4) 4 y e−φ∂ ∑ − ∑ = −ν_μ Q ν_{μ ⎢⎣}⎡ Rν_μ− δν_μ R− ∇ ∇ − ∇ ∇_μ νφ _μφ νφ

(

)

1 4 ν α α μ α α δ φ φ φ ⎤ + ∇ ∇ + ∇ ∇ _⎥⎦, (V.71) 2 ( 2 3 12 4Q l R α β β α ⎡ 4) ⎤ − ∑ ∑ = _{+ ⎣ ⎦ ,} (V.72) 2 2 1 4 4 y e Q Q l φ αβ α αβ α φ αφ φ − _{∂ − − ∑ ∑ = ∇ ∇ + ∇ ∇ −}α , (V.73) 3 0 4 Q ν ν μ μ ∇ ∑ − ∇ = , (V.74)

Dan syarat junction diberikan oleh

(

2 ( ) ( ) 0 3 4 Q _y 2 T

)

ν ν ν ν μ μ μ μ κ δ σ δ+ + = ⎡_{∑ −} ⎤ _{= − +} ⎢ ⎥ ⎣ ⎦ , (V.75)

(

2 ( ) ( ) 3 4 Q _{y l} 2 T

)

ν ν ν ν μ μ μ μ κ δ σ δ− − = ⎡_{∑ −} ⎤ _{= − − +} ⎢ ⎥ ⎣ ⎦ . (V.76)

Bagian traceless dan trace dari kurvatur ekstrinsik didefinisikan 1 4 e K−φ _μν = ∑ +_μν g_μν K , Q e log g y φ − ∂ = − ∂ − . (V.77)

d(x)

y=0

y=l

y

Dengan menggunakan prosedur yang sama seperti pada sub bab sebelumnya, persamaan-persamaan Einstein pada masing-masing brane, sampai pada orde-1, dapat ditulis secara serempak sebagai berikut

2 ( ) ( ) 2 ( ) G T l l μν μν κ μν χ ± _{= ±} ± ₋ ± , (V.78) di manaχ_μν( )± adalah konstanta integrasi. Tanda ± di dalam persamaan (V.78) masing-masing berhubungan dengan brane yang memiliki tegangan positif dan negatif. Metrik induksi pada masing-masing brane dihubungkan melalui transformasi konformal

( ) 2 ( )

h_μν− = Ω h_μν+ , (V.79) dengan faktor konformal diberikan oleh

( )

exp eφ

Ω = − . (V.80)

Untuk sistem dua buah brane adalah mungkin mengeleminasi kuantitas non lokal,

( )

μν χ ±

, di dalam persamaan (V.78) sehingga diperoleh persamaan Einstein lokal pada masing-masing brane. Hal ini dapat dilakukan jika hubungan antaraχ_μν( )+ dan

( )

μν χ −

diketahui. Dengan menggunakan persamaan evolusi dari tensor Weyl terproyeksi (IV.75) untuk orde-1 dan persamaan (V.79), tensor Weyl terproyeksi adalah dihubungan secara konformal,

( )(1) 2 ( )(1)

E − _μν = Ω− E + _μν. (V.81) Berikut ini diturunkan persamaan Einstein pada masing-masing brane dalam bentuk tertutup.

V.4.2 Teori Efektif pada Brane

Dengan menggunakan persamaan (A.10) pada lampiran A, persamaan Einstein pada brane yang memiliki tegangan negatif dapat dinyatakan dalam ungkapan kuantitas-kuantitas pada brane yang memilki tegangan positif,

G_μν( )− =G_μν( )+ − 2

(

D_μ( )+D_ν( )+Ω −h_μν( )+D_α( )+ D( )+αΩ

)

Ω ( ) ( ) ( ) ( ) ( ) 2 4 1 4 D_μ+ D_ν+ h_μν+ D_α+ D+α ⎛ ⎞ + _⎜ Ω Ω − Ω _⎟ Ω ⎝ Ω⎠, (V.82)

Persamaan (V.81) bersama-sama dengan persamaan (V.29) untuk kasus dua brane, suku non lokalχ_μν( )± dihubungakan secara konformal sebagai berikut

( ) 2 ( )

μν μν

χ − _{= Ω}− χ +

. (V.83)

Eleminasi χ_μν( )± pada persamaan (V.78) mengimplikasikan bahwa

(

2 ( ) 2 ( ) ( ) 2 ( ) G G T T l μν μν μν μν κ + _{= Ω} − ₊ + _{+ Ω} −

)

. (V.84)

Suku pertama pada ruas kanan persamaan (V.84), G_μν( )− , dapat dieleminasi dengan menggunakan persamaan (V.82). Dengan mendefinisikan sebuah medan skalar Ψ oleh

2

1

Ψ = − Ω , (V.85)

persamaan Eintein pada brane yang memiliki tegangan positif diperoleh

(

(

)

)

(

)

2 ( ) ( ) ( ) 1 ( ) ( ) ( ) ( ) ( ) 1 G T T D D h D D l α μν+ =κ_Ψ μν+ + − Ψ μν− + _Ψ μ+ ν+Ψ − μν+ α+ + Ψ

(

3

)

( ) ( ) 1 ( ) ( ) ( ) 2 1 D D 2h D D α μ+ ν+ μν+ α+ + ⎛ ⎞ + _⎜ Ψ Ψ − Ψ _⎟ Ψ − Ψ ⎝ Ψ . ⎠ (V.86)

Dengan hasil ini, kuantitas non lokal dapat dinyatakan dalam ungkapan kuantitas-kuantitas pada brane,

(

)

(

)

(

)

2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 2 2 l T T D D h D D α μν κ μν μν μ ν μν α χ + _{= − − Ψ} + ₊ − ₋ + +_{Ψ −} + + _Ψ Ψ Ψ +

(

3

)

( ) ( ) 1 ( ) ( ) ( ) 4 1 2 l D_μ+ D_ν+ h_μν+D_α+ D+α ⎛ ⎞ − _⎜ Ψ Ψ − Ψ Ψ_⎟ Ψ − Ψ ⎝ ⎠. (V.87)

Karena Ω (atau ekuivalen dengan Ψ ) mengandung informasi jarak antara kedua

brane, (atau ) dinamakan radion. Persamaan gerak untuk medan skalar radion diperoleh dengan mengambil trace persamaan (V.87),

Ω Ψ

(

)

(

)

(

)

2 ( ) ( ) 1 ( ) ( ) ( ) ( ) 1 1 2 1 3 D D D D T T l α α α+ + Ψ + _{− Ψ} α+Ψ + Ψ =κ − Ψ ⎣⎡ + + − Ψ − ⎤⎦, (V.88) di mana ( ) ( ) ( ) . T − =h T_μν− −μν (V.89)

Persamaan-persamaan (V.86) dan (V.88) merepresentasikan sebuah teori gravitasi skalar-tensor pada brane yang memiliki tegangan positif dan dapat diturunkan dari aksi efektif 4-dimensi:

(

)

( ) 4 ( ) ( ) ( ) ( ) 2 3 2 2 1 l S d h R D_α D α κ + _{= −} + ⎛_⎜Ψ + ₋ +_Ψ ⎞_⎟ ⎜ _{− Ψ} ⎟ ⎝ ⎠

∫

+ _Ψ

(

)

2 4 ( ) ( ) 4 ( ) ( 1 d h+ L+ d h+ L ) +

∫

− +

∫

− − Ψ − . (V.90)

Prosedur yang sama juga dapat digunakan untuk memperoleh persamaan-persamaan efektif pada brane yang memiliki tegangan negatif dan diperoleh:

(

(

)

)

(

)

2 ( ) ( ) ( ) 1 ( ) ( ) ( ) ( ) ( ) 1 G T T D D h D D l α μν μν μν μ ν μν α κ − ₌ − _{+ + Φ} + ₊ − −_{Φ −} − − − Φ Φ Φ

(

3

)

( ) ( ) 1 ( ) ( ) ( ) 2 1 D D 2h D D α μ− ν− μν− α− − ⎛ ⎞ − _⎜ Φ Φ − Φ _⎟ Φ + Φ ⎝ Φ . ⎠ (V.91)

(

)

(

)

(

)

2 ( ) ( ) 1 ( ) ( ) ( ) ( ) 1 1 2 1 3 D D D D T T l α α α α κ − − _{Φ −} −_Φ − _{Φ = + Φ ⎡} − _{+ + Φ} + _⎤ ⎣ ⎦ + Φ , (V.92)

(

)

(

)

(

)

2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 2 2 l T T D D h D D α μν μν μν μ ν μν α κ χ − _{= − + Φ} − ₊ + ₋ − −_{Φ −} − − _Φ Φ Φ −

(

3

)

( ) ( ) 1 ( ) ( ) ( ) 4 1 2 l D_μ− D_ν− h D_μν− _α− D−α ⎛ ⎞ + _⎜ Φ Φ − Φ Φ_⎟ Φ + Φ ⎝ ⎠. (V.93)

Aksi efektif 4-dimensi untuk brane yang memiliki tegangan negatif diberikan oleh

(

)

( ) 4 ( ) ( ) ( ) ( ) 2 3 2 2 1 l S d h R D_α D α κ − _{= −} − ⎛_Φ − ₊ −_Φ ⎞ ⎜ ⎟ ⎜ _{+ Φ} ⎟ ⎝ ⎠

∫

− _Φ

(

)

2 4 ( ) ( ) 4 ( ) ( 1 d h− L− d h− L ) +

_∫

− +

_∫

− + Φ + , (V.94) di mana 2 1 − Φ = Ω − . (V.95)

Hasil-hasil di atas memperlihatkan bahwa jika dinamika dari sebuah brane diketahui maka dinamika pada brane yang lain juga dapat diperoleh. Ketidakbebasan dinamika pada kedua brane dapat dinyatakan melalui hubungan berikut:

1 Ψ Φ =

− Ψ. (V.96)

Persamaan-persamaan Einstein dan persamaan-persamaan gerak untuk medan skalar pada brane adalah tertutup, yang dapat direpresentasikan melalui kekekalan materi pada masing-masing brane,

( ) ( )

0

D T_μ± ±_νμ = . (V.97)

Terhadap metrik pada brane yang memiliki tegangan positif, h_μν( )+ , persamaan kekekalan (V.97) dapat dituliskan menjadi

( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 ( ) 0, 1 2 1 D D D T_{μ ν}μ D T_{μ ν}μ μ T _νμ ν T + + + + ₌ + − ₌ Ψ − ₋ Ψ − − Ψ − Ψ . (V.98)

Jadi terhadap metrik h_μν( )+ , tensor energi-momentum pada brane yang memiliki tegangan positif memenuhi hukum kekekalan sedangkan divergensi tensor energi-momentum pada brane yang lain ditentukan oleh jarak antara kedua brane.

Aksi-aksi efektif yang digambarkan oleh persamaan-persamaan (V.90) dan (V.94) tidak lain adalah aksi gravitasi skalar-tensor di mana kopling gravitasional pada masing-masing brane ditentukan oleh medan skalar Brans-Dicke Φ untuk brane yang memiliki tegangan negatif dan Ψ untuk brane yang memiliki tegangan positif. Gravitasi skalar-tensor pada masing-masing brane dibedakan oleh ungkapan parameter kopling ω( )Φ = −3 / 2 1Φ

(

+ Φ

)

untuk brane yang memiliki tegangan negatif dan ω( )Ψ = Ψ3 / 2 1

(

− Ψ

)

untuk brane yang memiliki tegangan positif.

V.5 Implikasi Kosmologi Sistem Dua Buah Brane

Pada sub bab ini dibahas implikasi kosmologi untuk sistem dua buah brane. Persamaan-persamaan efektif 4-dimensi untuk brane yang memiliki tegangan positif dapat dinyatakan kembali dalam bentuk persamaan dinamika berikut:

(

)

2 2 ( ) ( ) 1 ( ) 1 ( ) 1 ( ) 2 2 R T T T T l l ν ν ν ν ν μ μ μ μ μ κ κ _{δ δ} + ₌ ⎛ + ₋ + ⎞₊ − Ψ ⎛ − ₋ ⎜ ⎟ ⎜ Ψ_{⎝ ⎠} Ψ _⎝ − ⎞ ⎟ ⎠

( )

( ) ( ) ( ) ( ) ( ) ( ) 2 1 1 2 D D D D D D ν α ν μ α μ μ ω δ + + + + Ψ + + + Ψ + Ψ + Ψ Ψ Ψ Ψ ν_{Ψ ,} (V.99) 2 ( ) ( ) ( ) ( ) 1 ( ) ( ) 2 3 2 3 d D D D D d l α α α _ω ω α κ T _ω T + − + + _{Ψ +} +_Ψ + _{Ψ =} + + Ψ + , (V.100)

dengan parameter koplingω

( )

Ψ didefinisikan oleh

( )

3

2 1

ω Ψ = Ψ

Medan skalar Ψ dalam ungkapan medan φ adalah

(

)

1 exp 2eφ

Ψ = − − , (V.102)

yang mengimplikasikan Ψ ∈

[ ]

0,1 . Dalam limit Ψ →1 berhubungan dengan gravitasi dalam relativitas umum dan terkait dengan keadaan di mana kedua brane terpisah pada jarak yang sangat besar,

(

)

( ) ln 1 ,

2

l

d x =leφ = − − Ψ → ∞ φ → +∞ . (V.103) Sedangkan dalam limit berhubungan dengan sebuah keadaan di mana kedua brane bertumbukan: ,

0 Ψ →

0

d → φ→ −∞ .

Materi fluida pada brane yang memilki tegangan positif adalah fluida ideal,

(

)

(

)

( ) , T_μν+ = ρ+P U U_{μ ν} +Pg_μν P= Γ −1 t , (V.104) di mana Γ adalah indeks barotropik. Misalnya, Γ = 4/3 menyatakan materi radiasi dan Γ = 0 berhubungan dengan konstanta kosmologi. Pada brane yang memilki tegangan negatif, tensor energi-momentumnya diberikan oleh

( ) ( )

( )

T −_μν =λ− δν_μ , (V.105) Jika metrik induksi pada brane diberikan oleh metrik FRW, persamaan (V.62), maka menghasilkan hukum kekekalan untuk fluida ideal,

3 0 3 a , a a ρ _{= − Γ} ρ _⇒ ρ ρ₌ − Γ , (V.106)

dan persaman untukλ( )− adalah

( ) ( ) 1 λ λ − − Ψ = − − Ψ. (V.107)

Solusi persamaan ini adalah

(

)

(

)

( ) ( ) ( ) 0 1 0 exp 2e φ λ − ₌λ − _{− Ψ =}λ − ₋ . (V.108)

Jadi evolusi dari materi pada brane yang memilki tegangan negatif diparameterisasi oleh jarak wajar antara kedua brane. Jika φ adalah besar (jarak antara brane menjadi besar) materi pada brane yang memilki tegangan negatif menjadi lenyap . Sebaliknya, jika jarak antara brane menjadi kecil, maka materi pada brane yang memilki tegangan negatif, nilainya tidak nol.

( )

0 λ − _→

Dengan metrik FRW, persamaan medan 4-dimesi (V.99) dan (V.100) dapat diperoleh sebagai berikut:

(

)

(

)(

)

(

) (

)

2 2 2 2 ( ) 0 1 4 3 4 1 4 3 3 2 1 3 3 H l l κ κ ρ λ − − Ψ − Γ − Ψ − Γ Ψ Ψ + Ψ + = − − Ψ , (V.109)

(

)

2 2 4 3 2 6 H H l κ ρ − Γ + = , (V.110)

(

)

(

(

)

2 2 2 2 ( 0 1 1 4 1 3 H H l κ _ρ − Ψ Ψ + − = − − Ψ Ψ Ψ − Ψ Ψ

)

) λ . (V.111)

Persamaan (V.109) dan (V.110) berturut-turut adalah persamaan dinamika untuk Ψ dan H dan persamaan (V.111) adalah persamaan Friedmann. Persamaan (V.110) tidak mengandung suku tambahan yang menggambarkan pengaruh dari

brane yang memilki tegangan negatif dan medan skalar. Sedangkan persamaan

(V.109) mengandung suku tambahan pada ruas kanan persamaannya yang menunjukan ketidaklinearan persamaan. Berikut ini dikaji solusi-solusi khusus dari persamaan-persamaan tersebut.

V.5.1 Dinamika Radion

Pertama tinjau kasus Γ = 0 (konstanta kosmologi). Hukum kekekalan (V.106) menghasilkan ρ ρ= ₀ =konstan, dan persamaan (V.110) menjadi

2 2 0 2 2 3 H H l κ ρ + = , (V.112)

Solusi trivial dari persamaan ini diberikan oleh parameter Hubble konstan,

2 2

0

( / 3 )

H = κ l ρ tetapi ini bukan solusi umum (lihat pasal V.5.4). Untuk solusi

trivial menghasilkan evolusi faktor skala dalam bentuk eksponensial:

2 0exp 3 a a t l κ ρ ⎛ ⎞ = _⎜⎜ ⎝ 0 ⎠⎟⎟ . (V.113)

Persamaan (V.111) dapat diselesaikan secara aljabar dan menghasilkan solusi

2 2 ( ) 0 0 0 0 1 exp 3 A t l κ ρ ρ ρ λ − − ⎡ ⎛ ⎞ ⎤ ⎢ Ψ = − ⎜_⎜ ⎟_⎟± ⎢ _{⎝ ⎠} ⎥ ⎣ ⎦ ⎥ , (V.114)

di mana A adalah konstanta integrasi. Dengan memilih kontanta integrasi

(

_{( )}

)

1 / 2 0/ 0 A= ρ λ− maka 2 2 0 0 ( ) 0 1 exp 1 3l t ρ _{κ ρ} λ − − ⎡ ⎛ ⎞ ⎤ ⎢ ⎥ Ψ = − ⎜_⎜ ⎟_⎟± ⎢ _{⎝ ⎠} ⎥ ⎣ ⎦ , (V.115)

Solusi persamaan (V.114) menentukan jarak wajar antara kedua brane

2 ( ( ) 0 0 0 ( ) ln exp 3 t d t le l A t l φ κ _ρ λ ρ −) ⎡ ⎛ ⎞ ⎤ ⎢ ⎥ = = ⎜_⎜ ⎟_⎟± ⎢ _{⎝ ⎠} ⎥ ⎣ ⎦ , (V.116) Untuk t → + ∞ maka d → + ∞ dan juga diperoleh sebuah solusi

(

)

1 ( ) 0 0 2 0 3 ln 1 / , 0 c l t t A λ ρ d κ ρ ± ⎡ − − ⎤ = = _{⎢ ⎥} = ⎣ ∓ ⎦ . (V.117)

Solusi persamaan (V.114) tidak memiliki singularitas ketika brane bertumbukan dan dapat diteruskan untuk daerah di mana Ini dapat diinterpretasikan sebagai suatu perubahan kedudukan kedua brane sepanjang sumbu-y: untuk perubahan kedudukan (

0

d = d t( )<0.

( ) ( )

,

σ + σ − _{) berhubungan dengan}

dan untuk arah sebaliknya (

( ) 0 d t > ( ) 0 d t < ( ) ( ) , σ − σ + ). Kanno, dkk., (2003) memperkenalkan skenario kosmologi BAB (Born-Again-Braneworld) bahwa tanda dari tegangan brane dapat berubah setelah tumbukan, σ( )− _↔σ( )+ _{. Dari}

pembahasan di atas mekanisma ini muncul secara alamiah. Misalnya untuk kasus

(

1

)

2

l

d = − − Ψ ≤ , 0 (V.118)

berhubungan dengan perluasan domain Ψ yaitu Ψ ∈ −∞[ , 0] . Berikut ditinjau evolusi dari jarak wajar untuk ( )d t < untuk masing-masing tanda yang 0 diberikan oleh solusi persamaan (V.115).

Untuk solusi ”negatif”, jika t− = maka 0 . Kemudian jarak wajar antara

brane memiliki domain pada seluruh sumbu riil

d→ −∞

[ ,

d∈ −∞ ∞ untuk ] dan faktor skala tidak pernah lenyap. Sedangkan untuk solusi ”positif”

[0, ] t∈ +∞ ( ) a t ( ) 0 0 , ln t d l λ ρ − +_{→ −∞ = < 0} , (V.119)

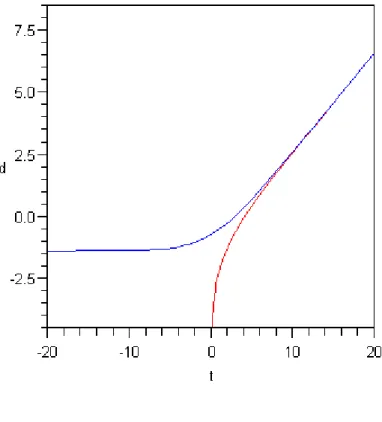
Gambar V.2 Jarak wajar antara dua buah brane untuk Γ = 0, tanpa pengaruh radiasi gelap. Warna merah adalah kurva untuk log(0.25(exp(0.4 t)-1)) dan kurva warna biru untuk log(0.25(exp(0.4 t)-t)-1)).

Dalam hal ini dua buah brane dipisahkan pada jarak berhingga dan faktor skala eksponensial (V.113) pada brane yang memiliki tegangan positif cenderung menuju nol (alam semesta memiliki singularitas t ). Situasi ini diperlihatkan pada Gambar V.2. Konstanta-konstanta ditetapkan sebagai berikut :

dan . + _{→ −∞}

(

_{( )}

)

1 / 2 0/ 0 0.25, A= ρ λ − = (κ λ2 ₀( )− / 3 )l 1 / 2 =0.1 .4 Γ 2 1 / 2 0 (κ ρ / 3 )l =0

Berikutnya tinjau untuk faktor skala pada brane yang memiliki tegangan positif yang digambarkan oleh sebuah fungsi pangkat . Dari persamaan (V.110) dan hukum kekekalan, solusi untuk indek pangkatnya adalah , Γ ≠ 0, dan sebuah kendala untuk nilai awal adalah

0 m a=a t 2 / 3 m=

( )

2 3 0 2 4 3l 9 a κ ρ 0 Γ = Γ . (V.120)

2 / 3 1 0 2 ( ) , 3 a t =a t Γ H = t− Γ . (V.121)

Persamaan-persamaan evolusi ini terkait dengan jarak wajar yang diberikan oleh

2 ( ) 0 2 / 3 1 3 / 3 2 ( ) ln , 3 2 3 l d t l A t κ λ t − Γ ⎛ _Γ ⎞ ⎜ ⎟ = Γ ⎜ Γ − ⎟ ⎝ ⎠ ∓ ≠ , (V.122) 2 ( ) 2 0 2 ( ) ln ln , 3 3 d t l A t t l κ λ − ⎛ ⎞ = ⎜_⎜ ⎟_⎟ Γ ⎝ ∓ ⎠ = , (V.123)

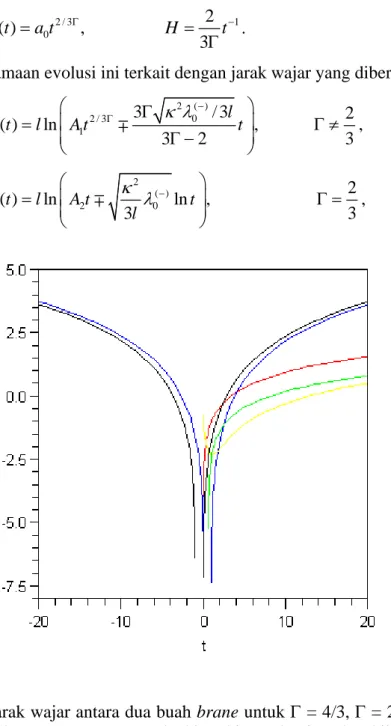
Gambar V.3 Jarak wajar antara dua buah brane untuk Γ = 4/3, Γ = 2/3 dan Γ = 1/3. Kurva warna merah, biru, hitam, kuning dan hijau masing-masing untuk kurva: log(0.2(t0.5+t)), log(0.1(t2-t)), log(0.1(t2+t)), log(0.1(t-log(t))) dan log(0.1(t+log(t))).

di mana A1 dan A2 adalah konstanta integrasi. Dari ungkapan ini dapat ditentukan

waktu terjadi tumbukan, , antara kedua brane. Dalam hal ini diperoleh . Berarti bahwa faktor skala adalah regular pada saat terjadi tumbukan dan bagi pengamat yang berada pada brane yang memiliki tegangan positif tumbukan ini tidak diamati, karena tidak ada pengaruh evolusi dari faktor skala. Pada saat t = 0

c

adalah singular, jarak antara kedua brane cenderung menuju −∞ dan faktor skala menuju nol (singularitas). Jika konstanta integrasi A₁ dipilih sebagai berikut

2 ( ) 0 1 3 / 3 2 l A κ λ − Γ = 3 Γ − , (V.124) maka diperoleh

(

2 2 2 / 3 ( ) 0 3 2 3 1 3 l t t κ λ

)

− Γ − Γ − ⎛ ⎞ Ψ = − ⎜_{⎝ Γ} ⎟_⎠ ∓ , (V.125)

Dapat dilihat bahwa untuk t→ ∞ (late times) maka Ψ →1 dan solusinya mendekati solusi relativitas umum. Situasi ini ditunjukan pada Gambar V.3.

V.5.2 Pengaruh Radiasi Gelap

Secara umum persamaan (V.110) adalah persamaan diferensial orde dua untuk factor skala:

( )

₍

₎

2 2 ₂ 2 3 0 2 4 3 3 d a a dt κ ρl − Γ = − Γ . (V.112)

Integrasi pertama terhadap waktu menghasilkan

( )

2 ₂ 0 4 3 2 0 2 3 3 d a dt l l a C κ ρ κ ρ − Γ = + , (V.113)

di mana C adalah konstanta integrasi sebagai suku radiasi gelap yang membawa informasi pengaruh bulk pada brane. Persamaan (V.113) menghasilkan persamaan Friedmann 2 2 4 3 C H l a κ ρ = + , (V.114)

Berikut ini ditinjau untuk berbagai nilai dari indeks barotropik Γ : • Γ =0. Solusi dari persamaan (V.113) adalah

(

)

(

)

2 2 0 0 2 2 0 0 0 1 3 exp 2 2 3 2 exp 2 3 lC a t t l t t l κ ρ κ ρ κ ρ ⎛ ⎞ = ⎜_⎜ − ⎟_⎟− ⎛ ⎞ ⎝ ⎠ _{⎜ − ⎟} ⎜ ⎟ ⎝ ⎠ , (V.115) • Γ =4 / 3.

(

)

(

)

2 2 0 0 0 1 2 , 3 ₂ a C t t H l _{t t} κ ρ = + − = − , (V.116)

Jadi untuk kasus materi radiasi, radiasi gelap tidak berpengaruh pada parameter Hubble dari brane yang memilki tegangan positif.

• Γ =2 / 3.

(

)

(

)

2 2 2 0 2 0 0 0 2 2 0 3 , 3 3 t t lC a t t H l l κ ρ κ ρ κ ρ − = − − = a . (V.117) • Γ =1 1/ 3 2 1/ 3 1 2 2 a= β + C β− + , C (V.118) di mana

(

)

4 2 2 3 0 0 8 3l t t C κ ρ β =⎛_⎜ ⎞_⎟ − ⎝ ⎠ −

(

)

(

)

8 4 2 2 4 ₃ 2 0 0 0 0 3 9 16 3l t t C 3l t t κ ρ κ ρ ⎛ ⎞ ⎛ ⎞ + _{⎜ ⎟} − − _{⎜ ⎟} ⎝ ⎠ ⎝ ⎠ − . (V.119)

Persamaan (V.111) dapat digunakan untuk mencari solusi numerik dari medan Ψ dengan bentuk sebagai berikut

(

)

2 2 2 ( ) 0 0 3 4 (1 ) (1 ) 3 4 1 3 C H la l a κ ρ κ λ − Γ − Ψ Ψ Ψ − Ψ − + − = Ψ Ψ Ψ − Ψ Ψ 2 < , (V.120) dengan H dan a ditentukan dari persamaan (V.113).

V.6 Rangkuman

Pada bab ini telah diperoleh persamaan-persamaan gravitasional energi rendah pada brane untuk sistem satu buah brane dan dua buah brane. Persamaan-persamaan evolusi bulk diselesaikan secara iteratif dengan mengekspansi persamaan-persamaan yang relevan dalam parameter ekspansi , dengan l adalah skala kurvatur bulk dan L adalah skala kurvatur brane. Ekspansi orde-0 menghasilkan ketertalaan antara tegangan brane dan konstanta kosmologi

bulk. Persamaan relativitas umum dengan suku-suku koreksi diperoleh untuk

ekspansi orde-1 dan seterusnya. Untuk sistem satu buah brane, terdapat suku non lokal

2

( / )l L 1 ε = <

μν

kebebasan bulk. Disamping itu pula, persamaan medan gravitasional menjadi tertutup, yaitu dapat ditentukan melalui besaran-besaran pada brane.

Aspek kosmologi untuk masing-masing konfigurasi menghasilkan persamaan Friedmaan termodifikasi oleh keberadaan tensor Weyl terproyeksi yang diinterpretasikan sebagai radiasi gelap dalam model kosmologi FRW. Ditinjau pula sebuah skenario kosmologi di mana dua buah brane bergerak dan bertumbukan di dalam ruang-waktu bulk 5-dimensi. Materi pada brane yang memiliki tegangan positif digambarkan oleh fluida ideal dan pada brane yang memiliki tegangan negatif adalah konstanta kosmologi bergantung waktu. Diperoleh solusi-solusi khusus untuk faktor skala pada brane yang memiliki tegangan positif dan radion yang menentukan jarak wajar antara kedua brane. Dari solusi analitik juga menunjukkan bahwa evolusi dari faktor skala adalah berbeda untuk latar belakang materi dengan indeks barotropik berbeda.