BILANGAN TERHUBUNG PELANGI DAN
BILANGAN TERHUBUNG KUAT PELANGI
PADA AMALGAMASI GRAF ANTIPRISMA AP3
Alfiatus Syifa
PROGRAM STUDI MATEMATIKA
FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS ISLAM NEGERI
SYARIF HIDAYATULLAH
JAKARTA
2018 M / 1439 H
BILANGAN TERHUBUNG PELANGI DAN
BILANGAN TERHUBUNG KUAT PELANGI
PADA AMALGAMASI GRAF ANTIPRISMA AP3
Skripsi
Sebagai Salah Satu Syarat untuk Memperoleh Gelar Sarjana Matematika (S.Mat)
Fakultas Sains dan Teknologi
Universitas Islam Negeri (UIN) Syarif Hidayatullah Jakarta
Oleh:
Alfiatus Syifa
1113094000018
PROGRAM STUDI MATEMATIKA
FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS ISLAM NEGERI
SYARIF HIDAYATULLAH
JAKARTA
2018 M / 1439 H
iv
PERSEMBAHAN
Untuk manusia yang masih menyimpan Allah dalam hatinya:
v
MOTTO
“Ketika kau tetap mendayung sampan sendirian ditengah sungai yang penuh beban dan tangis. Ketika kau terus maju mendayung bukan karena tak bisa kembali, tetapi meyakini bahwa itu akan membawa janji masa depan yang lebih
vi
KATA PENGANTAR
Dengan mengucap puji dan syukur kepada Allah SWT yang telah meberikan rahmat dan karunia-Nya sehinga skripsi yang berjudul “Bilangan Terhubung Pelangi dan Bilangan Terhubung Kuat Pelangi pada Amalgamasi Graf Antiprisma AP3” dapat terselesaikan dengan baik. Tak lupa
shalawat serta salam semoga senantiasa tercurahkan kepada Nabi Muhammad SAW, bagi keluarga, sahabat serta orang-orang yang mengikutinya dengan
istiqomah sampai akhir zaman.
Pada kesempatan ini juga, penulis mengucapkan banyak terima kasih kepada berbagai pihak yang telah ikut membantu dalam menyelesaikan skripsi ini, khusunya pada:
1. Allah subhanahu wa taala, sumber segala kehidupan saya. Terima kasih sudah menjadikanku sesempurnanya manusia yang tidak sempurna.
2. Bapak Dr. Agus Salim, M.Si selaku Dekan Fakultas Sains dan Teknologi, UIN Syarif Hidayatullah Jakarta.
3. Ibu Nina Fitriyati, M.Kom dan Bapak Muhaza Liebenlito, M.Si selaku Kepala Program Studi Matematika dan Sekretaris Program Studi Matematika.
4. Ibu Yanne Irene, M.Si dan Ibu Irmatul Hasanah, M.Si selaku dosen pembimbing yang dengan sabar telah memberikan bimbingan, nasehat, pengarahan, dan saran yang berguna bagi penulis.
5. Bapak Dr. Taufik Edy Sutanto dan Bapak Budi Harianto, M.Si selaku dosen penguji yang telah memberikan saran yang baik untuk perbaikan penulisan skripsi ini.
6. Segenap staff, karyawan, dan dosen pengajar Program Studi Matematika, yang telah memberikan pengalaman dan bekal imu kepada penulis selama menjalani studi.
7. Abah dan Mama tercinta yang telah memberikan atas kasih sayang teriring doa, semangat, serta dorongan dalam menyelesaikan skripsi ini.
vii
8. Adik kandung penulis, Laila Qudrah Fikriyah dan Aleya Senna yang sudah menjadi motivasi penulis untuk segera menyelesaikan skripsi ini. 9. Teman-teman terbaik penulis, Imas, Dayinta, Ayu, Cynthia, Nadya, Sofi,
Sarah, Oot. Terima kasih atas segala kesabaran, tenaga, dan pikiran yang kalian sampaikan pada otak saya yang bebal. Semoga selalu hidup dalam lindungan Allah SWT.
10. Teman-teman Matematika 2013, yang telah berjuang bersama-sama untuk mencapai kesuksesan yang diimpikan.
11. Keluarga Matematika, kakak kelas dan adik kelas yang menemani penulis selama menjalani studi. Terima kasih telah sudi menjadi teman sekelas di beberapa mata kuliah.
12. Tim pelindung penulis selama menjalani kehidupan di Ciputat, HMI Komfastek, KOHATI Cabang Ciputat, Ebi Bag, YOT Tangerang, Indonesian Youth Conference, CeweQuat. Terima kasih atas pengalaman yang sangat luar biasa!
13. Semua pihak yang telah membantu, baik secara langsung maupun tidak langsung, yang tidak bisa penulis sebutkan satu persatu.
Penulis menyadari bahwa dalam penulisan dan penyusunan skripsi ini masih terdapat kekurangan-kekurangan dan masih jauh dari sempurna. Untuk itu, penulis sangat mengharapkan kritik dan saran yang membangun dan dapat menyempurnakan tulisan skripsi ini di masa mendatang. Kritik dan saran dapat disampaikan langsung kepada penulis atau dikirimkan melalui email
alfiatus.syifa18@mhs.uinjkt.ac.id. Akhir kata, penulis berharap semoga skripsi ini dapat memberikan manfaat bagi penulis dan pembaca pada umumnya.
Jakarta, Mei 2018
Alfiatus Syifa NIM. 1113094000018
viii
DAFTAR ISI
LEMBAR PENGESAHAN ... ii PERNYATAAN ... ii PERSEMBAHAN ... iv MOTTO ... v KATA PENGANTAR ... viDAFTAR ISI ... viii
DAFTAR GAMBAR ... ix
ABSTRAK ... x
ABSTRACT ... xi
BAB I PENDAHULUAN ... 1
1.1 Latar Belakang Masalah ... 1
1.2 Rumusan Masalah ... 2
1.3 Pembatasan Masalah ... 2
1.4 Tujuan Penelitian ... 2
1.5 Manfaat Penelitian ... 2
1.6 Sistematika Penulisan ... 2
BAB II STUDI PUSTAKA ... 4
2.1 Terminologi Dasar Graf ... 4
2.2 Jenis Graf ... 6
2.3 Diameter pada Graf ... 7
2.4 Beberapa Graf Khusus dan Operasi pada Graf ... 7
2.5 Bilangan Terhubung Pelangi dan Bilangan Terhubung Kuat Pelangi... 10
BAB III PEMBAHASAN ... 13
3.1 Bilangan Terhubung Pelangi pada (( ) ) ... 14
3.2 Bilangan Terhubung Kuat Pelangi pada (( ) ) ... 18
BAB IV PENUTUP ... 23
4.1 Kesimpulan ... 23
4.2 Saran ... 23
ix
DAFTAR GAMBAR
2.1 Graf dengan order 4 dan size 5 ... 5
2.2 (a) Graf Sederhana (b) Graf Ganda (c) Graf Semu ... 6
2.3 Graf ... 7
2.4 Graf Lintasan ... 8
2.5 Graf Lingkaran ... 8
2.6 Graf P3,2 ... 8
2.7 Graf APn ... 9
2.8 Graf Hasil Operasi Amalgamasi C3 ... 9
2.9 Rainbow–3–Coloring pada Graf Petersen ... 11
2.10 Strong Rainbow–4–Coloring pada Graf Petersen ... 11
2.11 Rainbow–2–Coloring pada Graf ... 12
3.1 Amalgamasi dari Himpunan Graf dengan t = 3 ... 14
3.2 Rainbow–4–Coloring dari Amalgamasi Graf dengan t = 2 ... 16
3.3 Rainbow–4–Coloring dari Amalgamasi Graf dengan t = 3 ... 17
3.4 Rainbow–4–Coloring dari Amalgamasi Graf dengan t = 4 ...17
3.5 Rainbow–4–Coloring dari Amalgamasi Graf dengan t = 5 ...18
3.6 Strong Rainbow–4–Coloring dari Amalgamasi Graf dengan t = 2 ... 21
3.7 Strong Rainbow–5–Coloring dari Amalgamasi Graf dengan t = 3 ... 21
3.8 Strong Rainbow–6–Coloring dari Amalgamasi Graf dengan t = 4 ...22
x
ABSTRAK
Bilangan Terhubung Pelangi dan Bilangan Terhubung Kuat Pelangi pada Amalgamasi Graf Antiprisma
Oleh
Alfiatus Syifa 1113094000018
Bilangan terhubung pelangi dari graf terhubung G, dinotasikan dengan ( ), adalah minimum dari banyaknya warna yang dibutuhkan untuk mewarnai G sehingga G bersifat rainbow connected. Selanjutnya, G dikatakan strong rainbow
connected jika untuk setiap titik di G terdapat rainbow path yang panjangnya
sama dengan jarak terpendek u dan v. Bilangan terhubung kuat pelangi dari graf
G, dinotasikan ( ), adalah minimum dari banyaknya warna yang dibutuhkan untuk mewarnai G sehingga G bersifat strong rainbow connected. Pada penelitian ini akan dibahas bilangan terhubung pelangi dan bilangan terhubung kuat pelangi pada amalgamasi graf antiprisma , dinotasikan ( ) dimana . Bilangan terhubung pelangi pada ( ) adalah 4 dan bilangan terhubung kuat pelangi adalah .
Kata kunci: Amalgamasi, bilangan terhubung pelangi, bilangan terhubung kuat pelangi, graf antiprisma.
xi
ABSTRACT
Rainbow Connection Number and Strong Rainbow Connection Number from Amalgamation of Antiprism Graph
Rainbow connection number of connected graph G, denoted by ( ), is the minimum number of colors needed to color its edges, so that G is rainbow connected. Graph G is strongly rainbow connected if for any two vertices and in G, there exists at least one shortest rainbow path. Bilangan terhubung kuat pelangi of G, denoted by ( ), is the minimum number of colors needed to color its edges, so that G is strongly rainbow connected. This paper, deals with rainbow connection number and strong rainbow connection number of the amalgamation of antiprism graph , denoted by ( ) where . Rainbow connection number for ( ) is 4, and strong rainbow connection number is .
Keyword: Amalgamation, antiprism graph, rainbow connection number, strong rainbow connection number.
1
BAB I
PENDAHULUAN
1.1 Latar Belakang Masalah
Teori graf merupakan salah satu cabang dari ilmu matematika yang menarik untuk diteliti, saat ini topik menarik yang banyak dikembangkan dalam teori graf adalah tentang pelabelan dan pewarnaan. Bilangan terhubung pelangi merupakan salah satu pengembangan dari pewarnaan pada teori graf.
Bilangan terhubung pelangi pertama kali diperkenalkan oleh Chartrand, dkk pada tahun 2006 [1]. Misal adalah graf terhubung tak trivial yang terdefinisi pada sebuah pewarnaan sisi-sisi pada , pewarnaan c adalah pemetaan dari E(G) ke bilangan k, dengan , dimana sisi yang bertetangga dapat diwarnai sama. Pewarnaan c disebut rainbow coloring di graf jika graf merupakan rainbow
connected, yaitu untuk setiap dua titik dan di mengandung lintasan rainbow. Jika telah digunakan warna, maka dikatakan rainbow-k-coloring. Minimum dari yang terdapat pada rainbow-k-coloring graf merupakan bilangan terhubung pelangi pada graf dan dinotasikan dengan ( ).
Dalam tesisnya pada tahun 2015, Darmawan [2] melakukan penelitian bilangan terhubung pelangi (rainbow connection number) dan bilangan terhubung kuat pelangi (strong rainbow connection number) pada beberapa jenis graf khusus, salah satunya pada graf antiprisma ( ).
Pada tahun 2016, Salman, dkk [4] melakukan penelitian mengenai bilangan terhubung kuat pelangi pada amalgamasi beberapa graf cycle, amalgamasi graf pohon, dan amalgamasi pada graf komplit.
Berdasarkan beberapa penelitian tersebut, peneliti akan meneliti bilangan terhubung pelangi dan bilangan terhubung kuat pelangi pada amalgamasi graf antiprisma AP3 sebagai tugas akhir.
2
1.2 Rumusan Masalah
Berdasarkan latar belakang yang telah diuraikan, permasalahan yang akan diteliti dalam penelitian ini adalah menentukan bilangan terhubung pelangi dan bilangan terhubung kuat pelangi pada amalgamasi graf antiprisma AP3.
1.3 Pembatasan Masalah
Agar pembahasan tidak meluas maka peneliti membatasi objek kajian, yaitu: 1. Graf yang digunakan adalah graf sederhana, tidak berarah, terhubung,
dan tak trivial.
2. Graf khusus yang digunakan adalah graf antriprisma AP3.
3. Operasi yang digunakan pada pengoperasian graf khusus adalah amalgamasi.
1.4 Tujuan Penelitian
Tujuan yang ingin dicapai peneliti dalam penelitian ini adalah menentukan bilangan terhubung pelangi dan bilangan terhubung kuat pelangi pada amalgamasi graf antiprisma AP3.
1.5 Manfaat Penelitian
1. Dapat menentukan bilangan terhubung pelangi dan bilangan terhubung kuat pelangi pada amalgamasi graf antiprisma AP3.
2. Dapat menjadi acuan penelitian selanjutnya bagi peneliti dalam bidang Teori Graf.
3. Dapat menjadi tambahan referensi, sehingga dapat menambah wawasan bagi pembaca.
1.6 Sistematika Penulisan
Penulisan Tugas Akhir ini dibagi dalam empat bab dengan rinciannya sebagai berikut: bab 1 sebagai pendahuluan terdiri dari latar belakang masalah, rumusan masalah, batasan masalah, tujuan penelitian, manfaat penelitian, dan sistematika penulisan. Pada bab 2 akan dijelaskan mengenai studi pustaka yang
3
akan digunakan pada penelitian. Selanjutnya pada bab 3 akan dijelaskan bilangan terhubung pelangi dan bilangan terhubung kuat pelangi pada amalgamasi graf antiprisma AP3. Terakhir pada bab 4 sebagai kesimpulan dan saran dari
4
BAB II
STUDI PUSTAKA
Dalam bab ini akan diberikan penjelasan studi pustaka yang akan digunakan dalam penelitian ini. Studi pustaka diawali dengan materi terminologi dasar graf, jenis graf, diameter pada graf, beberapa graf khusus dan operasinya, kemudian akan dibahas bilangan terhubung pelangi dan bilangan terhubung kuat pelangi.
2.1 Terminologi Dasar Graf
Pada subbab kali ini akan dijelaskan terminologi dasar graf berdasarkan buku Discrete Mathematics and Its Applications dengan Kenneth H. Rosen sebagai penulisnya [3].
Definisi 2.1.1 Graf (graph) adalah pasangan himpunan ( ) terdiri dari dua
bagian:
i. Suatu himpunan ( ) * + himpunan tak kosong yang
memiliki elemen yang disebut titik (vertex).
ii. Suatu himpunan ( ) * + *( ) ( )+
himpunan tak kosong yang memiliki elemen yang disebut sisi (edge) yang menghubungkan sepasang titik.
Sebuah graf dimungkinkan tidak mempunyai sisi satu buah pun, tetapi titiknya harus ada minimal satu. Graf yang hanya memiliki satu buah titik tanpa sebuah sisi pun dinamakan graf trivial (trivial graph).
Suatu graf dengan buah titik dan buah sisi ditulis dengan ( ). Secara umum graf dapat digambarkan dengan suatu diagram dimana titik yang ditunjukkan sebagai titik yang dinotasikan dengan dengan dan sisi yang digambarkan dengan sebuah garis lurus atau dengan garis lengkung yang menghubungkan dua titik dinotasikan dimana disebut dengan titik - titik titik dari . Titik pada graf dapat dinomori dengan huruf, atau bilangan asli, atau dengan menggunakan keduanya.
5
Jumlah titik di dalam sebuah graf disebut order dinotasikan | ( )| dan jumlah sisi di dalam sebuah graf disebut size dinotasikan | ( )|. Gambar 2.1 akan mengilustrasikan bentuk graf.
Gambar 2.1 Graf dengan order 4 dan size 5
Dua buah titik dikatakan bertetangga jika terdapat sisi yang menempel pada kedua titiknya. Untuk sebarang ( ) dapat dikatakan bersisian dengan titik dan titik . Tinjau graf , disimpulkan ( ) adalah sebuah sisi pada graf, maka didapat bahwa dan bersisian, dan bersisian, serta dan bertetangga di . Disimpulkan pula tidak bersisian dengan serta tidak bertetangga dengan .
Jumlah atau banyaknya sisi yang terkait dengan suatu titik disebut derajat (degree) dari titik tersebut dinotasikan ( ) dimana . Contoh pada Gambar 2.1, terlihat bahwa untuk setiap titik di derajat titiknya adalah ( ) , ( ) , ( ) , ( ) .
Pada graf terdapat lintasan. Lintasan di adalah barisan berhingga, tak kosong suku-sukunya bergantian titik dan sisi, sedemikian sehingga ( ), ( ),…, ( ) adalah sisi pada graf.
dan berturut-turut disebut titik awal dan titik akhir . Panjang dari lintasan adalah banyaknya sisi dalam , ditulis . Jika lintasan dimulai dan diakhiri di titik yang sama, dinamakan siklus atau sirkuit.
Dua buah titik dikatakan terhubung jika terdapat lintasan dari dan kedua titiknya. dikatakan graf terhubung (connected graph) jika untuk setiap pasang
6
titik dan dalam himpunan terdapat lintasan dari dan . Jika tidak, maka dikatakan graf tak terhubung (disconnected graph).
2.2 Jenis Graf
Secara umum, graf terbagi menjadi dua yaitu graf sederhana dan graf tak sederhana.
1. Graf Sederhana (Simple Graph)
Graf sederhana adalah graf yang tidak mempunyai sisi ganda dan atau gelang (loop). Loop adalah sisi yang menghubungkan sebuah titik dengan dirinya sendiri. Sisi ganda adalah sekumpulan sisi yang menghubungkan sepasang titik yang sama. Pada graf sederhana, sisi adalah pasangan tak terurut (unordered pairs).
2. Graf tak Sederhana (Non simple Graph)
Graf tak Sederhana yang mengandung sisi ganda atau gelang (loop). Ada dua macam graf tak sederhana, yaitu graf ganda (multigraph) atau graf semu (pseudograph). Graf ganda adalah graf yang mengandung sisi ganda. Graf semu adalah graf yang mengandung sisi ganda dan gelang (loop). Gambar 2.2 akan mengilustrasikan bentuk graf sederhana, graf ganda, dan graf semu
Gambar 2.2 (a) Graf Sederhana (b) Graf Ganda (c) Graf Semu
Pengelompokan berdasarkan orientasi arah pada sisinya digolongkan menjadi dua yaitu graf berarah dan graf tak berarah.
1. Graf Berarah
Graf berarah adalah graf yang setiap sisinya memiliki orientasi arah. Sisi pada graf berarah disebut busur (arc). Pada graf berarah, ( ) dan ( ) menyatakan dua buah busur yang berbeda. Jadi ( ) ( ). Untuk busur ( ), titik dinamakan titik asal (initial vertex)
7
dan titik dinamakan titik terminal (terminal vertex). Pada graf berarah, adanya gelang diperbolehkan, tetapi sisi ganda tidak.
2. Graf tak Berarah
Graf tak berarah adalah graf yang sisinya tidak mempunyai orientasi arah. Urutan pasangan titik yang dihubungkan oleh sisi tidak diperhatikan, jadi ( ) dan ( ) adalah sisi yang sama.
2.3 Diameter pada Graf
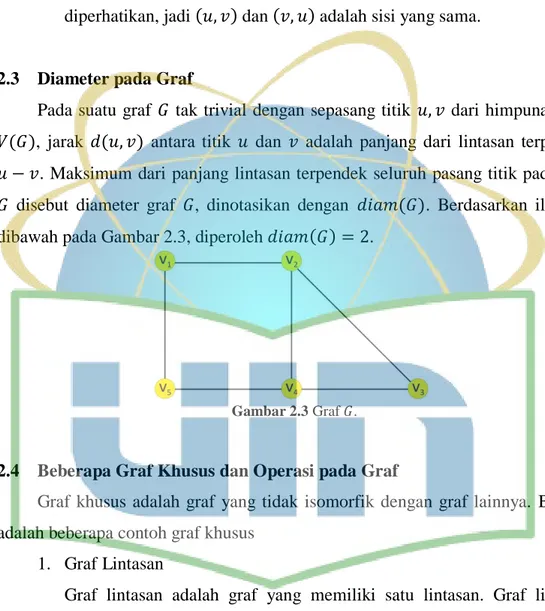
Pada suatu graf tak trivial dengan sepasang titik dari himpunan titik ( ), jarak ( ) antara titik dan adalah panjang dari lintasan terpendek . Maksimum dari panjang lintasan terpendek seluruh pasang titik pada graf disebut diameter graf , dinotasikan dengan ( ). Berdasarkan ilustrasi dibawah pada Gambar 2.3, diperoleh ( ) .
Gambar 2.3 Graf .
2.4 Beberapa Graf Khusus dan Operasi pada Graf
Graf khusus adalah graf yang tidak isomorfik dengan graf lainnya. Berikut adalah beberapa contoh graf khusus
1. Graf Lintasan
Graf lintasan adalah graf yang memiliki satu lintasan. Graf lintasan dengan n titik dilambangkan Pn dimana . Gambar 2.4 merupakan
ilustrasi dari graf lintasan
8
2. Graf Cycle (Lingkaran)
Graf Lingkaran adalah graf sederhana yang setiap titiknya berderajat dua. Graf lingkaran dengan n titik dilambangkan dengan Cn, dimana
. Gambar 2.5 adalah ilustrasi dari graf lingkaran.
Gambar 2.5 Graf Lingkaran . 3. Graf Prisma
Graf Prisma dinotasikan Pm,n dengan himpunan titiknya ( )
{ | } dan himpunan sisinya ( )
{{ | } { | }
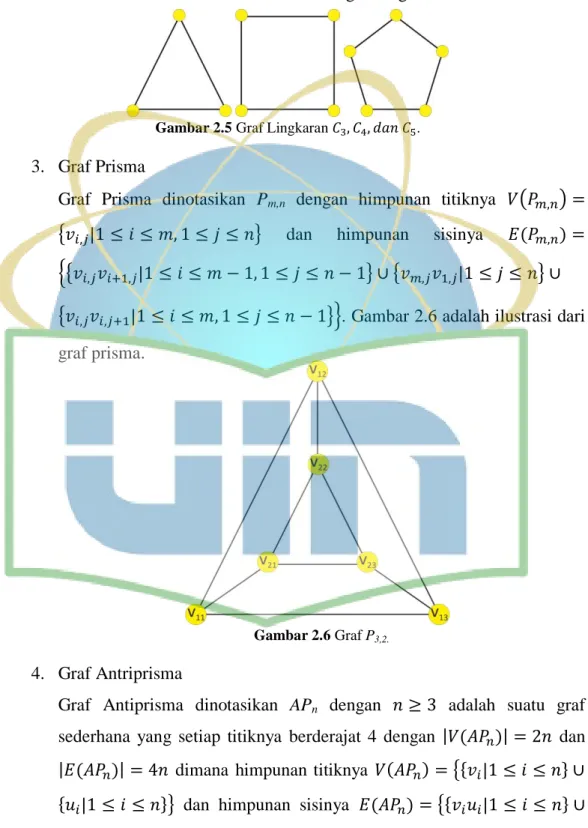
{ | }}. Gambar 2.6 adalah ilustrasi dari
graf prisma.
Gambar 2.6 Graf P3,2.
4. Graf Antriprisma
Graf Antiprisma dinotasikan APn dengan adalah suatu graf
sederhana yang setiap titiknya berderajat 4 dengan | ( )| dan | ( )| dimana himpunan titiknya ( ) {* | + * | +} dan himpunan sisinya ( ) {* | + * | + * + * + * | +
9
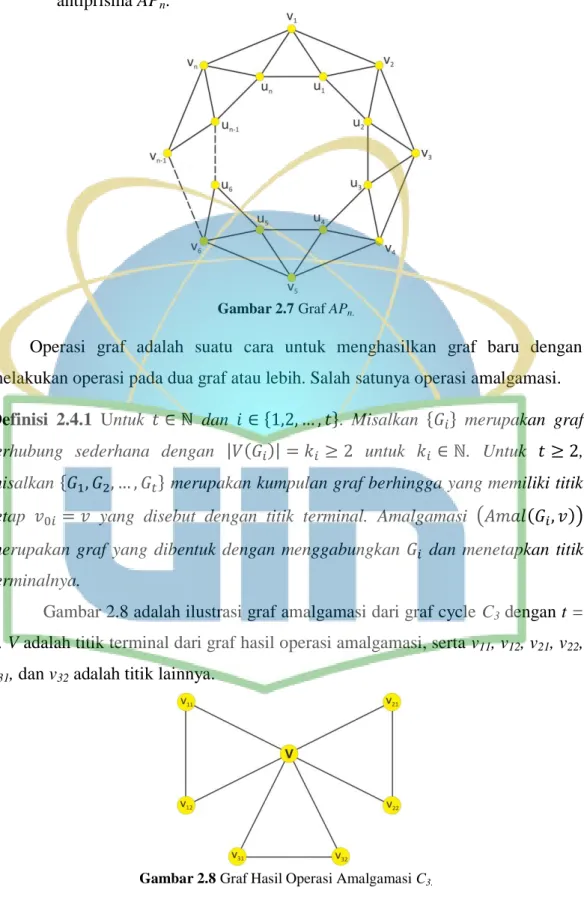
* | + * +}. Gambar 2.7 adalah ilustrasi dari graf antiprisma APn.
Gambar 2.7 Graf APn.
Operasi graf adalah suatu cara untuk menghasilkan graf baru dengan melakukan operasi pada dua graf atau lebih. Salah satunya operasi amalgamasi. Definisi 2.4.1 Untuk dan * +. Misalkan * + merupakan graf
terhubung sederhana dengan | ( )| untuk . Untuk ,
misalkan * + merupakan kumpulan graf berhingga yang memiliki titik
tetap yang disebut dengan titik terminal. Amalgamasi ( ( ))
merupakan graf yang dibentuk dengan menggabungkan dan menetapkan titik terminalnya.
Gambar 2.8 adalah ilustrasi graf amalgamasi dari graf cycle C3 dengan t =
3. V adalah titik terminal dari graf hasil operasi amalgamasi, serta v11, v12, v21, v22,
v31, dan v32 adalah titik lainnya.
10
2.5 Bilangan Terhubung Pelangi dan Bilangan Terhubung Kuat Pelangi Konsep rainbow connection pada graf pertama kali diperkenalkan pada tahun 2006 oleh Chartrand, dkk [1]. Misalkan adalah graf terhubung nontrivial dengan pewarnaan sisi ( ) * + untuk dengan sisi-sisi yang bertetangga boleh mempunyai warna yang sama. Suatu lintasan dikatakan
rainbow path jika tidak terdapat dua sisi di lintasan yang diwarnai sama. Sebuah edge−coloring graf adalah rainbow connected jika sebarang dua titik yang
terhubung dihubungkan oleh jalur rainbow. Graf disebut rainbow connected dengan pewarnaan jika memuat suatu rainbow path untuk setiap dua titik . Dalam hal ini, pewarnaan dikatakan rainbow coloring di .
Jelas bahwa jika graf adalah rainbow connected maka pasti terhubung. Jika pewarnaan menggunakan sebanyak warna, maka disebut
rainbow-k-coloring. Minimum dari yang terdapat pada rainbow-k-coloring pada graf merupakan bilangan terhubung pelangi pada graf dan dinotasikan dengan ( ).
Sebuah lintasan geodesic antara titik u dan v dari graf G adalah lintasan u –
v dengan panjang minimum. Misal suatu rainbow coloring pada suatu graf terhubung . Untuk sebarang titik dan di , rainbow geodesic di adalah rainbow path dengan panjang ( ), dimana ( ) adalah jarak antara titik dan . Graf dikatakan strongly rainbow connected jika mengandung satu rainbow geodesic untuk setiap pasang titik dan di . Dalam hal ini, dikatakan strong rainbow coloring dari Nilai minimum dari pewarnaan sisi ( ) * + yang dibutuhkan untuk mewarnai graf menjadi
strongly rainbow connected merupakan bilangan terhubung kuat pelangi pada graf
dan dinotasikan dengan ( ).
Chartrand, dkk [1] telah melakukan penelitian tentang batas bawah dan batas atas dari bilangan terhubung pelangi dan bilangan terhubung kuat pelangi. Teorema 2.5.1 Misal adalah graf terhubung tak trivial dengan size m yang
diameternya ( ), maka
11
Untuk mengilustrasikan konsep di atas akan diberikan contoh bilangan terhubung pelangi pada graf petersen pada Gambar 2.9. Akan ditunjukkan ( ) . Jika dan adalah titik-titik yang tidak bertetangga pada , maka ( ) dan panjang lintasan sekurang kurangnya adalah 2. Jadi setiap pewarnaan rainbow di digunakan adalah ( ) . Jika memuat pewarnaan-2 rainbow, maka terdapat dua sisi bertetangga di yang diwarnai sama, misal
dan adalah kedua sisi yang diwarnai sama. Karena terdapat tepat satu lintasan dengan panjang 2 di , maka tidak terdapat lintasan rainbow di . Berdasarkan asumsi ( ) terjadi kontradiksi sehingga haruslah ( ) . Oleh karena itu ( ) . Selanjutnya, diketahui setiap pewarnaan-3 pada sisi-sisi di dimana dua sisi bertetangga dan diberikan warna yang sama. Karena adalah satu-satunya lintasan
geodesic di , maka pewarnaan bukan merupakan pewarnaan strong rainbow. Pewarnaan-4 pada sisi di yang ditunjukkan pada Gambar 2.10 adalah pewarnaan strong rainbow, ( ) .
Gambar 2.9 Rainbow–3–Coloring pada Graf Petersen.
12
Selanjutnya, Darmawan melakukan penelitian menentukan bilangan terhubung kuat pelangi pada graf antiprisma. [3]
Teorema 2.5.2 Untuk , bilangan terhubung pelangi pada graf antiprisma adalah
( ) { ⌈ ⌉ .
Gambar 2.11 adalah ilustrasi bilangan terhubung pelangi pada graf antiprisma dengan ( ) * +.
Gambar 2.11 Rainbow – 2 – Coloring pada Graf .
Pada tahun 2016, Salman, dkk [5], melakukan penelitian berjudul bilangan terhubung pelangi pada amalgamasi dari beberapa graf. Dari hasil penelitian tersebut diperoleh batas atas dan batas bawah untuk bilangan terhubung pelangi pada amalgamasi dari graf sebarang.
Teorema 2.5.3 Untuk , Misal { | * +} adalah kumpulan
graf berhingga dan tiap memiliki titik tetap yang disebut terminal. Jika amalgamasi adalah dari ( ), maka
( ) ( ) ∑ ( )
13
BAB III
PEMBAHASAN
Dalam bab ini akan diberikan penjelasan hasil penelitian berdasarkan rumusan masalah yang telah dijelaskan pada bab sebelumnya. Penelitian diawali dengan menentukan graf khusus yaitu graf antiprisma yang kemudian akan dilakukan operasi graf yaitu amalgamasi. Hasil amalgamasi yang diperoleh tersebut akan diterapkan pewarnaan rainbow, kemudian akan diuji apakah pewarnaannya sudah optimal dan membentuk suatu pola dengan menggunakan teorema-teorema yang sudah ada. Jika pewarnaan sudah optimal dan membentuk suatu pola maka akan dibentuk fungsi dari ( ). Hasil akhir dari penelitian ini adalah teorema baru beserta pembuktiannya tentang bilangan terhubung pelangi dan bilangan terhubung kuat pelangi pada ( ) dimana .
Definisi 3.1 Graf merupakan graf antiprisma yang memiliki himpunan titik
( ) {* | + * | +} dengan | ( )| dan himpunan sisi ( ) {* | + * | + * + * + * | + * | + * +} dengan
| ( )| .
Definisi 3.2 Suatu operasi graf amalgamasi dari graf antiprisma
( ) ( ) ( ) , untuk * + dengan titik tetap dinotasikan
dengan (( ) ). Misal (( ) ). Graf memiliki
himpunan titik ( ) {* + * | +} dengan | ( )|
dan ( ) {* | + * |
+ * | + * | +
* | +} adalah himpunan sisinya dengan | ( )| .
Gambar 3.1 merupakan ilustrasi dari amalgamasi graf antiprisma AP3
14
Gambar 3.1 Amalgamasi dari Himpunan Graf AP3 dengan t = 3.
3.1 Bilangan Terhubung Pelangi pada (( ) )
Pada subbab ini akan ditunjukkan bahwa bilangan terhubung pelangi adalah ( ) .
Teorema 3.1.1 Misalkan dimana dan (( ) ) untuk
setiap * + maka ( )
Bukti. Diketahui ( ) . Berdasarkan Teorema 2.5.3 maka: ( ) ( ) ∑ ( )
( ) ( ( ) ( ) ( )) ( ) ( ( ) ( ) ( )) ( ) ( ( ))
Berdasarkan Teorema 2.5.2 didapat ( ) , dan persamaannya menjadi ( ) . Maka, nilai ( ) yang mungkin adalah . Selanjutnya, akan ditunjukkan ( ) , didefiniskan pewarnaan sisi ( ) * + sebagai berikut. ( ) { *( ) ( ) ( )+ *( ) ( ) ( )+ *( ) ( ) ( )+ *( ) ( ) ( )+
Selanjutnya, akan ditunjukkan terdapat suatu lintasan pelangi untuk setiap dua titik yang ada pada graf . Jika dan bertetangga, jelas selalu
15
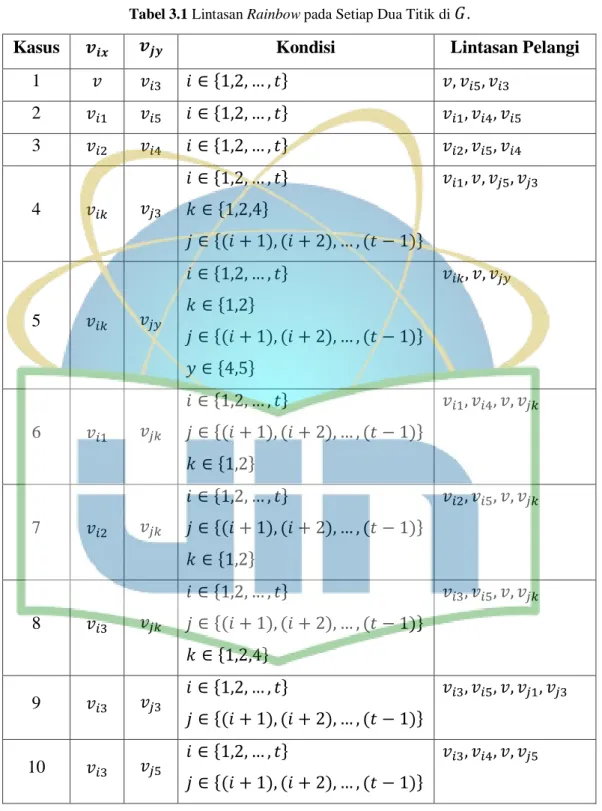
terdapat lintasan pelangi. Jika dan tidak bertetangga, dapat ditunjukkan bahwa terdapat lintasan pelangi seperti pada Tabel 3.1 dibawah ini.
Tabel 3.1 Lintasan Rainbow pada Setiap Dua Titik di .
Kasus Kondisi Lintasan Pelangi
1 * + 2 * + 3 * + 4 * + * + *( ) ( ) ( )+ 5 * + * + *( ) ( ) ( )+ * + 6 * + *( ) ( ) ( )+ * + 7 * + *( ) ( ) ( )+ * + 8 * + *( ) ( ) ( )+ * + 9 * + *( ) ( ) ( )+ 10 * + *( ) ( ) ( )+
16 11 * + *( ) ( ) ( )+ * + 12 * + *( ) ( ) ( )+ 13 * + *( ) ( ) ( )+ * + 14 * + *( ) ( ) ( )+ * +
Dapat disimpulkan bahwa pewarnaan pada graf memenuhi asumsi rainbow
connected. Maka, diperoleh ( ) . Pada gambar 3.2, gambar 3.3, gambar 3.4, dan gambar 3.5 akan diberikan ilustrasi pewarnaan bilangan terhubung pelangi pada graf (( ) ):
17
Gambar 3.3 Rainbow–4–Coloring dari Amalgamasi Graf dengan t = 3.
18
Gambar 3.5 Rainbow–4–Coloring dari Amalgamasi Graf dengan t = 5.
3.2 Bilangan Terhubung Kuat Pelangi pada (( ) )
Pada subbab 3.1 telah ditunjukkan bahwa bilangan terhubung pelangi dari graf (( ) ) adalah ( ) . Pada subbab ini akan ditunjukkan bahwa bilangan terhubung kuat pelangi adalah ( ) . Karena ( ) , berdasarkan Teorema 2.5.1, diperoleh ( ) sehingga nilai ( ) yang mungkin adalah .
Teorema 3.2.1 Misalkan dimana dan (( ) ) untuk
setiap * + maka ( )
Bukti. Andaikan pewarnaan sisi ( (( ) )) * + adalah pewarnaan strong rainbow.
Tanpa mengurangi perumuman, misalkan ( ) dan ( ) .
Diketahui ( ) dengan * +, * + dan hanya mempunyai satu-satunya lintasan terpendek adalah .
Untuk memenuhi asumsi strongly rainbow connected, didapat ( ) ( ) maka graf membutuhkan warna.
19
Pandang ( ) dengan * +, * +, * ( )+, * + dan hanya mempunyai satu-satunya lintasan terpendek adalah .
Untuk memenuhi asumsi strongly rainbow connected, didapat ( ) ( )
maka graf membutuhkan warna.
Diketahui ( ) dengan * + dan . Pandang lintasan .
Untuk memenuhi asumsi strongly rainbow connected, didapat ( ) ( ), ( ) ( ), ( ) ( ), ( ) ( ), ( ) ( ), ( ) ( ) dan membutuhkan warna.
Diketahui ( ) dengan * + dan . Pandang lintasan .
Untuk memenuhi asumsi strongly rainbow connected, didapat ( ) ( ), ( ) ( ), ( ) ( ), ( ) ( ), ( ) ( ), ( ) ( ).
Untuk .
Diketahui ( ) .
Pandang lintasan .
Untuk memenuhi asumsi strongly rainbow connected, didapat ( ) ( ) dan membutuhkan warna. Hal ini kontradiksi dengan asumsi
awal. Selanjutnya, definisikan pewarnaan sisi ( ) * + sebagai berikut.
20 ( ) { *( ) ( ) ( ) ( ) + *( ) ( ) ( ) ( ) ( ) ( ) ( )+ *( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )+ {( ( ) ( ) ) ( ( ) ( ) ) ( ( ) ( ) ) ( ( ) ( ) ) ( ) ( ( ) ( ) ) ( ( ) ( ) ) ( ( ) ( ) ) ( ) ( ) ( ) ( )} {( ( ) ( ) ) ( ( ) ( ) ) ( ( ) ( ) ) ( ( ) ( ) ) ( ) ( ) ( )+ *( ) ( ) ( ) ( )+
Selanjutnya, akan ditunjukkan terdapat suatu rainbow geodesic untuk
setiap dua titik yang ada pada graf . Jika dan bertetangga, jelas selalu terdapat lintasan pelangi. Jika dan tidak bertetangga, dapat ditunjukkan bahwa terdapat lintasan pelangi kuat seperti pada Tabel 3.2 dibawah.
Tabel 3.2 Lintasan Strong Rainbow pada Setiap Dua Titik di .
Kasus Kondisi Rainbow Geodesic
1 * + * + 2 * + 3 * + 4 * + 5 * + * + *( ) ( ) ( )+ 6 * + * + *( ) ( ) ( )+ 7 * + *( ) ( ) ( )+ * + 8 * + *( ) ( ) ( )+
21
Dapat disimpulkan bahwa pewarnaan pada graf memenuhi asumsi strongly
rainbow connected. Maka, diperoleh ( ) . Pada Gambar 3.6, Gambar 3.7, Gambar 3.8, dan Gambar 3.9 akan diberikan ilustrasi pewarnaan bilangan terhubung kuat pelangi pada graf (( ) ):
Gambar 3.6 Strong Rainbow–4–Coloring dari Amalgamasi Graf dengan t = 2.
22
Gambar 3.8 Strong Rainbow–6–Coloring dari Amalgamasi Graf dengan t = 4.
23
BAB IV
PENUTUP
4.1 Kesimpulan
Berdasarkan Teorema 3.1.1 diperoleh bilangan terhubung pelangi pada amalgamasi graf antiprisma , yaitu ( ) untuk adalah bilangan bulat positif . Sedangkan bilangan terhubung kuat pelangi pada amalgamasi graf berdasarkan Teorema 3.2.1 yaitu ( ) . Sehingga dapat disimpulkan dalam sebuah teorema baru, yaitu misal * + dengan bilangan bulat positif dimana dan (( ) ), maka ( ) dan ( ) .
4.2 Saran
Saran yang dapat diberikan peneliti kepada pembaca adalah dengan melanjutkan penelitian penentuan bilangan terhubung pelangi dan bilangan terhubung kuat pelangi pada amalgamasi graf dengan .
24
REFERENSI
[1] Chartrand, G., & dkk. (2008). Rainbow Connection in Graphs. Math Bohem 133(1), 85-98.
[2] Darmawan, R. N. (2015). Analisis Bilangan terhubung kuat pelangi pada
Graf Khusus dan Hasil Operasinya. thesis. Pascasarjana Universitas Jember.
[3] Rosen, K.H. (2012). Discrete Mathematics and Its Application 7th Edition. New York: Mac Graw-Hill, inc.
[4] Salman, A. N. M. dan D. Fitriani. (2016). Rainbow Connection Number of Amalgamation of Some Graphs. AKCE International J. Graph and
Combinatorics 13: h.90-99.
[5] Shulhany, M. A. dan Salman, A. N. M. (2015). Bilangan Terhubung Pelangi Graf Berlian. Prosiding Seminar Nasional Matematika dan Pendidikan