5 BAB II
TINJAUAN PUSTAKA
2.1 Definisi Aljabar Boolean
Aljabar Boolean pertama kali ditemukan pada tahun 1854 oleh seorang ahli matematika berkebangsaan Inggris bernama George Boole (1815-1864). Boole dalam penelitiannya memaparkan beberapa aturan dasar logika manusia dalam aturan nilai-nilai matematis pada bukunya yang berjudul An Investigation of The laws of Though, on Which are Founded the Mathematical Theorities of Logic and Probabilities, yang dalam bukunya disebut sebagai logika Boolean [5]. Logika Boolean ini secara sistem matematika dikenal sebagai Aljabar Boolean yang kemudian menjadi salah satu dasar perancangan rangkaian dari teknologi komputer digital.
Logika Boolean didasari pada penerapan aturan hubungan antara nilai-nilai matematis yang dibatasi pada dua nilai yaitu true dan false yang kemudian disimbolkan sebagai angka 1 dan 0 dimana 0 disebut elemen zero, sedangkan 1 disebut elemen unit. Aljabar Boolean adalah aljabar yang terdiri atas himpunan B yang memiliki dua operator biner yaitu: + (penjumlahan) dan • (perkalian) sehingga untuk setiap x, y, z ϵ B berlaku aksioma atau postulat sebagai berikut [6].
1. Closure : (i) x + y ϵ B (ii) x • y ϵ B
2. Identitas : (i) terdapat elemen tunggal yaitu 0 ϵ B sehingga berlaku: x + 0 = 0 + x = x
(ii) terdapat elemen tunggal 0 ϵ B sehingga berlaku:
x • 1 = 1 • x = 1
3. Komutatif : (i) x + y = y + x (ii) x • y = y • x
4. Distributif : (i) x • (y+z) = (x • y) + (x • z) (ii) x + (y • z) = (x+y) • (x+z) (iii) (x • y) + z = (x+z) • (y+z)
5. Komplemen : Setiap x ϵ B terdapat elemen tunggal x’ ϵ B sedemikian sehingga berlaku: x + x’ = 1 dan x • x’ = 0
6
6. Terdapat sedikitnya dua elemen, x dan y ϵ B sedemikian hingga berlaku: x ≠ y
7. Asosiatif : (i) x + (y+z) = (x+y) + z (ii) x • (y • z) = (x • y) • z 8. Idempoten : (i) x • x = x
(ii) x + x = x
Aksioma satu sampai enam disebut dengan Postulat Huntington. Hal ini karena aksioma tersebut diformulasikan oleh E.V. Huntington, syarat Aljabar Boolean berdasarkan aksioma yang dijelaskan adalah sebagai berikut [7].
1. Elemen himpunan B
2. Kaidah operasi adalah untuk dua operator biner
3. Himpunan B bersama-sama dengan dua operator biner harus memenuhi Postulat Huntington (aksioma 1 sampai dengan 6)
Terdapat beberapa perbedaan antara Aljabar Boolean dengan aljabar biasa untuk aritmetika bilangan riil. Perbedaan tersebut adalah sebagai berikut [1]. 1. Hukum distributif pertama pada aksioma yaitu x • (y+z) = (x • y) + (x • z) dapat
berarti Aljabar Boolean juga aljabar biasa. Namun untuk hukum distributif kedua yaitu x + (y • z) = (x+y) • (x+z) tidak benar untuk aljabar biasa namun benar untuk Aljabar Boolean
2. Aljabar Boolean tidak memiliki operasi pembagian dan pengurangan hal ini karena Aljabar Boolean tidak memiliki kebalikan perkalian (multipicative inverse) dan kebalikan penjumlahan
3. Aksioma komplemen pada Aljabar Boolean tidak tersedia pada aljabar biasa 4. Aljabar biasa memperlakukan himpunan bilangan riil dengan elemen yang tidak
berhingga. Sedangkan Aljabar Boolean memperlakukan himpunan B didefinisikan hanya dengan dua nilai yaitu 0 dan 1.
2.2 Aljabar Boolean Dua Nilai
Sebagaimana disebutkan sebelumnya, Aljabar Boolean mendefinisikan himpunan dengan dua buah elemen yaitu: B = {0,1} yang sering disebut dengan bit- atau binary digit dengan kaidah operator biner terdiri dari dua operasi yaitu + (penjumlahan) dan • (perkalian) serta adanya operator ‘ (uner) [5]. Hal ini ditunjukkan pada Tabel 2.1 berikut:
7
Tabel 2.1 Operator Biner untuk Penjumlahan dan Perkalian Logika
Tabel 2.2 Operator Uner
Operasi-operasi yang terdapat pada Tabel 2.1 dan Tabel 2.2 harus memenuhi aksioma yang ada. Hal ini dapat dibuktikan pada penjelasan berikut: 1. Closure. Pada tabel dapat dilihat bahwa 0 dan 1 ϵ B
2. Identitas. Dapat terlihat pada masing-masing tabel operator penjumlahan dan perkalian yang memenuhi elemen identitas 0 dan 1 yaitu:
(i) 0 + 1 = 1 + 0 = 1 (ii) 1 • 0 = 0 • 1 = 0
3. Komutatif. Dapat dilihat dari simetri tabel antara kolom x dan kolom y
4. Distributif. Jelas terpenuhi pada distributif (i) yaitu x • (y+z) = (x • y) + (x • z) dapat dibuktikan dengan membuat tabel kebenaran dengan semua nilai x dan y berasal dari Tabel 2.1. Sedangkan hukum distributif (ii) yaitu x + (y • z) = (x+y) • (x+z) juga sama dapat dibuktikan dengan membuat tabel kebenaran distributif (i). Adapun tabel kebenaran untuk distributif (i) seperti pada Lampiran 1. 5. Komplemen. Dapat dilihat pada Tabel 2.2 yang memperlihatkan bahwa:
(i) x + x’ = 1 (ii) x • x’ = 0
6. Aksioma 6 jelas terpenuhi karena Aljabar Boolean memiliki dua nilai yaitu 0 dan 1 sehingga 0 ≠ 1. x y x • y 0 0 0 0 1 0 1 0 0 1 1 1 x y x + y 0 0 0 0 1 1 1 0 1 1 1 1 x x’ 0 1 1 0
8 2.3 Prinsip Dualitas
Pada Aljabar Boolean, kerap ditemukan kesamaan identitas misalnya pada dua aksioma distributif (i) dan (ii) yaitu:
(i) x • (y+z) = (x • y) + (x • z) (ii) x + (y • z) = (x+y) • (x+z)
Berdasarkan aksioma distributif, aksioma distributif (ii) memiliki kesamaan dengan distributif (i) dengan hanya mengganti (•) dengan (+). Persamaan ini disebut dengan prinsip dualitas yang mana juga ditemukan dalam teori himpunan maupun logika. Adapun prinsip dualitas dapat disebutkan sebagai berikut [8].
(•) mempertukarkan dengan (+), begitupun sebaliknya (1) mempertukarkan dengan (0), begitupun sebaliknya.
Berdasarkan aksioma yang disebutkan sebelumnya, prinsip dualitas masing-masing aksioma adalah sebagai berikut.
1. Komutatif : x + y = y + x Dualitas: x • y = y • x
2. Asosiatif : x + (y+z) = (x+y) + z Dualitas: x • (y•z) = (x•y) + z 3. Distributif : x + (y•z) = (x+y) •(x+z)
Dualitas: x • (y+z) = (x•y) + (x•z) 2.4 Hukum – Hukum Aljabar Boolean
Aljabar Boolean sebagaimana disebutkan sebelumnya memiliki aturan atau hukum. Adapun hukum-hukum Aljabar Boolean adalah sebagai berikut [5].
Tabel 2.3 Hukum-hukum Aljabar Boolean 1. Hukum Identitas: (i) x + 0 = x (ii) x • 1 = x 2. Hukum Idempoten: (i) x + x = x (ii) x • x = x 3. Hukum Komplemen: (i) x + x’ = 1 (ii) x • x’ = 0 4. Hukum Dominansi: (i) x • 0 = 0 (ii) x + 1 = 1
9 5. Hukum Involusi:
(i) (a’)’ = a
6. Hukum penyerapan (absorbsi): (i) x + xy = x (ii) x(x+y) = x 7. Hukum Komutatif: (i) x + y = y + x (ii) xy = yx 8. Hukum Asosiatif: (i) x (x+z) = (x+y) + z (ii) x(yz) = (xy)z
9. Hukum Distributif:
(i) x + (yz) = (x+y) + (x+z) (ii) x(y+z) = xy + xz
10. Hukum De Morgan: (i) (x+y)’ = x’y’ (ii) (xy)’ = x’ + y’
11. Hukum 0/1: (i) 0’ = 1 (ii) 1’ = 0
Hukum-hukum Aljabar Boolean dapat diperoleh dari hukum-hukum aljabar biasa dengan mempertukarkan beberapa simbol dalam aljabar biasa diantaranya sebagai berikut.
∪ dan ˅ ditukar dengan + ∩ dan ˄ ditukar dengan •
U dan T ditukar dengan 1
Ø atau F ditukar dengan 0 2.5 Fungsi Boolean
Fungsi Boolean atau dikenal juga dengan istilah fungsi Biner adalah ekspresi dari bentuk variabel biner dua operator yaitu biner (+) dan (•) serta komplementer atau uner (‘) dengan adanya tanda kurung () dan tanda sama dengan (=). Setiap variabel Boolean disebut literal [2]. Adapun contoh-contoh penulisan fungsi Boolean adalah sebagai berikut [7].
10 1. f (x) = x’
2. f (x,y) = x’y + x’y + y 3. f (x,y,z) = xy’z + yz 4. f (x,y,z) = x + (y’z) 5. f (x,y,z) = xy’z
Ekspresi xy merupakan singkatan penulisan dari x•y. Dari lima contoh fungsi, contoh kelima yaitu xy’z memiliki tiga variabel yaitu x , y’ , z. Jika diambil nilai x = 1, y = 0 dan z = 1 diperoleh nilai fungsi untuk contoh kelima adalah 1. Tabel kebenaran untuk fungsi f(x,y,z) = xy’z terdapat dalam Lampiran 2.
2.6 Komplemen Fungsi Boolean
Fungsi Boolean dapat dikomplemenkan menjadi fungsi komplemen yang berfungsi saat menyederhakan suatu fungsi Boolean. Fungsi komplemen dapat dicari dengan menukarkan nilai 0 menjadi 1, serta nilai 1 menjadi 0. Fungsi komplemen dari fungsi f adalah f’ dan dapat dicari dengan dua cara yaitu [1]: 1. Menggunakan hukum De Morgan.
• Untuk dua variabel 𝑥1 dan 𝑥2 maka: (i) (x1 + x2)’ = x1’x2’
(ii) (x1•x2)’ = x1’ + x2’
• Untuk tiga variabel x1, x2, x3, maka:
(i) (x1 + x2 + x3)’ = (x1 + y)’ dimana y = x2 + x3
= x1’y’
= x1’(x2 + x3)’
= x1’x2’x3’
(ii) dualnya adalah = (x1•x2•x3)’ = x1’ + x2’ + x3’
• Untuk n variabel x1,x2,x3,....,xn maka :
(i) (x1 + x2 + x3 + ... + xn)’ = x1’x2’x3’...xn’
11 2. Menggunakan prinsip dualitas
Cara mencari fungsi komplemen dengan prinsip dualitas adalah pertama tentukan terlebih dahulu ekspresi Boolean yang mempresentasikan f, lalu komplemenkan dari setiap variabel di dalam dual tersebut sehingga membentuk ekspresi akhir yang disebut fungsi komplemen. Contoh menggunakan prinsip dualitas adalah sebagai berikut:
Contoh 2.1
f(x,y,z) = x(y’z’ + yz) (menyatakan ekspresi fungsi f)
= x + (y’ + z’) (y+z) (menentukan dual dari ekspresi Fungsi f)
= x’ + (y + z) (y’ + z’) = f’ (hasil komplemen dari tiap variabel dual diatas)
Sehingga diperoleh f’(x,y,x) = x’ + (y + z) )y’ + z’) sebagai bentuk fungsi komplemen dari f(x,y,z) = x(y’z’ + yz).
2.7 Bentuk Kanonik
Ekspresi Boolean yang menspesifikan suatu fungsi disajikan dalam dua bentuk yaitu fungsi Boolean yang merupakan jumlah dari hasil kali atau dikenal dengan istilah sum-of-product (SOP) atau minterm dan hasil kali dari jumlah atau dikenal dengan istilah product-of-sum (POS) atau maxterm dengan setiap sukunya mengandung variabel lengkap dimana ekspresi ini disebut dengan bentuk kanonik [5]. Ekspresi Boolean minterm dapat diselesaikan dengan mengoperasikan fungsi Boolean dengan operasi AND dan hasilnya dioperasikan dengan operasi OR sedangkan Aljabar Boolean maxterm dapat diselesaikan dengan mengoperasikan fungsi Boolean dengan operasi OR dan hasilnya dioperasikan dengan operasi AND [9]. Contoh bentuk minterm atau SOP sebagai penjumlahan dari hasil kali seperti berikut [5].
Contoh 2.2 Bentuk minterm SOP: f (x,y,z) = x’y’z’ + x’y’z + xyz
Contoh 2.3 Tentukan POS dari fungsi Contoh 2.2:
Untuk mengubah fungsi minterm bentuk SOP menjadi POS dengan menggunakan prinsip dualitas komplemen, sebagai berikut.
12
Kedua ekspresi Boolean pada Contoh 2.2 dan Contoh 2.3 baik minterm maupun maxterm memiliki hasil yang sama sehingga keduanya adalah fungsi yang sama. Ekspresi Boolean yang dinyatakan dalam satu atau lebih minterm ataupun maxterm disebut sebagai bentuk kanonik. Minterm dilambangkan sebagai huruf m kecil berindeks. Indeks menyatakan nilai desimal dari string biner yang mempresentasikan term. Pada 2 variabel x dan y indeks 0 pada momenyatakan nilai
desimal dari 00 yang berarti (x = 0 dan y = 0), sedangkan indeks 1 pada m1 berarti
nilai desimal dari 01 dengan x = 0 dan y = 1, sedangkan indeks 2 pada m2
menyatakan nilai desimal dari 10 dengan x = 1 dan y = 0. Untuk indeks 3 pada m3
menyatakan nilai desimal dari 11 dengan x = 1 dan y = 1 [5].
Sedangkan maxterm dilambangkan dengan huruf M besar berindeks. Indeks pada maxtermmenyatakan nilai desimal dari string biner dengan ekspresi x + y karena maxterm merupakan bentuk dari hasil kali dari jumlah. Sama halnya dengan minterm, Pada 2 variabel x dan y indeks 0 pada M0 menyatakan nilai desimal dari 00 yang berarti (x = 0 dan y = 0) dan seterusnya. Untuk 3 variabel misalnya x, y, z baik pada minterm maupun maxterm memiliki pola indeks yang sama. Misal indeks 0 untuk 3 variabel pada m0 menyatakan nilai desimal dari 000 yang berarti (x = 0,
y = 0, z = 0). Begitupun dengan m1 menyatakan nilai desimal dari 0001 yang berarti
(x = 0, y = 0, z = 1). Untuk itu, indeks 6 pada m6 berarti menyatakan nilai desimal
dari 110 yang merupakan bilangan biner dengan (x = 1, y = 1, z = 0) [5]. Secara singkat, penjelasan mengenai indeks pada ekspresi bentuk minterm maupun maxterm dapat dijelaskan pada Lampiran 3 dan 4.
Untuk membentuk minterm tinjau kombinasi variabel-variabel yang dapat menghasilkan nilai 1 seperti 001, 100, 111 seperti:
x’y’z, xy’z, dan xyz
Sedangkan untuk membentuk maxterm tinjau kombinasi variabel-variabel yang dapat menghasilkan nilai 0. Seperti kombinasi 000, 010, 101, dan 110 seperti: (x + y + z), (x + y’ + z), (x’ + y + z’), dan (x’ + y’ + z’).
Perlu diketahui, bahwa mengekspresikan fungsi Boolean tidak selalu unik yang berarti dua fungsi Boolean yang berbeda ekspresi dapat menyatakan dua buah fungsi yang sama sehingga disebut tidak unik (tidak beda). Sebagai contoh, fungsi f dan g memiliki dua fungsi yang berbeda yaitu [10]:
13 f (x,y,z) = x’y’z + x’yz + xy’
g (x,y,z) = x’z + xy’
Walaupun memiliki perbedaan ekspresi fungsi, kedua fungsi tersebut memiliki nilai fungsi Boolean yang sama. Hal ini dapat dilihat pada tabel kebenaran pada Lampiran 5.
Dapat dilihat pada Lampiran 5 walaupun fungsi f dan g memiliki bentuk ekspresi yang berbeda namun keduanya memiliki nilai yang sama yang menandakan tidak unik. Jika fungsi Boolean tidak unik dalam representasi ekspresinya, fungsi ini dapat dapat diubah spesifikasinya menjadi fungsi lain dengan memanipulasi aljabar terhadap ekspresi Boolean. Fungsi f (x,yz) = x’y’z + x’yz + xy’ agar membentuk fungsi yang unik dapat dilakukan manipulasi aljabar sebagai berikut [10].
f (x,y,z) = x’y’z + x’yz + xy’
= x’z (y’+y) + xy’ (menggunakan hukum distributif) = x’z (1) + xy’ (menggunakan hukum komplemen) = x’z + xy’ (menggunakan hukum identitas) Dengan manipulasi aljabar seperti yang dilakukan pada fungsi f maka akan didapatkan fungsi yang unik dengan nilai yang berbeda dengan fungsi g. Manipulasi aljabar ini juga disebut dengan istilah penyederhanaan fungsi Boolean. 2.8 Konversi Fungsi Boolean
Dalam fungsi Boolean minterm dilambangan dengan huruf kecil m berindeks. Indeks menyatakan nilai desimal dari bit string biner yang mempresentasikan term. Dari berbagai buku, fungsi Boolean ada dua bentuk. Ada yang berbentuk bilangan desimal dan ada yang berbentuk menggunakan variabel. Untuk mengubah bentuk desimal menjadi bentuk variabel maka harus dikonversikan terlebih dahulu menjadi bit string. Hal ini berguna juga untuk proses penyederhanaan fungsi Boolean menggunakan metode peta Karnaugh, metode Quine-McCluskey serta teknik covering dari teori graf.
14
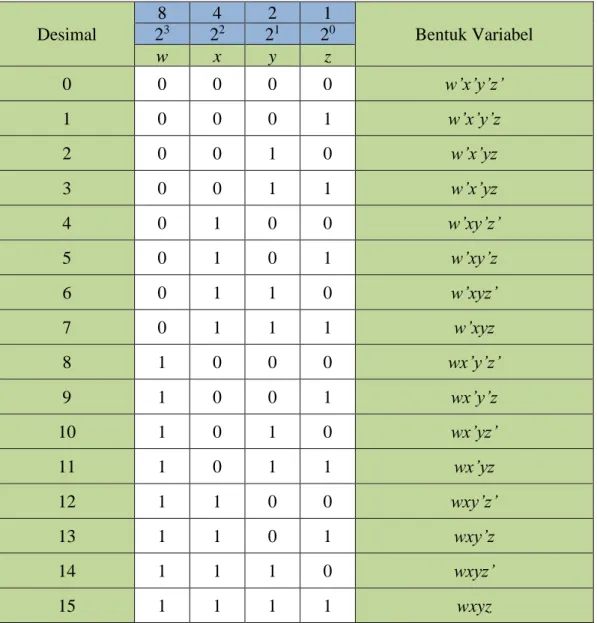
Tabel 2.4 Konversi fungsi Boolean ke bit string
Desimal 8 4 2 1 Bentuk Variabel 23 22 21 20 w x y z 0 0 0 0 0 w’x’y’z’ 1 0 0 0 1 w’x’y’z 2 0 0 1 0 w’x’yz 3 0 0 1 1 w’x’yz 4 0 1 0 0 w’xy’z’ 5 0 1 0 1 w’xy’z 6 0 1 1 0 w’xyz’ 7 0 1 1 1 w’xyz 8 1 0 0 0 wx’y’z’ 9 1 0 0 1 wx’y’z 10 1 0 1 0 wx’yz’ 11 1 0 1 1 wx’yz 12 1 1 0 0 wxy’z’ 13 1 1 0 1 wxy’z 14 1 1 1 0 wxyz’ 15 1 1 1 1 wxyz
Dari Tabel 2.3 dapat dilihat pada baris berwarna biru merupakan peubah untuk mengubah desimal menjadi bit string, 2 menyatakan bilangan biner 0 dan 1 kemudian dipangkatkan sesuai jumlah variabel yang digunakan. Sebagai contoh bilangan desimal 6 untuk diubah ke biner dengan cara tambahkan 4 dan 2 kemudian dari kedua angka yang ditambahkan tersebut maka pada variabel angka tersebut yaitu x dan y pada bit string binernya menjadi 1.
2.9 Penyederhanaan Fungsi Boolean
Sebagaimana yang telah dijelaskan sebelumnya mengenai fungsi f dan fungsi g, fungsi Boolean terkadang memiliki operasi-operasi aljabar yang tidak
15
perlu atau dengan kata lain variabel yang berlebihan. Untuk itu, fungsi Boolean dapat disederhanakan menjadi bentuk aljabar yang lebih sederhana. Penyederhanaan fungsi Boolean berarti mencari bentuk fungsi lain yang ekuivalen namun dengan jumlah variabel atau operasi yang lebih sedikit atau sederhana. Penyederhanaan fungsi Boolean disebut juga manipulasi aljabar atau minimisasi fungsi [5].
Fungsi Boolean yang lebih sederhana memiliki arti bahwa rangkaian logika yang ada didalamnya juga lebih sederhana (menggunakan jumlah gerbang logika yang lebih sedikit). Sebelumnya, fungsi f (x,y,z) = x’y’z + x’yz + xy’ sudah disederhanakan menjadi fungsi f (x,y,z) = x’z + xy’. Penyederhanaan ini menggunakan hukum-hukum aljabar pada fungsi Boolean sehingga cara penyederhanaan ini disebut juga dengan cara Aljabar Boolean. Ada tiga cara yang dapat dipilih dalam penyederhanaan fungsi Boolean yaitu sebagai berikut [7].
1. Aljabar Boolean 2. Peta Karnaugh 3. Quine McCluskey
Penyederhanaan fungsi Boolean dengan memanfaatkan hukum Aljabar Boolean membutuhkan waktu yang lama serta hasil yang diperoleh tidak dapat dijamin sebagai fungsi yang paling sederhana karena diduga cara Aljabar Boolean mengandalkan proses try & error dalam penetuan solusi akhir. Selain itu, untuk variabel yang lebih banyak tentunya menggunakan cara Aljabar Boolean yang secara manual dapat memakan waktu dan tenaga yang tidak sedikit. Cara kedua yaitu menggunakan Peta Karnaugh dengan menggunakan prosedur yang lebih mudah dibandingkan cara Aljabar Boolean. Secara visual, penyederhanaan fungsi Boolean menggunakan Peta Karnaugh diwujudkan dalam tabel kebenaran yang merupakan perluasan dari Diagram Venn. Metode Peta Karnaugh disebut juga metode grafis karena menggunakan diagram atau peta yang terbentuk dari kotak-kota bujursangkar yang bersisian. Setiap kotak-kotak mempresentasikan sebuah minterm yaitu bentuk term yang merupakan hasil kali [2].
Peta Karnaugh memang memiliki prosedur yang lebih mudah dibandingkan menggunakan Aljabar Boolean namun metode ini juga memiliki kekurangan yaitu fungsi Boolean yang memiliki variabel lebih dari empat lebih sulit untuk
16
disederhanakan menggunakan Peta Karnaugh. Hal ini dikarenakan semakin banyak variabel maka ukuran peta pada Peta Karnaugh juga akan semakin besar sehingga lebih sulit untuk diprogram dengan komputer karena memerlukan pengamatan visual dalam mengidentifikasi minterm-minterm yang ada dalam setiap kotak.
Untuk menyempurnakan metode Peta Karnaugh, cara lain dalam menyederhanakan Fungsi Boolean adalah dengan menggunakan metode Quine McCluskey atau lebih dikenal dengan istilah metode tabulasi. Metode ini dapat menyelesaikan penyederhanaan fungsi lebih dari lima variabel dan dapat dikerjakan dengan mesin atau program komputer. Metode Quine McCluskey menjamin pernyataan fungsi Boolean bentuk baku yang lebih sederhana. Oleh karenanya, metode Quine McCluskey lebih efektif dikerjakan dengan menggunakan bantuan mesin komputer [10].
2.10 Metode Quine Mc-Cluskey
Metode Quine McCluskey sebagaimana disebutkan sebelumnya merupakan salah satu metode untuk menyederhanakan fungsi Boolean. Metode ini bersifat lebih fleksibel untuk menyederhanakan fungsi Boolean dengan variabel lebih dari empat dibandingkan dengan Peta Karnaugh karena metode ini menggunakan tabulasi. Metode ini diambil dari nama penemunya yaitu W.V.Quine dan E.J. McCluskey yang mengembangkan metode ini pada tahun 1950. Metode Quine McCluskey menyederhanakan fungsi Boolean menjadi sebuah himpunan bentuk prima, dengan menghilangkan peubah (mengeliminasi variabel) secara maksimal hingga diperoleh bentuk ekspresi fungsi Boolean yang paling sederhana [9].
Metode Quine McCluskey berupaya untuk mengubah suatu fungsi Boolean menjadi sebuah himpunan bentuk prima. Dalam hal ini digunakan sebanyak mungkin variable yang dieliminasi atau dihilangkan secara maksimal hingga diperoleh fungsi Boolean dengan ekspresi aljabar yang paling sederhana [1]. 2.11 Graf
Graf G adalah himpunan berpasangan (V,E) dengan V(G) adalah himpunan tidak kosong dan berhingga dari objek yang disebut titik sedangkan E(G) adalah himpunan yang dapat kosong berpasangan tak berurutan dari titik-titik berbeda di V(G) yang disebut sebagai sisi. Himpunan titik di G dinotasikan sebagai V(G)
17
sedangkan himpunan sisi dinotasikan sebagai E(G). Banyaknya unsur di V disebut orde dari G yang dilambangkan dengan p(G) dan banyaknya unsur di E disebut size dari G dan dilambangkan dengan q(G). Jika hanya ada graf G, maka orde dan size dari G dapat ditulis dengan G(p,q) [12]. Berikut contoh graf G:
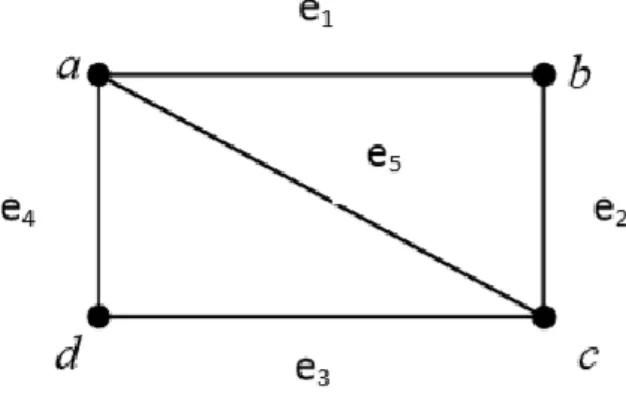
Gambar 2.1 Graf G
Pada Gambar 2.1 graf G memiliki orde 4 dan 5 sisi yang kemudian dapat dinyatakan dengan G = (V(G), E(G)) dengan V(G) = {a,b,c,d} dan E(G) = {(a,b), (b,c),(c,d),(a,d),(a,c)} atau dapat ditulis dengan V(G) = {a,b,c,d} dan E(G) = {e1,e2,
e3, e4, e5}. Sisi yang menghubungkan dua titik yang sama disebut loop. Jika terdapat
lebih dari satu sisi yang menghubungkan dua titik, maka sisi tersebut dinamakan sisi ganda. Graf digolongkan menjadi dua jenis yaitu graf sederhana dan graf tidak sederhana. Graf sederhana adalah graf yang tidak memiliki sisi ganda sedangkan graf tidak sederhana adalah graf yang memiliki sisi ganda sehingga disebut juga graf ganda serta graf gelang adalah suatu graf didalamnya terdapat sisi yang menghubungkan satu titik yang sama atau disebut juga graf semu [5].
2.12 Incident dan Adjacent
Sebagaimana yang disebutkan sebelumnya, suatu graf memiliki setidaknya satu titik. Jika graf tersebut memiliki lebih dari satu titik maka antar titik dapat dihubungkan oleh garis. Misal, sisi a = (v,u) yang berarti sisi a menghubungkan titik v dan u. titik u dan v disebut dengan adjacent (bertetangga) dan titik u dan v disebut incident (menempel) dengan sisi a.
18
Gambar 2.2 Adjacent dan incident pada graf
Pada Gambar 2.2 titik v adjacent dengan titik u, dan titik u dan v menempel sisi a. 2.13 Covering Graf
Pada suatu graf G, terdapat g dinyatakan sebagai sisi dan dikatakan menutup pada graf G jika setiap titik di G incident terhadap satu sisi di g. Sisi-sisi yang menutup titik-titik di G disebut covering sisi atau biasa disebut dengan covering dari graf G. Suatu titik covering di G merupakan himpunan dari titik-titik yang menutup semua sisi di G dan sisi covering pada G merupakan himpunan sisi-sisi yang menutup titik-titik di G [13]. Berikut contoh covering graf:
Gambar 2.3 Graf G
Pada Gambar 2.3, sisi 𝑒2 dan 𝑒4 adalah anggota dari covering G karena 𝑒2 dan 𝑒4 cover (menutup) G, sehingga {e2, e4} disebut covering dari graf G karena covering merupakan himpunan yang anggotanya sisi atau garis. Konsep covering graf ini digunakan pada banyak aplikasi pemecahan masalah dalam kehidupan sehari-hari seperti menemukan solusi atas permasalahan penempatan lokasi rumah yang berada diantaranya tempat wisata, atau menemukan solusi atas pemilihan produk rumah tangga dengan harga murah namun memenuhi semua standar kualitas produk, dan sebagainya [13]. Prinsip covering graf digunakan untuk mereduksi semua syarat dari suatu himpunan atau permasalahan agar solusi yang diperoleh efektif dan efisien.
Himpunan covering menurut penelitian oleh [4] pada dasarnya dikatakan minimal jika menggunakan paling sedikit jumlah titik. Pada Gambar 2.3 memiliki himpunan minimal covering adalah {𝑒2, 𝑒4}. Terdapat beberapa hal yang harus diperhatikan dalam minimal covering [13]:
19
1. Covering graf jika dan hanya jika graf tersebut tidak memiliki titik yang terisolasi. Titik terisolasi artinya titik yang tidak memiliki sisi atau bisa dikatakan dengan titik yang memiliki derajat 0. Derajat merupakan banyaknya sisi yang terhubung pada titik tersebut.
2. Covering dari graf n-titik akan memiliki setidaknya [𝑛 2] sisi. 3. Setiap covering memiliki minimal covering.
4. Misalkan g merupakan himpunan dari covering pada graf G, jika (G-g) menyatakan sebagai himpunan sisi yang tersisa dari G, maka g covering dari G jika dan hanya jika untuk setiap titik v di G, berlaku derajat titik di (G-g) ≤ (derajat titik v di G)-1
5. Tidak ada minimal covering yang dapat memuat sirkuit. Sirkuit merupakan jalan tertutup atau barisan titik-sisi yang diawali dan diakhiri oleh titik yang sama. karena dapat dihilangkan sisi dari sirkuit tanpa meninggalkan titik apapun dalam sirkuit yang tidak tertutup. Oleh karena itu, minimal covering dari graf n-titik dapat memuat tidak lebih dari n-1 sisi.
6. Secara umum sebuah graf memiliki banyak minimal covering dan mungkin memiliki ukuran yang berbeda (jumlah sisi yang berbeda). Jumlah sisi dalam minimal covering dari ukuran terkecil disebut dengan nomor covering pada graf.
Pada penelitian yang telah dilakukan oleh [15] , untuk menentukan minimal covering dari sebuah graf lintasan dilakukan perhitungan untuk jumlah sisi genap maka 𝑛
2 , sedangkan untuk jumlah sisinya ganjil maka 𝑛+1
2 , dimana untuk n = jumlah sisi dari sebuah graf. Perhitungan berikut merupakan maksimal dari covering sebuah graf. Contoh dari minimal covering dalam kehidupan sehari-hari adalah membagi daerah pada mobil patroli pada daerah yang memiliki catatan rawan kriminal.
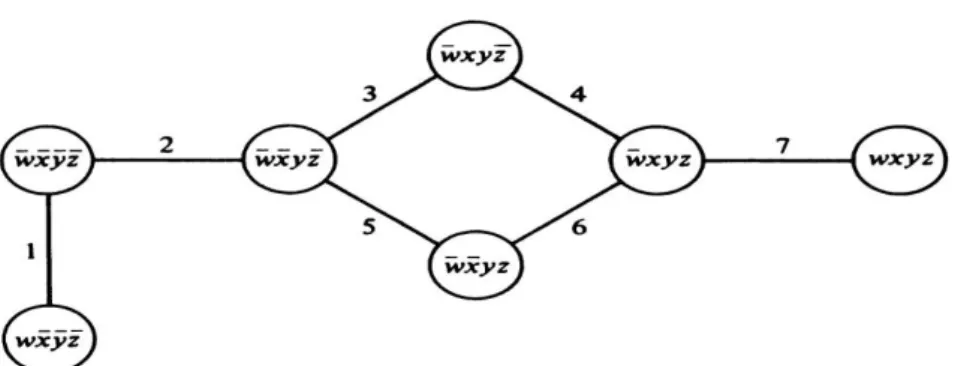
Jika dalam ilmu teknologi minimal covering dapat digunakan dalam meminimasi atau menyederhanakan fungsi Boolean sebelum diimplementasikan menjadi rangkaian logika. fungsi Boolean dibuat menjadi sebuah rangkaian graf sesuai dengan fungsi yang tersedia dengan titik pada graf merupakan minterm pada fungsi Boolean. Berikut contoh gambaran penyederhanaan fungsi Boolean menggunakan covering:
20