BAB III PEMBAHASAN. dengan retensi pelanggan yang membatalkan antrian, nilai harapan banyaknya

45 BAB III

PEMBAHASAN

Pada bab ini akan dibahas tentang penurunan sistem persamaan lengkap untuk sistem antrian M/M/1/N dengan retensi pelanggan yang membatalkan antrian. Sistem persamaan lengkap tersebut terdiri dari persamaan probabilitas sistem antrian M/M/1/N dengan retensi pelanggan yang membatalkan antrian, nilai harapan banyaknya pelanggan dalam sistem antrian (𝐿_𝑠), nilai harapan banyaknya pelanggan dalan antrian (𝐿_𝑞), nilai harapan waktu tunggu dalam sistem antrian (𝑊_𝑠) dan nilai harapan waktu tunggu dalam antrian (𝑊_𝑞).

A. Probabilitas Model Antrian M/M/1/N dengan Retensi Pelanggan yang Membatalkan Antrian

Langkah pertama yang dilakukan dalam menentukan karakteristik model antrian M/M/1/N dengan retensi pelanggan yang membatalkan antrian adalah menentukan probabilitas kejadian terdapat 𝑛 pelanggan dalam sistem (𝑃_𝑛).

Sebelumnya akan dijelaskan terlebih dahulu notasi-notasi yang digunakan untuk menentukan probabilitas kejadian terdapat 𝑛 pelanggan dalam sistem, yaitu:

𝜆_𝑛 : laju kedatangan jika ada 𝑛 pelanggan dalam sistem, jika laju kedatangan konstan untuk semua 𝑛 maka cukup ditulis dengan 𝜆

µ_𝑛 : laju pelayanan jika ada 𝑛 pelanggan dalam sistem, jika laju pelayanan konstan untuk semua 𝑛 maka cukup ditulis dengan µ

46

𝜉 : reneging times (dalam waktu: jam, menit, atau detik) 𝑝 : probabilitas dari reneging

𝑜(∆𝑡) : probabilitas terjadi lebih dari 1 kejadian pada kondisi saat 𝑡 sampai 𝑡 + ∆𝑡 yang bernilai sangat kecil, sehingga 𝑜(∆𝑡) dapat diabaikan.

Kemudian ditentukan bebarapa probabilitas-probabilitas sebagai berikut:

1. Probabilitas ada satu kedatangan dari t sampai 𝑡 + ∆𝑡, dinyatakan dengan

𝑃 ((𝑋(𝑡 + ∆𝑡) − 𝑋(𝑡)) = 1) = 𝜆_𝑛∆𝑡 + 𝑜(∆𝑡) (3.1) 2. Probabilitas tidak ada kedatangan dari 𝑡 sampai 𝑡 + ∆𝑡, dinyatakan dengan

𝑃 ((𝑋(𝑡 + ∆𝑡) − 𝑋(𝑡)) = 0) = 1 − 𝜆_𝑛∆𝑡 + 𝑜(∆𝑡) (3.2) 3. Probabilitas ada satu kepergian dari 𝑡 sampai 𝑡 + ∆𝑡, dinyatakan dengan

𝑃 ((𝑋(𝑡 + ∆𝑡) − 𝑋(𝑡)) = 1) = µ_𝑛∆𝑡 + 𝑜(∆𝑡) (3.3) 4. Probabilitas tidak ada kepergian dari 𝑡 sampai 𝑡 + ∆𝑡, dinyatakan dengan

𝑃 ((𝑋(𝑡 + ∆𝑡) − 𝑋(𝑡)) = 0) = 1 − µ_𝑛∆𝑡 + 𝑜(∆𝑡) (3.4) 5. Probabilitas ada satu customer reneging dari 𝑡 sampai 𝑡 + ∆𝑡, dinyatakan dengan 𝑃 ((𝑋(𝑡 + ∆𝑡) − 𝑋(𝑡)) = 1) = 𝑛𝜉𝑝∆𝑡 + 0(∆𝑡) (3.5) 6. Probabilitas tidak ada customer reneging dari 𝑡 sampai 𝑡 + ∆𝑡, dinyatakan dengan 𝑃 ((𝑋(𝑡 + ∆𝑡) − 𝑋(𝑡)) = 0) = 1 − (𝑛 − 1)𝜉𝑝∆𝑡 + 0(∆𝑡) (3.6)

47

7. Probalititas terjadi lebih dari satu kejadian pada selang waktu yang sangat pendek adalah sangat kecil sehingga dapat diabaikan, dapat dinyatakan dengan

𝑃 ((𝑋(𝑡 + ∆𝑡) − 𝑋(𝑡)) > 1) = 𝑜(∆𝑡) (3.7) Dari probabilitas-probabilitas yang telah didapatkan, probabilitas-probabilitas tersebut dapat digambarkan dalam bentuk state flow sebagai berikut:

Gambar 3.1 Proses kedatangan dan kepergian dalam sistem antrian M/M/1/N Berdasarkan gambar 3.1 terdapat 3 kondisi yang berbeda pada state flow tersebut sehingga kemungkinan-kemungkinan kejadian saling bebas yang dapat terjadi jika terdapat 𝑛 pelanggan dalam sistem pada waktu 𝑡 + ∆𝑡 dapat dibagi menjadi 3 kasus kemungkinan kejadian, yaitu :

1. Kemungkinan kejadian terdapat 𝑛 pelanggan dalam sistem untuk 1 ≤ 𝑛 ≤ 𝑁 − 1 adalah :

a. Kemungkinan kejadian terdapat 𝑛 pelanggan pada waktu 𝑡 dan terdapat 𝑛 pelanggan pada waktu 𝑡 + ∆𝑡 adalah :

1. Tidak ada kedatangan, tidak ada kepergian, dan tidak ada reneging 2. Ada kedatangan, ada kepergian, dan tidak ada reneging

3. Ada kedatangan, tidak ada kepergian, dan ada reneging

0 1 2

. . .

n-1 n n+1

. . .

N-1 N





N-1

n-1 n



 n n+1 N

n+2

n+2

n+1

48

b. Kemungkinan kejadian terdapat 𝑛 + 1 pelanggan pada waktu 𝑡 dan terdapat 𝑛 pelanggan pada waktu 𝑡 + ∆𝑡 adalah :

1. Tidak ada kedatangan, ada kepergian, dan tidak ada reneging 2. Tidak ada kedatangan, tidak ada keperian, dan ada reneging

c. Kemungkinan kejadian terdapat 𝑛 + 2 pelanggan pada waktu 𝑡 dan terdapat 𝑛 pelanggan pada waktu 𝑡 + ∆𝑡 adalah : tidak ada kedatangan, ada kepergian, dan ada reneging

d. Kemungkinan kejadian terdapat 𝑛 − 1 pelanggan pada waktu 𝑡 dan terdapat 𝑛 pelanggan pada waktu 𝑡 + ∆𝑡 adalah : ada kedatangan, tidak ada kepergian, dan tidak ada reneging.

Dari kemungkinan-kemungkinan yang telah diperoleh, kemudian disajikan kedalam tabel sebagai berikut ini.

Tabel 3.1 Kemungkinan Kejadian Terdapat 𝑛 Pelanggan dalam Sistem pada Saat 𝑡 +

∆𝑡 dengan 1 ≤ 𝑛 ≤ 𝑁 − 1

Kasus

Jumlah pelanggan pada waktu

𝑡

Jumlah kedatangan pada waktu

∆𝑡

Jumlah kepergian pada waktu

∆𝑡

Jumlah reneging

pada waktu ∆𝑡

Jumlah pelanggan pada waktu

𝑡 + ∆𝑡

1 𝑛 0 0 0 𝑛

2 𝑛 1 1 0 𝑛

49 Kasus

Jumlah pelanggan pada waktu

𝑡

Jumlah kedatangan pada waktu

∆𝑡

Jumlah kepergian pada waktu

∆𝑡

Jumlah reneging

pada waktu ∆𝑡

Jumlah pelanggan pada waktu

𝑡 + ∆𝑡

3 𝑛 1 0 1 𝑛

4 𝑛 + 1 0 1 0 𝑛

5 𝑛 + 1 0 0 1 𝑛

6 𝑛 + 2 0 1 1 𝑛

7 𝑛 − 1 1 0 0 𝑛

Menurut asumsi (vi) mengacu dari bab 2, kedatangan dan kepergian merupakan kejadian-kejadian yang saling bebas, sehingga kejadian-kejadian pada interval waktu tertentu tidak mempengaruhi kejadian ada interval waktu sesudahnya maka peluangdari masing-masing kejadian tersebut adalah sebagai berikut:

1. Probabilitas kasus 1 =

𝑃_𝑛(𝑡)(1 − 𝜆_𝑛∆𝑡 + 𝑜(∆𝑡))(1 − µ_𝑛∆𝑡 + 𝑜(∆𝑡))(1 − (𝑛 − 1)𝜉𝑝∆𝑡 + 𝑜(∆𝑡)) (3.8) 2. Probablitas kasus 2 =

𝑃_𝑛(𝑡)(𝜆_𝑛∆𝑡 + 𝑜(∆𝑡))(µ_𝑛∆𝑡 + 𝑜(∆𝑡))(1 − (𝑛 − 1)𝜉𝑝∆𝑡 + 𝑜(∆𝑡)) = 𝑜(∆𝑡) (3.9) 3. Probabilitas kasus 3 =

𝑃_𝑛(𝑡)(𝜆_𝑛∆𝑡 + 𝑜(∆𝑡))(1 − µ_𝑛∆𝑡 + 𝑜(∆𝑡))(𝑛𝜉𝑝∆𝑡 + 𝑜(∆𝑡)) = 𝑜(∆𝑡) (3.10)

50 4. Probabilitas kasus 4 =

𝑃_𝑛+1(𝑡)(1 − 𝜆_𝑛+1∆𝑡 + 𝑜(∆𝑡))(µ_𝑛+1∆𝑡 + 𝑜(∆𝑡))(1 − (𝑛 − 1)𝜉𝑝∆𝑡 + 𝑜(∆𝑡)) (3.11) 5. Probabilitas kasus 5 =

𝑃_𝑛+1(𝑡)(1 − 𝜆_𝑛+1∆𝑡 + 𝑜(∆𝑡))(1 − µ_𝑛+1∆𝑡 + 𝑜(∆𝑡))(𝑛𝜉𝑝∆𝑡 + 𝑜(∆𝑡)) (3.12) 6. Probabilitas kasus 6 =

𝑃_𝑛+2(𝑡)(1 − 𝜆_𝑛+2∆𝑡 + 𝑜(∆𝑡))(µ_𝑛+2∆𝑡 + 𝑜(∆𝑡))(𝑛𝜉𝑝∆𝑡 + 𝑜(∆𝑡)) = 𝑜(∆𝑡) (3.13) 7. Probabilitas kasus 7 =

𝑃_𝑛−1(𝑡)(𝜆_𝑛−1∆𝑡 + 𝑜(∆𝑡))(1 − µ_𝑛−1∆𝑡 + 𝑜(∆𝑡))(1 − (𝑛 − 1)𝜉𝑝∆𝑡 + 𝑜(∆𝑡)) (3.14) Maka probabilitas terdapat 𝑛 pelanggan dalam sistem dengan 1 ≤ 𝑛 ≤ 𝑁 − 1 pada saat (𝑡 + ∆𝑡) dinyatakan dengan:

𝑃_𝑛(𝑡 + ∆𝑡) = 𝑃 (kasus 1 atau kasus 2 atau kasus 3 atau kasus 4 atau kasus 5 atau kasus 6 atau kasus 7)

Karena kasus-kasus tersebut tidak dapat terjadi secara bersamaan atau saling asing, maka probabilitasnya adalah:

𝑃_𝑛(𝑡 + ∆𝑡) =(probabilitas kasus 1 + probabilitas kasus + probabilitas kasus 2 + probabilitas kasus 3 + probabilitas kasus 4 + probabilitas kasus 5 + probabilitas kasus 6 + probabilitas kasus 7) (3.15)

51

Substitusi persamaan (3.8), (3.9), (3.10), (3.11), (3.12), (3.13) dan (3.14) ke persamaan (3.15), sehingga didapatkan:

𝑃_𝑛(𝑡 + ∆𝑡) = 𝑃_𝑛(𝑡)(1 − 𝜆_𝑛∆𝑡 + 𝑜(∆𝑡))(1 − µ_𝑛∆𝑡 + 𝑜(∆𝑡))(1 − (𝑛 − 1)𝜉𝑝∆𝑡 + 𝑜(∆𝑡)) + 𝑜(∆𝑡) + 𝑜(∆𝑡)

+ 𝑃_𝑛+1(𝑡)(1 − 𝜆_𝑛+1∆𝑡 + 𝑜(∆𝑡))(µ_𝑛+1∆𝑡 + 𝑜(∆𝑡))(1 − (𝑛 − 1)𝜉𝑝∆𝑡 + 𝑜(∆𝑡))

+ 𝑃_𝑛+1(𝑡)(1 − 𝜆_𝑛+1∆𝑡 + 𝑜(∆𝑡))(1 − µ_𝑛+1∆𝑡 + 𝑜(∆𝑡))(𝑛𝜉𝑝∆𝑡 + 𝑜(∆𝑡)) + 𝑜(∆𝑡)

+ 𝑃_𝑛−1(𝑡)(𝜆_𝑛−1∆𝑡 + 𝑜(∆𝑡))(1 − µ_𝑛−1∆𝑡 + 𝑜(∆𝑡))(1 − (𝑛 − 1)𝜉𝑝∆𝑡 + 𝑜(∆𝑡))

𝑃_𝑛(𝑡 + ∆𝑡) = 𝑃_𝑛(𝑡)(1 − 𝜆_𝑛∆𝑡 + µ_𝑛∆𝑡)(1 − (𝑛 − 1)𝜉𝑝∆𝑡 + 𝑜(∆𝑡)) + 𝑃_𝑛+1(𝑡)(µ_𝑛+1∆𝑡)(1 − (𝑛 − 1)𝜉𝑝∆𝑡 + 𝑜(∆𝑡)) + 𝑃_𝑛+1(𝑡)(1 − 𝜆_𝑛∆𝑡 + µ_𝑛∆𝑡)(𝑛𝜉𝑝∆𝑡 + 𝑜(∆𝑡))

+ 𝑃_𝑛−1(𝑡)(𝜆_𝑛−1∆𝑡)(1 − (𝑛 − 1)𝜉𝑝∆𝑡 + 𝑜(∆𝑡)) + 𝑜(∆𝑡) 𝑃_𝑛(𝑡 + ∆𝑡) = 𝑃_𝑛(𝑡)(1 − 𝜆_𝑛∆𝑡 − µ_𝑛∆𝑡 − (𝑛 − 1)𝜉𝑝∆𝑡) + 𝑃_𝑛+1(𝑡)(µ_𝑛+1∆𝑡)

+ 𝑃_𝑛+1(𝑡)(𝑛𝜉𝑝∆𝑡) + 𝑃_𝑛−1(𝑡)(𝜆_𝑛−1∆𝑡) + 𝑜(∆𝑡)

𝑃_𝑛(𝑡 + ∆𝑡) = 𝑃_𝑛(𝑡) − 𝑃_𝑛(𝑡)(𝜆_𝑛∆𝑡) − 𝑃_𝑛(𝑡)(µ_𝑛∆𝑡) − 𝑃_𝑛(𝑡)((𝑛 − 1)𝜉𝑝∆𝑡) +

𝑃_𝑛+1(𝑡)(µ_𝑛+1∆𝑡) + 𝑃_𝑛+1(𝑡)(𝑛𝜉𝑝∆𝑡) + 𝑃_𝑛−1(𝑡)(𝜆_𝑛−1∆𝑡) + 𝑜(∆𝑡) (3.16)

52

Pada persamaan (3.16) dikurangkan 𝑃_𝑛(𝑡) pada ruas kiri dan kanan kemudian dibagi dengan ∆𝑡 maka diperoleh:

𝑃_𝑛(𝑡 + ∆𝑡) − 𝑃_𝑛(𝑡)

= −𝑃_𝑛(𝑡)(𝜆_𝑛∆𝑡) − 𝑃_𝑛(𝑡)(µ_𝑛∆𝑡) − 𝑃_𝑛(𝑡)((𝑛 − 1)𝜉𝑝∆𝑡) + 𝑃_𝑛+1(𝑡)(µ_𝑛+1∆𝑡) + 𝑃_𝑛+1(𝑡)(𝑛𝜉𝑝∆𝑡) + 𝑃_𝑛−1(𝑡)(𝜆_𝑛−1∆𝑡)

𝑃_𝑛(𝑡+∆𝑡)−𝑃𝑛(𝑡)

∆𝑡 = −𝑃_𝑛(𝑡)(𝜆_𝑛) − 𝑃_𝑛(𝑡)(µ_𝑛) − 𝑃_𝑛(𝑡)((𝑛 − 1)𝜉𝑝) + 𝑃_𝑛+1(𝑡)(µ_𝑛+1) + 𝑃_𝑛+1(𝑡)(𝑛𝜉𝑝) + 𝑃_𝑛−1(𝑡)(𝜆_𝑛−1) (3.17) Karena ∆𝑡 sangat kecil dan mendekati nol, maka berdasarkan Definisi 2.7 didapatkan:

∆𝑡→0lim

𝑃_𝑛(𝑡 + ∆𝑡) − 𝑃_𝑛(𝑡)

∆𝑡

= lim

∆𝑡→0[−𝑃_𝑛(𝑡)(𝜆_𝑛) − 𝑃_𝑛(𝑡)(µ_𝑛) − 𝑃_𝑛(𝑡)((𝑛 − 1)𝜉𝑝) + 𝑃_𝑛+1(𝑡)(µ_𝑛+1) + 𝑃_𝑛+1(𝑡)(𝑛𝜉𝑝) + 𝑃_𝑛−1(𝑡)(𝜆_𝑛−1)]

𝑑𝑃_𝑛(𝑡)

𝑑𝑡 = −𝑃_𝑛(𝑡)(𝜆_𝑛) − 𝑃_𝑛(𝑡)(µ_𝑛) − 𝑃_𝑛(𝑡)((𝑛 − 1)𝜉𝑝) + 𝑃_𝑛+1(𝑡)(µ_𝑛+1) + 𝑃_𝑛+1(𝑡)(𝑛𝜉𝑝) + 𝑃_𝑛−1(𝑡)(𝜆_𝑛−1)

𝑑𝑃_𝑛(𝑡)

𝑑𝑡 = −(𝜆_𝑛+ µ_𝑛 + (𝑛 − 1)𝜉𝑝)𝑃_𝑛(𝑡) + (µ_𝑛+1+ 𝑛𝜉𝑝)𝑃_𝑛+1(𝑡) + (𝜆_𝑛−1)𝑃_𝑛−1(𝑡) (3.18) 2. Kemungkinan kejadian terdapat 𝑛 pelanggan dalam sistem pada saat 𝑛 = 0 adalah:

a. Kemungkinan kejadian terdapat 0 pelanggan pada waktu 𝑡 dan terdapat 0 pelanggan pada waktu 𝑡 + ∆𝑡 adalah :

1. Tidak ada kedatangan, tidak ada kepergian dan tidak ada reneging

53

2. Ada kedatangan, ada kepergian dan tidak ada reneging

b. Kemungkinan kejadian terdapat 𝑛 + 1 pelanggan pada waktu 𝑡 dan terdapat 𝑛 pelanggan pada waktu 𝑡 + ∆𝑡 adalah :

1. Tidak ada kedatangan, ada kepergian dan tidak ada reneging 2. Tidak ada kedatangan,tidak ada kepergian, dan ada reneging

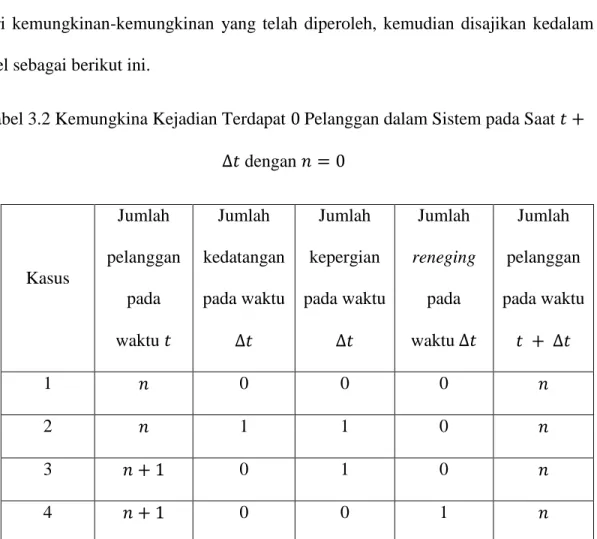
Dari kemungkinan-kemungkinan yang telah diperoleh, kemudian disajikan kedalam tabel sebagai berikut ini.

Tabel 3.2 Kemungkina Kejadian Terdapat 0 Pelanggan dalam Sistem pada Saat 𝑡 +

∆𝑡 dengan 𝑛 = 0

Kasus

Jumlah pelanggan

pada waktu 𝑡

Jumlah kedatangan pada waktu

∆𝑡

Jumlah kepergian pada waktu

∆𝑡

Jumlah reneging

pada waktu ∆𝑡

Jumlah pelanggan pada waktu

𝑡 + ∆𝑡

1 𝑛 0 0 0 𝑛

2 𝑛 1 1 0 𝑛

3 𝑛 + 1 0 1 0 𝑛

4 𝑛 + 1 0 0 1 𝑛

Selanjutnya akan dibahas secara khusus probabilitas terdapat 𝑛 pelanggan untuk nilai 𝑛 = 0. Pada saat jumlah pelanggan dalam sistem adalah nol, maka probabilitas

54

terjadinya nol kepergian pada kasus 1 dan kasus 4 serta nol reneging pada kasus 1, kasus 2 dan kasus 3 adalah satu.

Menurut asumsi (vi) mengacu dari bab 2, kedatangan dan kepergian merupakan kejadian-kejadian yang saling bebas, sehingga kejadian-kejadian pada interval waktu tertentu tidak mempengaruhi kejadian ada interval waktu sesudahnya maka peluangdari masing-masing kejadian tersebut adalah sebagai berikut:

1. Probabilitas kasus 1 =

𝑃_𝑛(𝑡)(1 − 𝜆_𝑛∆𝑡 + 𝑜(∆𝑡))(1)(1) (3.19) 2. Probablitas kasus 2 =

𝑃_𝑛(𝑡)(𝜆_𝑛∆𝑡 + 𝑜(∆𝑡))(µ_𝑛+1∆𝑡 + 𝑜(∆𝑡))(1) = 𝑜(∆𝑡) (3.20) 3. Probabilitas kasus 3 =

𝑃_𝑛+1(𝑡)(1 − 𝜆_𝑛+1∆𝑡 + 𝑜(∆𝑡))(µ_𝑛+1∆𝑡 + 𝑜(∆𝑡))(1) (3.21) 4. Probabilitas kasus 4 =

𝑃_𝑛+1(𝑡)(1 − 𝜆_𝑛+1∆𝑡 + 𝑜(∆𝑡))(1)(𝑛𝜉𝑝∆𝑡 + 𝑜(∆𝑡)) (3.22)

Probabilitas terdapat 𝑛 pelanggan dalam sistem dengan 𝑛 = 0 pada saat (𝑡 + ∆𝑡) adalah :

𝑃_𝑛(𝑡 + ∆𝑡) = 𝑃 (kasus 1 atau kasus 2 atau kasus 3 atau kasus 4)

Karena kasus-kasus tersebut tidak dapat terjadi secara bersamaan atau saling asing, maka probabilitas terdapat 𝑛 pelanggan dalam sistem dengan 𝑛 = 0 pada saat (𝑡 + ∆𝑡) dinyatakan dengan:

55

𝑃_𝑛(𝑡 + ∆𝑡) = (Probabilitas kasus 1 + Probabilitas kasus 2 + Probabilitas kasus 3 +

Probabilitas kasus 4) (3.23)

Substitusikan persamaan (3.19), (3.20), (3.21), dan (3.22) ke persamaan (3.23) sehingga didapatkan :

𝑃_𝑛(𝑡 + ∆𝑡) = 𝑃_𝑛(𝑡)(1 − 𝜆_𝑛∆𝑡 + 𝑜(∆𝑡))(1)(1) + 𝑜(∆𝑡)

+ 𝑃_𝑛+1(𝑡)(1 − 𝜆_𝑛+1∆𝑡 + 𝑜(∆𝑡))(µ_𝑛+1∆𝑡 + 𝑜(∆𝑡))(1) + 𝑃_𝑛+1(𝑡)(1 − 𝜆_𝑛+1∆𝑡 + 𝑜(∆𝑡))(1)(𝑛𝜉𝑝∆𝑡 + 𝑜(∆𝑡))

𝑃_𝑛(𝑡 + ∆𝑡) = 𝑃_𝑛(𝑡)(1 − 𝜆_𝑛∆𝑡 + 𝑜(∆𝑡)) + 𝑃_𝑛+1(𝑡)(µ_𝑛+1∆𝑡 + 𝑜(∆𝑡)) +

𝑃_𝑛+1(𝑡)(𝑛𝜉𝑝∆𝑡 + 𝑜(∆𝑡)) + 𝑜(∆𝑡) (3.24) Substitusi 𝑛 = 0 pada persamaan (3.24), diperoleh :

𝑃₀(𝑡 + ∆𝑡) = 𝑃₀(𝑡)(1 − 𝜆₀∆𝑡 + 𝑜(∆𝑡)) + 𝑃₁(𝑡)(µ₁∆𝑡 + 𝑜(∆𝑡)) + 𝑃₁(𝑡)(0𝜉𝑝∆𝑡 + 𝑜(∆𝑡)) + 𝑜(∆𝑡)

𝑃₀(𝑡 + ∆𝑡) = 𝑃₀(𝑡)(1 − 𝜆₀∆𝑡 + 𝑜(∆𝑡)) + 𝑃₁(𝑡)(µ₁∆𝑡 + 𝑜(∆𝑡)) + 𝑜(∆𝑡) 𝑃₀(𝑡 + ∆𝑡) = 𝑃₀(𝑡) − (𝜆₀∆𝑡)𝑃₀(𝑡) + (µ₁∆𝑡)𝑃₁(𝑡) + 𝑜(∆𝑡) (3.25) Pada persamaan (3.25) dikurangkan 𝑃₀(𝑡) pada ruas kiri dan kanan kemudian dibagi dengan ∆𝑡 maka diperoleh:

𝑃₀(𝑡 + ∆𝑡) − 𝑃₀(𝑡) = −(𝜆₀∆𝑡)𝑃₀(𝑡) + (µ₁∆𝑡)𝑃₁(𝑡)

56

𝑃₀(𝑡+∆𝑡)−𝑃0(𝑡)

∆𝑡 = −(𝜆₀)𝑃₀(𝑡) + (µ₁)𝑃₁(𝑡) (3.26) Karena ∆𝑡 sangat kecil dan mendakati nol, maka berdasarkan Definisi 2.7 didapatkan:

∆𝑡→0lim

𝑃₀(𝑡 + ∆𝑡) − 𝑃₀(𝑡)

∆𝑡 = lim

∆𝑡→0(−(𝜆₀)𝑃₀(𝑡) + (µ₁)𝑃₁(𝑡))

𝑑𝑃₀(𝑡)

𝑑𝑡 = −(𝜆₀)𝑃₀(𝑡) + (µ₁)𝑃₁(𝑡) (3.27)

3. Kemungkinan kejadian terdapat 𝑛 pelanggan dalam sistem pada saat 𝑛 = 𝑁 adalah:

a. Kemungkinan kejadian terdapat 𝑛 pelanggan pada waktu 𝑡 dan terdapat 𝑛 pelanggan pada waktu 𝑡 + ∆𝑡 adalah :

1. Tidak ada kedatangan, tidak ada kepergian dan tidak ada reneging 2. Ada kedatangan, ada kepergian dan tidak ada reneging

3. Ada kedatangan, tidak ada kepergian, dan ada reneging

b. Kemungkinan kejadian terdapat 𝑛 − 1 pelanggan pada waktu 𝑡 dan terdapat 𝑛 pelanggan pada waktu 𝑡 + ∆𝑡 adalah : tidak ada kedatangan, ada kepergian dan tidak ada reneging.

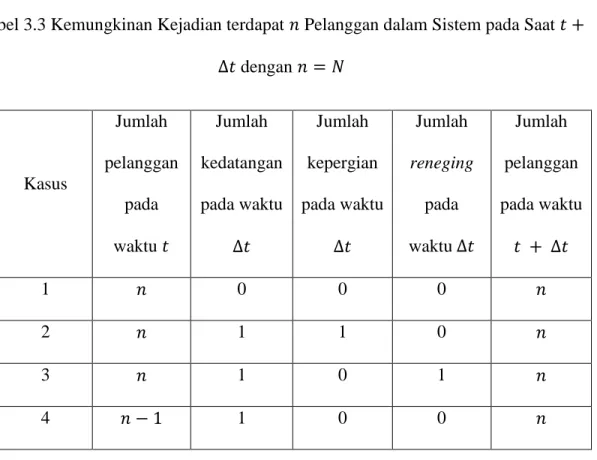
Dari kemungkinan-kemungkinan yang telah diperoleh, kemudian disajikan kedalam tabel sebagai berikut ini.

57

Tabel 3.3 Kemungkinan Kejadian terdapat 𝑛 Pelanggan dalam Sistem pada Saat 𝑡 +

∆𝑡 dengan 𝑛 = 𝑁

Kasus

Jumlah pelanggan

pada waktu 𝑡

Jumlah kedatangan pada waktu

∆𝑡

Jumlah kepergian pada waktu

∆𝑡

Jumlah reneging

pada waktu ∆𝑡

Jumlah pelanggan pada waktu

𝑡 + ∆𝑡

1 𝑛 0 0 0 𝑛

2 𝑛 1 1 0 𝑛

3 𝑛 1 0 1 𝑛

4 𝑛 − 1 1 0 0 𝑛

Selanjutnya akan dibahas secara khusus probabilitas terdapat 𝑛 pelanggan untuk nilai 𝑛 = 𝑁. Pada saat jumlah pelanggan dalam sistem adalah N, maka probabilitas terjadinya nol kedatangan pada kasus 1 adalah satu.

Menurut asumsi (vi) mengacu dari bab 2, kedatangan dan kepergian merupakan kejadian-kejadian yang saling bebas, sehingga kejadian-kejadian pada interval waktu tertentu tidak mempengaruhi kejadian ada interval waktu sesudahnya maka peluangdari masing-masing kejadian tersebut adalah sebagai berikut:

1. Probabilitas kasus 1 =

𝑃_𝑛(𝑡)(1)(1 − µ_𝑛∆𝑡 + 𝑜(∆𝑡))(1 − (𝑛 − 1)𝜉𝑝∆𝑡 + 𝑜(∆𝑡)) (3.28)

58 2. Probablitas kasus 2 =

𝑃_𝑛(𝑡)(𝜆_𝑛∆𝑡 + 𝑜(∆𝑡))(µ_𝑛∆𝑡 + 𝑜(∆𝑡))(1 − (𝑛 − 1)𝜉𝑝∆𝑡 + 𝑜(∆𝑡)) = 𝑜(∆𝑡) (3.29) 3. Probabilitas kasus 3 =

𝑃_𝑛(𝑡)(𝜆_𝑛∆𝑡 + 𝑜(∆𝑡))(1 − µ_𝑛∆𝑡 + 𝑜(∆𝑡))(𝑛𝜉𝑝∆𝑡 + 𝑜(∆𝑡)) = 𝑜(∆𝑡)

(3.30) 4. Probabilitas kasus 4 =

𝑃_𝑛−1(𝑡)(𝜆_𝑛−1∆𝑡 + 𝑜(∆𝑡))(1 − µ_𝑛−1∆𝑡 + 𝑜(∆𝑡))(1 − (𝑛 − 1)𝜉𝑝∆𝑡 + 𝑜(∆𝑡)) (3.31) Probabilitas terdapat 𝑛 pelanggan dalam sistem dengan 𝑛 = 𝑁 dalam waktu (𝑡 +

∆𝑡) adalah:

𝑃_𝑛(𝑡 + ∆𝑡) = 𝑃 (kasus 1 atau kasus 2 atau kasus 3 atau kasus 4)

Karena kasus-kasus tersebut tidak dapat terjadi secara bersamaan atau saling asing, maka probabilitas terdapat 𝑛 pelanggan dalam sistem dengan 𝑛 = 𝑁 pada saat (𝑡 + ∆𝑡) dinyatakan dengan:

𝑃_𝑛(𝑡 + ∆𝑡) = (Probabilitas kasus 1 + Probabilitas kasus 2 + Probabilitas kasus 3 +

Probabilitas kasus 4) (3.32)

Substitusi persamaan (3.28), (3.29), (3.30), dan (3.31) pada persamaan (3.32) sehingga diperoleh :

59

𝑃_𝑛(𝑡 + ∆𝑡) = 𝑃_𝑛(𝑡)(1)(1 − µ_𝑛∆𝑡 + 𝑜(∆𝑡))(1 − (𝑛 − 1)𝜉𝑝∆𝑡 + 𝑜(∆𝑡)) + 𝑜(∆𝑡) + 𝑜(∆𝑡) + 𝑃_𝑛−1(𝑡)(𝜆_𝑛−1∆𝑡 + 𝑜(∆𝑡))(1 − µ_𝑛−1∆𝑡 + 𝑜(∆𝑡))(1

− (𝑛 − 1)𝜉𝑝∆𝑡 + 𝑜(∆𝑡))

𝑃_𝑛(𝑡 + ∆𝑡) = 𝑃_𝑛(𝑡)(1 − µ_𝑛∆𝑡 − (𝑛 − 1)𝜉𝑝∆𝑡) + 𝑃_𝑛−1(𝑡)(𝜆_𝑛∆𝑡) + 𝑜(∆𝑡)

𝑃_𝑛(𝑡 + ∆𝑡) = 𝑃_𝑛(𝑡) − (µ_𝑛∆𝑡)𝑃_𝑛(𝑡) − ((𝑛 − 1)𝜉𝑝∆𝑡)𝑃_𝑛(𝑡) + (𝜆_𝑛∆𝑡)𝑃_𝑛−1(𝑡) +

𝑜(∆𝑡) (3.33)

Pada persamaan (3.33) dikurangkan 𝑃_𝑛(𝑡) pada ruas kiri dan kanan kemudian dibagi dengan ∆𝑡 maka diperoleh:

𝑃_𝑛(𝑡 + ∆𝑡) − 𝑃_𝑛(𝑡) = −(µ_𝑛∆𝑡)𝑃_𝑛(𝑡) − ((𝑛 − 1)𝜉𝑝∆𝑡)𝑃_𝑛(𝑡) + (𝜆_𝑛∆𝑡)𝑃_𝑛−1(𝑡)

𝑃_𝑛(𝑡+∆𝑡)−𝑃_𝑛(𝑡)

∆𝑡 = −(µ_𝑛)𝑃_𝑛(𝑡) − ((𝑛 − 1)𝜉𝑝)𝑃_𝑛(𝑡) + (𝜆_𝑛)𝑃_𝑛−1(𝑡) (3.34) Karena ∆𝑡 sangat kecil dan mendakati nol, maka berdasarkan Definisi 2.7 didapatkan:

∆𝑡→0lim

𝑃_𝑛(𝑡 + ∆𝑡) − 𝑃_𝑛(𝑡)

∆𝑡 = lim

∆𝑡→0(−(µ_𝑛)𝑃_𝑛(𝑡) − ((𝑛 − 1)𝜉𝑝)𝑃_𝑛(𝑡) + (𝜆_𝑛)𝑃_𝑛−1(𝑡)) 𝑑𝑃_𝑛(𝑡)

𝑑𝑡 = −(µ_𝑛)𝑃_𝑛(𝑡) − ((𝑛 − 1)𝜉𝑝)𝑃_𝑛(𝑡) + (𝜆_𝑛)𝑃_𝑛−1(𝑡) 𝑑𝑃_𝑛(𝑡)

𝑑𝑡 = (𝜆_𝑛)𝑃_𝑛−1(𝑡) − (µ_𝑛− (𝑛 − 1)𝜉𝑝)𝑃_𝑛(𝑡) Substitusi nilai 𝑛 = 𝑁 maka diperoleh :

𝑑𝑃𝑁(𝑡)

𝑑𝑡 = (𝜆_𝑁)𝑃_𝑁−1(𝑡) − (µ_𝑁− (𝑁 − 1)𝜉𝑝)𝑃_𝑁(𝑡) (3.35)

60

Jadi dari ke tiga kasus kemungkinan-kemungkinan kejadian saling asing yang dapat terjadi jika terdapat 𝑛 pelanggan dalam sistem pada waktu 𝑡 + ∆𝑡 diperoleh tiga sistem persamaan diferensial, yaitu persamaan (3.11), (3.20), dan (3.28) sebagai berikut :

1. ^{𝑑𝑃𝑛(𝑡)}

𝑑𝑡 = −(𝜆_𝑛+ µ_𝑛 + (𝑛 − 1)𝜉𝑝)𝑃_𝑛(𝑡) + (µ_𝑛+1+ 𝑛𝜉𝑝)𝑃_𝑛+1(𝑡) +

(𝜆_𝑛−1)𝑃_𝑛−1(𝑡) ; 1 ≤ 𝑛 ≤ 𝑁 − 1

2. ^{𝑑𝑃0(𝑡)}

𝑑𝑡 = −(𝜆₀)𝑃₀(𝑡) + (µ₁)𝑃₁(𝑡) ; 𝑛 = 0 3. ^{𝑑𝑃𝑁(𝑡)}

𝑑𝑡 = (𝜆_𝑁)𝑃_𝑁−1(𝑡) − (µ_𝑁− (𝑁 − 1)𝜉𝑝)𝑃_𝑁(𝑡) ; 𝑛 = 𝑁

Dari ke tiga persamaan diferensial tersebut, karena pada kasus ini laju kedatangan (𝜆_𝑛) dan laju pelayanan (µ_𝑛) konstan untuk semua 𝑛 maka dapat ditulis menjadi :

1. ^{𝑑𝑃𝑛(𝑡)}

𝑑𝑡 = −(𝜆 + µ + (𝑛 − 1)𝜉𝑝)𝑃_𝑛(𝑡) + (µ + 𝑛𝜉𝑝)𝑃_𝑛+1(𝑡) + (𝜆)𝑃_𝑛−1(𝑡) ; 1 ≤

𝑛 ≤ 𝑁 − 1 (3.36)

2. ^{𝑑𝑃0(𝑡)}

𝑑𝑡 = µ𝑃₁(𝑡) − 𝜆𝑃₀(𝑡) ; 𝑛 = 0 (3.37)

3. ^{𝑑𝑃𝑁(𝑡)}

𝑑𝑡 = 𝜆𝑃_𝑁−1(𝑡) − (µ − (𝑁 − 1)𝜉𝑝)𝑃_𝑁(𝑡) ; 𝑛 = 𝑁 (3.38) Dalam kondisi steady-state lim

𝑡→∞𝑃_𝑛(𝑡) = 𝑃_𝑛, oleh karena itu ^{𝑑𝑃𝑛(𝑡)}

𝑑𝑡 = 0 untuk 𝑡 →

∞. Kondisi steady-state yaitu keadaan sistem yang tidak bergantung pada keadaan awal maupun waktu yang telah dilalui. Untuk memperoleh kondisi steady-state,

61 substitusikan ^{𝑑𝑃𝑛(𝑡)}

𝑑𝑡 = 0 dan 𝑃_𝑛(𝑡) = 𝑃_𝑛 ke persamaan (3.36), (3.37), dan (3.38) sehingga diperoleh persamaan sebagai berikut :

1. 0 = −(𝜆 + µ + (𝑛 − 1)𝜉𝑝)𝑃_𝑛+ (µ + 𝑛𝜉𝑝)𝑃_𝑛+1+ (𝜆)𝑃_𝑛−1 ; 1 ≤ 𝑛 ≤ 𝑁 − 1 (3.39)

2. 0 = µ𝑃₁− 𝜆𝑃₀ ; 𝑛 = 0 (3.40)

3. 0 = 𝜆𝑃_𝑁−1− (µ − (𝑁 − 1)𝜉𝑝)𝑃_𝑁 ; 𝑛 = 𝑁 (3.41) Atau

1. (𝜆 + µ + (𝑛 − 1)𝜉𝑝)𝑃_𝑛 = (µ + 𝑛𝜉𝑝)𝑃_𝑛+1+ (𝜆)𝑃_𝑛−1 (3.42) 2. 𝜆𝑃₀ = 𝑃₁µ

𝑃₁ = ^𝜆

µ𝑃₀ (3.43)

3. (µ − (𝑁 − 1)𝜉𝑝)𝑃_𝑁= (𝜆)𝑃_𝑁−1

𝑃_𝑁 = ^(𝜆)

(µ−(𝑁−1)𝜉𝑝)𝑃_𝑁−1 (3.44)

Untuk mencari solusi rekursif dari kondisi steady-state, dilakukan perhitungan sebagai berikut:

substitusi 𝑛 = 1 pada persamaan (3.42), sehingga

[𝜆 + µ + (1 − 1)𝜉𝑝]𝑃₁ = (µ + 1𝜉𝑝)𝑃₁₊₁+ 𝜆𝑃₁₋₁ Jadi,

(𝜆 + µ)𝑃₁= (µ + 𝜉𝑝)𝑃₂+ 𝜆𝑃₀

62

(µ + 𝜉𝑝)𝑃₂ = (𝜆 + µ)𝑃₁− 𝜆𝑃₀

(µ + 𝜉𝑝)𝑃₂ = 𝜆𝑃₁+ (µ𝑃₁− 𝜆𝑃₀) (3.45)

Dengan menggunakan persamaan (3.40) yaitu µ𝑃₁− 𝜆𝑃₀ = 0, persamaan (3.45) menjadi

(µ + 𝜉𝑝)𝑃₂ = 𝜆𝑃₁ (3.46) Kemudian persamaan (3.46) dibagi dengan (µ + 𝜉𝑝) menjadi

𝑃₂ = ^𝜆𝑃1

(µ+𝜉𝑝) (3.47)

Substitusikan persamaan (3.43) pada persamaan (3.47) sehingga diperoleh

𝑃₂ = 𝜆 (𝜆

µ) 𝑃₀ (µ + 𝜉𝑝)

𝑃₂ = 𝑃₀(𝜆 µ) 𝜆

(µ + 𝜉𝑝)

𝑃₂ = 𝑃₀( 𝜆

µ + 0𝜉𝑝) ( 𝜆 (µ + 𝜉𝑝))

𝑃₂ = 𝑃₀( ^𝜆

µ+(1−1)𝜉𝑝) ( ^𝜆

(µ+(2−1)𝜉𝑝)) (4.48) Dengan menggunakan notasi sigma, maka persamaan (3.41) menjadi,

𝑃₂ = 𝑃₀∏ ^𝜆

µ+(𝑘−1)𝜉𝑝

2𝑘=1 (3.49)

63 Substitusi 𝑛 = 2 pada persamaan (3.42), sehingga

[𝜆 + µ + (2 − 1)𝜉𝑝]𝑃₂ = (µ + 2𝜉𝑝)𝑃₂₊₁+ 𝜆𝑃₂₋₁ Jadi,

(µ + 2𝜉𝑝)𝑃₃ = [𝜆 + µ + 𝜉𝑝]𝑃₂− 𝜆𝑃₁

(µ + 2𝜉𝑝)𝑃₃ = 𝜆𝑃₂+ (µ𝑃₂+ 𝜉𝑝𝑃₂) − 𝜆𝑃₁ (3.50)

Dengan menggunakan persamaan (3.46) yaitu (µ + 𝜉𝑝)𝑃₂ = 𝜆𝑃₁, persamaan (3.50) menjadi

(µ + 2𝜉𝑝)𝑃₃ = 𝜆𝑃₂+ 𝜆𝑃₁− 𝜆𝑃₁

sehingga

(µ + 2𝜉𝑝)𝑃₃ = 𝜆𝑃₂ (3.51) Kemudian persamaan (3.44) dibagi dengan (µ + 2𝜉𝑝) maka menjadi

𝑃₃ = ^𝜆𝑃2

(µ+2𝜉𝑝) (3.52)

Substitusi persamaan (3.49) pada persamaan (3.52) sehingga

𝑃₃ = ^𝜆

(µ+2𝜉𝑝)𝑃₀∏ ^𝜆

µ+(𝑘−1)𝜉𝑝

2𝑘=1 (3.53)

Dengan menggunakan notasi sigma, maka persamaan (3.53) menjadi,

𝑃₃ = 𝑃₀∏ ^𝜆

µ+(𝑘−1)𝜉𝑝

3𝑘=1 (3.54)

64 Substitusi 𝑛 = 3 pada persamaan (3.35), sehingga

[𝜆 + µ + (3 − 1)𝜉𝑝]𝑃₃ = (µ + 3𝜉𝑝)𝑃₃₊₁+ 𝜆𝑃₃₋₁ Jadi,

(µ + 3𝜉𝑝)𝑃₄ = [𝜆 + µ + 2𝜉𝑝]𝑃₃− 𝜆𝑃₂

(µ + 3𝜉𝑝)𝑃₄ = 𝜆𝑃₃+ (µ𝑃₃+ 2𝜉𝑝𝑃₃) − 𝜆𝑃₂ (3.55)

Dengan menggunakan persamaan (3.44) yaitu (µ + 2𝜉𝑝)𝑃₃ = 𝜆𝑃₂, persamaan (3.48) menjadi

(µ + 3𝜉𝑝)𝑃₄ = 𝜆𝑃₃+ 𝜆𝑃₂− 𝜆𝑃₂

Sehingga

(µ + 3𝜉𝑝)𝑃₄ = 𝜆𝑃₃ (3.56) Kemudian persamaan (3.56) dibagi dengan (µ + 3𝜉𝑝) maka menjadi

𝑃₄ = ^𝜆𝑃3

(µ+3𝜉𝑝) (3.57) Substitusi persamaan (3.54) pada persamaan (3.57) sehingga

𝑃₄ = ^𝜆

(µ+3𝜉𝑝)𝑃₀∏ ^𝜆

µ+(𝑘−1)𝜉𝑝

3𝑘=1 (3.58)

Dengan menggunakan notasi sigma, maka persamaan (3.58) menjadi,

𝑃₄ = 𝑃₀∏ ^𝜆

µ+(𝑘−1)𝜉𝑝

4𝑘=1 (3.59)

65

Untuk 4 ≤ 𝑛 ≤ 𝑁 − 1 dengan menggunakan cara yang sama, maka diperoleh:

𝑃_𝑛 = 𝑃₀∏ ^𝜆

µ+(𝑘−1)𝜉𝑝

𝑛𝑘=1 ; 1 ≤ 𝑛 ≤ 𝑁 − 1 (3.60)

Untuk = 𝑁 , substitusikan persamaan (3.60) pada persamaan (3.44)

𝑃_𝑁= 𝜆𝑃_𝑁−1 [µ + (𝑁 − 1)𝜉𝑝]

Jadi,

𝑃_𝑁 = ^𝜆

[µ+(𝑁−1)𝜉𝑝]𝑃₀∏ ^𝜆

µ+(𝑘−1)𝜉𝑝

𝑁−1𝑘=1 (3.61)

Dengan menggunakan notasi sigma, maka persamaan (3.61) menjadi,

𝑃_𝑁= 𝑃₀∏ ^𝜆

µ+(𝑘−1)𝜉𝑝

𝑁𝑘=1 (3.62)

Selanjutnya, akan dicari probabilitas nol pelanggan dalam sistem. Jumlah kumpulan dari berbagai kemungkinan terjadinya probabilitas terdapat n pelanggan dalam sistem (𝑃_𝑛) adalah sama dengan 1. Dalam kalimat matematika ditulis:

∑^𝑁_𝑛=0𝑃_𝑛 = 1 (3.63) Oleh karena itu dapat dicari probabilitas nol pelanggan dalam sistem, yaitu

𝑃₀+ ∑^𝑁_𝑛=1𝑃_𝑛 = 1 (3.64) Substitusi persamaan persamaan (3.60) ke persamaan (3.64) sehingga

𝑃₀+ ∑ ∏ ^𝜆

µ+(𝑘−1)𝜉𝑝

𝑛𝑘=1 𝑃₀ = 1

𝑁𝑛=1 (3.65)

66

Dengan menggunakan operasi pemfaktoran pada persamaan (3.65) menjadi

[1 + ∑ ∏ ^𝜆

µ+(𝑘−1)𝜉𝑝 𝑛𝑘=1

𝑁𝑛=1 ] 𝑃₀ = 1 (3.66)

Kemudian persamaan (3.66) dibagi dengan [1 + ∑ ∏ ^𝜆

µ+(𝑘−1)𝜉𝑝 𝑛𝑘=1

𝑁𝑛=1 ] diperoleh

𝑃₀ = ¹

1+∑ ∏ ^𝜆

µ+(𝑘−1)𝜉𝑝 𝑛𝑘=1

𝑁𝑛=1

(3.67)

Jadi persamaan rekursif kondisi steady-state dari model adalah:

𝑃_𝑛 = 𝑃₀∏ 𝜆 µ + (𝑘 − 1)𝜉𝑝

𝑛

𝑘=1

; 0 ≤ 𝑛 ≤ 𝑁

dengan

𝑃₀ = 1

1 + ∑ ∏ 𝜆

µ + (𝑘 − 1)𝜉𝑝

𝑛𝑘=1 𝑁𝑛=1

B. Ukuran Keefektifan Sistem Antrian M/M/1/N dengan Retensi Pelanggan yang Membatalkan Antrian

Nilai harapan banyaknya pelanggan dalam sistem (𝐿_𝑠) mempunyai hubungan sederhana antara jumlah pelanggan yang antri (𝑛) dan berbagai kemungkinan 𝑃_𝑛 dengan batas maksimum tempat antrian sebesar 𝑁.

67

Akan dicari nilai harapan banyaknya pelanggan dalam sistem (𝐿_𝑠) menggunakan persamaan umum nilai harapan berdasarkan persamaan (2.50)

𝐿_𝑠 = ∑ 𝑛𝑃_𝑛

𝑁

𝑛=0

Substitusi persamaan (3.60) pada persamaan (2.50) sehingga

𝐿_𝑠 = ∑^𝑁_𝑛=0𝑛𝑃₀(∏ ^𝜆

µ+(𝑘−1)𝜉𝑝

𝑛𝑘=1 ) (3.68)

Rata-rata waktu tunggu dalam sistem (𝑊_𝑠) dipengaruhi jumlah rata-rata pelanggan dalam sistem dibanding tingkat kedatangan dalam sistem.

Akan dicari nilai harapan waktu tunggu dalam sistem (𝑊_𝑠) menggunakan little formula berdasarkan persamaan (2.52) sebagai berikut:

𝐿_𝑠 = 𝜆𝑊_𝑠

𝑊_𝑠 = ^𝐿𝑠

𝜆 (3.69)

Substitusi persamaan (3.68) ke persamaan (3.69) sehingga diperoleh

𝑊_𝑠 =^{∑ 𝑛}

𝑁𝑛=0 𝑃0(∏^𝑛_{𝑘=1µ+(𝑘−1)𝜉𝑝}^𝜆 )

𝜆 (3.70)

Rata-rata waktu tunggu dalam antrian (𝑊_𝑞) dipengaruhi oleh rata-rata waktu menunggu dalam sistem dengan waktu pelayanan.

68

Akan dicari nilai harapan waktu tunggu dalam antrian (𝑊_𝑞) menggunakan little formula sebagai berikut:

𝑊_𝑞 = 𝑊_𝑠 −¹

µ (3.71)

Substitusi persamaan (3.70) pada persamaan (3.71) sehingga diperoleh

𝑊_𝑞= ^{∑ 𝑛}

𝑁𝑛=0 𝑃0(∏^𝑛_{𝑘=1µ+(𝑘−1)𝜉𝑝}^𝜆 )

𝜆 −¹

µ (3.72) Nilai harapan banyaknya pelanggan dalam antrian (𝐿_𝑞) berkaitan erat dengan lamanya tingkat kedatangan dikali rata-rata waktu menunggu pelanggan dalam antrian.

Akan dicari nilai harapan waktu tunggu dalam sistem (𝑊_𝑠) menggunakan little formula berdasarkan persamaan (2.53) sebagai berikut:

𝐿_𝑞= 𝜆𝑊_𝑞

Substitusi persamaan (3.72) pada persamaan (2.53) sehingga diperoleh

𝐿_𝑞 = 𝜆 (^{∑ 𝑛}

𝑁𝑛=0 𝑃0(∏^𝑛_{𝑘=1µ+(𝑘−1)𝜉𝑝}^𝜆 )

𝜆 −¹

µ) (3.73)

Dengan operasi perkalian biasa pada persamaan (3.73) sehingga diperoleh nilai 𝐿_𝑞 sebagai berikut

𝐿_𝑞 = ∑^𝑁_𝑛=0𝑛𝑃₀(∏ ^𝜆

µ+(𝑘−1)𝜉𝑝

𝑛𝑘=1 ) −^𝜆

µ (7.74)

69 C. SIMULASI

Simulasi yang dilakukan adalah membandingkan hasil perhitungan probabilitas terdapat 𝑛 pelanggan dalam sistem serta perhitungan ukuran keefektifan pada sistem antrian M/M/1/N dengan sistem antrian M/M/1/N dengan retensi pelanggan yang membatalkan antrian.

Contoh kasus sistem antrian M/M/1/N

Dalam sebuah sarana jasa pembersihan mobil, informasi yang dikumpulkan menunjukan bahwa kedatangan mobil terdistribusi Poisson dengan rata-rata 2 mobil perjam. Waktu untuk mencuci mobil bervariasi, tetapi mengikuti distribusi eksponensial dengan rata-rata 20 menit per mobil. Sarana pelayanan hanya dapat menangani satu mobil setiap saat serta tempat pakir yang tersedia hanya dapat memuat sebanyak 9 mobil. Tentukan ukuran keefektifan dari sistem antrian sarana jasa pembersihan mobil tersebut jika diketahui probabilitas dari retention adalah sebesar 0.6 dan reneging times 0.1 jam.

Diketahui : 𝜆 = 2 mobil/jam

1

µ= 20 menit/mobil , µ = 3 mobil/jam Kapasitas sistem (𝑁) = 10 mobil Probabilitas dari retention (𝑞) = 0.6

70 Probabilitas dari reneging (𝑝) = 1 − 𝑞 = 0.4 Reneging times (𝜉) = 0.1 jam

Ditanyakan:

1. Probabilitas terdapat 𝑛 pelanggan dalam sistem (𝑃_𝑛) 2. Nilai harapan banyaknya pelanggan dalam sistem (𝐿_𝑠) 3. Nilai harapan banyaknya pelanggan dalam antrian (𝐿_𝑞) 4. Nilai harapan waktu tunggu pelanggan dalam sistem (𝑊_𝑠) 5. Nilai harapan waktu tunggu pelanggan dalam antrian (𝑊_𝑞)

Jawab:

A. Menentukan probabilitas dan ukuran keefektifan sistem antrian M/M/1/N sederhana:

1. Menentuka probabilitas terdapat 𝑛 pelanggan dalam sistem (𝑃_𝑛)

𝑃_𝑛 = (𝜆 µ)

𝑁

𝑃₀

dengan

𝑃₀ =

1 − (𝜆 µ) 1 − (𝜆

µ)

𝑁+1

untuk 𝑁 = 10, maka nilai 𝑃₀

71 𝑃₀ = 1 − (2

3) 1 − (2

3)

10+1

𝑃₀ =1 − 0.66667

1 − 0.01156= 0.33728 untuk 𝑛 = 𝑁 = 10, maka nilai 𝑃₁₀

𝑃₁₀ = (2 3)

10

𝑃₀

𝑃₁₀ = (0.01734)(0.33728) 𝑃₁₀ = 0.00585

Jadi probabilitas terdapat 𝑛 pelanggan dalam sistem adalah 𝑃_𝑛 = (^𝜆

µ)^𝑁𝑃₀ dan probabilitas terdapat 10 pelanggan dalam sistem adalah sebesar 0.00585.

2. Menentukan nilai harapan banyaknya pelanggan dalam sistem (𝐿_𝑠)

𝐿_𝑠 = (𝜆

µ) (1 −(𝑁 + 1) (𝜆 µ)

𝑁

+ 𝑁 (𝜆 µ)

𝑁+1

) (1 − (𝜆

µ)) (1 − ( 𝜆 µ)

𝑁+1

)

𝐿_𝑠 = (2

3) (1 −(10 + 1) (2 3)

10

+ 10 (2 3)

10+1

) (1 − (2

3)) (1 − ( 2 3)

10+1

)

𝐿_𝑠 = (2

3) (1 −(11) (2 3)

10

+ 10 (2 3)

11

) (1 − (2

3)) (1 − ( 2 3)

11

)

72 𝐿_𝑠 = ^0.61657

0.32948= 1.87134

Jadi nilai harapan banyaknya pelanggan dalam sistem adalah sebesar 1.87134 pelanggan.

3. Menentukan nilai harapan banyaknya pelanggan dalam antrian (𝐿_𝑞)

𝐿_𝑞 = (𝜆

µ) (1 −(𝑁 + 1) (𝜆 µ)

𝑁

+ 𝑁 (𝜆 µ)

𝑁+1

) (1 − (𝜆

µ)) (1 − ( 𝜆 µ)

𝑁+1

)

−𝜆(1 − 𝑃_𝑁) µ

𝐿_𝑞 = 𝐿_𝑠−𝜆(1 − 𝑃_𝑁) µ

𝐿_𝑞= 1.87134 −2(1 − 0.00585) 3

𝐿_𝑞 = 1.87134 − 0.66278 = 1.20857

Jadi nilai harapan banyaknya pelanggan dalam antrian adalah sebesar 1.20857 pelanggan.

4. Menentukan nilai harapan waktu tunggu pelanggan dalam sistem (𝑊_𝑠)

𝑊_𝑠 = 𝐿_𝑠 𝜆(1 − 𝑃_𝑁)

𝑊_𝑠 = 1.87134

2(1 − 0.00585)= 0.94118

Jadi nilai harapan waktu tunggu dalam sistem adalah sebesar 0.94118 jam.

5. Menentukan nilai harapan waktu tunggu pelanggan dalam antrian (𝑊_𝑞) 𝑊_𝑞 = 𝐿_𝑞

𝜆(1 − 𝑃_𝑁) 𝑊_𝑞= 1.20857

2(1 − 0.00585)= 0.60784

73

Jadi nilai harapan waktu tunggu dalam antrian adalah sebesar 0.60784 jam.

B. Menentukan probabilitas dan ukuran keefektifan sistem antrian M/M/1/N dengan reneging customers:

1. Menentukan probabilitas terdapat 𝑛 pelanggan dalam sistem (𝑃_𝑛)

𝑃_𝑛 = 𝑃₀∏ 𝜆 µ + (𝑘 − 1)𝜉𝑝

𝑛

𝑘=1

; 𝑛 = 0,1,2, … 𝑁

dengan

𝑃₀ = 1

1 + ∑ ∏ 𝜆

µ + (𝑘 − 1)𝜉𝑝

𝑛𝑘=1 𝑁𝑛=1

untuk 𝑁 = 10, maka nilai 𝑃_0

𝑃₀ = 1

1 + ∑ ∏ 2

3 + (𝑘 − 1)(0.1)(0.4)

𝑛𝑘=1 10𝑛=1

dengan menggunakan Microsoft exel diperoleh 𝑃₀ = 0.34986 untuk 𝑛 = 𝑁 = 10, maka nilai 𝑃₁₀

𝑃₁₀= 𝑃₀∏ 2

3 + (𝑘 − 1)(0.1)(0.4)

𝑛

𝑘=1

𝑃₁₀ = (0.34986)(0.00975) 𝑃₁₀ = 0.00341

74 Jadi 𝑃_𝑛 = 𝑃₀∏ ^𝜆

µ+(𝑘−1)𝜉𝑝

𝑛𝑘=1 dan probabilitas terdapat 10 pelanggan dalam sistem adalah sebesar 0.00341.

2. Menentukan nilai harapan banyaknya pelanggan dalam sistem (𝐿_𝑠)

𝐿_𝑠 = ∑ 𝑛

𝑁

𝑛=0

𝑃₀(∏ 𝜆

µ + (𝑘 − 1)𝜉𝑝

𝑛

𝑘=1

)

𝐿_𝑠 = ∑ 𝑛

10

𝑛=0

𝑃₀(∏ 𝜆

µ + (𝑘 − 1)𝜉𝑝

10

𝑘=1

)

𝐿_𝑠 = 1𝑃₀𝑘₁+ 2𝑃₀𝑘₂+ ⋯ + 10𝑃₀𝑘₁₀

𝐿_𝑠 = (1)(0.34986)(0.66667) + (2)(0.34986)(0.43859) + ⋯ + (10)(0.34986)(0.00975)

𝐿_𝑠 = 0.23324 + 0.30689 + ⋯ + 0.03410 𝐿_𝑠 = 1.71920

jadi diperoleh nilai harapan banyaknya pelanggan dalam sistem adalah sebesar 1.71920 pelanggan.

3. Menentukan nilai harapan banyaknya pelanggan dalam antrian (𝐿_𝑞)

𝐿_𝑞= ∑ 𝑛

𝑁

𝑛=0

𝑃₀(∏ 𝜆

µ + (𝑘 − 1)𝜉𝑝

𝑛

𝑘=1

) −𝜆 µ

𝐿_𝑞= 𝐿_𝑠−𝜆 µ

75

𝐿_𝑞 = 1.71920 −2 3

𝐿_𝑞 = 1.71920 − 0.66667 = 1.05253

jadi nilai harapan banyaknya pelanggan dalam antrian adalah sebesar 1.05253 pelanggan.

4. Menentukan nilai harapan waktu tunggu dalam sistem (𝑊_𝑠)

𝑊_𝑠 =

∑^𝑁_𝑛=0𝑛𝑃₀(∏ 𝜆 µ + (𝑘 − 1)𝜉𝑝

𝑛𝑘=1 )

𝜆 𝑊_𝑠 = 𝐿_𝑠 𝜆 𝑊_𝑠 =1.71920

2 = 0.85960

Jadi nilai harapan waktu tunggu dalam sistem adalah sebesar 0.85960 jam.

5. Menentukan nilai harapan waktu tunggu dalam antrian (𝑊_𝑞)

𝑊_𝑞 =

∑^𝑁_𝑛=0𝑛𝑃₀(∏ 𝜆 µ + (𝑘 − 1)𝜉𝑝

𝑛𝑘=1 )

𝜆 −1

µ 𝑊_𝑞 = 𝑊_𝑠 −1

µ 𝑊_𝑞 = 0.85960 −1

3= 0.53637

Jadi nilai harapan waktu tunggu dalam antrian adalah sebesar 0.53637 jam.

76

Tabel 3.4 Perbandingan Probabilitas dan Ukuran-ukuran Keefektifan Sistem Antrian M/M/1/N dengan Sistem Antrian M/M/1/N dengan Retensi Pelanggan yang

Membatalkan Antrian

Dari tabel diatas dapat disimpulkan bahwa adanya reneging pada sistem antrian berpengaruh terhadap ukuran sistem yang diharapkan dan ukuran-ukuran keefektifan pada sistem antrian M/M/1/N lebih tinggi daripada ukuran-ukuran keefektifan sistem antrian M/M/1/N dengan retensi pelanggan yang membatalkan antrian.