MATRIKS SOLUSI PERSAMAAN LINEAR

(1)

Äfisika-komputasi⊇

47

MATRIKS &

SOLUSI PERSAMAAN

LINEAR

Pada bab ini dibahas konsep dasar dan metode di dalam menyelesaikan

persamaan linear dengan pendekatan matriks terutama berkaitan dengan kasus-kasus

khusus dalam fisika. Disajikan beberapa metode komputasi numerik, meliputi

metode eliminasi Gauss dengan pivoting, metode Gauss-Seidel, dan matriks

Tridiagonal yang cukup familiar di terapkan dalam masalah nilai eigen dalam fisika

kuantum, sebagai stimulan untuk pemahaman yang lebih intensif terhadap

metode-metode yang lain menyangkut solusi fenomena fisis dalam formulasi persamaan

linear.

A. SASARAN UMUM

Sasaran umum dari perkuliahan ini adalah memberikan pemahaman kepada

mahasiswa mengenai proses penyelesaian kasus fisika dalam formulasi persamaan

linear secara komputasi numerik, dan memberikan keleluasaan wawasan tentang

beberapa metode dari sekian banyak metode yang bisa diimplementasikan.

B. SASARAN KHUSUS

Setelah perkuliahan selesai dilaksanakan, mahasiswa diharapkan mampu:

1. Memformulasikan fenomena fisis bentuk persamaan linear ke dalam formula

iteratif komputasi numerik.

2. Menyebutkan beberapa metode komputasi numerik dalam kasus penyelesaian

persamaan linear

3. Menjelaskan perilaku metode eliminasi Gauss, metode Gauss-Seidel dan matriks

Tridiagonal di dalam menanga ni kasus persamaan linear yang ditangani.

4. Mengembangkan pemahaman dengan menggunakan karakteristik metode-metode

(2)

48

5. Meng-implementasikan metode komputasi numerik bercirikan matriks untuk

persamaan linear dalam program komputer.

C. URAIAN MATERI

Tinjau sistem linear Ax=b, yang mempunyai satu dan hanya satu

penyelesaian untuk setiap sisi kanan b, dan batasi perhatian pada sistem yang

mempunyai jumlah persamaan tepat sama dengan jumlah variabelnya, yakni untuk

matriks yang koefisiennya A dan dapat diinvers-kan.

Suatu uji coba yang seringkali dikutip untuk meneliti dapat tidaknya suatu

matriks diinverskan, didasarkan pada konsep determinan. Teorema penting yang

bersangkutan menyatakan bahwa matriks A dapat diinverskan, jika hanya jika

det(A)≠0 sebagaimana Dalil Cramer yang menyatakan penyelesaian dari Ax=b

dalam determinan. Nsmun demikian, determinan tidak penting untuk praktek

penyelesaian sistem linear, karena perhitungan determinan biasanya mempunyai

kesulitan yang sama dengan penyelesaian sistem linear. Karena alasan tersebut tidak

digunakan determinan dalam penyelesaian sistem linear dan juga tidak perlu

mendefinisikan determinan itu sendiri.

Metode komputasi numerik untuk penyelesaian sistem persamaan linear

dapat dibagi dalam dua jenis, langsung (direct) dan iterasi(iterative). Metode

langsung adalah metode dengan tidak adanya kesalahan pembulatan atau

lain-lainnya, akan memberikan penyelesaian yang tepat dalam jumlah operasi aritmetika

elementer yang terbatas banyaknya. Metode dasar yang digunakan adalah eliminasi

Gauss dan ada berbagai pilihan metode yang bervariasi dalam efisiensi dan

kecermatan hitungan. Metode iterasi adalah dimulai dengan pendekatan permulaan

menggunakan algoritma yang sesuai, untuk mendapatkan hasil pendekatan yang

lebih baik. Metode iterasi bervariasi dalam algoritma dan kecepatan konvergensi.

Kelebihan metode iterasi adalah kesederhanaan dan keseragamannya dari operasi

yang dilakukan.

Matriks yang berkaitan dengan sistem linear juga digolongkan dalam padat

(dense) atau longgar (sparse). Matriks padat mempunyai sedikit sekali unsur-unsur

nol, dan orde matriks itu cenderung menjadi relatif kecil– mungkin berorde 100 atau

(3)

49

matriks semacam itu dengan metode langsung. Matriks longgar mempunyai sedikit

sekali unsur-unsur tak nol. Biasanya timbul dari usaha -usaha untuk menyelesaiakan

persamaan diferensial dengan metode selisih terhingga. Tingkat matriks semacam ini

mungkin besar sekali, dan secara ideal sangat cocok untuk penyelesaian dengan

metode iterasi.

Berikut ini adalah beberapa metode di dalam menyelesaikan persamaan linear

dengan pendekatan matriks, antara lain:

a. Kaidah Cramer

b. ÄEliminasi Gauss (dengan pivoting)

(Stability:– ,Precision:Affected by Round-off error, Breadth of

Application:General, Programming Effort:Moderat)

c. Gauss Jordan

d. ÄDekomposisi LU(Matriks Spesial–Tridiagonal)

(Stability:– ,Precision:Affected by Round-off error, Breadth of

Application:General, Programming Effort:Mode rat)

e. ÄGauss Seidel

(Stability:may not converge if not diagonally dominant,

Precision:Excellent, Breadth of Application:Appropriate only

for diagonally dominant system, Programming Effort:Easy)

3.1 Eliminasi Gauss (dengan pivoting)

Matriks menjadi skema yang efisien ketika semua koefisien sistem linear

Ax=b berada dalam deret berorde Nx(N+1). Koefisien-koefisien b disimpan dalam

kolom N+1 dari deret ( yaitu ai,N+1=bi ). Tiap baris memuat semua koefisien yang

diperlukan untuk menyatakan satu persamaan dalam sistem linear. Matriks lengkap

dinyatakan oleh [A,b] dan sistem linear itu dinyatakan sebagai berikut:













=

N NN N

N

N N

b a a

a

b b a

a

b a a

a

b A

...

... ... ... ... ...

... ...

] , [

2 1

2 2 22

21

1 1 12

11

(4)

50

Sistem Ax=b, dapat diselesaikan dengan melakukan OBE (operasi-operasi

baris elementer) pada matriks lengkap [A,b]. Var iabel-variabel xk adalah pemegang

posisi untuk koefisien-koefisien dan dapat dihilangkan sampai akhir perhitungan.

Operasi berikut merupakan operasi baris elementar yang dapat diterapkan

pada matriks lengkap dan menghasilkan sistem yang setara, meliputi:

(a) Pertukaran : urutan dua baris dapat ditukar

(b) Penskalaan : Perkalian sebuah baris dengan tetapan tidak nol

(c) Penggantian : Sebuah baris dapat digantikan oleh jumlah baris itu dengan

kelipatan sebarang baris lainnya.

Tumpuan (pivoting) adalah salah satu bentuk penyelesaian eliminasi Gauss

dengan menentukan bilangan akk pada posisi (k,k) untuk mengeliminasi xk dalam

baris k+1,k+2,…,N. Jika akk=0, maka baris k tidak dapat dipakai untuk

menghilangkan elemen-elemen pada kolom k, dan baris k harus ditukar dengan baris

lainnya di bawah diagonal untuk memperoleh elemen tumpuan yang tidak nol. Jika

ini tidak dapat dilakukan maka sistem persamaan tidak mempunyai selesaian tunggal.

Metode eliminasi Gauss memerlukan dua tahap di dalam menyelesaikan

sua tu sistem persamaan linear. Pertama, tahap eliminasi maju (forward elimination)

bertujuan mengubah matriks koefisien menjadi matriks segitiga atas. Kedua, adalah

subtitusi balik (back subtitution).

Contoh 3.1

Sistem persamaan umum dengan n=3, dituliskan sebagai berikut

3 3 33 2 32 1 31

2 2 23 2 22 1 21

1 3 13 2 12 1 11

b x a x a x a

=

+

=

+

=

+

) 3 (

) 2 (

) 1 (

P P P

(3.2)

selesaikan persamaan linear silmultan diatas menggunakan metode eliminasi Gauss

Solusi

Tahap Pertama: Eliminasi Maju

langkah pertama, adalah eliminasi xi dari P(2) dan P(3) dengan asumsi a1 1≠0.

Definisikan

11 21 21

a a

P

=

dan

11 31 31

(5)

51

lakukan operasi-operasi berikut P(2) – P21* P(1) dan P(3) – P31* P(1), maka

persamaan linear pada (3.2) menjadi:

' ' ' ' ' ' 3 3 33 2 32 2 2 23 2 22 1 3 13 2 12 1 11 b x a x a b x a x a b x a x a x a

=

+

=

+

=

+

) 3 ( ) 2 ( ) 1 ( P P P (3.3)

koefisien-koefisien aij’ didefinisikan oleh

1 1 1 1 ' ' b P b b a P a a i i i j i ij ij

−

=

−

=

3 , 2 3 , 2 ,

=

i j i

Langkah kedua adalah eliminasi x2 dari P(3). Asumsikan bahwa a2 2’≠0

Definisikan ' ' 22 32 32 a a P

=

lakukan operasi-operasi berikut P(3) – P32* P(2) maka persamaan linear pada (3.3)

menjadi: " " ' ' ' 3 3 33 2 2 23 2 22 1 3 13 2 12 1 11 b x a b x a x a b x a x a x a

=

+

=

+

) 3 ( ) 2 ( ) 1 ( P P P (3.4)

koefisien-koefisien yang baru didefinisikan oleh

2 32 2 3 23 32 33 33 ' " ' ' " b P b b a P a a

−

=

−

=

3 , 2 3 , 2 ,

=

i j i

Tahap Kedua: Subtitusi Balik

Dengan subtitusi balik, secara beruntun didapatkan x1,x2 dan x3:

11 3 13 2 12 1 1 22 3 23 2 2 33 3 3 / ) ( ' / ) ' ' ( " / " a x a x a b x a x a b x a b x

−

=

−

=

(3.5)

Contoh 3.2

Gunakan eliminasi Gauss untuk menyelesaikan

4 , 71 10 2 , 0 3 , 0 3 , 19 3 , 0 7 1 , 0 85 , 7 2 , 0 1 , 0 3 3 2 1 3 2 1 3 2 1

=

+

−

=

−

+

=

−

x x x x x x x x x ) 3 ( ) 2 ( ) 1 ( P P P (3.6)

(6)

52

solusi

Tahap Pertama: Eliminasi Maju

Operasi-operasi eliminasi adalah P(2)– 0,1/3*P(1) dan P(3)– 0,3/3*P(1) akan

memberikan perubahan pada persamaan 3.6 menjadi:

6150 , 70 0200 , 10 190000 , 0 5617 , 19 293333 , 0 00333 , 7 85 , 7 2 , 0 1 , 0 3 3 2 3 2 3 2 1

=

+

−

=

−

=

−

x x x x x x x ) 3 ( ) 2 ( ) 1 ( P P P (3.7)

Untuk melengkapi eliminasi maju, x2 harus dihilangkan dari P(3) dengan operasi

P(3)– 0,19000/7,00333*P(2), sehingga sistem tereduksi menjadi bentuk segitiga atas

sebagai berikut: 0843 , 70 0200 , 10 5617 , 19 293333 , 0 00333 , 7 85 , 7 2 , 0 1 , 0 3 3 3 2 3 2 1

=

−

=

−

=

−

x x x x x x ) 3 ( ) 2 ( ) 1 ( P P P (3.8)

Tahap Kedua: Subtitusi Balik

00003 , 7 0200 , 10 0843 . 70

3

=

x 50000 , 2 00333 , 7 ) 00003 , 7 ( 293333 , 0 5617 , 19

2

=

−

+

=

−

x 00000 , 3 3 ) 00003 , 7 ( 2 , 0 ) 50000 , 2 ( 1 , 0 85 , 7

1

=

+

−

+

=

x

Langkah-langkah untuk n=3 pada contoh 3.1 dan 3.2 secara mudah dapat

diimplementasikan untuk sistem n persamaan linear yang tidak singular, dimana

matriks segitiga atas karena proses eliminasi dituliskan,

) 1 ( ) 1 ( 3 3 3 33 2 2 2 23 2 22 1 1 3 13 2 12 1 11 ... ... " " ... " ' ' ... ' ' ... − −

=

+

=

+

=

+

n n n n nn n n n n n n b x a b x a x a b x a x a x a b x a x a x a x a (3.9)

(7)

53

) 1 (

− −

=

_n

nn n n n

a b

x (3. 10)

Hasilnya kemudian disubtitusi balik pada persamaan yang ke (n– 1). Prosedurenya

akan berulang untuk mengevaluasi nilai-nilai x, dengan formula:

) 1 (

1 ) 1 ( )

1 (

− + =

−

∑

=

_i

ij n

i j

j i ij i

i

a

x a b

x untuk i

=

n

−

1,n

−

2,...,1 (3. 11)

Algoritma Eliminasi Gauss

Pseudocode untuk implementasi eliminasi Gauss dan proses subtitusi balik

disajikan dibawah ini:

DO k=1,n– 1 DO i=k+1,n

factor=ai k/ak,k

DO j=k+1 to n

ai,j=ai,j–factor.ak,j

END DO bi=bi– factor.bk

END DO END DO

xn=bn/an,n

DO i=n–1,1,–1 sum=0 DO j=i+1,n

sum=sum+ai,j.xj

END DO xi=(bi–sum)/ai,j

END DO

Contoh 3.3

Buatlah program untuk menyelesaikan set persamaan simultan dalam bentuk matriks

berikut dengan eliminasi Gauss !













−

1 3 4 2

0 1 2 2

0 2 1 0

(8)

54

/* Eliminasi Gauss */

#include <stio.h> #include <stdlib.h> #include <math.h> #define TRUE 1

/* a[i][j] : elemen matriks, a[I,j]

n : orde matriks

*/ main() {

int i, j, _i, _r; static n=3;

static float a_init[10][11]= { { 0, – 1, 2, 0}, {–2, 2, –1, 0}, {–2, 4, 3, 1} }; double a[10][11];

void gauss(); static int _aini = 1;

printf ( “ Eliminasi Gauss \n\n”); printf (“ Elemen Matriks\n”); for ( i=1; i<=n; i++) {

for ( j=1; j<= n+1; j++ ) {

a[i][j]=a_init[i– 1][j– 1]; printf( “ %12.5”, a[i][j] );

}

printf ( “\n”); }

gauss ( n, a); printf ( “ Solusi\n”);

printf ( “ ---\n”);

printf ( “ i x(i)\n”);

printf ( “ ---\n”); for ( i=1; i<=n; i++ ) printf ( “ %5d %16.6e\n”, i, a[i] [n+1] ); printf ( “ ---\n\n”); exit(0);

}

void gauss (n, a) int n; double a[ ] [11]; {

int i, j, jc, k, kc, nv, pv; r, temp, tm, va;

for ( i = 1; i < =(n-1); i++){

for (jr = i+1; jr<=n; jr++){ /* eliminasi dibawah diagonal */ if ( a[jr][i] ! = 0 ) {

r = a[jr][i] / a[i][i];

for (kc = i + 1; kc<= (n+1); kc++){ temp = a[jr][kc];

(9)

55

}

} }

for ( i=1; i<=n; i++){ /* subtitusi balik */ a[n][n+1] = a[n] [n+1]/a[n][n]; for ( nv=n– 1; nv >=1; nv– – ){

va = a[nv][n+1];

for ( k=nv+1; k <= n; k++) { va=va– a[nv][k]*a[k][n+1]; }

a[nv][n+1] = va/a[nv][nv]; }

return; }

}

Hasil program Elemen matriks

0.00000e+00 – 1.0000e+00 2.00000e+00 0.00000e+00 – 2.00000e+00 2.00000e+00 – 1.00000e+00 0.00000e+00

– 2.00000e+00 4.00000e+00 3.00000e+00 1.00000e+00

Solusi

---

I x[i]

---

1 2.187500e+00

2 1.750000e+00

3 1.250000e –01

---

3.2 Metode Gauss-Seidel

Dalam sub-bahasan ini akan dibahas metode penyelesaian sistem persamaan

linear secara tak langsung atau iteratif. Metode perhitungan secara langsung sudah

dibahas dalam sub-bahasan di depan, yaitu eliminasi Gauss. Metode Gauss-Seidel

adalah metode iteratif yang secara luas telah digunakan sebagai alternatif metode

eliminasi.

Tinjau satu set dari n persamaan: [A]{X}={B}, dengan asumsi merupakan

persamaan 3x3. Jika elemen diagonal tidak nol dan nilainya tidak diketahui,

persamaan pertama bisa diselesaikan sebagai x1, persamaan kedua sebagai x2 dan

(10)

56

11

3 13 2 12 1 1

a

x a x a b

x

=

−

(3.12a)

22

3 23 1 21 2 2

a

x a x a b

x

=

−

(3.12b)

33

2 32 1 31 3 3

a

x a x a b

x

=

−

(3.12c)

Tahap selanjutnya dimulai proses penyelesaian dengan memilih nilai coba

untuk x. Langkah sederhana untuk menentukan nilai coba dengan mengasumsikan

bahwa semua nilai awal adalah nol. Jika disubtitusikan pada persamaan (3.12a),

maka didapatkan nilai baru untuk x1=b1/a11. Kemudian kita subtitusikan nilai baru x1

dan nilai awal bernilai nol untuk x3 pada persamaan (3.12b) untuk menghitung nilai

baru x2. Proses diulang pada persamaan (3.12c) untuk mendapatkan nilai baru x3.

Kemudian kembali diulang untuk persamaan dan prosedur berulang sampai

penyelesaian konvergen cukup rapat untuk nilai kebenaran. Konvergensi bisa dicek

menggunakan kriteria

s j

i j i j i i

a e

x x x

e

=

−

<

− % 100 1

,

untuk semua i, dimana j dan j– 1 adalah iterasi saat itu dan sebelumnya.

Contoh 3.4

Pandang suatu sistem persamaan

4 , 71 10

2 , 0 3 , 0

3 , 19 3

, 0 7 1 , 0

85 , 7 2 , 0 1

, 0 3

3 2

1

3 2

1

3 2

1

=

+

−

=

−

+

=

−

+

−

x x x

x x

x

x x

x

(3.15)

solusi acuan yang benar adalah x1=3, x2=– 2,5 dan x3=7

Solusi

pertama, selesaikan setiap persamaan untuk diagonal yang belum diketahui

3 2 , 0 1 , 0 85 ,

7 ₂ ₃

1

x x

x

=

+

(3.13a)

7

3 , 0 1 , 0 3 ,

19 ₁ ₃

2

x x

(11)

57

10

2 , 0 3 , 0 4 ,

71 ₁ ₂

3

x x

x

=

−

+

(3.13c)

dengan asumsi x2 dan x3 adalah nol, maka (3.13a) menjadi

616667 , 2 3

0 0 85 , 7

1

=

+

=

x

nilai ini dan asumsi x3=0, disubtitusikan pada (3.12b) memberikan hitungan

794524 , 2 7

0 ) 616667 , 2 ( 1 , 0 3 , 19

2

=

−

+

−

=

x

iterasi pertama dilengkapi dengan subtitusi hasil perhitungan nilai x1 dan x2 ke

dalam persamaan (3.12c) berikut

005610 , 7 10

) 794524 , 2 ( 2 , 0 ) 61667 , 2 ( 3 , 0 4 , 71

3

=

−

+

−

=

x

Untuk iterasi kedua, proses yang sama berulang dan memberikan hasil berikut:

990557 , 2 3

) 005610 , 7 ( 2 , 0 ) 794524 , 2 ( 1 , 0 85 , 7

1

=

+

−

+

=

x e_t

=

0,31%

499625 , 2 7

) 005610 , 7 ( 3 , 0 ) 990557 , 2 ( 1 , 0 3 , 19

2

=

−

+

−

=

x e_t

=

0,015%

000291 , 7 10

) 499625 , 2 ( 2 , 0 ) 990557 , 2 ( 3 , 0 4 , 71

3

=

−

+

−

=

x e_t

=

0,042%

metode ini, lebih jauh, konvergen pada nilai benar. Kelanjutan iterasi akan

memberikan jawaban yang lebih tepat.

Algoritma Gauss-Seidel

Pseudocode untuk implementasi metode Gauss-Seidel disajikan dibawah ini:

SUBROUTINE Gseid(a,b,n,x,imax,es,lambda) DO i=1,n

dummy =ai,i

DO j=1, n

ai,j=ai,j /dummy

END DO bi=bi /dummy

END DO DO i=1,n

sum= bi

(12)

58

IF i≠j THEN sum=sum–ai,j.xj

END DO xi=sumj

END DO iter=1 DO

sentinel=1 DO i=1,n

old=xi

sum=bi

DO j=1,n

IF i≠j THEN sum=sum– ai,j.xj

END DO

xi=lambda*sum+(1,–lambda)*0ld

IF sentinel= 1 AND xi ≠ 0. THEN ea=ABS((xi–old)/xi)*100.

IF ea>es THEN sentinel=0 END IF

END DO iter=iter+1

IF sentinel=1 OR (iter ≥ imax) EXIT END DO

END Gseid

3.3 Matriks spesial Tridiagonal & Nilai Eigen

Banyak masalah terapan melibatkan matriks dengan kebanyakan elemennya

nol. Salah satu bentuk matriks yang elemen nolnya berpola adalah matriks pita

(banded matrix). Lebar pita adalah maksimum banyaknya elemen taknol pada

baris-baris suatu matriks pita. Matriks pita yang terkecil adalah yang lebar pitanya tiga

atau dikenal sebagai matriks tridiagonal, seperti ditunjukkan pada persamaan (3.12)

sebagai Sistem linear tridiagonal NxN.

(13)

59













− − −

N N

N N N

f e

g f

e g

f e

g f e

g f

1 1

1 3

3 3

2 2 2

1 1

.. .. ..





















−

N N

x x

x x x

1 3 2 1

. . .

=





















−

N N

r r

r r r

1 3 2 1

. . .

(3.12)

Jika eliminasi Gauss langsung diterapkan pada sistem (3.12) maka banyak

operasi yang sebenarnya tidak perlu dilakukan. Agar metode lebih efisien diperlukan

modifikasi. Pivoting tidak diperlukan, karena pada umumnya persamaan (3.12) yang

dijumpai dalam praktek bersifat dominan secara diagonal. Setelah eliminasi akan

dihasilkan matriks bidiagonal atas.

Beberapa metode bisa digunakan untuk menyelesaikan sistem tridiagonal,

diantaranya adalah Secant, Gauss Seidel dan lainnya tergantung dari korelasi

perilaku elemen matriks tridiagonal. Di fisika seringkali dijumpai kasus penyelesaian

nilai eigen dan fungsi eigen dari suatu fungsi keadaan. Akhir bahasan pada studi

kasus akan disinggung tentang nilai eigen dan fungsi eigen untuk partikel yang

berada dalam sumur potensial.

Metode yang efisien untuk menyelesaikan sistem tridiagonal diantaranya

adalah algortima Thomas (Thomas Algorithm). Seperti pada dekomposisi konvensial

LU, algoritma terdiri dari tiga langkah yaitu dekomposisi, subtitusi maju dan

subtitusi balik.

Berikut ini adalah algoritma Thomas:

(a) Dekomposisi DO k=2,n

ek=ek/fk–1 fk=fk –ek.gk – 1 END DO

(b) Subtitusi Maju DO k=2,n

rk=rk–ek.rk– 1 END DO

(14)

60

xk=(rk– gk.xk+1)/fk END DO

Contoh 3.4

Selesaikan sistem tridiagonal berikut dengan algoritma Thomas













−

04 , 2 1 1 04 , 2 1 1 04 , 2 1 1 04 , 2

=





















4 3 2 1 T T T T





















8 , 200 8 , 0 8 , 0 8 , 40 (3.13) Solusi

Pertama, dekomposisi diimplementasikan sebagai berikut

323 , 1 ) 1 )( 717 , 0 ( 04 , 2 717 , 0 395 , 1 / 1 395 , 1 ) 1 )( 645 , 0 ( 04 , 2 645 , 0 550 , 1 / 1 550 , 1 ) 1 )( 49 , 0 ( 04 . 2 49 , 0 04 , 2 / 1 4 4 3 3 2 2

=

−

=

−

=

−

=

−

=

−

=

−

=

−

=

−

=

−

=

f e f e f e

kemudian matriks bertransformasi menjadi













−

323 , 1 717 , 0 1 395 , 1 645 , 0 1 550 , 1 49 , 0 1 04 , 2

dan dekomposisi LU memberikan

] ][ [ ]

[A

=

L U =













−

1 717 , 0 1 645 , 0 1 49 , 0 1













−

323 , 1 1 395 , 1 1 550 , 1 1 04 , 2

Subtitusi maju me mberikan perhitungan:

(15)

61

dan modifikasi vektor





















996 , 210

221 , 14

8 , 20

8 , 40

yang kemudian digunaka n dalam konjungsi dengan matriks U dalam subtitusi balik

dan memberikan solusi,

970 , 65 040 , 2 / ] 778 , 93 ) 1 ( 800 , 40 [ 1

778 , 93 550 , 1 / ] 538 , 124 ) 1 ( 800 , 20 [ 2

538 , 124 395 , 1 / ] 48 , 159 ) 1 ( 221 , 14 [ 3

480 , 159 323 , 1 / 996 , 210 4

=

−

=

−

=

−

=

T T T T

Jawaban dari algoritma Thomas ini bisa dicek dengan menggunakan software

komputasi populer, dalam hal ini dipilih MATLAB (MATrix LABoratory) sebagai

fasilitas manipulasi matriks, dan sistem tridiagonal pada persamaan (3.13)

diselesaikan dengan sangat akurat, seperti pada gambar 3.1.

Gambar 3. 1 proses MATLAB dalam menyelesaikan sistem tridiagonal

(16)

62

Arus dan Tegangan dalam Rangkaian Resistor

Untuk menentukan besar arus dan tegangan pada rangkaian kombinasi

resistor, digunakan kaidah Kirchoff tentang arus dengan formulasi:

∑

i

=

0 dan

kaidah Kirchoff tentang tegangan dalam loop:

∑ ∑

ξ

−

iR

=

0, dimana ξ adalah

gaya gerak listrik dari sumber tegangan.

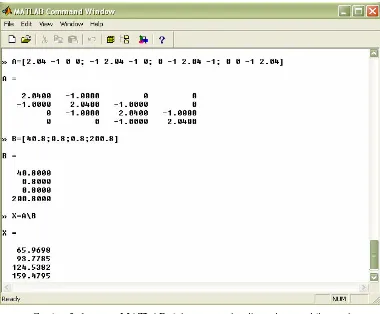
Tinjau rangkaian pada gambar 3. 2. Arus dalam rangkaian belum diketahui

baik besar maupun arahnya.Bukan menjadi persoalan yang rumit karena dengan

asumsi yang sederhana, arah dicari pada tiap aliran arus. Jika hasil dari kaidah

Kirchoff negatif, maka asumsi arah tentunya diperbaiki.

[a] [b]

Gambar 3. 2 [a] Rangkaian resistor dievaluasi dengan persamaan linear simultan, dan [b] Asumsi arah arus

Berdasarkan asumsi pada gambar 3.2 [b], kaidah Kirchoff tentang arus pada

setiap node memberikan:

0 0

43 54

32 43

54 52 65

32 52 12

=

−

=

−

=

−

=

+

i i

i i i

(3.14)

dan kaidah tegangan pada 2 loop adalah:

0 200

0

12 12 52 52 65 65

52 52 32 32 43 43 54 54

=

−

+

−

=

+

−

R i R i R i

R i R i R i R i

(3.15)

Lebih lanjut sejumlah permasalahan diselesaikan dengan enam set persamaan dimana

terdapat enam besaran arus yang tidak diketahui, seperti terlihat pada pemodelan

10 Ω 10 Ω

5 Ω

20 Ω 15 Ω 5

2 3

4

1

6 5 Ω

V6=0 V V1=200 V

6

i52 i32

i43

i65 i54

5 2 3

4

1

(17)

63

matriks. Disamping tidak praktis diselesaikan dengan tangan, sistem ini amat mudah

ditangani dengan metode eliminasi.





















=





































−

200 0 0 0 0 0

0 0 20 0

10 5

5 15 0

10 10

0

1 1 0 0 0 0

1 0 0 1 0

0

0 1 1

0 1 0

0 0 0 1 1 1

43 54 65 32 52 12

i i i i i i

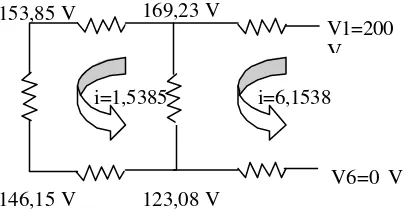
Selanjutnya dalam kasus ini, solusi didapatkan:

1538 , 6 1538 , 6

65 12

−

=

i i

5385 , 1

6154 , 4

54 52

−

=

−

=

i i

5385 , 1

43 32

−

=

−

=

i i

besar dan arah arus dan tegangan pada node dan loop ditunjukkan pada gambar

dibawah:

Gambar 3. 3 Besar dan arah arus dan tegangan pada rangkaian resistor

Lebih lanjut, dengan menggunakan algoritma komputasi numerik dan

pemrograman komputer, tipe kasus seperti ini menjadi lebih sederhana.

Nilai Eigen dan Fungsi Eigen pada Sumur Potensial

Solusi Persamaan Schrodinger Dimensi Satu dalam sistem Kuantum

153,85 V

146,15 V

i=6,1538

123,08 V 6 169,23 V

V6=0 V V1=200 V

(18)

64

Persamaan Schrodinger tak

tergantung waktu menjadi acuan dalam

kasus ini.

0 ) ( ) ( 2 ) ( 2 2

=

−

+

∂

x V E m

x x

ψ

h

(3.16)

dimana

ψ

(x) adalah fungsi eigen, dan

E adalah nilai eigen.

Dilakukan normalisasi de ngan

mensubtitusikan:

2 2

2 ,

2mb V v mb E

h

=

= λ

dan x =by,

maka diperoleh

0 ) ( ) ( ) ( 2 2

=

−

+

∂

y v y

y

ψ

λ

ψ

(3.17)

dengan mengubah persamaan (3.17) ke dalam bentuk komputasi numerik,

memberikan persamaan iterasi berikut:

0 2

)

( ₁ ₁ ₂

2

−

+

=

+

λ

ψ

_o h v (3.18)

0 2

)

( ₂ ₂ ₃

2

1

+

λ

−

ψ

+

ψ

=

ψ

h v (3.19)

dan seterusnya hingga

0 2

)

( ₁ ₁

2

+

−

+

=

− n n n

n h

λ

v

ψ

(3.20)

dimana v1 adalah potensial di titik i.

Dengan menerapkan syarat batas

ψ

_o

=

0 pada x=– b atau y=–1 dan

ψ

_n

=

0 pada x=b atau y=1,

maka didapatkan bentuk lain dari persamaan (3.18), (3.19) dan (3.20) yaitu sistem

tridiagonal sebagai berikut,

V=∞ V=∞

Vo

(19)

65













−

− −

2 ) (

1

1 2

) (

1

.. ..

..

1 2 ) (

1

1 2

) ( 1

1 2

) (

1 2

2 2

3 2 2

2 1

2

n n

v h

v h v

h v

h

λ

(3.21)

dengan matriks fungsi sebagai berikut :





















− −

1 2 3 2 1

.

n n

ψ

(3.22)

Perkalian matriks koefisien dalam sistem tridiagonal dengan matriks fungsi sama

dengan nol.

Penyelesaian matriks diatas akan trivial jika determinan matriks paling kiri

tidak sama dengan nol. Agar tidak trivial maka determinan tidak boleh sama dengan

nol. Determinan matriks dapat dihitung dengan cara membuat sub-sub determinan

yang dihitung sebagai berikut:

2 )

( ₁

2

1

=

h

−

v

−

P

λ

(3.23)



2( ₂) 2



. ₁ 1

2

=

h

−

v

−

P

−

P

λ

(3.24)

dan seterusnya hingga diperoleh aturan umum untuk mencari setiap sub determinan

ini, yaitu





1 2 2

. 2 )

(

−

₋

−

₋

=

n n n

n h v P P

P

λ

(3.25)

Sehingga determinan keseluruhan dari matriks pada persamaan (3.21) adalah

C

1

0 −

=

n Pi

P (3.26)

Persamaan (3.26) ini merupakan polinom sehingga untuk menyelesaikannya dapat

(20)

66

didapat nilai-nilai λ yang memenuhi persamaan (3.26). Adapun metode Secant dalam

formula iteratifnya adalah

) ( ) ( ) (

1 1 1

− −

+

=

−

i i

i i i i i

P P

P

λ

(3.27)

Nilai-nilai

λ

yang diperoleh dari persamaan (3.27) merupakan nilai-nilai

eigen dari partikel-partikel pada kasus sumur potensial. Untuk setiap nilai

λ

disubtitusikan ke matriks (3.21), dan dengan menggunakan metode Gauss Seidel bisa

diperoleh fungsi eigen gelombang untuk

λ

terkait. Adapun subtitusi nilai awal untuk

metode Gauss Seidel (sebagaimana lazimnya metode Gauss Seidel) diberikan nilai –1 dan seterusnya, hingga akhirnya diperoleh satu buah nilai coba yang dapat memberikan nilai fungsi-fungsi gelombang yang ternornalkan.

Dengan demikian proses penyelesaian secara komputasi numerik memenuhi persyaratan penyelesaian sebagaimana penyelesaian analitik untuk persamaan Schrodinger.

D. SOAL_SOAL

(3.1) Selesaikan sistem segitiga atas berikut ini:

15 5

15 3

2

3 2

4

8 2

3

4 4 3

4 3 2

4 3 2 1

=

+

−

=

+

−

=

−

+

−

x x x

x x x x

6 3

10 2

3 2

0 7 2 6 2

4 2

2 4

5 5 4

5 4 3

5 4 3 2

5 4 3 2 1

=

−

=

−

=

+

−

=

−

+

−

x x x

x x x x

x x x x x

(3.2) Carilah parabol y=A+Bx+Cx2 yang melalui tiga titik:

(1,4), (2,7) dan (3,14)

(3.3) Menggunakan eliminasi Gauss dengan pivoting selesaikan sistem persamaan

linear berikut:

5 2 3

10 3

5

4 6

4 2

3 2 1

=

+

=

+

−

=

−

+

x x x

(3.4) Mulai dengan semua nila i awal nol gunakan iterasi Gauss-Seidel

(21)

67

3 4

11 8

2

10 5

=

+

−

=

−

+

=

+

−

z y x

Apakah iterasi Gauss Seidel akan konvergen ke selesaian?

(3.5) Buatlah program untuk studi kasus pertama dan kedua, dengan metode yang

dimaksud.

E. DAFTAR PUSTAKA

Chapra, S.C., and Canale, R.P., Numerical Methods for Engineers, McGraw-Hill,

1998

James, M.L., G.M. Smith, and J.C. Wolford, Applied Numerical Methods for Digital

Computations, 3rd ed. Harper & Row, 1985

Koonin, S.E., Computational Physics, Addison-Wesley Inc, 1986

Mathews, J.H., Numerical Methods for Mathematics, Science and Engineering,

Prentice -Hall Inc., 1992

McCracken, D. D., Computing for Engineers and Scientists with Fortran 77, Wiley,

1984

Morris,J.L., Computational Methods in Elementary Numerical Analysis, Wiley, 1983

Nakamura, S., Applied Numerical Methods in C, Prentice-Hall Inc. 1993

Yakowitz, S., and F. Szidarovszky, An Introduction to Numerical Computations,