DIKTAT GEOMETRI
DISUSUN UNTUK PERKULIAHAN GEOMETRI
PADA PROGRAM STUDI PENDIDIKAN MATEMATIKA
FKIP UNIVERSITAS SRIWIJAYA
PENYUSUN:
Nyimas Aisyah
UNIVERSITAS SRIWIJAYA
DAFTAR ISI A. Kedudukan Titik, Garis, dan Bidang dalam Ruang ... B. Proyeksi ... C. Jarak ... D. Sudut ... BAB V: IRISAN BIDANG ... A. Menggambar Irisan Bidang dengan Sumbu Afinitas ... B. Menggambar Irisan Bidang Menggunakan Perpotongan Bidang Diagonal C. Menggambar Irisan Bidang Menggunakan Perluasan Bidang Sisi
BAB 1
LUKISAN DASAR
A. MELUKIS SUDUT
1. Melukis Sudut yang Sama Dengan Sudut yang Diketahui
Untuk melukis suatu sudut yang besarnya sama dengan sudut lain dapat ditempuh dengan beberapa cara. Salah satu cara yang paling mudah adalah dengan mengukur sudut yang diketahui dengan menggunakan busur derajat. Namun cara ini kurang tepat terutama apabila pengukurannya kurang teliti. Agar hasil yang diperoleh lebih baik, maka alat bantu yang digunakan sebaiknya adalah jangka dan mistar. Adapun langkah-langkah untuk melukis sudut yang sama dengan sudut yang diketahui adalah sebagai berikut.
Diketahui: Sudut A
Lukislah: Sudut B = sudut A
Langkah-langkah melukis:
1. Buat busur lingkaran dengan titik pusat A memotong kedua kaki sudut di C dan D.
Pindahkan busur itu di B memotong garis l di titik E.
2. Buat busur lingkaran dengan titik pusat C melalui titik D. Pindahkan busur itu pada titik
E, sehingga memotong busur pertama tadi di titik F.
3. Tarik garis m memotong titik B dan titik F. Garis l dan m adalah kaki sudut. Sudut B
2. Melukis Sudut-sudut Istimewa
Untuk melukis sudut-sudut istimewa, sebenarnya Anda dapat menggunakan penggaris dam busur. Namun untuk mendapatkan hasil yang lebih baik lagi, Anda dapat menggunakan penggaris dan jangka. Adapun langkah-langkah untuk melukis sudut-sudut istimewa tersebut adalah sebagai berikut.
(a) Sudut 90o (Sudut Siku-siku)
Diketahui: garis l dan titik A
Lukislah: Sudut A = 90o
Langkah-langkah melukis (Cara I):
1. Buat busur lingkaran dengan titik pusat A memotong garis l di B.
2. Pindahkan busur itu ke titik B sehingga memotong busur pertama di C.
3. Pindahkan busur itu ke titik C sedemikian hingga memotong garis yang ditarik melalui titik B dan C di titik D.
4. Tarik garis m melalui A dan D, maka didapatlah sudut A = 90o (siku-siku).
Langkah-langkah melukis (Cara II):
1. Buat lingkaran sembarang yang memotong garis l di titik A dan B.
2. Tarik garis tengah lingkaran itu melalui titik B dan memotong lingkaran di C
Langkah-langkah melukis (Cara III):
1. Buat busur lingkaran dengan pusat titik A hingga memotong garis l di B dan C.
2. Buat busur lain dengan pusat di titik B
3. Pindahkan busur itu ke titik C hingga keduanya berpotongan di D.
4. Tarik garis m melalui A dan D, maka didapatlah sudut A = 90o (siku-siku).
(b) Sudut 60o
Diketahui: garis l dan titik A pada l.
Lukislah: sudut A = 60o
Langkah-langkah melukis:
1. Buat busur sembarang dengan titik pusat A dan memotong garis l di B.
2. Pindahkan busur itu ke titik B dan memotong busur pertama di C.
3. Tarik garis m melalui A dan C, maka didapat sudut A = 60o.
(c) Sudut 45o
Diketahui: garis l dan titik A pada l.
Lukislah: sudut A = 45o
Langkah-langkah melukis:
1. Ambil titik B sembarang pada garis l.
2. Buat garis t tegak lurus l melalui B
4. Tarik garis m melalui A dan C, maka didapat sudut A = 45o.
(d) Sudut 30o
Diketahui: garis l dan titik A pada l.
Lukislah: sudut A = 30o
Langkah-langkah melukis:
1. Buat busur sembarang dengan titik pusat A dan memotong garis l di B.
2. Pindahkan busur itu ke titik B dan memotong busur pertama di C.
3. Pindahkan lagi busur itu ke titik C hingga memotong busur kedua di D
4. Tarik garis m melalui A dan D, maka didapat sudut A = 30o.
Latihan
1. Lukislah dengan cermat ketiga garis tinggi segitiga lancip.?
2. Lukislah sudut yang sama besar dengan sudut-sudut di bawah ini.
(a) (b) B
A
B. MELUKIS GARIS
1. Melukis Sebuah Garis Tegak Lurus
Untuk melukis sebuah garis tegak lurus dengan garis lain yang melalui titik di luar garis lain itu sebenarnya dapat Anda lakukan dengan menggunakan sepasang penggaris siku-siku saja. Namun untuk mendapatkan lukisan yang lebih baik, Anda dapat menggunakan satu penggaris dan jangka. Adapun langkah-langkah untuk melukis garis tegak lurus dengan menggunakan jangka adalah sebagai berikut.
Diketahui: garis l dan titik A di luar garis l.
Lukislah: garis m l melalui A
Langkah-langkah melukis:
1. Buat busur sembarang dengan pusat A hingga memotong garis l di B dan C.
2. Pindahkan busur itu ke B dan C sehingga didapat perpotongan busur di D.
3. Tarik garis melalui A dan D, maka didapat garis m garis l.
2. Melukis Dua Garis yang Saling Sejajar
Untuk melukis dua garis yang sejajar dengan garis lain melalui yang diketahui sebenarnya dapat Anda lakukan dengan menggunakan sebuah penggaris siku-siku dan sebuah penggaris biasa. Namun untuk mendapatkan lukisan yang lebih baik, Anda dapat menggunakan satu penggaris dan jangka. Adapun langkah-langkah untuk melukis dua garis yang saling sejajar dengan menggunakan jangka adalah sebagai berikut.
Diketahui: garis l dan titik A di luar garis l.
Langkah-langkah melukis:
1. Buat garis sembarang melalui A dan memotong garis l di B.
2. Lukis sudut dengan A sebagai titik sudut yang besarnya sama dengan sudut B dan
berseberangan dengannya.
3. Didapatlah garis m // l
3. Melukis Sebuah Garis Bagi Sudut
Garis Bagi Sudut adalah garis yang ditarik dari salah satu titik sudut dan membagi sama besar sudut tersebut. Adapun langkah-langkah melukis garis bagi sudut tersebut adalah sebagai berikut.
Diketahui: sudut A
Lukislah : garis bagi sudut A
Langkah-langkah melukis:
1. Lukis busur lingkaran dengan pusat A dan jari-jari r1, sehingga busur tersebut memotong
kaki-kaki sudut A di titik B dan C.
2. Lukis busur lingkaran dengan pusat B dan C, jari-jari r2, sehingga kedua busur
berpotongan di titik D.
4. Melukis Garis Sumbu Sebuah Ruas Garis
Garis Sumbu sebuah ruas garis adalah garis tegak lurus terhadap ruas garis yang diketahui dan memotong sama panjang ruas garis diketahui tersebut. Untuk melukis sumbu ruas garis ini diperlukan penggaris dan mistar, dengan langkah-langkah sebagai berikut.
1. Diketahui ruas garis AB
2. Lukis dua busur lingkaran masing-masing di atas dan di bawah ruas garis AB dengan
pusat A dan jari-jari r.
3. Dengan cara yang sama lukis pula dua busur lingkaran dengan pusat B dan jari-jari r,
sehingga busur yang terletak di atas ruas garis AB berpotongan di titik K dan busur yang terletak di bawah ruas garis AB berpotongan di titik L.
4. Hubungkan K dan L, maka didapat garis KL yang merupakan sumbu ruas garis AB.
5. Membagi Ruas Garis Menjadi n Bagian yang Sama Panjang
Untuk menjamin ketepatan pembagian garis menjadi n bagian yang sama panjang, maka sebaiknya digunakan penggaris dan jangka. Adapun langkah-langkah membagi ruas garis tersebut adalah sebagai berikut.
Diketahui: garis AB
Lukislah : pembagian AB menjadi 5 bagia yang sama panjang
Langkah-langkah melukis:
1. Buatlah garis g sembarang melalui salah satu ujung ruang garis AB (misalkan di A)
dengan membentuk sudut tertentu (tidak nol) dengan AB.
2. Dengan menggunakan jangka, lukiskan pada garis g titik C, D, E, F, G sedemikian
3. Hubungkan B dan G.
4. Lukiskan garis-garis sejajar GB, yang masing-masing melalui titik-titik C, D, R, F.
Misalkan garis-garis ini memotong AB berturur-turut di K, L, M, dan N.
5. Maka didapatlah pembagian AB menjadi 5 bagian yang sama panjang.
Latihan
Kerjakan latihan berikut ini!
1. Bagilah garis AB = 6 cm menjadi 6 bagian yang sama panjang.
2. Lukislah garis berat melalui A dan garis bagi melalui B pada Δ ABC tumpul.
3. Lukislah sudut 15o
4. Lukislah belahketupat PQRS, dengan ketentuan sebagai berikut.
a. Salah satu diagonal belahketupat adalah garis g
b. Titik P di luar g
c. P merupakan salah satu titik sudut belahketupat.
C. MELUKIS SEGITIGA
Untuk melukis segitiga yang diketahui unsur-unsurnys tidak dapat hanya dengan menggunakan penggaris saja. Anda mungkin tidak akan mengalami kesulitan untuk mengukur sisi pertama dan kedua, tetapi akan mengalami kesulitan pada saat melukis sisi yang ketiga segitiga sesuai dengan ukuran yang ditetapkan. Oleh karena itu penggunaan penggaris dan jangka menjadi keharusan.
1. Melukis Segitiga Jika Diketahui Sisi-sisinya
Diketahui: ruas garis a, b, c
Lukislah : segitiga yang sisi-sisisnya a, b, c
Langkah-langkah melukis:
1. Buat ruas garis a = BC
2. Buat busur lingkaran dengan pusatnya salah satu ujung garis a jari-jarinya = b.
3. Buat busur lingkaran dengan jari-jari c dan pusatnya terletak pada ujung lain garis a.
4. Kedua busur tadi berpotongan di A.
5. Maka didapat Δ ABC dengan sisi-sisi a, b, c.
2. Melukis Segitiga Jika Diketahui Sisi, Sudut, Sisi
Diketahui: ruas garis a, sudut α, dan ruas garis b
Lukislah : segitiga
Langkah-langkah melukis:
1. Buat ruas garis b = AB
2. Ukur sudut α pada titik B
3. Melukis Segitiga Jika Diketahui Sudut, Sisi, Sudut
Diketahui: sudut α, ruas garis a, dan sudut β
Lukislah : segitiga
Langkah-langkah melukis:
1. Buat ruas garis a = BC
2. Dengan menggunakan busur derajat, ukur sudut α dengan A sebagai titik sudut dan ukur
sudut β dengan dan B sebagai titik sudut.
3. Dari pengukuran sudut α dan β didapat dua garis yang berpotongan di C.
4. Maka didapat Δ ABC.
4. Melukis Segitiga Jika Diketahui Sisi, Sisi, Sudut
Diketahui: ruas garis a, b dan sudut α
Lukislah : segitiga
Langkah-langkah melukis:
3. Gambar busur lingkaran dengan pusat B dan jari-jari r, sehingga meotong kaki sudut C di titik A (Selain A ada titik lain, makakah itu?)
4. Tarik garis BA, maka didapat Δ ABC.
Lukisan (Silahkan Anda coba!)
Latihan
Kerjakan latihan berikut ini!
1. Lukislah Δ ABC, jika diketahui AB = 6 cm, ABC = 75o dan BC = 7,5 cm.
2. Lukislah segitiga siku-siku samakaki dengan panjang kakinya 5 cm
3. Lukislah segitiga samasisi dengan panjang sisi 6 cm.
4. Lukislah Δ ABC, jika diketahui AB = 7 cm, BC = 3 cm, dan BCA = 100o
5. Lukislah Δ ABC, jika diketahui ABC = 60o, BC = 4 cm, dan BCA = 95o.
6. Lukis suatu Δ ABC jika diketahui
a. panjang alasnya AB adalah a satuan
b. tinggi dari titik C ke AB adalah t satuan
c. panjang salah satu kaki (BC) adalah b satuan
7. Lukis suatu Δ ABC jika diketahui
a. panjang alasnya AB adalah a satuan
b. panjang garis tinggi dari C sama dengan t satuan
c. besar sudut puncak C adalah α
8. Hidayat melakukan permainan pada suatu kegiatan pramuka. Hidayat harus menemukan
D. MELUKIS BANGUN RUANG
Bangun ruang dapat dilukiskan pada bidang datar. Untuk mendapatkan hasil lukis yang proporsional ada beberapa langkah dan istilah yang diperlukan. Istilah-istilah tersebut adalah sebagai berikut.
1. Bidang frontal adalah bidang gambar.
2. Bidang ortogonal adalah bidang yang tegak lurus dengan bidang frontal.
3. Garis frontaladalah garis yang terletak pada bidang frontal.
4. Garis ortogonal adalah garis yang tegak lurus terhadap bidang frontal.
5. Sudut surutadalah sudut antaraa bidang frontal dan ke arah kiri ke bidang ortogonal.
6. Perbandingan proyeksi adalah perbandingan panjang garis pada lukisan dengan
panjang garis yang sebenarnya.
Sedangkan langkah-langkah untuk melukiskan kubus adalah sebagai berikut.
1. Lukis bidang frontal dengan ukuran yang sebenarnya.
2. Cari panjang salah satu garis ortogonal dengan menggunakan perbandingan proyeksi.
3. Pada bidang frontal, tentukan titik yaang menjadi titik pertemuan antara garis frontal
dengan garis ortogonal.
4. Dengan menggunakan sudut surut dan ukuran garis ortogonal (langkah 2), buat garis
ortogonal.
5. Buat garis ortogonal lain.
6. Hubungkan titik-titik ujung dari garis ortogonal.
Contoh:
Lukislah kubus ABCD.EFGH dengan panjang rusuk 4 cm. Perbandingan proyeksinya ⅓, dan
sudut surutnya 450 serta bidang ABFE sebagai bidang frontalnya.
Langkah-langkah melukiskan kubus ABCD.EFGH di atas sebagai berikut.
1. Buat bidang frontal, yaitu bidang ABFE dengan ukuran 4 cm x 4 cm.
2. Salah satu garis ortogonal adalah AD, dengan panjang AD yang sebenarnya 4 cm.
Panjang AD pada lukisan = ⅓ x 4 cm = 1⅓ cm.
3. Titik A adalah titik pertemuan antara garis frontal AB dangaris ortogonal AD.
Pada titik A ini akan dibuat garis ortogonal dengan menggunakan busur derajat.
4. Letakkan titik tengah busur derajat berimpit dengan titik A.
Dari garis frontal AB, tentukan arah 450 berlawanan arah dengan jarum jam, beri tanda.
5. Buatlah garis ortogonal lainnya yaitu, EH, BC, dan FG dengan ukuran 1⅓ cm.
6. Hubungkan titik D dengan titik C, titik C dengan titik G, titik G dengan titik H, dan titik H dengan titik D, sehingga terbentuklah kubus ABCD.EFGH.
Contoh 2:
Diketahui kubus KLMN.PQRS berukuran 6 cm. Lukislah kubus tersebut dengan bidang LMRQ
sebagai bidang frontal, dengan perbandingan proyeksi ⅓ dan sudut surutnya 600.
Langkah-langkah melukis kubus KLMN. PQRS:
1. Bidang frontal adalah bidang ………., dengan ukuran ………….
2. Salah satu garis ortogonal adalah ……….. .
Panjang LK yang sebenarnya adalah ……….
Panjang LK pada lukisan adalah = ……..……..…….
3. Titik pertemuan garis frontal LM dengan gais orogonal LK adalah titik ……. .
4. Letakkan titik tengah busur berhimpit dengan titik …..
Dari garis frontal horizontal LM. Ditentukan arah ……. berlawanan arah dengan arah jarum jam, dan diberi tanda. Tarik garis dari titik L ke tampat yang telah diberi tanda tadi. Ukur dari titik L garis sepanjang 2 cm dan beri nama titik …… .
5. Buat garis ortogonal yang lain yang sejajar dengan LK yaitu:
1. Diketahui limas segiempat beraturan T.ABCD dengan ukuran alasnya 4 cm dan tinggi 6
cm. Titik K berada di tengah-tengah AD dan titik L berada di tengah-tengah BC. Bidang KLT sebagai bidang frontal, garis KL sebagai garis frontal horizontal dengan sudut surut
600 dan perbandingan proyeksinyaa ½. Lukislah limas tersebut.
2. Diketahui bidang empat beraturan T.ABC dengan TA = AB = 4 cm, D pertengahan
rusuk BC. Lukislah bidang empat tersebut dengan bidang TAD frontal, AD horizontal,
sudut surut 60o , dan perbandingan orthogonal
4 3
BAB 2
BANGUN RUANG
A.Bangun Ruang Sisi Datar
1. Macam-macam Bangun Ruang Sisi Datar a. Bangun Ruang Bidang Banyak
Suatu bangun ruang yang dibatasi oleh bidang-bidang datar disebut bidang banyak
(polihedron). Poligon yang membatasi polihedron ini disebut bidang sisi (permukaan). Segmen garis yang merupakan perpotongan dua bidang sisi disebut rusuk, dan titik ujung rusuk merupakan titik-titik sudut bangun ruang tersebut. Titik sudut merupakan titik persekutuan tiga atau lebih rusuk bangun ruang. Beberapa contoh bangun ruang bidang banyak ini adalah bidang empat (memiliki empat bidang batas), bidang enam (memiliki enam bidang batas), bidang dua belas (memiliki dua belas bidang batas), dan lain-lain. Perhatikan Gambar 4.1 berikut.
D
A C B
Gambar 4.1. Bidang Empat
Gambar 4.1 merupakan Bidang Empat ABCD. Bidang batasnya adalah ABC, ABD, BCD, dan ACD. Rusuknya adalah AB, BC, AC, AD, BD, dan CD Titik sudutnya adalah A, B, C, D.
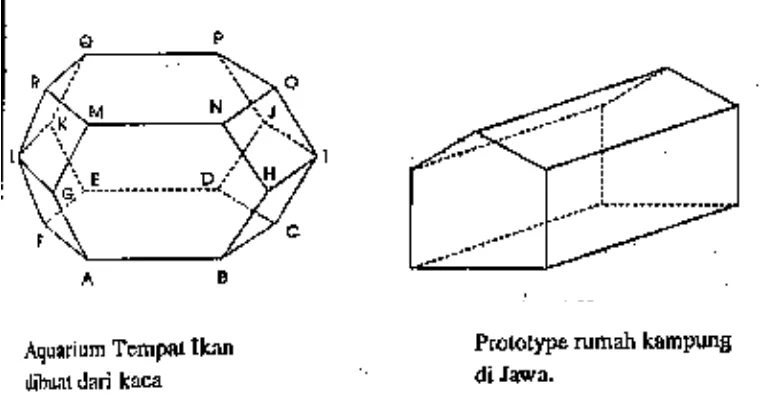
Gambar 4.2 adalah sketsa gambar aquarium terbuat dari kaca. Benda ini berbentuk bidang dua belas, karena memiliki 12 bidang batas berupa 8 persegi dan 4 segienam beraturan.
Gambar 4.3 adalah sketsa gambar rumah. Benda ini berbentuk bidang tujuh, karena memiliki 7 bidang batas berupa 5 persegi panjang dan 2 segilima.
Pada bagian selanjutnya akan dibahas lebih mendalam beberapa contoh bangun ruang bidang banyak seperti bidang banyak beraturan, prisma, limas, dan prismoide.
b. Bidang Banyak Beraturan
Bidang banyak ada yang dibatasi oleh satu macam segibanyak, tetapi ada juga yang dibatasi oleh beberapa macam segibanyak. Jika pembatas hanya terdiri dari satu macam segibanyak beraturan saja dan kongruen satu sama lain, maka bidang banyak ini dinamakan bidang banyak beraturan.
Bidang banyak beraturan adalah bangun ruang yang dibatasi oleh sejumlah poligon
beraturan kongruen yang sama pada setiap titik sudutnya. Karena pada setiap titik sudut bertemu
paling sedikit tiga rusuk, maka sudut poligon haruslah kurang dari 120o (Mengapa?). Berarti
poligon pembentuk yang mungkin hanya segitiga samasisi (3, 4, atau 5 segitiga samasisi pada setiap sudut). Dengan demikian hanya ada lima jenis bidang banyak beraturan yang dikenal
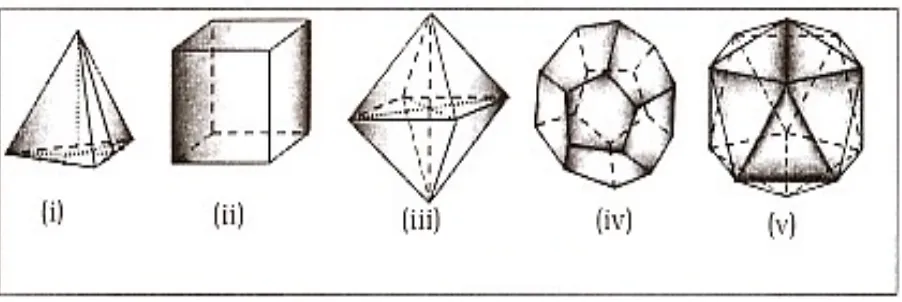
Gambar 4.4. Bidang Banyak Beraturan
a. Gambar 4.4. (i) adalah gambar bidang empat beraturan (tetraeder). Bangun ini
dibatasi oleh empat daerah/bidang segitiga kongruen. Pada setiap titik sudut terdapat tiga bidang segitiga samasisi dan tiga rusuk.
b. Gambar 4.4. (ii) adalah gambar bidang enam beraturan yang lebih dikenal
sebagai kubus (hexaeder). Bangun ini dibatasi oleh enam daerah persegi kongruen. Pada
setiap titik sudut terdapat tiga bidang persegi dan tiga rusuk.
c. Gambar 4.4. (iii) adalah gambar bidang delapan beraturan (octaeder). Bangun ini
dibatasi oleh delapan segitiga kongruen. Pada setiap titik sudut terdapat empat bidang segitiga samasisi, dan empat rusuk.
d. Gambar 4.4. (iv) adalah gambar bidang duabelas beraturan (icosaeder). Bangun
ini dibatasi oleh duabelas segilima. Pada setiap titik sudut terdapat tiga bidang segilima beraturan, dan tiga rusuk.
e. Gambar 4.4. (v) adalah gambar bidang duapuluh beraturan (dodecaeder).
Bangun ini dibatasi oleh duapuluh segitiga kongruen. Pada setiap titik sudut terdapat lima bidang segitiga samasisi, dan lima rusuk.
c. Prisma
Prisma adalah bidang banyak yang dibatasi oleh dua poligon yang sejajar dan
(i) (ii) (iii) (iv)
Gambar 4.5. Prisma
a. Gambar 4.5. (i) adalah gambar prisma miring. Bangun ini disebut prisma miring
karena rusuk tegaknya tidak tegak lurus bidang alas.
b. Gambar 4.5. (ii) adalah gambar prisma tegak. Bangun ini disebut prisma tegak
karena1 rusuk tegaknya tegak lurus bidang alas.
c. Gambar 4.5. (iii) adalah gambar prisma segi-n. Prisma ini memiliki sisi alas
berbentuk segi-n. Apabila alasnya berbentuk segi-n beraturan, maka disebut prisma segi-n beraturan.
d. Gambar 4.5. (iv) adalah gambar Parallelepipedum. Prisma ini alasnya berbentuk
jajargenjang. Jika alas parallelepipedum tegak berbetuk persegipanjang, maka disebut parallelepipedum siku-siku. Jika semua bidang sisi parallelepipedum siku-siku tersebut kongruen, maka disebut kubus. Parallelepipedum yang semua rusuknya sama panjang
disebut rhomboeder.
d. Limas
Limas atau piramid adalah bangun ruang yang dibatasi sebuah bidang datar atau
bidang alas yang berbentuk segi-n dan oleh bidang-bidang sisi tegak yang berbentuk segitiga. Garis alas segitiga itu berimpit dengan sisi-sisi segi-n dan titik puncak segitiga-segitiga itu bertemu atau berimpit di suatu titik Perhatikan Gambar 4.6 berikut.
Ditinjau dari bentuk alasnya, maka suatu limas dapat dibedakan menjadi:
1. limas segitiga, bidang alasnya berbentuk segitiga
2. limas segiempat, bidang alasnya berbentuk segiempat
3. limas segilima, bidang alasnya berbentuk segilima
Ditinjau dari teratur atau tidaknya bidang alas dan kedudukan titik puncak terhadap bidang sisi, maka suatu limas dapat dibedakan menjadi:
1. limas sembarang, yaitu apabila bidang alasnya berbentuk segi-n sembarang dan titik
puncaknya juga sembarang.
2. limas beraturan, yaitu apabila bidang alasnya berbentuk segi-n beraturan dan proyeksi
titik puncaknya berimpit dengan titik pusat bidang alas.
e. Prismoide
Prismoide adalah bangun ruang sisi datar yang dibatasi oleh dua bidang sejajar
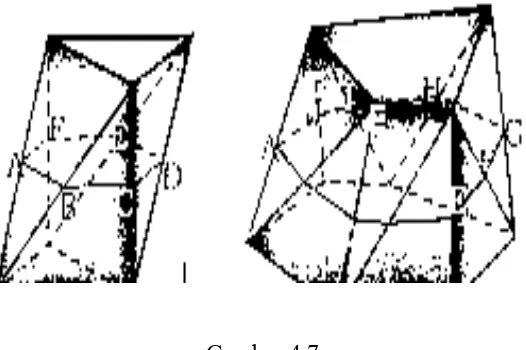
(bidang alas dan bidang atas) dan bidang-bidang segitiga atau trapesium sebagai bidang sisi tegak. Prisma dan limas terpancung merupakan bangun khusus prismoide. Perhatikan Gambar 4.7 berikut.
Gambar 4.7
2. JARING-JARING DAN LUAS BANGUN RUANG SISI DATAR
Secara sederhana, jaring-jaring sebuah bangun ruang dapat diperoleh apabila bangun
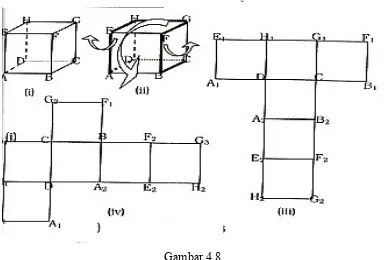
ruang tersebut diiris sepanjang rusuk-rusuk tertentu sedemikian hingga terbentang beberapa bidang datar pembentuknya. Perhatikan Gambar 4.8 berikut.
Gambar 4.8
Gambar 4.8 adalah gambar sebuah kubus yang diiris sepanjang rusuk yang dicetak tebal. Apabila direbahkan pada bidang datar, maka terjadilah jaring-jaring kubus seperti pada Gambar 4.8 (ii) dan 4.8 (iii). Masih sangat banyak model jaring-jaring kubus yang dapat dibuat sesuai dengan rusuk yang diiris. Begitu juga untuk bangun-bangun ruang sisi datar lainnya. Dari jaring-jaring bangun ruang ini, dengan mudah dapat ditentukan luas sisi bangun ruang tersebut. Hal ini karena luas sisi bangun ruang pada dasarnya sama dengan jumlah luas sisi-sisi dari bangun ruang yang dapat dihitung dari jaring-jaring kubus yang tersebut. Bagaimana jika bangun datar yang terbentuk tidak seluruhnya terdiri dari bangun-bangun datar yang dikenal, misalnya kotak kue yang berbentuk “love” yang sering digunakan untuk acara lamaran nikah.
3. VOLUM BANGUN RUANG SISI DATAR
dinamakan volum kubus/balok. Volum kubus/balok ini selanjutnya dapat digunakan untuk menentukan volum bangun-bangun ruang sisi datar lainnya.
a. Menentukan Volum Prisma
Balok adalah suatu prisma yang khusus. Dengan demikian, volum prisma dapat ditentukan dengan menggunakan volum balok. Hal ini dapat ditunjukkan dengan membagi suatu balok menjadi dua bagian yang volumnya sama (dibagi menurut salah satu bidang diagonalnya). Perhatikan Gambar 4.9 berikut.
= luas alas prisma ABD.EFH x tinggi prisma
Jadi, volum prisma ABD.EFH = luas alas x tinggi
Dengan cara mudah Anda juga dapat menentukan volum prisma segi-n tegak lainnya, karena prisma segi-n dapat dibentuk dari (n – 2) prisma segitiga tegak.
b. Menentukan Volum Limas
Untuk menentukan volum limas, dapat digunakan suatu kubus yang dibagi menjadi enam limas yang kongruen atau menggunakan prisma segitiga tegak yang dibagi menjadi tiga limas yang kongruen. Dengan memperhatikan kekongruenan dan prinsip dasar volum limas di atas,
tunjukkan bahwa volum limas = 13 x luas alas x tinggi.
c. Menentukan Volum Bangun Ruang dengan Prinsip Cavalleri.
Prinsip Cavalleri pertama kali diketemukan oleh Bonaventura Cavalleri, ahli matematika berkebangsaaan Italia. Berdasarkan prinsip Cavalleri:
“Jika dua benda tingginya sama dan bidang irisan mendatar pada ketinggian yang sama mempunyai luas yang sama, maka kedua benda tersebut mempunyai volum yang sama” Prinsip ini berlaku untuk semua bangun ruang termasuk bangun ruang sisi datar.
Gambar 4.10
Gambar 4.10 (i) adalah gambar sebuah prisma miring dan Gambar 4.10 (ii) adalah gambar prisma miring yang dipotong oleh irisan siku-siku (irisan yang tegak lurus rusuk tegaknya). Jika prisma bagian bawah irisan dipindahkan dan ditempatkan tepat di atas bagian atas irisan terjadilah bangun ruang baru seperti pada Gambar 4.10 (iii). Panjang rusuk tegaknya tidak berubah. Dengan demikian diperoleh:
Luas alas prisma miring = luas irisan siku-siku = luas alas prisma tegak Tinggi prisma miring = tinggi prisma tegak
Jadi : Volum prisma miring = Ls
x r
dengan Ls adalah luas irisan siku-siku dan r panjangrusuk tegak.
Latihan
Untuk soal nomor 1 – 10, pilih satu jawaban yang Anda anggap paling tepat!
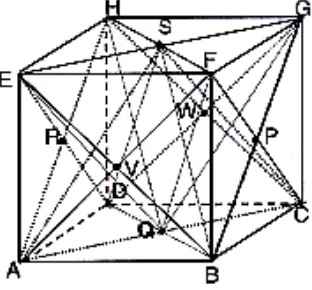
Untuk nomor 1 s.d 4, perhatikan Gambar di atas!
1. Pada kubus ABCD.EFGH di atas, limas G.ABD merupakan bidang empat ...
A. teratur
B. tegak
C. siku-siku
2. Salah satu bangun yang kongruen dengan G.ABD adalah ...
A. E.ABD
B. E.CBD
C. F.ABD
D. F.CBD
3. Bangun ACD.EGF pada kubus di atas merupakan bangun ...
A. prisma segitiga beraturan
B. prisma segitiga sembarang
C. bidang empat teratur
D. bidang empat sembarang
4. Volum bangun ABD.EFH pada soal nomor 4 adalah ... cm3
A. 500
6. Dari limas beraturan T.ABCD dibuat semua jaring-jaringnya. Banyaknya jaring-jaring yang satu sama lain berbeda adalah ……….
A. 6 B. 7 C. 8 D. 9
7.Sebuah limas yang alasnya berbentuk persegi mempunyai luas alas 100 cm2 dan tinggi
8.Diketahui prisma segitiga siku-siku dengan sisi-sisi 6 cm, 8 cm, dan 10 cm. Jika tinggi
prisma adalah 15 cm, maka volum prisma adalah ... cm3
A. 720
B. 360
C. 180
D. 120
9. Limas terpancung dengan alas berupa segitiga samasisi disebut ...
A. Bidang empat terpancung
B. Bidang empat beraturan terpancung
C. Bidang empat orthocentris terpancung
D. Bidang empat ortogonal terpancung
10. ABCD.EFGH adalah kubus dengan panjang rusuk 6 cm. Volum limas T.ABC adalah ... cm3
A. 216
B. 72
C. 36
D. 18
Untuk soal nomor 11, kerjakan dengan tepat dan jelas!
11. Perhatikan Gambar di bawah ini. Pertanyaan:
a. Apa nama bangun S.ABCD?
b. Sebutkan bangun yang
kongruen dengan S.ABCD!
c. Sebutkan nama bangun yang
berbentuk bidang empat!
d. Berapa luas permukaan dan
B. BANGUN RUANG SISI LENGKUNG
Jika sebuah bidang datar diputar mengelilingi suatu garis lurus yang termuat pada bidang itu, maka ruas garis yang terdapat dalam bidang itu akan membentuk suatu bidang lengkung yang disebut bidang putar. Jadi pada dasarnya bangun ruang sisi lengkung merupakan bangun yang terjadi apabila bangun datar diputar mengelilingi suatu garis lurus. Akibatnya sisi-sisi pembentuk bangun ruang sisi-sisi lengkung ini sebagian merupakan sisi-sisi lengkung. Hal inilah yang membedakan antara bangun ruang sisi datar dengan bangun ruang sisi lengkung. Namun secara umum sifat-sifat kedua bangun ruang ini adalah sama.
Oleh karena itu, agar materi bangun ruang sisi lengkung ini mudah Anda pahami, maka Anda dapat menggunakan materi bangun datar sisi datar sebagai referensi. Seperti pada bangun datar sisi datar, pembahasan tentang materi bangun ruang sisi lengkung akan diawali dengan mengenalkan macam-macam bangun ruang sisi lengkung tersebut, sebelum pembahahasan tentang luas dan volum.
1. MACAM-MACAM BANGUN RUANG SISI LENGKUNG a. Tabung
Jika persegi panjang ABCD diputar dengan AD sebagai sumbu putar, maka benda putar yang
terjadi disebut tabung. AD disebut poros (sumbu) tabung. Perhatikan Gambar 4.11
berikut.
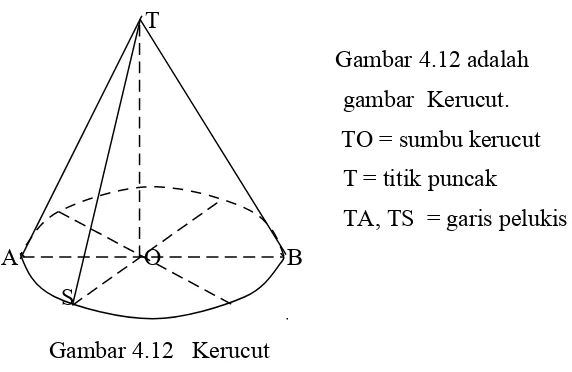
T Gambar 4.12 adalah gambar Kerucut.
TO = sumbu kerucut T = titik puncak
TA, TS = garis pelukis A O B
S
Gambar 4.12 Kerucut
c. Bola
Bola adalah suatu bidang putar yang terjadi bila setengah lingkaran diputar dengan garis tengahnya sebagai sumbu putar. Karena letak titik-titik pada setengah lingkaran terhadap titik-titik pusat lingkaran tidak berubah selama perputaran, maka titik-titik pada bidang bola itu berjarak sama terhadap titik pusat bola. Perhatikan Gambar 4.13 berikut.
PQ = tali busur AB = garis tengah
A, B = titik-titik diametral
Gambar 4.13. Bola
2. LUAS BANGUN RUANG SISI LENGKUNG a. Luas Tabung
Tabung terdiri dari tiga sisi, yaitu sisi atas dan sisi alas yang berbentuk lingkaran serta sisi tegak (berupa bidang lengkung). Sisi tegak ini biasa disebut selimut tabung.
Gambar 4.14. Jaring-jaring Tabung
Gambar 4.14 (i) adalah sebuah tabung dengan jari-jari r dan tinggi t, sedangkan Gambar 4.14 (ii) adalah jaring-jaring tabung tersebut. Dengan menggunakan Gambar 4.14 ini, coba Anda
tunjukkan bahwa luas tabung adalah L = 2 п r2 + 2 п r t
b. Luas Kerucut
Kerucut memiliki dua sisi, yaitu sisi alas berupa daerah lingkaran, dan sisi lengkung yang biasa disebut selimut tabung. Dengan demikian luas kerucut adalah jumlah dari luas sisi alas yang berupa lingkaran dan luas selimut. Untuk menentukannya, Anda dapat menggunakan jaring-jaring kerucut seperti pada Gambar 4.15 berikut.
Gambar 4.15. Jaring-jaring Kerucut
Dengan menggunakan Gambar 4.15 ini, coba Anda tunjukkan bahwa luas kerucut adalah L = п r2 + п r s
c. Luas Bola
Untuk menentukan luas bola, Anda dapat melakukan kegiatan lab. Mini berikut.
Lab. Mini – Mencari luas bola
Cara kerja:
1. Potonglah jeruk di tengah-tengah
2. Ukurlah garis tengahnya, dan buatlah lingkaran-lingkaran yang garis tengahnya
sama dengan garis tengah jeruk.
3. Kupaslah jeruk
4. Potong-potonglah kulit jeruk menjadi kecil-kecil
5. Tempelkan (dengan lem) potongan-potongan kulit jeruk tersebut di dalam
lingkaran-lingkaran yang telah dibuat, dengan penuh dan tidak tumpang tindih.
Ada berapa lingkaran yang penuh oleh kulit jeruk tersebut? Benarkah ada 4 lingkaran?. Jika demikian, dengan mudah Anda dapat tunjukkan bahwa Luas bola adalah:
LBola = 4 Lingkaran = 4 (п r2)
3. VOLUM BANGUN RUANG SISI LENGKUNG a. Volum Tabung
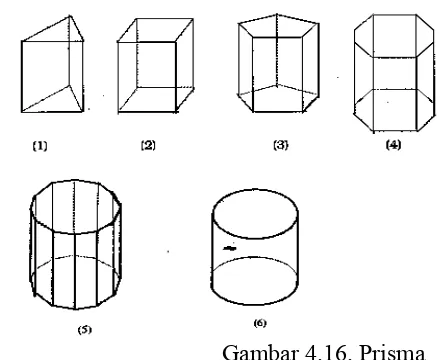
Perhatikan Gambar 4.16 berikut.
Gambar 4.16. Prisma
b. Volum Kerucut
Lab. Mini – Mencari Volum Kerucut
Bahan : Kertas manila, lem/perekat kertas, beras/pasir Alat : gunting/pisau, jangka, penggaris, busur derajat,. Cara kerja:
1. Buatlah model kerucut tanpa bidang alas dari kertas manila
2. Buatlah model tabung tanpa tutup dari kertas manila (Bagaimana caranya?)
3. Isilah kerucut sampai penuh dengan pasor/beras
4. Tuangkan beras/pasir tersebut ke dalam model tabung
5. Ulangi kegiatan a dan b sampai tabung pebuh dengan pasir/beras.
6. Apa kesimpulan yang Anda dapatkan?
c. Volum Bola
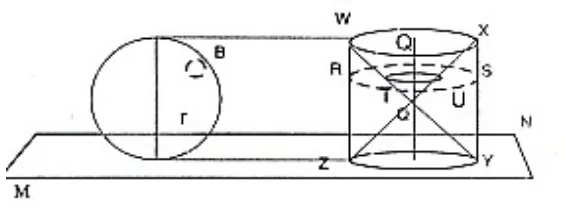
Volum bola dapat ditemukan dengan menggunakan kegiatan Lab.Mini seperti di atas (Bagaimana caranya?) dan dapat juga dengan menggunakan prinsip Cavalleri. Apabila Anda akan menunjukkannya dengan prinsip Cavalleri, maka Anda harus menggunakan dua bangun ruang yang tingginya sama. Bangun ruang yang pertama adalah bola itu sendiri (jari-jari = r), dan bangun yang kedua adalah sebuah tabung dengan (jari-jari-(jari-jari lingkaran alasnya adalah r sedangkan tingginya 2r. Di dalam tabung itu dibuat dua buah kerucut. Kerucut yang satu alasnya terletak di bawah (berimpit dengan lingkaran alas tabung), dan kerucut kedua alasnya terletak di atas (berimpit dengan lingkaran atas tabung). Titik puncak dari kedua kerucut ini berimpit, dan terletak tepat pada titik tengah dari sumbu tabung. Perhatikan Gambar 4.17.
Gambar 4.17. Prinsip Cavalleri
Berdasarkan Gambar 4.17 di atas, tunjukkan bahwa volum bola adalah: VBola = 3
4
Latihan
Untuk soal nomor 1 – 10, pilih salah satu jawaban yang paling tepat!
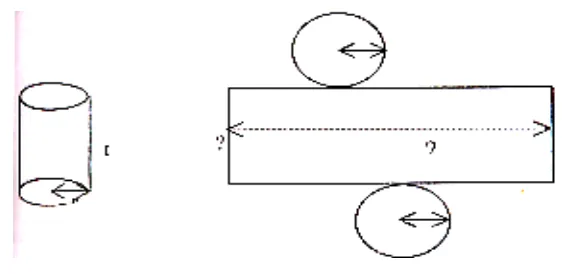
1. Sebuah tabung yang tinggi dan diameternya sama akan memiliki ketebalan selimut berbentuk persegi panjang dengan perbandingan panjang dan lebarnya adalah ... A. : 1
B. 2 : 1 C. 3 : 1 D. d : 1
2. Sebuah tandon air berbentuk tabung bertutup dengan tinggi bagian dalamnya 1,56 m terbuat dari tembaga. Untuk menjaga agar tembaga awet, maka bagian dalam tabung dilapisi dengan aspal setebal 1 cm. Volum aspal minimal yang diperlukan untuk melapis bagian dalam tandon adalah ... cm3
A. 48871,43 B. 96941,43 C. 48627,07 D. 116062,57
3. Diketahui sebuah tabung tanpa tutp dengan jari-jari alas 6 cm dan tingginya 10 cm. Jika = 3,14 maka luas tabung tanpa tutup tersebut adalah ... cm2
A. 602,88
A. sudut antara garis-garis pelukis sama dengan sudut bidang alas B. bidang alas kerucut adalah lingkaran
C. sumbu kerucut tegak lurus bidang alas
6. Diketahu kerucut dengan jari-jari alasnya 5 cm dan tingginya 12 cm. Jika п = 3,14
maka luas selimut kerucut adalah ………. cm2.
A. 62,8
9. Sebuah bola dimasukkan ke dalam tabung. Diameter bola sama dengan diameter tabung
= 12 cm. Jika tinggi tabung = 20 cm dan = 3,14 maka volum tabung di luar bola
Untuk soal nomor 11 – 13, kerjakan soal-soal berikut ini!
11. Gambarkan jaring-jaring kerucut dengan ukuran garis tengah alas 5 cm dan
tinggi 6 cm.
12. Buktikan volum tabung adalah VTabung = luas alas x tinggi
BAB 3
BANGUN DATAR
A. Bangun Datar Segitiga
1. Segitiga-segitiga Sebangun
Definisi : Suatu bangun B disebut sebangun dengan bangun C (B C), jika B dapat dikalikan
dengan suatu faktor, sehingga terjadilah bangun B’ yang sama dan sebangun dengan C (B’
C). Perhatikan Gambar 3-1 berikut.
b. sisi-sisi yang seletak mempunyai perbandingan yang seharga.
Dalil-dalil kesebangunan :
a. ABC dan PQR adalah sebangun, jika kedua segitiga itu mempunyai sepasang
sudut yang sama besar (misalnya A = P), sedangkan sisi-sisi yang mengapit sudut itu
mempunyai perbandingan yang seharga (misalnya AC : PR = AB : PQ).
b. ABC dan PQR adalah sebangun, jika sisi-sisinya mempunyai perbandingan yang
seharga.
c. ABC siku-siku di A dan PQR siku-siku di P adalah sebangun, jika satu buah sisi
2. Segitiga-segitiga Kongruen
Secara khusus syarat-syarat untuk dua segitiga kongruen ini adalah sebagai berikut. Teorema 1 :
Dua buah segitiga akan kongruen jika dua sisi yang bersesuaian sama panjang dan satu sudut yang diapit kedua sisi tersebut sama besar (S – Sd – S)
Bukti :
Perhatikan Gambar 3-3 di samping. B = Q (...)
AB = PQ dan BC = QR (...)
Tempatkan PQR pada ABC, sedemikian
sehingga titik sudut B berimpit dengan titik sudut Q. Akibatnya QP akan menutupi BA dan QR akan menutupi BC.
AB = PQ dan BC = QR P berimpit A dan
R berimpit C
Dengan demikian titik-titik sudut ABC berimpit
dengan titik-titik sudut PQR, yang membuktikan
Dua segitiga akan kongruen jika satu sisi yang seletak sama panjang dan dua sudut yang seletak pada sisi tersebut sama besar. (Sd – S – Sd).
Teorema 3 :
Dua segitiga akan kongruen jika satu sisi yang seletak sama panjang dan dua susut yang seletak sama besar (S – Sd – Sd)
Teorema 4 :
Dua segitiga akan kongruen jika ketiga sisi yang seletak sama panjang (S – S – S).
Latihan!
b. Tentukanlanh panjang AB, AC, DC, CE, AE, DF.
1. Garis tinggi
Garis tinggi suatu segitiga adalah garis yang membagi tegak lurus sisi di depan titik sudut segitiga tersebut.
Perhatikan ABC di samping, dan buktikanlah
bahwa ketiga garis tinggi dalam ABC tersebut
melalui satu titik. Bukti :
Perhatikan ABC pada Gambar di samping.
Melalui titik A, B, dan C ditarik garis-garis yang masing-masing sejajar dengan sisi dihadapan titik Berdasarkan sifat di atas, maka didapat bahwa OD = ..., OE = ..., dan OF = ...
Karena O AQ, O BR, dan O CP dan AQ,
BR, dan CP adalah garis tinggi pada ABC,
Garis berat suatu segitiga adalah garis yang membagi dua sama panjang sisi di depan titik
sudut tersebut. Perhatikan ABC pada gambar di bawah ini.
C
E P’ D P
A F B Buktikanlah :
Ketiga garis berat dalam ABC di atas melalui satu titik, yang disebut titik berat segitiga. Bukti :
Perhatikan ABC di atas.
AD dan BE adalah garis berat dalam ABC BD = DC dan AF = BF.
Misalkan AD dan BE berpotongan di P, akan dibuktikan bahwa CF juga akan melalui P.
Perhatikan CED dan CAB.
CE : CA = CD : CB = 2 : 1 (...) Akibatnya AB // ED dan ED : AB = CE : CA = 1 : 2.
DEP = ABP dan EPD = APB (...) EPD .... APB.
Akibatnya EP : PB = ED : AB = 1 : 2 = DP : AP.
Misalkan CF adalah garis berat yang melalui C dan memotong EB di P’, maka dengan cara yang sama dapat dibuktikan bahwa EP’ : P’B = 1 : 2.
Dengan demikian diperoleh EP = 31 EB dan EP’ = 31 EB atau .... = ...
Jadi terbukti bahwa CF adalah garis berat yang memotong EB di P.
3. Garis bagi
Garis bagi suatu segitiga adalah garis yang membagi dua sudut segitiga menjadi dua bagian
yang sama besar. Perhatikan ABC pada gambar berikut.
E D X
o o * A B
Karena Garis AD adalah garis bagi dari BAC, maka semua titik pada AD letaknya sama
jauh dari AC dan AB (Mengapa ?).
Karena Garis BE adalah garis bagi dari ABC, maka semua titik pada BE letaknya sama
jauh dari BA dan BC (Mengapa ?).
Misalkan AD dan BE berpotongan di titik X, maka berarti X letaknya sama jauh dari AC dan AB dan juga dari BA dan BC (Mengapa ?).
Jadi X letaknya sama jauh dari CA dan CB, yang berarti bahwa X terletak pada garis bagi
dari ACB atau CX adalah terletak pada garis bagi dari ACB.
Dengan demikian terbukti bahwa ketiga garis bagi ini melalui pada satu titik.
Latihan!
1. Dalam sebuah ABC, BD dan AE adalah garis-garis berat yang masing-masing melalui
titik sudut B dan A. Buktikan bahwa garis DE // AB.
2. Dalam sebuah ABC, BD dan AE adalah garis-garis berat yang masing-masing melalui
titik sudut B dan A. Kedua garis berat ini berpotongan di titik Z. Buktikan bahwa :
Misalkan pada ABC di atas, AD adalah garis bagi dari BAC, BE adalah garis bagi dari sudut luar CBF dan CH adalah garis bagi dari sudut luar GBC. Buktikan bahwa ketiga garis bagi ini akan berpotongan pada satu titik.
4. Buktikan bahwa garis tinggi suatu segitiga sama kaki akan membagi segitiga menjadi dua segitiga yang kongruen.
5. Garis tinggi pada hipotenusa suatu segitiga siku-siku sama kaki sama dengan setengah panjang hipotenusanya. Buktikan !
6. Buktikan bahwa kedua garis bagi sudut alas suatu segitiga sama kaki sama panjang.
B. Bangun Datar Segiempat
Untuk memahami macam-macam bangun segiempat secara baik, perhatikan Skema berikut.
Segiempat
Layang-layang Jajargenjang Trapesium
Persegipanjang Belahketupat
Persegi
Skema Segiempat
Dari skema di atas terlihat bahwa persegi panjang dan belah ketupat merupakan bentuk khusus dari jajargenjang, sedangkan persegi adalah bentuk khusus dari persegi panjang atau belahketupat. Secara rinci tentang bangun-bangun di atas akan dibahas berikut ini.
1. Jajargenjang
Definisi :
Jajargenjang adalah sebuah segiempat yang kedua pasang sisi yang berhadapan sejajar. Dalil-dalil tentang jajargenjang :
1. ABCD adalah jajargenjang sisi AB = CD dan BC = AD.
3. Pada setiap jajargenjang, kedua diagonalnya berpotongan di tengah-tengah.
4. Pada segiempat ABCD sisi AB = CD dan BC = AD ABCD adalah jajargenjang.
5. Jika pada suatu segiempat, kedua diagonalnya berpotongan di tengah-tengah, maka
segiempat itu adalah jajargenjang.
Sehingga AB = CD dan AD = BC (Terbukti).
(2) ABD CDB A = C dan B1,2 = D1,2 (Terbukti)
2. Persegipanjang
Definisi :
Persegipanjang adalah sebuah jajargenjang yang mempunyai sebuah sudut siku-siku.. Dalil-dalil tentang jajargenjang :
1. ABCD adalah persegipanjang panjang diagonal AC = diagonal BD.
2. Diagonal jajargenjang sama panjang jajargenjang itu persegipanjang.
Bukti :
Perhatikan Gambar 3-8 berikut.
D C
A B (1) Diketahui :
Buktikan : Bukti :
3. Belahketupat
Definisi :
Belahketupat adalah sebuah jajargenjang yang dua sisinya yang berurutan sama panjang Dalil-dalil tentang jajargenjang :
1. Setiap diagonal belahketupat merupakan garis bagi titik-titik sudut belahketupat itu.
Definisi :
Persegi adalah sebuah segiempat yang semua sisi-sisinya sama panjang dan salah satu sudutnya siku-siku.
Dalil-dalil tentang jajargenjang :
1. ABCD adalah persegi AC = BD.
2. Semua sudut pada persegi adalah siku-siku.
Bukti :
D C
Perhatikan Gambar 3–9 di samping
A B (1) Diketahui :
Buktikan : Bukti :
(2) Diketahui : Buktikan : Bukti :
Latihan!
1. Tuliskan definisi layang-layang dan dalil-dalil tentang layang-layang beserta buktinya. 2. Tuliskan definisi trapesium dan dalil-dalil tentang trapesium beserta buktinya.
3. Tuliskan sifat-sifat yang ada pada jajargenjang, persegipanjang, persegi, belahketupat, trapesium, dan layang-layang.
GEOMETRI DIMENSI TIGA
Sebelum membahas lebih lanjut tentang sifat-sifat di dalam geometri ruang, akan diperkenalkan terlebih dahulu beberapa singkatan tertentu yang biasa digunakan dalam pembicaraan geometri ruang, antara lain :
Titik (a, b) = titik potong garis a dan garis b
Titik (a, ) = titik tembus garis a terhadap bidang Garis (, ) = garis potong antara bidang dan bidang Bidang (ABC) = bidang melalui titik-titik A, B, dan C Bidang (a, P) = bidang melalui garis a dan titik P
Bidang (a, b) = bidang melalui garis a dan garis b
A. Kedudukan Titik, Garis, dan Bidang dalam Ruang
1. Kedudukan Garis terhadap Bidang
Di dalam ruang dimensi tiga, ada tiga kondisi untuk menentukan kedudukan garis terhadap bidang, yaitu:
(1) Garis terletak pada bidang Definisi 1.1:
Sebuah garis dikatakan terletak pada sebuah bidang, jika semua titik pada garis itu
terletak pada bidang tersebut.
Sebuah garis dan sebuah bidang dikatakan sejajar, jika garis dan bidang tersebut tidak
Definisi 1.3:
Sebuah garis dikatakan menembus sebuah bidang, jika garis dan bidang itu mempunyai
sebuah titik persekutuan yang disebut titik tembus garis terhadap bidang. l
Dua buah garis dikatakan sejajar, jika dua garis tersebut terletak dalam satu bidang dan
tidak memiliki titik persekutuan.
Dua buah garis dikatakan berpotongan, jika kedua garis itu terletak dalam satu bidang
dan mempunyai sebuah titik persekutuan.
Dua buah bidang dikatakan bersilangan, jika kedua garis itu tidak terletak dalam satu
(1) Dua bidang saling sejajar Definisi 1.7:
Dua buah bidang dikatakan sejajar, jika kedua bidang itu tidak mempunyai sebuah garis
persekutuan.
α
β
(2) Dua bidang saling berpotongan Definisi 1.5:
Dua buah bidang dikatakan berpotongan, jika kedua bidang itu mempunyai sebuah
garis persekutuan.
β
(α, β)
α
4. Beberapa teorema tentang kedudukan garis dan bidang dalam ruang Teorema 1.1:
Jika garis l sejajar garis m dan garis m terletak pada bidang α, maka garis l sejajar bidang α Diketahui: l // m dan m
αAkan dibuktikan : l // α
Jika melalui sebuah titik P yang tidak terletak pada bidang α dibuat garis g yang tegak lurus bidang α dan memotong bidang α dititik P1 maka P1 disebut titik kaki gari stegak lurus
yang dibuat melalui P pada bidang α.
Definisi 1.5 : Proyeksi sebuah titik pada sebuah bidang adalah titik kaki dari garis yang dibuat
melalui titik itu tegak lurus bidang tersebut.
Anda perhatikan Gambar 1.34 α disebut bidang proyeksi
P disebut titik yang diproyeksikan
P1 disebut titik hasil proyeksi atau proyeksi P pada bidang α
G disebut garis pemroyeksi
Kalau setiap bangun geometri dipandang sebagai himpunan titik-titik tertentu maka proyeksi suatu bangun pada sebuah bidang merupakan bangun lain yang terjadi dari himpunan proyeksi semua titik dari bangun itu pada bidang tersebut.
Pada gambar 1.35 ditunjukkan bahwa proyeksi dari sebuah kurva S adalah kurva S1.
S1 merupakan
titiknya pada bidang tersebut. Antara lain, jika Anda harus menentukan proyeksi dari sebuah garis lurus.
Anda perhatikan lebih dahulu sifat dari proyeksi sebuah garis lurus pada sebuah bidang seperti yang dikemukakan dalam teorema berikut.
Teorema 1.3 : Proyeksi sebuah garis pada sebuah bidang pada umumnya merupakan sebuah
garis lagi
Diketahui : garis g dan bidang α
g1 merupakan proyeksi garis g pada bidang
Dibuktikan : g1 merupakan garis lurus
Bukti : Garis-garis pemroyeksi dari titik-titik yang terletak pada garis g merupakan garis-garis yang memotong garis g dan sejajar satu sama lain, semuanya terletak pada sebuah bidang, misalnya bidang β.
Bidang β memotong bidang menurut garis lurus (α, β). Garis potong (α, β) tidak lain
adalah garis g1. Dengan perkataan lain proyeksi dari garis g pada bidang α, yaitu g1, merupakan
garis lurus.
Karena sebuah garis lurus letaknya ditentukan oleh dua buah titiknya, maka mendasarkan pada teorema 1.3 untuk menentukan proyeksi sebuah gris pada sebuah bidang, Anda cukup memproyeksikan dua buah titiknya saja dari garis itu. Pada Gambar 1.37, titik P
Setelah Anda mengenal pengertian dari proyeksi dan sifat dari proyeksi sebuah garis lurus pada sebuah bidang, maka diharapkan Anda dapat memahami pengertian sudut antara garis dan bidang.
Definisi 1.5 : Jika sebuah garis tidak tegak lurus pada sebuah bidang, maka sudut antara garis itu dan bidang tersebut adalah sudut lancip antara garis itu dengan proyeksi garis itu pada bidang tersebut.
Pada gambar 1.38 ditunjukan kepada Anda tentang sebuah garis g yang tidak tegak lurus pada
bidang α. Garis g1 adalah proyeksi garis g pada bidang α. Sehingga sudut antara garis g dan
bidang α adalah sudut lancip antara garis g dan g1, yaitu φ.
Proyeksi sebuah titik pada sebuah bidang adalah titik kali garis yang dibuat melalui titik itu dan tegak lurus pada bidang tersebut.
Proyeksi sebuah garis tidak tegak lurus pada sebuah bidang, maka yang dimaksud dengan sudut antara garis itu dan bidang tersebut adalah sudut lancip yang dibentuk oleh garis itu dengan proyeksinya pada bidang tersebut.
1. Proyeksi Titik Pada Bidang
Definisi : Jika dari titik T ditarik garis TT1 ( T1 pada bidang α ) yang tegak lurus pada bidang α,
maka T1 disebut proyeksi titik T pada bidang α.
T = titik yang diproyeksikan T1 = proyeksi
TT1 = garis pembuat proyeksi (proyektor)
2. Proyeksi Garis Pada Bidang
Proyeksi suatu bangun pada suatu bidang adalah himpunan proyeksi semua titik pada bangun itu ke bidang α.
Jika semua titik pada garis AB diproyeksikan ke bidang α, maka dapat dibuktikan bahwa semua proyektor terletak pada satu bidang yang disebut bidang proyektor. Dan semua proyeksinya terletak pada satu garis A1B1 disebut proyeksi garis AB pada bidang α (lihat
gambar (a)).
Jika garis CD tegak lurus pada bidang α, maka proyeksinya pada bidang α berupa sebuah titik (gambar (b)).
Jika garis PQ memotong bidang α di titik Q,maka untuk melukis proyeksinya cukup
dilukiskan titik P1 yang merupakan proyeksi dari titik P. Garis P1Q adalah proyeksi garis PQ
pada bidang α (lihat gambar(c)).
Contoh soal:
Diketahui kubus dengan bidang alas ABCD dan rusuk-rusuk tegaknya AE,BF, CG, dan DH. a. Buktikan bahwa BC tegak lurus bidang ABFE
b. Buktikan bahwa CD tegak lurus AH
c. Tentukan proyeksi dari titik C pada bidang ADHE d. Tentukan proyeksi dari DE pada bidang ABCD e. Tentukan sudut antara CH dan bidang EFGH
Jawab :
Jika Gambar 1.39 menunjukkan kubus yang dimaksud, maka:
a. Karena ABCD sebuah kubus, maka:
< CBA siku-siku atau CB ┴ BA < CBF siku-siku atau CB ┴ BF
BA dan BF pada bidang ABF dan berpotongan CB ┴ bidang ABFE
b. CD ┴ DA
CD ┴ DH
CD ┴ bidang ADHE
AH pada bidang ADHE, menurut teorema 1.2, maka CD ┴ AH
c. Pada jawaban pertanyaan (b) dikemukakan bahwa CD ┴ bidang ADHE. Berarti bahwa
D adalah titik kaki dari garis yang melalui C dan tegak lurus bidang ADHE; jadi proyeksi titik C pada bidang ADHE adalah titik D.
d. Untuk memproyeksikan ruas garis DE pada bidang ABCD, ditetapkan dua titiknya, dan
dipilih ujung-ujungnya D dan E. Proyeksi dari titik D pada bidang ABCD adalah titik D sendiri.
e. Sudut antara CH dengan proyeksinya pada bidang EFGH adalah sudut antara CH dengan
Latihan
1. Pada kubus ABCD.EFGH dengan AB = a cm, titik N adalah titik potong diagonal bidang atas EFGH dan garis CE memotong garis AN di titik K
a. Tentukan perbandingan antara panjang garis EK dan KC
b. Jika titik K’ adalah proyeksi titik K pada bidang ABCD, buktikan bahwa AK’ : K’C = EK : KC = 1 : 2
2. Diketahui limas T.ABCD. tentukan panjang proyeksi garis TA pada bidang ABCD dan
proyeksi garis TA pada bidang TBD. Jika panjang AB = 4 cm dan TA = 4 2cm.
3. Diketahui bidang empat T.ABC, dengan alas ΔABC, AB = BC = 10 cm, AC = 12 cm, dan TC = 8 cm. Garis TC tegak lurus bidang ABC. Panjang proyeksi garis TC pada bidang TAB adalah…………..
4. Diketahui kubus ABCD.EFGH dengan AB = 18 cm. titik P adalah titik tengah bidang EFGH. Dari titik P ditarik garis sejajar garis HB sehingga memotong rususk BF di titik Q. Panjang proyeksi garis GQ pada bidang ABCD adalah…………
5. Diketahui prisma tegak ABC.DEF, dengan AB = AC = 4 cm dan BC = AD = 4 2cm.
Melalui titik D dibuat bidang α yang sejajar dengan garis BC, membentuk sudut 450
dengan bidang ABC, dan memotong garis BE dan CF berturut-turut di titik P dan Q, sehingga:
a. BP : PE = 1 : 1
b. Proyeksi garis DP pada bidang BCFE adalah 2 2cm
c. Luas proyeksi bidang α pada bidang BCFE adalah 8 cm2
d. Volume limas D.PEFQ adalah 16/3 cm3
Pernyataan yang benar adalah…
6. Kubus ABCD.EFGH, memiliki panjang AB = 16 cm. Titik P dan Q bertutut-turut merupakan titik tengah rusuk AB dan BC. Titik M dan N adalah titik pusat bidang alas dan bidang alas
a. Proyeksi garis BN pada bidang ACGE adalah MN
b. Panjang proyeksi garis PN pada bidang BDHF adalah 12 2cm
c. Panjang proyeksi garis MN pada bidang NPQ adalah 32/3 2cm
d. Volume limas N.PBQM adalah 1024 cm3
C. Jarak
Dalam Geometri kata jarak diberi arti yang jelas. Kata jarak selalu dikaitkan dengan hubungan dari dua benda. Dalam Geometri benda-benda dipandang secara umum sebagai himpunan titik-titik tertentu, misalnya berupa sebuah titik, ruas garis, garis, bidang atau
bangunan Geometri yang lain. Jika secara umum sebuah bangun geometri dinamakan G1 dan G2,
D2 adalah jarak antara bangun G1 dan G 2. maka jelas bahwa jarak sebagai ruas garis terpendek
yang menghubungkan titin k-titik pada kedua bangun.
a. Jarak Titik
Suatu titik hanya ditentukan oleh letaknya, tetapi tidak mempunyai besaran (ukuran), dikatakan suatu titik tak berdimensi. Sebuah titik dilukiskan dengan tanda nokhtah, kemudian dibubuhkan dengan nama titik itu. Biasanya nama titik itu menggunakan huruf capital.A,,C,P,Q atau R. pada gambar diperlihatkan dua buah titik yaitu titik A dan titik B
A
.
.
B(a) titik A (b) titik B
b. Jarak Titik ke Garis
Kalau sebuah titik berada di luar garis maka terdapat jarak antara titik ke garis itu. Jarak antara sebuah titik A ke garis g (titik A berada di luar garis g) dapat dicari dengan cara sebagai berikut
Tariklah garis dari titik A tegak lurus terhadap garis , sehingga memotong garis tersebut di B, maka AB adalah jarak yang dimaksud itu.
Gambar
B g
A
c. Jarak Titik ke Bidang
Untuk Sebuah titik yang berada di luar bidang maka terdapat jarak antara titik ke bidang itu. Jarak antara titik A ke bidang α (titik A berada di luar bidang α) dapat dicari dengan cara sebagai berikut
Buatlah garis g melalui titk A dan tegak lurus bidang α sehingga menembus bidang α di titik B. AB adalah jarak dari titik A ke bidag α yang diminta.
α
A
.
BContoh Soal :
1. Diketahui balok ABCD.EFGH denga panjang rusuk AB = 10 cm, AD = 8cm, dan AE = 6 cm. Titik O merupakan titik potong diagonal bidang alas AC dan BD. Hitung:.
a) A ke bidang BCGF b) A ke bidang CDHG c) O ke bidang ABFE
H G
E F
D
O C
A B
a) Jarak titik A ke bidang BCGF adalah AB = 10 cm, sebab AB tegak lurus bidang BCGF. b) Jarak titik A ke bidang CDHG adalah AD = 8 cm, sebab AD tegak lurus bidang CDHG. c) Jarak titik O ke bidang ABFE adalah OP = ½ PQ = ½ 8 = 4 cm.
2. Diketahui kubus ABCD.EFGH dengan panjang rusuk 4 cm. Carilah jarak titik C ke bidang
BDG
H G E F
Jawab:
Jarak titik C ke bidang BDG adalah ruas garis yang dibuat melalui C dan tegak lurus terhadap garis GP.
Diagonal AC = a√2 = 4√2, sehimgga PC = ½ AC = 2√2 cm. Perhatikan ∆PCG:
PG2 = 42 + (2√2)2 = 24
PG = 2√6
Sin α = CG/ PG = 4/ 2√6 = 1/3 √6 Perhatikan ∆COP:
Sin α = CO/CP CO = CP Sin α CO = 2√2 (1/3 √6) CO = 4/3 √3 cm
Jadi, jarak titik C ke bidang BDG sama dengan 4/3 √3 cm
Latihan
1. Diketahui kubus ABCD.EFGH.
H G E F
D C A B
Tentukan jarak titik D ke bidang ACH.
2. Diketahui kubus ABCD.EFGH. dengan rusuk a cm. jika S merupakan proyeksi titik C
pada bidang AFH, maka jarak titik A ke titik S adalah H G
E F
A B
3. Jika panjang rusuk kubus adalah 9 cm. maka hitunglah jarak C ke diagonal FD adalah H G
E F
D C
A B
d. Jarak antara dua garis sejajar
Dalam hal dua garis sejajar maka terdapat jarak antara dua garis tersebut Definisi:
Jarak antara dua buah garis sejajar adalah ruas garis yang menghubungkan salah satu titik pada garis yang satu dengan proyeksi titik itu pada garis yang lain.
Jika garis g sejajar garis h, maka jarak antara kedua garis itu dapat ditentukan dengan cara sebagai berikut:
Garis g dan h membentuk bidang b (Dalil 4). Buatlah garis k yang memotong tegak lurus terhadap garis g dan h di titik A dan B. AB adalah jarak antara garis g dan h yang diminta.
Jarak antara dua garis sejajar, seperti AB dan CD pada gambar , adalah ruas garis PQ, garis tegak lurus diantara dua garis sejajar tersebut.
A P B
C Q D k
e. Dua garis bersilangan
Dua buah garis g dan h dikatakan bersilangan (tidak berpotongan dan tidak sejajar),jika kedua garis itu tidak terletak pada sebuah bidang
Gbr. Garis g bersilangan dengan garis h
Garis h menembus bidang di titik A, sedangkan titik A tidak terletak pada garis g. dalam hal demikian garis g dan h dikatakan bersilangan.
Latihan!
1. H G
Diketahui kubus ABCD EFGH dengan panjang rusuk 6cm. Hitunglah jarak AF ke bidang CDHG!
A B
2. T.ABC adalah bidang empat beraturan, degan AB = 16. jika P dan Q masing-masing
pertengahan TA dan BC, maka tentukan PQ.
3. Diketahui bidang empat D.ABC beraturan dengan AB = 10, dengan titik P dan Q
masing-masing merupakan titik tengah dari BA dan DC. Hitunglah jarak AB ke CD! h
A
g
f
. Jarak Bidang1.Jarak Antara Sebuah Titik dan Sebuah Bidang
Definisi
Ruas garis yang menghubungkan titik itu dengan proyeksinya pada bidang tersebut
Panjang ruas garis yang tegak lurus menghubungkan titik tersebut dengan bidang
A
Ruas garis d yang tegak lurus bidang V menunjukkan jarak antara
titik A dan bidang V.
A1 merupakan proyeksi titik A pada bidang V d
A1
V
Contoh :
1. Pada sebuah balok yang bidang alasnya ABCD dan rusuk-rusuk tegak AE, BF, CG dan DH. Tentukanlah ruas garis yang menyatakan jarak antara titik D
dan bidang BCGF!
Jawab :
C merupakan proyeksi D pada bidang BCGF, sehingga
Ruas garis DC merupakan jarak antara titik D dengan bidang BCGF. 2. Panjang rusuk kubus ABCD.EFGH di bawah ini adalah 6 cm. Hitunglah jarak antara titik F ke bidang ABCD.?
H G E F
Jawab:
Ruas garis BF merupakan ruas garis yang menunjukkan jarak antara titik F dengan bidang ABCD,sehingga jarak yang dimaksudkan adalah 6 cm
2. Jarak Antara Sebuah Garis dan Sebuah Bidang yang Saling Sejajar
Definisi
Diketahui balok ABCD.EFGH dengan panjang AB = 6 cm, BC = 4 cm dan BF = 8 cm. Hitunglah jarak antara garis AC dan bidang EFGH.?
H G
Jarak antara garis AC dan bidang EFGH dapat diwakili oleh ruas garis AE atau CG, sehingga jarak yang dimaksud adalah 8 cm
Panjang ruas garis yang masing-masing tegak lurus terhadap
garis dan bidang tersebut
Panjang ruas garis PQ dengan Q proyeksi P ke bidang V,
3. Jarak Antara Dua Bidang
1. Diketahui sebuah balok PQRS.TUVW. Tentukanlah ruas garis yang menyatakan jarak antara bidang PQUT dan bidang RSWV!
Jawab:
Ruas garis PS, QR, TW dan UV tegak lurus bidang PQUT dan bidang RSWV. Sehingga ruas garis tersebut dapat dinyatakan sebagai jarak antara bidang PQUT dan Bidang RSWV
Jarak bidang ABCD dengan bidang EFGH dapat diwakili oleh ruas garis AE, DH, BF dan CG,
2. Diketahui kubus PQRS.TUVW dengan panjang rusuk PQ = 6 cm. a. Carilah jarak antara PU dan bidang RSWV
b. Carilah jarak antara UW dan bidang PQRS
3. Kubus ABCD.EFGH dengan rusuk 10 cm. Titik P dan Q berturut-turut adalah titik tengah FG dan HG. Hitunglah jarak garis PQ ke bidang BDHF!
4. Sebuah kubus dengan rusuk a cm. Bidang alasnya ABCD, rusuk-rusuk tegaknya AE,BF,CG dan DH.
a. Carilah jarak antara bidang ACH dan bidang BEG b. Carilah jarak antara bidang BDE dan bidang CFH
5. Sebuah kubus yang bidang alasnya PQRS dan rusuk-rusuk tegaknya PT, QU, RV
D. Sudut
1. Sudut antara garis dan bidang
Jika sebuah garis tidak tegak lurus pada sebuah bidang, maka sudut antara garis itu dan bidang tersebut adalah sudut lancip antara garis itu dengan proyeksi garis itu pada bidang tersebut. Adapun sudut antara garis dan bidang dapat ditentukan sebagai berikut:
1. Tentukan titik tembus garis g berikut serta beri nama sudut yang dibentuk antara keduanya.
a. Garis AH dan bidang ABCD
b. Titik tembus GA dan ABCD adalah titik A. Proyeksi G pada ABCd adalah titik C (buktikan bahwa GC tegak lurusABCD). Jadi, proyeksi GA pada ABCD adalah CA. Sudut antara GA dan ABCD adalah sudat antara GA dan CA, yaitu sudut GAC, seperti pada gambar 2.
c. Titik tembus HF pada BCGF adalah titik F (buktikan bahwa HG tegak lurusBCGF). Jadi, proyeksi HF pada BCGF adalah GF. Sudut antar HF dan BCGF adalah sudut anatar HF dan GF yaitu sudut HFG, seperti pada gambar 3.
2. Diketahui limas tegak beraturan T.ABCD dengan rusuk 4 cm dan rusuk tegaknya 6 cm. a. Tunjukkan sudut antara garis AB dengan bidang ACT.
b. Hitunglah besar sudut antara garis AB dengan bidang ACT.
Jawab:
a. Jika pusat diagonal alas ABCD kita sebut P, maka proyeksi garis AB terhadap
bidang ACT adalahgaris AP, sehingga sudut antara AB dan bidang ACT adalah
BAP
b. Perhatikan segitiga siku-siku ABP. Jika sudut tersebut kita namakan α, maka: T
Sudut antara dua bidang yang berpotongan adalah sudut yang terbentuk antara dua garis pada masing masing bidang, dimana kedua garis itu tegak lurus pada suatu garis perpotongan kedua bidang. Adapun sudut antara dua bidang dapat ditentukan sebagai berikut:
m dan garis n, yaitu θ. Contoh Soal:
1. Pada kubus ABCD.EFGH, hitunglah sudut antara bidang BDE daan BDG. Jawab : bidang BDE dan BDG yang berpotongan dengan garis potong BD. Misalkan P titik pusat ABCD. Karena pada kubus ABCD.EFGH berlaku BD tegak lurus ACGE, maka BD tegek lurus EP, EP pada bidang BDE dan BD tegek lurus GP, GP pada bidang BDG. Jadi,
Dengan cara yang sama diperoleh CPG = 54,73°.
Jadi, θ = EPG = (BDE,BDG) = 180° - 2. 54,73° = 70.5°
2. Bidang empat (tetrahedron) T.ABC mempunyai alas segitiga siku-siku ABC, dengan sisi
Jawab
Dua buah garis dikatakan bersilangan jika keduanyatidak terletak dalam sebuah bidang. Jadi, sudut antara dua garis yang bersilangan adalah sudut yang diperoleh dari dua garis yang berpotongan yang masing-masing garis sejajar dengan garis yang bersilangan.
Adapun sudut antara dua garis yang bersilangan dapat ditentukan sebagai berikut:
1. Misal garis m dan garis n adalah dua
terbentuk antara dua garis yang bersilangan, yaitu θ.
Diketahui kubus ABCD.EFGH dengan panjang rusuk 4 cm.
a. Tunjukkan sudut antara garis CF dan garis EG.
b. Hitunglah sudut antara garis CF dan garis EG.
Jawab:
memotong CF adalah garis AC. Dengan demikian, sudut antara garis CF dan garis EG diwakili oleh sudut ACF.
b. Pada segitiga ACF, tampak bahwa
AC = CF = AF (diagonal sisi), sehingga segitiga tersebut merupakan segitiga sama sisi, oleh sebab itu sudut antara garis CF dan garis EG adalah 60°.
Latihan!
1. Pada kubus ABCD.EFGH, hitunglah sudut antara garis BG dengan bidang ACGE dan
BA dengan bidang ACGE.
2. P.ABCD merupakan limas beraturan. Panjang sisi persegi adalah 2 cm dan panjang
rusuk tegak PA adalah 3 cm. Jika α adalah sudut antara bidang PAB dan bidang PCD.
Hitunglah sin α.
3. Diketahui kubus ABCD.EFGH dengan rusuk 4. Titik T pada perpanjangan CG sehingga
CG = GT. Jika sudut antara TC dan bidang BDT adalah α, maka tan α = ... (UMPTN 1999)
4. Pada bidang empat T.ABC, bidang alas ABC merupakan sama sisi, TA teagk lurus pada
bidang alas, panjang TA sama dengan 1 dan besar sudut TBA adalah 30°. Jika α adalah sudut antara bidang TBC dan bidang alas, maka tan α = ... (UMPTN 1998)
Jika suatu bidang datar memotong suatu bangun ruang maka akan diperoleh bidang irisan. Suatu bidang yang memotong bangun ruang maka perpotongannya disebut bidang irisan. Untuk menentukan irisan bidang dengan bangun ruang dapat digukana 3 cara yaitu menggunakan :
1. sumbu affinitas
T dan S, serta memotong bidang CDHG di R dan S.
Garis-garis potong QR, RS, ST, TP, dan PQ ini membentuk bidang yang disebut irisan atau
penampang antara bidang α dengan kubus ABCD.EFGH.
Definisi Irisan:
“Irisan antara bidang dengan bangun ruang adalah sebuah bangun datar yang dibatasi oleh garis-garis potong antara bidang itu dengan bidang-bidang sisi dari bangun ruang, sehingga irisan itu membagi bangun ruang menjadi dua bagian.”
Perhatikan gambar di atas! Bidang irisan PQRST berpotongandengan bidang alas ABCD
pada garis potong PQ. Garis potong PQ disebut sumbu afinitas atau garis dasar atau garis
koliniasi.
Definisi Sumbu afinitas:
“Sumbu afinitas adalah garis potong antara bidang irisan dengan bidang alas bangun ruang yang diirisnya. Sumbu afinitas terletak pada bidang irisan dan bidang alas.”
Sumbu afinitas memegang peranan yang sangat penting untuk menyelesaikan gambar irisan suatu bidang dengan bangun ruang.
3. Menggunakan Sumbu Afinitas dalam Menggambar Irisan
1. Aksioma yang diperlukan dalam melukis bidang irisan:a. Dua titik menentukan garis.
b. Garis dapat diperpanjang pada kedua ujungnya. c. Bidang dapat diperluas.
2. Langkah menggambar bidang irisan dengan sumbu afinitas:
a. Pilih dua titik pada bidang irisan yang terletak sebidang pada bangun ruang. b. Lukislah garis yang melalui dua titik tersebut.
c. Perpanjang garis-garis pada alas bangun ruang sehingga memotong garis pada langkah 2.
d. Hubungkan 2 titik baru pada bidang alas bangun ruang. Garis yang diperoleh adalah sumbu afinitas.
e. Lengkapi gambar irisan bidang tersebut.
Contoh:
1.
Lukislah bidang irisan kubus ABCD.EFGH yang melalui titik P, Q, dan R!Langkah penyelesaian:
a. Lukislah garis yang melalui titik R dan Q.
b. Perpanjang garis DC sehingga memotong RQ di S
c.
Lukislah garis yang menghubungkan titik P dan S. Garis PS akan memotong BC diT. PT adalah sumbu afinitas.
d. Hubungkan titik R dan P, serta titik Q dan T.
Sumbu afinitas
LATIHAN
Soal 1 dan 2 menggunakan kubus ABCD.EFGH dengan panjang rusuk 4 cm.
1. Titik K terletak pada pertengahan rusuk AD, titik L terletak pada rusuk DH sehingga DL = ¾ DH. Bidang α melalui garis KL dan sejajar dengan rusuk AB.
a. Gambarlah irirsan bidang α dengan kubus.
b. Sebutkan bentuk bangun datar irisan itu, kemudian hitung luasnya.
2. Titik-titik K dan L adalah pertengahan rusuk AD, AB, dan BF. Bidang α melalui titik-titik K, L, M.
a. Gambarlah irisan bidang α dengan kubus.
b. Sebutkan bentuk bangun datar irisan itu, kemudian hitung luasnya.