Teori Kemacetan

BAB 2 BAB 2

LANDASAN TEORI LANDASAN TEORI

2.1 Pengertian

2.1 Pengertian KemaceKemacetantan

Kemacetan adalah situasi atau keadaan tersendatnya atau bahkan terhentinya Kemacetan adalah situasi atau keadaan tersendatnya atau bahkan terhentinya lalulalu lintas

lintas yang disebabkan oleh banyaknya jumlah kendaraan melebihi kapasitasyang disebabkan oleh banyaknya jumlah kendaraan melebihi kapasitas  jalan.

 jalan. Kemacetan Kemacetan banyak banyak terjadi terjadi didi kota-kotakota-kota  besar,  besar, terutamanya terutamanya yang yang tidaktidak mempunyai

mempunyai transportasi publiktransportasi publik yang baik atau memadai ataupun juga tidakyang baik atau memadai ataupun juga tidak seimbangnya kebutuhan jalan dengan ke

seimbangnya kebutuhan jalan dengan kepadatan penduduk, misalnyapadatan penduduk, misalnya Jakarta. Jakarta. Kemacetan lalu lintas menjadi permasalahan sehari-hari di

Kemacetan lalu lintas menjadi permasalahan sehari-hari di Jakarta,Jakarta, Surabaya,

Surabaya, Bandung,Bandung, Medan,Medan,  Semarang, Makassar, Palembang, Denpasar,  Semarang, Makassar, Palembang, Denpasar, Jogjakarta, dan kota-kota besar lainnya di

Jogjakarta, dan kota-kota besar lainnya di Indonesia.Indonesia.  Jika arus lalu lintas  Jika arus lalu lintas mendekati kapasitas, kemacetan mulai terjadi. Kemacetan semakin meningkat mendekati kapasitas, kemacetan mulai terjadi. Kemacetan semakin meningkat apabila arus begitu besarnya sehingga kendaraan sangat berdekatan satu sama apabila arus begitu besarnya sehingga kendaraan sangat berdekatan satu sama lain.

lain. Kemacetan Kemacetan total total terjadi terjadi apabila kendaraan apabila kendaraan harus harus berhenti berhenti atau atau bergerakbergerak lambat.

lambat.

Kemacetan adalah kondisi dimana arus lalu lintas yang lewat pada ruas Kemacetan adalah kondisi dimana arus lalu lintas yang lewat pada ruas  jalan

 jalan yang ditinjau meleyang ditinjau melebihi kapasitas bihi kapasitas rencana jalan rencana jalan tersebut yang metersebut yang mengakibatkanngakibatkan kecepatan bebas ruas jalan tersebut mendekati atau melebihi 0 km/jam sehingga kecepatan bebas ruas jalan tersebut mendekati atau melebihi 0 km/jam sehingga menyebabkan terjadinya antrian. Pada saat terjadinya kemacetan, nilai derajat menyebabkan terjadinya antrian. Pada saat terjadinya kemacetan, nilai derajat kejenuhan pada ruas jalan akan ditinjau dimana kemacetan akan terjadi bila nilai kejenuhan pada ruas jalan akan ditinjau dimana kemacetan akan terjadi bila nilai derajat kejenuhan mencapai lebih dari 0,5.

derajat kejenuhan mencapai lebih dari 0,5.

Sudradjat, Tony Sumartono, Asropi (2011) dalam jurnalnya menyebutkan Sudradjat, Tony Sumartono, Asropi (2011) dalam jurnalnya menyebutkan  bahwa

 bahwa kemacetan kemacetan lalu lalu lintas lintas biasanya biasanya meningkat meningkat sesuai sesuai dengan dengan meningkatnymeningkatnyaa mobilitas manusia pengguna transportasi, terutama pada saat-saat sibuk. mobilitas manusia pengguna transportasi, terutama pada saat-saat sibuk. Kemacetan

Kemacetan terjadi karena berbagai sebab terjadi karena berbagai sebab diantaranya disebabkan odiantaranya disebabkan oleh kelemahanleh kelemahan sistem

sistem pengaturan pengaturan lampu lampu lalu lalu lintas, lintas, banyaknybanyaknya a persimpangan persimpangan jalan, jalan, banyaknyabanyaknya kendaraan yang turun ke jalan, musim, kondisi jalan, dan lain-lain. Berbagai usaha kendaraan yang turun ke jalan, musim, kondisi jalan, dan lain-lain. Berbagai usaha untuk menanggulangi kemacetan lalu lintas yang dilakukan adalah dengan untuk menanggulangi kemacetan lalu lintas yang dilakukan adalah dengan

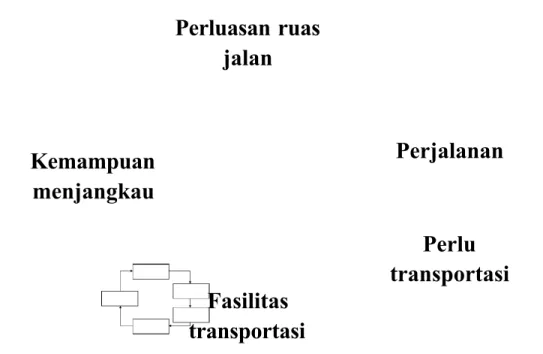
 penambahan sarana jalan, pembangunan jalan tol, jalan layang, terowongan, sistem pengaturan lampu  ATCS  ( Area Traffic Control System), dan lain-lain. Transportasi sangat erat kaitannya dengan perluasan lahan tanah. Drewe menggambarkan hubungan antara perkembangan transportasi dengan perluasan lahan tanah yang digambarkan seperti pada gambar.

Gambar 2.1 Diagram Siklus Perluasan Ruas Jalan dan Transportasi

2.2 Definisi Transportasi

Menurut Morlok (1991), transportasi adalah memindahkan atau mengangkut  barang atau penumpang dari suatu tempat ke tempat lain. Transportasi dikatakan  baik, apabila perjalanan cukup cepat, tidak mengalami kemacetan, frekuensi  pelayanan cukup, aman, bebas dari kemungkinan kecelakaan dan kondisi  pelayanan yang nyaman. Untuk mencapai kondisi yang ideal seperti, sangat ditentukan oleh berbagai faktor yang menjadi komponen transportasi ini, yaitu kondisi prasarana (jalan), sistem jaringan jalan, kondisi sarana (kendaraan) dan sikap mental pemakai fasilitas transportasi tersebut (Budi D.Sinulingga, 1999).

Perluasan ruas  jalan Perjalanan Perlu transportasi Fasilitas transportasi Kemampuan menjangkau

2.3 Teknik Perlalulintasan(Tr affi c Technique) 

Suatu transportasi dikatakan baik, apabila waktu perjalanan cukup cepat tidak mengalami kemacetan, frekuensi pelayanan cukup, aman bebas dari kemungkinan kecelakaan dan kondisi pelayanan yang nyaman. Untuk mencapai kondisi yang ideal seperti itu sangat ditentukan oleh berbagai faktor yang menjadi komponen transportasi, yaitu kondisi prasarana (jalan) serta sistem jaringannya dan kondisi sarana (kendaraan),serta yang tak kalah pentingnya ialah sikap mental pemakai fasilitas transportasi tersebut.

Untuk mengetahui tentang transportasi kota dalam aspek perencanaan dan  pelaksanaannya, maka penting sekali untuk memahami aspek teknik  perlalulintasan (traffic technique). Teknik lalu lintas angkutan darat meliputi: karakteristik volume lalu lintas, kapasitas jalan, satuan mobil penumpang, asal dan tujuan lalu lintas, dan pembangkit lalu lintas (Sinulingga, 1999).

2.4 Karakteristik Volume Lalu Lintas

Di dalam suatu perlalulintasan dikenal lalu lintas harian atau AADT ( Average  Annual Daily Traffic) yaitu jumlah kendaraan yang lewat secara rata-rata dalam sehari (24 jam) pada suatu ruas jalan tertentu, besarnya lalu lintas harian akan menentukan dimensi penampang jalan yang akan di bangun. Volume lalu lintas ini bervariasi besarnya, tidak tetap, tergantung waktu, variasi dalam sehari, seminggu maupun sebulan dan setahun. Di dalam satu hari biasanya terdapat dua waktu jam sibuk, yaitu pagi dan sore hari. Tapi ada juga jalan-jalan yang mempunyai variasi volume lalu lintas agak merata. Volume lalu lintas selama jam sibuk dapat digunakan untuk merencanakan dimensi untuk menampung lalu lintas. Semakin tinggi volumenya, semakin besar dimensi yang diperlukan. Suatu volume yang over estimate akan membuat perencanaan menjadi boros, sedangkan volume yang under estimate akan membuat jaringan jalan cepat mengalami kemacetan, sehingga memerlukan pengembangan pula.

2.5 Teori Graf

Graf adalah suatu diagram yang memuat informasi tertentu jika diinterpretasikan secara tepat. Dalam kehidupan sehari-hari, graf digunakan untuk menggambarkan  berbagai macam struktur yang ada. Tujuannya adalah sebagai visualisasi

objek-objek agar lebih mudah dimengerti.

Teori graf merupakan pokok bahasan yang sudah tua usianya namun memiliki banyak terapan sampai saat ini. Di ilmu matematika dan komputer teori graf adalah himpunan benda-benda yang disebut verteks ( vertex atau node) yang terhubung oleh jalur-jalur (edges). Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Representasi visual dari graf adalah dengan menyatakan objek sebagai noktah, bulatan atau verteks, sedangkan hubungan di antara objek dinyatakan dengan garis (jalur).

Banyak sekali struktur yang bisa direpresentasikan dengan graf, dan banyak masalah yang bisa diselesaikan dengan bantuan graf. Jaringan jalan raya pada sebuah wilayah bisa direpresentasikan dengan graf. Verteks-verteksnya adalah kota-kota yang terdapat pada wilayah tersebut dan ada jalur antara kota A dan kota B dihubungkan oleh sebuah jalan.

Sebuah struktur graf dikembangkan dengan memberi bobot pada tiap jal ur. Graf berbobot dapat digunakan untuk melambangkan berbagai konsep. Sebagai contoh jika suatu graf melambangkan jaringan jalan maka bobotnya bisa berarti  panjang jalan maupun batas kecepatan tertinggi jalur tertentu. Ekstensi lain pada

graf adalah dengan membuat jalurnnya berarah, yang secara teknis disebut graf  berarah atau digraph (directed graph). Digraf dan jalur berbobot disebut jaringan. Jaringan banyak digunakan pada cabang praktis teori graf yaitu analisis jaringan. Pada analisis jaringan, definisi kata jaringan bisa berbeda dan sering berarti graf sederhana (tanpa bobot dan arah).

Graf G  didefinisikan sebagai pasangan terurut (V ,  E ) dan dilambangkan dengan G = (V , E ) dimana:

1. V  = {v1, v2, ... , vn} adalah himpunan tak kosong yang terbatas dan

anggota-anggotanya dinamakan simpul

2.  E = {e1, e2, ... , en} adalah himpunan sisi yang menghubungkan sepasang

simpul (Munir, 2003).

Definisi diatas menyatakan bahwa V   tidak boleh kosong, sedangkan  E   boleh kosong. Jadi sebuah graf dimungkinkan tidak mempunyai sisi satu buah  pun, tetapi simpulnya harus ada minimal satu. Graf yang hanya mempunyai satu  buah simpul tanpa sebuah jalur dinamakan graf trivial. Jumlah simpul pada suatu

graf dinyatakan dengan V   dan jumlah sisi dinyatakan dengan  E  .

Simpul pada graf dapat dinomori dengan huruf, seperti a, b, c, ..., v, w, ..., dengan bilangan asli 1, 2, 3, ..., 3 atau gabungan keduanya. Sedangkan sisi yang menghubungkan simpul u dengan simpul v dinyatakan dengan pasangan (u, v) atau dinyatakan dengan lambang



1,



2… Dengan kata lain, jika e adalah sisi yang menghubungkan simpul u dengan simpul v, maka e dapat ditulis sebagai e = (u, v). Nama suatu jalur dapat dituliskan dengan pasangan simpulnya, misalnya dari gambar graf dibawah jalur



2.

b



3 c a



2



4



1 e



₅ d

Gambar 2.2 Graf G dengan Lima Simpul dan Lima Sisi

Suatu graf dapat disajikan dalam bentuk diagram seperti pada gambar 2.2 di atas. Selain itu graf dapat juga disajikan dalam bentuk matriks yaitu matriks  berelasi dan matriks berisisian seperti berikut ini.

Andaikan G = (V ,  E ) adalah graf sederhana dengan banyak simpul di V  adalah n. Misalkan simpul-simpul dari G  adalah v1, v2, ... , vn. Matriks berelasi

dari suatu graf G adalah matriks nol satu n  n dengan 1 sebagai entri dari a_ij jika vi dan v j berelasi artinya (vi, v j)  E , dan 0 sebagai entri dari aij jika vidan v jtidak

 berelasi artinya v_i,v _j  E . Dengan kata lain jika matriks berdekatan, maka

entrinya adalah:

1, jika vi, v j  E

0, jika vi, v j  E 

Matriks berdekatan dari graf sederhana adalah simetrik, yaitu a_ij a  _ji.

Kedua entri itu sama dengan 1 bila v_i  dan v _j berdekatan dan keduanya sama dengan 0 bila v_idan v _jtidak berdekatan. Selanjutnya karena matriks dari graf sederhana tidak mempunyai loop, maka setiap entri aij  untuk i =  j  adalah 0.

Matriks berdekatan dapat juga digunakan untuk menyajikan graf tidak berarah yang mempunya loop dan jalur ganda. Suatu loop pada simpul v_i atau v _jdiwakili oleh 1 pada posisi v_i ke v _jdengan i = j sehingga aij = 1 untuk



=

 

 pada matriks

 berdekatan. Untuk jalur ganda bahwa entri aij  pada matriks berdekatan adalah

sama dengan banyaknya jalur yang berhubungan v_i dengan v _jdengan i = . Semua graf tidak berarah yang mempunyai jalur ganda dan pseudograf mempunyai matriks berdekatan yang simetris.

Contoh matriks berdekatan untuk menyajikan graf pada gambar 2.2. Kalau urutan simpul-simpulnya adalah a, b, c, d , e maka dapat dianggap v a

1 , v2 b,

c

v3  , v₄ d , v5 e. Dari gambar 2.2 diperoleh  E  = {ac, ae, be, dc, de} berarti 13

a  = 1, a15 = 1, a25 = 1, a43= 1, dan a₄₅ 1, sedang selainnya entrinya 0. Matriks

yang menyajikan graf tersebut adalah sebagai berikut:



0 0 1 0 1 0 0 0 0 1 1 0 0 1 0 0 0 1 0 1 1 1 0 1 0



ai =

Jika matriks bersisian digunakan untuk merepresentasikan hubungan antara simpul-simpul graf, maka untuk menunjukkan hubungan antara simpul-simpul dan jalur-jalur pada graf digunakan matriks berelasi. Definisi dari matriks berelasi disajikan sebagai berikut.

Misalkan G = (V , E ) adalah graf tidak berarah dengan V 



v₁,v₂,



,v_k 



 dan



e e ek 



 E  ₁, ₂,



,  maka matriks bersisian yang berkenaan dengan urutan V  dan E 

adalah matriks m  n, dengan entrinya adalah :

1, jika jalur ei berinsiden dengan vi

0, jika jalur ei tidak berinsiden dengan vi

Selain untuk menyajikan graf sederhana, matriks bersisian dapat juga digunakan pada jalur-jalur ganda dan loop. Untuk mewakili jalur-jalur ganda pada matriks bersisian menggunakan kolom sebagai jalur dan baris sebagai simpul. Kalau jalurnya ganda berarti jalur-jalur ini bersisian dengan pasangan simpul yang sama. Kalau terdapat loop berarti jalur itu bersisian dengan tepat satu simpul sehingga entrinya sama dengan 1.

Matriks bersisian dari graf pada gambar 2.2. simpul vi bersisian dengan jalur

e1 dan e1maka m11 = 1, dan m13 = 1, simpul v2 bersisian dengan jalur e2 maka, m22

= 1, simpul v3 bersisian dengan jalur e3 dan e4 maka m33 = 1, dan e4 =1, simpul v4

 bersisian dengan jalur e4  dan e5  maka m44  =1 dan m45  = 1, simpul v5  bersisian

dengan jalur e1, e2, dan e5 maka m51  = 1, m52  = 1, dan m55  = 1. Jadi matriks

 bersisian dari graf pada gambar 3.1 tersebut adalah



0 0 1 0 1   0 0 0 0 1   1 0 0 1 0   0 0 1 0 1   1 1 0 1 0



Setiap garis pada graf berhubungan dengan satu atau dua titik. Titik-titik tersebut dinamakan titik ujung. Garis yang hanya berhubungan dengan satu titik ujung disebut loop. Dua garis berbeda yang menghubungkan titik yang sama

disebut garis paralel. Perlu diketahui bahwa panjang garis, kelengkungan garis, dan letak titik tidak berpengaruh dalam suatu graf.

Menurut teori graf, persoalan lintasan terpendek (the shortest path  problem) adalah suatu persoalan untuk mencari lintasan antara dua buah simpul  pada graf berbobot yang memiliki gabungan nilai jumlah bobot pada sisi graf

yang dilalui dengan jumlah yang paling minimum. 2.5.1 Macam-macam Graf

Berdasarkan arah dan bobotnya graf digolongkan atas 4 jenis, yaitu:

1. Graf berarah dan berbobot yaitu graf yang setiap sisinya memiliki orientasi arah dan bobot.

2. Graf berarah dan tak berbobot yaitu graf yang sisinya mempunyai arah dan tidak berbobot.

3. Graf tidak berarah dan berbobot yaitu graf yang setiap sisinya tidak mempunyai arah tetapi memiliki bobot.

Graf tidak berarah dan tidak berbobot yaitu graf yang setiap sisinya tidak memiliki arah dan bobot.

2.5.2 Terminologi dalam Graf

Terminologi (istilah) yang berkaitan dengan graf akan sering digunakan. Di  bawah ini didefinisikan beberapa istilah yang sering dipakai dan berhubungan

dengan maximum spanning tree.

1. Walk   adalah suatu barisan berhingga dari verteks dan edge secara  bergantian, yang diawali dari verteks dan diakhiri dengan verteks. Bentuk

umum dari walk  adalah:

n n n n e v e v v v e v_{0 0 1 1},



, ₁ ₁

Dalam hal ini



0 merupakan verteks awal dan





 merupakan verteks akhir. Jika verteks awal dan verteks akhir dari suatu walk adalah sama, maka walk  disebut close walk (walk  tertutup).

2. Trail adalah suatu walk dengan setiap edge-nya berlainan. 3.  Path adalah suatu walk dengan setiap verteksnya berbeda.

4. Cycle adalah suatu  path yang memiliki verteks awal sama dengan verteks akhir.

5.  Length (panjang) adalah bilangan yang menyatakan banyaknya edge  yang muncul dalam suatu walk .

6.  Edge e adalah sebuah jembatan untuk G  jika G dengan e tidak terhubung. Secara umum edge e adalah jembatan untuk suatu graf G jika G dengan e mempunyai komponen terhubung lebih dari G.

2.5.3 Graf Terhubung, Graf Berbobot, dan Subgraf 1. Graf Terhubung

Misalkan u dan v adalah titik yang berbeda pada graf G. Maka titik u dan v dapat dikatakan terhubung (connected ), jika terdapat lintasan u-v di G. Sedangkan suatu graf G dapat dikatakan terhubung (connected ), jika untuk setiap titik u  dan v di G  terhubung. Keterhubungan adalah sifat yang dimiliki oleh graf. Graf terhubung dapat dilihat atau dibuktikan dari keterhubungan antara u dan v. Untuk lebih menguatkan kondisi ( u, v):

Gambar 2.3 Graf Terhubung (Connected Graph)

2. Graf berbobot (weighed graph)

Graf berbobot adalah graf yang setiap sisinya diberi sebuah bobot. Bobot  pada tiap sisi dapat berbeda-beda bergantung pada masalah yang

dimodelkan dengan graf (Munir, 2005). Contohnya,

 A  E

 D C

8 3 5 ₁ 2 4 ₆ 6 3 10 7  D

Gambar 2.4 Graf Berbobot (Weighted Graph)

Graf G pada gambar 2.4 dikatakan berbobot karena pada setiap edge diberi sebuah bobot.

3. Graf berarah dan berbobot (directed graph)

Graf yang setiap sisinya diberikan orientasi arah disebut sebagai graf  berarah. Secara umum sisi berarah disebut dengan busur (arc). Pada graf  berarah (u,v) dan (v,u) menyatakan dua buah busur yang berbeda, dalam arti kata bahwa (u,v)  (v,u). Jadi untuk busur (u,v) simpul u dinamakan simpul asal dan simpul v dinamakan simpul terminal atau simpul tujuan. Graf berarah sering dipakai untuk menggambarkan aliran proses, peta lintas kota dan lain sebagainya. Sehingga pada graf berarah gelang atau looping diperbolehkan tetapi sisi ganda tidak diperbolehkan. Contohnya,

Gambar 2.5 Graf Berarah dan Berbobot  A  E _C  B 7 5 9 8 6 4 A D B C E F

4. Subgraf

Graf  H  disebut subgraf jika setiap titik dari graf  H  juga merupakan titik dari graf G  dan setiap edge  pada  H   juga merupakan edge  pada graf G.

Contoh dari subgraf adalah:



2

Gambar 2.6 Graf dan Subgrafnya



_

₅



1 Graf G



3



2



1



3



5



2



1



4



3



1



4



2

2.6 Algoritma Dijkstra

Algoritma Dijkstra untuk menentukan rute terpendek. Algoritma Dijkstra digunakan pada graf berarah dan berbobot. Jika bobot graf > 0, maka digunakan Dijkstra dengan level satu, dan bila bobot graf ada yang negatif akan digunakan level dua. Dalam penelitian ini akan dipakai algoritma Dijkstra yang memakai  bobot > 0, karena bobot graf merepresentasikan jarak antar titik sehingga  bobotnya positif.

Algoritma ini diberi nama sesuai nama penemunya, Edsger Wybe Dijkstra. Algoritma Dijkstra mencari lintasan terpendek dalam sejumlah langkah. Algoritma ini menggunakan prinsip Greedy yang menyatakan bahwa pada setiap langkah kita memilih sisi yang berbobot minimum dan memasukkannya ke dalam himpunan solusi. Input algoritma ini adalah sebuah graf berarah yang berbobot (weighted directed graph) G dan sebuah sumber verteks S  dalam G dan V  adalah himpunan semua verteks dalam graf G (Munir, 2005).

Ada beberapa versi algoritma Dijkstra, salah satunya adalah sebagai  berikut. Misalkan,

V (G) :



v₁,v₂,



,v_n



.

 L : himpunan titik-titik V (G) yang sudah terpilih dalam alur  path (jalur) terpendek.

 D( j) : jumlah bobot path (jalur) terkecil dari vi ke v j.

W (i, j) : bobot garis dari titik vi ke titik v j.

W*(i, j): jumlah bobot path terkecil dari vi ke v j.

Secara formal, algoritma Dijkstra untuk mencari jalur terpendek adalah sebagai berikut.

1.  L 

 

V =



v₁,v₂,



,v_n



.

2. Untuk  j = 2, … , n, lakukan D( j)W (1, j)

3. Selama vn L lakukan :

} {v_k   L

 L .

 b. Untuk setiap keadaan v1mempuyai edge ke v j lakukan :

Jika D( j) D(k )W (k , j) maka ganti D( j) dengan D(k ) + W (k, j)

4. Untuk setiap keadaan edge dari v1 ke v j adalah terkecil , maka W*(i, j) =

 D( j).

Menurut algoritma tersebut,  path  (jalur) terpendek dari titik vi ke vn  adalah

melalui titik-titik dalam secara berurutan, dan jumlah bobot  path  (jalur) terkecilnya adalah D(n).

Dalam jurnalnya, Deiby T. Salaki (2011) mengatakan bahwa salah satu masalah umum yang dapat diselesaikan dengan menggunakan teori graf adalah Masalah Lintasan Terpendek (Shortest Path Problem atau SPP ) yang mencari lintasan dengan jumlah bobot paling minimum. Algoritma Dijkstra merupakan salah satu algoritma untuk menyelesaikan masalah ini. Penelitian tersebut ditujukan untuk membuat lintasan terpendek yang dapat dilalui kendaraan roda empat dari Fakultas MIPA ke Fakultas lainnya di kampus UNSRAT dengan menggunakan Algoritma Dijkstra. Shortest Path Problem (SPP ) adalah suatu  persoalan untuk mencari lintasan antara dua atau lebih simpul pada graf berbobot yang gabungan bobot sisi graf yang dilalui berjumlah paling minimum. Persoalan ini juga merupakan suatu persoalan optimasi yang menggunakan graf berbobot, dimana bobot dapat menyatakan jarak antar kota, waktu pengiriman pesan, ongkos pembangunan, dan sebagainya (Pradana, 2009).

Algoritma Dijkstra adalah algoritma yang dikhususkan untuk pencarian  jalan terbaik dalam sebuah graf (Willy Setiawan, 2010).