BAB 9 DERET FOURIER. Ir. A.Rachman Hasibuan dan Naemah Mubarakah, ST

BAB 9

DERET FOURIER

Oleh :

Oleh :

Ir. A.Rachman Hasibuan dan

Naemah Mubarakah, ST

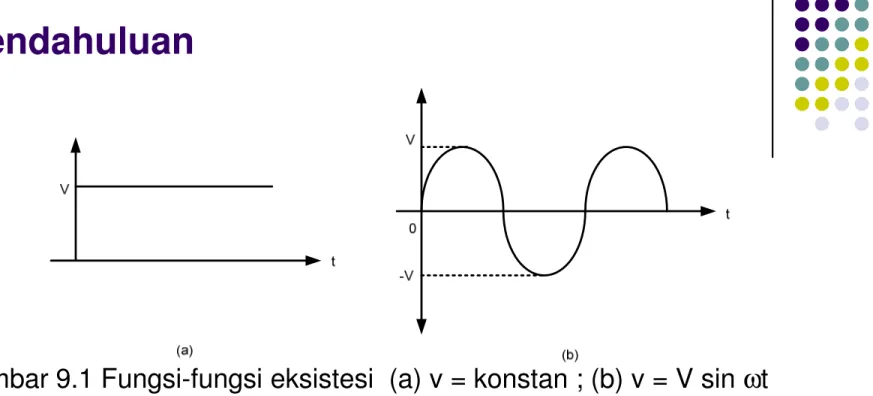
9.1 Pendahuluan

Gambar 9.1 Fungsi-fungsi eksistesi (a) v = konstan ; (b) v = V sin ωt Gambar 9.1 Fungsi-fungsi eksistesi (a) v = konstan ; (b) v = V sin ωt

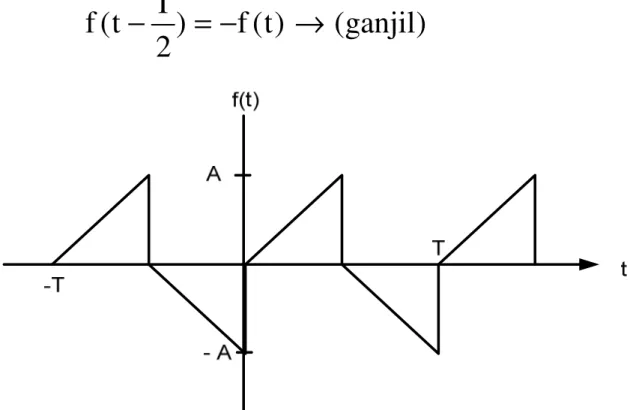
Gambar 9.2 Gelombang gigi gergaji

Gelombang gergaji ini dapat dinyatakan sebagai f(t) = (V/T)t dalam interval 0 < t < T dan oleh f(t) = (V/T)(t – T) dalam interval T < t < 2T.

9.2 Deret Fourier Trigonometri

Suatu fungsi f (t) dikatakan periodik apabila :

f(t) = f(t + nT)

dimana n adalah bilangan bulat/integer dan T adalah periode dari f (t), Menurut teori Fourier setiap fungsi periodik dengan frekuensi ω_o dapat di ekspresikan sebagai perjumlahan dari fungsi sinus ataupun kosinus atau :

{ 4 4 4 4 4 3 4 4 4 4 4 2 1 ac ) t n sin b t n cos a ( dc a f(t) 1 n o n o n o ↓ ↓

∑

∞ = ω + ω + =

ω_o = 2π/T disebut sebagai frekuensi dasar

sin nωot atau cos nωot merupakan harmonisa yang ke-n dari f (t) dan bila n merupakan bilangan ganjil disebut harmonisa ganjil dan bila genap

Suatu fungsi f(t) dapat dinyatakan dengan sebuah deret Fourier apabila : 1. f(t) memiliki nilai tunggal untuk setiap t.

2. Jika f(t) tidak kontinyu maka hanya terdapat jumlah diskontinuitas terbatas pada periode T.

3. Memiliki jumlah maksimum dan minimum yang terbatas dalam periode.

4. Untuk setiap t₀.

syarat-syarat ini disebut sebagai syarat Dirichlet

∫

t +T

<

∞

t 0 0

dt

|

)

t

(

f

∫

∫

∫

→ = ω ω ≠ → = ω → = ω T T 0 o T 0 o ) c ( .... m , n semua 0 dt t n n cos t n sin ) b ( .. ... ... 0 n semua 0 dt n cos ) a ( ... ... ... n semua 0 dt n sin

Adapun proses untuk menentukan koefisien a_o ; a_n dan b_n disebut sebagai analisa. Fourier, dimana dalam analisa Fourier ini ada beberapa bentuk integral trigonometri yang sangat membantu diantaranya :

∫

∫

∫

∫

∫

→ = ω → = ω ≠ → = ω ω ≠ → = ω ω → = ω ω T 0 o 2 T 0 o 2 T 0 o o T 0 o o T 0 o o ) g ( ... ... m semua 2 / T dt t m cos ) f ( ... ... n semua 2 / T dt n cos ) e ( ... ... m n 0 dt t m cos n cos ) d ( ... ... m n 0 dt t n sin n sin ) c ( .... m , n semua 0 dt t n n cos t n sin

∫

= T 0 o f(t)dt T 1 a =

∫

ω T 0 o n f(t)cosn tdt T 2 a =

∫

ω T 0 o n f(t)sinn tdt T 2 b

Dari analisa Fourir, didapat :

∑

∞ = φ + ω + = 1 n n o n o A cos(n t ) a ) t ( f ∞ ∞ ; dan Maka :

∑

∑

∞ = ∞ = ω φ − ω φ + = φ + ω + 1 n o n n o n n o 1 n o n

o A cos(n t n) a (A cos )cosn t (A sin )sinn t

a n n n

A

cos

a

=

φ

b_n = −(A_n sinφ_n) A_n = a_n2 + b_n2 n n 1 n a b tan− − = φ

dalam bentuk kompleks :

A

_n

∠

φ

_n

=

a

_n

−

jb

_n

Sehingga :

Carilah bentuk deret Fourier gelombang dibawah ini dan gambarkan juga spektrum amplitudo dan spektrum fasa dari gelombang tersebut.

Contoh :

Jawab :

Adapun deret Fourier :

∑

∞ = ω + ω + = 1 n o n o n o (a cosn t b sinn t) a f(t)

Adapun bentuk persamaan gelombang diatas :

   < < → < < → = 2 t 1 0 1 t 0 1 ) t ( f

2 1 t 2 1 dt 0 dt 1 2 1 dt ) t ( f T 1 a 0 1 2 0 1 0 T 0 o  = =    + = =

∫

∫

∫

0 0 dt t n cos 0 1 0 t sin n 1 dt t n cos 1 2 2 dt t n cos ) t ( f T 2 a 2 1 1 0 T 0 o n =                         π + π π π = ω = ↓ ↓

∫

∫

∫

4 4 3 4 4 2 1 4 43 4 42 1 0 n _  π ) 1 n (cos n 1 0 dt t n sin 0 1 0 t n cos n 1 dt t n sin 1 2 2 dt t n sin ) t ( f T 2 b 2 1 1 0 T 0 o n π− π − =                         π + π π − π = ω = ↓ ↓

∫

∫

∫

4 4 3 4 4 2 1 43 42 1

[

]

    → → π = − − π = genap n harga untuk 0 ganjil n harga untuk n 2 ) 1 ( 1 n 1 b_n n

Harga-harga a₀, a_n dan b_n yang telah diperoleh disubstitusikan ke persamaan umum deret fourier, maka deret Fourier dari bentuk gelombang diatas adalah :

...

t

5

sin

5

2

t

3

sin

3

2

t

sin

2

2

1

)

t

(

f

π

+

π

+

π

π

+

π

π

+

=

1 k 2 n : ini hal dalam t n sin n 1 2 2 1 ) t ( f 1 k − = → π π + =

∑

∞ =

untuk mendapatkan spektrum amplitudo dan spektrum fasa : untuk mendapatkan spektrum amplitudo dan spektrum fasa :

{ {     → → π = = → π = + = ↓ ↓ 0 ngenap ganjil n n 2 b ganjil n n 2 n b b 0 a An _n2 _n2 _n    → ° → ° − = − = φ − ganjil n 0 genap n 90 a b tan n n 1 n

Telah diketahui didepan bahwa ω0 = π dan harga An dan φn untuk beberapa harga n maka hasilnya seperti pada tabel dibawah ini.

maka spektrum amplitudo : π 2 π 3 2 2 n φ o ω π 2π 3π 4π 5π 6π π 3 π 5 2 o ω π 2π 3π 4π 5π 6π

9.3 Kesimetrisan

9.3.1 Simetris Genap

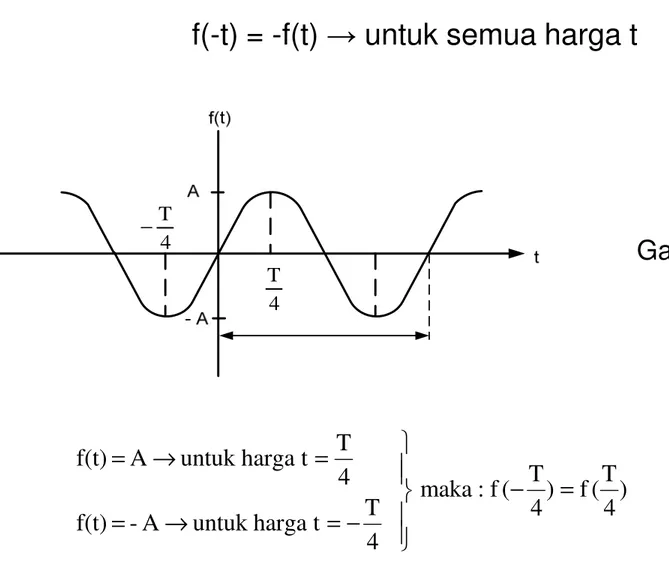
f(t) = f(-t) → untuk semua harga t

T T − 2 T 2 T −

Gambar 9.3 Fungsi Genap

) 2 / T ( f ) 2 / T ( f : maka T/2 t harga untuk A -f(t) T/2 t harga untuk A -f(t) − =    − = → = = → =

Adapun sifat yang utama dari fungsi genap ini adalah :

∫

∫

=

− 2 / T 0 e 2 / T 2 / T e

(

t

)

dt

2

f

(

t

)

dt

f

dimana notasi e pada f_e(t) untuk melambangkan fungsi genap (even).

didapat koefisien-koefisien Fourier-nya :

∫

= 2 / T 0 0 f(t)dt T 2 a

∫

ω = 2 / T 0 0 n f(t)cosn tdt T 4 a b_n = 0

9.3.2 Simetris Ganjil

f(-t) = -f(t) → untuk semua harga t

4 T −

Gambar 9.4 Fungsi Ganjil

4 T

4 _{Gambar 9.4 Fungsi Ganjil}

) 4 T ( f ) 4 T ( f : maka 4 T t harga untuk A -f(t) 4 T t harga untuk A f(t) = −       − = → = = → =

Adapun bentuk umum fungsi ini adalah :

0

dt

)

t

(

f

2 / T 2 / T o

=

∫

−

dimana f_o(t) hanya berupa simbol dari fungsi ganjil (Odd).

Untuk fungsi ganjil ini harga-harga : A₀ = 0 an = 0 an = 0

∫

ω

=

2 / T 0 0 n

f

(

t

)

sin

n

t

dt

T

4

b

Setiap fungsi periodik f(t) dapat merupakan gabungan fungsi-fungsi genap atau ganjil saja ataupun gabungan fungsi genap atau ganjil

) t ( f ) t ( f ganjil t n sin b genap t n sin a a ) t ( f _{e o} 1 n 0 n 1 n 0 n 0 + ω + ω = + = ↓ ↓

∑

∑

∞ = ∞ =_{4 4443 14 24 4 34} 4 4 2 1

9.3.3 Simetris Gelombang Setengah

Suatu fungsi dikatakan simetris gelombang setengah apabila :

) ganjil ( ) t ( f ) 2 T t ( f − = − →

Koefisien Fourier nya :         + = =

∫

∫

∫

− − 2 / T 0 0 2 / T 2 / T 2 / T 0 f(t)dt f(t)dt T 1 dt ) t ( f T 1 a f(x)dx f(t)dt 0 T 1 a 2 / T 0 2 / T 0 0 =         + − =

∫

∫

→

















ω

+

ω

=

∫

∫

− 2 / T 0 0 0 2 / T 0 n

f

(

t

)

cos

n

t

dt

f

(

t

)

cos

n

t

dt

T

2

a





_{−T/2 0}

T

[

]

     ω = ω − − =

∫

∫

genap n untuk . ... ... ... ... 0 ganjil n untuk . ... dt t n cos ) t ( f T 4 dt t n cos ) t ( f ) 1 ( 1 T 2 a 2 / T 0 0 2 / T 0 0 n n











ω

=

∫

genap

n

untuk

.

...

...

...

...

0

ganjil

n

untuk

.

...

dt

t

n

sin

)

t

(

f

T

4

b

2 / T 0 0 n

Contoh :

Carilah deret Fourir dari f(t) yang tergambar di bawah ini :

Jawab :

Fungsi ini adalah fungsi ganjil sehingga a₀ = 0 = a_n dimana 2

2π π π

Fungsi ini adalah fungsi ganjil sehingga a₀ = 0 = a_n dimana periodenya T = 4 sehingga 2 4 2 T 2 0 π = π = π = ω , maka :

∫

ω = 2 / T 0 0 n f(t)sinn tdt T 4 b

















_π

+

π

=

∫

∫

2 1 1 0 n

t

dt

2

n

sin

0

dt

t

2

n

sin

1

4

4

b

→

      π − π = π π − = 2 n cos 1 n 2 2 t n cos n 2 b 1 0 n

∑

∞ = π       π − π = 1 n 2 n sin 2 n cos 1 n 1 2 ) t ( f

→

Contoh :

Carilah deret Fourir dari fungsi di bawah ini :

Jawab :

Fungsi adalah gelombang ganjil setengah simetris, sehingga a₀ = 0 = a_n dengan periode T = 4 dan

2 4 2 T 2 0 π = π = π = ω f(t) = 1 → -1 < t < 1 . Maka :

∫

ω = 2 / T 0 0 n f(t)sinn tdt T 4 b Maka :

→

n₂ cos n 4 2 n sin n 8 b 2 2 n π π − π π =

karena sin (-x) = - sin x pada fungsi ganjil dan cos (-x) = cos x pada fungsi genap, maka :













=

=

−

π

=

=

−

π

=

+ −

...

,

6

,

4

,

2

genap

n

untuk

)

1

(

n

4

...

,

5

,

3

,

1

ganjil

n

untuk

)

1

(

n

8

b

2 / ) 2 n ( 2 / ) 1 n ( 2 2 n

 π

n

sehingga :

∑

∞ =

π

=

1 n n

t

2

n

sin

b

)

t

(

f

9.4 Pemakaian Pada Rangkaian Listrik

Adapun langkah-langkah yang diperlukan diantaranya :

Untuk mendapatkan respons steady state rangkaian terhadap eksitasi non-sinusoidal periodik ini diperlukan pemakaian deret Fourier, analisis fasor ac dan prinsip superposisi.

Adapun langkah-langkah yang diperlukan diantaranya : 1. Nyatakan eksitasi dalam deret Fourier.

2. Transformasikan rangkaian dari bentuk wawasan waktu menjadi wawasan frekuensi.

3. Cari resonse komponen dc dan ac dalam deret Fourier. 4. Jumlahkan masing-masing response secara superposisi.

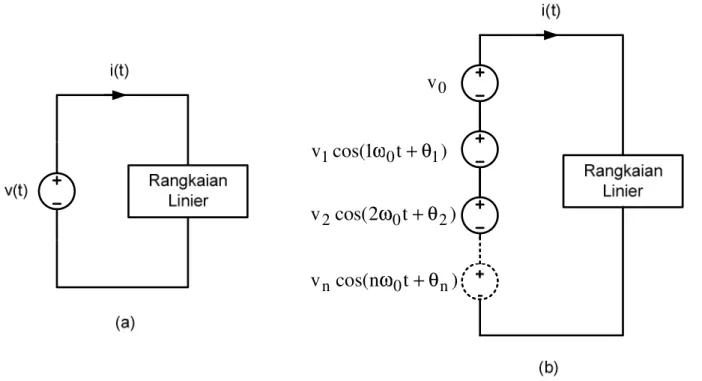
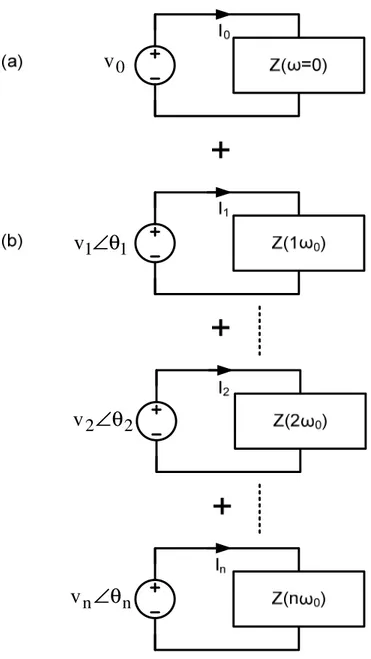
) t 1 cos( v₁ ω₀ +θ₁ ) t 2 cos( v₂ ω₀ +θ₂ ) t n cos( v_n ω₀ +θ_n 0 v

Gambar 9.6 a) Rangkaian linier dengan sumber tegangan periodik b) Merepresentasekan deret Fourier (wawasaan waktu)

adapun pernyataan deret Fourier-nya :

∑

∞ = θ + ω + = 1 n n 0 n 0 V cos(n t ) V ) t ( v

0

v

1 1

v ∠θ

Gambar 9.7 a) Respons steady state komponen dc b) Respons steady state komponen ac (wawasan frekuensi)

n n v ∠θ 2 2 v ∠θ

∑

∞ = Ψ + ω + = 1 n n 0 0 In cos(n t ) i ) t ( i

Contoh :

Rangkaian seperti di bawah ini :

Bilamana sumber tegangan v_s(t) pada rangkaian berbentuk :

1 k 2 n t n sin n 1 2 2 1 ) t ( v 1 k s π → = − π + =

∑

∞ = Carilah v₀(t). (*)

Jawab : s s n n 0 V n 2 j 5 n 2 j V L j R L j V π + π = ω + ω =

(

π

)

π + =       → π + π = j2n n 2 j 5 1 V 1 V : atau n 2 j 5 n 2 j V V s 0 s 0 ) 90 2 ( n 1 ) 2 j ( n 1 2 j 1 n 1 n 2 j 1 V : atau n 2 j V 1 s s ° − ∠ π = − π =       π = π = → π = ° − ∠ = 2 90 V_s _     ° − ∠ π π + π = 90 n 2 n 2 j 5 n 2 j V₀

→

° − ∠ π = 90 n V_s = _{+ π}_{ π} ∠ −90°_ n n 2 j 5 V₀ 2 2 1 0 n 4 25 5 n 2 tan 4 V π +       π − ∠ = −

→

dan dalam wawasan waktu :

1 k 2 n : untuk 5 n 2 tan t n cos n 4 25 4 ) t ( V 1 1 k 2 2 0  → = −      π − π π + = ∞ − =

∑

maka dengan mensubstitusikan harga ( k = 1, 2, 3, … atau n = 1, 3, 5,…) untuk harmonisa ganjil akan diperoleh :

Volt ... ) 96 , 80 t 5 ( cos 1257 , 0 ) 14 , 75 t 3 ( cos 2051 , 0 ) 49 , 51 t 1 ( cos 4981 , 0 ) t ( 0 V + ° − π + ° − π + ° − π =

dan kalau digambarkan spektrum amplitudo-nya :

ω

π 2π 3π 4π 5π 6π 7π

0

9.5 Daya Rata-rata dan RMS

Untuk mendapatkan harga daya rata-rata yang diserap oleh suatu rangkaian dengan sumber suatu fungsi periodik , yaitu :

∑

∞ = θ ω + = 1 n n 0 n dc V cos(n t - ) V ) t ( v

∑

∞ = φ ω + = I_dc V_m cos(m ₀t - _m) ) t ( i

∑

=1 m

sedangkan sebagaimana diketahui bahwa daya rata-rata adalah :

∫

= T 0 vi dt T 1 P

∑

∞ = φ θ + = 1 n n n n n dc dc V I cos( - ) 2 1 I V P

harga efektif (rms) dari suatu f(t) adalah :

∫

= T 0 2 rms f (t) dt T 1 F

∑

(

)

∞ = + + = 1 n 2 n 2 n 2 0 rms a b 2 1 a F

→

→

Contoh :

Rangkaian seperti di bawah ini :

Carilah daya rata-rata yang diberikan oleh sumber ke rangkaian bilamana : A ) 35 t 3 cos( 6 ) 10 t cos( 10 2 ) t ( i = + + ° + + °

Jawab : Impedansi rangkaian : ω + = ω + ω       ω =       ω +       ω = + = 20 j 1 10 2 j 1 20 j 2 j 10 2 j 1 10 2 j 1 10 X R X . R Z C C maka : ω ∠ ω + = ω ∠ ω + = ω + = ω + = = − − _{1 400 tan 20} I . 10 1 20 tan ) 20 ( 1 I . 10 20 j 1 I . 10 20 j 1 10 . I Z . I V 1 2 1 2 2 untuk komponen dc (ω = 0) : 1 untuk komponen dc (ω = 0) : I = 2 A

→

20v ) 0 ( 20 tan ) 0 ( 400 1 ) 2 ( 10 V 1 2_∠ = + = −

untuk ω = 1 rad/det, maka :

° − ∠ = ° ∠ ° ∠ = ∠ + ° ∠ = → ° ∠ = − _{20 87,14} 5 77,14 10 100 ) 1 ( 20 tan ) 1 ( 400 1 ) 10 10 ( 10 V dan 10 10 I 1 2

untuk ω = 3 rad/det, maka :

° − ∠ = ° ∠ ° ∠ = ∠ + ° ∠ = → ° ∠ = − 60 89,04 1 54,04 35 60 ) 3 ( 20 tan ) 3 ( 400 1 ) 35 6 ( 10 V dan 35 6 I 1 2

sehingga dalam wawasan waktu : V ) 04 , 54 t 3 cos( 1 ) 14 , 77 t cos( 5 20 ) t ( v = + − ° + − °

Adapun daya rata-rata dapat dihitung dengan :

∑

∞ = φ θ + = 1 n n n n n dc dc V I cos( - ) 2 1 I V P

[

77,14 ( 10 )

]

1 (1)(6)cos

[

54,04 ( 35 )

]

cos ) 10 )( 5 ( 1 ) 2 ( 20 P = +

[

°− − °

]

+ (1)(6)cos

[

54,04°−(−35°)

]

2 1 ) 10 ( 14 , 77 cos ) 10 )( 5 ( 2 1 ) 2 ( 20 P = + °− − ° + °− − ° P = 40 + 1,247 + 0,05 = 41,297 W cara lain : W 30 , 41 06 , 0 25 , 1 40 10 1 2 1 10 5 2 1 10 20 R V 2 1 R V P 2 2 2 1 n 2 n 2 dc _{+ = + + = + + =} =

∑

∞ =

Contoh :

Suatu tegangan diekspresikan dengan :

... ) 7 , 78 t 4 cos( 4851 , 0 ) 56 , 71 t 3 cos( 6345 , 0 ) 45 , 63 t 2 cos( 8944 , 0 ) 45 t cos( 414 , 1 1 ) t ( v + ° + − + ° + − ° + + ° + − =

carilah harga rms dari tegangan ini.

Jawab : Jawab : Dengan menggunakan :

∑

∞ = + = 1 n 2 n 2 0 rms A 2 1 a F maka :

[

( 1,414) (0,8944) ( 0,6345) ( 0,4851)

]

1,649 V 2 1 1 V_rms = 2 + − 2 + 2 + − 2 + − 2 =

9.6 Bentuk Eksponensial Deret Fourier

∑

∞ −∞ = ω = n t jn ne o c ) t ( f

Untuk mendapatkan harga rms

∑

∞ + + = 2 n 2 n 2 a b a F

→

=

∫

T − ω 0 t jn n

f

(

t

)

e

dt

T

1

c

o

∑

= + + = 1 n n n 2 0 rms 2 b a a F 2 b a c 2 n 2 n n + = 2 0 2 0

a

c

=

∑

∞ = + = 1 n 2 n 2 0 rms c 2 c F Karena : Maka : dan

Contoh :

Carilah bentuk eksponensial deret Fourier dari :

) t ( f ) 2 t ( f : dengan 2 t 0 ; e ) t ( f = t < < π + π = Jawab :

1

T

2

maka

2

T

Karena

=

π

→

ω

₀

=

π

=

maka :

∫

∫

− ω = π − = 1 T jn t 1 2 t jnt π − = 2 t ) jn 1 ( e 1 1 c

→

∫

∫

− ω = _π π − = 2 0 jnt t T 0 t jn n e e dt 2 1 dt e ) t ( f T 1 c o − − π = 0 t ) jn 1 ( n e jn 1 1 2 1 c

[

e

e

1

]

)

jn

1

(

2

1

c

_n 2 j2 n

−

−

π

=

π − π e−j2πn = cos2πn − jsin2πn =1− j0 =1

[

]

) jn 1 ( 51 , 85 1 e ) jn 1 ( 2 1 c_n 2 − = − − π = π

sehingga deret Fourier-nya : jnt

e ) jn 1 ( 51 , 85 ) t ( f

∑

∞ ∞ − − =

→

→