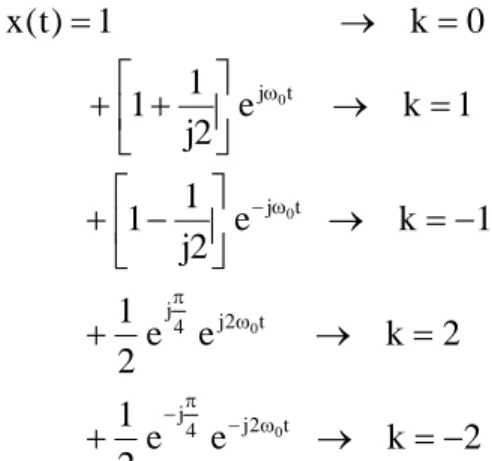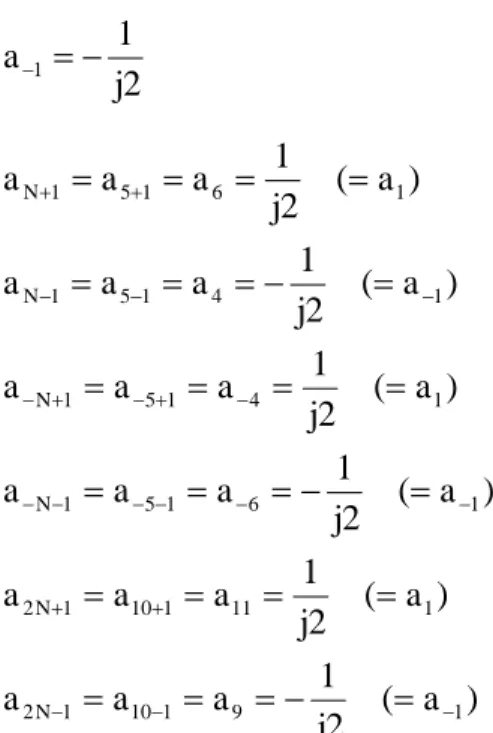ISYARAT DAN SISTEM Bab 4 Deret Fourier Untuk Isyarat Periodik

ISYARAT DAN SISTEM

Bab 4 – Deret Fourier Untuk Isyarat Periodik

Indah Susilawati, S.T., M.Eng.

Program Studi Teknik Elektro

Fakultas Teknik dan Ilmu Komputer

Universitas Mercu Buana Yogyakarta

B A B I V

DERET FOURIER UNTUK ISYARAT PERIODIK

Tujuan Instruksional

1. Umum

Setelah menyelesaikan mata kuliah ini, mahasiswa dapat melakukan analisis dan sintesis sistem yang sangat bermanfaat untuk menunjang kreativitas perekayasaan terutama dalam desain sistem.

2. Khusus

Setelah menyelesaikan bab ini, diharapkan:

- Mahasiswa dapat menyatakan deret Fourier isyarat periodik waktu kontinyu.

- Mahasiswa dapat memahami sifat-sifat deret Fourier waktu kontinyu.

- Mahasiswa dapat menyatakan deret Fourier isyarat periodik waktu diskrit.

- Mahasiswa dapat memahami sifat-sifat deret Fourier waktu diskrit. - Mahasiswa dapat menentukan tanggapan frekuensi sistem LTI. - Mahasiswa dapat memahami tentang filter-filter pemilih frekuensi.

4.1. Tanggapan Sistem LTI Terhadap Eksponensial Kompleks

Tanggapan sistem LTI terhadap masukan eksponensial merupakan isyarat eksponensial yang sama tetapi dengan perubahan amplitudo. Hal ini dapat dinyatakan sebagai:

est → H(s) est (sistem waktu kontinyu) zn → H[z] zn (sistem waktu diskrit)

Suatu isyarat yang menghasilkan keluaran yang merupakan hasil kali suatu konstanta dengan masukannya tersebut, disebut eigenfunction dari sistem tersebut (dalam hal ini adalah est atau zn). Sedangkan faktor amplitudonya disebut dengan eigenvalue sistem tersebut (dalam hal ini adalah H(s) atau H[z]) .

Berikut adalah ilustrasi pada sistem LTI waktu kontinyu.

Terdapat sistem LTI waktu kontinyu dengan tanggapan impuls h(t). Untuk masukan x(t) = est maka keluarannya dapat ditentukan dengan integral konvolusi, yaitu:

) s ( H e d e ) ( h e d e e ) ( h d e ) ( h d ) t ( x ) ( h ) t ( y st s st s st ) t ( s = τ τ = τ τ = τ τ = τ τ − τ =

∫

∫

∫

∫

∞ + ∞ − τ − ∞ + ∞ − τ − ∞ + ∞ − τ − +∞ ∞ − dengan

est merupakan eigenfunction sistem

∫

−+∞∞ τ − _τ τ = h( )e d ) s (

H s merupakan eigenvalue sistem

Sedangkan ilustrasi pada sistem LTI waktu diskrit dapat dijelaskan sebagai berikut.

Sistem LTI waktu diskrit dengan tanggapan impuls h[n] mempunyai masukan

x[n] = zn

maka keluaran sistem dapat ditentukan dengan jumlah konvolusi sebagai ] z [ H z z ] k [ h z z z ] k [ h z ] k [ h ] k n [ x ] k [ h ] n [ y n k k n k k n k k n k = = = = − =

∑

∑

∑

∑

∞ −∞ = − ∞ −∞ = − ∞ −∞ = − ∞ −∞ = dengan

zn merupakan eigenfunction sistem

∑

∞ −∞ = − = k k z ] k [ h ] z [

H

merupakan eigenvalue sistem

4.2. Sifat Superposisi

Sistem LTI memiliki sifat superposisi. Jika x(t) merupakan kombinasi linier yang dinyatakan dengan persamaan

t s 3 t s 2 t s 1 3 2 1 _{a e a e} e a ) t ( x = + +

maka tanggapan sistem LTI waktu kontinyu yang dihasilkan merupakan jumlahan (superposisi) dari tanggapan masing-masing komponen yang membentuk masukannya. Perhatikan:

t s 3 3 3 t s 3 3 t s 2 2 2 t s 2 2 t s 1 1 1 t s 1 1 3 3 2 2 1 1 e ) s ( H a ) t ( y e a ) t ( x e ) s ( H a ) t ( y e a ) t ( x e ) s ( H a ) t ( y e a ) t ( x = → = = → = = → = +

∑

∑

→ → k t s k k k t s k k k _{a H(s )e} e a ) t ( y ) t ( x

Dengan demikian, keluaran y(t) dapat dinyatakan sebagai

∑

= k t s k k k e ) s ( H a ) t ( y

Sifat superposisi juga terdapat pada sistem LTI waktu diskrit. Jika masukan x[n] merupakan kombinasi linier yang dinyatakan sebagai

∑

= k n k k z a ] n [ x

maka tanggapan sistem LTI waktu diskrit yang dihasilkan juga merupakan jumlahan (superposisi) dari tanggapan masing-masing komponen yang membentuk masukannya. Dengan cara yang sama, maka keluaran y[n] dapat dinyatakan dengan

∑

= k n k k k H[z ] z a ] n [ y

4.2.1. Contoh Soal dan Penyelesaian

1. Sebuah sistem LTI waktu kontinyu mempunyai hubungan masukan dan keluaran sebagai berikut:

y(t) = x(t – 3)

Jika masukannya adalah x(t) = e j2t, maka tentukanlah keluaran sistem tersebut.

Penyelesaian

Cara 1

Dengan masukan x(t) = e j2t, maka y(t) = x(t – 3)

= e j2(t – 3) = e – j6 e j2t

Dalam hal ini e j2t merupakan eigenfunction dan eigenvalue untuk s = j2 dituliskan sebagai

H(s) = H(j2) = e – j6

Cara 2

H(s) dapat ditemukan dengan rumusan , dengan h(t) = δ(t – 3), sehingga

∫

−+∞∞ − _τ τ = h( )e d ) s ( H st s 3 s 3 s 3 s s e d ) 3 ( e d ) 3 ( e d e ) 3 ( d e ) ( h ) s ( H − ∞ + ∞ − − ∞ + ∞ − − ∞ + ∞ − τ − +∞ ∞ − τ − = τ − τ δ = τ − τ δ = τ − τ δ = τ τ =

∫

∫

∫

∫

Jika x(t) = e j2t, maka s = j2 dan dengan demikian H(j2) = e – 3s

2. Untuk sistem LTI yang sama dengan pada contoh soal no. 1, maka tentukanlah keluaran sistem jika masukannya adalah

x(t) = cos 4t + cos 7t Penyelesaian

Masukan x(t) merupakan kombinasi linear yang terdiri atas dua komponen, sehingga soal ini dapat diselesaikan dengan sifat superposisi yang dimiliki sistem LTI. Masukan x(t) dapat diuraikan menggunakan rumus Euler menjadi:

{

j4t j4t

} {

j7t j7t

}

e e 2 1 e e 2 1 t 7 cos t 4 cos ) t ( x − − _{+ +} + = + =

maka keluaran y(t) dapat ditemukan sebagai

{

4(t 3)

}

cos

{

7(t 3)

}

cos e 2 1 e 2 1 e 2 1 e 2 1 ) 3 t ( x ) t ( y ) 3 t ( 7 j ) 3 t ( 7 j ) 3 t ( 4 j ) 3 t ( 4 j − + − = + + + = − = − − − − − −

Eigenfunction dan eigenvalue untuk masing-masing komponen diperlihatkan pada tabel 4.1.

Tabel 4.1. Eigenfunction dan eigenvalue untuk masing-masing komponen untuk contoh soal no. 2

Komponen Eigenfunction Eigenvalue

e j4(t – 3) e j4t ½ e j12 e – j4(t – 3) e – j4t ½ e – j12

e j7(t – 3) e j7t ½ e j21 e – j7(t – 3) e – j7t ½ e – j21

4.2.2. Soal-soal Tambahan

1. Sebuah sistem LTI waktu kontinyu mempunyai hubungan keluaran dan masukan yang dinyatakan dengan persamaan

y(t) = 2 x(t – 1)

Jika masukannya adalah x(t) = e j3t, maka tentukanlah keluaran sistem. 2. Sebuah sistem LTI waktu kontinyu mempunyai hubungan keluaran dan

masukan yang dinyatakan dengan persamaan y(t) = x(t) + 2 x(t – 1)

Jika masukannya adalah x(t) = e j3t, maka tentukanlah keluaran sistem.

4.3. Representasi Deret Fourier Pada Isyarat Periodik Waktu Kontinyu

Untuk isyarat periodik waktu kontinyu x(t) yang mempunyai perioda dasar T dan frekuensi dasar ω0 = 2π/T, maka deret Fourier atas x(t) didefinisikan sebagai berikut:

∑

∑

∞ + −∞ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ π +∞ −∞ = ω = = k t T 2 jk k k t jk k e a e a ) t ( x 0 dengan

∫

∫

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ π − ω − = = T t T 2 jk T t jk k dt e ) t ( x T 1 dt e ) t ( x T 1 a 0

Koefisien ak disebut koefisien deret Fourier atau koefisien spektral dari x(t). Koefisien a0 (yaitu ak saat k = 0) disebut komponen dc atau konstan dari x(t), yang ditentukan oleh:

∫

= T 0 x(t)dt T 1 a

Besarnya ak menunjukkan besarnya sinyal x(t) pada setiap harmonik dari komponen dasar. Pada subab berikut akan diberikan beberapa contoh soal berikut penyelesaiannya dalam hal menyatakan sebuah isyarat menjadi deret Fouriernya.

4.3.1. Contoh Soal dan Penyelesaian

1. Isyarat x(t) = sin ω0 t mempunyai frekuensi dasar ω0. Tentukanlah deret Fourier untuk menyatakan x(t).

Penyelesaian

Salah satu cara untuk menentukan deret Fourier untuk x(t) = sin ω0 t adalah dengan menguraikan x(t) menggunakan rumus Euler.

{

}

t j t j t j t j 0 0 0 0 0 e 2 j 1 e 2 j 1 e e 2 j 1 t sin ) t ( x ω − ω ω − ω − = − = ω =

Dari penguraian x(t) dapat diketahui bahwa a −1 = 2 j 1 − a0 = 0 a1 = 2 j 1

dan ak = 0 untuk nilai k yang lain.

2. Isyarat x(t) didefinisikan sebagai berikut:

x(t) = 1 + sin ω0 t + 2 cos ω0 t + cos (2ω0 t + π/4) Nyatakanlah x(t) dalam deret Fourier.

Penyelesaian

Isyarat x(t) mempunyai frekuensi dasar ω0 dan dapat diuraikan menjadi:

{

} {

}

t 2 j 4 j t 2 j 4 j t j t j 4 t 2 j t j t j t j t j 0 0 0 0 0 0 0 4 t 0 2 j 0 0 0 0 0 e e 2 1 e e 2 1 e 2 j 1 1 e 2 j 1 1 1 e e 2 1 e e e e 2 j 1 1 4 t 2 cos t cos 2 t sin 1 ) t ( x ω − π − ω π ω − ω ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{ω +}π ω − ω ω − ω + + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + = ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ − + + + − + = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{ω +} π + ω + ω + = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{ω +}π − maka

2 k e e 2 1 2 k e e 2 1 1 k e 2 j 1 1 1 k e 2 j 1 1 0 k 1 ) t ( x t 2 j 4 j t 2 j 4 j t j t j 0 0 0 0 − = → + = → + − = → ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + = → ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + = → = ω − π − ω π ω − ω

dan dapat diketahui bahwa:

2 k untuk 0 a ) j 1 ( 4 2 e 2 1 a ) j 1 ( 4 2 e 2 1 a 2 1 j 1 2 j 1 1 a 2 1 j 1 2 j 1 1 a 1 a k 4 j 2 4 j 2 1 1 0 > = − = = + = = + = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − = − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ₊ = = π − − π −

Koefisien ak dapat diplot seperti pada gambar 4.1.

-3 -2 -1 0 1 2 3 k

Gambar 4.1 Plot koefisien-koefisien deret Fourier pada soal no. 2

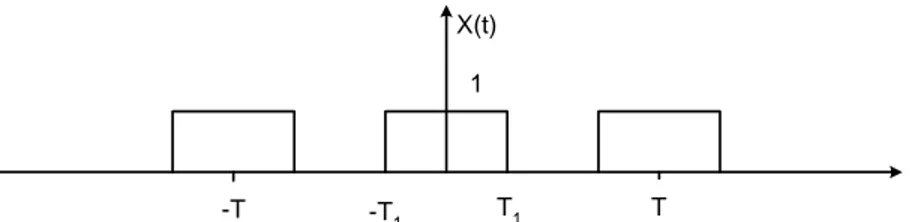
3. Isyarat x(t) pada gambar 4.2 dapat dinyatakan sebagai

⎪⎩ ⎪ ⎨ ⎧ < < < = 2 , 0 , 1 ) ( 1 1 T t T T t t x

X(t) 1

-T -T₁ T1 T

Gambar 4.2 Isyarat x(t) untuk soal no. 3 Penyelesaian

Isyarat x(t) merupakan isyarat yang periodik, maka untuk satu periode x(t) dapat ditemukan koefisien ak.

• Saat k = 0, maka

[

]

T T 2 ) T ( T T 1 t T 1 dt 1 . 1 T 1 dt e ) t ( x T 1 a 1 1 1 T T T T T T t jk 0 1 1 1 1 1 1 0 = − − = = = = − − − ω −

∫

∫

• Saat k ≠ 0, maka

[

]

[

]

2 j e e T k 2 e e T jk 1 e e T jk 1 T T e jk 1 T 1 dt e T 1 dt e ) t ( x T 1 a 1 0 1 0 1 0 1 0 1 0 1 0 0 1 1 0 1 1 0 T jk T jk 0 T jk T jk 0 T jk T jk 0 1 1 t jk 0 T T t jk T T t jk k ω − ω ω − ω ω ω − ω − − ω − − ω − − × ω = − × ω = − × ω − = − × ω − × = = =

∫

∫

π ω = ω ω = ω × ω = k ) T k sin( T k ) T k sin( 2 ) T k ( sin T k 2 1 0 0 1 0 1 0 0 Ingat bahwa T 2 0 π = ω

Sebagai gambaran, maka dapat dimisalkan suatu kasus jika T = 4T1 sehingga 1 0 T 4 2 T 2 π = π = ω atau 2 T₁ 0 π =

ω . Dengan pemisalan ini dapat

ditemukan nilai-nilai koefisien deret Fourier x(t) untuk berbagai harga k.

seterusnya dan a a 5 1 5 ) 2 / 5 sin( a a a 0 4 2 sin a a a 3 1 3 ) 2 / 3 sin( a a a 0 2 sin a a a 1 ) 2 / sin( a maka k 2 k sin k ) T k sin( a 2 1 T 4 T 2 T T 2 a 5 5 5 4 4 4 3 3 3 2 2 2 1 1 1 1 0 k 1 1 1 0 = → π = π π = = → = π π = = → π − = π π = = → = π π = = → π = π π = π ⎥⎦ ⎤ ⎢⎣ ⎡ π = π ω = = = = − − − − −

Koefisien ak dapat diplot seperti pada gambar 4.3.

-5 -4 -3 -2 -1 0 1 2 3 4 5 k ak

4.3.2 Soal-soal Tambahan

1. Untuk soal yang sama dengan contoh soal no. 3, tentukanlah koefisien deret Fourier dari x(t) jika:

a. T = 8T1 b. T = 16T1

c. Apa kesimpulan anda?

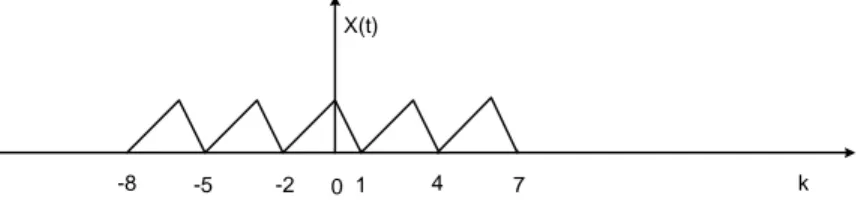
2. Tentukanlah deret Fourier untuk isayarat x(t) yang diperlihatkan pada gambar 4.4 berikut ini.

X(t)

0 -2 -5

-8 1 4 7 k

Gambar 4.4 Isyarat x(t) untuk soal no. 2

4.4. Sifat-sifat Deret Fourier Waktu Kontinyu

Untuk kepentingan kemudahan dalam pembahasan tentang sifat-sifat deret Fourier waktu kontinyu, maka koefisien deret Fourier dari sebuah isyarat x(t), yaitu ak , akan dituliskan dengan notasi:

k FS a ) t ( x ←⎯→

Artinya, isyarat x(t) dapat dinyatakan dengan deret Fourier dengan koefisien-koefisien ak (FS = Fourier Series = Deret Fourier).

Berikut adalah sifat-sifat deret Fourier waktu kontinyu: 1. Linearitas

Jika x(t) dan y(t) adalah isyarat periodik dengan periode T dan k FS a ) t ( x ←⎯→ k FS b ) t ( y ←⎯→

maka untuk isyarat z(t) yang didefinisikan sebagai z(t) = A x(t) + B y(t)

berlaku sifat linearitas sebagai berikut: k k k FS b B a A c ) t ( z ←⎯→ = +

yaitu koefisien deret Fourier dari z(t) adalah ck = A ak + B bk , dengan A dan B adalah konstanta.

2. Pergeseran waktu

Jika x(t) adalah isyarat periodik dengan periode T dengan k FS a ) t ( x ←⎯→

dan y(t) merupakan isyarat tergeser waktu dari x(t) yang dinyatakan sebagai

y(t) = x(t – t0) maka berlaku sifat

0 0 0 t T 2 jk k t jk k FS e . a e . a ) t ( y π − ω − ₌ ⎯→ ←

yaitu koefisien deret Fourier dari y(t) merupakan perkalian ak dengan

0 0 0 t T 2 jk t jk e e π − ω − ₌ . 3. Waktu-balikan

Jika x(t) adalah isyarat periodik dengan periode T dengan k FS a ) t ( x ←⎯→

maka untuk isyarat waktu balikan dari x(t) yaitu x(-t) berlaku sifat sebagai berikut: k FS a ) t ( x − ←⎯→ ₋ 4. Perkalian

Jika x(t) dan y(t) adalah isyarat periodik dengan periode T dan k FS a ) t ( x ←⎯→ k FS b ) t ( y ←⎯→ maka berlaku

∑

∞ −∞ = − = ⎯→ ← l l l k k FS b a h ) t ( y ) t ( x

yaitu koefisien deret Fourier dari perkalian x(t) dan y(t) merupakan jumlah konvolusi diskrit dari ak dan bk.

5. Penskalaan waktu (time scalling)

∑

∞ −∞ = ω = k t jk k 0 e a ) t ( x

maka isyarat x(t) yang terskala waktu (sebesar α) mempunyai deret Fourier yang dinyatakan sebagai

∑

∞ −∞ = αω = α k t ) ( jk k 0 e a ) t ( x

6. Konjugat dan simetri konjugat

Jika x(t) adalah isyarat periodik dengan periode T dengan k FS a ) t ( x ←⎯→ maka k FS a ) t ( x ←⎯→ ₋

dimana x(t) adalah konjugat kompleks dari x(t) dan a_k adalah konjugat kompleks dari ak .

Jika x(t) merupakan bilangan riil murni, maka x(t) = x(t) dan koefisien deret Fourier akan menjadi simetri konjugat, yaitu:

k

k a

a₋ =

4.5. Deret Fourier Isyarat Periodik Waktu Diskrit

Jika isyarat periodik waktu kontinyu x[n] periodik dengan periode dasar N dan frekuensi dasar ω0 = 2π / N , maka x[n] dapat dinyatakan sebagai deret Fourier waktu diskrit sebagai berikut:

∑

∑

= π = ω = = N k n N 2 jk k N k n jk k e a e a ] n [ x 0

dengan ak adalah koefisien deret Fourier untuk isyarat x[n], dan didefinisikan dengan pernyataan

∑

∑

= π − = ω − = = N k n N 2 jk N k n jk k e ] n [ x N 1 e ] n [ x N 1 a 0

4.5.1. Contoh Soal dan Penyelesaian

1. Jika x[n] = sin ω0 n, maka tentukan deret Fourier untuk x[n]. Penyelesaian

Isyarat x[n] = sin ω0 n periodik hanya jika 2π/ω0 merupakan bilangan bulat atau perbandingan bilangan bulat. Jika

N 2 0 π = ω , maka x[n] periodik

dengan periode dasar N dan x[n] dapat diuraikan menjadi deret Fourier sebagai berikut: n N 2 j n N 2 j 0 e 2 j 1 e 2 j 1 n N 2 sin n sin ] n [ x π − π − = ⎥⎦ ⎤ ⎢⎣ ⎡ π = ω =

Dengan demikian, koefisien deret Fouriernya adalah

lain yang k untuk ? ... a 2 j 1 a 2 j 1 a k 1 1 = − = = −

Untuk harga k yang lain, dapat dicari dengan cara berikut. Oleh karena x[n] periodik dengan periode dasar N, maka koefisien-koefisien deret Fourier x[n] juga akan berulang dengan periode N, sehingga

1 1 N 1 1 N a dan a a a ₊ = ₋ = ₋

Misalkan diambil periode dasar N = 5, maka dapat ditentukan:

2 j

1 a₁ =

2 j 1 a₋₁ =− ) a ( 2 j 1 a a a ) a ( 2 j 1 a a a ) a ( 2 j 1 a a a ) a ( 2 j 1 a a a ) a ( 2 j 1 a a a ) a ( 2 j 1 a a a 1 9 1 10 1 N 2 1 11 1 10 1 N 2 1 6 1 5 1 N 1 4 1 5 1 N 1 4 1 5 1 N 1 6 1 5 1 N − − − + + − − − − − − − + − + − − − − + + = − = = = = = = = = − = = = = = = = = − = = = = = = =

Koefisien ak dapat diplot seperti pada gambar 4.5.

-6 -5 -1/j2 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 k a_k 1/j2

Gambar 4.5 Plot koefisien-koefisien deret Fourier pada soal no. 1 2. Untuk soal yang sama dengan soal no. 1, maka misalkan 2π/ω0 merupakan

perbandingan bilangan bulat sebagai berikut:

M N 2 atau M N 2 0 0 = ω π π = ω

maka nyatakanlah koefisien-koefisien deret Fourier untuk x[n]. Penyelesaian Dengan mensubsitusikan M N 2 0 π =

ω pada persamaan isyarat x[n], maka

n N 2 jM n N 2 jM 0 e 2 j 1 e 2 j 1 n M N 2 sin n sin ] n [ x π − π − = ⎥⎦ ⎤ ⎢⎣ ⎡ π = ω = Sehingga 2 j 1 a_M = 2 j 1 a_−M =−

Isyarat x[n] periodik dengan periode dasar N, jika dipilih M = 3 dan N = 5, maka diperoleh: 2 j 1 a aM = 3 = 2 j 1 a a_−M = ₋₃ =− ) a ( 2 j 1 a a a ) a ( 2 j 1 a a a ) a ( 2 j 1 a a a ) a ( 2 j 1 a a a ) a ( 2 j 1 a a a ) a ( 2 j 1 a a a ) a ( 2 j 1 a a a ) a ( 2 j 1 a a a 3 13 3 10 M N 2 3 7 3 10 M N 2 3 7 3 10 M N 2 3 13 3 10 M N 2 3 8 3 5 M N 3 2 3 5 M N 3 2 3 5 M N 3 8 3 5 M N − − − − − − − + − + − − − − + + − − − − − − − + − + − − − − + + = − = = = = = = = = − = = = = = = = = − = = = = = = = = − = = = = = = =

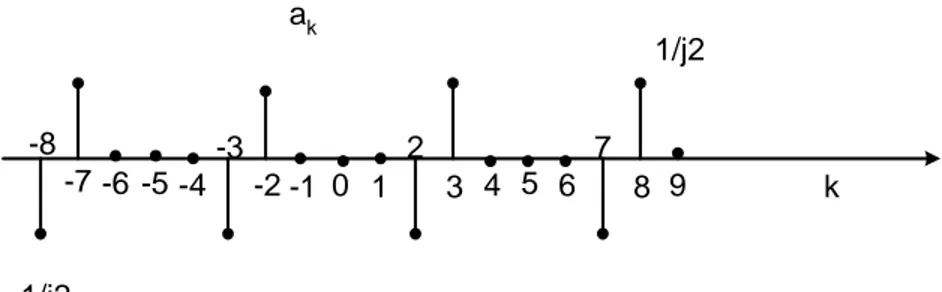
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 k a_k 1/j2 -1/j2

Gambar 4.6 Plot koefisien-koefisien deret Fourier pada soal no. 2 3. Tentukanlah deret Fourier untuk isyarat n

N 2 cos 3 n N 2 sin 1 ] n [ x ⎥⎦ ⎤ ⎢⎣ ⎡ π + ⎥⎦ ⎤ ⎢⎣ ⎡ π + = Penyelesaian

Isyarat x[n] periodik dengan periode dasar N, dan dapat diuraikan menjadi: n N 2 j n N 2 j n N 2 j n N 2 j n N 2 j n N 2 j n N 2 j e 2 j 1 2 3 e 2 j 1 2 3 e 2 j 1 2 3 1 e e 2 3 e e 2 j 1 1 n N 2 cos 3 n N 2 sin 1 ] n [ x ⎥⎦ ⎤ ⎢⎣ ⎡ π ⎥⎦ ⎤ ⎢⎣ ⎡ π − ⎥⎦ ⎤ ⎢⎣ ⎡ π ⎥⎦ ⎤ ⎢⎣ ⎡ π − ⎥⎦ ⎤ ⎢⎣ ⎡ π ⎥⎦ ⎤ ⎢⎣ ⎡ π − ⎥⎦ ⎤ ⎢⎣ ⎡ π ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − + ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + + = ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ + + ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ − + = ⎥⎦ ⎤ ⎢⎣ ⎡ π + ⎥⎦ ⎤ ⎢⎣ ⎡ π + = Sehingga diperoleh: 2 1 j 2 3 2 j 1 2 3 a 2 1 j 2 3 2 j 1 2 3 a 1 a 1 1 0 + = − = − = + = = −

4. Tentukanlah koefisien-koefisien deret Fourier untuk isyarat x[n] jika isyarat x[n] diperlihatkan pada gambar 4.7.

X[n]

1

-N -N₁ 0 N₁ N n

Penyelesaian

Dari gambar isyarat x[n] di atas, diketahui bahwa x[n] = 1 untuk harga –N1 < n < N1 , maka dapat dinyatakan:

∑

− = ⎥⎦ ⎤ ⎢⎣ ⎡ π − = 1 1 N N n n N 2 jk k e N 1 a

Dengan menganggap bahwa m = n + N1 , maka

.... , N 2 , N , 0 k ; N k sin N 5 , 0 N k 2 sin N 1 e e e e e e N 1 e 1 e . e e N 1 e 1 e 1 e N 1 ) e e N 1 e N 1 a 1 N 2 2 jk N 2 2 jk N 5 , 0 N 2 jk N 5 , 0 N 2 jk N 2 2 jk N 2 2 jk N 2 jk N 1 N 2 2 jk N N 2 jk N N 2 jk N 2 jk N 1 N 2 2 jk N N 2 jk * N 2 0 m N 2 jk N N 2 jk N 2 0 m ) N m ( N 2 jk k 1 1 1 1 1 1 1 1 m 1 1 ₁ ± ± ≠ ⎥⎦ ⎤ ⎢⎣ ⎡π ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + π × = ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ − ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ − × × = ⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ − − = ⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ − − = = = ⎥⎦ ⎤ ⎢⎣ ⎡ π − ⎥⎦ ⎤ ⎢⎣ ⎡ π ⎥⎦ ⎤ ⎢⎣ ⎡ + π − ⎥⎦ ⎤ ⎢⎣ ⎡ + π ⎥⎦ ⎤ ⎢⎣ ⎡ π − ⎥⎦ ⎤ ⎢⎣ ⎡ π − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ π − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + π − ⎥⎦ ⎤ ⎢⎣ ⎡ π ⎥⎦ ⎤ ⎢⎣ ⎡ π ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ π − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + π − ⎥⎦ ⎤ ⎢⎣ ⎡ π = ⎥⎦ ⎤ ⎢⎣ ⎡ π − ⎥⎦ ⎤ ⎢⎣ ⎡ π = − ⎥⎦ ⎤ ⎢⎣ ⎡ π −

∑

∑

Catatan )* Suku

∑

= ⎥⎦ ⎤ ⎢⎣ ⎡ π − 1 m N 2 0 m N 2 jk

e merupakan sebuah deret geometri dengan 2N1+1 suku, sehingga

jumlah deret geometri tersebut dapat diketahui menggunakan rumus jumlah deret geometri.

Sedangkan untuk k = 0, ±N, ±2N, … maka koefisien deret Fouriernya adalah

N 1 N 2 a 1 k + =

Sebagai contoh, koefisien-koefisien ak untuk (2N1 + 1) = 5 dapat digambarkan untuk berbagai nilai N, misalnya N = 10.

• Untuk k = 0, ±10, ±20, … maka 2 1 10 5 N 1 N 2 a 1 k = = + = • Untuk k ≠ 0, ±10, ±20, … maka ⎥⎦ ⎤ ⎢⎣ ⎡ π ⎥⎦ ⎤ ⎢⎣ ⎡ π = ⎥⎦ ⎤ ⎢⎣ ⎡ π ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + π × = ⎥⎦ ⎤ ⎢⎣ ⎡ π ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + π × = 10 k sin 2 k sin 10 1 N k sin N 1 N 2 k sin N 1 N k sin N 5 , 0 N k 2 sin N 1 a 1 1 k Sehingga diperoleh: 4 4 4 3 3 3 2 2 2 1 1 1 a a 0 10 4 sin 2 sin 10 1 a a a 124 , 0 10 3 sin 2 3 sin 10 1 a a a 0 5 sin sin 10 1 a a a 3 , 0 10 sin 2 sin 10 1 a = → = ⎥⎦ ⎤ ⎢⎣ ⎡ π π = = → − = ⎥⎦ ⎤ ⎢⎣ ⎡ π⎥⎦ ⎤ ⎢⎣ ⎡ π = = → = ⎥⎦ ⎤ ⎢⎣ ⎡π π = = → = ⎥⎦ ⎤ ⎢⎣ ⎡ π⎥⎦ ⎤ ⎢⎣ ⎡π = − − − −

6 6 6 5 5 5 a a 0 5 3 sin 3 sin 10 1 a a a 1 , 0 2 sin 2 5 sin 10 1 a = → = ⎥⎦ ⎤ ⎢⎣ ⎡ π π = = → = ⎥⎦ ⎤ ⎢⎣ ⎡π⎥⎦ ⎤ ⎢⎣ ⎡ π = − − 9 9 9 8 8 8 7 7 7 a a 3 , 0 10 9 sin 2 9 sin 10 1 a a a 0 5 4 sin 4 sin 10 1 a a a 124 , 0 10 7 sin 2 7 sin 10 1 a = → = ⎥⎦ ⎤ ⎢⎣ ⎡ π ⎥⎦ ⎤ ⎢⎣ ⎡ π = = → = ⎥⎦ ⎤ ⎢⎣ ⎡ π π = = → − = ⎥⎦ ⎤ ⎢⎣ ⎡ π ⎥⎦ ⎤ ⎢⎣ ⎡ π = − − −

Karena sifatnya yang periodik dengan periode N = 10, maka

... a a a a a a a a a a a a .... a a a a a a a a 22 22 2 22 21 21 1 21 19 19 9 19 12 12 2 12 11 11 1 11 = → = = → = = → = = → = = → = − − − − −

Koefisien ak dapat diplot seperti pada gambar 4.8.

a_k 0 1 2 3 4 5 6 7 8 9 1011 -1 -3 -5 -7 -10 k

4.5.2. Soal-soal Tambahan

1. Untuk soal yang sama dengan pada contoh soal no. 3, tentukanlah koefisien-koefisien deret Fourier untuk x[n] jika

a. N = 5 b. N =10 c. N = 15

Gambarkan plot dari koefisien-koefisien tersebut.

2. Untuk soal yang sama dengan pada contoh soal no. 4, tentukanlah koefisien-koefisien deret Fourier untuk x[n] jika

a. N = 20 b. N = 40

Gambarkan plot dari koefisien-koefisien tersebut.

4.6. Sifat-sifat Deret Fourier Waktu Diskrit

Untuk isyarat waktu diskrit x[n] yang periodik dengan periode N dan mempunyai koefisien deret Fourier ak, maka hubungan ini akan ditulis sebagai berikut: k FS a ] n [ x ←⎯→

Berikut ini adalah sifat-sifat deret Fourier waktu diskrit. 1. Perkalian

Jika x[n] dan y[n] adalah isyarat periodik dengan periode N dan k FS a ] n [ x ←⎯→ k FS b ] n [ y ←⎯→ maka berlaku

∑

= − = ⎯→ ← N k k FS b a d ] n [ y ]. n [ x l l l 2. Diferensiasi pertama

Jika x[n] adalah isyarat periodik dengan periode N dan k FS a ] n [ x ←⎯→

maka koefisien deret Fourier yang sesuai dengan diferensiasi pertama dari x[n] dinyatakan sebagai: ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − ⎯→ ← − − ⎟⎠ ⎞ ⎜ ⎝ ⎛ π − N 2 jk k FS e 1 a ] 1 n [ x ] n [ x

dimana frekuensi dasar x[n] adalah ω0 = 2π/N.

4.7. Deret Fourier dan Sistem LTI

Dalam waktu kontinyu, jika x(t) = est merupakan input atau masukan sistem LTI waktu kontinyu, maka keluarannya adalah

y(t) = H(s) est dengan

∫

−+∞∞ τ − _τ τ = h( )e d ) s ( H s

dan h(t) merupakan tanggapan impuls sistem LTI. Jika s = jω maka e st = e jωt

sehingga masukan LTI merupakan eksponensial kompleks dengan frekuensi

ω. Dalam hal ini, maka H(s) = H(jω) yang dinyatakan:

∫

−+∞∞ τ − _τ τ = ω) h( )e d j ( H s

H(jω) disebut dengan istilah tanggapan frekuensi (frequency response) sistem LTI.

Jika isyarat masukan x(t) dinyatakan dalam deret Fourier sebagai berikut

∑

+∞ −∞ = ω = k t jk k 0 e a ] n [ x

maka keluaran sistem LTI dapat dinyatakan dengan

∑

+∞ −∞ = ω ω = k t jk 0 k 0 e ) jk ( H a ] n [ y

dimana dalam hal ini sk = jkω0 , dan koefisien dari y(t) adalah bk = ak H(jkω0)

Dengan cara yang sama, dalam waktu diskrit jika x[n] = zn merupakan masukan sistem LTI waktu diskrit, maka keluarannya adalah

y[n] = H(z) zn dengan

∑

∞ −∞ = − = k k z ] k [ h ) z ( H

dan h[n] adalah tanggapan impuls sistem LTI.

Jika harga z dipilih sedemikian rupa sehingga ⎢z⎥ = 1, maka z = e jω

dan

zn = e jωn

Dengan demikian, maka diperoleh persamaan yang menyatakan tanggapan frekuensinya, yaitu:

( )

_∑

+∞ −∞ = ω − ω ₌ n n j j e ] n [ h e H

Jika isyarat masukan x[n] merupakan isyarat periodik yang dinyatakan dalam deret Fourier sebagai

∑

= ⎥⎦ ⎤ ⎢⎣ ⎡ π = N k n N 2 jk k e a ] n [ x

maka keluaran sistem LTI (dengan tanggapan impuls h[n]) adalah

∑

= ⎥⎦ ⎤ ⎢⎣ ⎡ π ⎥⎦ ⎤ ⎢⎣ ⎡ π = N k n N 2 jk N 2 jk k H(e )e a ] n [ y

dimana koefisien y[n] adalah bk = ak H(e j2πk/N)

4.7.1. Contoh Soal dan Penyelesaian

1. Sebuah sistem LTI waktu kontinyu mempunyai tanggapan impuls h(t) = e−t u(t)

∑

− = π = 3 3 k t 2 jk k e a ] n [ x dengan a0 = 1 a1 = a−1 = ¼ a2 = a−2 = ½ a3 = a−3 = 13

maka tentukanlah tanggapan frekuensi dan keluaran sistem LTI tersebut. Penyelesaian

Tanggapan frekuensi dapat ditemukan sebagai berikut:

ω + = ω + − = = = = = ω ∞ ω + − ∞ ω + − ∞ ω − − ∞ ∞ − ω − − ∞ ∞ − ω −

∫

∫

∫

∫

j 1 1 e j 1 1 dt e dt e e dt e ) t ( u e dt e ) t ( h ) j ( H 0 t ) j 1 ( 0 t ) j 1 ( 0 t j t t j t t j

Oleh karena isyarat x(t) mempunyai frekuensi dasar ω0 = 2π maka keluaran sistem LTI tersebut adalah

∑

− = π = 3 3 k t 2 jk k e b ] n [ y dengan bk = ak H( jk2π )

sehingga dapat ditentukan besaranya bk untuk harga-harga k yang berbeda sebagai berikut.

π − × = π − = π − × = π − = π + × = π = π + × = π = π + × = π = = = − − − − 4 j 1 1 2 1 ) 4 j ( H a b 2 j 1 1 4 1 ) 2 j ( H a b 6 j 1 1 3 1 ) 6 j ( H a b 4 j 1 1 2 1 ) 4 j ( H a b 2 j 1 1 4 1 ) 2 j ( H a b 1 ) 0 ( H a b 2 2 1 1 3 3 2 2 1 1 0 0 π − × = π − = ₋ − 6 j 1 1 3 1 ) 6 j ( H a b _{3 3}

2. Sebuah sistem LTI waktu diskrit mempunyai tanggapan impuls h[n] = α n u[n]

dimana −1 < α < 1. Jika masukan sistem ini adalah

N n 2 cos ] n [ x = π

maka tentukanlah tanggapan frekuensi sistem tersebut. Penyelesaian n N 2 j n N 2 j e 2 1 e 2 1 N n 2 cos ] n [ x π − π + = π =

maka dapat diperoleh tanggapan frekuensi untuk jω = j2π/N dan jω = −j2π/N, sebagai berikut:

(

)

[

]

∑

∑

∑

∞ + = π − ∞ + −∞ = π − +∞ −∞ = π − π α = α = = 0 n n ) N / 2 ( j n n ) N / 2 ( j n n n ) N / 2 ( j N / 2 j e e ] n [ u e ] n [ h e H N / 2 j e 1 1 π − α − =

dan

(

)

[

]

N / 2 j 0 n n ) N / 2 ( j n n ) N / 2 ( j n n n ) N / 2 ( j N / 2 j e 1 1 e e ] n [ u e ] n [ h e H π ∞ + = π ∞ + −∞ = π +∞ −∞ = π π − α − = α = α = =

∑

∑

∑

Secara umum, tanggapan frekuensinya dapat dinyatakan dengan

( )

−ω ω α − = _j j e 1 1 e H

Cara lain untuk menentukan tanggapan frekuensi sistem adalah sebagai berikut. Masukan x[n] dapat ditulis sebagai deret Fourier

n N 2 j n N 2 j e 2 1 e 2 1 ] n [ x ⎥⎦ ⎤ ⎢⎣ ⎡ π − ⎥⎦ ⎤ ⎢⎣ ⎡ π + =

dan tanggapan frekuensinya adalah

( )

ω − ∞ = ω − ∞ = ω − ∞ + −∞ = ω − +∞ −∞ = ω − ω α − = α = α = α = =

∑

∑

∑

∑

j 0 n n j n 0 n n j n n n j n n n j j e 1 1 e e e ] n [ u e ] n [ h e H

Dengan demikian, keluaran sistem dapat dinyatakan sebagai:

n N 2 j N / 2 j n N 2 j N / 2 j n N 2 j N / 2 j n N 2 j N / 2 j N k n N 2 jk N / k 2 j k e e 1 1 2 1 e e 1 1 2 1 e ) e ( H 2 1 e ) e ( H 2 1 e ) e ( H a ] n [ y π − π π π − π − π − π π = π π ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ α − + ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ α − = + = =

∑

4.7.2. Soal-soal Tambahan

1. Sebuah sistem LTI waktu diskrit mempunyai tanggapan impuls n 2 1 ] n [ h ⎥⎦ ⎤ ⎢⎣ ⎡ =

maka tentukanlah representasi deret Fourier dari y[n] jika masukan x[n] adalah isyarat periodik dengan periode 6 dan dinyatakan sebagai berikut

⎩ ⎨ ⎧ ± ± = ± = = 3 , 2 n , 0 1 , 0 n , 1 ] n [ x

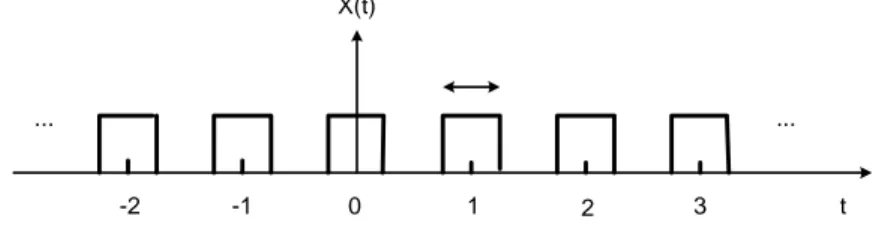
2. Sebuah sistem LTI waktu kontiyu dengan tanggapan impuls h(t) = e −4⎜t⎥

maka tentukanlah representasi deret Fourier dari y(t) jika masukan x(t) seperti pada gambar berikut.

X(t)

-2 -1 0 1 2 3 t

... ...

Gambar 4.9 Isyarat x(t) untuk soal no. 2

4.8. Filter-filter Pemilih Frekuensi

Tanggapan frekuensi suatu filter dalam waktu kontinyu, secara garis besar dibedakan menjadi:

1. Lowpass ideal

Filter ini melewatkan frekuensi rendah saja. Perhatikan gambar 4.10.

H(jω)

1

ω

−ω_c 0 ωc

2. Highpass ideal

Filter ini melewatkan frekuensi tinggi saja. Perhatikan gambar 4.11.

H(jω)

1

ω

−ω_c 0 ωc

Gambar 4.11 Tanggapan frekuensi filter highpass ideal (waktu kontinyu)

3. Bandpass ideal

Tanggapan frekuensi filter bandpass ideal diperlihatkan pada gambar 4.12.

H(jω) 1

−ω₂ −ω₁ ω₁ ω₂

ω

Gambar 4.12 Tanggapan frekuensi filter bandpass ideal (waktu kontinyu)

Sedangkan tanggapan frekuensi suatu filter dalam waktu diskrit, secara garis besar juga dibedakan menjadi:

1. Lowpass ideal

Tanggapan frekuensi filter bandpass ideal diperlihatkan pada gambar 4.13.

H(e jω₎ −ω1 ω1 1 0 π −π 2π −2π ω

Gambar 4.13 Tanggapan frekuensi filter lowpass ideal (waktu diskrit)

2. Highpass ideal

H(e jω₎ 1 0 π −π 2π −2π ω Gambar 4.14 Tanggapan frekuensi filter highpass ideal (waktu diskrit)

3. Bandpass ideal

Tanggapan frekuensi filter bandpass ideal diperlihatkan pada gambar 4.15.

H(e jω₎

1

0 π

−π 2π

−2π ω

Gambar 4.15 Tanggapan frekuensi filter bandpass ideal (waktu diskrit)

4.8.1. Contoh Soal dan Penyelesaian

1. Sebuah rangkaian filter lowpass RC sederhana pada gambar 4.16. Jika masukan sistem adalah Vs(t) dan keluarannya adalah Vc(t), tentukanlah persamaan yang menyatakan hubungan antara keluaran dan masukan sistem. R C i(t) Vc(t) V_s(t)

Gambar 4.16 Rangkaian filter RC lowpass sederhana

Penyelesaian

Dengan Vs(t) sebagai masukan sistem dan Vc(t) sebagai keluarannya, maka untuk rangkaian RC di atas berlaku:

) t ( V ) t ( V ) t ( V dt d RC ) t ( V ) t ( V ) t ( i R ) t ( V ) t ( V ) t ( V S C C S C S C R = + = + = +

Jika masukan Vs(t) = e jωt maka keluaran Vc(t) harus menjadi Vc(t) = H(jω) e jωt Sehingga diperoleh

{

}

[

]

1 RCj 1 ) j ( H 1 ) j ( H 1 RCj 1 ) j ( H ) j ( H RCj e e ) j ( H e ) j ( H RCj e e ) j ( H e ) j ( H dt d RC t j t j t j t j t j t j + ω = ω = ω + ω = ω + ω ω = ω + ω ω = ω + ω ω ω ω ω ω ω Jika

ω≈ 0 maka ⎢H(jω)⎥≈ 1 dan ω > 0 maka ⎢H(jω)⎥ <<

Tanggapan frekuensi filter ini dapat digambarkan secara grafis pada gambar 4.17.

-1/RC 1/RC

1

IH(Jω)I

ω

Gambar 4.17 Tanggapan filter lowpass RC pada soal no. 1

Filter lowpass RC sederhana pada contoh soal no. 1 ini merupakan filter yang non-ideal.

2. Sebuah rangkaian filter highpass RC sederhana pada gambar 4.18. Jika masukan sistem adalah Vs(t) dan keluarannya adalah VR(t), tentukanlah persamaan yang menyatakan hubungan antara keluaran dan masukan sistem.

R i(t) VR(t) C Vs(t)

Gambar 4.18 Rangkaian filter RC highpass sederhana

Penyelesaian

Dengan Vs(t) sebagai masukan sistem dan VR(t) sebagai keluarannya, maka untuk rangkaian RC di atas berlaku:

) t ( V dt d RC ) t ( V ) t ( V dt d RC ) t ( V dt ) t ( V RC 1 ) t ( V ) t ( V dt R ) t ( V C 1 ) t ( V ) t ( V dt ) t ( i C 1 ) t ( V ) t ( V ) t ( V ) t ( V S R R S R R S R R S R S C R = + = + = + = + = +

∫

∫

∫

Jika masukan Vs(t) = e jωt maka keluaran VR(t) harus menjadi VR(t) = H(jω) e jωt Sehingga diperoleh

[

]

1 RCj RCj ) j ( H RCj ) j ( H ) 1 RCj ( e . RCj e ). j ( H e ) j ( H . RCj e dt d RC e ). j ( H e ). j ( H dt d RC ) t ( V dt d RC ) t ( V ) t ( V dt d RC t j t j t j t j t j t j S R R + ω ω = ω ω = ω + ω ω = ω + ω ω = ω + ω = + ω ω ω ω ω ω

Terlihat dari persamaan tanggapan frekuensi sistem, bahwa jika

⎜ω⎟ >> 1/RC maka terjadi redaman. Dengan kata lain, jika ω mendekati nol maka ⎢H(jω)⎥ << dan jika ⎜ω⎟ = 1/RC maka ⎢H(jω)⎥ = 1.

Tanggapan frekuensi filter ini dapat digambarkan secara grafis pada gambar 4.19. -1/RC 1/RC 1 IH(Jω)I ω

Gambar 4.19 Tanggapan filter highpass RC pada soal no. 2

Filter highpass RC sederhana pada contoh soal no. 2 ini merupakan filter yang non-ideal.