PROSES PERCABANGAN PADA DISTRIBUSI GEOMETRIK

Arantika Desmawati, Respatiwulan, dan Dewi Retno Sari S

Program Studi Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sebelas Maret

Abstrak. _{Proses percabangan muncul secara alami dalam berbagai hal terutama} reproduksi individu. Dalam proses percabangan dipelajari fungsi pembangkit pro-babilitas yang merepresentasikan propro-babilitas suatu kejadian. Salah satu persoalan proses percabangan yang tertua yaitu tentang kepunahan nama keluarga. Nama ke-luarga hanya dapat diwariskan oleh keturunan laki-laki. Kepunahan nama keke-luarga sesuai dengan distribusi geometrik. Tujuan penelitian ini adalah menurunkan ulang dan menerapkan proses percabangan pada distribusi geometrik. Berdasarkan pe-nurunan ulang tersebut, diperoleh fungsi pembangkit probabilitas yang digunakan untuk menentukan rata-rata dan variansi banyaknya generasi sampai nama keluarga punah. Berdasarkan penerapan proses percabangan untuk rantai keturunan laki-laki di Amerika diperoleh hasil bahwa proses percabangan pada distribusi geometrik de-ngan probabilitas sukses sebesar b = 0, 4107, probabilitas tidak memiliki keturunan laki-laki sebesar p0= 0, 4825 dan probabilitas memiliki j keturunan laki-laki sebesar pj = (0, 2126)(0, 5893)(j−1) untuk j ≥ 1 mempunyai rata-rata banyaknya generasi sampai nama keluarga di Amerika punah sebesar µ = 1, 4349 dengan variansi sebesar 3, 4937.

Kata kunci _{: proses percabangan, distribusi geometrik, probabilitas, rata-rata,} vari-ansi

1. PENDAHULUAN

Proses percabangan muncul secara alami pada berbagai hal dalam kehidup-an. Proses percabangan erat kaitannya dengan reproduksi individu. Individu-individu yang diamati saling independen dan hidup dalam suatu rentang waktu. Tiap individu akan mempunyai sejumlah keturunan dan kemudian mati. Bebera-pa kasus proses percabangan yang menonjol yaitu penggandaan elektron, reaksi rantai neutron, dan penurunan nama keluarga (Taylor dan Karlin [8]). Proses per-cabangan juga berperan dalam biologi tentang bermacam-macam karsinogenesis (Meza [4]), teori jaringan (Newman [6]) dan reaksi berantai polimerase (Kimmel dan Axelrod [3]).

Proses percabangan dapat digunakan dalam mempelajari populasi makhluk hidup yang ditinjau dari sudut pandang matematika. Dalam proses percabangan dipelajari fungsi pembangkit probabilitas yang merepresentasikan probabilitas dari suatu kejadian (Reluga [7]). Untuk mempelajari fungsi pembangkit, perlu diketahui distribusi probabilitas dari variabel random yang diamati. Variabel random dalam proses percabangan dapat mengikuti suatu distribusi antara lain distribusi Bernoulli, binomial, Poisson, geometrik atau binomial negatif.

Salah satu persoalan proses percabangan yang tertua yaitu tentang nama keluarga bangsawan Inggris yang hanya diturunkan kepada keturunan laki-laki (Kimmel dan Axelrod [3]). Nama keluarga yang diturunkan oleh leluhur akan pu-nah apabila semua keturunan laki-laki meninggal tanpa mewariskannya kepada anak laki-laki mereka. Dalam suatu keluarga, terdapat dua kemungkinan jenis ke-lamin dari keturunan mereka yaitu laki-laki dan perempuan. Apabila keturunan mereka berjenis kelamin laki-laki maka keturunan mereka akan membawa nama keluarga, tetapi tidak bila keturunan mereka berjenis kelamin perempuan. Nama keluarga tidak dapat diturunkan apabila keturunan berjenis kelamin perempuan. Kepunahan nama keluarga sesuai dengan karakterisrik distribusi geometrik. Asumsikan jenis kelamin tiap kelahiran bersifat independen. Kelahiran keturunan pada suatu generasi diandaikan sebagai suatu percobaan Bernoulli. Untuk me-ngetahui kepunahaan nama keluarga, dikatakan percobaan Bernoulli memperoleh hasil sukses apabila pada suatu generasi setiap kelahiran memberikan keturunan berjenis kelamin perempuan dan gagal apabila terdapat kelahiran yang membe-rikan keturunan berjenis kelamin laki-laki sehingga nama keluarga masih dapat diturunkan. Serangkaian percobaan Bernoulli yang terjadi sampai pertama kali diperoleh hasil sukses ini merupakan distribusi geometrik. Pada penelitian ini di-kaji ulang tentang proses percabangan dengan banyaknya generasi sampai punah berdistribusi geometrik dan penerapannya.

2. PROSES PERCABANGAN

Proses percabangan dikemukakan pertama kali oleh Bienayme pada tahun 1845. Sekitar tahun 1870, model tersebut dikembangkan oleh seorang ahli mate-matika bernama Henry William Watson bersama seorang ahli biometri bernama Francis Galton. Pengembangan tersebut khususnya dalam hal penurunan nama keluarga yang hanya diturunkan untuk keturunan laki-laki (Mode [5]). Menu-rut Allen [1], proses percabangan waktu diskrit merupakan suatu rantai Markov waktu diskrit dengan variabel waktu dan ruang state diskrit. State pada waktu n+ 1 hanya dipengaruhi oleh state pada waktu n.

Dimisalkan variabel random X adalah banyaknya keturunan pada generasi tertentu dan setiap individu menghasilkan keturunan berjumlah random sebanyak ξ dengan distribusi probabilitas P r(ξ = k) = pk untuk k = 0, 1, 2, . . . dengan pk ≥ 0 dan

P∞

k pk = 1. Banyaknya keturunan pada generasi ke-n adalah Xn dan ukuran total populasi pada generasi ke-n adalah Zn dengan n = 0, 1, 2, . . .. Menurut Allen [1], pada proses percabangan terdapat tiga asumsi yaitu

(1) probabilitas individu menghasilkan keturunan adalah p yang bernilai sama untuk setiap individu,

(2) setiap individu menghasilkan keturunan secara independen, dan (3) proses dimulai dengan individu tunggal pada waktu n = 0.

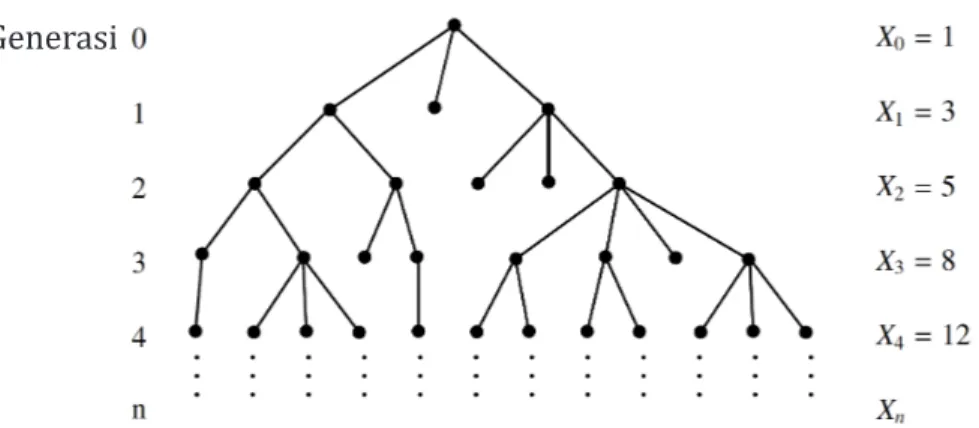
Asumsi 1 dan 2 memberikan definisi proses percabangan Galton-Watson waktu diskrit yaitu rantai Markov waktu diskrit yang menggambarkan pertum-buhan populasi yang bereproduksi dengan percabangan sederhana dan proses tidak harus dimulai dengan individu tunggal. Ilustrasi dari contoh proses perca-bangan Galton-Watson waktu diskrit dapat dilihat pada Gambar 1. Asumsi 3 menyatakan bahwa Z0 = 1.

Generasi

Gambar 1. Proses percabangan Galton-Watson waktu diskrit

Pada generasi ke-n, Xn secara independen menghasilkan keturunan berjum-lah ξ₁(n), ξ₂(n), . . . , ξ_X(n)

n sehingga kumulatif banyaknya keturunan yang dihasilkan

pada generasi ke-(n + 1) adalah

Xn+1 = ξ1(n)+ ξ (n)

2 + . . . + ξ (n) Xn.

Total populasi pada generasi ke-(n) adalah

Zn= X0+ X1+ X2+ . . . + Xn. 3. DISTRIBUSI GEOMETRIK

Distribusi geometrik merupakan distribusi yang muncul dari serangkaian percobaan Bernoulli yang saling independen. Percobaan Bernoulli adalah perco-baan yang memiliki dua kemungkinan hasil yaitu sukses (R) dengan P (R) = b dan gagal (F ) dengan P (F ) = 1 − b = c. Andaikan percobaan Bernoulli dila-kukan hingga terjadi sukses yang pertama, maka banyaknya sukses adalah satu dan banyaknya percobaan Bernoulli yang dilakukan merupakan variabel random berdistribusi geometrik. Banyaknya percobaan Bernoulli yang diperlukan sampai menghasilkan sukses yang pertama dinotasikan dengan Y . Nilai Y yang mungkin

adalah 1, 2, 3, . . . dengan Y = y terjadi jika dan hanya jika terdapat serangkaian y −1 kegagalan dan 1 sukses. Dengan syarat bahwa percobaan saling independen, maka berlaku

f(y) = P [Y = y] = P [F F . . . F R] = cy−1b, y= 1, 2, 3, . . . . 4. FUNGSI PEMBANGKIT

Fungsi pembangkit sangat berguna untuk menentukan nilai ekspektasi. Menurut Bain dan Engelhardt [2], jika Y adalah suatu variabel random, ma-ka nilai ekspektasi MY(s) = E(esY) disebut fungsi pembangkit momen dari Y . Untuk variabel random yang bernilai bilangan bulat tak negatif seperti dalam kasus proses percabangan, lebih mudah dikerjakan dengan ekspektasi tipe la-in yang dikenal dengan momen faktorial. Momen faktorial ke-r dari Y adalah E[Y (Y − 1) . . . (Y − r + 1)] dan fungsi pembangkit momen faktorial dari Y adalah

GY(s) = E(sY)

apabila nilai ekspektasi ada untuk setiap s dalam interval 1 − h < s < 1 + h. Fungsi pembangkit momen faktorial juga disebut fungsi pembangkit proba-bilitas karena variabel random Y yang bernilai bilangan bulat tak negatif. Fungsi pembangkit probabilitas menentukan distribusi dari variabel random tersebut. Jika Y mempunyai suatu fungsi pembangkit probabilitas, GY(s), maka

G′_Y(1) = E[Y ],

G′′_Y(1) = E[Y (Y − 1)],

G(r)_Y (1) = E[Y (Y − 1) . . . (Y − r + 1)]. 5. HASIL DAN PEMBAHASAN

5.1. Proses Percabangan pada Distribusi Geometrik. Suatu individu yang ingin melestarikan jenisnya, ia harus melakukan reproduksi. Reproduksi adalah proses suatu individu menghasilkan individu baru. Proses inilah cara dasar indi-vidu untuk mempertahankan jenisnya sehingga memiliki keturunan yang hidup pada generasi selanjutnya. Suatu populasi terdiri atas individu yang melakukan reproduksi misalnya hewan, bakteri, dan virus komputer.

Reproduksi mengakibatkan meningkatnya jumlah individu dalam suatu po-pulasi. Setiap keturunan hasil reproduksi dapat memiliki sifat yang sama dengan individu induk dan dapat pula berbeda. Sifat-sifat yang dimaksud misalnya ada-lah jenis kelamin, bentuk fisik ataupun kepemilikan penyakit menurun. Apabila keturunan memiliki dua kemungkinan sifat, maka reproduksi dapat dipandang sebagai percobaan Bernoulli.

Mengacu pada pengertian proses percabangan, reproduksi pada suatu gene-rasi dianggap sebagai suatu percobaan Bernoulli yang memiliki keturunan sukses (R) apabila diperoleh keturunan dengan keadaan yang diharapkan dan keturunan gagal (F ) apabila diperoleh keturunan dengan keadaan yang tidak diharapkan. Probabilitas untuk memiliki keturunan sukses sebesar b dan probabilitas untuk memiliki keturunan sukses sebesar 1 − b = c. Reproduksi akan dilakukan hing-ga diperoleh keturunan denhing-gan keadaan yang diharapkan atau denhing-gan kata lain hingga percobaan Bernoulli memiliki keturunan sukses. Apabila variabel random Y adalah banyak generasi sampai diperoleh keturunan dengan keadaan yang di-harapkan untuk pertama kalinya maka Y berdistribusi geometrik. Variabel ran-dom dalam proses percabangan berkaitan dengan fungsi pembangkit probabilitas. Fungsi pembangkit probabilitas merupakan alat utama untuk analisis proses per-cabangan. Fungsi pembangkit probabilitas dapat digunakan untuk menentukan rata-rata dan variansi. Untuk mengetahui fungsi pembangkit probabilitas dari suatu variabel random, harus diketahui terlebih dahulu distribusi dari variabel random tersebut.

5.2. Rata-rata dan Variansi. Rata-rata dan variansi pada proses percabangan ditentukan berdasarkan fungsi pembangkit probabilitas sesuai distribusi dari va-riabel random. Fungsi pembangkit probabililtas diturunkan untuk memperoleh rata-rata dan variansi. Turunan pertama fungsi pembangkit probabilitas pada distribusi geometrik adalah

G′_Y(s) = E(Y sY −1). Untuk s = 1, diperoleh

G′_Y(1) = E(Y 1Y −1) = E(Y ).

Nilai ekspektasi variabel random Y adalah rata-rata populasi yang diamati se-hingga

G′_Y(1) = µ. (5.1)

Fungsi pembangkit probabilitas untuk variabel random Y dengan probabi-litas memiliki keturunan sukses sebesar b adalah

GY(s) =

b

1 − (1 − b)s. (5.2)

Turunan pertama untuk persamaan (5.2) adalah G′

Y(s) = b(1−b) (1−(1−b)s)2 dan untuk nilai s = 1, diperoleh G′Y(1) = b(1−b) b2 = 1−b

b . Jadi nilai rata-rata variabel random Y yaitu

µ= 1 − b

Mengacu pada Bain dan Engelhardt [2], diberikan definisi variansi sebagai σ2 = E(Y2_{) − (E(Y ))}2_{. (5.4)} Turunan kedua fungsi pembangkit probabilitas adalah

G′′_Y(s) = E(Y (Y − 1)sY −2) = E((Y2−Y)sY −2). Untuk s = 1, diperoleh G′′

Y(1) = E((Y2−Y)1Y −2) dan untuk y = 0, 1, 2, 3, . . ., diperoleh nilai 1Y −2 _{= 1 sehingga}

G′′_Y(1) = E((Y2−Y)) = E(Y2_{) − E(Y )} atau

E(Y2) = G′′_Y(1) + E(Y ). (5.5) Berdasarkan persamaan (5.5), persamaan (5.4) dapat dinyatakan sebagai

σ2 = G′′Y(1) + E(Y ) − (E(Y ))2. (5.6) Turunan kedua fungsi pembangkit probabilitas untuk variabel random Y sebagaimana pada persamaan (5.2) adalah

G′′_Y(s) = 2b(1 − b) 2 (1 − (1 − b)s)3. Untuk nilai s = 1, diperoleh

G′′_Y(1) = 2(1 − b) 2

b2 . (5.7)

Berdasarkan persamaan (5.3) dan (5.7), variansi pada persamaan (5.6) dapat dinyatakan sebagai σ2 = 2(1 − b) 2 b + 1 − b b −( 1 − b b ) 2 = (1 − b) 2 b2 + 1 − b b . Jadi variansi variabel random Y adalah

σ2 = (1 − b) 2 b2 +

1 − b b .

5.3. Penerapan. Proses percabangan mulai muncul sejak Galton menyampai-kan persoalan tentang punahnya nama keluarga pada suatu populasi. Nama ke-luarga hanya dapat diturunkan oleh keturunan laki-laki sehingga nama keke-luarga akan berhenti diturunkan apabila keturunan berjenis kelamin perempuan. Pada 1931, Alfred Lotka mengasumsikan suatu distribusi geometrik untuk menyesuai-kan distribusi keturunan populasi laki-laki Amerika pada tahun 1920. Teori proses percabangan dengan distribusi geometrik digunakan untuk membahas kepunah-an nama keluarga. Karena nama keluarga diturunkkepunah-an oleh keturunkepunah-an laki-laki maka hanya jumlah keturunan laki-laki yang diperhitungkan. Probabilitas bahwa seorang laki-laki memiliki j keturunan laki-laki adalah

pj = (1 − p0)(1 − b)(j−1)b, j = 1, 2, 3, . . . , j ≥ 1.

Probabilitas bahwa seorang laki-laki tidak memiliki keturunan laki-laki adalah p0. Probabilitas sukses atau dengan kata lain nama keluarga akan punah adalah b. Lotka memberikan estimasi probabilitas untuk distribusi geometrik yaitu b = 0, 4107 dan p0 = 0, 4825 sehingga diperoleh pj = (0, 2126)(0, 5893)(j−1).

Dari pembahasan yang telah diuraikan, diketahui bahwa rata-rata banyak-nya generasi sampai nama keluarga punah sebesar µ = 1−b_b = 1, 4349. Dike-tahui bahwa variansi banyaknya generasi sampai nama keluarga punah adalah σ2 = (1−b)_b2 2 + 1−b_b = 3, 4937. Hal ini berarti bahwa rata-rata nama keluarga

di Amerika pada tahun 1920 akan punah pada generasi ke-1, 4349 dan memiliki ukuran penyebaran sebesar 3, 4937 terhadap nilai rata-rata. Berdasarkan simu-lasi untuk beberapa nilai b pada interval 0, 20 sampai 0, 50 dapat disimpulkan jika besarnya probabilitas sukses punah yaitu b semakin kecil, maka rata-rata banyaknya generasi sampai nama keluarga punah semakin besar dengan variansi yang semakin besar pula.

6. KESIMPULAN

Dari hasil dan pembahasan yang telah dilakukan, diperoleh dua kesimpulan berikut.

(1) Rata-rata dan variansi proses percabangan pada distribusi geometrik ada-lah µ= 1 − b b dan σ2 = (1 − b) 2 b2 + 1 − b b .

(2) Penerapan proses percabangan pada distribusi geometrik dengan probabi-litas sukses punah sebesar 0, 4107, probabiprobabi-litas tidak memiliki keturunan

laki-laki sebesar 0, 4825 dan probabilitas memiliki j keturunan laki-laki sebesar (0, 2126)(0, 5893)(j−1) _{untuk j ≥ 1 diperoleh µ = 1, 4349 dengan} variansi sebesar 3, 4937. Hal ini berarti bahwa rata-rata nama keluarga di Amerika pada tahun 1920 akan punah pada generasi ke-1, 4349 namun memiliki ukuran penyebaran sebesar 3, 4937 terhadap nilai rata-rata.

DAFTAR PUSTAKA

[1] Allen, L. J. S. An Introduction to Stochastic Processes with Applications to Biology. Prentice Hall, New Jersey, 2003.

[2] Bain, L. J. and M. Engelhardt. Introducton to Probability and Mathematical Statistics. Duxbury Press, California, 1991.

[3] Kimmel, M and D. E. Axelrod. Branching Process in Biology. Springer-Verlag, New York, 2002.

[4] Meza, R. Age-specific Incidence of Cancer: Phases, Transitions, and Biological Implications. Proceedings of the National Academy of Science, 105(42), 2008.

[5] Mode, C. J. Multitype Branching Process Theory and Applications. Elsevier, New York, 1971.

[6] Newman, M. E. J. et al. Random Graph with Arbitrary Degree Distributions and Their Applications. Physical Review E, 64(2), 2001.

[7] Reluga, T. C. Branching Process and Noncommuting Random Variables in Population Bi-ology. Canadian Applied Mathemathics Quarterly, 17:397–407, 2009.

[8] Taylor, H. M. and S. Karlin. An Introduction to Stochastic Modeling. Academic Press, San Diego, 1998.