(The Method of Separation of Variables). Metode ini dapat digunakan pada PDP linier, khususnya PDP dengan koefisien konstan.

METODE PEMISAHAN PEUBAH

(The Method of Separation of Variables). Metode ini dapat digunakan pada PDP linier, khususnya PDP dengan koefisien konstan.

Tujuan Instruksional :

Setelah mengikuti perkuliahan mahasiswa dapat:

1. Menjelaskan prinsip metode pemisahan peubah

2. Menyelesaikan jenis-jenis PDP yang memenuhi syarat batas

3. Menggunakan deret Fourier untuk menemukan penyelesaian persamaan tersebut yang memenuhi syarat awal.

4.2. METODE PEMISAHAN PEUBAH

4.

Gagasan metode ini adalah :

- Memisahkan peubah untuk memperoleh dua persamaan diferensial biasa. - Menentukan penyelesaian yang memenuhi syarat batas.

- Menggunakan deret Fourier untuk menemukan penyelesaian persamaan tersebut yang memenuhi syarat awal.

4.2.1. Persamaan Gelombang

Sebagai ilustrasi penggunaaan metode ini pada persamaan gelombang, . 0 , 2 2 2 2 2 L x x u c t u       

dengan tiga macam syarat batas , yaitu; i. u(0,t)0,u(L,t)0.

ii. u_x(0,t)u_x(L,t)0.

iii. u(0,t)u(L,t), u_x(0,t)u_x(L,t). Dan syarat awal :

. 0 ), ( ) 0 , ( ), ( ) 0 , (x x u x x x L u  _t   

Disini kita akan menyelesaikan untuk syarat batas (i) saja. Asumsikan bahwa u(x,t) dapat ditulis sebagai perkalian fungsi xdan fungsi t, yaitu u x t( , ) X x T t( ) ( ).

Kita peroleh u_tt XT'' dan u_xx  X T'' , sehingga XT''c X T2 '' . Selanjutnya kita dapatkan T₂'' X'' ,

c T  X   konstan.

Kita peroleh dua persamaaan diferensial biasa (PDB) orde dua, yaitu

'' 0

X X  dan T''c T2 0.

Dari syarat batas u(0, )t u L t( , )0 atau X(0) ( )T t X L T t( ) ( )0 kita dapatkan

(0) ( ) 0

X X L  . Jadi kita peroleh X''X 0, 0 x L dengan syarat batas

(0) ( ) 0

X X L  .

Masalah ini dapat dipandang sebagai masalah nilai eigen  karena ₂ x 

 dapat dipandang sebagai suatu operator diferensial yang bersifat linier.

Selanjutnya kita akan mencari penyelesaian persamaan diferensial tersebut dengan memandangnya sebagai masalah nilai eigen. Penyelesaiannya akan kita lihat dalam tiga kasus :

Kasus I, 2 0.   

Dalam kasus ini kita dapatkan X''2X 0 yang memiliki penyelesaian umum X x( )AcosxBsinx, dengan A B, konstan. Dengan mengingat syarat batas X(0)X L( )0 kita akanmendapatkan X_n( )x sinn x

L 

 , yang merupakan fungsi eigen untuk nilai eigen

2 n n L   _{ } _   , n1, 2,3,...

Kasus II,  0.

Kita peroleh persamaan X''0 dengan syarat batas X(0) X L( )0. Sehingga X x( )AxB, dengan A B, konstan. Karena X(0)X L( )0 maka

(0) 0

X  B dan X L( ) AL B 0. Akibatnya A B 0. Kita dapatkan penyelesaian trivial X x( )0. Jadi 0 bukan nilai eigen.

Kasus III, 2 0    .

Kita peroleh X''2X 0 dengan syarat batas X(0) X L( )0. Penyelesaiannya X x( )AeLBeL 0, dengan A B, konstan. Karena

(0) ( ) 0

X X L  maka X(0)  A B 0 danX L( ) AeLBeL 0. sehingga

A B dan AeLBeL AeLAeL  A e( LeL)0.

Karena eLeL 0, maka A B 0. Kita peroleh penyelesaian trivial. Jadi untuk 0 bukan nilai eigen.

Jadi untuk masalah nilai eigen tersebut kita dapatkan bahwa nilai eigennya adalah 2 n n L   _{ } _

  , n1, 2,3,... , dan fungsi eigennya n( ) sin n

X x x

L 

 .

Secara sama untuk syarat batas (ii) dan (iii) kita akan mendapatkan nilai eigen dan fungsi eigen adalah

Untuk syarat batas (ii)

L x n x X x X L n n n     0, ; ₀( ) 1, ( ) cos 2 0            ,

Syarat batas (iii)

L x n B L x n A x X x X L n n n     ₀ 0, 2 ; ₀( )1, ( ) cos2  sin2         , n = 1,2, . . .

Selanjutnya pada kasus dengan syarat batas (i) penyelesaian PDB yang kedua 2

'' 0

T c T  yang bersesuaian dengan n 2 L  _{ } _   adalah ( ) cos sin n n n n c n c T t A t B t L L     dengan A B_n, _n konstan. Maka kita peroleh penyelesaian

( , ) cos sin sin

n n n n c n c n u x t A t B t x L L L      _  _  

yang memenuhi syarat batas (i). Superposisinya juga merupakan penyelesaian dari persamaan gelombang yang juga memenuhi syarat batas.

Jadi penyelesaian yang memenuhi syarat batas adalah

1

1

( , ) ( , )

cos sin sin .

n n n n n u x t u x t n c n c n A t B t x L L L            _  _  





Selanjutnya akan kita tentukan penyelesaian yang memenuhi syarat awal ( , 0) ( ), ( , 0)_t ( ) u x  x u x  x .  ) (x  1 ( , 0) nsin n n u x A x L    



dan 1 ( , 0) n sin t n B n c n u x x L L     



(x), dengan 0 2 ( ) sin L n n A x xdx L L   



dan 0 2 ( ) sin L n n B x xdx nLc L   



.

Jadi penyelesaian persamaan gelombang yang memenuhi syarat batas dan syarat awal (i) adalah,

1

( , ) ncos nsin sin

n n c n c n u x t A t B t x L L L         _  _  



.

Contoh : Misalkan u(x,0) f(x)sinx dan 0  0   ) ( ) , (x g x t u

, maka kita punyai

Bn = 0 untuk semua n, D1 = 1, dan Dn = 0 untuk n > 1. (Tunjukkan)

Soal 1. Selesaikan ₂, 0 . 2 2 2 2 L x x u c t u       

x x f x u( ,0) ( )sin dan x g x x x u sin ) ( ) , (     0 .

2. Seperti pada nnnomor 1, buktikan bahwa jika

. maka

3. Dengan pemisahan peubah, tentukan penyelesaian persamaan

4.2.2. Persamaan Panas

Persamaan panas akan diturunkan pada aliran padas pada baangan baja.Dalam hal ini u(x,t) menyatakan suhu pada saat t di x. Aliran panas sebanding dengan perubahan suhu

, yaitu

Perhatikan poongan batangan baja antara x dan xx. Jumlah panas pada poongan tersebut, pada saat t adalah

dimana adalah panas jenis baja dan  adalah massa per sauan panjang. Pada saat t t, jumlah panas adalah

Dengan demikian perubahan panasnya adalah

Peruahan panas ini harus sama dengan aliran panas yang masuk di x dikurangi panas yang keluar melalui xx selama waktu t. Diperoleh

Dengan menyamakan kedua persamaan dan membagi dengan dan diperoleh,

Dimana konsanta

  K

c2 adalah thermal conductivity dan

2 2 x y   adalah thermal conduction.

Penyelesaian persamaan panas

Sebagai ilustrasi akan diselesaikan persamaan panas dengan kondisi diriclet,

Dengan syara batas

Dan kondisi awal

Dengan pemisahan peubah,

Sehingga diperoleh

Selanjunya dengan cara seperti pada penyelesaian persamaan gelombang, akhirnya diperoleh penyelesaian yang memenuhi syarat batas adalah

Mengingat syarat awal

(2.59)

(2.60) Untuk semua bilangan bulat n.

Contoh : Selesaikan

Dengan syara baas

dan syarat awal

Penyelesaiannya berbentuk dengan Untuk n = 2m dan untuk n ganjil Soal 1. Selesaikan

yang memenuhi syarat batas

dan syarat awal

2. Selesaikan

dengan

3. Selesaikan persamaan panas yang memenuhi syarat batas

dan syarat awal

4. Selesaikan persamaan panas dengan syaat batas Newmann berikut 0 , 0 ), , ( ) , (x t u x t xl t  u_{t xx} 0 ) , ( ) , (x t u l t 

u_{x x} dan syarat awal u(x,0)g(x)

4.2.3.Persamaan Laplace

Jika proses difusi atau gelombang idak dipengaruhi oleh waktu , maka u_t 0 dan 0

 tt

u dan diperoleh persamaan Laplace , yaitu

 u_xx 0 , persamaan Laplace dalam satu dimensi.  uu_xx u_yy 0, dua dimensi.

Dalam versi non homogen dipunyai persamaan Poissonu f . Masalah Dirichlet untuk plat segiempat

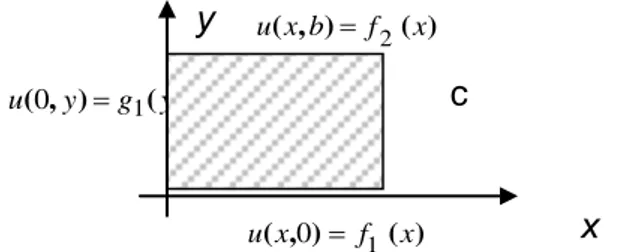
Akan kita bahas persamaan laplace dua dimensi pada plat segiempat seperti pada gambar

y u(x,b) f₂(x)

u(0,y)g₁(y) c

u(x,0) f₁(x) x

Gambar : Masalah Dirichlet plat segiempat. Formulasi masalah : 0   _yy xx u u Syarat batas : u(x,0) f₁(x), u(x,b) f₂(x), 0 < x < a u(0,y)g₁(y)u(a,y) g₂(y), 0 < y < b. Penyelesaian dengan pemisahan peubah

Sebagai ilustrasi akan kita selesaikan untuk syarat batas berbentuk 0 0 0) ( , ) ( , ) , (x u y u x b u dan u(a,y)g₂(y). Dengan pemisahan peubah, u(x,y)X(x)Y(y). Diperoleh dua PD Biasa

. ' ' ' ' 0 0       Y Y X X Syarat batas 0 0 0 0) , ( ) ( ) ( Y Y b X . Diperoleh ,... , , , 123 2           n b n b y n y Y_n( )sin  , b x n B b x n A x X_n( ) _ncosh   _nsinh  . Nasukkan syarat batas, diperoleh An = 0 dan

. sinh ) ( b x n B x X_n  _n 

Prinsip superposisi memberikan

. sin sinh ) , ( b y n b x n B y x u _n n   



 1 dengan . sin ) ( sinh dy b y n y g b b a n B b n   



0 2 2

Contoh : Jika pada kasus di atas g₂(y)10, maka

. ) ( sin ) ( sinh sinh ) ( ) , ( ) ( _b y n n x n n y x u b a n n         _{ } 



2 1 2 1 1 2 1 40 1 2 1 Soal

Selesaikan persamaan laplace pada plat segiempat dengan syarat batas yang diberikan berikut

1. u(x,0)u(0,y)u(x,)0 dan u(,y)siny. (a = b =) 2. u(x,0)u(0,y)u(x,1)0 dan u(1,y)y.