BAB 2 LANDASAN TEORI

LANDASAN TEORI

Sebagian besar dari persoalan manajemen berkenaan dengan penggunaan sumber secara efisien atau alokasi sumber-sumber yang terbatas (tenaga kerja terampil, bahan mentah, modal) untuk mencapai tujuan yang diinginkan (desired objective) seperti penerimaan hasil penjualan yang harus maksimum, penerimaan devisa hasil ekspor nonmigas harus maksimum; jumlah biaya transport harus minimum; lamanya waktu antrian untuk menerima pelayanan sependek mungkin; kemakmuran rakyat sebesar-besarnya.

Dalam keadaan sumber yang terbatas harus dicapai suatu hasil yang optimum. Dengan perkataan lain bagaimana caranya agar dengan masukan (input) yang serba terbatas dapat dicapai hasil kerja yaitu keluaran (output) berupa produksi barang atau jasa yang optimum. Linear programming akan memberikan banyak sekali hasil pemecahan persoalan, sebagai alternatif pengambilan tindakan, akan tetapi hanya ada satu yang optimum (maksimum atau minimum). Ingat bahwa mengambil keputusan berarti memilih alternatif, yang jelas harus alternatif yang terbaik (the best alternative).

Jika diperhatikan keadaan dalam praktek di mana pimpinan perusahaan bermaksud atau bertujuan untuk mencapai hasil penjualan sebesar mungkin (maximum revenue), logikanya adalah pimpinan perusahaan tersebut memutuskan untuk memproduksi sebanyak-banyaknya, maka kalau semua barang tersebut laku dijual, tentu akan diperoleh jumlah hasil penjualan sebanyak-banyaknya. Akan tetapi, keadaan belum tentu seperti itu, pimpinan perusahaan tersebut sebagai pembuat keputusan (decision maker), ternyata akan menghadapi pembatasan-pembatasan (limitation or constraints), misalnya jumlah permintaan masyarakat tidak sebanyak yang diproduksi, sehingga barang susah dijual. Pembatasan bukan berhenti disitu saja sebab mungkin dia menghadapi pembatasan seperti persediaan bahan mentah ternyata hanya tersedia terbatas, tenaga terampil yang aktif dan kreatif

terbatas, machine hours untuk memproses produksi terbatas, modal terbatas, ruangan (storage) untuk menyimpan barang hasil produksi terbatas dan permintaan masyarakat ternyata juga terbatas (limited demand).

Persoalan yang timbul kemudian adalah bagaimana dapat mencapai hasil (output) yang optimum dengan memperhatikan input (men, money, material, time) yang tersedianya memang terbatas. Jadi mencari suatu pemecahan yang optimum dengan memperhatikan pembatasan-pembatasan input. Inilah yang menjadi sasaran linear programming. Pimpinan perusahaan atau pengambil keputusan dalam menghadapi product-mix harus mencari pemecahan agar diperoleh maximum revenue atau maximum profit atau sebaliknya minimum cost of production.

2.1 Persoalan Transportasi

Persoalan transportasi merupakan persoalan linear programming. Bahkan aplikasi dari teknik linear programming pertama kali ialah dalam merumuskan persoalan transportasi dan memecahkannya. Persoalan tranportasi yang dasar pada mulanya dikembangkan oleh F.L Hitchcock pada tahun 1941 dalam studinya yang berjudul: The distribution of a product from several sources to numerous locations. Ini merupakan ciri dari persoalan transportasi yaitu mengangkut sejenis produk tertentu katakan beras, minyak, daging, telur, tekstil, pupuk dan jenis produk lainnya dari beberapa daerah asal (pusat produksi, depot minyak, gudang barang) ke beberapa daerah tujuan (pasar, tempat proyek, pemukiman, daerah trasmigrasi), pengaturan harus dilakukan sedemikian rupa agar jumlah biaya transportasi minimum.

Pada tahun 1947, T.C Koopmans secara terpisah menerbitkan suatu hasil studi mengenai : Optimum utilization of the transportation system. Selanjutnya, perumusan persoalan linear programming, dan cara pemecahan yang sistematis dikembangkan oleh Prof. George Danzig yang sering disebut Bapak linear programming. Prosedur pemecahan yang sistematis tersebut disebut metode simpleks.

Ciri-ciri khusus metode transportasi :

1. Terdapat sejumlah sumber dan sejumlah tujuan tertentu.

2. Jumlah yang didistribusikan dari setiap sumber dan yang diminta oleh setiap tujuan adalah tertentu .

3. Jumlah yang dikirim atau diangkut dari suatu sumber ke suatu tujuan sesuai dengan permintaan atau kapasitas sumber. Jumlah permintaan dan penawaran seimbang dan apabila jumlah permintaan tidak sama dengan penawaran, maka harus ditambahkan variabel dummy.

4. Biaya transportasi dari suatu sumber ke suatu tujuan adalah tertentu.

5. Jumlah variabel dasar m + n - 1, dimana m adalah jumlah baris dan n adalah jumlah kolom. Apabila jumlah variabel dasar kurang dari m + n – 1 yang disebut dengan degenerasi, maka harus ditambahkan variabel dasar dengan nilai nol.

2.1.1 Model Matematis Metode Transportasi

Dalam menggambarkan masalah transportasi, perlu digunakan istilah istilah yang tidak khusus karena masalah transportasi adalah masalah yang umum, yaitu pendistribusian berbagai komoditi dari berbagai kelompok pusat penerima yang disebut tujuan, sedemikian rupa sehingga meminimalisasi biaya distribusi total.

Secara umum, sumber i (i = 1, 2, ..., m) mempunyai supply si unit yang akan didistribusikan ke tujuan-tujuan dan tujuan (j = 1, 2, ...,n) mempunyai permintaan di unit yang dikirim dari sumber-sumber. Asumsi dasar metode transportasi ini adalah biaya mendistribusikan unit-unit dari sumber i ke tujuan j berbanding langsung dengan jumlah yang akan didistribusikan, dimana c menyatakan biaya per unit _ij yang didistribusikan.

Apabila Z merupakan biaya distribusi total dan x ( i = 1, 2, ..., m ; j = 1, 2, _ij ..., n) adalah jumlah unit yang harus didistribusikan dari sumber i ke tujuan j, maka formulasi pemrograman linier masalah transportasi. Dari penjelasan di atas, maka rumus metode transportasi dapat diformulasikan sebagai berikut :

Meminimumkan :

∑∑

= = = m i n j ij ijx c Z 1 1 Batasan : 0 , 2 , 1 ; , 2 , 1 ; ≥ = = = =

∑

∑

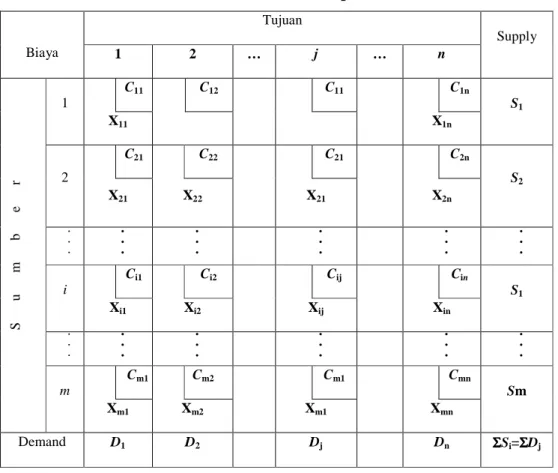
ij j ij i ij X n j b X m i a X K K

Untuk memudahkan pemahaman model transportasi, berikut ini diberikan ilustrasinya pada gambar di bawah ini. Gambar di bawah menjelaskan bahwa terdapat tiga sumber dalam sebuah perusahaan, yaitu m1, m2, dan m3. Dari ketiga sumber tersebut dapat dikirimkan ke tujuan n1, n2, dan n3. Untuk mengetahui seberapa besar masing-masing sumber didistribusikan ke masing-masing tujuan, maka digunakan model transportasi. Dengan menggunakan model transportasi, akan dihasilkan pendistribusian yang akan meminimalisasikan biaya transportasi.

Ilustrasi model transportasi gambar diterjemahkan ke dalam tabel model transportasi dengan mebedakan antara sumber dengan tujuan. Sumber diletakkan pada baris, sedangkan tujuan diletakkan pada kolom. Jumlah penawaran dari masing-masing sumber diletakkan pada kolom paling akhir dan jumlah masing-masing-masing-masing permintaan diletakkan pada baris paling akhir.

Segi empat kecil yang berisi c _,c _,Kc_mn

12

11 merupakan biaya pendistribusian

dari sumber ke tujuan, sedangkan segi empat besar merupakan jumlah yang akan didistribusikan dari setiap sumber ke setiap tujuan. Sebagai gambaran yang lebih konkret, berikut dituangkan model transportasi pada tabel, dengan menggunakan tabel akan memudahkan mencari penyelesaian dari setiap permasalahan transportasi.

Tabel 2.1 Persoalan Transportasi Tujuan Biaya 1 2 … j … n Supply C11 C12 C11 C1n 1 X11 X1n S1 C21 C22 C21 C2n 2 X21 X22 X21 X2n S2 . . . . . . . . . . . . . . . . . . Ci1 Ci2 Cij Cin i Xi1 Xi2 Xij Xin S1 . . . . . . . . . . . . . . . . . . Cm1 Cm2 Cm1 Cmn S u m b e r m Xm1 Xm2 Xm1 Xmn Sm Demand D1 D2 Dj Dn ΣΣΣΣSi=ΣΣΣΣDj

2.1.2 Langkah-Langkah Penyelesaian Masalah Model Transportasi

Dalam menyelesaikan masalah transportasi, terdapat dua langkah yang harus dilakukan, yaitu :

1. Mencari penyelesaian layak pada variabel dasar. Untuk mencari penyelesaian yang layak dapat dipilih salah satu metode yang tersedia. Metode yang dapat digunakan adalah Northwest Corner ( sudut barat laut), Least Cost (biaya terkecil) dan Vogel Approximation ( VAM).

a. Metode Northwest Corner (NWCR)

1. Pendistribusian dimulai dari pojok kiri atas dan, diakhiri pada pojok kanan bawah.

2. Setiap pendistribusian dipilih nilai sebanyak mungkin tanpa menyimpang dari sumber/ tujuan.

3. Apabila variabel dasar sudah terisi semua, maka dihitung jumlah biaya yang akan dikeluarkan oleh perusahaan.

b. Metode Least Cost

1. Pendistribusian dimulai dari biaya terkecil dan, apabila terdapat biaya terkecil lebih dari satu, maka dipilih salah satu.

2. Setiap pendistribusian dipilih nilai sebanyak mungkin tanpa mengabaikan jumlah sumber/tujuan.

c. Vogel Approximation Method ( VAM )

1. Menghitung opportunity cost yang didasarkan pada dua biaya terkecil pada setiap baris dan kolom dan mengurangkan keduanya, hasil perhitungannya disebut dengan penalty cost. 2. Memilih nilai penalty cost terbesar di antara baris dan kolom. 3. Memilih biaya terkecil dari nilai penalty cost terbesar dan

mendistribusikan sejumlah nilai. Baris/ kolom penalti yang sudah terpilih diabaikan untuk langkah selanjutnya.

4. Menyesuaikan jumlah permintaan dan penawaran untuk menunjukkan alokasi yang sudah dilakukan. Menghilangkan semua baris dan kolom dimana penawaran dan permintaan telah dihabiskan.

5. Apabila jumlah penawaran dan permintaan belum sesuai, maka ulangi langkah pertama sampai terisi semua.

2. Menguji hasil penyelesaian. Dengan menggunakan salah satu metode yang tersedia akan didapatkan solusi awal yang layak, akan tetapi penyelesaian yang layak ini belum tentu menjadi penyelesaian yang optimal. Oleh karena itu, perlu dilakukan pengujian agar hasil penyelesaian model transportasi optimal yaitu menghasilkan biaya minimal. Pengujian optimalisasi menggunakan dua metode yaitu :

a. Metode Stepping Stone

1. Memilih satu water square (segi empat yang masih kosong/variabel non basis) dan 3 atau lebih variabel basis (segi empat yang terisi).

2. Mengisi water square (entering variable) dengan memperhatikan variabel basis dan menyesuaikan dengan jumlah penawaran dan permintaan.

3. Memberikan tanda + (positif) pada water square yang akan diisi dan variabel basis yang nilainya bertambah.

4. Memberikan tanda – (negatif) pada variabel basis yang nilainya dipindahkan pada water square.

5. Menguji hasil stepping stone dengan mencari nilai perubahan biaya yang masih negatif.

6. Mengulangi langkah di atas dengan memilih nilai terkecil.

b. Metode MODI

Metode MODI merupakan variasi dari model stepping stone yang didasarkan pada rumusan dual. Perbedaannya dengan metode stepping stone adalah pada metode ini tidak harus menentukan semua jalur

tertutup variabel non basis, kecuali pada saat akan melakukan perpindahan pengisian tabel. Dengan demikian MODI merupakan cara yang efisien untuk menghitung variabel non basis. Dalam metode MODI terdapat persamaan sebagai berikut :

Di mana : mi = Nilai setiap sel baris

nj = Nilai setiap kolom

Cij = Biaya transportasi per unit

Adapun langkah-langkah dalam metode MODI adalah :

1) Mentukan nilai mi untuk setiap baris dan nilai-nilai nj untuk setiap kolom dengan menggunakan hubungan Cij = mi + nj untuk semua variabel basis dan menentukan nilai mi = 0.

2) Menghitung perubahan biaya Cij untuk setiap variabel non basis dengan menggunakan rumus Cij - mi - nj.

3) Apabila hasil perhitungan terdapat nilai Cij negatif, maka solusi belum optimal. Oleh karena itu, dipilih Xij dengan nilai Cij negatif terbesar sebagai entering variabel.

4) Mengalokasikan sejumlah nilai ke entering variabel Xij sesuai dengan proses stepping stone dan mengulangi langkah pertama.

2.1.3 Perumusan Persoalan Transportasi Secara Umum

Misalkan suatu jenis barang diangkut dari beberapa daerah asal ke beberapa daerah tujuan . Misalnya ada m daerah asal: A₁,A₂,...,A_i,...,A_mdan n daerah tujuan :T₁,T₂,...,T_j,...,T_n. Di daerah asal A , tersedia barang yang akan diangkut (supply) _i

sebanyak S dan di tempat tujuan barang tersebut diminta sebanyak _i d (demand). _j

ij

x = jumlah barang yang diangkut (dalam satuan) dari A ke _i T _j

ij

c = besarnya biaya untuk 1 unit barang tersebut dari A ke _i T _j

Dengan demikian untuk mengangkut x diperlukan biaya _ij c_ijx_i. Jumlah permintaan (total demand) = jumlah penawaran (total supply).

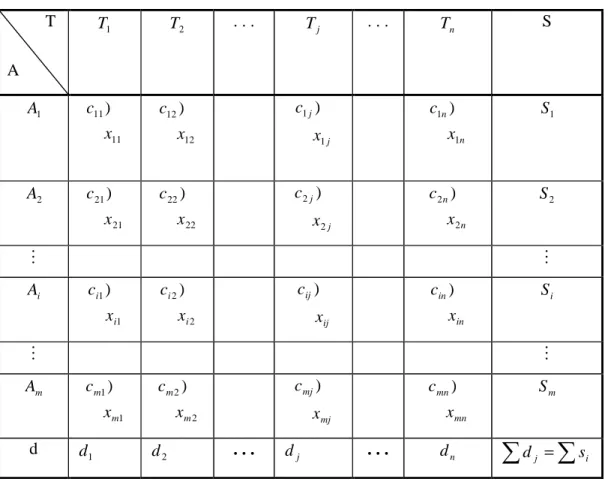
Perhatikan tabel berikut yang menggambarkan permintaan dari setiap tempat tujuan dan penawaran/persediaan dari setiap tempat asal, juga besarnya biaya

ij

c dengan tanda kurung buka.

Tabel 2.2 Perumusan Transportasi Secara Umum T A 1 T T ₂ . . . T _j . . . T _n S 1 A 11 11) x c 12 12) x c j j x c 1 1 ) n n x c 1 1 ) S1 2 A 21 21) x c 22 22) x c j j x c 2 2 ) n n x c 2 2 ) S2 M M i A 1 1) i i x c 2 2) i i x c ij ij x c ) in in x c ) S_i M M m A 1 1) m m x c 2 2) m m x c mj mj x c ) mn mn x c ) S_m d d₁ d₂ . . . d _j . . . d_n

_∑

d_j =

_∑

s_i

Perumusan persoalan linear programming menjadi : Minimum :

∑∑

= = = m i n j ij ijx c Z 1 1 Dengan kendala :

∑

∑

∑∑

∑ ∑

∑

∑

= = = = = = = = ≥ = → = ≥ ≤ n j ij j m i i n j m i ij m i n j ij m i j ij n j i ij x d S x x d x S x 1 1 1 1 1 1 1 1 0 , 2.1.4 Model Transshipment (Persinggahan)

Model transportasi standar mengasumsikan bahwa rute langsung antara sebuah sumber dan sebuah tujuan adalah rute berbiaya minimum. Ini berarti bahwa perhitungan persiapan yang melibatkan penentuan rute terdekat harus dilakukan sebelum biaya unit dari model transportasi standar dapat ditentukan. Perhitungan ini dapat dilakukan dengan menerapkan algoritma rute terdekat terhadap pasangan node yang diinginkan.

Satu prosedur alternatif dari penggunaan model transportasi biasa (dengan algoritma rute terdekat yang dimasukkan ke dalamnya) adalah model

transshipment. Model yang baru ini memiliki ciri tambahan yang mengijinkan

unit-unit yang dikirimkan dari semua sumber untuk melewati node-node antara atau sementara sebelum pada akhirnya mencapai tujuan mereka. Dengan kata lain model transshipment digunakan pada saat terdapat suatu node-node antara yang diijinkan menjadi tempat persinggahan unit dari sumber sebelum pada akhirnya mencapai tujuan. Akibatnya, algoritma baru ini menggabungkan baik algoritma transportasi biasa dengan algoritma rute terdekat menjadi satu prosedur.

Model transshipment merupakan perluasan dari model transportasi. Perbedaannya adalah, pada model transshipment semua simpul berpotensi

menjadi tempat persinggahan barang atau titik transshipment,sedang pada model transportasi pengiriman barang langsung dari gudang yang kelebihan barang ke gudang yang membutuhkan barang. Dalam model transshipment diasumsikan bahwa:

1. Barang yang dikirim adalah homogen, 2. Biaya penyimpanan tidak diperhitungkan,

3. Alat pengangkutan telah ditentukan untuk pengiriman barang dari suatu gudang ke gudang lain,

4. Biaya pengiriman barang dari suatu gudang ke gudang dihitung untuk tiap unit barang yang dipindahkan,

5. Biaya persinggahan pada titik transshipment dihitung untuk tiap unit barang yang dipindahkan.

Langkah-langkah yang ditempuh untuk menyelesaikan masalah transshipment adalah sebagai berikut :

1. Membuat model transshipment,

2. Mengubah model transshipment menjadi model transportasi, 3. Mencari solusi fisibel basis,

4. Mencari solusi optimal.

Berdasarkan Nasendi (1985),masalah transshipment (persinggahan) merupakan suatu bentuk umum dari model transportasi, sedangkan model transportasi adalah bentuk khususnya di mana terdapat pusat-pusat asal atau sumber-sumber asli, pusat-pusat tujuan yang asli, dan titik-titik

transshipmentnya. Titik-titik transshipment tersebut bisa terdapat pada pusat

asal maupun pusat tujuan. Dalam model ini setiap pusat dapat mengirim dan menerima arus barang angkutan. Hal ini berarti terdapat keleluasaan dalam penetapan rute arus barang dari titik i ke titik j, selain rutenya yang langsung.

Ada beberapa cara untuk merumuskan masalah transshipment secara matematis. Pendekatan yang disajikan ini termasuk relatif lebih singkat dan

tegas. Andaikan : X = jumlah yang diangkut dari titik i ke titik j ; _ij n j i j i≠ ; , =1,2,K, _. ij

C = biaya angkutan dari titik i ke titik j ; C_ij ≥0.

i

r = kebutuhan bersih (sisa) di titik i.

Setiap titik atau lokasi yang ada harus dapat memenuhi suatu rumusan keseimbangan yaitu antara arus barang yang keluar (diangkut) dikurangi arus barang yang masuk(diterima) harus sama dengan kebutuhan bersih. Secara simbolik, rumusan model umum transshipment adalah sebagai berikut :

Minimumkan : Z C X i j n i n j ij ij ≠ =

∑∑

= = dimana , 1 1 Dengan kendala : j i n j i X n i r X X ij i n i j ji n j i ij ≠ = ≥ = = −

∑

∑

≠= ≠ = ; , , 2 , 1 , ; 0 dan , , 2 , 1 untuk 1 1 1 1 K K

Apabila kita inginkan agar jumlah permintaan sama dengan jumlah suplai (artinya

∑

_ir_i =0) maka model transshipmentnya menjadi :

Minimumkan : Z C X i j n i n j ij ij ≠ =

∑∑

= = dimana , 1 1 Dengan kendala : j i n j i X n i X X ij n i j ji n j i ij ≠ = ≥ = = −

∑

∑

≠= ≠ = ; , , 2 , 1 , ; 0 dan , , 2 , 1 untuk 0 1 1 1 1 K K

2.2 Terminologi Dasar Graph

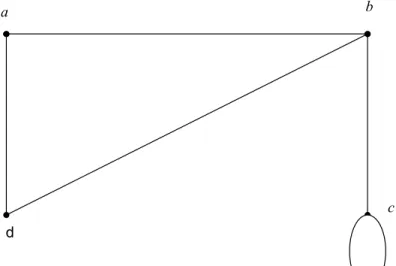
Graph berarah (directed graph) didefinisikan secara abstrak sebagai suatu pasangan terurut (V,E), dengan V suatu himpunan dan E suatu relasi biner pada V. Graph berarah dapat digambarkan secara geometris sebagai suatu himpunan titik-titik V dengan suatu himpunan tanda panah E antara pasangan titik-titik. Sebagai misal Gambar di bawah ini menunjukkan sebuah graph berarah. Unsur-unsur di dalam V dinamakan verteks (vertex), sedangkan psangan terurut di dalam E dinamakan rusuk (edge) graph berarah tersebut. Sebuah rusuk dikatakan berinsidensi (incident) dengan kedua verteks yang dihubungkannya.

Gambar 2.2 Graph Berarah

Sebagai misal, rusuk (a,b) berinsidensi dengan verteks a dan verteks b. Kadang-kadang, bila diinginkan lebih rinci lagi, dapat dikatakan bahwa rusuk (a,b) berinsidensi dari a dan berinsidensi ke b. Untuk rusuk (a,b), verteks a dinamakan verteks awal (initial vertex). Suatu rusuk yang berinsidensi dari dan ke verteks yang sama, misalnya (c,c) di dalam Gambar, dinamakan lup (loop).

Dua verteks dikatakan berdekatan (adjacent) jika keduanya dihubungkan oleh sebuah rusuk. Selain itu, untuk rusuk (a,b), verteks a dikatakan berdekatan ke (adjacent to) verteks b, sedangkan verteks b dikatakan berdekatan dari (adjacent

form) verteks a. Sebuah verteks dinamakan verteks terasing atau terisolasi

(isolated vertex) jika tidak ada rusuk yang beinsidensi dengannya.

Graph tak berarah (undirected graph) G didefinisikan secara abstrak sebagai suatu pasangan terurut (V, E), dengan V suatu himpunan dan E suatu himpunan yang unsur-unsurnya berupa multi himpunan dengan dua unsur dari V. Sebagai misal, G = ({a, b, c, d}, {{a, b}, {a, d}, {b, c}, {b, d}, {c, c}}) adalah sebuah graph tak berarah. Graph tak berarah G diatas digambarkan secara geometrik dalam Gambar. Sebagai ilustrasi lain, misalkan V = {a, b, c, d, e} sebuah himpunan program komputer. Gambar menunjukkan sebuah graph tak berarah dengan dua verteks dihubungkan oleh sebuah rusuk jika kedua program yang direpresentasikan oleh kedua verteks itu bisa menerima data yang sama.

a b

c d

Gambar 2.3 Graph Tak Berarah

2.2.1 Graph Ganda dan Graph Berbobot

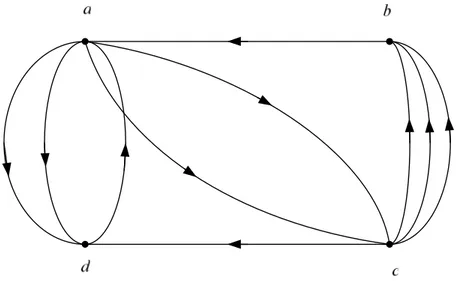
Definisi graph dapat diperluas dalam beberapa cara. Misalkan G = (V, E), dengan V suatu himpunan dan E suatu himpunan ganda yang unsur-unsurnya

berupa pasangan terurut dari V x V. Graph G ini dinamakan graph ganda berarah (directed multigraph). Secara geometris, graph ganda berarah dapat dinyatakan sebagai suatu himpunan titik-titik V dengan suatu himpunan tanda panah E antara titik-titik tanpa ada kendala mengenai banyaknya tanda panah dari satu titik ke titik lainnya. Sebagai misal, Gambar di bawah menunjukkan sebuah graph ganda. Selanjutnya perhatikan representasi grafis sebuah peta jalan raya dengan rusuk antara dua kota menyatakan sebuah jalur pada jalan raya antara kedua kota. Karena jalan raya antara dua kota sering mempunyai banyak lajur, representasi ini akan menghasilkan sebuah graph ganda. Gagasan graph ganda tak berarah (undirected multigraph) dapat didefinisikan dengan cara serupa.

Gambar 2.4 Graph Ganda Berarah

Ketika memodelkan suatu masalah fisik sebagai suatu graph abstrak, seringkali ditambahkan informasi lain kepada verteks-verteks dan/atau rusuk-rusuk graph tersebut. Sebagai misal, di dalam graph yang menggambarkan jaringan jalan raya antara kota-kota, ditambahkan sebuah bilangan pada setiap rusuk untuk menunjukkan jarak antara kedua kota yang dihubungkan oleh rusuk tersebut. Secara umum, graph berbobot (weighted graph) didefinisikan sebagai sebuah pasangan terurut ganda empat (V, E, f, g), atau sebuah pasangan terurut ganda tiga (V, E, g); dalam hal ini V himpunan semua verteksnya, E

himpunan semua rusuknya, f sebuah fungsi dengan daerah asal (domain) V, dan

g sebuah fungsi dengan daerah asal E. Fungsi f memberi pembobot (weights)

pada verteks, sedangkan fungsi g memberi pembobot pada rusuk. Pembobot itu bisa berupa bilangan, lambang, atau besaran apa pun yang ingin kita berikan kepada verteks dan rusuk.

2.2.2 Lintasan dan Rangkaian

Di dalam graph berarah, lintasan ialah suatu barisan rusuk ) , , , ( 2 1 i ik i e e

e K _{sedemikian rupa sehingga verteks terminal}

j i e berimpit dengan verteks awal ) 1 (j+ i

e untuk 1≤ j≤k−1. Suatu lintasan dikatakan sederhana (simple)

jika ia tidak mencakup rusuk yang sama dua kali. Suatu lintasan dikatakan elementer (elementary) jika ia tidak bertemu verteks yang sama dua kali.

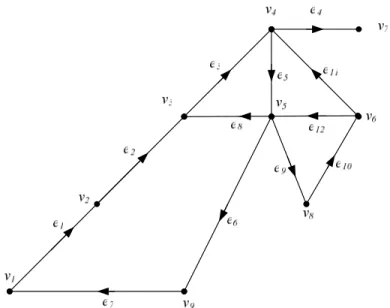
Dalam Gambar di bawah ini, (e1, e2, e3, e4) adalah sebuah lintasan ; (e1, e2,

e3, e5, e8, e3, e4) adalah sebuah lintasan,namun bukan yang sederhana ; (e1, e2, e3,

e5, e9, e10, e11, e4) adalah sebuah lintasan sederhana, namun bukan yang elementer.

Rangkaian (circuit) ialah suatu lintasan ( , , , ) 2 1 i ik i e e e K _{yang verteks} terminalnya, k i

e . Suatu rangkaian dikatakan sederhana (simple) jika ia tidak mencakup rusuk yang sama dua kali. Suatu rangkaian dikatakan elementer (elementary) jika ia tidak bertemu verteks yang sama dua kali. Di dalam Gambar, (e1, e2, e3, e5, e9, e10, e12, e6, e7) adalah sebuah rangkaian sederhana, namun bukan elementer, sedangkan (e1, e2, e3, e5, e6, e7) adalah sebuah rangkaian elementer.

Suatu lintasan atau suatu rangkaian dapat direpresentasikan juga dengan barisan verteks-verteks yang ditemuinya. Sebagai misal, lintasan (e1, e2,

e3, e4) di dalam Gambar, dapat juga direpresentasikan sebagai (v1, v2, v3, v4, v7), sedangkan rangkaian (e5, e9, e10, e11) dapat direpresentasikan sebagai (v4, v5, v8,

v6, v4).

Suatu graph tak berarah dikatakan terhubungkan (connected) jika ada suatu lintasan antara setiap dua verteks, dan jika tidak demikian dikatakan tidak terhubungkan (disconnected). Suatu graph berarah dikatakan terhubungkan jika graph tak berarah yang diperoleh dengan mengabaikan arah-arah rusuk-rusuknya ternyata terhubungkan, dan jika tidak demikian dikatakan tidak terhubungkan. Dengan demikian, suatu graph tidak terhubungkan terdiri dari dua atau lebih komponen yang masing-masingnya berupa sebuah graph terhubungkan. Suatu graph berarah dikatakan terhubungkan erat (strongly connected) jika untuk setiap dua verteks a dan b di dalam graph itu, ada lintasan dari a ke b maupun dari b ke a.

2.2.3 Lintasan dan Sirkuit Euler

Misalkan G adalah suatu graph. Lintasan Euler G adalah lintasan yang melalui masing-masing sisi di dalam graph G tepat satu kali..

Sirkuit Euler ialah sirkuit yang melewati masing-masing sisi tepat satu kali dan graph yang mempunyai sirkuit Euler disebut graph Euler (Eulerian

graph). Graph yang mempunyai lintasan Euler dinamakan juga graph

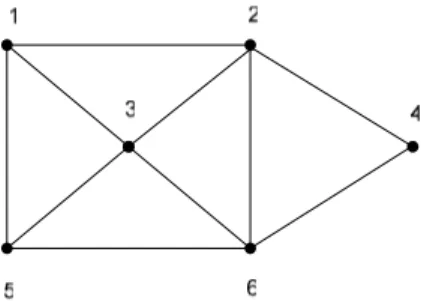
semi-Euler (semi-semi-Eulerian graph). Gambar di bawah ini merepresentasikan sebuah graph Euler dengan lintasan eulernya : 1, 2, 4, 6, 2, 3, 6, 5, 1, 3

Gambar 2.6 Graph Euler

2.2.4 Lintasan dan Sirkuit Hamilton

Suatu graph terhubung G disebut lintasan Hamilton bila ada lintasan yang melalui tiap simpul di dalam graph G tepat satu kali. Sirkuit Hamilton ialah sirkuit yang melalui tiap simpul di dalam graph tepat satu kali, kecuali simpul asal (sekaligus simpul akhir) yang dilalui dua kali. Graph yang memiliki sirkuit Hamilton dinamakan graph Hamilton, sedangkan graph yang hanya memiliki lintasan Hamilton disebut graph semi-Hamilton.

Dalam sirkuit Euler, semua garis harus dilalui tepat satu kali, sedangkan semua titiknya boleh dikunjungi lebih dari satu kali. Sebaliknya, dalam sirkuit Hamilton semua titik harus dikunjungi tepat satu kali dan tidak harus melalui semua garisnya. Dalam sirkuit Euler, yang dipentingkan adalah garisnya. Sebaliknya dalam sirkuit Hamilton, yang dipentingkan adalah kunjungan pada titiknya. Gambar di bawah ini merepresentasikan sebuah contoh graph Hamilton dengan lintasannya adalah : 1, 2, 3, 4, 1.

Gambar 2.7 Graph Hamilton

2.2.5 Lintasan Terpendek Di Dalam Graph Berbobot

Misalkan G = (V, E, w) sebuah graph berbobot ; dalam hal ini w suatu fungsi dari E ke himpunan bilangan nyata positif. Misalkan V sebuah himpunan kota-kota dan E himpunan jalan-jalan raya yang menghubungkan kota-kota-kota-kota tersebut. Pembobot rusuk {i, j}, dilambangkan w(i, j), biasanya dinamakan panjang rusuk {i, j}, yang dalam hal ini dapat ditafsirkan sebagai jarak antara kota i dan kota j. Panjang suatu lintasan di dalam graph G didefinisikan sebagai jumlah panjang rusuk-rusuk di dalam lintasan itu.

Misalkan diinginkan suatu lintasan terpendek dari verteks a ke verteks z di dalam graph G. Mula-mula ditentukan lintasan terpendek dari a ke suatu verteks lain, lalu ditentukan lagi lintasan terpendek dari a ke suatu verteks lain lagi, dan demikian seterusnya. Pada akhirnya, prosedur demikian ini akan berakhir bila lintasan terpendek dari a ke z diperoleh.

Masalah lintasan terpendek adalah masalah yang menyangkut node, panjang jalur, arah lintasan. Dalam lintasan ini perlu diperhatikan khusus yaitu node supply (node awal) dan node demand ( node akhir). Untuk menyelesaikan masalah lintasan terpendek, terdapat suatu algoritma yang bisa dipakai yaitu :

1. Tujuan pada iterasi ke-n ; Tentukan node terdekat dari titik awal (node awal)

2. Input pada iterasi ke-n ; node terdekat ke n-1 ke node awal, termasuk di dalamnya lintasan terpendek dan jarak dari node awal. (node-node ini ditambah dengan node awal disebut node terselesaikan, yang lain node belum terselesaikan).

3. Kandidat untuk node terdekat ke-n ; setiap node terselesaikan yang langsung berhubungan dengan satu atau lebih node belum terselesaikan sebagai kandidat node belum terselesaikan yang mempunyai hubungan terpendek.

4. Perhitungan node terdekat ke-n ; untuk setiap node terselesaikan dan node kandidat, ditambah dengan jarak diantaranya. Kandidat yang mempunyai total jarak terpendek ke-n.

2.3 Jaringan Transportasi

Suatu graph berbobot dinamakan jaringan transportasi (transport network) jika sejumlah syarat berikut dipenuhi :

1. Ia terhubungkan dan tidak mempunyai lup.

2. Ada satu dan hanya satu verteks di dalam graph itu yang tidak mempunyai rusuk masuk.

3. Ada satu dan hanya satu verteks di dalam graph itu yang tidak mempunyai rusuk keluar.

4. Pembobot setiap rusuk berupa sebuah bilangan nyata tidak negatif.

Di dalam suatu jaringan transportasi, verteks yang tidak mempunyai rusuk masuk dinamakan sumber (source) dan dilambangkan dengan a ; verteks yang tidak mempunyai rusuk keluar dinamakan pembuangan (sink) dan dilambangkan dengan z. Pembobot suatu rusuk dinamakan kapasitas (capacity) rusuk tersebut. Kapasitas rusuk (i, j) dilambangkan dengan w(i, j)

Suatu jaringan transportasi merepresentasikan suatu model umum bagi transportasi benda/barang dari tempat asal pasokan ke tujuan melalui berbagai

rute pengiriman, dengan kendala berupa batas maksimum terhadap banyaknya barang yang dapat dikirimkan melalui rute-rute tersebut.

Aliran (flow) di dalam suatu jaringan transportasi,φ,ialah pemberian suatu bilangan tidak negatif φ( ji, ) kepada setiap rusuk (i, j) sedemikian rupa sehingga syarat-syarat berikut dipenuhi :

1. φ(i,j)≤w(i, j) untuk setiap rusuk (i,j).

2.

∑

∑

∝ = ∝ = = 0 0 ) , ( ) , ( k i k j j i φ

φ untuk setiap verteks j kecuali sumber a dan pembuangan z.

Dalam kaitan dengan transportasi barang/benda, φ( ji, ) adalah banyaknya barang yang akan dikirim melalui rute (i, j). Syarat 1 berarti bahwa banyaknya barang yang akan dikirim melalui suatu rute tidak boleh melebihi kapasits rute tersebut. Syarat 2 berarti bahwa, kecuali di sumber dan di pembuangan, banyaknya barang yang mengalir menuju suatu verteks harus sama dengan banyaknya barang yang keluar dari verteks bersangkutan. Besaran

∑

∝ =0 ) , ( i i a

φ dinamakan nilai aliran φ (value of the flow φ) dan dilambangkan dengan φ_v,sehingga :

∑

∑

∝ = ∝ = = = 0 0 ) , ( ) , ( k i v φ a i φ k z φ

yang berarti bahwa total aliran keluar di titik sumber sama dengan total aliran masuk di titik pembuangan. Untuk suatu aliran, rusuk (i, j) dikatakan jenuh (saturated) jika φ(i, j)=w(i,j) , dan dikatakan belum jenuh (unsaturated) jika

) , ( ) , (i j <wi j

φ . Aliran maksimum (maximum flow) di dalam suatu jaringan transportasi ialah suatu aliran yang mencapai nilai tertinggi yang mungkin dicapai.

Potongan (a cut) di dalam suatu jaringan transportasi ialah suatu himpunan potongan dari graph tak terhubungkan (yang diperoleh dari jaringan transportasi itu dengan mengabaikan arah rusuk-rusuknya) yang memisahkan titik sumber dari titik pembuangannya. Notasi (P,P) digunakan untuk menyatakan suatu potongan yang membagi verteks-verteks itu menjadi dua himpunan bagian P dan P , dengan P mengandung titik sumber dan P mengandung titik pembuangan. Kapasitas suatu potongan,dilambangkan dengan w(P,P), didefinisikan sebagai jumlah kapasitas rusuk-rusuk yang berinsidensi dari verteks-verteks di dalam P ke verteks-verteks di dalam P; dengan kata lain :

∑

∈ ∈ = P j P i j i w P P w & & , ) , ( ) , ( .