SEMI DISKRITISASI METODE GALERKIN PADA PERSAMAAN PANASDUA DIMENSI SEMI DISCRETIZATION OF GALERKIN METHOD ON TWO DIMENSIONAL HEAT EQUATION

(1)

SEMI–DISKRITISASI METODE GALERKIN PADA PERSAMAAN PANASDUA DIMENSI

SEMI–DISCRETIZATION OF GALERKIN METHOD ON TWO DIMENSIONAL HEAT EQUATION

Marwan Sam, Jeffry Kusuma, Mawardi

Program Studi Matematika Terapan, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Hasanuddin

Alamat Korespondensi: Marwan Sam

Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Hasanuddin

Makassar,

HP: 085330245132

(2)

Abstrak

Sebuah persamaan panas dua dimensi memiliki dua buah variabel yakni variabel x dan y yang keduanya dipengaruhi oleh variabel waktu t. Tujuan penelitian ini adalah mereduksi persamaan panas dua dimensi menjadi persamaan panas satu dimensi. Proses reduksi ini menggunakan berbagai macam cara, salah satunya dengan menggunakan metode Semi Diskritisasi dari metode Galerkin yang merupakan salah satu dari berbagai macam metode yang terdapat dalam metode Elemen Hingga. Persamaan panas dua dimensi akan didiskritisasi terhadap koordinat x. Metode Galerkin dapat digunakan dengan mengambil fungsi terboboti sebagai fungsi interpolasi. Untuk memenuhi syarat pada fungsi interpolasi, maka dilakukan reduksi dengan menerapkan teorema Green–Gauss. Dari sini diperoleh sebuah persamaan panas yanbg hanya memiliki satu variabel. Dinamakan persamaan panas satu dimensi. Berikutnya hasil yang diperoleh akan didiskritisasi terhadap koordinat x. Diskritisasi terhadap x memungkinkan solusi dari beberapa matriks koefisien. Dapat dilihat bahwa matriks – matriks tersebut adalah matriks simetris. Dua diantaranya positif definit dan yang lainnya positif semi-definit yang menandakan kestabilan dari metode ini. Dari penelitian ini dapat disimpulkan bahwa persamaan panas dua dimensi dapat direduksi menjadi persamaan panas satu dimensi dengan menggunakan tehnik semi-diskritisasi dari Metode Galerkin.

Kata Kunci : persamaan panas dua dimensi, semi–diskritisasi , metode Galerkin

Abstract

A two dimensional heat equation have two variable. They are x dan y that both of them are influenced by times variable. The purpose of this research is to reduce a two dimensional heat equation be a one dimensional heat equation. This proccess can be done by many methods, one of them is semi–discretization of Galerkin Method which are the part of Finite Elemen method. The two dimensional heat equation will be discretizated in xcoordinat. Galerkin Method can be used by taking the weighted function as an interpolation function. To satisfy the condition of the function, the function will be reduced by Green–Gauss Theorem. From here, we find an equation which have just one variable. It’s called one dimensional heat equation. This result will be discretizated by x-coordinate. Some matrices can be found by discretization of x. It can be seen that the matrices are all symmetric. One of them is positive semi–definite and the others are positive definite. So, It can be said that the two dimensional heat equation can be reduced to be an one dimentional heat equation by using semi-discretization technique from Galerkin Method.

(3)

PENDAHULUAN

Persamaan differensial biasa muncul secara alami ketika memodelkan fenomena fisik, seperti osilasi mekanik dan osilasi elektrik. Jika sebuah fenomena meliputi fungsi–fungsi yang lebih dari satu variabel, maka permodelan akan meliputi beberapa turunan parsial dan mengarahkannya ke sebuah persamaan differensial parsial. Persamaan differensial parsial muncul dalam studi tentang getaran–getaran.Seperti mekanika membran, balok dan flat, migrasi persamaan gelombang, aliran panas, teori potensial, elektromagnetis, elastisitas dan yang sejenisnya (Hoffman, 2003).

Terdapat beberapa contoh yang menarik untuk dibahas berkaitan dengan persamaan differensial parsial adalah yang berkaitan dengan perpindahan panas dan persamaan gelombang (Asmar, 2005).

Salah satu jenis persamaan differensial parsial yaitu migrasi persamaan gelombang 2D diselesaikan dengan menggunakan metode Semi–Diskritisasi Galerkin yang diambil dari gabungan Metode Elemen Hingga dan Beda Hingga dalam domain spasial. Dengan menggunakan teknik semi-diskritisasi galerkin dari Metode Elemen Hingga dalam domain spasial, persamaan gelombang 2D tersebut dapat dituliskan sebagai persamaan differensial parsial dengan dimensi yang lebih rendah yang secara kontinu bergantung pada ruang dan waktu. Metode Beda Hingga digunakan untuk menyelesaikan PDP tersebut (Bancroft dkk., 2003).

Sementara itu, persamaan panas diselesaikan dengan menggunakan teknik semi-diskritisasi dari Metode Elemen Hingga dengan syarat batas Neuman dan Dirichlet yang kemudian dilanjutkan dengan Metode Elemen Hingga Theta (Tamaz Szabo, 2009).

Persamaan panas yang berdimensi dua yang dapat diselesaikan dengan menggunakan Metode Elemen Hingga dan Beda Hingga dapat diselesaikan dengan cepat dan mudah dengan menggunakan gabungan kedua metode tersebut yang pada Metode Elemen Hingga menggunakan Semi–Diskritisasi Galerkin sehingga dimensi dari persamaan panas menjadi lebih rendah sehingga jauh lebih mudah untuk diselesaikan. Dalam penelitian ini akan dilakukan Semi– Diskritisasi terhadap koordinat x dengan menggunakan Metode Galerkin (Yang dkk., 2005).

Tujuan penelitian ini adalah mengubah dimensi dari persamaan panas yang awalnya dua dimensi menjadi satu dimensi dengan menggunakan Metode Galerkin sehingga lebih mudah diselesaikan dengan metode – metode yang lainnya.

(4)

BAHAN DAN METODE

Lokasi dan Waktu Penelitian

Penelitian ini dilaksanakan di Program Studi Matematika Terapan Fakultas Matematika dan Ilmu Pengetahuan Alam selama satu bulan yaitu pada bulan Mei hingga Juli 2013.

Sumber Data

Data yang digunakan pada penelitian ini diambil dari hasil running timedengan syarat batas dan syarat awal yang sudah ditentukan.

Rancangan Penelitian

Metode yang digunakan adalah Metode Galerkin yang merupakan bagian dari Metode Elemen Hingga. Selanjutnya persamaan – persamaan yang ada diselesaikan dengan menggunakan bantuan program Maple 11.

Persamaan Perambatan Panas

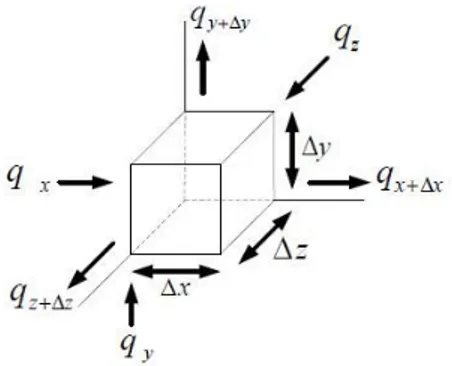
Persamaan konduksi pada tiga dimensi dapat diturunkan dari bentuk control volume yang sisi – sisinya  ,x ydan  masing – masing sejajar dengan sumbuz x, dany z seperti yang ditunjukkan pada gambar 2.Karena volume dari elemen tersebut adalahV xyz, maka massanya adalah (Ardian, 2010)

z y x V m        

Jumlah panas pada elemen ini saat waktu adalah :

.. ... )... , , , ( ) , , , ( ) , , , , , (x y z x y z c mU x y z t c x y zU x y z t Q          (1)

Gambar 1. Control volume benda pada koordinat Cartesius dimensi tiga.

Rata – rata perubahan jumlah panas pada elemen ini diberikan oleh :

... ... ... ... ... ... ... )... , , , (x y z t t U z y x c dt dQ        (2)

(5)

Sesuai dengan prinsip kekekalan energi, yaitu rata – rata perubahan panas harus sama dengan aliran panas yang masuk dikurangi aliran panas yang keluar, maka diperoleh (Asmar, 2005) ... ... ... ... ... ... z z y y x x z y x q q q q q q dt dQ             (3)

Kuantitas panas yang masuk dan yang keluar pada elemen volume arah sumbu x adalah (Holman, 2003) : ... ... ... ... ... ... ... ... ... ... x U z y k q_x       (4) ... ... ... ... ... ... ... z y x x U k x x U k q_x _x _                         (5)

Kuantitas panas yang masuk dan yang keluar pada elemen volume arah sumbu y adalah (Holman, 2003) : ... ... ... ... ... ... ... ... ... ... y U z x k q_y       (6) ... ... ... ... ... ... ... z x y y U k y y U k q_y _y _                         (7)

Sedangkan kuantitas panas yang masuk dan yang keluar pada elemen volume arah sumbu

zadalah (Holman, 2003) : ... ... ... ... ... ... ... ... ... ... z U y x k q_z       (8) .... ... ... ... ... ... ... y x z z U k z z U k q_z _z _                         (9)

Substitusikan persamaan (2) dan persamaan (4) sampai persamaan (9) ke persamaan (3) kemudian bagi dengan xyz_{diperoleh (Holman, 2003) :}

. ... ... ... ... ... ... ... 2 2 2 2 2 2                  z U y U x U k t U c (10)

(6)

... ... ... ... ... ... ... 1 2 2 2 2 2 2 2 U z U y U x U t U               (11) dengan k c   1

adalah konstanta penghamburan panas atau koefisien difusi thermal dan 2U

adalah operator Laplace. Persamaan (11) inilah yang disebut sebagai persamaan panas pada benda dimensi tiga dalam koordinat cartesius (Ardian, 2010).

Dari persamaan (11) di atas, dapat ditentukan pula bentuk persamaan panas benda satu dimensi dengan menghilangkan variabel y dan zpada U dan persamaan panas pada benda dimensi dua dengan menghilangkan variabel zpadaU .

Persamaan Panas Satu Dimensi

Persamaan panas benda satu dimensi berdasarkan persamaan (11) adalah :

... ... ... ... ... ... ... ... ... ... 1 2 2 x U t U       (12)

Persamaan Panas Dua Dimensi

Sedangkan persamaan panas benda dua dimensi berdasarkan persamaan (11) adalah : ... ... ... ... ... ... ... ... ... 1 2 2 2 2 y U x U t U          (13)

Persamaan (13) inilah yang dimensinya akan diubah menjadi persamaan panas satu dimensi seperti pada persamaan (12) dengan syarat batas dan syarat awal untuk U(x,y,t)disepanjang interval 0 x L diberikan melalui

0 ) , , ( ) , ( ) 0 , , ( 0 , 0 0 ), , ( ) , , (             T t y x t U y x t y x U y y t x t y x U   ……….(14)

(7)

Metode Semi–Diskritisasi Galerkin adalah teknik analisis–numerik turunan dari Elemen Hingga dan Beda Hingga yang menggunakan elemen hingga untuk variabel spasial dan memodelkan waktu atau variabel yang seperti waktu dengan menggunakan beda hingga.

Metode Pengumpulan Data

Pengumpulan data dilakukan dengan memperhatikan syarat awal dan syarat batas dari persamaan panas dua dimensi yang akan disemi-diskritisasi dengan menggunakan metode galerkin.

Analisis Data

Data – data dari hasil observasi akan dianalisis dengan menggunakan syarat awal dan syarat batas yang telah ditentukan.

HASIL

Hasil dari penelitian ini adalah persamaan panas satu dimensi yang berasal dari persamaan panas dua dimensi dengan semi-diskritisasi dari metode galerkin dengan syarat batas dan syarat awal yang telah ditentukan. Berikut merupakan persamaan panas satu dimensi yang dihasilkan

... ... ... ... ... ... ... ... ... 2 2 y u H Ku t u M       (15)

dengan syarat batas dan syarat awal

0 ) , ( ) ( ) 0 , ( 0 , 0 0 ), ( ) , (             T t y t u y g t y u y y t f t y u ……….(16)

Dari persamaan (15) dan (16) dapat dilihat bahwa variabel yang tersisa adalah variabel y,

begitu pun dengan syarat batas dan syarat awalnya.

PEMBAHASAN

Penelitian ini menunjukkan perubahan yang terjadi pada persamaan panas dua dimensi dengan syarat batas dan syarat awal yang diberikan berubah menjadi persamaan panas satu

(8)

dimensi. Perubahan persamaan panas dari dua dimensi menjadi persamaan panas satu dimensi ini diikuti dengan perubahan syarat awal dan syarat batas dengan mereduksi variabel x, sehingga yang tersisa adalah syarat batas dan syarat awal dengan variabel y dan t.

Substitusikan sebuah solusi pendekatan untuk U ,

... ... ... ... ... ... ... ... ) ( ) , ( ) , , ( 1



  M i i i y t N x t y x u  (17)

ke dalam persamaan (13) dan terapkan metode residu terboboti sehingga diperoleh :

... ... ... ... ... ,..., 2 , 1 , 0 1 0 2 2 2 2 M j dx t u y u x u W L j                



    (18)

Kemudian gunakan metode galerkin klasik dengan mengambil fungsi terboboti sebagai fungsi interpolasi :

) (x N W_j  _j

Oleh karena itu persamaan (18) menjadi

. ... ... ... ... ... 0 1 0 0 2 2 0 2 2         



L j L j L j dx t u N dx y u N dx x u N     (19)

Agar memenuhi syarat kekontinuan untuk fungsi interpolasi linear maka perlu direduksi persamaan (19) dengan menerapkan Teorema Green Gauss. Teorema green gauss menyederhanakan bentuk integral sehingga diperoleh (Meade, 2003)

, 0 1 0 0 2 2 0          

_

dx t u N dx y u N dx x u dx dN L j L j L j   

(9)

... ... ... ... ... 0 1 0 0 2 2 0         



dx t u N dx y u N dx x u dx dN L j L j L j    (20)

Substitusikan solusi pendekatan untuk ₂

2 , , y u x u u       dan t u   berikut , 1



    M i i i dx dN x u   , 1 2 2 2 2



      M i i i y N y u 



      M i i i t N t u 1 ,  

ke dalam persamaan (20) menghasilkan persamaan elemen hingga berikut :

... ... 0 0 1 1 1 2 2 0 1       

_

_

_

_





    dx t N N dx y N N dx dx dN dx dN L _M i i i j L i M i i i j L _M i i i j     (21) kemudian misalkan dx dx dN dx dN A L i j ji 



0 dan ... 0 dx N N B L i j ji 



(22)

maka dari persamaan (21) diperoleh bentuk sebagai berikut:

. ... ... ... ... ... 0 1 1 1 2 2 1       

_



   M i i ji M i i ji M i i ji t B y B A     (23)

(10)

Diskritisasi waktu terhadap x memungkinkan solusi dari A dan _ji B diperoleh terlebih ji dahulu. Unsur–unsurdari matriks A dan _ji B dapat diselesaikan secara exact dengan _ji menggunakan kuadratur Gaussian jika pangkat polynomial yang lebih rendah dipilih sebagai fungsi interpolasi (Munir, 2003).

Misalkan ... ... ... ... ... ... , , 1 1 1 1 2



      M i ji M i ji M i ji K A H B B M  (24)

danui, maka persamaan (23) berubah bentuk menjadi

2 2 y u H Ku t u M      

dengan syarat batas dan syarat awal

0 ) , ( ) ( ) 0 , ( 0 , 0 0 ), ( ) , (             T t y t u y g t y u y y t f t y u

KESIMPULAN DAN SARAN

Dari penelitian di atas dapat disimpulkan bahwa semi-diskritisasi galerkin dapat mengubah dimensi dari sebuah persamaan panas dari dua dimensi menjadi satu dimensi.Demikian pula halnya persamaan gelombang yang mempunyai sifat dan karakter yang mirip dengan persamaan panas.

(11)

Namun, metode ini masih perlu penyempurnaan untuk menghasilkan solusi numeric yang lebih akurat dengan menggabungkannya dengan metode – metode yang lain, salah satunya adalah dengan metode Beda Hingga.

DAFTAR PUSTAKA

Ardian.(2010).Analisa Persamaan Panas dan Nilai Sterilisasi pada Proses Sterilisasi Makanan Kaleng. Surabaya: Jurusan Matematika ITS.

Asmar, Nakhle H.(2005).Partial Differential Equations with Fourier Series and Boundary Value Problems; 2nd Edition. New Jersey: Upper Saddle River.

Bancroft, John C;sDu, Xiang;Dong, Yuan.(2003).2D Wave-Equation Migration by Joint Finite Elemen Method and Finite Difference Method. UK: CREWES Research Report.Volume 15.

Hoffman, Joe D.(2003).Numerical Methods for Engineers and Scientist; 2ndEdition.Indiana: Department of Mechanical Engineering Purdue University.

Holman, J.P.(2003).Perpindahan Kalor. Jakarta: Erlangga.

Kushartantya, Kurniatuti A.(2003).Efek Diskritisasi Metode Galerkin Semi Diskret Terhadap Akurasi dari Solusi Model Rambatan Panas Tanpa Konveksi. Indonesia: Jurnal Matematika dan Komputer Vol. 4. No. 3, 160 – 166.

Meade, Andrew J.(2003).The Semi-Discrete Galerkin Finite Elemen Modelling of Compressible Viscous Flow Past an Airfoil. Texas: Department of Mechanical Engineering, Rice University.

Munir, Rinaldi.(2003).Metode Numerik, Revisi ketiga. Buku Teks Ilmu Komputer. Bandung: Informatika.

Szabo, Tamaz.(2009).On The Discretization Time-Step in The Finite Element Theta-Method of The two –Dimensional Discrete Heat Equation. Hungaria: Eotvos Lorand University. Yang, Won Y;Cao, Wenwu;Chung, Tae-Sang;Morris, John.(2005).Applied Numerical Methods