Bipolar Neutrosophic Graph Structures | Akram | Journal of the Indonesian Mathematical Society 442 946 1 PB

Vol. 23, No. 1 (2017), pp. 55–80.

BIPOLAR NEUTROSOPHIC GRAPH STRUCTURES

Muhammad Akram

1

and Muzzamal Sitara

2

1

Department of Mathematics, University of the Punjab, New Campus, Lahore, Pakistan,

makrammath@yahoo.com

2

Department of Mathematics, University of the Punjab, New Campus, Lahore, Pakistan,

muzzamalsitara@gmail.com

Abstract.In this research study, we introduce the concept of bipolar single-valued neutrosophic graph structures. We discuss certain notions of bipolar single-valued neutrosophic graph structures with examples. We present some methods of con-struction of bipolar single-valued neutrosophic graph structures. We also investigate some of their prosperities.

Key words and Phrases: Graph structure, bipolar single-valued neutrosophic graph structure, operations.

Abstrak. Pada penelitian ini, kami memperkenalkan konsep struktur graf neu-trosofik bipolar bernilai tunggal. Kami mengkaji ide-ide tertentu dari struktur graf neutrosofik bipolar bernilai tunggal berserta contoh-contohnya. Kami menya-jikan beberapa metode konstruksi struktur graf neutrosofik bipolar bernilai tunggal. Kami juga memeriksa beberapa sifat-sifat mereka.

Kata kunci: Striktur graf, struktur graf neutrosofik bipolar bernilai tunggal, operasi

1. Introduction

Fuzzy graph theory has a number of applications in modeling real time sys-tems where the level of information inherent in the system varies with different levels of precision. Fuzzy models are becoming useful because of their aim in re-ducing the differences between the traditional numerical models used in engineering and sciences and the symbolic models used in expert systems. In 1973, Kauffmann [13] illustrated the notion of fuzzy graphs based on Zadeh’s fuzzy relations [24]. Rosenfeld [16] discussed several basic graph-theoretic concepts, including bridges,

2000 Mathematics Subject Classification: 03E72, 68R10, 68R05. Received: 02-02-2017, revised: 02-03-2017, accepted: 03-02-2017.

cut-nodes, connectedness, trees and cycles. Later on, Bhattacharya [8] gave some remarks on fuzzy graphs. In 1994, Mordeson and Chang-Shyh [14] defined some operations on fuzzy graphs. The complement of fuzzy graph was defined in [14]. Further, this concept was discussed by Sunitha and Vijayakumar [20]. Akram de-scribed bipolar fuzzy graphs in 2011 [1]. Akram and Shahzadi [5] dede-scribed the concept of neutrosophic soft graphs with applications. Dinesh and Ramakrishnan [12] introduced the concept of the fuzzy graph structure and investigated some re-lated properties. Akram and Akmal [4] proposed the notion of bipolar fuzzy graph structures. On the other hand, Dhavaseelan et al. [10] defined strong neutrosophic graphs. Akram and Sarwar [3] portrayed bipolar neutrosophic graphs with appli-cations. Akram and Shahzadi [5] introduced the notion of neutrosophic soft graphs with applications. Akram [2] introduced the notion of single-valued neutrosophic planar graphs. Representation of graphs using intuitionistic neutrosophic soft sets was discussed in [6]. Single-valued neutrosophic minimum spanning tree and its clustering method were studied by Ye [22]. In this research study, we introduce the concept of bipolar single-valued neutrosophic graph structures. We discuss certain notions of bipolar single-valued neutrosophic graph structures with examples. We present some methods of construction of bipolar single-valued neutrosophic graph structures. We also investigate some of their prosperities.

2. BIPOLAR SINGLE-VALUED NEUTROSOPHIC GRAPH

STRUCTURES

Smarandache [19] introduced neutrosophic sets as a generalization of fuzzy sets and intuitionistic fuzzy sets. A neutrosophic set has three constituents: truth-membership, indeterminacy-membership and falsity-truth-membership, in which each membership value is a real standard or non-standard subset of the unit interval ]0−

,1+_{[. In real-life problems, neutrosophic sets can be applied more appropriately}

by using the single-valued neutrosophic sets defined by Smarandache [19] and Wang et al [21].

Definition 2.1. [19] Aneutrosophic set N on a non-empty setV is an object of the form

N ={(v, TN(v), IN(v), FN(v)) :v∈V} where, TN, IN, FN :V →]0

−

,1+_{[ and there is no restriction on the sum of T}

N(v),

IN(v) andFN(v) for allv∈V.

Definition 2.2. [21]A single-valued neutrosophic set N on a non-empty set V is an object of the form

N ={(v, TN(v), IN(v), FN(v)) :v∈V}

Deli et al. [9] defined bipolar neutrosophic sets a generalization of bipolar fuzzy sets. They also studied some operations and applications in decision making problems.

Definition 2.3. [9]Abipolar single-valued neutrosophic seton a non-empty setV

is an object of the form

B={(v, TP B(v), I

P B(v), F

P B(v), T

N B(v), I

N B(v), F

N

B(v)) :v∈V}

where, TP B, I

P B, F

P

B :V →[0,1] andT N B, I

N B, F

N

B :V →[−1,0]. The positive values

TP B(v), I

P B(v), F

P

B(v) denote the truth, indeterminacy and falsity membership values of an element v ∈ V, whereas negative valuesTN

B(v), I N B(v), F

N

B(v) indicates the implicit counter property of truth, indeterminacy and falsity membership values of an elementv∈V.

Definition 2.4. A bipolar single-valued neutrosophic graphon a non-empty setV

is a pairG= (B, R), whereBis a bipolar single-valued neutrosophic set onV and

R is a bipolar single-valued neutrosophic relation inV such that

TP

R(bd)≤T P B(b)∧T

P B(d), I

P

R(bd)≤I P B(b)∧I

P

B(d), F P

R(bd)≤F P B(b)∨F

P B(d),

TN

R(bd)≥T N B(b)∨T

N B(d), I

N

R(bd)≥I N B(b)∨I

N

B(d), F N

R(bd)≥F N B(b)∧F

N B(d), for allb, d∈V.

We now define bipolar single-valued neutrosophic graph structure.

Definition 2.5. Gˇbn= (B, B1, B2, . . . , Bm) is calledbipolar single-valued

neutro-sophic graph structure(BSVNGS) of graph structure ˇGs = (V, V1, V2, . . . , Vm) if

B=< b, TP (b), IP

(b), FP (b), TN

(b), IN (b), FN

(b)>and

Bk =<(b, d), T P k (b, d), I

P k(b, d), F

P k (b, d), T

N k (b, d), I

N k (b, d), F

N

k (b, d)>are bipolar single-valued neutrosophic(BSVN) sets onV andVk, respectively, such that

TP

k (b, d)≤min{T P

(b), TP

(d)},IP

k (b, d)≤min{I P

(b), IP (d)},

FP

k (b, d)≤max{F P

(b), FP

(d)}, TN

k (b, d)≥max{T N

(b), TN (d)},

IN

k (b, d)≥max{I N

(b), IN

(d)},FN

k (b, d)≥min{F N

(b), FN (d)},

for allb, d∈V.Note that 0≤TP

k (b, d) +I P

k (b, d) +F P

k (b, d)≤3,

−3≤TN

k (b, d) +I N

k (b, d) +F N

k (b, d)≤0 for all (b, d)∈Vk.

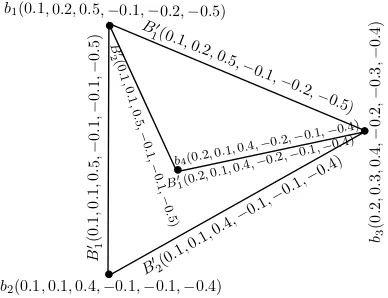
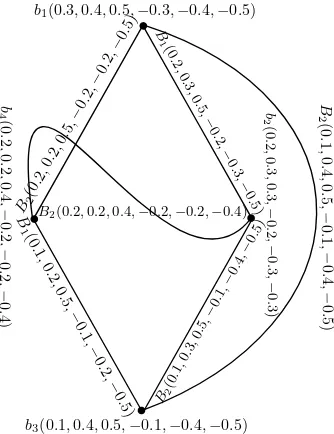
Example 2.6. Consider graph structure(GSR) ˇGs = (V, V1, V2) such that V =

{b1, b2, b3, b4},V1={b1b3, b1b2, b3b4},V2={b1b4, b2b3}. By defining bipolar

single-valued neutrosophic setsB,B1andB2onV,V1 andV2, respectively, we can draw

a bipolar SVNGS as depicted in Fig. 1.

Definition 2.7. Let ˇGbn = (B, B1, B2, . . . , Bm) be a BSVNGS of GS ˇGs. If ˇ

Hbn= (B

′ , B′

1, B ′ 2, . . . , B

′

m) is a BSVNGS of ˇGs such that

T′P

(b)≤TP (k), I′P

(b)≤IP (b), F′P

(b)≥FP (b),

T′N

(b)≥TP (k), I′N

(b)≥IP (b), F′N

b

Figure 1. _{A bipolar single-valued neutrosophic graph structure}

b

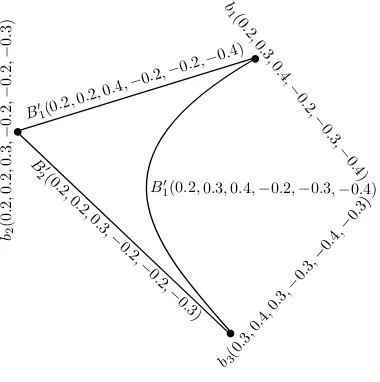
Figure 2. _{A BSVN subgraph structure}

T′P

Then ˇHbn is named as abipolar single-valued neutrosophic(BSVN) subgraph

struc-tureof BSVNGS ˇGbn.

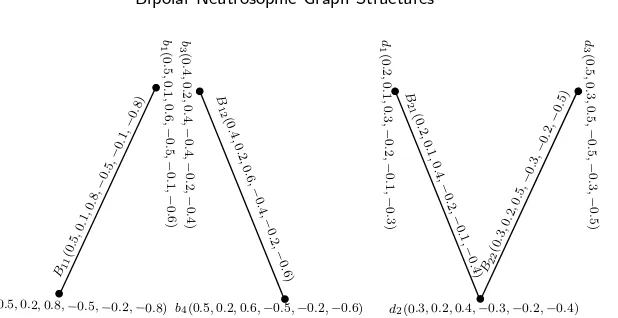
Example 2.8. Consider a BSVNGS ˇHbn = (B′, B₁′, B₂′) of GS ˇGs = (V, V₁, V₂) as depicted in Fig. 2. Routine calculations indicate that ˇHbnis BSVN subgraph-structure of BSVNGS ˇGbn.

Definition 2.9. A BSVNGS ˇHbn= (B′, B₁′, B′₂, . . . , Bm′ ) is called aBSVN induced

b

b

b

b3(0 .3,0

.4,0 .3,−

0.3, −0.

4,− 0.3) b2

(0

.

2

,

0

.

2

,

0

.

3

,

−

0

.

2

,

−

0

.

2

,

−

0

.

3

)

b₁

(0_. 2_,

0_. 3_,

0_. 4_,

− 0_.

2_, −

0_. 3_,

− 0_.

4)

B′

1(0.2,0.3,0.4,−0.2,−0.3,−0.4)

B′

2₍₀

.2_, 0_.

2_, 0_.

3_, −

0_.2

,₋

0_. 2_,

− 0_.

3) B′1(0.2

,0.2,0.4,−0.2,−0.2,−0.4)

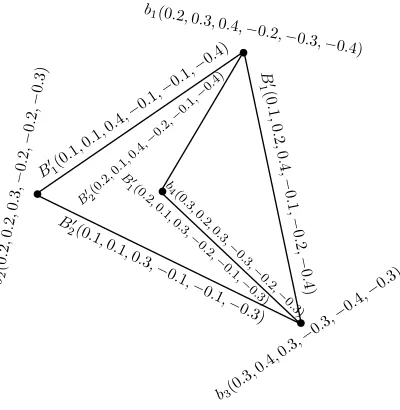
Figure 3. _{A BSVN induced subgraph-structure}

T′P

(b) =TP (b), I′P

(b) =IP (b), F′P

(b) =FP (b),

T′N

(b) =TN (b), I′N

(b) =IN

(b), F′N

(b) =FN (b),

T′P

k (b, d) =T P k (b, d),I

′P

k (b, d) =I P

k(b, d),F

′P

k (b, d) =F P k (b, d),

T′N

k (b, d) =T N

k (b, d),I

′N

k (b, d) =I N

k (b, d),F

′N

k (b, d) =F N k (b, d), ∀b, d∈Q,k= 1,2, . . . , m.

Example 2.10. A BSVNGS depicted in Fig.3 is a BSVN induced subgraph-structure of BSVNGS represented in Fig. 1.

Definition 2.11. A BSVNGS ˇHbn= (B′, B₁′, B′₂, . . . , Bm′ ) is calledBSVN spanning

subgraph-structureof BSVNGS ˇGbn= (B, B1, B2, . . . , Bm) ifB

′

=B and

T′P

k (b, d)≤T P k (b, d),I

′P

k (b, d)≤I P

k(b, d),F

′P

k (b, d)≥F P k (b, d),

T′N

k (b, d)≥T N

k (b, d),I

′N

k (b, d)≥I N

k (b, d),F

′N

k (b, d)≤F N

k (b, d), k= 1,2, . . . , m.

Example 2.12. A BSVNGS represented in Fig. 4 is a BSVN spanning subgraph-structure of BSVNGS represented in Fig. 1.

Definition 2.13. Let ˇGbn= (B, B₁, B₂, . . . , Bm) be a BSVNGS. Thenbd∈Bk is called aBSVNBk-edgeor shortlyBk-edge, if

TP

k (b, d)> 0 orI P

k(b, d)> 0 orF P

k (b, d)> 0 orT N

k (b, d) <0 or I N

k (b, d)< 0 or

FN

b

b

b

b

B ′ 1

(0_. 1_, 0_. 2_, 0_. 4_, − 0_. 1_, − 0_. 2_, − 0_. 4) b₄

(0_. 3,₀

.₂ ,₀

.₃ ,−

0.₃ ,−

0.₂ ,−

0.₃₎

b3(0 .3,0.4

,0.3, −0.3

,−0 .4,−0

.3) b2(0

.2, 0.2

,0. 3,−

0.2 ,−

0.2 ,−

0.3)

b1(0.2,0.3,0.4,−0.2,−0.3,−0.4)

B′2(0

.2,0

.1,0

.4,

−0

.2,

−0

.1,− 0.4)

B_′ 1₍₀

._2, 0.₁

,_0. 3,−

0._2, −

0.₁ ,−

0.₃₎

B′

2(0_. 1,_0.

1,_0. 3,−₀

.1,−₀ .1,−₀

.₃₎ B′1(0

.1,0.1 ,0.4,

−0.1 ,−0.

1,−0

.4)

Figure 4. _{A BSVN spanning subgraph-structure}

supp(Bk) = {bd ∈ Bk : T P

k (b, d) > 0} ∪ {bd ∈ Bk : I

P

k(b, d) > 0} ∪ {bd ∈ Bk :

FP

k (b, d)>0} ∪ {bd∈Bk :T

N

k (b, d)<0} ∪ {bd∈Bk :I

N

k (b, d)<0} ∪ {bd∈Bk :

FN

k (b, d)<0},k= 1,2, . . . , m.

Definition 2.14. Bk-path in BSVNGS ˇGbn = (B, B1, B2, . . . , Bm) is a sequence

b1, b2, . . . , bmof distinct nodes(vertices) (exceptbm=b1) inV such that bk−1bk is a BSVNBk-edge for allk= 2, . . . , m.

Definition 2.15. A BSVNGS ˇGbn = (B, B1, B2, . . . , Bm) is Bk-strong for any

k∈ {1,2, . . . , m}if

TP

k (b, d) = min{T P

(b), TP

(d)},IP

k (b, d) = min{I P

(b), IP (d)},

FP

k (b, d) = max{F P

(b), FP

(d)}, TN

k (b, d) = max{T N

(b), TN (d)},

IN

k (b, d) = max{I N

(b), IN

(d)},FN

k (b, d) = min{F N

(b), FN (d)},

∀ bd∈supp(Bk). If ˇGbn isBk-strong for allk∈ {1,2, . . . , m}, then ˇGbn is called

strong BSVNGS.

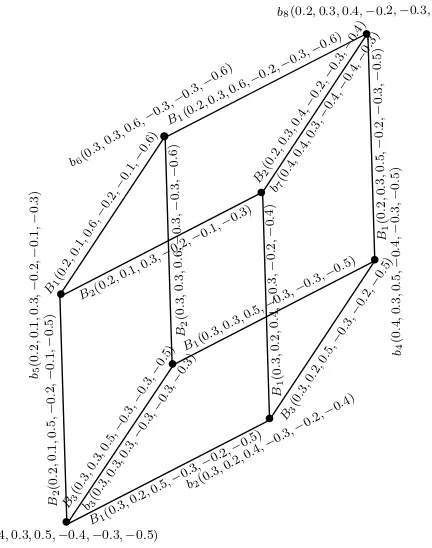
Example 2.16. Consider BSVNGS ˇGbn = (B, B1, B2, B3) as depicted in Fig. 5.

Then ˇGbnis strong BSVNGS, since it isB₁−,B₂−andB₃−strong.

b

Figure 5. _{A Strong BSVNGS}

(1) ˇGbnis strong BSVNGS.

(2) supp(Bk)6=∅, for all k = 1, 2, . . . , m. (3) For allb, d∈V,bdis aBk−edgefor some k.

Example 2.18. Let ˇGbn = (B, B₁, B₂) be BSVNGS of GS ˇG = (V, V₁, V₂), such that V ={b1, b2, b3, b4},V1={b1b2, b3b4}, V2={b1b3, b2b3, b1b4, b2b4}.

b

Figure 6. _{A complete BSVNGS}

b b

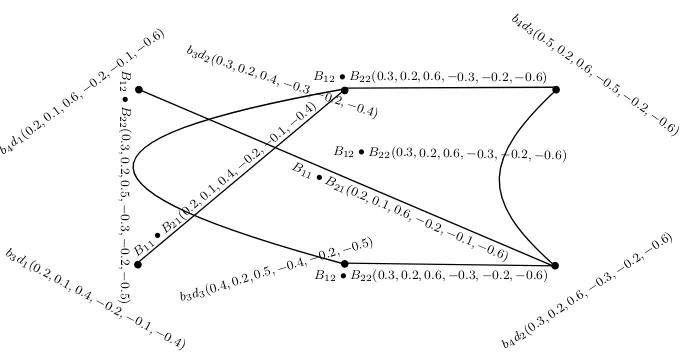
Lexicographic product of BSVNGSs ˇGb1and ˇGb2 shown in Fig. 7 is defined as:

ˇ

b

b4d 2(0.3,

0.2,0.6 ,−0.3

,−0.2 ,−0.6)

b

b b b

b3_d 1₍₀

.2,₀ ._1,

0._4, −

0._2, −

0._1, −

0.₄₎

b3d3(0

.4,0.2,0.5,−0.4, −0.2,

−0.5)

b4_d 3₍₀

.₅ ,_0.

2,_0. 6,−

0._5, −

0.₂ ,−

0.₆₎

b4d 1(0

.2,0

.1,0.6 ,−0.

2,−0.

1,−0

.6)

b3d2₍₀ .3,_0.

2,_0.4 ,−₀

._3,− 0._2,−

0.₄₎

B 11•_B

21₍₀ ._2,

0._1, 0._6,−

0._2,− 0._1,−

0.₆₎ B11

•B 21(0

.2,0 .1,0

.4,− 0.2,

−0

.1,

−0

.4)

B

1

2

•

B

2

2

(0

.

3

,

0

.

2

,

0

.

5

,

−

0

.

3

,

−

0

.

2

,

−

0

.

5

)

b

B12•_B22(0.3,0.2,0.6,−0.3,−0.2,−₀.6)

B12•B22(0.3,0.2,0.6,−0.3,−₀.2,−0.6) B12•B22(0.3,0.2,0.6,−₀.3,−₀.2,−0.6)

Figure 8. _Gˇb₁•Gˇb₂

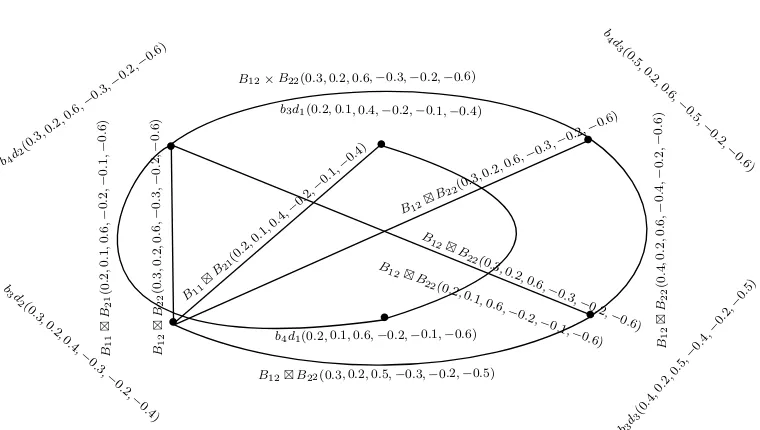
Theorem 2.21. Lexicographic product ˇGb1•Gˇb2 = (B1•B2, B11• B21, B12• B22, . . . , B1m•B2m) of two BSVNSGSs of GSs Gˇs1 and Gˇs2 is a BSVNGS of

ˇ

Gs₁•Gˇs₂.

proof. _{Consider two cases:}

Case 1.: Forb∈V1,d1d2∈V2k

TP

(B

1k•B₂k)((bd1)(bd2)) =T P B

1(b)∧T P B

2k(d1d2)

≤TBP

1(b)∧[T P B

2(d1)∧T P B

2(d2)] = [TP

B₁(b)∧T P

B₂(d1)]∧[T

P B₁(b)∧T

P B₂(d2)]

=T(PB₁•B₂)(bd1)∧T

P

(B₁•B₂)(bd2), T(NB

1k•B

2k)((bd1)(bd2)) =T N B

1(b)∨T N B

2k(d1d2)

≥TBN

1(b)∨[T N B

2(d1)∨T N B

2(d2)] = [TN

B₁(b)∨T N

B₂(d1)]∨[T

N B₁(b)∨T

N B₂(d2)]

=T(NB₁•B₂)(bd1)∨T

N

(B₁•B₂)(bd2),

IP

(B

1k•B₂k)((bd1)(bd2)) =I P B₁(b)∧I

P B

2k(d1d2)

≤IP

B₁(b)∧[I P

B₂(d1)∧I P B₂(d2)] = [IP

B 1(b)∧I

P B

2(d1)]∧[I P B

1(b)∧I P B

2(d2)] =IP

I(NB

1k•B₂k)((bd1)(bd2)) =I N B

1(b)∨I N B

2k(d1d2)

≥IN

B

1(b)∨[I N B

2(d1)∨I N B

2(d2)] = [IN

B₁(b)∨I N

B₂(d1)]∨[I N B₁(b)∨I

N B₂(d2)] =IN

(B

1•B2)(bd1)∨I N

(B

1•B2)(bd2),

FP

(B

1k•B₂k)((bd1)(bd2)) =F P B₁(b)∨F

P B

2k(d1d2)

≤FP

B₁(b)∨[F P

B₂(d1)∨F P B₂(d2)] = [FP

B

1(b)∨F P B

2(d1)]∨[F P B

1(b)∨F P B

2(d2)] =FP

(B₁•B₂)(bd1)∨F(PB₁•B₂)(bd2),

FN

(B

1k•B₂k)((bd1)(bd2)) =F N B₁(b)∧F

N

B₂k(d1d2)

≥FN

B

1(b)∧[F N B

2(d1)∧F N B

2(d2)] = [FN

B

1(b)∧F N B

2(d1)]∧[F N B

1(b)∧F N B

2(d2)] =FN

(B

1•B2)(bd1)∧F N

(B

1•B2)(bd2), forbd1, bd2∈V1•V2.

Case 2.: Forb1b2∈V1k,d₁d₂∈V₂k

TP

(B

1k•B₂k)((b1d1)(b2d2)) =T P B

1k(b1b2)∧T P B

2k(d1d2)

≤[TP

B₁(b1)∧T P

B₁(b2]∧[T P

B₂(d1)∧T P B₂(d2)] = [TP

B

1(b1)∧T P B

2(d1)]∧[T P B

1(b2)∧T P B

2(d2)] =TP

(B₁•B₂)(b1d1)∧T(PB₁•B₂)(b2d2),

TN

(B

1k•B₂k)((b1d1)(b2d2)) =T N

B₁k(b1b2)∨T N

B₂k(d1d2)

≥[TN

B

1(b1)∨T N B

1(b2]∨[T N B

2(d1)∨T N B

2(d2)] = [TN

B

1(b1)∨T N B

2(d1)]∨[T N B

1(b2)∨T N B

2(d2)] =TN

(B

1•B2)(b1d1)∨T N

(B

1•B2)(b2d2),

IP

(B

1k•B₂k)((b1d1)(b2d2)) =I P B

1k(b1b2)∧I P B

2k(d1d2)

≤[IP

B₁(b1)∧I P

B₁(b2]∧[I P

B₂(d1)∧I P B₂(d2)] = [IP

B

1(b1)∧I P B

2(d1)]∧[I P B

1(b2)∧I P B

2(d2)] =IP

I(NB is defined as:

b

I(NB

1k⊠B₂k)((bd1)(bd2)) =I N B

1(b)∨I N B

2k(d1d2)

≥IN

B

1(b)∨[I N B

2(d1)∨I N B

2(d2)] = [IN

B₁(b)∨I N

B₂(d1)]∨[I N B₁(b)∨I

N B₂(d2)] =IN

(B_1⊠B

2)(bd1)∨I N

(B_1⊠B 2)(bd2),

FP

(B

1k⊠B₂k)((bd1)(bd2)) =F P B₁(b)∨F

P B

2k(d1d2)

≤FP

B₁(b)∨[F P

B₂(d1)∨F P B₂(d2)] = [FP

B

1(b)∨F P B

2(d1)]∨[F P B

1(b)∨F P B

2(d2)] =FP

(B_1⊠B₂)(bd1)∨F(PB_1⊠B₂)(bd2),

FN

(B

1k⊠B₂k)((bd1)(bd2)) =F N B₁(b)∧F

N

B₂k(d1d2)

≥FN

B

1(b)∧[F N B

2(d1)∧F N B

2(d2)] = [FN

B

1(b)∧F N B

2(d1)]∧[F N B

1(b)∧F N B

2(d2)] =FN

(B_1⊠B

2)(bd1)∧F N

(B_1⊠B 2)(bd2), forbd1, bd2∈V1⊠V2.

Case 2.: Forb∈V2,d1d2∈V1k

TP

(B

1k⊠B₂k)((d1b)(d2b)) =T P B₂(b)∧T

P B

1k(d1d2)

≤TP

B₂(b)∧[T P

B₁(d1)∧T P B₁(d2)] = [TP

B 2(b)∧T

P B

1(d1)]∧[T P B

2(b)∧T P B

1(d2)] =TP

(B_1⊠B₂)(d1b)∧T(PB_1⊠B₂)(d2b),

TN

(B

1k⊠B₂k)((d1b)(d2b)) =T N B₂(b)∨T

N

B₁k(d1d2)

≥TN

B

2(b)∨[T N B

1(d1)∨T P B

1(d2)] = [TN

B 2(b)∨T

N B

1(d1)]∨[T N B

2(b)∨T N B

1(d2)] =TN

(B_1⊠B

2)(d1b)∨T N

(B_1⊠B 2)(d2b),

IP

(B

1k⊠B₂k)((d1b)(d2b)) =I P B₂(b)∧I

P B

1k(d1d2)

≤IP

B₂(b)∧[I P

B₁(d1)∧I P B₁(d2)] = [IP

B 2(b)∧I

P B

1(d1)]∧[I P B

2(b)∧I P B

1(d2)] =IP

I(NB

1k⊠B₂k)((d1b)(d2b)) =I N B

2(b)∨I N B

1k(d1d2)

≥IN

B

2(b)∨[I N B

1(d1)∨I N B

1(d2)] = [IN

B₂(b)∨I N

B₁(d1)]∨[I N B₂(b)∨I

N B₁(d2)] =IN

(B_1⊠B

2)(d1b)∨I N

(B_1⊠B 2)(d2b),

FP

(B

1k⊠B₂k)((d1b)(d2b)) =F P B₂(b)∨F

P B

1k(d1d2)

≤FP

B₂(b)∨[F P

B₁(d1)∨F P B₁(d2)] = [FP

B

2(b)∨F P B

1(d1)]∨[F P B

2(b)∨F P B

1(d2)] =FP

(B_1⊠B₂)(d1b)∨F(PB_1⊠B₂)(d2b),

FN

(B

1k⊠B₂k)((d1b)(d2b)) =F N B₂(b)∧F

N

B₁k(d1d2)

≥FN

B

2(b)∧[F N B

1(d1)∧F N B

1(d2)] = [FN

B

2(b)∧F N B

1(d1)]∧[F N B

2(b)∧F N B

1(d2)] =FN

(B_1⊠B

2)(d1b)∧F N

(B_1⊠B 2)(d2b), ford1b, d2b∈V1⊠V2.

Case 3.: Forb1b2∈V1k,d₁d₂∈V₂k

TP

(B

1k⊠B₂k)((b1d1)(b2d2)) =T P B

1k(b1b2)∧T P B

2k(d1d2)

≤[TP

B₁(b1)∧T P

B₁(b2]∧[T P

B₂(d1)∧T P B₂(d2)] = [TP

B

1(b1)∧T P B

2(d1)]∧[T P B

1(b2)∧T P B

2(d2)] =TP

(B_1⊠B₂)(b1d1)∧T(PB_1⊠B₂)(b2d2),

TN

(B

1k⊠B₂k)((b1d1)(b2d2)) =T N

B₁k(b1b2)∨T N

B₂k(d1d2)

≥[TN

B

1(b1)∨T N B

1(b2]∨[T N B

2(d1)∨T N B

2(d2)] = [TN

B

1(b1)∨T N B

2(d1)]∨[T N B

1(b2)∨T N B

2(d2)] =TN

(B_1⊠B

2)(b1d1)∨T N

(B_1⊠B

2)(b2d2),

IP

(B

1k⊠B₂k)((b1d1)(b2d2)) =I P B

1k(b1b2)∧I P B

2k(d1d2)

≤[IP

B₁(b1)∧I P

B₁(b2]∧[I P

B₂(d1)∧I P B₂(d2)] = [IP

B

1(b1)∧I P B

2(d1)]∧[I P B

1(b2)∧I P B

2(d2)] =IP

I(NB is defined as:

b b

b b b

b

b

B11∪B21(0.2,0.05,0.4,−0.2,−₀.05,−₀.4) B12∪B22(0.3,0.1,0.5,−0.3,−0.1,−0.5)

B12∪B22(0.4,0.1,0.6,−0.4,−0.1,−0.6) B11∪B21(0.5,0.05,0.8,−0.5,−0.05,−₀.8)

b3(0.4,0.1,0.4,−0.4,−₀.1,−0.4) d1(0.2,0.05,0.3,−0.2,−0.05,−0.3)

b1(0.5,0.05,0.6,−0.5,−0.05,−0.6) d3(0.5,0.15,0.5,−₀.5,−0.15,−₀.5)

b

2

(0

.

5

,

0

.

1

,

0

.

8

,

−

0

.

5

,

−

0_.

1

,

−

0

.

8

)

b

4

(0

.

5

,

0

.

1

,

0

.

6

,

−

0

.

5

,

−

0

.

1

,

−

0

.

6

)

d2(0.3,0.1,0.4,−0.3,−0.1,−0.4)

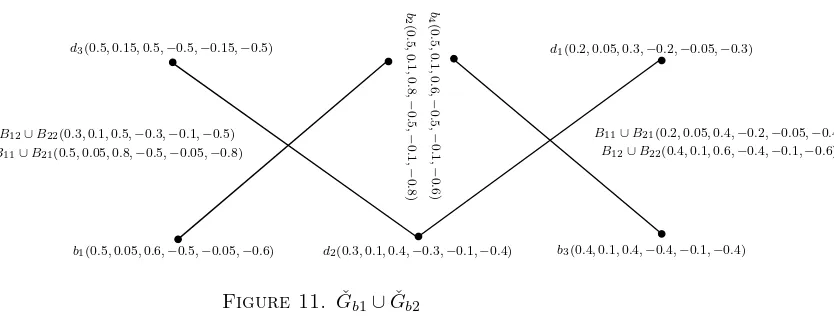
Figure 11. _Gˇb1∪Gˇb2

Example 2.26. Union of two BSVNGSs ˇGb₁ and ˇGb₂ shown in Fig. 7 is defined as ˇGb1∪Gˇb2={B1∪B2, B11∪B21, B12∪B22}and is depicted in Fig. 11.

Theorem 2.27. Union ˇGb₁∪Gˇb₂= (B₁∪B₂, B₁₁∪B₂₁, B₁₂∪B₂₂, . . . , B₁m∪B₂m) of two BSVNGSs of the GSs ˇG1 and ˇG2 is BSVNGS of ˇG1∪Gˇ2.

proof._Letb1b2∈V1k∪V2k. Two cases arise:

Case 1.: Forb1, b2∈V1, by definition 2.25 TP

B

2(b1) = T P B

2(b2) =T P B

2k(b1b2) = 0, I P B

2(b1) = I P B

2(b2) =I P B

2k(b1b2) = 0,

FP B

2(b1) =F P B

2(b2) =F P B

2k(b1b2) = 1,

TN

B₂(b1) = T N

B₂(b2) =T N B

2k(b1b2) = 0, I N

B₂(b1) = I N

B₂(b2) =I N B

2k(b1b2) = 0,

FN B

2(b1) =F N B

2(b2) =F N B

2k(b1b2) =−1, so

T(PB₁k∪B₂k)(b1b2) =T P B

1k(b1b2)∨T P B

2k(b1b2) =TBP

1k(b1b2)∨0

≤[TP

B₁(b1)∧T P

B₁(b2)]∨0 = [TP

B

1(b1)∨0]∧[T P B

1(b2)∨0] = [TP

B

1(b1)∨T P B

2(b1)]∧[T P B

1(b2)∨T P B

2(b2)] =TP

(B

1∪B2)(b1)∧T P

(B

1∪B2)(b2),

TN

(B

1k∪B₂k)(b1b2) =T N B

1k(b1b2)∧T N B

2k(b1b2) =TN

B

1k(b1b2)∧0

≥[TBN

1(b1)∨T N B

1(b2)]∧0 = [TN

B₁(b1)∧0]∨[T N

B₁(b2)∧0] = [TN

B

1(b1)∧T N B

2(b1)]∨[T N B

1(b2)∧T N B

2(b2)] =TN

F(PB

1k∪B₂k)(b1b2) =F P B

1k(b1b2)∧F P B

2k(b1b2) =FP

B

1k(b1b2)∧1

≤[FP

B₁(b1)∨F P

B₁(b2)]∧1 = [FP

B

1(b1)∧1]∨[F P B

1(b2)∧1] = [FBP

1(b1)∧F P B

2(b1)]∨[F P B

1(b2)∧F P B

2(b2)] =FP

(B

1∪B2)(b1)∨F P

(B

1∪B2)(b2),

FN

(B

1k∪B₂k)(b1b2) =F N

B₁k(b1b2)∨F N B₂k(b1b2) =FN

B

1k(b1b2)∨ −1

≥[FN

B

1(b1)∧F N B

1(b2)]∨ −1 = [FBN

1(b1)∨ −1]∧[F N B

1(b2)∨ −1] = [FN

B₁(b1)∨F

N

B₂(b1)]∧[F

N

B₁(b2)∨F

N B₂(b2)]

=F(NB₁∪B₂)(b1)∧F

N

(B₁∪B₂)(b2),

IP

(B

1k∪B₂k)(b1b2) =

IP B

1k(b1b2) +I P B

2k(b1b2) 2

=I P B

1k(b1b2) + 0 2

≤[I

P B

1(b1)∧I P B

1(b2)] + 0 2

= [I P B₁(b1)

2 + 0]∧[

IP B₁(b2)

2 + 0]

=[I P B

1(b1) +I P B

2(b1)]

2 ∧

[IP B

1(b2) +I P B

2(b2)] 2

=IP

I(NB 1k∪B

2k)(b1b2) =

IN B

1k(b1b2) +I N B

2k(b1b2) 2

=I N B

1k(b1b2) + 0 2

≥[I

N B

1(b1)∨I N B

1(b2)] + 0 2

= [I N B

1(b1)

2 + 0]∨[

IN B

1(b2)

2 + 0]

=[I N B

1(b1) +I N B

2(b1)]

2 ∨

[IN B

1(b2) +I N B

2(b2)] 2

=IN

(B

1∪B2)(b1)∨I N

(B

1∪B2)(b2),

forb1, b2∈V1∪V2.

Case 2.: Forb1, b2∈V2, by definition 2.25 TP

B

1(b1) = T P B

1(b2) =T P B

1k(b1b2) = 0, I P B

1(b1) = I P B

1(b2) =I P B

1k(b1b2) = 0,

FP B

1(b1) =F P B

2(b2) =F P B

1k(b1b2) = 1,

TN

B₁(b1) = T N

B₁(b2) =T N B

1k(b1b2) = 0, I N

B₁(b1) = I N

B₁(b2) =I N B

1k(b1b2) = 0,

FN B

1(b1) =F N B

2(b2) =F N B

1k(b1b2) =−1, so

TP

(B

1k∪B₂k)(b1b2) =T P B

1k(b1b2)∨T P B

2k(b1b2) =TP

B

2k(b1b2)∨0

≤[TBP

2(b1)∧T P B

2(b2)]∨0 = [TP

B₂(b1)∨0]∧[T

P

B₂(b2)∨0]

= [TP B

2(b1)∨T P B

1(b1)]∧[T P B

2(b2)∨T P B

1(b2)] =TP

(B

1∪B2)(b1)∧T P

(B

1∪B2)(b2),

TN

(B

1k∪B₂k)(b1b2) =T N B

1k(b1b2)∧T N B

2k(b1b2) =TN

B

2k(b1b2)∧0

≥[TBN

2(b1)∨T N B

2(b2)]∧0 = [TN

B₂(b1)∧0]∨[T N

B₂(b2)∧0] = [TN

B

2(b1)∧T N B

1(b1)]∨[T N B

2(b2)∧T N B

1(b2)] =TN

F(PB

1k∪B₂k)(b1b2) =F P B

1k(b1b2)∧F P B

2k(b1b2) =FP

B

2k(b1b2)∧(1)

≤[FP

B₂(b1)∨F P

B₂(b2)]∧(1) = [FP

B

2(b1)∧(1)]∨[F P B

2(b2)∧(1)] = [FBP

2(b1)∧F P B

1(b1)]∨[F P B

2(b2)∧F P B

1(b2)] =FP

(B

1∪B2)(b1)∨F P

(B

1∪B2)(b2),

FN

(B

1k∪B₂k)(b1b2) =F N

B₁k(b1b2)∨F N B₂k(b1b2) =FN

B

2k(b1b2)∨(−1)

≥[FN

B

2(b1)∧F N B

2(b2)]∨(−1) = [FBN

2(b1)∨(−1)]∧[F N B

2(b2)∨(−1)] = [FN

B₂(b1)∨F

N

B₁(b1)]∧[F

N

B₂(b2)∨F

N B₁(b2)]

=F(NB₁∪B₂)(b1)∧F

N

(B₁∪B₂)(b2),

IP

(B

1k∪B₂k)(b1b2) =

IP B

1k(b1b2) +I P B

2k(b1b2) 2

=I P B

2k(b1b2) + 0 2

≤[I

P B

2(b1)∧I P B

2(b2)] + 0 2

= [I P B₂(b1)

2 + 0]∧[

IP B₂(b2)

2 + 0]

=[I P B

2(b1) +I P B

1(b1)]

2 ∧

[IP B

2(b2) +I P B

1(b2)] 2

=IP

Definition 2.29. Let ˇGb1= (B1, B11, B12, . . . , B1m) and ˇGb2= (B2, B21, B22, . . . , B2m) be BSVNGSs and letV1∩V2 =∅. Joinof ˇGb1 and ˇGb2, denoted by

ˇ

Gb₁+ ˇGb₂= (B₁+B₂, B₁₁+B₂₁, B₁₂+B₂₂, . . . , B₁m+B₂m), is defined as:

(i)

3. CONCLUDING REMARKS

b

(3) BSVN interval-valued hypergraph structures, and(4) BSVN rough hypergraph structures.

Acknowledgement. The authors are highly thankful to Executive Editor and the referees for their valuable comments and suggestions.

References

[1] Akram, M., ”Bipolar fuzzy graphs”, Information Sciences”,181:24_{(2011), 5548-5564.}

[2] Akram, M., ”Single-valued neutrosophic planar graphs”,International Journal of Algebra and Statistics,5_{(2) (2016), 157-167.}

[3] Akram, M. and Sarwar, M., ”Novel multiple criteria decision making methods based on bipolar neutrosophic sets and bipolar neutrosophic graphs”, viXra:1701.0190, 2015. [4] Akram, M. and Akmal, R., ”Application of bipolar fuzzy sets in graph structures”,Applied

Computational Intelligence and Soft Computing, (2016), 13 pages.

[5] Akram, M. and Shahzadi, S., ”Neutrosophic soft graphs with application”,Journal of Intel-ligent & Fuzzy Systems,32(2017), 841-858.

[6] Akram, M. and Shahzadi, S., ”Representation of graphs using intuitionistic neutrosophic soft sets”,Journal of Mathematical Analysis,7:6(2016), 31-53.

[7] Atanassov, K., ”Intuitionistic fuzzy sets”,Fuzzy Sets and Systems,20:1(1986), 87-96. [8] Bhattacharya, P., ”Some remarks on fuzzy graphs”,Pattern Recognition Letters,6:5(1987),

297-302.

[10] Dhavaseelan, R., Vikramaprasad, R. and Krishnaraj, V., ”Certain types of neutrosophic graphs”,Int. Jr. of Mathematical Sciences and Applications,5:_{) (2015), 333-339.}

[11] Dinesh, T., A study on graph structures, incidence algebras and their fuzzy ana-logues[Ph.D.thesis], Kannur University, Kannur, India, (2011).

[12] Dinesh, T. and Ramakrishnan, T.V., ”On generalised fuzzy graph structures”,Applied Math-ematical Sciences,5:4_{(2011), 173-180.}

[13] Kauffman, A.,Introduction a la Theorie des Sous-emsembles Flous, Masson et Cie, Vol.1

(1973).

[14] Mordeson, J.N. and Chang-Shyh, P., ”Operations on fuzzy graphs”,Information Sciences,

79(1994), 159-170.

[15] Peng, J.J., Wang, J.Q., Zhang, H.Y. and Chen, X.H, ”An outranking approach for multi-criteria decision-making problems with simplified neutrosophic sets”,Applied Soft Comput-ing,25(2014), 336-346.

[16] Rosenfeld, A., ”Fuzzy graphs”, In Fuzzy Sets and their Applications( L.A.Zadeh, K.S.Fu, M.Shimura, Eds.), Academic Press, New York, (1975), 77-95.

[17] Sampathkumar, E., ”Generalized graph structures”,Bulletin of Kerala Mathematics Asso-ciation,3:2_{(2006), 65-123.}

[18] Shah, N. and Hussain, A., ”Neutrosophic soft graphs”, Neutrosophic Set and Systems,11

(2016), 31-44.

[19] Smarandache, F., Neutrosophy Neutrosophic Probability, Set, and Logic, Amer Res Press, Rehoboth, USA, (1998).

[20] Sunitha, M.S. and Vijayakumar, A., ”Complement of a fuzzy graph”,Indian Journal of Pure and Applied Mathematics,33:) (2002), 1451-1464.

[21] Wang, H., Smarandache, F., Zhang, Y.Q. and Sunderraman, R., ”Single valued neutrosophic sets”,Multispace and Multistructure,4(2010), 410-413.

[22] Ye, J., ”Single-valued neutrosophic minimum spanning tree and its clustering method”, Jour-nal of Intelligent Systems,23:3(2014), 311-324.

[23] Zadeh, L.A., ”Fuzzy sets”,Information and control,8:3(1965), 338-353.

[24] Zadeh, L.A., ”Similarity relations and fuzzy orderings”, Information Sciences,3:2(1971), 177-200.