STUDI SIMULASI DALAM ESTIMASI BAYESIAN OBYEKTIF
Adi Setiawan
Program Studi Matematika Industri dan Statistika, Fakultas Sains dan Matematika
Universitas Kristen Satya Wacana Jl
Diponegoro 52-60 Salatiga 50711, Indonesia
e-mail: [email protected]
Abstrak Dengan pemilihan distribusi prior dan fungsi kerugian khusus, metode Bayesian obyektif menghasilkan suatu estimasi yang hanya tergantung pada distribusi anggapan dari populasi dan data yang ada. Dalam makalah ini, akan dilakukan studi simulasi tentang estimasi Bayesian obyektif untuk berbagai distribusi anggapan populasi yang biasa digunakan metode Bayesian obyektif digunakan untuk menentukan estimator titik dari suatu parameter populasi. Kata kunci :distribusi prior,fungsi kerugian,studi simulasi,metode Bayesian obyektif. 1. Pendahuluan
Dalam metode Bayesian, pemilihan prior dan fungsi kerugian sangatlah penting. Dalam metode Bayesian obyektif digunakan prior yang nantinya akan memberikan pengaruh minimal dalam inferensi dan menggunakan fungsi kerugian deskrepansi intrinsik. Dalam makalah ini akan dijelaskan bagaimana metode Bayesian obyektif digunakan dalam menentukan estimasi titik jika dimiliki sampel yang dianggap berasal dari populasi yang berdistribusi eksponensial atau populasi yang berdistribusi seragam.
2. Dasar Teori
Dalam pandangan Bayesian, hasil dari sembarang masalah inferensi yang dinyatakan dalam distribusi posterior merupakan gabungan dari informasi yang disediakan oleh data dan informasi prior relevan yang tersedia. Akan tetapi apabila tidak tersedia informasi prior, akan dipilih fungsi prior yang relatif uninformative artinya fungsi prior yang memberikan pengaruh minimum pada inferensi fungsi posterior.
Misalkan bahwa mekanisme probabilitas yang membangkitkan data yang tersedia x dianggap sebagai p(x| ) untuk suatu dan kuantitas yang menjadi perhatian adalah fungsi yang bernilai real () dari . Tanpa menghilangkan keumuman, hal itu juga dapat dijelaskan berikut ini. Misalkan model probabilitas yang digunakan berbentuk {p(x|
,
)} dengan adalah parameter nuisance yang dipilih. Dalam hal ini diperlukan untuk mengidentifikasi fungsi prior bersama (,) yang akan mempunyai pengaruh minimal pada distribusi posterior marginal dengan kuantitas yang menjadi perhatianyaitu
(
|
x
)
p
(
x
|
,
)
(
,
)
d
.Reference prior digunakan sebagai prior yang dapat memberikan pengaruh minimal pada
distribusi posterior. Dalam kasus dimensi satu,reference priormerupakan prior Jeffry. Dengan menggunakan prior ini maka penyelesaian masalah estimasi hanya tergantung pada model anggapan dan data pengamatan sehingga estimasi titik yang menggunakan metode ini dinamakan sebagai estimasi titik Bayesian obyektif (Bernardo dan Juarez, 2003).
(
(
)
|
(
)
)
,
(
(
)
|
(
)
)
min
)
,
(
p
1p
2
K
p
2x
p
1x
K
p
1x
p
2x
dengan
X
dx x p
x p x p x p x p K
) (
) ( log ) ( )) ( | ) ( (
2 1 1
2
1 .
Untuk dua keluarga fungsi densitas
1(
|
)
,
1(
)
,
1
p
x
x
M
dan
2(
|
)
,
2(
)
,
2
p
x
x
M
dapat didefinisikan diskrepansi intrinsik
(
|
)
,
(
|
)
min
)
,
(
*
1 2, 2
1
M
M
p
x
p
x
.Fungsi kerugian (loss function) dalam kasus ini adalah diskrepansi intrinsik. Misalkan bahwa deskripsi yang sesuai dari tingkah laku probabilistik dari kuantitas random x diberikan oleh model
} ,
, ), , | (
{p x
x
. Diskrepansi intrinsik antara p(x|
,
) dan keluarga densitas}
),
,
|
(
{
p
x
0
adalah
)
,
;
,
(
inf
)
;
,
(
*
0 0 00
dengan
(
,
|
,
)
,
(
,
|
,
)
min
)
,
;
,
(
0
0
0
0
0
0
K
K
.Misalkan {p(x|
,
),x,
,
} adalah model parametrik yang dapat digunakan untuk menggambarkan tingkah laku kuantitas random x. Didefinisikan intrinsik statistik(intrinsic statistic) sebagai
x
E
x
x
d
d
d
(
0|
)
[
*
|
]
*
(
,
;
0)
*(
,
|
)
*
dengan
*(
,
|
x
)
adalah posterior referensi untuk parameter dari model p(x|
,
)bila)
;
,
(
*
0
adalah parameter yang menjadi perhatian. Intrinsik statistik merupakan ukuran dari kekuatan bukti melawan penggunaanp
(
x
|
0,
)
sebagaiproxy untuk p(x|
,
). Proxyterbaik dicapai pada suatu nilai yang menghasilkan kerugian terkecil.
Misalkan {p(x|
,
),x,
,
} adalah model parametrik yang sesuai untuk menggambarkan tingkah laku probabilistik dari kuantitas random x. Estimator intrinsik(intrinsic estimator) atau estimasi titik Bayesian obyektif didefinisikan sebagai yaitu parameter
yang meminimalkan statistik intrinsik
) | ( min arg ) ( * *
~
~
x d
x
.
Populasi Eksponensial
Misalkan dimiliki sampel x1, x2, ...., xn dari distribusi eksponensial dengan fungsi kepadatan
probabilitas
x
e
x
f
(
|
)
]
)
|
(
,
)
|
(
[
min
)
,
(
0
0
0
x
n
dengan
dx
x
f
x
f
x
f
i j j j i
)
|
(
)
|
(
ln
)
|
(
)
|
(
0
= j i j i 1 ln .Akibatnya 0 0 0 0 0 , ) / ( , ) / ( ) , ( g g x .
dengang(x)= (x-1)-ln(x). Dapat dibuktikan bahwareference priordari parameter yang menjadi perhatianadalah() =-1 danreference posterioryang terkait adalah
nt
n Gamma n t e
x
x1,...., ) ( | , ) 1
|
(
.Diperoleh intrinsik statistik
0 0 0
1
0 | ,...., ) ( | , ) ( , ) ( | , )
(
x x d
t n n
Gamma
n t d
d n x
dengan
n i ix
t
1 . Populasi SeragamMisalkanx1,x2, ....,xn sampel dari distribusi seragam dengan fungsi kepadatan probabilitas 1
)
|
(
x
f
untuk 0 x , > 0 dan misalkan t= max{ x1, x2, ....,xn }. Deskrepansi intrinsik dari
distribusi eksponensial adalah
]
)
|
(
,
)
|
(
[
min
)
,
(
0
0
0
x
n
dengan
. , , / log / ln ) | ( 0 1 i j i j j i j i j j i j dx
Akibatnya|
)
/
ln(
|
)
,
(
0
0
x
n
.Karena ruang sampel dariX= [ 0,] tergantung dari parameter maka hal ini bukan masalah regular. Fungsi
t
^
merupakan statistik cukup, estimator konsisten dari yang mempunyai distribusi sampling n nt
n
t
p
(
|
)
1
untuk 0 <t<. Dapat dibuktikan bahwareference priordari parameter yang menjadi perhatian
adalah() =-1 danreference posterioryang terkait adalah . , ) ...., , |
( x1 x nt ( 1) t
n n
n
Diperoleh intrinsik statistik
t n n
n d t n n nt d
x x
3. Studi Simulasi dan Pembahasan Kasus Sampel dari Populasi Eksponensial
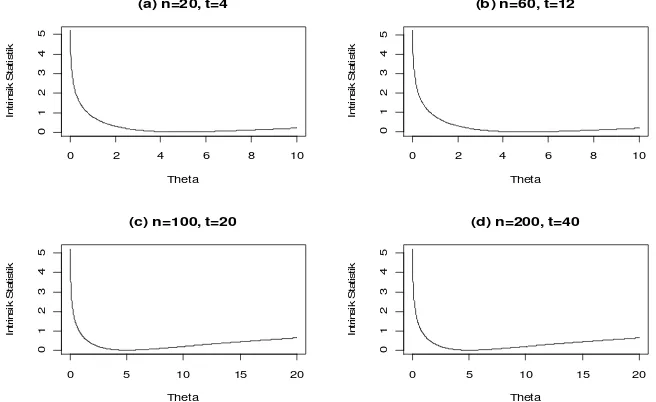
Apabila diberikan ukuran sampel n dan statistik cukup t dengan sampel dianggap berasal dari populasi yang berdistribusi eksponensial maka dapat ditentukan estimator titik Bayesian obyektif yaitu nilai parameter * yang meminimalkan intrinsik statistik. Pada Gambar 1 diberikan gambar yang merupakan hasil perhitungan intrinsik statistik jika diberikan beberapa nilai n dant. Pada Gambar 1, estimator titik Bayesian obyektif dan MLE dari masing-masing berturut-turut adalah 1,91, 3,91, 7,90, 4,98 dan 2, 4, 8, 5. Pada Gambar 2 diberikan estimator titik Bayesian obyektif dengan n dan t yang bersesuaian sehingga menghasilkan estimator titik Bayesian obyektif berturut-turut adalah 4,88, 4,96, 4,98 dan 4,99. Terlihat bahwa untuk ukuran sampel yang membesar maka estimator tersebut akan mendekati nilai MLE yaitu 5.
0 2 4 6 8 10
0
1
2
3
4
(a) n=10, t=5
Theta
In
tr
in
s
ik
S
ta
ti
s
ti
k
0 2 4 6 8 10
0
1
2
3
4
5
(b) n=20, t=5
Theta
In
tr
in
s
ik
S
ta
ti
s
ti
k
0 5 10 15 20
0
1
2
3
4
5
(c) n=40, t=5
Theta
In
tr
in
s
ik
S
ta
ti
s
ti
k
0 5 10 15 20
0
1
2
3
4
5
(d) n=100, t=20
Theta
In
tr
in
s
ik
S
ta
ti
s
ti
[image:4.595.117.437.275.514.2]k
Gambar 1. Gambar nilai intrinsik statistik untuk beberapa nilaindantyang diberikan.
0 2 4 6 8 10
0
1
2
3
4
5
(a) n=20, t=4
Theta
In
tr
in
s
ik
S
ta
ti
s
ti
k
0 2 4 6 8 10
0
1
2
3
4
5
(b) n=60, t=12
Theta
In
tr
in
s
ik
S
ta
ti
s
ti
k
0 5 10 15 20
0
1
2
3
4
5
(c) n=100, t=20
Theta
In
tr
in
s
ik
S
ta
ti
s
ti
k
0 5 10 15 20
0
1
2
3
4
5
(d) n=200, t=40
Theta
In
tr
in
s
ik
S
ta
ti
s
ti
k
[image:4.595.114.442.544.745.2]Simulasi dilakukan dengan cara membangkitkan sampel ukuran n dari distribusi eksponensial dengan parameter dan dengan sampel tersebut akan diestimasi (ulang) parameter dengan metode Bayesian obyektif. Apabila hal itu dilakukan sebanyak bilangan besar B (dalam makalah ini digunakan B=100) maka untuk beberapa nilai n dan yang digunakan, akan diperoleh histogram pada Gambar 3.
(a) Histogram Estimasi Theta jika n=10, theta=5
2 3 4 5 6 7 8
0
.0
0
0
.1
0
0
.2
0
(b) Histogram Estimasi Theta jika n=30, theta=2
1.0 1.5 2.0 2.5 3.0 3.5 4.0
0
.0
0
.4
0
.8
(c) Histogram Estimasi Theta jika n=60, theta=5
3.5 4.0 4.5 5.0 5.5 6.0 6.5 7.0
0
.0
0
.2
0
.4
0
.6
(d) Histogram Estimasi Theta jika n=100, theta=10
8.0 8.5 9.0 9.5
0
.0
0
.5
1
.0
1
[image:5.595.143.481.158.406.2].5
Gambar 3. Histogram hasil simulasi untuk beberapa ukuran sampelndan yang digunakan dalam simulasi.
[image:5.595.148.466.543.744.2]Kasus Sampel dari Populasi Uniform
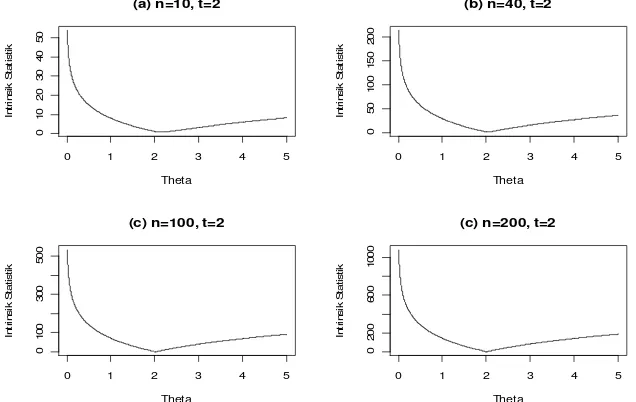
Gambar 4 merupakan hasil perhitungan intrinsik statistik jika diberikan beberapa nilaindan
t = 2 dengan sampel dianggap berasal dari populasi yang berdistribusi seragam sehingga estimator titik Bayesian obyektif dan MLE dari masing-masing berturut-turut adalah 2,135, 2,025, 2,005, 1,995dan 2. Hal itu berarti bahwa untuk ukuran sampel yang membesar maka estimator tersebut akan cenderung mendekati nilai MLE yaitu 2.
0 1 2 3 4 5
0
1
0
2
0
3
0
4
0
5
0
(a) n=10, t=2
Theta
In
tr
in
s
ik
S
ta
ti
s
ti
k
0 1 2 3 4 5
0
5
0
1
0
0
1
5
0
2
0
0
(b) n=40, t=2
Theta
In
tr
in
s
ik
S
ta
ti
s
ti
k
0 1 2 3 4 5
0
1
0
0
3
0
0
5
0
0
(c) n=100, t=2
Theta
In
tr
in
s
ik
S
ta
ti
s
ti
k
0 1 2 3 4 5
0
2
0
0
6
0
0
1
0
0
0
(c) n=200, t=2
Theta
In
tr
in
s
ik
S
ta
ti
s
ti
k
Simulasi dilakukan dengan cara membangkitkan sampel ukuran n dari distribusi seragam pada (0, ) dengan parameter dan dengan sampel tersebut akan diestimasi (ulang) parameter dengan metode Bayesian obyektif. Apabila hal itu dilakukan sebanyak bilangan besar B (dalam makalah ini digunakan B=1000) maka untuk beberapa nilai n = 10, 40, 60, 100 dan=2 yang digunakan, akan diperoleh histogram pada Gambar 5. Terlihat bahwa makin besar ukuran sampel akan makin kecil variansi estimasinya.
(a) n=10, theta=2
1.0 1.2 1.4 1.6 1.8 2.0
0
2
4
6
8
1
0
(b) n=10, theta=2
1.0 1.2 1.4 1.6 1.8 2.0
0
5
1
0
1
5
2
0
(c) n=10, theta=2
1.0 1.2 1.4 1.6 1.8 2.0
0
5
1
0
2
0
3
0
(d) n=10, theta=2
1.0 1.2 1.4 1.6 1.8 2.0
0
2
0
4
0
6
0
8
[image:6.595.127.443.175.387.2]0
Gambar 5. Histogram hasil simulasi untuk beberapa ukuran sampeln= 10, 40, 60, 100 dan = 2 yang digunakan dalam simulasi.
4. Kesimpulan dan Saran
Estimasi titik Bayesian obyektif dapat digunakan untuk kasus sampel dari distribusi eksponensial dan sampel dari distribusi seragam. Penelitian ini dapat dikembangkan untuk berbagai macam distribusi yang lain.
Daftar Pustaka
[1] Bernardo, J. M. ( 2009 ) Statistics : Bayesian Methodology in Statistics, Comprehensive
Chemometrics ( S. Brown, R. Tauler dan R. Walczak eds) Oxford : Elsevier.
[2] Bernardo, J. M. dan M. A. Juarez ( 2003 ) Intrinsic Estimation, Bayesian Statistics 7, Oxford : University Press.
[3] Bernardo, J. M. and Rueda, R. ( 2002 ) Bayesian hypothesis testing: A reference approach.
International Statistical Review70, 351-372.
[4] Juarez, M. A. ( 2004 ) Objective Bayesian Methods for Estimation and Hypothesis Testing, Valencia : University of Valencia.
[5] Setiawan, A. (2009) Estimasi Titik Bayesian Obyektif, Prosiding Seminar Sains dan