Ebook Matematika: Imapact Mathematic 1 UNDUH IMPACT Math 1

(1)

Algebra and More

Course 1

(2)

Algebra and More

(3)

(4)

Algebra and More

Course 1

Developed by

Education Development Center, Inc.

Peter Braunfeld, Ricky Carter, Haim Eshach, Sydney Foster, Susan Janssen, Phil Lewis, Joan Lukas, Michelle Manes, Cynthia J. Orrell, Melanie Palma,

(5)

The algebra content for Impact Mathematicswas adapted from the series, Access to Algebra, by Neville Grace, Jayne Johnston, Barry Kissane, Ian Lowe, and Sue Willis. Permission to adapt this material was obtained from the publisher, Curriculum Corporation of Level 5, 2 Lonsdale Street, Melbourne, Australia.

Copyright © 2004 by the McGraw-Hill Companies, Inc. All rights reserved. Printed in the United States of America. Except as permitted under the United States Copyright Act, no part of this publication may be reproduced or distributed in any form or by any means, or stored in a database or retrieval system, without prior written permission from the publisher.

Send all inquiries to: Glencoe/McGraw-Hill 8787 Orion Place Columbus, OH 43240

ISBN: 0-07-860909-7

(6)

v Marcie Abramson

Thurston Middle School Boston, Massachusetts Denise Airola

Fayetteville Public Schools Fayetteville, Arizona Chadley Anderson

Syracuse Junior High School Syracuse, Utah

Jeanne A. Arnold Mead Junior High Elk Grove Village, Illinois Joanne J. Astin

Lincoln Middle School Forrest City, Arkansas Jack Beard

Urbana Junior High Urbana, Ohio Chad Cluver

Maroa-Forsyth Junior High Maroa, Illinois

Robert C. Bieringer

Patchogue-Medford School Dist. Center Moriches, New York Susan Coppleman

Nathaniel H. Wixon Middle School South Dennis, Massachusetts Sandi Curtiss

Gateway Middle School Everett, Washington

Alan Dallman

Amherst Middle School Amherst, Massachusetts Sharon DeCarlo

Sudbury Public Schools Sudbury, Massachusetts David P. DeLeon

Preston Area School Lakewood, Pennsylvania Jacob J. Dick

Cedar Grove School Cedar Grove, Wisconsin Sharon Ann Dudek Holabird Middle School Baltimore, Maryland Cheryl Elisara

Centennial Middle School Spokane, Washington Patricia Elsroth

Wayne Highlands Middle School Honesdale, Pennsylvania Dianne Fink

Bell Junior High San Diego, California Terry Fleenore

E.B. Stanley Middle School Abingdon, Virginia Kathleen Forgac Waring School Massachusetts

Steven J. Fox

Bendle Middle School Burton, Michigan Kenneth L. Goodwin Jr. Middletown Middle School Middletown, Delaware Fred E. Gross

Sudbury Public Schools Sudbury, Massachusetts Penny Hauben

Murray Avenue School Huntingdon, Pennsylvania Jean Hawkins

James River Day School Lynchburg, Virginia Robert Kalac Butler Junior High Frombell, Pennsylvania Robin S. Kalder Somers High School Somers, New York Darrin Kamps

Lucille Umbarge Elementary Burlington, Washington Sandra Keller

Middletown Middle School Middletown, Delaware Pat King

Holmes Junior High Davis, California Peter Braunfeld

Professor of Mathematics Emeritus University of Illinois

Sherry L. Meier

Assistant Professor of Mathematics Illinois State University

Judith Roitman

Professor of Mathematics University of Kansas

Impact Mathematics Project Reviewers

Education Development Center appreciates all the feedback from the curriculum specialists and teachers who participated in review and testing.

(7)

Kim Lazarus

San Diego Jewish Academy La Jolla, California Ophria Levant Webber Academy Calgary, Alberta Canada Mary Lundquist Farmington High School Farmington, Connecticut Ellen McDonald-Knight

San Diego Unified School District San Diego, California

Ann Miller

Castle Rock Middle School Castle Rock, Colorado Julie Mootz

Ecker Hill Middle School Park City, Utah

Jeanne Nelson

New Lisbon Junior High New Lisbon, Wisconsin DeAnne Oakley-Wimbush Pulaski Middle School Chester, Pennsylvania Tom Patterson

Ponderosa Jr. High School Klamath Falls, Oregon Maria Peterson Chenery Middle School Belmont, Massachusetts Lonnie Pilar

Tri-County Middle School Howard City, Michigan

Karen Pizarek

Northern Hills Middle School Grand Rapids, Michigan Debbie Ryan

Overbrook Cluster Philadelphia, Pennsylvania Sue Saunders

Abell Jr. High School Midland, Texas Ivy Schram

Massachusetts Department of Youth Services

Massachusetts Robert Segall

Windham Public Schools Willimantic, Connecticut Kassandra Segars Hubert Middle School Savannah, Georgia Laurie Shappee Larson Middle School Troy, Michigan Sandra Silver

Windham Public Schools Willimantic, Connecticut Karen Smith

East Middle School Braintree, Massachusetts Kim Spillane

Oxford Central School Oxford, New Jersey Carol Struchtemeyer Lexington R-5 Schools Lexington, Missouri

Kathy L. Terwelp Summit Public Schools Summit, New Jersey Laura Sosnoski Tracey Somerville, Massachusetts Marcia Uhls

Truesdale Middle School Wichita, Kansas Vendula Vogel

Westridge School for Girls Pasadena, California Judith A. Webber

Grand Blanc Middle School Grand Blanc, Michigan Sandy Weishaar Woodland Junior High Fayetteville, Arkansas Tamara L. Weiss

Forest Hills Middle School Forest Hills, Michigan Kerrin Wertz

Haverford Middle School Havertown, Pennsylvania Anthony Williams

Jackie Robinson Middle School Brooklyn, New York

Deborah Winkler The Baker School Brookline, Massachusetts Lucy Zizka

(8)

vii

All About Patterns . . . .2

Lesson 1.1: Looking for Patterns . . . .4

Investigation 1: Pascal’s Triangle and Sequences . 5 On Your Own Exercises . . . .10

Lesson 1.2: Following Rules . . . .14

Investigation 1: Sequences and Rules . . . .15

Investigation 2: Order of Operations . . . .19

On Your Own Exercises . . . .23

Lesson 1.3: Writing Rules for Patterns . . . .28

Investigation 1: Finding Rules . . . .29

Investigation 2: Connecting Numbers . . . .32

On Your Own Exercises . . . .36

Lesson 1.4: Patterns in Geometry . . . .42

Investigation 1: Polygons . . . .42

Investigation 2: Angles . . . .46

Investigation 3: Classifying Polygons . . . .50

Investigation 4: Triangles . . . .54

Lab Investigation: Polygons to Polyhedra . . . .58

Review and Self-Assessment . . . .69

All About Numbers . . . .74

Lesson 2.1: Factors and Multiples . . . .76

Investigation 1: Factors . . . .77

Investigation 2: Prime Numbers . . . .79

Investigation 3: Common Factors . . . .82

Investigation 4: Multiples . . . .85

Lab Investigation: A Locker Problem . . . .88

Lesson 2.2: Patterns in Fractions . . . .96

Investigation 1: Visualizing Fractions . . . .97

Investigation 2: Equivalent Fractions . . . .99

Investigation 3: Comparing Fractions . . . .102

Investigation 4: Estimating with Fractions . . . .104

On Your Own Exercises . . . .106

Lesson 2.3: Patterns in Decimals . . . .112

Investigation 1: Understanding Decimals . . . . .113

Investigation 2: Measuring with Decimals . . . . .117

Investigation 3: Comparing and Ordering Decimals . . . .120

Lesson 2.4: Fractions and Decimals . . . .128

Investigation 1: Estimating Fraction and Decimal Equivalents . . . .128

Investigation 2: Changing Fractions to Decimals 131 Investigation 3: Patterns in Fractions and Decimals . . . .134

On Your Own Exercises . . . .137

Lesson 2.5: Negative Numbers . . . .142

Investigation 1: Understanding Negative Numbers . . . .143

(9)

Chapter Four

Chapter Three

Working with Fractions and

Decimals . . . .152

Lesson 3.1: Adding and Subtracting Fractions . . . . .154

Investigation 1: Adding and Subtracting with Fraction Pieces . . . .154

Investigation 2: Adding and Subtracting Using Common Denominators . . . .157

Investigation 3: Adding and Subtracting Mixed Numbers . . . .161

Lab Investigation: Using a Fraction Calculator . .164 On Your Own Exercises . . . .166

Lesson 3.2: Multiplying and Dividing with Fractions . . . .172

Investigation 1: Multiplying Fractions and Whole Numbers . . . .172

Investigation 2: A Model for Multiplying Fractions . . . .175

Investigation 3: More Multiplying with Fractions . . . .178

Investigation 4: Dividing Whole Numbers by Fractions . . . .182

Investigation 5: Dividing Fractions by Fractions . . . .185

Lesson 3.3: Multiplying and Dividing with Decimals 198 Investigation 1: Multiplying Whole Numbers and Decimals . . . .198

Investigation 2: Multiplying Decimals as Fractions . . . .201

Investigation 3: Multiplying Decimals in Real Life . . . .204

Investigation 4: Dividing Decimals . . . .207

Investigation 5: Multiplying or Dividing? . . . . .210

Making Sense of Percents . . . .224

Lesson 4.1: Using Percents . . . .226

Investigation 1: Understanding Percents . . . .227

Investigation 2: Making a Circle Graph . . . .230

Investigation 3: Parts of Different Wholes . . . .234

Investigation 4: Linking Percents, Fractions, and Decimals . . . .236

Lesson 4.2: Finding a Percent of a Quantity . . . .248

Investigation 1: Modeling with a Grid . . . .249

Investigation 2: Using a Shortcut . . . .252

On Your Own Exercises . . . .256

Lesson 4.3: Percents and Wholes . . . .260

Investigation 1: Finding the Percent . . . .261

Investigation 2: Finding the Whole . . . .264

Lab Investigation: Playing Percent Ball . . . .268

(10)

ix

Exploring Graphs . . . .276

Lesson 5.1: Interpreting Graphs . . . .278

Investigation 1: Using Points to Display Information . . . .278

Investigation 2: Interpreting Points . . . .282

Investigation 3: Interpreting Lines and Curves . . . .286

Lesson 5.2: Drawing and Labeling Graphs . . . .300

Investigation 1: Drawing Your Own Graphs . . .301

Investigation 2: Plotting Points . . . .302

Investigation 3: Choosing Scales . . . .306

On Your Own Exercises . . . .311

Lesson 5.3: Using Graphs to Find Relationships . . .316

Investigation 1: Looking for a Connection . . . . .317

Investigation 2: How Some Things Grow . . . . .319

Investigation 3: Making Predictions From Graphs . . . .320

Lab Investigation: Graphing with Spreadsheets . . . .324

Analyzing Data . . . .340

Lesson 6.1: Using Graphs to Understand Data . . . .342

Investigation 1: Using Line Graphs to Solve a Mystery . . . .343

Investigation 2: Using Bar Graphs to Analyze Data . . . .346

Investigation 3: Making Histograms . . . .350

Lesson 6.2: What Is Typical? . . . .362

Investigation 1: Mode and Median . . . .362

Investigation 2: Stem-and-Leaf Plots . . . .366

Investigation 3: The Meaning of Mean_{. . . .370}

Investigation 4: Mean or Median? . . . .373

Investigation 5: Analyzing Data . . . .377

Lesson 6.3: Collecting and Analyzing Data . . . .390

Investigation 1: Planning Your Analysis . . . .391

Investigation 2: Carrying Out Your Analysis . . .394

Lab Investigation: Statistics and Spreadsheets . .396 On Your Own Exercises . . . .399

(11)

Chapter Seven

Chapter Eight

Variables and Rules . . . .408

Lesson 7.1: Patterns and Variables . . . .410

Investigation 1: Sequences, Rules, and Variables . . . .411

Investigation 2: Are These Rules the Same? . . .414

Investigation 3: What’s My Rule? . . . .419

Lesson 7.2: Rules in Real Life . . . .430

Investigation 1: Rules in Context . . . .431

Lab Investigation: Crossing a Bridge . . . .433

Investigation 2: Translating Words into Symbols . . . .436

Investigation 3: Equivalent Rules . . . .439

Lesson 7.3: Explaining Number Relationships . . . . .450

Investigation 1: Think of a Number . . . .451

Investigation 2: Consecutive Numbers . . . .455

Geometry and Measurement . . . .464

Lesson 8.1: Angles . . . .466

Investigation 1: Measuring Angles . . . .467

Investigation 2: Investigating Angle Relationships . . . .472

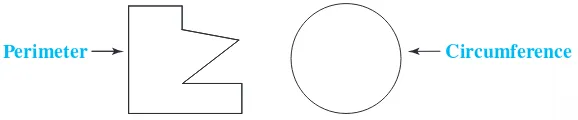
Lesson 8.2: Measuring Around . . . .482

Investigation 1: Finding Perimeter . . . .482

Investigation 2: Approximating

π

. . . .486

Lesson 8.3: Areas and Squares . . . .494

Investigation 1: Counting Square Units . . . .495

Investigation 2: Squaring . . . .498

Investigation 3: More about Squaring . . . .501

Investigation 4: Taking Square Roots . . . .504

Lesson 8.4: Calculating Areas . . . .514

Investigation 1: Areas of Parallelograms . . . . .515

Investigation 2: Areas of Triangles . . . .518

Investigation 3: Areas of Circles . . . .522

Lab Investigation: Using a Spreadsheet to Maximize Area . . . .525

Lesson 8.5: The Pythagorean Theorem . . . .536

Investigation 1: Right Triangles and Squares . . .536

Investigation 2: Using the Pythagorean Theorem . . . .540

(12)

1

Solving Equations . . . .556

Lesson 9.1: Understanding Equations . . . .558

Investigation 1: Equations and Inequalities . . . .559

Investigation 2: Equations with Variables . . . . .560

Lab Investigation: Just Undo It! . . . .563

Lesson 9.2: Backtracking . . . .570

Investigation 1: Learning to Backtrack . . . .571

Investigation 2: Practicing Backtracking . . . .574

Investigation 3: Using Backtracking to Solve Problems . . . .576

Lesson 9.3: Guess-Check-and-Improve . . . .586

Investigation 1: Using Guess-Check-and-Improve . . . .586

Investigation 2: Solving Problems Using Guess-Check-and-Improve . . . .589

Investigation 3: Choosing a Method . . . .592

Understanding Probability . . . .602

Lesson 10.1: The Language of Chance . . . .604

Investigation 1: Probability in Everyday Life . . .605

Investigation 2: Theoretical Probability . . . .608

Lab Investigation: The Spinning Top Game . . . . .613

Lesson 10.2: Analyzing Games . . . .620

Investigation 1: Who’s Greater?_{. . . .621}

Investigation 2: Dice Sums . . . .623

Investigation 3: Rolling Differences . . . .624

Investigation 4: Geometric Probability . . . .626

On Your Own Exercises . . . .631

Lesson 10.3: Making Matches . . . .638

Investigation 1: Matching Colors . . . .639

Investigation 2: Matching Cards . . . .643

Glossary . . . 656

Index . . . 666

Photo Credits . . . 675

(13)

A Bee Tree

Although a female honeybee has two parents, a male honeybee has only a mother. The family tree of a male honeybee’s ancestors reveals an interest-ing pattern of numbers.

The numbers of bees in the generations—1, 1, 2, 3, 5, 8, and so on—form a famous list of numbers known

as the Fibonacci sequence.

Think About It

Can you discover a pattern in the family tree or the list of numbers that will help you find the next two or three numbers in the Fibonacci sequence? M

F

M F

F M F

M F F M F

F M F M F F M F

1 male bee

1 parent

2 grandparents

3 great-grandparents

5 great-great-grandparents

8 great-great-great-grandparents

All about Patterns

(14)

Fa

mi

ly

Le

tt

e

r

Dear Student and Family Members,

Our class is about to begin an exciting year of mathematics. Don’t worry—mathematics is more than just adding and subtracting numbers. Mathematics has been called the “science of patterns.” Recognizing and describing patterns and using patterns to make predictions are important mathematical skills.

We’ll begin by looking for patterns in Pascal’s triangle, a number triangle containing many patterns.

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

Can you describe any patterns in the triangle? Try to predict the numbers in the next row of the table. Don’t worry if you can’t find any patterns yet. We’ll be learning lots about this triangle in the next few days.

We’ll also be looking for shape patterns. For example, the surface of a honeycomb, like the one shown here in the background, is made up of a pattern of hexagons that fit together with no overlaps. Can you make a similar pattern with squares? How about with triangles?

Vocabulary

Along the way, you’ll be learning about these new terms:

angle regular polygon

concave polygon sequence

line symmetry term

order of operations triangle inequality

polygon vertex

What can you do at home?

During the next few weeks, your student may show interest in patterns and rules. Ask him or her to think about common occurrences of patterns and rules, such as this rule to estimate how many miles you are from a lightning strike:Count the number of seconds between seeing the lightning and hearing the thunder, and then divide by 5.

(15)

Patterns are everywhere! You can see patterns in wallpaper, fabric, buildings, flowers, and insects. You can hear patterns in music and song lyrics and even in the sound of a person’s voice. You can follow patterns to catch a bus or a train or to locate a store with a particular address.

Patterns are an important part of mathematics. You use them every time you read a number, perform a mathematical operation, interpret a graph, or identify a shape. In this lesson, you will search for, describe, and extend many types of patterns.

Explore

In this diagram, you can begin at “Start” and trace a path, following the arrows, to any of the letters.

How many different paths are there from Start to A? Describe each path.

How many paths are there from Start to D? Describe each path.

How many paths are there from Start to G? Describe each path.

There are four paths from Start to K. Describe all four.

Add another row of circles to a copy of the diagram, following the pattern of arrows and letters. How many paths are there from Start to S? Describe them.

On a new copy of the diagram, replace each letter with the number of paths from Start to that letter. For example, replace A with 1 and K with 4.

The triangle of numbers you just created is quite famous. You will learn more about the triangle and the patterns it contains in Investigation 1.

Start

B

E D A

C

G

F H I

K

J L M N

(16)

Investigation

1

Pascal’s Triangle

and Sequences

The number triangle you created in the Explore has fascinated mathemati-cians for centuries because of the many patterns it contains. Chinese and Islamic mathematicians worked with the triangle as early as A.D. 1100.

Blaise Pascal, a French mathematician who studied it in 1653, called it the arithmetic triangle.It is now known as Pascal’s trianglein his honor.

Problem Set

A

Below is a copy of the diagram you made in the Explore. The word “Start” has been replaced by the numeral 1, and the rows have been labeled.

There are many patterns in this triangle. For example, each row reads the same forward as it does backward.

1. Describe as many patterns in the triangle as you can.

2. To add more rows to the triangle, you could count paths as you did in the Explore—but that might take a lot of time. Instead, use some of the patterns you found in Problem 1 to extend the triangle to Row 7. You may not be able to figure out all the numbers, but fill in as many as you can.

3. One way to add new rows to the triangle is to consider how each number is related to the two numbers just above it to the left and right. Look at the numbers in Rows 3 and 4. Describe a rule for finding the numbers in Row 4 from those in Row 3. Does your rule work for other rows of the triangle as well?

4. Use your rule from Problem 3 to complete the triangle to Row 9.

1 Row 0

Row 1 Row 2 Row 3 Row 4 Row 5 2

6

1 1

3

10 3

10

1 1

4 4

1

5

1

5 1

1

1 1

The number triangle as it appears in Precious Mirror of the Four Elements,written by Chinese mathematician Chu Shih-Chieh in 1303

(17)

&

Pascal’s triangle has many interesting patterns in it. You have probably worked with other patterns in the form of puzzles like these:

Fill in the blanks.

Puzzle A:2, 5, 8, 11, __, __ , __

Puzzle B:16, 8, 4, 2, __, __, __

Puzzle C:3, 2, 3, 2, __, __, __

Puzzle D:★,✻,★,✻, __, __, __

To solve these puzzles, you need to find a pattern in the part of the list given and use it to figure out the next few items. Ordered lists like these are called sequences.Each item in a sequence is called a term. Terms may also be referred to as stages.

Think Discuss

Here is Puzzle A. Describe a rule you can follow to get from one term to the next.

2, 5, 8, 11, __, __ , __

According to your rule, what are the next three terms?

Now look at Puzzle B. Describe the pattern you see.

16, 8, 4, 2, __, __, __

According to the pattern you described, what are the next three terms?

What pattern do you see in Puzzle C: 3, 2, 3, 2, __, __, __?

According to the pattern, what are the next three terms?

Sequences don’t always involve numbers. Look at Puzzle D, for example.

★,✻,★,✻, __, __, __

Describe the pattern, and give the next three terms.

In Puzzles A and B, each term is found by applying a rule to the term before it. In Puzzles C and D, the terms follow a repeating pattern. In the next problem set, you will explore more sequences of both types.

V O C A B U L A R Y

sequence

(18)

Problem Set

B

1. The sequences in Parts a–e follow a repeating pattern. Give the next three terms or stages of each sequence.

a.

b.3, 6, 9, 3, 6, 9, 3, 6, . . .

c.

d.7, 1, 1, 7, 1, 1, 7, 1, 1, . . .

e.ᎏ1₂ᎏ,ᎏ2₃ᎏ,ᎏ1₂ᎏ,ᎏ2₃ᎏ,ᎏ1₂ᎏ,ᎏ2₃ᎏ, . . .

2. In Parts a–e, each term in the sequence is found by applying a rule to the term before it (the precedingterm). Give the next three terms of each sequence.

a.3, 6, 9, 12, . . .

b.

c.100, 98.5, 97, . . .

d.3, 5, 8, 12, . . .

e.ᎏ1₂ᎏ,ᎏ1₃ᎏ,ᎏ1₄ᎏ,ᎏ1₅ᎏ, . . .

M A T E R I A L S

• toothpicks

(optional)

• counters (optional)

(19)

3. Below are two sequences, one made with toothpicks and the other with counters. You and your partner should each choose a different sequence. Do Parts a–c on your own using your sequence.

a.Make or draw the next three terms of your sequence.

b.How many toothpicks or counters will be in the tenth term? Check by making or drawing the tenth term.

c.Give a number sequence that describes the number of toothpicks or counters in each term of your pattern.

d.Compare your answers to Parts a–c with your partner’s. What is the same about your answers? What is different?

4. Describe the pattern in each number sequence, and use the pattern to fill in the missing terms.

a.5, 12, 19, 26, __ , __ , __

b.0, 9, 18, 27, __ , __ , __

c.125, 250, __ , 1,000, __ , __ , 8,000

d.1, 0.1, __, 0.001, __, 0.00001, __

e.4, 6, 9, 11, 14, 16, 19, __, __, __

5. Consider this sequence of symbols:

⌬,⌬,⌬,⍀,⍀,⌬,⌬,⌬,⍀,⍀,⌬,⌬,⌬,⍀,⍀, . . .

a.If this repeating pattern continues, what will the next six terms be?

b.What will the 30th term be?

c.How could you find the 100th term without drawing 100 symbols? What will the 100th term be?

Sequence B Sequence A

The symbols in Problem 5 are letters of the Greek alphabet. ⌬is the letter delta,and ⍀ is the letter omega.

Greek letters are used frequently in physics and advanced mathematics.

facts

Just

(20)

&

L E S S O N 1 . 1 Looking for Patterns 9

6. The sequence below is known as the Fibonacci sequenceafter the mathematician who studied it. The Fibonacci sequence is interesting because it appears often in both natural and manufactured things.

1, 1, 2, 3, 5, 8, 13, . . .

a.Study the sequence carefully to see whether you can discover the pattern. Give the next three terms of the sequence.

b.Write instructions for continuing the Fibonacci sequence.

Share

Summarize

1.The diagram from the Explore on page 4 is repeated below. How is Pascal’s triangle related to the number of paths from Start to each letter in this diagram?

2.You discovered that each number in Pascal’s triangle is the sum of the two numbers just above it. Explain what this means in terms of the number of paths to a particular letter in the diagram above.

3.Describe some strategies you use when searching for a pattern in a sequence.

Start

B

E D A

C

G

F H I

K

J L M N

The Fibonacci

numbers—the numbers in the sequence—can be found in the arrange-ments of leaves and flowers on plants and of scales on pine cones and pineapples.

facts

Just

(21)

On Your Own Exercises

&

Practice

Apply

In mathematics, the symbol ⌬represents the amount of change in a quantity, and the symbol ⬁represents infinity.

facts

Just

t h e

1 Row 0

Row 1 Row 2 Row 3 2

1 1

3 3

1 1

1. Here are the first few rows of Pascal’s triangle:

a.How many numbers are in each row shown?

b.How many numbers are in Row 4? In Row 5? In Row 6?

c.If you are given a row number, how can you determine how many numbers are in that row?

d.In some rows, every number appears twice. Other rows have a middle number that appears only once. Will Row 10 have a mid-dle number? Will Row 9? How do you know?

2. A certain row of Pascal’s triangle has 252 as the middle number and 210 just to the right of the middle number.

a.What is the number just to the left of the middle number? How do you know?

b.What is the middle number two rows later? How do you know?

Describe the pattern in each sequence, and use the pattern to find the next three terms.

3. 3, 12, 48, 192, __ , __ , __

4. 0.1, 0.4, 0.7, 1.0, __ , __ , __

5. 2, 5, 4, 7, 6, 9, __, __, __

6. _⌬,⬁,⌬,⌬,⬁,⌬,⌬,⌬,⬁, __, __, __

7. ⫺_5,⫺_4,⫺_3,⫺_{2 , __ , __, __}

8. a, c, e, g, __, __, __

? 252 ?

? ?

(22)

9. Some patterns in Pascal’s triangle appear in unexpected ways. For example, look at the pattern in the sums of the rows.

a.Find the sum of each row shown above.

b.Describe the pattern in the row sums.

10. The pattern below involves two rows of numbers. If the pattern were continued, what number would be directly to the right of 98? Explain how you know.

3 6 9 12 15 18

1 2 4 5 7 8 10 11 13 14 16 17

11. Look at this pattern of numbers. If it were continued, what number would be directly below 100?

1

2 3 4

5 6 7 8 9

10 11 12 13 14 15 16

1 Row 0 Sum ⴝ 1

Row 1 Sum ⴝ 2 Row 2 Sum ⴝ 4

2 6 1 1 3 10

3 10

1 1

4 4

1 5

1 5 1

1

1 1

ⴙ

ⴙ ⴙ ⴙ

ⴙ ⴙ

ⴙ

ⴙ ⴙ

&

Connect

Extend

(23)

12. For this problem, you may want to draw the shapes on graph paper.

a.Find the next term in this sequence:

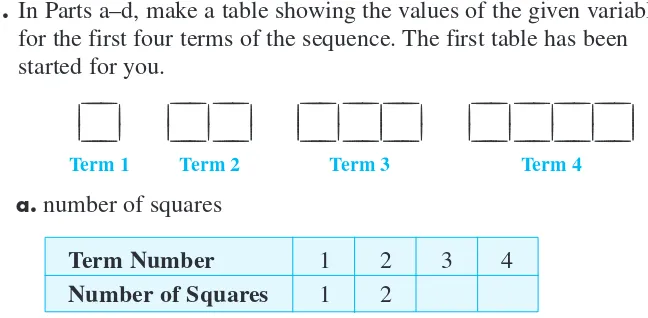
b.This table shows the number of squares in the bottom rows of Terms 1 and 2. Copy and complete the table to show the number of squares in the bottom rows of the next two terms.

Squares in Term Bottom Row

1 1

2 3

3 4

c.Look at your table carefully. Describe the pattern of numbers in the second column. Use your pattern to extend the table to show the number of squares in the bottom rows of Terms 5 and 6.

d.Predict the number of squares in the bottom row of Term 30.

e.Now make a table to show the total number of squaresin each of the first five terms.

Term Total Number of Squares

1 1

2 4

3 4 5

f.Look for a pattern in your table from Part e. Use the pattern to predict the total number of squares in Term 10.

Term 3 Term 2

Term 1

What is a pattern? Is every sequence of numbers a pattern? Is every sequence of shapes a pattern? Explain your answers.

own

In

y o u r

(24)

L E S S O N 1 . 1 Looking for Patterns 13

13. Imagine that an ant is standing in the square labeled A on the grid below. The ant can move horizontally or vertically, with each step taking him one square from where he started.

a.On a copy of the grid, color each square (except the center square) according to the least number of steps it takes the ant to get there. Use one color for all squares that are one step away, another color for all squares that are two steps away, and so on.

b.What shapes are formed by squares of the same color? How many squares of each color are there? What other patterns do you notice?

Find each sum or difference without using a calculator.

14. 5,853 ⫺788 15. 1,054 ⫹1,492 16. 47,745 ⫺2,943

17. Write thirty-two thousand, five hundred sixty-threein standard form.

18. Write fourteen million, three hundred two thousand, twoin standard form.

19. Write 324 in words. 20. Write 12,640 in words.

21. Geometry Imagine that you have 12 square tiles, each measuring 1 inch on a side.

a.In how many different ways can you put all 12 tiles together to make a rectangle? Sketch each possible rectangle.

b.Which of your rectangles has the greatest perimeter? What is its perimeter?

c.Which of your rectangles has the least perimeter? What is its perimeter?

1 in. 1 in.

A

Review

Mixed

Remember

Writing a number in

standard formmeans writing it using digits. For example, standard form for seventeenis 17.

(25)

&

Jing drew a rectangle. She then wrote a rule for generating a sequence of shapes starting with her rectangle.

Starting rectangle:

Rule:Draw a rectangle twice the size of the preceding rectangle.

By following Jing’s rule, Caroline drew this sequence:

Jahmal followed Jing’s rule and drew this sequence:

Think Discuss

Could both sequences above be correct? Explain your answer.

Rosita also followed Jing’s rule. The sequence she drew was differ-ent from both Caroline’s and Jahmal’s. What might Rosita’s

sequence look like?

Rewrite the rule so that Caroline’s sequence is correct but Jahmal’s is not. Try to make your rule clear enough that anyone following it would get the sequence Caroline did.

(26)

Investigation

L E S S O N 1 . 2 Following Rules 15

1

Sequences and Rules

You have just seen how three students could follow the same rule yet draw three different sequences. This is because Jing’s rule is ambiguous— it can be interpreted in more than one way. In both mathematics and everyday life, it is often important to state rules in such a way that everyone will get the same result.

Problem Set

A

1. Create a sequence of shapes in which each shape can be made by applying a rule to the preceding shape. On a blank sheet of paper, draw the first shape of your sequence and write the rule. Try to make your rule clear enough that anyone following it will get the sequence you have in mind.

2. Exchange starting shapes and rules with your partner. Follow your partner’s rule to draw at least the next three shapes in the sequence.

3. Compare the sequence you drew in Problem 2 with your partner’s original sequence. Are they the same? If not, describe how they are different and why. If either your rule or your partner’s rule is ambiguous, work together to rewrite it to make it clear.

Rules are often used to describe how two quantities are related. For example, a rule might tell you how to calculate one quantity from another.

An adult dose of SniffleLess cold medicine is 2 ounces. The dose for a child under 12 can be calculated by using this rule:

Divide the child’s age by 12, and multiply the result by 2 ounces.

This rule tells how a child’s dose is related to the age of the child. If you know the child’s age, you can use the rule to calculate the dose.

You can apply the rule to calculate the dose for a 3-year-old child:

dose ⫽3 ⫼12 ⫻2 ounces

⫽0.25 ⫻2 ounces

(27)

In Problem Set B, you will look at some common rules for finding one quantity from another.

Problem Set

B

1. You can use this rule to estimate how many miles away a bolt of lightning struck:

Count the seconds between seeing the lightning flash and hearing the thunder, and divide by 5.

Use the rule to estimate how far away a bolt of lightning struck if you counted 15 seconds between the flash and the thunder.

2. Hannah’s grandmother uses this rule to figure out how many spoon-fuls of tea to put in her teapot:

Use one spoonful for each person, and then add one extra spoonful.

a.How much tea would Hannah’s grandmother use for four people?

b.Hannah’s grandfather thinks this rule makes the tea too strong. Make up a rule he might like better.

c.Using your rule from Part b, how many spoonfuls of tea are needed for four people?

d.Hannah’s cousin Amy likes her tea much stronger than Hannah’s grandmother does. Make up a rule Amy might like, and use it to figure out how many spoon-fuls of tea would be needed for four people.

3. A cookbook gives this rule for roasting beef:

Cook for 20 minutes at 475°F. Then lower the heat to 375°F and cook for 15 minutes per pound. If you like rare beef, remove the roast from the oven. If you like it medium, cook it an additional 7 minutes. If you like it well done, cook it an additional 14 minutes.

What is the total cooking time for a 4-pound beef roast if you like it medium?

It is believed that people first began drinking hot tea more than 5,000 years ago in China. Iced tea wasn’t introduced until 1904 at the St. Louis World’s Fair, when an Englishman named Richard Blechynden added ice to the drink because no one was buying his hot tea.

facts

Just

(28)

L E S S O N 1 . 2 Following Rules 17 The rules in Problem Set B are fairly simple. Many rules involve more complicated calculations. If you don’t need to find an exact value, you can sometimes use a simpler rule to find an approximation.

Problem Set

C

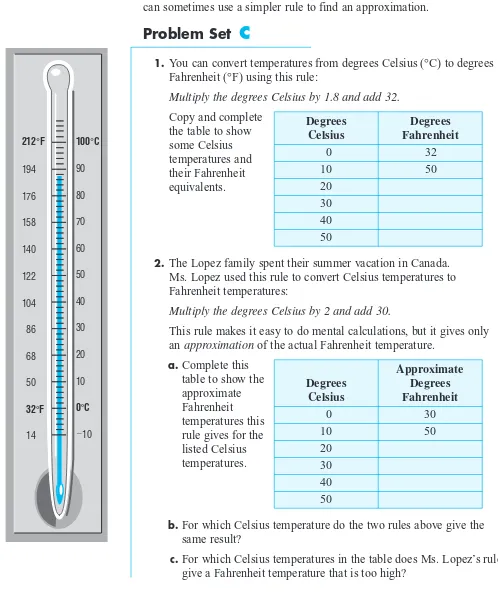
1. You can convert temperatures from degrees Celsius (°C) to degrees Fahrenheit (°F) using this rule:

Multiply the degrees Celsius by 1.8 and add 32.

Copy and complete the table to show some Celsius temperatures and their Fahrenheit equivalents.

2. The Lopez family spent their summer vacation in Canada. Ms. Lopez used this rule to convert Celsius temperatures to Fahrenheit temperatures:

Multiply the degrees Celsius by 2 and add 30.

This rule makes it easy to do mental calculations, but it gives only an approximationof the actual Fahrenheit temperature.

a.Complete this table to show the approximate Fahrenheit temperatures this rule gives for the listed Celsius temperatures.

b.For which Celsius temperature do the two rules above give the same result?

c.For which Celsius temperatures in the table does Ms. Lopez’s rule give a Fahrenheit temperature that is too high?

212°F

194 176 158 140 122 104 86 68 50

32°F

14

90 80

100°C

70 60 50 40 30 20 10

0°C

(29)

&

3. One day the Lopez family flew from Toronto, where the temperature was 37°C, to Winnipeg, where the temperature was 23°C.

a.Use the rule from Problem 1 to find the exact Fahrenheit tempera-tures for the two cities.

b.Use Ms. Lopez’s rule from Problem 2 to find the approximate Fahrenheit temperatures for the two cities.

c.For which city did Ms. Lopez’s rule give the more accurate temperature?

4. Look back at your answers to Problems 2 and 3. What happens to the Fahrenheit approximation as the Celsius temperature increases?

Share

Summarize

1.Below are the first term and a rule for a sequence.

First term:20

Rule:Write the number that is 2 units from the preceding number on the number line.

a. Give the first few terms of two sequences that fit the rule.

b. Rewrite the rule so that only one of your sequences is correct.

2.At the corner market, bananas cost 49¢ a pound. Write a rule for calculating the cost of a bunch of bananas.

(30)

facts

Investigation

2

Order of Operations

A conventionis a rule people have agreed to follow because it is helpful or convenient for everyone to do the same thing. The rules “When you drive, keep to the right” and “In the grocery store, wait in line to pay for your selections” are two conventions.

Reading across the page from left to right is a convention that English-speaking people have adopted. When you see the words “dog bites child,” you know to read “dog” then “bites” then “child” and not “child bites dog.” Not all languages follow this convention. For example, Hebrew is read across the page from right to left, and Japanese is read down the page from left to right.

To do mathematics, you need to know how to read mathematical expres-sions. For example, how would you read this expression?

5 ⫹3 ⫻7

There are several possibilities:

• Left to right:Add 5 and 3 to get 8, and then multiply by 7. The result is 56.

• Right to left:Multiply 7 and 3 to get 21, and then add 5. The result is 26.

• Multiply and then add:Multiply 3 and 7 to get 21, and then add 5. The result is 26.

To communicate in the language of mathematics, people follow a con-vention for reading and evaluating expressions. The concon-vention, called the order of operations,says that expressions should be evaluated in this order:

• Evaluate any expressions inside parentheses.

• Do multiplications and divisions from left to right.

• Do additions and subtractions from left to right.

To evaluate 5 ⫹3 ⫻7, you multiply first and then add:

5 ⫹3 ⫻7 ⫽5 ⫹21 ⫽26

If you want to indicate that the addition should be done first, you would use parentheses:

(5 ⫹3) ⫻7 ⫽8 ⫻7 ⫽56

Conventions are not unchangeable like the physical law “When you drop an object, it falls to the ground.” People can agree to change a convention and do something different.

Just

t h e

V O C A B U L A R Y

order of

operations

Remember

(31)

These calculations follow the order of operations:

15 ⫺3 ⫻4 ⫽15 ⫺12 ⫽3

1 ⫹4 ⫻(2 ⫹3) ⫽1 ⫹4 ⫻5 ⫽1 ⫹20 ⫽21 3 ⫹6 ⫼2 ⫺1 ⫽3 ⫹3 ⫺1 ⫽6 ⫺1 ⫽5 E X A M P L E

Another convention in mathematics involves the symbols used to repre-sent multiplication. You are familiar with the ⫻symbol. An asterisk or a small dot between two numbers also means to multiply. So, each of these expressions means “three times four”:

3 ⫻4 3 ⴢ4 _{3 * 4}

Problem Set

D

In Problems 1–4, use the order of operations to decide which of the expressions are equal.

1. 8 ⴢ4 ⫹6 (8 ⴢ4) ⫹6 8 ⫻(4 ⫹6)

2. 2 ⫹8 ⴢ4 ⫹6 (2 ⫹8) ⫻(4 ⫹6) 2 ⫹(8 ⴢ4) ⫹6

3. (10 ⫺4) ⫻2 10 ⫺(4 * 2) 10 ⫺4 * 2

4. 24 ⫼6 * 2 (24 ⫼6) ⫻2 24 ⫼(6 ⴢ2)

5. Make up a mathematical expression with at least three operations, and calculate the result. Then write your expression on a separate sheet of paper, and swap expressions with your partner. Evaluate your partner’s expression, and have your partner check your result.

6. Most modern calculators follow the order of operations.

a.Use your calculator to compute 2 ⫹3 ⫻4. What is the result? Did your calculator follow the order of operations?

(32)

Problem Set

E

Mr. Conte gets electricity and gas from the Smallville Power Company. The company uses this rule to calculate a customer’s bill:

Charge 12.05 cents per kilowatt-hour (kwh) of electricity used and 65.7 cents per therm of gas used.

1. This month, Mr. Conte’s household used 726 units of electricity and 51.7 units of gas. How much should his bill be? Give your answer in dollars and cents.

2. The computer system at Smallville Power crashed, so the clerks have to use calculators to determine the bills. The calculators do not use the order of operations. Instead, they evaluate the operations in the order they are entered. To figure out Mr. Conte’s bill, the clerk enters the expression below. Will the result be correct, too little, or too much? Explain.

726 ⫻12.05 ⫹51.7 ⫻65.7

3. Suppose the clerk enters the calculation below instead. Will the result be correct, too much, or too little? Explain.

(33)

&

A fraction bar is often used to indicate division. For example, these expressions both mean “divide 10 by 2” or “10 divided by 2”:

10 ⫼2 ᎏ1₂0ᎏ

Sometimes a fraction bar is used in more complicated expressions:

ᎏ2₄⫹_⫹ᎏ3₄

In expressions such as this, the bar not only means “divide,” it also acts as a grouping symbol—grouping the numbers and operations above the bar and grouping the numbers and operations below the bar. It is as if the expressions above and below the bar are inside parentheses.

The expression ᎏ2₄⫹_⫹ᎏ3₄ means “Add 2 ⫹3, then add 4 ⫹4, and divide the results.” So this expression means ᎏ5₈ᎏ, or 0.625.

This more complete order of operations includes the fraction bar:

• Evaluate expressions inside parentheses and above and below fraction bars.

• Do multiplications and divisions from left to right.

• Do additions and subtractions from left to right.

Problem Set

F

Find the value of each expression.

1. ᎏ2₁⫹_⫹ᎏ2₁ 2. 2⫹ᎏ₁_⫹2ᎏ₁

3. Your calculator does not have a fraction bar as a grouping symbol, so you have to be careful when entering expressions like ᎏ2₁⫹_⫹ᎏ2₁.

a.What result does your calculator give if you enter 2⫹2/1 ⫹1 (or 2 ⫹2 ⫼1 ⫹1)? Can you explain why you get that result?

b.What should you enter to evaluate ᎏ2₁⫹_⫹ᎏ2₁?

Share

Summarize

(34)

On Your Own Exercises

&

Practice

Apply

Use the first term and rule given to create a sequence. Tell whether your sequence is the only one possible. If it isn’t, give another sequence that fits the rule.

1. First term:40

Rule:Divide the preceding term by 2.

2. First term:

Rule:Draw a shape with one more side than the preceding shape.

3. Starting with a closed geometric figure with straight sides, you can use the rule below to create a design.

Find the midpoint (middle point) of each side of the figure. Connect the midpoints, in order, to make a new shape. (It will be the same shape as the original, but smaller.)

a.Copy this square. Follow the rule three times, each time starting with the figure you drew the previous time.

b.Copy this triangle. Follow the rule three times, each time starting with the figure you drew the previous time.

c.Draw your own shape, and follow the rule three times to make a design.

4. Measurement Luis is making a dessert that requires three eggs for each cup of flour.

a.How many eggs does he need for three cups of flour?

b.For a party, Luis made a large batch of his dessert using a dozen eggs. How much flour did he use?

(35)

5. Economics Althea uses this rule to figure out how much to charge for baby-sitting:

Charge $5 per hour for one child, plus $2 per hour for each additional child.

a.Last Saturday she watched the Newsome twins for 3 hours. How much money did she earn? Explain how you found your answer.

b.Mr. Foster hires Althea to watch his three children for 2 hours. How much will she charge?

c.Does Althea earn more for watching two children for 3 hours or three children for 2 hours?

d.Althea hopes to earn $25 next weekend to buy her sister a birthday present. Describe two ways she could earn at least $25 baby-sitting.

6. Measurement You can convert speeds from kilometers per hour to miles per hour by using this rule:

Multiply the number of kilometers per hour by 0.62.

a.Convert each kilometers-per-hour value in the table below to miles per hour.

Kilometers Miles per

per Hour Hour

50 60 70 80 90 100 110 120

b.As part of his job, Mr. Lopez does a lot of driving in Canada. He uses this rule to approximate the speed in miles per hour from a given speed in kilometers per hour:

Divide the number of kilometers per hour by 2 and add 10.

Use Mr. Lopez’s rule to convert each kilometers-per-hour value in the table to an approximate miles-per-hour value.

c.For which kilometers-per-hour values from the tables are the results for the two rules closest?

(36)

Evaluate each expression.

7. 3 ⫹3 ⴢ2 ⫹2 8. (3 ⫹3) ⫻(2 ⫹2)

9. (3 ⫹3) ⫹2 ⫼2 10. ᎏ7₁⫹₁6

⫺ ⫺

5 2

ⴢ2

ⴢ6

ᎏ

Tell whether each expression was evaluated correctly using the order of operations. If not, give the correct result.

11. 10 ⫻(1 ⫹5) ⫺7 ⫽8 12. 54 ⫺27 ⫼3 ⫽45

13. (16 ⫺4 ⴢ2) ⫺(14 ⫼2) ⫽5 14. 100 ⫺33 ⴢ2 ⫺(4 ⫹8) ⫽22

15. You can produce a sequence of numbers by applying this rule to each term:

If the number is even, get the next number by dividing by 2. If the number is odd, get the next number by multiplying by 3 and adding 1.

a.Use this rule to produce a sequence with 1 as the first term. Describe the pattern in the sequence.

b.Now use the rule to produce a sequence with 8 as the first term. Keep finding new terms until you see a pattern in the sequence. Describe what happens.

c.Use the rule to generate two more sequences. Keep finding new terms until you see a pattern.

d.Using your calculator and the rule, generate a sequence with 331 as its first term. Again, keep finding new terms until you see a pattern.

e.Describe what you discovered in Parts a–d.

&

Connect

Extend

(37)

16. Measurement One mile is about 1.6 kilometers.

a.Which is the greater distance, 1 mile or 1 kilometer?

b.Los Angeles and New York City are about 2,460 miles apart. How many kilometers apart are they?

c.If the speed limit on a road in Canada is 50 kilometers per hour, what is the speed limit in miles per hour?

d.In Investigation 2, you learned that lightning is 1 mile away for every 5 seconds you count between the lightning and the following clap of thunder. About how many seconds would it take you to hear the thunder if the lightning were 1 kilometer away?

17. Economics Calls on a particular pay telephone are charged according to this rule:

Charge 25 cents for the call, plus 10 cents for every 3 minutes, or part of 3 minutes, after the first 3 minutes.

a.How much would it cost you to make a 10-minute call?

b.If you have $1.15 in change, how long can you talk if you make a single call?

In Exercises 18–21, tell whether each rule is

• a convention, or

• a rule we can’t change

18. Nine times a number is equal to the difference between 10 times the number and the number.

19. In an expression involving only addition and multiplication and no parentheses, such as 2 ⴢ3 ⫹4 ⴢ5 ⫹6, do the multiplication first.

20. 4 ⫹3 ⫽7

21. Use a decimal point to separate the integer part of a number from the fractional part.

Explain the mathe-matical convention that tells you how to read a three-digit whole number like 645 and know that it is different from a number like 546.

own

In

y o u r

(38)

22. This computation gives the same result whether you compute correctly (using order of operations) or whether you do the com-putations from left to right:

16 ⫺6 ⴢ2 ⫺15 ⫼5

a.Find the value of the expression both ways, and show that you get the same result.

b.Find another computation that you should not evaluate from left to right, but that gives the correct result if you do.

Find each sum or difference without using a calculator.

23. 73.97 ⫺12.43 24. 4.642 ⫺2.1 25. 37.13 ⫺16.4

26. 194.5 ⫹73.94 27. 54.32 ⫹45.68 28. 73.7654 ⫺5

29. Lucita drew this grid:

a.What fraction of the squares contain dots?

b.What percent of the squares are striped?

c.What fraction of the squares have hearts?

d.Describe how Lucita could fill in the blank squares to create a grid in which 50% of the squares contain dots,ᎏ1₄ᎏhave hearts, and 25% have stripes.

e.Describe how Lucita could fill in the blank squares to create a grid in which ᎏ2

3ᎏof the squares have the same pattern.

30. What number is halfway between 1.8 and 3.2 on the number line?

Review

(39)

There is a pattern in the page numbers of a newspaper. The following activity will help you discover it.

Explore

Each person in your group should take one sheet from the same sec-tion of a newspaper.

Notice that your sheet contains four printed pages, two on each side. Write down the pair of page numbers on one side of the sheet and the pair of page numbers on the other side.

Compare the two page numbers on one side of your sheet with the two on the other side. Describe any patterns you notice.

Now compare your two pairs of numbers with those of the other students in your group. Describe any patterns that fit every pair of numbers.

Now work with your group to solve this problem:

A section of a newspaper has 48 pages (numbered from 1 to 48). What is the sum of all the page numbers in the section?

Explain how you found your answer. (Try to find your answer with-out adding all the numbers.)

Writing Rules

for Patterns

M A T E R I A L S

a section of

(40)

Investigation

L E S S O N 1 . 3 Writing Rules for Patterns 29

1

Finding Rules

A fun way to practice recognizing patterns and finding rules is to play a game called What’s My Rule?In this game, one player thinks of a rule about numbers, and the other players try to guess the rule.

Hannah, Jahmal, and Miguel were playing What’s My Rule? E X A M P L E

Now you will have a chance to play What’s My Rule?As you play, try to come up with some strategies for finding the rule quickly.

? !

Ok, I've got my rule. Give me a number, Jahmal. 2

2 gives 5. The rule is "add 3."

I know the rule.

Ok, Miguel, with your rule, what

would 11 give? 11 gives 14.

No! With my rule, 11

gives 23! Try again.

What does 4 give?

9

I've got it!

So what would 6 give with your rule,

Jahmal?

6 gives 13.

YES! What's

(41)

&

Problem Set

A

1. Play What’s My Rule?at least six times with your group. Take turns making up the rule. Do the following for each game you play:

• Write down the name of the person who made up the rule.

• Make a table showing the numbers the players guess and the results the rule gives for those numbers.

• After a player correctly guesses the rule, write it down.

2. Work with your group to create a list of strategies for playing What’s My Rule?

In What’s My Rule?you try to guess a rule that another student made up. Now you will play a rule-guessing game that doesn’t require a partner.

To play, imagine that a machine has taken some inputnumbers, applied a rule to each one, and given the resulting outputnumbers. Your job is to guess the rule the machine used.

Think Discuss

Here are the outputs one machine gave for the inputs 6, 3, 10, and 11. What rule did the machine use?

?

6

20

?

3

11

?

10

32

?

11

35 Rule

Input

(42)

&

Problem Set

B

Each table shows the outputs a particular machine produced for the given inputs. Find a rule the machine could have used. Check to make sure your rule works for all the inputs listed.

1. Input 3 5 8 4 1

Output 2 4 7 3 0

2. Input 4 7 10 3 0

Output 2 3.5 5 1.5 0

3. Input 10 6 3 4 0 100

Output 23 15 9 11 3 203

Share

Summarize

1.In one game of What’s My Rule?the first clue was “2 gives 4.” Write at least two rules that fit this clue.

2.The next clue in the same game was “3 gives 9.” Write at least two rules that fit this clue. Do any of the rules you wrote for the first clue work for this clue as well?

3.The third clue was “10 gives 100.” Give a rule that fits all three clues. How did you find the rule?

4. Describe some strategies you use to find a rule for an input/output table.

(43)

Investigation

M A T E R I A L S

toothpicks (optional)

2

Connecting Numbers

In Investigation 1, you found rules relating input and output numbers. Now you will write rules connecting pairs of numbers in a pattern of toothpicks. You will discover that finding a rule can help you figure out the number of toothpicks in any part of the pattern without building every step along the way.

Problem Set

C

Look at this sequence of toothpick figures.

In this sequence, there are 4 toothpicks in Term 1, 7 toothpicks in Term 2, and 10 toothpicks in Term 3.

1. How many toothpicks are in Term 4? If you continued the pattern, how many

toothpicks would you need to make Term 5? Term 6? Term 10?

2. It would take a long time to build or draw Term 100. Describe a shortcut for finding the number of toothpicks in Term 100.

3. Could you use your shortcut to find the number of toothpicks for anyterm of the sequence? Write a rule for finding the number of toothpicks needed for any term, and explain why it works. (Hint: It is not enough to show that your rule works in a few specific cases. Try to explain why it works based on how the terms are built.)

Term 1 Term 2 Term 3 Term 4

Term Toothpicks

1 4

2 7

(44)

L E S S O N 1 . 3 Writing Rules for Patterns 33 Ms. Washington asked her students to write reports about how they found their rules in Problem Set C.

Here is Rosita, Conor, and Marcus’ report. E X A M P L E

Term 1 Term 2 Term 3

Term 8

Report by Rosita, Conor, and Marcus

Term 1 is a square with 4 toothpicks. Three more toothpicks are added at each term to make another square. So, Term 2 has 4 plus one group of 3. Term 3 has 4 plus two groups of 3, and so on.

We checked our rule for Term 8: it should have 4 toothpicks plus 7 groups of 3. That’s 4 + 7 x 3 = 25 toothpicks altogether. When we drew the shape, it took 25 toothpicks.

We found two ways to write our rule.

One way is this:

To find the number of toothpicks for any term, start with 4 toothpicks, and add the number of the term minus 1, times 3.

A shorter way is this:

(45)

A second group found their rule a different way.

Here is Luke, Althea, and Miguel’s report. E X A M P L E

In Problem Set D, you will practice writing rules for sequences and explaining why your rules work. You may find it helpful to build the patterns with toothpicks.

Report by Luke, Althea, and Miguel

We made a table to show the number of toothpicks at each term. Term Toothpicks

1 4

2 7

3 10

4 13

The pattern in the second column is 4, 7, 10, 13, . . . . The numbers go up by 3 for each new term. It would take a long time to do this up to Term 100, so we looked for a connection between the term number and the number of toothpicks.

We guessed “add 3 to the term number,” but that worked for only the first row (1 + 3 = 4). It didn’t work for the second row (2 + 3 = 7).

Then we noticed that the rule “multiply the term number by 3 and add 1” worked for the first two rows. We checked, and it worked for the other rows too.

We drew diagrams to show why the rule works.

We can see that our rule will work for any term because each new term needs 3 new toothpicks, and there is always 1 extra toothpick.

(46)

&

Problem Set

D

Do Parts a–d for each sequence of shapes below.

a.Figure out how many toothpicks are in each of the first five terms. Record your results in a table.

b.Tell how many toothpicks are in Term 100.

c.Write a rule that connects the number of toothpicks to the term number. Use your rule to predict the

number of toothpicks in Terms 6 and 7, and check your predic-tions by building or drawing those terms. If your rule doesn’t work, revise it until it does.

d.Explain why your rule will work for any term number.

1.

2.

3.

Share

Summarize

Caroline asked, “How can I know that a rule for a toothpick sequence is correct unless I check it for every term?” Write a sentence or two answering Caroline’s question.

Term 1 Term 2 Term 3

Term 1 Term 2 Term 3

Term 3 Term 2

Term 1

M A T E R I A L S

toothpicks (optional)

Term Toothpicks 1

(47)

On Your Own Exercises

Find a rule that works for all the pairs in each input/output table. Use your rule to find the missing outputs.

1. Input 0 1 2 5 8 12

Output 4 5 6 9

2. Input 3 24 36 12 45 60

Output 1 8 12 4

3. Input 2 10 16 22 32 44

Output 0 4 7 10

4. Input 1 2 3 4 6 10

Output 9 19 29 39

5. Consider this sequence of figures:

a.Sketch the next two terms in the sequence.

b.Complete the table to show the number of toothpicks in each term.

Term 1 2 3 4 5

Toothpicks 6

c.Predict the number of toothpicks in Term 100.

Term 1 Term 2 Term 3

&

Practice

(48)

6. Conor and Althea both found a rule for predicting the number of toothpicks in each term of this sequence:

Conor’s rule was “Add 1 to the term number, and multiply what you get by 5.”

Althea’s rule was “Multiply the term number by 5, and add 5 more.”

a.Do both rules fit the three terms shown?

b.Use both rules to predict the number of toothpicks in Term 100. Do the rules give the same result?

c.Choose one of the rules, and explain why it is correct.

7. This sequence of figures is made from stars:

a.Figure out how many stars are in each of the first five terms, and record your results in a table.

b.How many stars are needed for Term 100?

c.Write a rule that connects the number of stars to the term number. Use your rule to predict the number of stars in Terms 6 and 7, and check your predictions by building or drawing those terms. If your rule doesn’t work, revise it until it does.

✮ ✮

Term 1 Term 2 Term 3 Term 4

(49)

8. This sequence of figures is made from flowers:

a.Figure out how many flowers are in each of the first five terms, and record your results in a table.

b.How many flowers are needed for Term 100?

c.Write a rule that connects the number of flowers to the term number. Use your rule to predict the number of flowers in Terms 6 and 7, and check your predictions by building or drawing those terms. If your rule doesn’t work, revise it until it does.

9. Not all input/output tables involve numbers. In this table, the inputs are words and the outputs are letters.

Input Alice Justin Kiran Marcus Jimmy Sarah

Output i s r r

a.Complete the last two columns of the table.

b.What would be the output for your name?

c.Describe a rule for finding the output letter for any input word.

d.Are there input words that have no outputs? Explain your answer.

10. In this input/output table, the inputs are numbers and the outputs are letters.

Input 1 2 3 4 5 6

Output O T T F F S

a.What would be the outputs for the inputs 7 and 8?

b.Describe a rule for finding the output letter for any input number.

❀ ❀

❀

❀ ❀

❀

Term 1 Term 2 Term 3

&

Connect

(50)

11. Rosita was trying to find a relationship between the number of letters in a word and the number of different ways the letters can be arranged. She considered only words in which all the letters are different.

Number of Number of

Letters Example Arrangements

1 A 1 (A)

2 OF 2 (OF, FO)

3 CAT 6 (CAT, CTA, ACT, ATC, TAC, TCA)

a.Continue Rosita’s table, finding the number of arrangements of four different letters. (You could use MATH as your example, since it has four different letters.)

b.Challenge Predict the number of arrangements of five different letters. Explain how you found your answer.

12. Life ScienceGeese often fly in a V-shaped pattern. Below is a sequence of such patterns.

a.Draw Terms 4 and 5. Use dots or other shapes to represent each bird.

b.How many geese are in Term 100?

c.Find a rule relating the number of geese to the term number.

d.Can such a V-pattern have exactly 41,390,132 geese? Explain.

Term 1 Term 2 Term 3

An anagram is a word or phrase formed by reordering the letters of another word or phrase. Anagrams were popular in 17th-century France. King Louis XIII even had a Royal Anagrammatist who worked full time creating anagrams to amuse Louis and his guests.

facts

Just

t h e

Flying in a V-shaped pattern is an efficient way to travel. As each goose flaps its wings, it creates an “uplift” for the birds behind it. When the lead goose tires, it moves out of position, allowing another bird to take its place.

facts

Just

(51)

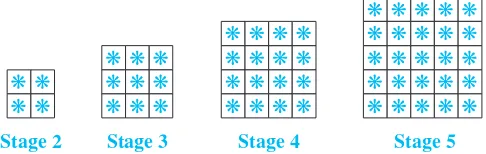
13. Consider this sequence of stars:

Could there be a term in this sequence with exactly 12,239 stars? Explain.

14. You can create a sequence of squares of increasing size by arranging identical copies of a small square. The first three terms in such a sequence are shown here.

a.Draw the next two terms in the sequence.

b.The numbers of small squares in the terms of this sequence are called square numbers.The first square number is 1, the second square number is 4, and so on. Give the third, fourth, and fifth square numbers.

c.Without drawing a picture, find the 25th square number.

d.Write a rule for finding the square number for any term in the sequence.

15. You can create a sequence of triangles of increasing size by arrang-ing identical copies of a sma