TURUNAN FUNGSI ALJABAR

(1)

1 | M A T E M A T I K A X I I P S S M A G O N Z A G A / T U R U N A N / 2 0 2 0 - 2 0 2 1

TURUNAN FUNGSI ALJABAR

INDIKATOR:

Menyelesaikan soal aplikasi turunan fungsi aljabar.

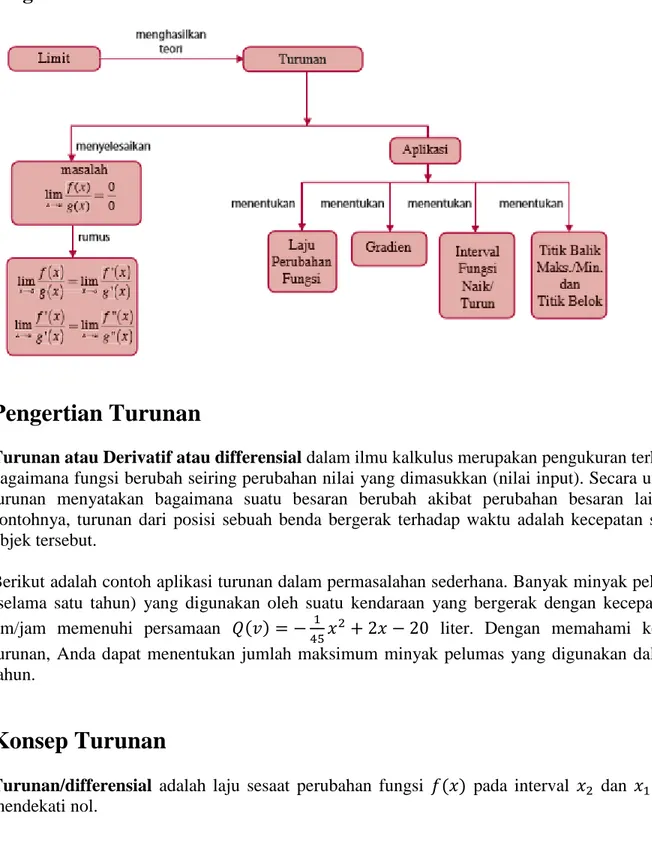
Diagram Alur

Pengertian Turunan

Turunan atau Derivatif atau differensial dalam ilmu kalkulus merupakan pengukuran terhadap bagaimana fungsi berubah seiring perubahan nilai yang dimasukkan (nilai input). Secara umum, turunan menyatakan bagaimana suatu besaran berubah akibat perubahan besaran lainnya;

contohnya, turunan dari posisi sebuah benda bergerak terhadap waktu adalah kecepatan sesaat objek tersebut.

Berikut adalah contoh aplikasi turunan dalam permasalahan sederhana. Banyak minyak pelumas (selama satu tahun) yang digunakan oleh suatu kendaraan yang bergerak dengan kecepatan 𝑣 km/jam memenuhi persamaan 𝑄(𝑣) = − ¹

45𝑥²+ 2𝑥 − 20 liter. Dengan memahami konsep turunan, Anda dapat menentukan jumlah maksimum minyak pelumas yang digunakan dalam 4 tahun.

Konsep Turunan

Turunan/differensial adalah laju sesaat perubahan fungsi 𝑓(𝑥) pada interval 𝑥₂ dan 𝑥₁ yang mendekati nol.

(2)

Laju rata-rata perubahan fungsi

Jika 𝑥₁ = 𝑎, 𝑥₂ = 𝑎 + 𝑏, dan 𝑎 adalah domain dari 𝑓(𝑥), maka:

∆𝑦

∆𝑥

=

^𝑓(𝑥²^{)−𝑓(𝑥}¹⁾

𝑥₂−𝑥₁

=

𝑓(𝑎+𝑏)−𝑓(𝑎) (𝑎+𝑏)−𝑎

∆𝑦

∆𝑥

=

𝑓(𝑥+𝑏)−𝑓(𝑥)

𝑏

Laju sesaat perubahan fungsi (turunan)

Adalah nilai limit dari laju rata-rata perubahan fungsi 𝑓(𝑥) pada interval 𝑥₂ dan 𝑥₁ mendekati nol.

Jika 𝑥₁ = 𝑎, 𝑥₂ = 𝑎 + 𝑏, dan 𝑎 adalah domain dari 𝑓(𝑥), dan nilai 𝑏 mendekati nol, maka

:

𝑑𝑦

𝑑𝑥

= lim

𝑏→0

∆𝑦

∆𝑥

= lim

𝑏→0

𝑓(𝑥₂)−𝑓(𝑥₁)

𝑥₂−𝑥₁

= lim

𝑏→0

𝑓(𝑎+𝑏)−𝑓(𝑎) (𝑎+𝑏)−𝑎

𝑑𝑦

𝑑𝑥

=

^{𝑑[𝑓(𝑥)]}

𝑑𝑥

= 𝑦

^′

= 𝑓′(𝑥) = lim

𝑏→0

𝑓(𝑥+𝑏)−𝑓(𝑥)

𝑏

Untuk memahami konsep dasar turunan, tinjaulah dua masalah berikut ini. Masalah pertama adalah masalah garis singgung, sedangkan masalah kedua adalah masalah kecepatan sesaat. Satu dari kedua masalah itu menyangkut geometrid an lainnya menyangkut mekanika, terlihat seperti tidak ada hubungan. Sebenarnya, kedua masalah itu merupakan kembaran yang identik.

Garis singgung

Amati gambar 1. Misalkan A adalah suatu titik tetap pada grafik 𝑦 = 𝑓(𝑥) dan B adalah sebuah titik berdekatan yang dapat dipindah-pindahkan sepanjang grafik 𝑦 = 𝑓(𝑥). Misalkan, titik A berkoordinat (𝑎, 𝑓(𝑎)) maka titik B berkoordinat (𝑎 +

∆𝑥, 𝑓(𝑎 + ∆𝑥)). Garis yang melalui A dan B mempunyai gradient (kemiringan) 𝑓(𝑎+∆𝑥)−𝑓(𝑎)

∆𝑥 . Garis ini memotong grafik di dua titik A dan B yang berbeda.

Jika titik B bergerak sepanjang kurva 𝑦 = 𝑓(𝑥) mendekati titik A (amati gambar 2) maka nilai ∆𝑥 mendekati nol maka titik b akan berimpit dengan titik A. akibatnya, garis singgung (jika tidak tegak lurus pada sumbu X) adalah garis yang melalui 𝐴(𝑎, 𝑓(𝑎)) dengan gradient

𝒎

_𝑨𝑩

= 𝐥𝐢𝐦

∆𝒙→𝟎

𝒇(𝒂+∆𝒙)−𝒇(𝒂)

∆𝒙 …………(1)

Mengapa persamaan garis singgung tidak boleh tegak lurus sumbu X?

Gambar 1

Gambar 2

(3)

3 | M A T E M A T I K A X I I P S S M A G O N Z A G A / T U R U N A N / 2 0 2 0 - 2 0 2 1 Contoh 1:

Tentukan gradient garis singgung pada kurva a. 𝑓(𝑥) = 𝑥² di titik dengan absis 2

b. 𝑓(𝑥) = 𝑥³ di titik dengan absis 2 Penyelesaian:

a.

𝑚 = lim

∆𝑥→0

𝑓(2+∆𝑥)−𝑓(2)

∆𝑥

= lim

∆𝑥→0

(2+∆𝑥)²−2²

∆𝑥

= lim

∆𝑥→0

4+4∆𝑥+(∆𝑥)²−4

∆𝑥

= lim

∆𝑥→0

4∆𝑥+(∆𝑥)²

∆𝑥

= lim

∆𝑥→0

∆𝑥(4+∆𝑥)

∆𝑥

= lim

∆𝑥→0

(4 + ∆𝑥) = 4

Jadi, gradient garis singgung kurva 𝑓(𝑥) = 𝑥² di titik dengan absis 2 adalah

𝑚 = 4.

b.

𝑚 = lim

∆𝑥→0

𝑓(3+∆𝑥)−𝑓(3)

∆𝑥

= lim

∆𝑥→0

(3+∆𝑥)³−3³

∆𝑥

= lim

∆𝑥→0

3³+3∙3²∆𝑥+3∙3(∆𝑥)²+(∆𝑥)³−3³

∆𝑥

= lim

∆𝑥→0

27∆𝑥+9(∆𝑥)²+(∆𝑥)³

∆𝑥

= lim

∆𝑥→0

∆𝑥(27+9∆𝑥+(∆𝑥)²)

∆𝑥

= lim

∆𝑥→0

(27 + 9∆𝑥 + (∆𝑥)

²

) = 27

Jadi, gradient garis singgung kurva 𝑓(𝑥) = 𝑥³ di titik dengan absis 2 adalah

𝑚 = 27.

Kecepatan sesaat

Misalkan, fungsi 𝑓(𝑥) = 15𝑥²+ 20𝑥 menyatakan jarak (dalam km) yang ditempuh sebuah mobil setelah 𝑥 jam perjalanan selama selang waktu 0 ≤ 𝑥 ≤ 2. Kecepatan rata-rata mobil itu selama perjalanannya adalah:

∆𝑓

∆𝑥

=

^{𝑓(2)−𝑓(0)}

2−0

=

^[15(2)²+20(2)]−[15(0)²+20(0)]

2

= 50 𝑘𝑚/𝑗𝑎𝑚

Sekarang, coba amati kecepatan rata-rata mobil dalam selang 𝑐 ≤ 𝑥 ≤ 𝑑 seperti pada tabel di samping. Nilai ^∆𝑓

∆𝑥 mendekati ke bilangan 50 jika lebar selang waktunya dibuat semakin mengecil (∆𝑥 mendekati nol). Nilai 50 tersebut disebut kecepatan (sesaat) pada 𝑥 = 1.

Sekarang, dapat dipahami bahwa kecepatan sesaat diperoleh melalui proses limit terhadap kecepatan rata-rata dengan cara membuat nilai-nilai 𝑥 mendekati ke-1 atau ∆𝑥 sekat ke nol. Dalam lambang matematika kecepatan sesaat pada 𝑥 = 1 ditulis:

∆𝑥→0

lim

∆𝑓

∆𝑥 =

lim

∆𝑥→0

𝑓(1+∆𝑥)−𝑓(1)

∆𝑥

=

lim

∆𝑥→0

[15(1+∆𝑥)²+20(1+∆𝑥)]−[15(1)²+20(1)]

∆𝑥

=

lim

∆𝑥→0

[15(1+2∆𝑥+(∆𝑥)²)+20+20∆𝑥]−[15+20]

∆𝑥

(4)

=

lim

∆𝑥→0

50∆𝑥+(∆𝑥)²

∆𝑥

= lim

∆𝑥→0

∆𝑥(50+∆𝑥)

∆𝑥

= 50

Jadi, kecepatan mobil pada saat 𝑥 = 1 adalah 50 km/jam.

Uraian tersebut menggambarkan definisi kecepatan sesaat 𝑣 di 𝑥 = 𝑎, yaitu:

𝒗 = 𝐥𝐢𝐦

∆𝒙→𝟎

𝒗

_{𝒓𝒂𝒕𝒂−𝒓𝒂𝒕𝒂}

= 𝐥𝐢𝐦

∆𝒙→𝟎

𝒇(𝒂+∆𝒙)−𝒇(𝒂)

∆𝒙

……….(2)

Contoh 2:

Sebuah benda bergerak sepanjang garis lurus sehingga kedudukannya setelah 𝑥 detik memenuhi persamaan 𝑓(𝑥) = 6𝑥³+ 𝑥², dengan 𝑓(𝑥) dinyatakan dalam meter.

a. Tentukan kecepatan rata-rata benda dalam selang waktu 2 ≤ 𝑥 ≤ 3.

b. Berapa kecepatan sesaat benda pada 𝑥 = 2 detik?

Penyelesaian:

a. ^∆𝑓

∆𝑥

=

^{𝑓(3)−𝑓(2)}

3−2

=

^[⁶⁽³⁾³⁺⁽³⁾²^]−[⁶⁽²⁾³⁺⁽²⁾²^]

1

= 119

Jadi, kecepatan rata-ratanya adalah 119 m/s b.

lim

∆𝑥→0

𝑓(2+∆𝑥)−𝑓(2)

∆𝑥

= lim

∆𝑥→0

[6(2+∆𝑥)³+(2+∆𝑥)²]−[6(2)³+(2)²]

∆𝑥

= lim

∆𝑥→0

[6((2)³+3∙(2)²∆𝑥+3∙2(∆𝑥)²+(∆𝑥)³)+(4+4∆𝑥+(∆𝑥)²)]−52

∆𝑥

= lim

∆𝑥→0

[6(8+12∆𝑥+6(∆𝑥)²+(∆𝑥)³)+4+4∆𝑥+(∆𝑥)²]−52

∆𝑥

= lim

∆𝑥→0

[48+72∆𝑥+36(∆𝑥)²+6(∆𝑥)³+4+4∆𝑥+(∆𝑥)²]−52

∆𝑥

= lim

∆𝑥→0

[6(∆𝑥)³+37(∆𝑥)²+76∆𝑥]

∆𝑥

= lim

∆𝑥→0

∆𝑥[6(∆𝑥)²+37∆𝑥+76]

∆𝑥

=

lim

∆𝑥→0 [

6(∆𝑥)

²

+ 37∆𝑥 + 76

]

= 76

Jadi, kecepatan pada saat 𝑥 = 2 atau pada detik kedua adalah 76 m/s.

LATIHAN 1

1. Gunakan konsep limit untuk menyelesaikan soal-soal berikut.

a. Jika 𝑓(𝑥) = 𝑥²+ 3𝑥, tentukan 𝑓′(𝑥).

b. Jika 𝑓(𝑥) = 𝑥²− 2𝑥 + 6, tentukan 𝑓′(𝑥).

c. Jika 𝑓(𝑥) = √2𝑥, tentukan 𝑓′(𝑥).

d. Jika 𝑓(𝑥) = 1 +¹

𝑥, tentukan 𝑓′(𝑥).

2. Gunakan konsep limit untuk menyelesaikan soal-soal berikut.

a. Jika 𝑓(𝑥) = 4 − 𝑥², tentukan 𝑓′(−3).

b. Jika 𝑓(𝑥) = 6𝑥 − 2𝑥³, tentukan 𝑓′(2).

c. Jika 𝑓(𝑥) = ^𝑥

𝑥−1, tentukan 𝑓′(5).

(5)

5 | M A T E M A T I K A X I I P S S M A G O N Z A G A / T U R U N A N / 2 0 2 0 - 2 0 2 1 d. Jika 𝑓(𝑥) = 𝑥²+ ^𝑥

𝑥+1, tentukan 𝑓′(1).

3. Dengan menggunakan konsep limit, tentukan gradient garis singgung pada kurva berikut ini.

a. 𝑓(𝑥) = 5𝑥² di titik dengan absis 𝑥 = 2

b. 𝑓(𝑥) = 𝑥² + 𝑥 − 5 di titik dengan absis 𝑥 = −1 c. 𝑓(𝑥) = ^𝑥

𝑥² di titik dengan absis 𝑥 = −2 d. 𝑓(𝑥) = √𝑥 + 𝑥 di titik dengan absis 𝑥 = 4 Gunakan konsep limit untuk soal-soal berikut.

4. Sebuah benda bergerak, kedudukannya setelah 𝑡 sekon memenuhi persamaan 𝑆(𝑡) = 3𝑡²+ 4𝑡.

a. Berapa kecepatan rata-rata pada selang waktu 𝑡 = 3 sekon dan 𝑡 = 5 sekon?

b. Berapa kecepatan sesaat pada waktu 𝑡 = 2 sekon?

5. Sebuah perusahaan mendapatkan keuntungan setelah 𝑡 tahun sebesar 2.500.000𝑡²− 5.000𝑡.

a. Berapa besar keuntungan antara 𝑡 = 3 tahun dan 𝑡 = 4 tahun?

b. Berapa laju keuntungan sesaat pada 𝑡 = 2 tahun?

MENENTUKAN TURUNAN FUNGSI ALJABAR

RUMUS:

- Jika 𝑦 = 𝑎𝑥^𝑛 maka 𝑦^′= 𝑎𝑛𝑥^𝑛−1 dengan 𝑎 konstanta, 𝑛 ∈ 𝑅 (rumus dasar) - Rumus turunan fungsi aljabar:

 Jika 𝑦 = 𝑢 ∙ 𝑣 maka 𝑦^′ = 𝑢^′∙ 𝑣 + 𝑢 ∙ 𝑣′ (rumus perkalian)

 Jika 𝑦 =^𝑢

𝑣 maka

𝑦

^′

=

^𝑢^′^{∙𝑣−𝑢∙𝑣′}

𝑣² (rumus pecahan)

 Jika 𝑦 = 𝑢^𝑛 maka 𝑦^′= 𝑛𝑢^𝑛−1∙ 𝑢′ (rumus aturan rantai/rumus komposisi)

Contoh 1:

Carilah 𝑓′(𝑥) jika diketahui fungsi berikut.

a. 𝑓(𝑥) = √𝑥

³ ²

c. 𝑓(𝑥) = 4𝑥

³

b. 𝑓(𝑥) =

⁵

𝑥²

d. 𝑓(𝑥) =

^2𝑥²

3√𝑥

Penyelesaian:

a. 𝑓(𝑥) = √𝑥

³ ²

= 𝑥

²³

𝑓

^′

(𝑥) =

²

3

𝑥

²³⁻¹

=

²

3

𝑥

⁻¹³

=

²

3𝑥 1 3

=

²

3 √𝑥³

b. 𝑓(𝑥) =

⁵

𝑥²

= 5𝑥

⁻²

𝑓

^′

(𝑥) = 5(−2)𝑥

⁻²⁻¹

= −10𝑥

⁻³

=

⁻¹⁰

𝑥³

c. 𝑓(𝑥) = 4𝑥

³

(6)

𝑓

^′

(𝑥) = 4 ∙ 3𝑥

³⁻¹

= 12𝑥

²

d. 𝑓(𝑥) =

^2𝑥²

3√𝑥

=

²

3

𝑥

²⁻¹²

=

²

3

𝑥

³²

𝑓′(𝑥) =

²

3

∙

³

2

𝑥

¹²

= 𝑥

¹²

= √𝑥

a. b.

c. d.

Contoh 2:

Carilah 𝑓′(𝑥) jika diketahui:

a. 𝑓(𝑥) = 3𝑥² + 7𝑥 c. 𝑓(𝑥) = 4𝑥³− 5𝑥 + ³

𝑥²

b. 𝑓(𝑥) = −𝑥³− 8𝑥² d. 𝑓(𝑥) = 6𝑥 − √𝑥³ ²+ 3 Penyelesaian:

a. 𝑓(𝑥) = 3𝑥² + 7𝑥

𝑓^′(𝑥) = 3 ∙ 2𝑥²⁻¹+ 7 ∙ 1𝑥¹⁻¹ 𝑓^′(𝑥) = 6𝑥 + 7

b. 𝑓(𝑥) = −𝑥³− 8𝑥²

𝑓^′(𝑥) = −3𝑥³⁻¹− 8 ∙ 2𝑥²⁻¹

(7)

7 | M A T E M A T I K A X I I P S S M A G O N Z A G A / T U R U N A N / 2 0 2 0 - 2 0 2 1 𝑓^′(𝑥) = −3𝑥²− 16𝑥

c. 𝑓(𝑥) = 4𝑥³ − 5𝑥 + ³

𝑥² = 4𝑥³ − 5𝑥 + 3𝑥⁻² 𝑓^′(𝑥) = 4 ∙ 3𝑥³⁻¹− 5 ∙ 1𝑥¹⁻¹+ 3 ∙ (−2)𝑥⁻²⁻¹ 𝑓^′(𝑥) = 12𝑥²− 5 − 6𝑥⁻³

d. 𝑓(𝑥) = 6𝑥 − √𝑥³ ²+ 3 = 6𝑥 − 𝑥

2 3+ 3 𝑓^′(𝑥) = 6 ∙ 1𝑥¹⁻¹−²

3𝑥

2 3−1

+ 0 𝑓^′(𝑥) = 6 −²

3𝑥⁻

1 3

a. b.

c. d.

(8)

Carilah ^𝑑𝑦

𝑑𝑥 jika diketahui:

a. 𝑦 = (𝑥²− 7)(2𝑥 − 3) b. 𝑦 = (2𝑥³− 4𝑥²)(𝑥⁵+ 3𝑥²) Penyelesaian:

a. 𝑦 = (𝑥²− 7)(2𝑥 − 3) 𝑢 = 𝑥²− 7 → 𝑢^′= 2𝑥 𝑣 = 2𝑥 − 3 → 𝑣^′ = 2 Jadi jika 𝑦 = 𝑢 ∙ 𝑣, maka ^𝑑𝑦

𝑑𝑥 = 𝑦^′= 𝑢^′∙ 𝑣 + 𝑢 ∙ 𝑣′

= 2𝑥(2𝑥 − 3 ) + (𝑥²− 7)2

= 4𝑥²− 6𝑥 + 2𝑥² + 14

= 6𝑥²− 6𝑥 + 14 b. 𝑦 = (2𝑥³− 4𝑥²)(𝑥⁵+ 3𝑥²)

𝑢 = 2𝑥³− 4𝑥² → 𝑢^′= 6𝑥²− 8𝑥 𝑣 = 𝑥⁵ + 3𝑥² → 𝑣^′ = 5𝑥⁴+ 6𝑥 Jadi, ^𝑑𝑦

𝑑𝑥 = 𝑦^′= 𝑢^′∙ 𝑣 + 𝑢 ∙ 𝑣′

= (6𝑥²− 8𝑥 )(𝑥⁵ + 3𝑥²) + (2𝑥³ − 4𝑥²)(5𝑥⁴+ 6𝑥 )

= (6𝑥⁷− 8𝑥⁶+ 18𝑥⁴ − 24𝑥³) + (10𝑥⁷ − 20𝑥⁶ + 12𝑥⁴− 24𝑥³)

= 16𝑥⁷− 28𝑥⁶+ 30𝑥⁴− 48𝑥³

a. b.

(9)

Carilah turunan pertama dari:

a.

𝑦 =

^3𝑥−2

5𝑥+6 c. 𝑦 = (𝑥³ − 3𝑥)² b.

𝑦 =

^𝑥²^+2𝑥

𝑥−3 d. 𝑦 = (2 + 5𝑥²)⁵ Penyelesaian:

a.

𝑦 =

^3𝑥−2

5𝑥+6

𝑢 = 3𝑥 − 2 → 𝑢^′= 3 𝑣 = 5𝑥 + 6 → 𝑣^′ = 5 Jika =^𝑢

𝑣 , maka

𝑦

^′

=

^𝑢^′^{∙𝑣−𝑢∙𝑣}^′

𝑣²

=

3(5𝑥+6)−(3𝑥−2)5 (5𝑥+6)²

=

15𝑥+18−15𝑥+10 (5𝑥+6)²

=

²⁸

(5𝑥+6)²

b.

𝑦 =

^𝑥²^+2𝑥

𝑥−3

𝑢 = 𝑥²+ 2𝑥 → 𝑢^′ = 2𝑥 + 2 𝑣 = 𝑥 − 3 → 𝑣^′ = 1

Jadi,

𝑦

^′

=

^𝑢^′^{∙𝑣−𝑢∙𝑣}^′

𝑣²

=

(2𝑥+2)(𝑥−3)−(𝑥²+2𝑥)∙1 (𝑥−3)²

=

^2𝑥²^{−6𝑥+2𝑥−6−𝑥}²^−2𝑥

(𝑥−3)²

=

^𝑥²^−6𝑥−6

(𝑥−3)²

c. 𝑦 = (𝑥³− 3𝑥)²

Misal: 𝑢 = 𝑥³− 3𝑥 → 𝑢^′= 3𝑥²− 3 Jika 𝑦 = 𝑢^𝑛, maka 𝑦^′ = 𝑛 ∙ 𝑢^𝑛−1∙ 𝑢′

= 2(𝑥³− 3𝑥)²⁻¹∙ (3𝑥²− 3)

= 2(𝑥³− 3𝑥)(3𝑥²− 3)

= 2(3𝑥⁵− 3𝑥³− 9𝑥³+ 9𝑥)

= 2(3𝑥⁵− 12𝑥³+ 9𝑥)

= 6𝑥⁵ − 24𝑥³+ 18𝑥 d. 𝑦 = (2 + 5𝑥²)⁵

Misal: 𝑢 = 2 + 5𝑥² → 𝑢^′= 10𝑥 Jika 𝑦 = 𝑢^𝑛, maka 𝑦^′ = 𝑛 ∙ 𝑢^𝑛−1∙ 𝑢′

= 5(2 + 5𝑥²)⁵⁻¹∙ 10𝑥

= 50𝑥(2 + 5𝑥²)⁴

(10)

a. b.

c. d.

(11)

Latihan 2

1. Dengan menggunakan rumus turunan, tentuan turunan dari masing-masing fungsi berikut.

a. 𝑓(𝑥) = (2𝑥 + 1)(3𝑥 − 2) b. 𝑓(𝑥) = 4𝑥

²

+ 𝑥

2

3

− √𝑥

c. 𝑓(𝑥) = 4√𝑥 + 2𝑥√𝑥 +

³₈

𝑥

²

√𝑥 d. 𝑓(𝑥) = 𝑥

²

√𝑥 −

⁴

√𝑥

e. 𝑓(𝑥) =

²

𝑥√𝑥

−

³

8𝑥²

√𝑥 f. 𝑓(𝑥) =

^𝑥²^−2𝑥+1

√𝑥

g. 𝑦 = (𝑥

²

+ 2𝑥)(2𝑥

³

+ 𝑥

²

+ 1) h. 𝑦 = (𝑥

²

+ 2)(𝑥

²

− 2)

i. 𝑦 = (𝑥

²

+ 4)(√𝑥 − 4)(√𝑥 + 4) j. 𝑓(𝑥) =

^(𝑥+2)²

√𝑥

k. 𝑓(𝑥) = √

^3𝑥+2

2𝑥+1

l. 𝑓(𝑥) = (𝑥

²

+ 3)

⁴³

m. 𝑓(𝑥) = √𝑥

²

− 5𝑥

n. 𝑓(𝑥) = (2𝑥 − 5)√𝑥

²

− 5𝑥 o. 𝑓(𝑥) = (𝑥

²

− 1)√𝑥

²

− 4𝑥 + 3

2. a. Jika

𝑦 =

^2𝑥²^+3𝑥−5

𝑥−1

,

maka ^𝑑𝑦

𝑑𝑥

= ⋯

b. Jika

𝑦 = 𝑎𝑥

³

+ 𝑏𝑥

²

+ 2

dan ^𝑑𝑦

𝑑𝑥

= 12𝑥

²

+ 𝑥

maka nilai 𝑎 + 𝑏 = ⋯ c. Jika

𝑦 = (4𝑥 + 5)

³²

,

maka^𝑑𝑦

𝑑𝑥

= ⋯

d. Jika

𝑦 = (6 − 𝑥

²

)

³

,

maka^𝑑𝑦

𝑑𝑥

= ⋯

e. Jika

𝑓(𝑥) =

^𝑥²^−3𝑥

3√𝑥

,

maka 𝑓′(8) = ⋯.

f. Jika

𝑔(𝑥) = (2𝑥 +

¹

2𝑥

)

², maka 𝑔′(1) = ⋯.

g. Jika

𝑓(𝑥) = 2𝑥

³

√8 − 𝑥

²

,

maka tentukan nilai 𝑓′(2) h. Jika 𝑓(𝑥) = 4 √³

(3𝑥

²

− 4)

²

,

maka tentukan nilai 𝑓′(2)

(12)

TERAPAN TURUNAN

- Menentukan gradient garis singgung dan persamaan garis singgung kurva

Jika 𝑦 = 𝑓(𝑥) maka gradient garis singgung kurva tersebut di 𝑥 = 𝑎 adalah 𝑚 = 𝑓′(𝑎) Persamaan garis singgung dari kurva 𝑦 = 𝑓(𝑥) melalui (𝑥₁, 𝑦₁) adalah:

(𝑦 − 𝑦₁) = 𝑚(𝑥 − 𝑥₁) atau 𝑦 = 𝑚𝑥 + 𝑐 - Menentukan fungsi naik dan fungsi turun

Fungsi 𝑓(𝑥) dikatakan naik jika 𝑓^′(𝑥) > 0, dan fungsi 𝑓(𝑥) dikatakan turun jika 𝑓^′(𝑥) < 0.

- Menentukan titik stasioner serta jenisnya

Fungsi 𝑓(𝑥) dikatakan stasioner jika 𝑓^′(𝑥) = 0 Jenis titik stasioner ada 3 yaitu:

 Titik balik maksimum (naik-turun)

 Titik balik minimum (turun-naik)

 Titik belok positif (naik-naik)

 Titik belok negatif. (turun-turun)

(13)

13 | M A T E M A T I K A X I I P S S M A G O N Z A G A / T U R U N A N / 2 0 2 0 - 2 0 2 1 - Turunan kedua

Turunan kedua dari suatu fungsi 𝑦 = 𝑓(𝑥) adalah turunan dari turunan pertama dan diberi lambang:

𝑦^′′ = 𝑓^′′(𝑥) =^𝑑²^𝑦

𝑑𝑥² = ^𝑑²^𝑓

𝑑𝑥²

Menentukan jenis titik stasioner dengan turunan kedua

 Titik balik maksimum, syarat 𝑓^′(𝑥) = 0 dan 𝑓^′′(𝑥) < 0

 Titik balik minimum, syarat 𝑓^′(𝑥) = 0 dan 𝑓^′′(𝑥) > 0

- Menentukan nilai maksimum dan nilai minimum pada interval tertutup 𝒂 ≤ 𝒙 ≤ 𝒃 Langkah-langkah:

1. Cari nilai stasioner, terlebih dahulu cari nilai 𝑥 pembuat nol

2. Cari nilai untuk 𝑥 pada ujung-ujung interval, yaitu nilai 𝑓(𝑎) dan 𝑓(𝑏) 3. Nilai terkecil yang didapat dari langkah 1 dan 2 sebagai nilai minimum 4. Nilai terbesar yang didapat dari langkah 1 dan 2 sebagai nilai maksimum Contoh 5:

Tentukan persamaan garis singgung kurva:

a. 𝑦 = 𝑥³− 3𝑥 + 4 pada titik (2, 6)

b. 𝑦 = √𝑥 − 3 yang tegak lurus garis 6𝑥 + 3𝑦 − 4 = 0 Penyelesaian:

(14)

14 | M A T E M A T I K A X I I P S S M A G O N Z A G A / T U R U N A N / 2 0 2 0 - 2 0 2 1 a. 𝑦 = 𝑥³ − 3𝑥 + 4

𝑦^′= 𝑓′(𝑥) = 3𝑥²− 3

Gradient garis singgung kurva di titik (2, 6) adalah 𝑚_𝑔𝑠= 𝑓^′(2) = 3(2)²− 3 = 12 − 3 = 9

Jadi, persamaan garis singgung kurva di titik (2, 6) adalah 𝑦 − 6 = 9(𝑥 − 2)

𝑦 = 9𝑥 − 12 b. 𝑦 = √𝑥 − 3 = (𝑥 − 3)¹²

Jika (𝑥₁, 𝑦₁) titik singgung pada kurva, maka kemiringan garis singgung di titik itu adalah:

𝑚

₁

= 𝑦

^′

=

¹

2√𝑥−3

Garis 6𝑥 + 3𝑦 − 4 = 0 dapat dituliskan dengan

𝑦 = −2𝑥 +

⁴

3, sehingga kemiringan garis ini adalah 𝑚₂ = −2. Dua garis saling tegak lurus jika:

𝑚₁∙ 𝑚₂ = −1 ↔ 𝑚₁(−2) = −1 ↔ 𝑚₁ =¹

2

Maka,

𝑚

₁

= 𝑦

^′

=

¹

2√𝑥−3

↔

¹

2

=

¹

2√𝑥−3

↔

¹

𝑥−3

= 1

↔ 𝑥 − 3 = 1

↔ 𝑥 = 4

Substitusikan 𝑥 = 4 ke dalam persamaan kurva 𝑦 = √𝑥 − 3 sehingga didapat 𝑦 = √4 − 3 = 1. Jadi, koordinat titik singgung adalah (4, 1), dan persamaan garis

singgungnya adalah:

(𝑦 − 𝑦₁) = 𝑚(𝑥 − 𝑥₁) (𝑦 − 1) =¹

2(𝑥 − 4) 𝑦 =¹

2𝑥 − 1 a

.

b .

(15)

Diketahui 𝑓(𝑥) =¹

3𝑥³− 2𝑥² − 5𝑥 + 10. Tentukan interval agar:

a. Kurva 𝑦 = 𝑓(𝑥) naik b. Kurva 𝑦 = 𝑓(𝑥) turun.

Penyelesaian:

𝑓(𝑥) =¹

3𝑥³− 2𝑥²− 5𝑥 + 10 𝑓^′(𝑥) = 𝑥² − 4𝑥 − 5

a. Syarat fungsi naik:

𝑓^′(𝑥) > 0 𝑥² − 4𝑥 − 5 > 0 (𝑥 + 1)(𝑥 − 5) > 0 𝑥 + 1 = 0 atau 𝑥 − 5 = 0 𝑥 = −1 atau 𝑥 = 5

Jadi, interval 𝑥 agar kurva naik adalah 𝑥 < −1 atau 𝑥 > 5.

b. Syarat fungsi turun:

𝑓^′(𝑥) < 0

Jadi, interval 𝑥 agar kurva naik adalah −1 < 𝑥 < 5.

+ – +

-1 5

+ – +

-1 5

(16)

Tentukan titik stasioner dan jenisnya dari fungsi 𝑓(𝑥) = 𝑥²+ 2𝑥 Penyelesaian:

Syarat stasioner, 𝑓′(𝑥) = 0 𝑓^′(𝑥) = 2𝑥 + 2 = 0

2𝑥 = −2 → 𝑥 = −1

Nilai stasioner, 𝑓(−1) = (−1)²+ 2(−1) = 1 − 2 = −1 Sehingga diperoleh titik stasioner (−1, −1)

Untuk menentukan jenisnya, perhatikan garis bilangan berikut.

Cek gradient di sebelah kiri 𝑥 = −1, misalkan 𝑥 = −2 substitusi ke 𝑓^′(𝑥) = 2𝑥 + 2

→ 𝑓^′(−2) = 2(−2) + 2 = −2 (karena negatif maka grafik di sebelah kiri turun)

Cek gradient di sebelah kanan 𝑥 = −1, misalkan 𝑥 = 0 → 𝑓^′(0) = 2(0) + 2 = 2 (karena positif maka grafik di kanan naik).

Jadi, titik (−1, −1) adalah titik balik minimum.

Atau dengan cara turunan kedua:

Syarat stasioner, 𝑓′(𝑥) = 0 𝑓^′(𝑥) = 2𝑥 + 2 = 0

2𝑥 = −2 → 𝑥 = −1

Nilai stasioner, 𝑓(−1) = (−1)²+ 2(−1) = 1 − 2 = −1 Sehingga diperoleh titik stasioner (−1, −1)

Cek dengan turunan kedua

𝑓^′(𝑥) = 2𝑥 + 2 → 𝑓′′(𝑥) = 2 > 0

Karena hasil turunan keduanya positif, maka jenis titik baliknya adalah minimum.

(17)

Tentukan titik stasioner dan jenisnya dari fungsi 𝑓(𝑥) =¹

3𝑥³− 2𝑥² − 5𝑥 + 10.

Penyelesaian:

Syarat stasioner, 𝑓′(𝑥) = 0 𝑓^′(𝑥) = 𝑥² − 4𝑥 − 5 = 0 (𝑥 + 1)(𝑥 − 5) = 0 𝑥 + 1 = 0 atau 𝑥 − 5 = 0 𝑥 = −1 atau 𝑥 = 5

Untuk x = −1, 𝑓(−1) =¹

3(−1)³− 2(−1)²− 5(−1) + 10 = −¹

3− 2 + 5 + 10 = 12²

3 Untuk x = 5, 𝑓(5) =¹

3(5)³− 2(5)²− 5(5) + 10 = 41²

3− 50 − 25 + 10 = −23¹

3

Cek garis bilangan,

Titik balik maksimum (−1, 12²

3), dan nilai maksimum 12²

3 Titik balik maksimum (5, −23¹

3), dan nilai minimum −23¹

3

Cek dengan cara turunan kedua, Syarat stasioner, 𝑓′(𝑥) = 0 𝑓^′(𝑥) = 𝑥² − 4𝑥 − 5 = 0 (𝑥 + 1)(𝑥 − 5) = 0 𝑥 + 1 = 0 atau 𝑥 − 5 = 0 𝑥 = −1 atau 𝑥 = 5

Turunan pertama: 𝑓^′(𝑥) = 𝑥² − 4𝑥 − 5 Turunan kedua: 𝑓^′′(𝑥) = 2𝑥 − 4

Untuk 𝑥 = −1, 𝑓^′′(−1) = 2(−1) − 4 = −6 → karena𝑓^′′(−1) < 0, maka x = −1 pembuat maksimum. Nilai maksimummya 𝑓(−1) =¹

3(−1)³− 2(−1)²− 5(−1) + 10 = 12²

3

Titik balik maksimum (−1, 12²

3), dan nilai maksimum 12²

3

Untuk 𝑥 = 5, 𝑓^′′(5) = 2(5) − 4 = 6 → karena𝑓^′′(5) > 0, maka 𝑥 = 5 pembuat minimum.

Titik balik minimum (5, −23¹

3) dan nilai minimumnya −23¹

3.

(18)

Tentukan nilai maksimum dan minimum untuk fungsi 𝑓(𝑥) = 6𝑥² − 𝑥³ pada interval

−1 ≤ 𝑥 ≤ 3.

Penyelesaian:

Fungsi 𝑓(𝑥) = 6𝑥²− 𝑥³ pada interval −1 < 𝑥 < 3 Nilai fungsi pada batas interval:

𝑓(−1) = 6(−1)²− (−1)³ = 6 + 1 = 7 𝑓(3) = 6(3)²− (3)³ = 54 − 27 = 27 Nilai stasioner fungsi:

𝑓^′(𝑥) = 12𝑥 − 3𝑥² → 12𝑥 − 3𝑥² = 0 3𝑥(4 − 𝑥) = 0 𝑥 = 0 atau 𝑥 = 4

𝑥 = 0 di dalam interval −1 < 𝑥 < 3, maka dicari nilai fungsinya.

𝑓(0) = 6(0)²− (0)³ = 0

𝑥 = 4 di luar interval −1 < 𝑥 < 3, maka tidak perlu dicari nilai fungsinya.

Jadi, nilai maksimum adalah 27 dan nilai minimum adalah 0.

(19)

Sebuah bola dilempar vertikal ke atas. Dalam waktu 𝑡 detik ketinggian yang dicapai oleh bola dengan persamaan ℎ(𝑡) = 72𝑡 − 9𝑡².

a. Tentukan waktu (t) yang diperlukan sehingga tinggi bola maksimum.

b. Tentukan tinggi maksimum yang dicapai bola itu.

Penyelesaian:

a. ℎ(𝑡) = 72𝑡 − 9𝑡² ℎ^′(𝑡) = 72 − 18𝑡

Agar mencapai maksimum maka ℎ^′(𝑡) = 0 ℎ^′(𝑡) = 72 − 18𝑡

0 = 72 − 18𝑡 18𝑡 = 72

𝑡 = 4 detik

b. tinggi maksimum yang dicapai bola itu adalah:

ℎ(𝑡) = 72𝑡 − 9𝑡²

ℎ(4) = 72(4) − 9(4)² = 288 − 144 = 144 meter Contoh 11:

Kawat sepanjang 120 m akan dibuat kerangka seperti pada gambar di bawah ini. Agar luasnya maksimum, maka hitunglah panjang kerangka (p) tersebut.

Penyelesaian:

Persamaan kerangka: 3𝑝 + 4𝑙 = 120 4𝑙 = 120 − 3𝑝 𝑙 = 30 −³

4𝑝 Persamaan luas:

𝐿 = 𝑝 ∙ 2𝑙 = 𝑝 ∙ 2 (30 −³

4𝑝) = 60𝑝 −³

2𝑝² Luas akan maksimum jika 𝐿^′ = 0 → 60 − 3𝑝 = 0

𝑝 = 20 Jadi, panjang kerangka agar luas maksimum adalah 20 m.

Contoh 12:

Luas permukaan balok dengan alas persegi adalah 150𝑐𝑚². Agar diperoleh volume balok yang maksimum, maka tentukan panjang alas balok.

Penyelesaian:

Karena alas berbentuk persegi, maka 𝑝 = 𝑙 Luas permukaan: 𝐿 = 150

2(𝑝𝑙 + 𝑝𝑡 + 𝑙𝑡) = 150

(20)

20 | M A T E M A T I K A X I I P S S M A G O N Z A G A / T U R U N A N / 2 0 2 0 - 2 0 2 1 𝑝𝑙 + 𝑝𝑡 + 𝑙𝑡 = 75, karena 𝑝 = 𝑙 maka didapat: 𝑝²+ 𝑝𝑡 + 𝑝𝑡 = 75

→ 2𝑝𝑡 = 75 − 𝑝²

→ 𝑡 =

^75−𝑝²

2𝑝

……(1)

Persamaan volume: 𝑉 = 𝑝 ∙ 𝑙 ∙ 𝑡, karena 𝑝 = 𝑙, maka 𝑉 = 𝑝 ∙ 𝑝 ∙ 𝑡

= 𝑝²(^75−𝑝_2𝑝²)

=

^75𝑝₂

−

^𝑝₂³

Volume akan maksimum jika 𝑉^′ = 0

75 2 −^3𝑝²

2 = 0 (kali 2) 75 − 3𝑝² = 0

𝑝² = 25 → 𝑝 = 5

Jadi, volume akan maksimum jika panjang balok 5 cm.

Contoh 13:

Dari selembar karton berbentuk persegi yang berukuran sisi 18 cm akan dibuat kotak tanpa tutup, dengan cara menggunting empat buah persegi di setiap pojok karton, seperti pada gambar berikut.

Tentukan volume maksimum kotak yang bisa dibuat.

Penyelesaian:

Kotak yang terbentuk memiliki alas sepanjang (18 − 2𝑥) dan tingginya 𝑥. Perhatikan gambar!

Syarat: sisi dari kotak tidak boleh negative, sehingga didapat:

𝑥 > 0 dan 18 − 2𝑥 > 0

18 > 2𝑥 atau 𝑥 < 9

Persamaan volume: 𝑉 = 𝑙𝑢𝑎𝑠 𝑎𝑙𝑎𝑠 × 𝑡𝑖𝑛𝑔𝑔𝑖 𝑉 = (18 − 2𝑥)²𝑥

𝑉 = (324 − 72𝑥 + 4𝑥²)𝑥 𝑉 = 324𝑥 − 72𝑥²+ 4𝑥³ Volume akan maksimum saat 𝑉^′= 0

324 − 144𝑥 + 12𝑥² = 0

12𝑥² − 144𝑥 + 324 = 0 (bagi 12) 𝑥² − 12𝑥 + 27 = 0

(𝑥 − 9)(𝑥 − 3) = 0 𝑥 = 9 atau 𝑥 = 3

Nilai 𝑥 yang memenuhi syarat adalah 𝑥 = 3

(21)

21 | M A T E M A T I K A X I I P S S M A G O N Z A G A / T U R U N A N / 2 0 2 0 - 2 0 2 1 𝑉 = (18 − 2𝑥)²𝑥

𝑉 = (18 − 2 ∙ 3)²∙ 3 = 432𝑐𝑚²

Jadi, volume maksimum kotak yang bisa dibuat adalah 432𝑐𝑚³. Contoh 14:

Seorang pedagang memproduksi 𝑥 unit barang dengan biaya (5𝑥²− 10𝑥 + 30) dalam ribu rupiah untuk tiap unit. Jika barang tersebut terjual habis dengan harga Rp50.000,00 tiap unit, maka tentukan keuntungan maksimum yang diperoleh pedagang tersebut.

Penyelesaian:

Biaya produksi 𝑥 unit: (5𝑥²− 10𝑥 + 30)𝑥 (dalam ribu rupiah) Biaya penjualan 𝑥 unit: 50𝑥 (dalam ribu rupiah)

Keuntungan/laba: Biaya penjualan – Biaya produksi 𝐿(𝑥) = 50𝑥 − (5𝑥²− 10𝑥 + 30)𝑥

= 50𝑥 − 5𝑥³+ 10𝑥²− 30𝑥 = −5𝑥³+ 10𝑥²+ 20𝑥

Keuntungan akan maksimum jika 𝐿′(𝑥) = 0

−15𝑥²+ 20𝑥 + 20 = 0 (bagi – 5) 3𝑥² − 4𝑥 − 4 = 0

(3𝑥 + 2)(𝑥 − 2) = 0 𝑥 = −²

3 atau 𝑥 = 2

Jadi, keuntungan akan maksimum jika memproduksi 2 unit barang dengan keuntungan maksimumnya adalah:

𝐿(2) = −5(2)³+ 10(2)²+ 20(2) = −40 + 40 + 40 = 40 (dalam ribu rupiah)

Latihan 3:

1. Tentukan persamaan garis singgung pada kurva:

a. 𝑦 = 𝑥²− 2𝑥 − 3 di titik (3, 1) b. 𝑦 = 𝑥 − 2𝑥² di titik dengan absis 1

c. 𝑦 = (2 − 𝑥)(2𝑥 + 1) di titik dengan ordinat 0 2. Tentukanlah:

a. Persamaan garis singgung kurva 𝑦 = 3 + 2𝑥 − 𝑥² yang sejajar dengan garis 4𝑥 + 𝑦 = 3

b. Persamaan garis singgung kurva 𝑦 = 2𝑥² + 𝑥 + 1 yang tegak lurus dengan garis 𝑥 + 5𝑦 = −7

c. Koordinat titik singgung jika garis 𝑦 = 𝑥 + 3 menyinggung kurva 𝑦 = 𝑥²− 3𝑥 + 7 d. Nilai 𝑎 jika garis 𝑦 = −𝑥 menyinggung kurva 𝑦 = 𝑎 +¹

𝑥

e. Nilai 𝑏 jika garis 𝑦 = 4𝑥 + 1 menyinggung kurva 𝑦 = 𝑎𝑥²+ 𝑏𝑥 di titik yang berabsis 2 f. Nilai 𝑏 jika garis 𝑦 = 2𝑥 menyinggung kurva 𝑦 = 𝑥²+ 𝑎𝑥 + 𝑏 di titik (2, 4)

g. Nilai 𝑎 + 𝑏 jika diketahui kurva 𝑦 = 𝑎√𝑥 + ^𝑏

√𝑥 melalui titik 𝐴(4, 8) dan garis singgung kurva di titik A tegak lurus dengan garis 2𝑥 + 𝑦 − 1 = 0

(22)

22 | M A T E M A T I K A X I I P S S M A G O N Z A G A / T U R U N A N / 2 0 2 0 - 2 0 2 1 3. Tentukan interval fungsi naik dan interval fungsi turun dari fungsi berikut ini.

a. 𝑓(𝑥) = 𝑥² − 6𝑥 b. 𝑓(𝑥) =¹

3𝑥³+ 4𝑥²− 20𝑥 + 2 c. 𝑓(𝑥) = (𝑥²− 1)(𝑥 + 1) d.

𝑓(𝑥) =

^𝑥+1

𝑥²+8

e.

𝑓(𝑥) =

^𝑥

𝑥+1

4. Tentukanlah:

a. Nilai 𝑎 − 𝑏 jika fungsi 𝑔(𝑥) = −𝑥³ + 6𝑥² + 15𝑥 − 2 pada interval −2 < 𝑥 < 6 mempunyai nilai maksimum 𝑎 dan nilai minimum 𝑏

b. Nilai minimum fungsi ℎ(𝑥) = 2𝑥³− 6𝑥²− 48𝑥 + 5 dalam interval −3 ≤ 𝑥 ≤ 4 c. Nilai maksimum fungsi 𝑦 = 𝑥³− 3𝑥²+ 3 pada selang −1 ≤ 𝑥 ≤ 2

d. Nilai minimum fungsi 𝑓(𝑥) = 𝑎𝑥⁴+ 𝑏𝑥³ + 𝑐𝑥² pada selang −1 ≤ 𝑥 ≤ 3 jika diketahui 𝑓(2) = 0 = 𝑓′(2) dan 𝑓(1) = −¹

2

e. Nilai 𝑝 jika fungsi 𝑓(𝑥) = 𝑥³+ 𝑝𝑥²− 19𝑥 hanya didefinisikan pada interval

−5 ≤ 𝑥 ≤ 0 dan mencapai maksimum pada saat 𝑥 = −3.

5. Tentukan nilai stasioner dan jenisnya pada fungsi berikut.

a. 𝑓(𝑥) = 𝑥² − 6𝑥

b. 𝑓(𝑥) = 2𝑥³ − 9𝑥²+ 12𝑥 c. 𝑓(𝑥) = 2𝑥³ + 6𝑥²+ 9𝑥 + 7 d. 𝑓(𝑥) =¹

4𝑥⁴−¹

2𝑥² e. 𝑓(𝑥) = 𝑥⁴ − 8𝑥² − 9 f.

𝑓(𝑥) =

^(𝑥−1)²

𝑥−4

6. Jumlah dari bilangan pertama dan kuadrat bilangan kedua adalah 75. Hitunglah nilai terbesar dari hasil kali kedua bilangan tersebut.

7. Jika 𝑥₁ dan 𝑥₂ akar-akar persamaan 𝑥² + 𝑘𝑥 + 𝑘 = 0, maka hitunglah nilai 𝑘 agar 𝑥₁²+ 𝑥₂² mencapai nilai minimum.

8. Dua kandang berdampingan masing-masing dengan ukuran 𝑥 meter, 𝑦 meter, dan luasnya 12𝑚². Agar panjang pagar yang diperlukan sesedikit mungkin, maka hitunglah ukuran 𝑥 dan 𝑦 yang mungkin.

9. Selembar kertas karton berukuran 6dm × 6dm akan dibuat kotak tanpa tutup dengan keempat sudut kertas itu digunting sehingga potongannya berbentuk persegi dengan panjang sisinya 𝑥 dm. tentukan nilai 𝑥 agar volume kotak itu mencapai maksimum.

10. Sebuah kotak tanpa tutup yang alasnya berbentuk persegi, mempunyai volume 4𝑚³ terbuat dari selembar karton. Tentukanlah ukuran kotak tersebut agar karton yang diperlukan sesedikit mungkin.

11. Sebuah benda bergerak dengan percepatan pada setiap saat 𝑡 ditentukan oleh 𝑎(𝑡) = 5 − 𝑡 meter/detik². Jika kecepatannya pada saat 𝑡 = 0 adalah ¹

6𝑚/𝑠 dan posisi pada saat 𝑡 = 0 adalah 6 meter, maka hitunglah jarak tempuh benda tersebut dalam waktu 4 detik.

12. Jarak yang ditempuh sebuah mobil dalam waktu 𝑡 diberikan oleh fungsi 𝑆(𝑡) = −¹

3𝑡³+ 3𝑡² − 5𝑡. Tentukan waktu yang dibutuhkan agar kecepatan mobil mencapai maksimum.

(23)

13. Untuk memproduksi 𝑥 unit barang per hari diperlukan biaya (𝑥³− 2.000𝑥²+ 3.000.000𝑥) rupiah. Jika barang itu harus diproduksi, maka hitunglah banyak barang yang harus diproduksi per hari agar biaya produksi per unit mencapai minimum.

14. Suatu proyek pembangunan gedung sekolah dapat diselesaikan dalam 𝑥 hari dengan biaya proyek perhari (3𝑥 − 900 +¹²⁰

𝑥 ) ratus ribu rupiah. Agar biaya proyek minimum maka terntukan berapa hari proyek tersebut harus diselesaikan.

15. Suatu perusahaan menghasilkan 𝑥 produk dengan biaya total sebesar (75 + 2𝑥 + 0,1𝑥²) juta rupiah. Jika semua produk perusahaan tersebut terjual dengan harga Rp40.000.000,00 untuk setiap produknya, maka hitunglah laba maksimum yang diperoleh perusahaan tersebut.