BAB II LANDASAN TEORI 2.1. Penelitian Terkait - Sistem Penjadwalan Kuliah dengan Menggunakan Algoritma Genetika Studi Kasus Fakultas Teknik Universitas Sumatera Utara

BAB II

LANDASAN TEORI

2.1. Penelitian Terkait

Penelitian terkait yang menggunakan algoritma genetika untuk menemukan solusi dalam menyelesaikan permasalahan penjadwalan kuliah telah banyak dilakukan. Sam’ani [3] melakukan penelitian tentang penjadwalan kuliah dan ujian

akhir semester program studi Diploma III Manajemen Informatika STMIK Palangkaraya dengan menggunakan algoritma genetika. Teknik pengkodean dalam penelitian tersebut menggunakan string bit atau varchar untuk teknik pengkodean,

populasi awal dibentuk secara acak (random), fungsi fitness digunakan untuk meminimalkan jumlah pelanggaran antar jadwal, metode seleksi dengan roulette-wheel, pindah silang satu titik potong (one-point crossover), mutasi dengan pengkodean nilai, menggunakan elitisme dan kondisi selesai ditentukan bila iterasi maksimum telah tercapai. Hasil output dari sistem berupa susunan penjadwalan kuliah dan ujian akhir semester dan didapatkan hasil terbaik dengan semua nilai

fitness tiap generasi bernilai satu dan waktu tercepat dicapai pada generasi ke-5, populasi ke-5, probabilitas pindah silang 25% dan mutasi 2%.

algoritma penjadwalan tersendiri yang berbeda dengan agoritma genetika. Proses penjadwalan pertama sekali dilakukan dengan algoritma penjadwalan dengan menjadwalkan kuliah berdasarkan urutan tertentu yang dapat mengatasi hard constraint dan soft constraint. Algoritma penjadwalan terbatas pada pencarian solusi yang paling optimum dari masalah yang dihadapi di dalam proses penjadwalan. Untuk mengatasi keterbatasan tersebut, jadwal yang dihasilkan nantinya akan dievaluasi berdasarkan kesesuaiannya dan dijadikan sebagai dasar dalam operasi algoritma genetika. Dalam penelitian ini, pencarian solusi dengan menggunakan 5000 generasi tidak dapat menghasilkan zero hard maupun soft constraint. Dari hasil diperoleh bahwa dengan algoritma genetika tidak dapat mengatur kepuasan seluruh

hard constraint, meskipun hubungan hasil yang diperoleh berdekatan, masih saja ditemukan dua kesalahan. Dengan kata lain, apabila hanya mengandalkan algoritma genetika saja, maka hasil yang diperoleh adalah hanya berupa soft constraint saja dan hasilnya lebih baik dibandingkan penjadwalan yang dibuat admin.

dan kursi yang tersisa untuk setiap ruang. Penjadwalan dimulai dari jumlah mata kuliah yang sedikit sehingga dihasilkan beberapa pilihan jadwal.

2.2. Penjadwalan Kuliah

Penjadwalan merupakan kumpulan kebijakan dan mekanisme dalam sistem operasi yang berkaitan dengan disain sistem, urutan kerja, daftar atau rencana kegiatan dengan pembagian waktu pelaksanaan yang terperinci. Penjadwalan digunakan untuk memutuskan prioritas yang harus dijalankan, waktu pelaksanaan pekerjaan dan teknik pelaksanaan pekerjaan [6].

Penjadwalan kuliah merupakan kegiatan administrasi yang mengalokasikan sejumlah aktivitas perkuliahan tertentu pada slot waktu dan ruang yang tersedia [7]. Dalam menyusun penjadwalan kuliah, terdapat beberapa pertimbangan penting yang harus diperhatikan, antara lain jumlah mata kuliah yang ditawarkan dalam satu semester, jenis mata kuliah (teori dan praktikum), jumlah dosen yang mengajar dalam satu semester, waktu kuliah dan ruang yang tersedia.

Konsep penjadwalan kuliah diawali dengan penugasan seluruh mata kuliah yang disusun dalam satu semester untuk diberikan kepada dosen pengajar. Selanjutnya mata kuliah dijadwalkan menurut waktu dan ruang yang tersedia dengan mempertimbangkan ketersediaan waktu mengajar dosen, sehingga nantinya diperoleh sistem penjadwalan kuliah yang baik.

a. Himpunan mata kuliah C = {c1c2,c3,….cn} yang merupakan kegiatan (peristiwa).

b. Himpunan waktu T={t1,t2,t3,….tN}. c. Himpunan ruang P={p1,p2,p3,…pN}. d. Himpuan dosen A={a1,a2,a3,….aN}.

Jika diimplementasikan dalam empat duplex (e,t,p,a), sedemikian sehingga e € E, t € T, p € P, dan a € A. Hal ini berarti bahwa peristiwa (e) berlangsung pada waktu

(t), yang terjadi pada tempat (p), dilakukan oleh dosen (a).

Apabila penjadwalan ditentukan oleh satu himpunan dosen {a1,a2,…}, satu set mata kuliah {c1,c2,…}, satu himpunan ruang {p1,p2,…}, dan satu set himpunan waktu {t1,t2,…}, maka dapat ditulis satu set rangkap tiga {ai,cj,pk} mewakili keperluan {dimana i=1,….n; j=1,….m; dan k=1,….q}. Setiap himpunan menunjukkan dosen ai,

mengajar mata kuliah cj di dalam kelas pk. Demikian seterusnya, jika set rangkap tiga ini ditambah elemen t1 {dimana l=1, ...s}, maka membentuk set rangkap empat yaitu {ai,cj,pk,tl} yang dapat diartikan bahwa dosen (ai) mengajar mata kuliah (cj) di kelas (pk) pada waktu (tl). Tiap dua set rangkap berempat misalnya {ai,cj,pk,tl} dan {aw,cx,py,tz} harus memenuhi persyaratan berikut:

Bila ai = aw, maka tl≠tz ……… (2.1)

Bila ai = aw, maka pk≠py ……….. (2.2) Bila cj = cx, maka tl≠tz ……… (2.3) Bila cj = cx, maka pk≠ty ……… (2.4)

Dari ketiga persamaan tersebut, maka persamaan (2.1) menyatakan tidak ada dosen dijadwalkan lebih dari satu kali pada waktu yang bersamaan. Persamaan (2.2) menyatakan bahwa tidak ada dosen dijadwalkan lebih dari satu kali pada ruang yang bersamaan. Persamaan (2.3) menyatakan tidak ada mata kuliah yang dijadwalkan lebih dari satu kali pada waktu yang bersamaan. Persamaan (2.4) menyatakan bahwa tidak ada mata kuliah yang dijadwalkan lebih dari satu kali pada ruang yang bersamaan. Persamaan (2.5) menyatakan bahwa tidak ada ruang yang dijadwalkan lebih dari satu kali dalam satu waktu.

Secara umum suatu penjadwalan kuliah sebaiknya berdasarkan ketentuan sebagai berikut:

a. Kegiatan perkuliahan dirancang selama satu semester yang diimplementasikan dalam bentuk kurikulum.

b. Seluruh beban mengajar didistribusikan secara adil dan merata untuk tiap dosen tanpa adanya perlakuan khusus kepada dosen tertentu.

c. Mengoptimalkan seluruh sarana dan prasarana penunjang perkuliahan. d. Melakukan evaluasi dan montioring dari tiap pencapaian kegiatan

perkuliahan selama satu semester.

2.3. Masalah Penjadwalan Kuliah

komponen utama yang menjadi pertimbangan penting dalam penyusunan jadwal kuliah. Komponen tersebut dibagi dalam lima kelompok besar, yaitu:

a. Kelompok dosen. b. Kelompok mata kuliah. c. Kelompok kurikulum. d. Kelompok waktu. e. Kelompok ruang.

Dosen, mata kuliah dan kurikulum disusun membentuk suatu aktivitas perkuliahan. Apabila ketiga kelompok ini ditempatkan ke dalam slot waktu dan ruang, maka akan timbul permasalahan. Permasalahan tersebut antara lain sulitnya mendapatkan alokasi waktu yang tepat terhadap ketersediaan waktu dosen dengan mata kuliah yang ditawarkan. Selain itu penggunaan ruang yang terbatas untuk menampung aktivitas perkuliahan turut menjadi pertimbangan penting sebelum menyusun jadwal. Solusi dikatakan optimal jika seluruh aktivitas perkuliahan dapat disusun dalam waktu singkat sehingga pelanggaran terhadap persyaratan-persyaratan yang ada dapat ditekan sekecil mungkin.

2.4. Persyaratan Penjadwalan

a. Seluruh mata kuliah terjadwal dan dinyatakan dalam waktu yang jelas. b. Kelas yang terjadwal harus memberikan kemungkinan gabungan dari

aktivitas perkuliahan yaitu dosen, mata kuliah dan mahasiswa.

c. Seorang dosen hanya boleh mengajar pada satu kelas untuk waktu yang bersamaan.

d. Seorang mahasiswa hanya boleh mengambil mata kuliah pada satu kelas untuk waktu yang bersamaan.

e. Kegiatan perkuliahan hanya boleh dilaksanakan sebanyak satu kali dalam satu ruang dalam satu waktu tertentu.

f. Satu ruang disesuaikan dengan daya tampung mahasiswa yang akan mengikuti perkuliahan.

g. Setiap dosen diberi batasan minimum dan maksimum untuk mengajar dalam satu minggu (Senin s.d Jumat).

h. Selang waktu tiap pergantian mata kuliah agar diusahakan sekecil mungkin.

i. Seorang dosen tidak diperbolehkan melakukan perpindahan ruang untuk mata kuliah yang sama jika dosen yang bersangkutan berhalangan hadir.

2.5. Kesulitan dalam Penjadwalan Kuliah

Beberapa kesulitan yang sering dihadapi saat penjadwalan kuliah adalah:

b. Merancang suatu penjadwalan kuliah yang efektif bukanlah suatu pekerjaan yang mudah untuk dilakukan. Penempatan dosen, mata kuliah, kurikulum dan waktu pada ruang yang terbatas menjadi masalah yang menarik dalam penjadwalan kuliah.

c. Adanya persyaratan tertentu yang ditambahkan dapat mempengaruhi lama waktu penyelesaian sehingga masalah penjadwalan kelihatannya lebih kompleks dan sulit untuk diselesaikan.

d. Masalah penjadwalan sering terkendala oleh persyaratan nyata ketika diaplikasikan dilapangan, seperti dosen mengajar satu kali pertemuan maksimum 3 SKS.

2.6. Algoritma Genetika

2.6.1. Tahapan Algoritma Genetika

Beberapa tahapan penting dalam proses algoritma genetika antara lain [10] [11]: a. Inisialisasi populasi.

b. Evaluasi populasi.

c. Memilih anggota populasi yang terbaik untuk membentuk populasi baru atau disebut dengan proses seleksi.

d. Membentuk kromosom baru dengan cara rekombinasi dan mutasi. e. Evaluasi kromosom yang baru dan memasukkan ke dalam populasi.

f. Jika memenuhi kriteria termination, proses berhenti dan mengembalikan kromosom terbaik, jika belum maka kembali ke tahap dua.

Contoh penggunaan algoritma genetika yang dibandingkan dengan algoritma optimasi sederhana ditunjukkan pada Gambar 2.1.

Gambar 2.1. Flowchart Algoritma Genetika ya

tidak

Lakukan inisialisasi populasi

seleksi individu yang akan dikawinkan

mutasikan keturunan

masukkan keturunan ke dalam populasi

Selesai kriteria kepuasan

2.6.2. Komponen Utama Algoritma Genetika

Algoritma Genetika harus memiliki lima komponen antara lain [12]:

a. Representasi genetik dari setiap solusi yang mungkin dari suatu permasalahan.

b. Cara pembentukan populasi awal atau inisialisasi populasi.

c. Fungsi evaluasi yang berperan menilai fitness dari solusi yang mungkin. d. Operator genetika yang mengubah komposisi kromosom.

e. Nilai parameter yang digunakan dalam Algoritma Genetika, meliputi ukuran populasi, nilai probabilitas yang ditetapkan dalam operator genetika (seleksi, crossover, mutasi).

2.7. Pengkodean

Pengkodean merupakan teknik penyederhanaan masalah ke dalam bentuk bilangan tertentu. Bilangan yang terbentuk merupakan gambaran dari susunan kromosom. Pada pengkodean, terdapat beberapa teknik atau cara yang seluruhnya bergantung dari masalah yang diselesaikan [13].

2.7.1. Pengkodean Biner

yang ditulis dalam bit 1 dan 0 seperti ditunjukkan pada Tabel 2.1, dimana angka tiap posisi menunjukkan nilai dari beberapa masalah.

Tabel 2.1. Kromosom dengan pengkodean biner Kromosom 1 101010101100110011100 Kromosom 2 111111000000011111100

Holland mengkodekan kromosom dalam bentuk bilangan biner. Sejumlah properti pada pengkodean biner bekerja menyederhanakan algoritma genetika. Selain itu, terdapat beberapa cara pembuatan gen, dimana masing-masing cara tersebut memiliki keunggulan tersendiri. Langkah penyederhanaan masalah ke dalam bentuk gen dilakukan dengan mengumpulkan informasi yang menunjukkan kebenaran dari masalah. Sebagai contoh, menyusun suatu penjadwalan kuliah dalam satu semester melibatkan sejumlah item yang ditampilkan dalam sejumlah kolom.

2.7.2. Pengkodean Nilai

(neural network). Penggunaannya berawal dari adanya masukan yang diberikan kepada neuron untuk membiasakan jaringan supaya menghasilkan keluaran yang sesuai [13]. Tabel 2.2. menunjukkan contoh kromosom dengan pengkodean nilai.

Tabel 2.2. Kromosom dengan pengkodean nilai

Kromosom A 1.3532, 6.566, 2.9234, 4.3241 Kromosom B P, Q, R, S, T, U, V,

Kromosom C (atas), (bawah), (depan), (belakang)

2.7.3. Pengkodean Pohon

Pengkodean ini banyak digunakan pada pemrograman genetika. Kromosom digambarkan sebagai pohon dari seluruh objek, seperti fungsi atau perintah dalam bahasa pemrograman. Pengkodean ini digunakan untuk mencari fungsi berdasarkan nilai-nilai yang diberikan untuk mendapatkan nilai keturunan terbaik (sesuai dengan keinginan) untuk seluruh masukan. Masalah ini dapat dikodekan ke dalam pengkodean pohon dimana kromosom merupakan fungsi-fungsi yang dinyatakan dalam pengkodean pohon. Sebagai contoh, perhitungan fungsi berdasarkan nilai-nilai yang diberikan. Perhitungan tersebut nantinya harus menghasilkan nilai keluaran yang berbaik terhadap seluruh masukan yang diberikan [13].

2.7.4. Pengkodean Permutasi

Seluruh kromosom pada pengkodean ini terdiri dari barisan angka yang disusun dalam urutan tertentu seperti yang ditunjukkan pada Tabel 2.3.

Tabel 2.3. Kromosom dengan pengkodean permutasi Kromosom 1 1 5 3 2 6 4 7 9 8

Kromosom 2 8 5 6 7 2 3 1 4 9

Proses kawin silang dan mutasi pada pengkodean ini menghasilkan kromosom yang memiliki konsistensi tertentu. Teknik pengkodean ini sering ditemui pada masalah wiraniaga. Untuk dapat melalui sejumlah kota dengan jarak yang telah ditetapkan dalam satu kota, maka seorang wiraniaga tidak harus berkunjung ke seluruh kota, melainkan hanya melakukan beberapa kunjungan dengan cara menyusun urutan kota yang akan dikunjungi dengan jumlah jarak seminimal mungkin. Dengan demikian tiap kota diwakili dengan kromosom untuk setiap kota yang akan dikunjungi secara berurutan.

2.8. Inisialisasi Populasi

2.9. Operator dalam Algoritma Genetika

Algoritma genetika memiliki operator genetika yang sering digunakan, antara lain seleksi, crossover dan mutasi. Operator ini sangat berperan untuk mengubah komposisi suatu kromosom.

2.9.1. Seleksi

Seleksi merupakan proses pemilihan calon induk. Proses seleksi merupakan teknik pemilihan kromosom yang akan dikawinsilangkan dari bakal induk yang baik pada proses evolusi selanjutnya. Perubahan tiap individu dari satu generasi sangat ditentukan oleh nilai fitness. Tujuannya adalah menghasilkan keturunan yang terbaik dari suatu popuasi untuk diproses melalui rekombinasi dan mutasi. Dengan dasar inilah seleksi dilakukan dengan menggunakan tiga teknik, yaitu seleksi roda roullete

(fitness based selection), seleksi rangking (rank selection) dan seleksi turnamen (tournament selection). [15] Sebagai contoh, diberikan individu a dipasangkan dengan individu b seperti ditunjukkan pada Tabel 2.4.

Tabel 2.4. Contoh proses seleksi

Individu Kromosom Fitness

a 1011 3

b 0101 2

2.9.1.1. Seleksi Roda Roullete

Pada proses seleksi Roullete, induk ditentukan menurut nilai fitness. Untuk

yang terbaik, maka program sebaiknya melakukan seleksi dengan nilai fitness yang terendah [16]. Seleksi roda roulette merupakan metode seleksi yang paling disukai. Prosesnya ditunjukkan pada Gambar 2.2.

Gambar 2.2 Seleksi roda roulette [16]

Cara kerja roda tersebut adalah sebagai berikut: pertama, individu-individu dipetakan pada segmen garis yang berdekatan, sehingga masing-masing individu berukuran sama sesuai dengan fitness. Kedua, nomor acak dibangkitkan dan seluruh individu berada pada daerah nomor acak yang telah dipilih. Ketiga, proses kemudian diulangi sampai ditemukan nomor individu yang sesuai keinginan. Kromosom dalam kelompok yang terpilih disusun dalam roda roulette berdasarkan pada nilai fitness.

2.9.1.2. Seleksi Ranking

Seleksi roda roullete ternyata memiliki kekurangan. Hal ini akan nampak bila selisih yang terjadi pada nilai fitness cukup jauh. Misalkan, bila fitness kromosom terbaik menjadi 95% dari percobaan roda roullete, maka mengakibatkan kormosom lain memiliki kesempatan sangat kecil untuk dapat dipilih. Dengan dasar inilah lalu diperkenalkan teknik seleksi lain yaitu seleksi ranking. Prinsip kerja dari seleksi ini adalah melakukan ranking terlebih dahulu seluruh kromosom yang akan diseleksi berdasarkan nilai fitnes untuk mendapatkan nilai fitness baru. Seleksi ini memiliki prioritas tertentu mulai dari fitness terburuk yang bernilai 1, terburuk kedua bernilai 2, dan seterusnya sampai diperoleh fitness terbaik. Kromosom dengan nilai fitness

terbaik akan memiliki nilai fitness ke N, dimana N merupakan jumlah kromosom di dalam suatu populasi [13].Proses sebelum di-ranking ditunjukkan pada Tabel 2.5.

Tabel 2.5. Seleksi ranking sebelum di-ranking

Kromosom Fitness

P 12

Q 5

R 15

S 3

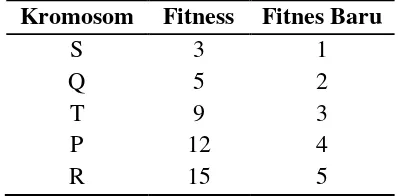
Proses seleksi setelah di-ranking ditunjukkan pada Tabel 2.6. Tabel 2.6. Seleksi ranking setelah di-ranking

Kromosom Fitness Fitnes Baru

S 3 1

Q 5 2

T 9 3

P 12 4

R 15 5

2.9.1.3. Seleksi Turnamen

Algoritma genetika menggunakan mekanisme seleksi untuk mendapatkan individu dari kumpulan populasi. Individu yang dikawinkan digunakan untuk membangkitkan keturunan baru (offspring) dan menjadi dasar membentuk generasi selanjutnya. Jika individu dalam kelompok dikawinkan, maka seluruh sifat gen baru akan diturunkan ke generasi selanjutnya. Hasil kawin ini diharapkan dapat menghasilkan individu yang baik. Mekanisme seleksi dalam algoritma genetika merupakan proses sederhana yang membantu seleksi individu yang lebih baik dalam populasi pada kelompok pasangan [17].

terdiri dari pemenang turnamen, memiliki nilai rata-rata fitness yang lebih tinggi dibandingkan dengan rata-rata fitness populasinya. Perbedaan dari nilai fitness ini memberikan tekanan seleksi, yang mengatur algoritma genetika untuk memperbaiki nilai fitness dari masing-masing generasi yang berhasil. Seleksi turnamen mirip dengan seleksi kedudukan (rank selection), tetapi perhitungannya lebih efisien dan lebih dapat dipertanggungjawabkan pada kasus yang lebih kompleks. Kedua individu dipilih secara acak dari populasi [13].

2.9.2. Kawin Silang

Kawin silang (crossover) sering digunakan untuk menghasilkan keturunan baru berdasarkan induk yang terpilih. Aturan kawin silang dalam algoritma genetika adalah mengkombinasikan bit dari solusi yang fit. Proses pengulangan banyak digunakan oleh operator crossover untuk mendapatkan gen populasi. Operator

crossover merupakan teknik yang sering digunakan dalam algoritma genetika dengan harapan bahwa kromosom baru berubah menjadi kromosom yang lebih baik [18].

2.9.2.1. Kawin Silang 1 titik

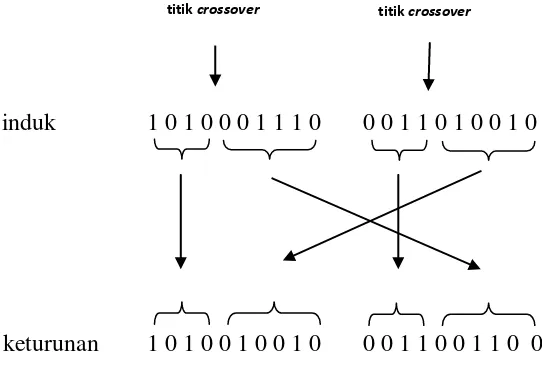
titik, dimana prinsip kerjanya adalah dengan mengambil dua induk, kemudian memotong kromosom string-nya beberapa posisi secara acak untuk menghasilkan dua bagian utama dan pendukung. Bagian pendukung kemudian ditukar untuk menghasilkan dua kromosom baru (lihat Gambar 2.3). Kedua induk yang dihasilkannya masing-masing mewarisi beberapa gen dari induknya. Teknik ini disebut kawin silang satu titik [19][20].

induk 1 0 1 0 0 0 1 1 1 0 0 0 1 1 0 1 0 0 1 0

keturunan 1 0 1 0 0 1 0 0 1 0 0 0 1 1 0 0 1 1 0 0

Gambar 2.3. Kawin silang 1 titik

2.9.2.2. Kawin Silang2 Titik

Perkawinan silang 2 titik merupakan perkembangan dari cara sebelumnya dengan memilih secara acak untuk melakukan pertukaran bit kromosom. Dalam kawin silang dua titik (two point crossover), kromosom ditampilkan sebagai loop

yang dibentuk berdasarkan penggabungan bersama. Untuk menukar bagian satu loop

dengan loop lain dibutuhkan seleksi dua titik potong, seperti yang ditunjukkan oleh

Gambar 2.4. Dalam hal ini, kawin silang satu titik ditampilkan sebagai kawin silang dua titik dengan satu titik potong pada string awal. Secara umum, kawin silang dua titik menunjukkan fungsi yang sama seperti kawin silang satu titik. Selain itu cara lain adalah dengan menyalin barisan bit kromosom orang tua pertama dari bit pertama sampai dengan titik perkawinan silang pertama dan dari titik perkawinan silang kedua sampai dengan bit terakhir. Perkawinan silang dengan dua titik lebih disukai daripada kawin silang satu titik [11] [14].

Gambar 2.4. Kawin silang 2 titik [14]

2.9.2.3. Kawin Silang Seragam

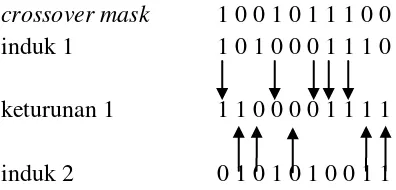
kawin silang tertutup bernilai 1, maka gen merupakan hasil salinan dari induk yang pertama, sebaliknya jika kawin silang terlindung bernilai 0, maka gen yang disalin merupakan hasil dari induk kedua. Proses diulangi dengan induk yang bergantian untuk menghasilkan keturunan yang kedua. Hasil kawin silang terlindung yang baru dibangkitkan secara acak pada pasangan dari tiap induk [18]. Untuk lebih jelasnya perhatikan Gambar 2.5.

crossover mask 1 0 0 1 0 1 1 1 0 0 induk 1 1 0 1 0 0 0 1 1 1 0

keturunan 1 1 1 0 0 0 0 1 1 1 1

induk 2 0 1 0 1 0 1 0 0 1 1 Gambar 2.5. Kawin silang seragam

2.9.2.4. Kawin Silang Rekombinasi

Kawin silang rekombinasi memilih secara acak dari semua gen yang ada pada induk untuk mendapatkan gen anak [11]. Contoh kawin silang rekombinasi diperlihatkan Tabel 2.7.

Tabel 2.7 Kawin silang rekombinasi Kromosom

2.9.3. Mutasi

Mutasi merupakan operator algoritma yang digunakan untuk menentukan perbedaan genetika dari satu generasi ke generasi lainnya. Setelah hasil kawin silang terbentuk tetapi sebelum keturunan terbentuk, terlebih dahulu harus menjalani tahap mutasi. Peristiwa ini mengacu pada perhitungan mutasi. Mutasi tidak selamanya menghasilkan gen baru, dan dapat merupakan hasil salinan gen induk. Tujuan dilaksanakannya mutasi adalah untuk menekan gangguan dan menghasilkan allele

baru dalam populasi [4]. Pemutaran mutasi ditetapkan jika dua allele diputar merubah susunan penjadwalan seperti pada Gambar 2.6. Jika perhitungan mutasi terlalu tinggi, dapat mengakibatkan keturunan yang baik akan hilang dan mengurangi harapan nilai

fitness yang tinggi dari ruang solusi. Beberapa sistem tidak menggunakan operator mutasi. Sebagai gantinya, sistem mempercayakan gangguan (noise) untuk mengacak populasi yang dihasilkan pada inisialisasi sehingga diperoleh gen yang dapat melakukan penggabungan ulang.

Gambar 2.6. Operasi mutasi dalam Algoritma Genetika keturunan

Pada Gambar 2.6 terlihat bahwa ketika gen telah diseleksi melalui mutasi, lalu gen hasilnya diubah menjadi angka. Pada kasus representasi biner, mutasi sederhana pada gen tunggal menyebabkan nilai gen menjadi komplit dari 1 menjadi 0 dan sebaliknya [14].

2.9.3.1. Mutasi Biner

Mutasi ini termasuk jenis yang paling sederhana. Cara kerjanya berdasarkan bit

pada kromosom yang dipilih secara acak, lalu nilainya diinversi dan diubah menjadi lawannya [11]. Untuk jelasnya perhatikan Tabel 2.8.

Tabel 2.8. Mutasi pada pengkodean biner Kromosom sebelum mutasi 1 1 1 0 0 0 1 1 Kromosom setelah mutasi 1 1 1 0 0 0 0 1

2.9.3.2. Mutasi Permutasi

Salah satu teknik yang dilakukan pada pengkodean permutasi adalah dengan memilih dua posisi pada kromosom lalu posisinya saling dipertukarkan. Tetapi perlu diingat bahwa proses mutasi pada pengkodean permutasi harus konsisten dalam mengurutkannya [11]. Untuk lebih jelasnya, perhatikan Tabel 2.9.

Tabel 2. 9. Mutasi pada pengkodean permutasi

2.9.3.3. Mutasi Nilai

Mutasi pada pengkodean biner dapat diaplikasikan pada pengkodean nilai karena urutan kromosomnya tidak perlu dijaga. Dalam hal ini prosesnya tidak menginversi bit. Sebagai contoh, nilai yang dinyatakan dalam bilangan nyata dimutasi dengan cara menukarkan nilai dari dua gen yang terdapat pada kromosom. Cara ini kurang efektif untuk mendapatkan nilai yang sama. Oleh karena itu ada cara lain yang lebih efektif yaitu dengan memilih posisi gen secara acak pada kromosom, kemudian menambah atau menguranginya dengan suatu nilai yang kecil secara acak [11]. Lebih jelasnya perhatikan Tabel 2.10.

Tabel 2.10 Contoh mutasi pada pengkodean nilai riil Kromosom sebelum dimutasi 1,43 1,09 4,51 9,11 6,94 Kromosom setelah dimutasi 1,43 1,19 4,51 9,01 6,94

2.10.Elitisme

2.11.Precedence Preservative Crossover (PPX)

Precedence preservative crossover (PPX) merupakan pengembangan dari masalah vehicle routing yang dijelaskan oleh Blanton dan Wainwright. Operator melewati hubungan operasi yang lebih dahulu diberikan dalam dua permutasi induk menjadi satu anak pada tingkatan yang sama, ketika tidak satupun hubungan yang lebih dahulu diperkenalkan. Metode ini sesungguhnya memberikan jawaban atas urutan gen dalam kromosom induk. Pertama-tama kromosom anak yang akan diinisialisasi bernilai kosong. Kemudian suatu vektor sepanjang n diisi secara acak pada sekumpulan elemen {1,2}. Vektor menggambarkan urutan yang dihasilkan oleh induk 1 dan 2. Setelah gen diwaliki oleh satu induk dan yang lainnya dihilangkan, maka hasilnya diberikan kepada kromosom anak. Langkah tersebut diulangi sampai kedua kromosom induk hilang dan kromosom anak berisi seluruh gen anak yang dimasukkan. Dalam hal ini gen dari induk dapat merupakan bilangan acak 1 dan 2 yang mewakili induk 1 dan induk 2 dan prosesnya ditunjukkan oleh Gambar 2.7 [19][20].

Gambar2.7 Precedence Presservative Crossover (PPX)

2.12.Konvergen

Jika algoritma genetika telah diimplementasikan dengan benar, maka populasi akan menyusun generasi secara berturut-turut sehingga menghasilkan nilai fitness