Proposal DAn Skripsi Revisi 2

(1)

PROPOSAL SKRIPSI

PEMODELAN ANOMALI GRAVITASI DAERAH MANIFESTASI PANASBUMI PARANGWEDANG BANTUL DIY

Dosen Pembimbing : Muhammad Faizal Zakaria, S.Si., M.T

Diajukan sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

Disusun oleh Muhammad Rofiqul A’la

12620004

PROGRAM STUDI FISIKA FAKULTAS SAINS DAN TEKNOLOGI

(2)

BAB I

PENDAHULUAN

1.1. Latar Belakang

Di daerah Parangwedang, Parangtritis, Kecamatan Kretek, Kabupaten Bantul, Daerah Istimewa Yogyakarta terdapat suatu manifestasi panasbumi yang berupa mata air panas. Manifestasi tersebut dimanfaatkan sebagai tempat wisata pemandian air panas Parangwedang. Berdasarkan fakta yang ada bahwa di daerah tersebut belum pernah dilakukan eksplorasi terkait sistem panas bumi yang ada di dalamnya. Berdasarkan Firman Allah SWT dalam QS Yunus Ayat 101 :

يِن ُت اَََمَو

ۡغ

ۚ ِض ۡر ۡلٱ

َأ َو ِتَٰوَٰم ََّسل يِف اَذاَََم ْاوُرََُظن ِلََُق

ٱ

َنوُنِم ُي ّل َق نَع ُرُذّنل َو ُتَٰي

ۡؤ

ٖم ۡو

ٱ

ٓأ

ۡلٱ

١٠١

Artinya :

“Katakanlah : Perhatikanlah apa yang ada di langit dan di bumi. Tidaklah bermanfaat tanda kekuasaan Allah dan rasul-rasul yang

memberi peringatan bagi orang-orang yang tidak beriman.” (QS

Yunus:101)

Dalam Ayat tersebut Allah memerintahkan kepada kita semua untuk memperhatikan sekaligus meneliti apa yang ada di langit dan bumi, termasuk potensi yang ada di dalamnya yaitu potensi panasbumi.

Dalam rangka memanfaatkan potensi tersebut secara optimal, maka diperlukan survei geofisika. Salah satu survey geofisika yang digunakan untuk eksplorasi panasbumi adalah metode gravitasi. Studi menggunakan

(3)

metode gravitasi di area vukanik dapat didemonstrasikan secara efektif bahwa metode ini memberikan bukti variasi densitas pada bawah permukaan yang dangkal, yang berasosiasi dengan struktur dan sejarah magmatik gunungapi (Ndombi, 1981).

Untuk mencapai target di atas, beberapa teknik pengolahan data gravitasi seperti reduksi data (konversi data, reduksi alat, koreksi pasang surut hingga koreksi medan), transformasi ke bidang datar, pemisahan anomali regiona-residual, analisis derivatif, dan pemodelan ke depan (forward modeling) dapat diaplikasikan. Dengan informasi geologi dan penelitan-penelitian sebelumnya diharapkan sebagian sistem panasbumi yang ada di Parangwedang dapat diidentifikasi dengan baik. Penelitian ini akan membahas mengenai Pemodelan anomali gravitasi dari system panasbumi yang ada di Parangwedang.

1.2. Rumusan Masalah

Adapun rumusan masalah pada penelitian kali ini adalah :

1. Bagaimanakan melakukan analisis derivatif pada data gravitasi ? 2. Bagaimana melakukan pemodelan pada data anomali bouger

lengkap ?

(4)

1.3. Tujuan Penelitian

Adapun tujuan yang ingin dicapai dalam penelitian ini adalah sebagai berikut :

1. Melakukan analisis derivatif pada data gravitasi.

2. Melakukan pemodelan pada peta anomaly bouger lengkap.

3. Melakukan interpretasi terhadap hasil pemodelan dan analisis derivatif pada daerah manifetasi panasbumi.

1.4. Batasan Penelitian

Adapun batasan yang dilakukan dalam penelitian ini meliputi :

1. Perhitungan anomali gravitasi dilakukan dengan reduksi data gravitasi yang terdiri atas perhitungan G observasi dan G teoritis.

2. Pemisahan anomali regional dan residual dilakukan dengan metode kontinuasi ke atas (upward continuation).

3. Analisis derivatif menggunakan First Horizontal Derivative (FHD) dan Second Vertical Derivative (SVD)

4. Pemodelan anomali gravitasi dengan menggunakan Forward Modeling

1.5. Manfaat Penelitian

Manfaat dari penelitian dapat berkontribusi bagi masyarakat, pemerintah dan dalam dunia akademisi, adapun manfaat yang diharapkan adalah :

(5)

1. Manfaat untuk peranan akademik

Hasil dari penelitian ini diharapkan dapat memberikan gambaran mengenai system panasbumi yang ada di daerah parangwedang melalui studi gravitasi. Selain itu juga diharapkan dapat memberikan referensi bagi peneliti lain tentang panasbumi dari berbagai aspek ilmu.

2. Manfaat untuk masyarakat dan pemerintahan

(6)

BAB II

TINJAUAN PUSTAKA

2.1. Studi Pustaka

Sebagai referensi, digunakan beberapa literatur penelitian sejenis sebelumnya. Adapun penelitian sejenis yang relevan dengan penelitian ini adalah:

Tabel 2.1. Penelitian yang relevan dengan studi gravitasi daerah manifestasi panasbumi

No Judul Peneliti Publikasi Metode Hasil Penelitian

1 Analisis Data Pemisahan anomali menggunakan metode moving average. Analisis derivatif FHD (First Horizontal Derivative) dan SVD (Second Vertical Derivatif) untuk menentukan batas struktur. Pemodelan inversi 3D.

Adanya anomaly rendah di daerah utara penelitian yang berhubungan adanya prospek geothermal. Dari pemodelan 3D menunjukkan daerah gedongsongo merupakan daerah prospek panasbumi dengan nilai densitas berkisar 2,2 – 2,5 gr/cc. Struktur yang mengontrol berarah Baratlaut – Baratdaya dan Barattimur Daerah reservoir Anomali bouger lengkap dibawa ke bidang datar dengan metode titik ekivalen sumber massa. Pemisahan anomali dengan Kontinuasi Keatas. Pemodelan 2D dan 3D.

Hasil pengolahan data pemodelan 2D dan 3D serta anomaly Bouger di daerah Blawan-Ijen dapat disimpukan bahwa dari ketiga penampang terlihat nilai densitas paling rendah ditunjukkan oleh batuan rho1 yang berwarna biru dengan nilai densitas sebesar 2.58 gr/cc yang merupakan reservoir panasbumi dengan porositas tinggi dan tingkat

(7)

No Judul Peneliti Publikasi Metode Hasil Penelitian

permeabilitas tinggi dengan volume sebesar 101.20 juta m3_.

dkk (2003) Kolokium Hasil Kegiatan Inventarisasi Geolistrik, Geomagnet dan Gravitasi. Aspek Geokimia meneliti fluida manifestasi panasbumi.

Penyelidikan terpadu Geologi, Geokimia dan Geofisika di daerah Parangwedang mengindikasikan Potensi panas bumi didaerah Parangtritis termasuk entalpi rendah (T bawah permukaan <125o_{C) dengan demikian kemungkinan} pemanfaatan sumber daya panasbumi didaerah ini adalah untuk kegiatan wisata pantai berupa pemandian dan balai pengobatan airpanas.

4 Analisis Struktur Pemisahan anomali menggunakan metode moving average. Analisis derivatif FHD (First Horizontal Derivative) dan SVD (Second Vertical Derivatif) untuk menentukan batas struktur. Anomali residual dimodelkan untuk melihat struktur bawah permukaan pengontrol system panasbumi.

Dari hasil interpretasi hasil pemodelan bawah permukaan terlihat bahwa batuan terobosan andesit menjadi sumber panas (heat source) di area manifestasi dan sesar normal diidentifikasi menjadi salah satu jalur migrasi bagi fluida yang muncul sebagai manifestasi.

(8)

2.2. Landasan Teori

2.2.1. Geologi

Geologi daerah manifestasi panas bumi merupakan data-data lapangan guna mengetahui potensi panas bumi di daerah Parangwedang berdasarkan penyelidikan Alanda idral et.al., (2003).

2.2.1.1. Stratigrafi

Stratigrafi daerah Parangtritis dan sekitarnya disusun oleh batuan Tersier yang terdiri dari batuan sedimen klastik vulkanik, batuan gunung api, dan sedimen klastik karbonat, serta endapan permukaan yang berumur Kuarter.

2.2.1.1.1. Batuan sedimen klastik Vulkanik

Batuan sedimen klastik, tufa, (Tomt), terdiri dari klastik vulkanik berbutiran abu hingga lapilli, tidak bersifat gampingan dan

tidak terdapat fosil. Ketebalan perlapisan Tufa tersingkap di Sindet mencapai 75 meter. Batuan tufa ini sangat kedap air karena permeabilitas primer sangat kecil akibat gravitasi perlapisan karena batuan ini menjadi batuan dasar di daerah penelitian.

2.2.1.1.2. Batuan Gunung api

Batuan gunung api tersier ini terdiri dari batuan breksi andesit (Tomb) Satuan Andesit (Toma), Satuan Lava Parangkusumo

(Tmlp).

(9)

Breksi andesit yang diselingi oleh aliran lava bersusunan andesitan yang mempunyai struktur lempeng dan telah terlapukkan, dan terubahkan dengan ditemukannuya mineral khlorit dan serisit.

Satuan andesit berupa lava berwarna hitam, memperlihatkan kekar tiang, terubahkan dengan ditemukannya mineral khlorit. Batuan lava Parangkusumo (Tmlp) berupa lava basal, kekar menunjukkan struktur aliran lava dan diselingi retas andesit hornblende berstruktur kekar lempeng. Batuan ini terubahkan dengan hadirnya mineral khlorit dan kalsit, tersingkap baik di daerah situs Parangkusumo. Selingan lava andesit hornblende sebagai paksa efusif lava basal berperan penting sebagai indikasi parameter pembentukan sumber panas dikedalaman daerah panas bumi Parangtritis.

2.2.1.1.3. Batuan Sedimen Klastik Karbonat

Penyebaran sedimen klastik karbonat terdapat dibagian Barat dan dibagian Timur daerah penelitian yang terdiri dari Batu Gamping

Terumbu (Tmlc) dan Batuan Gamping Pasiran(Tmls).

2.2.1.1.4. Endapan Permukaan

(10)

garis pasang berbentuk “barchans dune” karena perubahan bentuk oleh pengaruh angin. Ketinggian gumuk pasir mencapai 21 meter dpl.

2.2.1.2. Struktur Geologi

Dalam penyelidikan terpadu yang dilakukan oleh tim dari SUBDIT Panas Bumi diketahui pola struktur geologi yang terdapat di daerah penelitian sebagian besar berkaitan dengan gejala-gejala tektonik yang pernah berlangsung pada “Java Trench” dan pembentukan sistem pegunungan diselatan Jawa.

Bentuk struktur yang terdapat di daerah penelitian dan sekitarnya selain diperkuat oleh kenampakan permukaan juga di dukung oleh karakteristik anomaly geofisika (geomagnet, gayaberat dan head-on). Struktur yang ada di daerah penyelidikan adalah berupa sesar normal (Bantul, Bambang Lipuro, dan Mudal), sesar mendatar (Parangkusumo, Soka Nambangan dan Siluk), ketidakselarasan, kekar dan kelarasan (fracturing).

Pada umumnya orientasi sesar SE - NW berkisar antara N 275o_W

hingga N 310o_{W dan NE - SW berkisar antara N 20}o_{E hingga 50}o_E,

diantara sesar - sesar tersebut diatas sesar Parangkusumo dengan arah N 300o_{W, menunjam 80}o_{kearah barat daya, merupakan sesar yang penting}

karena mengontrol pemunculan mata air panas Parangtritis. Sudut penunjaman sesar menyebabkan pembukaan zona kekaran (fracturing zone).

(11)

2.2.1.3. Manifestasi Panas Bumi Parangwedang

Manifestasi panas bumi Parangtritis yang terlihat di permukaan adalah berupa mata air panas (MAP) di Parangwedang (Air panas Parangwedang 1), ketinggian 8 meter diatas permukaan laut. Air panas bersuhu 43,0 o_{C temperature udara 25,6}o_{C, pH 7,5-7,7, terasa asin, tidak}

berbau, debit air tidak terukur, daya hantar listrik 17750 μS/cm dan terakumulasi dalam kolam air panas. Di permukaan air kolam muncul gelembung gas dan endapan algae berwarna hijau kehitaman. Air panas ini dijumpai pada satuan alluvium.

Pemandian air panas (Air panas Parangwedang 2), airnya berasal dari sumur galian pada kedalaman ± 6 meter, berjarak 10 meter timur sumur air panas Parangwedang 1. Air panas berasa asin, tidak berwarna, tidak berbau, pH netral (7,49), temperature 49 o_{C pada temperature udara}

28,2 o_{C, debit air tidak bias diukur, daya hantar listrik 18110 17750}

(12)

⃗

r0

2.2.2. Prinsip Dasar Metode Gravitasi

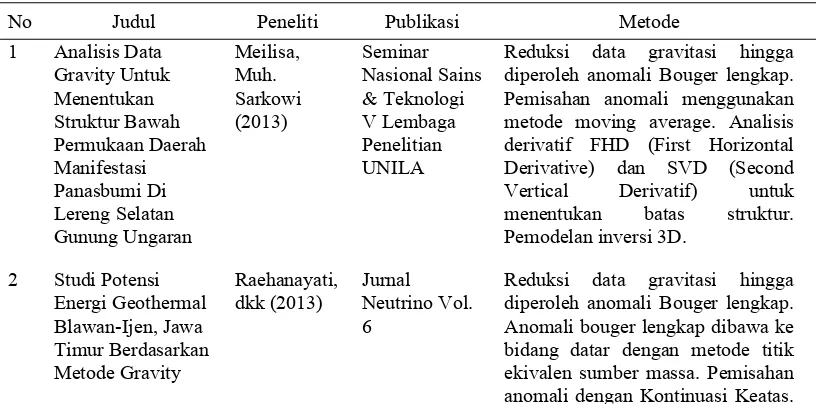
Metode gravitasi merupakan suatu metode yang berdasarkan pada hokum Newton tentang gaya tarik menarik antar partikel. Hukum Newton tersebut menyatakan bahwa gaya tarik menarik antara dua partikel dengan massa m1 dengan m2 yang terpisah sejauh r dari pusat massanya sebanding

dengan perkalian massa m1 dengan m2 dan berbanding terbalik dengan

kuadrat jaraknya (gambar 2.1). Gaya tersebut dijabarkan pada persamaan (2.1)

Gambar 2.1. Prinsip dasar Hukum Gravitasi Newton

(13)

Dengan F r

 

 

⃗ ⃗

adalah gaya yang bekerja pada m oleh karena adanya

0

m _{dan memiliki arah yang berlawanan dengan arah}r r⃗ ₀ ⃗

yaitu dari m0

menuju m. Dan untuk Gadalah konstanta umum gravitasi yang besarnya ( 6,67×10−11_{N m}2

/kg).

Dalam metode gravitasi, nilai yang terukur adalah suatu medan

gravitasi. Medan gravitasi dari partikel m0_{adalah besarnya gaya persatuan}

massa pada suatu titik sejauh r r 0

Dengan menganggap Bumi homogen, berbentuk sferis dan tidak

berotasi maka dapat diasumsikan m0_{adalah massa Bumi}



Me



_dengan

e

R _{adalah jari-jari Bumi dan}_r_ˆ_{adalah vektor satuan yang berarah radial}

dari pusat Bumi, serta arah g adalah menuju pusat Bumi. Maka besarnya

(14)

Medan gravitasi g sering disebut juga percepatan gravitasi atau percepatan

jatuh bebas. Satuan g dalam cgs adalah gal (1 cm/s2_{). Medan gravitasi}

merupakan medan konservatif, dimana usaha yang dilakukan terhadap suatu benda dalam medan gravitasi tidak tergantung pada lintasan yang dilalui, melainkan hanya tergantung pada posisi awal dan posisi akhir. Maka, medan gravitasi dapat diperoleh dari turunan sebagai fungsi potensial skalar yang ditunjukkan pada persamaan (2.4)

 

adalah potensial gravitasi dari massa m0_{yang dijabarkan}

sebagai persamaan (2.5) : menuju ke pusat bumi (Gambar 2.2). Arah percepatan gravitasi tersebut didefinisikan sebagai arah vertikal. Percepatan gravitasi yang disebabkan benda anomali memiliki arah yang bervariasi terhadap arah vertikal, tergantung pada kedudukan terhadap benda anomali.

14

(2.4)

(15)

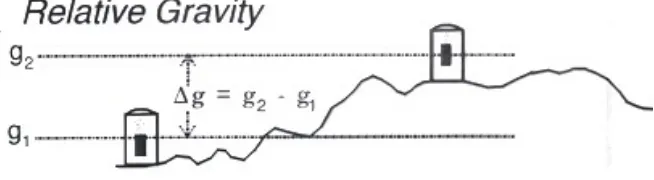
Perubahan percepatan gravitasi bumi yang disebabkan benda anomali lokal ini disebut dengan Anomali Gravitasi. Anomali tersebut dilambangkan dengan Δg ini bila dibandingkan dengan medan gravitasi bumi bernilai sangat kecil (Δg<<g). Anomali gravitasi hanya dapat diukur bersama medan gravitasi bumi pada arah yang sama.

x y z, ,



merupakan medan gravitasi teoritis di topografi (Dermawan, 2010).

Gambar 2.2. Arah percepatan gravitasi (Airlangga, 2010)

(16)

Untuk mendapat nilai medan gravitasi observasi, nilai yang didapatkan dari pengukuran dikoreksikan terhadap koreksi tinggi alat, koreksi pasang surut dan koreksi drift. Sedangkan medan gravitasi teoritis dipengaruhi oleh letak lintang, ketinggian dan massa topografi di sekitar titik ukur.

2.2.5.1. Konversi skala bacaan dan feedback ke mgal

Angka bacaan pada alat ukur biasanya belum menunjukkan nilai gravitasi yang sebenarnya. Angka bacaan pada alat ukur berupa angka dalam skala alat, yang masih harus dikonversi ke nilai gravitasi dalam skala miligal (mgal).

Gukur : nilai gravitasi terukur (mgal)

CR : counter reading yang diperoleh dari table alat

SB : skala bacaan (angka yang terbaca pada alat)

FFI : factor for interval yang diperoleh dari table alat

MVR : MVR yang digunakan di alat saat pengukuran

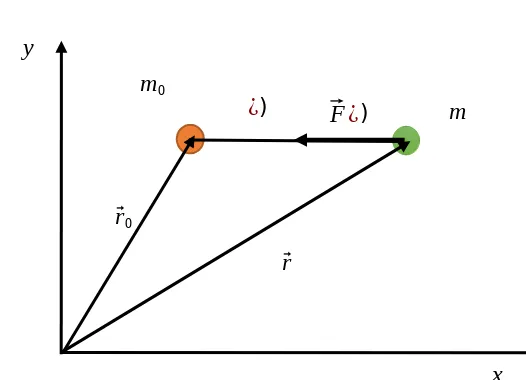
2.2.6. Koreksi Tinggi Alat

Koreksi tinggi alat dilakukan untuk membawa nilai pengukuran gravitasi sesuai posisi ketinggian topografi yang diperoleh Global

16

(2.7)

(2.8)

(17)

Positioning System (GPS). Beda ketinggian antara posisi gravitimeter

dengan GPS mempengaruhi nilai gravitasi, pada persamaan 2.9) GTerkoreksiTA = 0.30857 hTA

Dimana :

GTerkoreksiTA : Nilai Gukur yang telah terkonsentrasi tinggi alat (mgal)

hTA : Tinggi Alat (m)

2.2.7. Koreksi Pasang Surut (Tidal)

Pasang surut bulan dan matahari memberikan pengaruh ke perubahan nilai gravitasi di bumi sebesar 0,3 mgal, yaitu duapertiga dari pengaruh bulan dan sepertiga dari matahari. Perubahan nilai tersebut tergantung dari lokasi (posisi lintang), tanggal dan waktu pengukuran (Blakely, 1995).

Menurut Schureman, pengaruh pasang surut (tidal) pada arah vertikal dapat dihitung melalui persamaan (2.10).

hTa

Land Gravitymeter

GPS Geodetic

(18)

3 3

D _{= jarak dari Bumi ke matahari}

B

 _{= sudut geosentris terhadap bulan}

M

 _{= sudut geosentris terhadap matahari}

2.2.8. Koreksi Apungan (Drift)

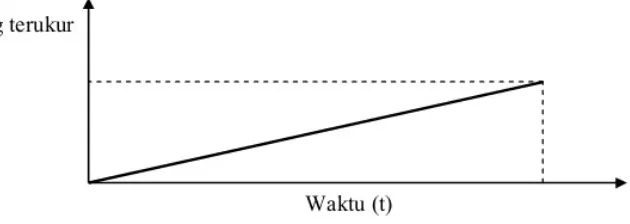
Alat gravitimeter sensitif terhadap pengaruh drift (apungan atau faktor kelelahan alat) yaitu perubahan nilai pengukuran gravitasi karena pengaruh perubahan mekanika dalam gravitimeter. Pengaruh tersebut berupa pegas yang semakin meregang terhadap waktu dan suhu. Faktor tersebut akan mempengaruhi pembacaan nilai gravitasi.

Untuk mengatasi pengaruh suhu, dipasang thermostat pada alat. Dengan demikian alat dapat bekerja konstan pada suhu tertentu, sedangkan untuk pengaruh waktu, dilakukan dengan cara mengukur kembali di titik base (base looping) untuk mengetahui besar perubahannya. Perubahan

nilai gravitasi tersebut terhadap waktu dianggap linier.

18

(19)

Selisih nilai pengukuran waktu awal dan akhir di titik base adalah besar gradien perubahan nilai tiap waktu pengukuran selama waktu looping (Gambar 2.5). Persamaan koreksi drift dapat dijabarkan persamaan

(2.11).

Koreksi Drift=

[

_TTi−Tawal

akhir−Tawal×(GBaseAwal−GBaseAkhir)

]

GTerkoreksiDrift=Gtitik−Koreksi Drift

Gambar 2.4. Proses looping untuk koreksi Drift (Airlangga, 2010)

2.2.9. Gravitasi

Observasi (gobs)

(2.11)

(20)

Nilai gravitasi yang terukur di titik amat adalah nilai gravitasi relatif. Disebut nilai gravitasi relatif karena nilai yang terukur adalah perbedaan nilai gravitasi dari satu titik terhadap titik lainnya. Nilai gravitasi mutlak didefinisikan sebagai nilai gravitasi yang sebenarnya di titik pengukuran. Untuk mendapatkan nilai gravitasi mutlak, maka nilai gravitasi relatif perlu diikatkan ke suatu titik yang dinamakan titik ikat gravitasi. Titik ikat gravitasi adalah titik yang sudah diketahui nilai gravitasi mutlaknya. Nilai gravitasi di titik ikat inilah yang akan ditambahkan ke nilai gravitasi relatif untuk mendapatkan nilai gravitasi mutlak di titik amat.

Persamaan untuk menentukan nilai gravitasi observasi (Arafin, 2004) adalah :

gobs gti



gd gdti



dengan, gobs_{= nilai gravitasi observasi di titik amat (mgal)}

ti

g _{= nilai gravitasi mutlak di titik ikat (mgal)}

d

g _{= nilai gravitasi terkoreksi drift di titik amat (mgal)}

gdti = nilai gravitasi terkoreksi drift di titik ikat (mgal)

20

(2.12)

(21)

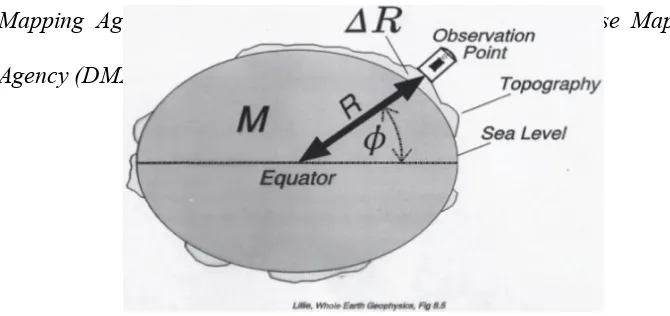
2.2.10. Gravitasi Teoritis

Untuk mendapatkan nilai medan gravitasi teoritis, pertama yang dilakukan adalah mencari nilai medan gravitasi normal analitis. Nilai medan gravitasi normal analitis, secara fisis terletak pada bidang referensi sferoida (z=0) sebagai titik referensi geodesi. Konsesi tentang rumusan medan gravitasi normal diterbitkan oleh dua badan, yaitu International Association of Geodesy (IAG) dan National Imagery and Mapping Agency

(NIMA, 2000).

(22)

dengan gBL



x y z, ,



_{adalah anomali medan gravitasi Bouger lengkap,}



, ,



obs



, ,



_{adalah koreksi medan (terrain).}

2.2.11. Koreksi Gravitasi Normal (gn)

Gravitasi normal adalah nilai gravitasi yang diperoleh atau diketahui dari bentuk bumi teoritis yang disebut referensi sferoida (Gambar 2.7). Formula gravitasi teoritis diterbitkan oleh dua badan, yaitu International Association of Geodesy (IAG) dan National Imagery and

Mapping Agency (NIMA) yang sebelumnya bernama Defense Mapping

Agency (DMA).

22

(2.14)

(23)

Formula terbaru yang diterbitkan NIMA adalah World Geodetic System yaitu pada persamaan 3.15. (Moritz, 1988).



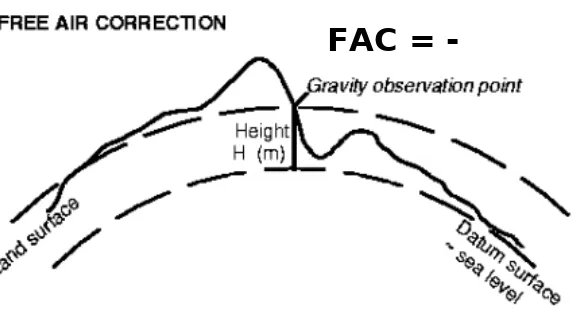
3.5.9. Koreksi Udara Bebas (Free Air Correction)

Koreksi udara bebas merupakan proses pemindahan medan gravitasi normal di referensi sferoida (z = 0) menjadi medan gravitasi normal di permukaan topografi (Gambar 2.8). Rumus matematis orde satu dari koreksi udara bebas pada persamaan (2.16).



_{0,3087691 0,0004398sin}2



fa

g     h

dengan gfa_{adalah nilai koreksi udara bebas dan}h_{adalah ketinggian titik}

amat dari referensi sferoida. Untuk 45o, diperoleh

0,3085672

fa

g   h

Persamaan (2.17) di atas disebut koreksi udara bebas karena hanya (2.15)

(2.16)

(2.17)

FAC =

(24)

dengan referensi sferoida. Sedangkan massa yang terletak di antara topografi dan referensi sferoida diabaikan.

Dengan koreksi udara bebas diperoleh anomali medan gravitasi udara bebas di topografi yang dirumuskan persamaan (2.18) atau (3.19).



, ,



, ,



, ,0



fa obs n fa

g x y z g x y z g x y g 

  _  _

atau



, ,



, ,



, ,



fa obs n

g x y z g x y z g x y z

  

dengan gn(x , y , z) adalah medan gravitasi normal di bidang topografi dan

∆ g_{fa adalah anomali medan gravitasi udara bebas (Li dan Gotze, 2001).}

3.5.10. Koreksi Medan (Terrain Correction)

Adanya massa yang terletak di bawah permukaan antara titik pengamatan pada ketinggian h dan bidang sferoida sangat mempengaruhi gaya gravitasi (gambar 2.9).

24

(2.18)

(2.19)

(25)

Koreksi Bouguer sederhana mencakup massa berbentuk slab horisontal tak hingga. Dalam koreksi Bouguer ini keberadaan massa di atas bidang Bouguer dan bagian massa yang hilang di bawah bidang Bouguer yakni lembah tidak diperhitungkan. Akibat dari massa ini disebut dengan efek medan (terrain effect) dan untuk mengatasinya dilakukan koreksi medan (terrain). Salah satu metode yang digunakan dalam koreksi medan (Terrain) adalah metode Hammer.

Dalam metode Hammer, daerah sekitar titik amat dibagi menjadi zona-zona melingkar dan tiap zona dibagi menjadi sektor-sektor dengan menggunakan diagram zona seperti terdapat pada gambar (2.10). Penjelasan lebih rinci tentang penggunaan metode Hammer dapat dilihat di Lampiran …..

(26)

Perhitungan nilai koreksi medan untuk tiap sector pada metode Hammer diperoleh berdasarkan rumus untuk menghitung gaya Tarik gravitasi dari sebuah silinder kosong vertikal sebagai berikut :



2 2 2 2

Dimana G merupakan konstanta gravitasi universal,  merupkan densitas

darimassa, r1_{merupakan jari-jari dalam dari zona tertentu,}r2_merupakan

jari-jari luar dari zona tertentu dan h merupakan tinggi dari silinder (yang merupakan rata-rata beda elevasi untuk setiap sector). Anomali yang dihasilkan setelah dilakukan koreksi Bouger dan Terrain disebut Anomali Bouger Lengkap (ABL) pada topografi.

3.5.11. Koreksi Bouger Sederhana

Koreksi Bouguer sederhana mencakup massa berbentuk lempeng (slab) horisontal dengan ketebalan tertentu yang panjangnya tak hingga. Massa ini terletak antara bidang Bouguer dengan referensi sferoida (Gambar 2.11). Dimana bidang Bouguer merupakan slab tak hingga yang melalui titik amat. Efek dari massa ini disebut dengan efek Bouguer. Model koreksi ini dikenal model slab horisontal tak hingga dengan ketebalan h relatif dari referensi sferoida ke bidang Bouguer letak titik amat. Besarnya koreksi Bouguer adalah persamaan (2.21).

(27)

dengan ρ adalah densitas massa Bouguer (massa topografi), G adalah konstanta gravitasi umum dan h adalah ketinggian titik amat dari referensi sferoida. Anomali Bouger sederhana didefinisikan sebagai berikut :



int



Obs L ang

SBA G  G FAC BC

dengan SBA adalah nilai anomali Bouger sederhana, GObs_{adalah nilai}

gravitasi observasi, GLintang_{adalah nilai gravitasi terkoreksi lintang,}FAC

adalah nilai koreksi free air dan BC adalah koreksi bouger.

3.5.12. Koreksi Bouger Lengkap

Anomali Bouger lengkap didapatkan setelah semua data gravitasi direduksi dan nilai gravitasi hanya dipengaruhi oleh densitas bawah permukaannya. Anomali Bouger lengkap didapat setelah terkoreksi medan yang sebelumnya disebut anomali Bouger sederhana. Persamaan untuk

(2.22)

(28)



int



Obs L ang

CBA G  G FAC BC TC 

dengan CBA adalah anomali Bouger lengkap, GObs_{adalah gravitasi}

observasi, GLintang_{adalah nilai gravitasi terkoreksi lintang,}FAC_adalah

koreksi free air, BC adalah koreksi Bouger dan TC adalah koreksi Terrain.

3.6. Reduksi ke Bidang Datar

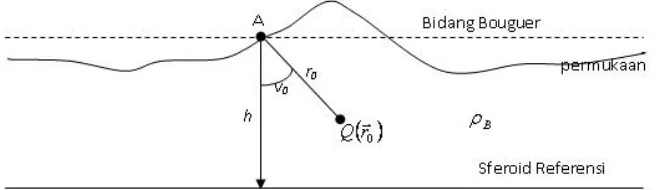
Anomali gravitasi Bouguer lengkap (ABL) adalah data anomali gravitasi yang masih terpapar pada topografi sehingga mempunyai ketinggian yang bervariasi. Variasi ini dapat menyebabkan distorsi pada data gravitasi. Untuk meminimalkan distorsi dilakukan dengan cara membawa ABL tersebut ke suatu bidang datar dengan ketinggian tertentu. Salah satu metode yang digunakan untuk membawa ABL ke suatu bidang datar adalah menggunakan metode sumber ekivalen titik massa yang dikemukakan oleh Dampney (1969).

Proses yang ditempuh dalam metode Dampney adalah menentukan sumber ekivalen titik massa diskrit pada kedalaman tertentu di bawah permukaan dengan memanfaatkan data ABL di permukaan. Kemudian dihitung medan gravitasi teoritis yang diakibatkan oleh sumber ekivalen tersebut pada suatu bidang datar dengan ketinggian tertentu (Gambar 2.12). Data anomali gravitasi yang terletak pada titik-titik yang tidak teratur dengan ketinggian yang bervariasi dapat dibuat suatu sumber

28

(29)

ekivalen titik-titik massa diskrit di atas bidang datar dengan kedalaman tertentu di bawah permukaan bumi. Kedalaman bidang sumber ekivalen titik-titik massa harus tetap dijaga dengan batas tertentu. Setelah sumber ekivalen diperoleh, maka secara teoritis dapat dihitung percepatan gravitasi yang diakibatkan oleh sumber tersebut pada bidang datar sembarang dengan grid yang diinginkan. Sifat dasar dari suatu medan gravitasi yaitu adanya ketidakteraturan yang selalu menyertai di dalam usaha untuk menentukan sumber penghasil medan gravitasi (Dampney, 1969).

Untuk mendapatkan nilai kedalaman sumber ekivalen titik massa yang terbaik, beberapa tes telah dilakukan sehingga diperoleh kesimpulan bahwa selisih jarak antara sumber ekivalen titik massa dan ketinggian bidang datar dari sferoida referensi minimal 2,5 kali jarak rata-rata antar stasiun pengukuran dan maksimal 6 kali jarak rata-rata antar stasiun

Gambar 2.12 Sumber ekivalen titik massa (Setyawan, 2005)

(30)



2,5 x h z  6 x

dengan Δx adalah jarak rata-rata antar stasiun pengamatan, h adalah kedalaman bidang ekivalen titik massa dan z adalah ketinggian titik pengamatan (Setyawan, 2005).

Anomali gravitasi di suatu titik yang disebabkan oleh sumber ekivalen tersebut dapat dihitung dengan menggunakan persamaan (Dampney,

adalah konstanta gravitasi umum, z adalah sumbu tegak yang menyatakan jarak dari topografi ke sferoida referensi dengan arah positif ke bawah dan h adalah kedalaman sumber ekivalen titik-titik massa dari sferoida

referensi.

Jika terdapat N buah titik data, maka dapat dihitung besarnya N buah titik massa pada kedalaman tertentu dengan menggunakan persamaan :

(31)



Selanjutnya, diperoleh anomaly gravitasi pada bidang datar :



anomali gravitasi di bidang datar.

3.7. Kontinuasi Ke Atas (Upward Kontinuation)

Data anomali gravitasi terjadi karena ketidakseragaman distribusi dari densitas semua massa yang ada di dalam Bumi. Jika batuan memiliki

densitas  berada diantara batuan lain yang memiliki densitas 0_maka

perbedaan densitas antara kedua batuan tersebut adalah     0_dan

disebut dengan kontras densitas. Jika kontras densitas batuan bernilai positif, anomali yang dihasilkan juga akan menunjukkan nilai positif sebaliknya jika kontras batuan bernilai negatif maka anomali yang dihasilkan akan negatif. Bentuk dari anomali gravitasi bergantung dari tiga hal yaitu bentuk dari batuan anomali, kontras densitas dan kedalaman anomali. Respon anomali gravitasi memiliki panjang gelombang yang beragam, untuk anomali dengan gelombang yang lebar dan amplitudo landai diakibatkan oleh batuan yang lebar dan dalam, anomali ini disebut anomali regional, sedangkan anomaly dengan panjang gelombang yang kecil dan (2.27)

(32)

memiliki amplitudo yang tajam diakibatkan oleh batuan yang kecil dan dangkal disebut sebagai anomali lokal (anomali residual).

, i1, 2,3,....

3.9. Second Vertical Derivative (SVD)

Second Vertical Derivative (SVD) ini memunculkan efek dangkal dari

pengaruh regionalnya sehingga proses pentapisan dengan metoda ini dapat

Gambar 2.13 Gradien horizontal terhadap anomali gravitasi pada model tabular (Blakely, 1996)

(34)

meyelesaikan masalah anomali residual yang tidak mampu dipisahkan dengan metode pemisahan residual-regional yang ada.

Secara teoritis, metoda ini diturunkan dari persamaan Laplace’s



derivatif orde dua horizontalnya, artinya bahwa anomali SVD dapat melalui derivatif orde dua horizontalnya yang lebih praktis dikerjakan.

3.10. Pemodelan Gravitasi

Setelah dilakukan pemisahan anomali residual dan regional, tahapan selanjutnya dengan melakukan pemodelan 2 dimensi (2D), yang dimaksud benda 2D adalah benda 3D yang memiliki penampang yang sama dimana saja sepanjang tak berhingga pada salah satu arahnya. Dengan pemodelan 2D dapat memperkirakan formasi bawah permukaan.

34

(2.31)

(2.32)

(35)

Pemodelan 2D ini dibuat berdasarkan prinsip Talwani. Dalam model 2D yang dikembangkan oleh Talwani, bentuk dari model Talwani dapat diwakili oleh suatu polygon berisi n. pemodelan ke depan untuk menghitung anomali gravitasi yang dinyatakan sebagai integral garis sepanjang sisi-sisi polygon dinyatakan Talwani dalam rumusan :

2

z

g  G

_

_

zd

Integral garis tertutup tersebut dapat pula dinyatakan sebagai jumlah integral tiap garis tiap sisinya, sehingga dapat ditulis sebagai :

1 polygon-poligon dalam system koordinat kartesian (gambar 2.14).



Gambar 2.14 Poligon model Talwani (Blakely, 1996)

(36)

(37)

BAB III

METODE PENELITIAN

3.1. Waktu dan Tempat Penelitian

Penelitian ini dilakukan pada bulan Januari hingga Juni 2016 dengan proses pengambilan data line pertama sampai line ketiga pada tanggal 26 – 28 Mei 2015 sedangkan line keempat pada tanggal 22 Oktober 2015. Penambahan line kelima sampai ketujuh sedang dalam rencana sekitar bulan Mei sampai Juni 2016. Lokasi penelitian berada di daerah Parangtritis Bantul Yogyakarta.

Daerah Penelitian

(38)

3.2. Alat dan Bahan Jumlah

Properti Lapangan (Akuisisi)

1. Gravitymeter La Coste & Romberg tipe G-1053 1 Buah

2. GPS Tremble Navigation 4600 LS 2 Buah

3. GPS Handheld 1 Buah

4. Tripod dan Bipod 1 Buah

5. Aki Kering 1 Buah

6. Meteran 1 Buah

7. Penggaris 1 Buah

8. Jam Digital 1 Buah

9. Log Sheet Pengambilan Data 1 Set

10. Peta Geologi dan RBI daerah Penelitian 1 Set

Properti Pengolahan (Processing)

1. Microsoft Office Excel 2013 1 Set

2. Golden Software Surfer 12 1 Set

3. Global Mapper 13 1 Set

4. Grav2dc 1 Set

5. Grav-TC 1 Set

6. Google Earth 1 Set

7. Rockworks99 1 Set

8. Geosoft Oasis Montaj 6 1 Set

9. Corel Draw X7 1 Set

10. Matlab R2009a 1 Set

(39)

3.3. Prosedur Kerja

Prosedur pelaksanaan penelitian secara umum dapat dilihat pada gambar 3.2

Gambar 3.2. Diagram Alir Pelaksanan Penelitian Mulai

Selesai

Processing Data

Interpretasi Data

Penulisan Laporan Skripsi Akuisisi Data Pembuatan Desain

(40)

Pelaksanaan penelitian secara lengkap diuraikan sebagai berikut :

3.3.1. Studi Pendahuluan

Studi pendahuluan meliputi pengkajian dan pencarian informasi mengenai calon lokasi penelitian mulai dari potensi apa yang akan dicari, target serta informasi geologi daerah tersebut sebelum masuk ke langkah pembuatan desain survey.

3.3.2. Pembuatan Desain Survey

Desain survey dibuat menggunakan Software Surfer 12 dengan metode Grid System dengan jarak antar titik sebesar 200 meter dan jarak antar lintasan sebesar 300 meter. Terdapat 7 lintasan dengan jumlah titik per lintasan sebanyak 11 titik. Sehingga dapat dihitung luas daerah penelitian sebesar 2 km x 1,8 km. Desain Survey di overlay dengan Peta Geologi dan Peta RBI daerah penelitian. Tampilan detail desain survey yang telah dibuat dapat dilihat pada gambar (3.2) dan gambar (3.3).

(41)

(42)

42

(43)

3.3.3. Akuisisi Data

Akuisi data dilakukan dengan metode looping, yaitu menggunakan satu titik acuan sebagai base. Pengukuran dimulai di base dan diakhiri di base kembali dalam periode harian.

Mulai

pengukuran dalam sehari Atur GPS (_{selama pengukuran}Rover) ON

Waktu

di OFF kan Merapikan Alat

(44)

3.3.4. Processing Data

(45)

Deskripsi Processing data dapat dijabarkan sebagai berikut : a. Konversi skala bacaan dan feedback ke mGal

Data output dari alat Gravitymeter masih dalam skala alat dan harus dikonversi ke miligal dengan bantuan tabel konversi (lampiran 1) dan dengan menggunakan persamaan (2.7) dan (2.8).

b. Menghitung koreksi tinggi alat

Selisih antara gravitymeter dan GPS Tremble menyumbang nilai pada hasil pengukuran sehingga harus dikoreksi. Proses perhitungan koreksi tinggi alat dengan menggunakan persamaan (2.9).

c. Menghitung koreksi pasang surut

Benda disekitar bumi (matahari dan bulan) turut menyumbang nilai dalam pengukuran gravitasi sehingga harus dikoreksi. Proses perhitungan nilai pasang surut menggunakan persamaan (2.10) dan proses perhitungan menggunakan software grav-tc.exe. Proses perhitungan nilai pasang surut menggunakan software grav-tc.exe dapat dilihat pada lampiran …..

d. Menghitung koreksi drift

Koreksi drift dilakukan karena kelelahan alat yang dibawa dari awal pengukuran ke titik-titik pengukuran di berbagai elevasi sehingga menyebabkan pegas tidak stabil dan harus dikalibrasi ulang. Proses perhitungan koreksi drift menggunakan persamaan (2.11).

(46)

Gravitasi observasi merupakan nilai gravitasi yang diperoleh dari pengukuran dilapangan dengan kondisi yang sebenarnya pada tiap titiknya. Proses perhitungan nilai gravitasi observasi mengunakan persamaan (2.12).

f. Menghitung G. Normal / G Lintang

G. Normal atau G. Lintang merupakan nilai gravitasi pada titik pengukuran secara teoritis dengan menganggap bumi berbentuk ellipsoid. Nilai gravitasi teoritis berubah terhadap posisi lintang. Pendekatan terbaru perhitungan G. Lintang adalah yang diterbitkan NIMA model bumi WGS84 dengan menggunakan persamaan (2.15).

g. Menghitung koreksi udara bebas (free air)

Efek free air perlu dihitung untuk membawa nilai pengukuran



x y, ,0



_menuju

_

x y z, ,

_

_{karena proses pengukuran dilakukan di}

topografi bukan di MSL (Mean Sea Level). Proses perhitungan koreksi free air menggunakan persamaan (2.16) kemudian didapatkan anomali free air dengan menggunakan persamaan (2.19).

h. Menghitung koreksi Medan (Terrain)

Lembah dan bukit disekitar titik pengukuran turut menyumbang nilai pada pengukuran. Untuk menghilangkan efek tersebut dilakukan koreksi terrain. Proses perhitungan secara fisis menggunakan persamaan (2.20). Proses pencarian koreksi Terrain menggunakan software Geosoft Oasis Montaj 6 dengan bekal peta DEM (Digital Elevation Model)

(47)

daerah penelitian untuk menentukan jari-jari local dan regionalnya (Lampiran …).

i. Menghitung koreksi Bouger

Pada koreksi free air membawa nilai gravitasi teoritis ke topografi

dengan asumsi dari



x y, ,0



menuju



x y z, ,



tidak ada apapun (kosong). Padahal sebenarnya antara keduanya terdapat massa. Koreksi Bouger untuk menghitung efek massa yang ada antara MSL (Mean Sea Level) dengan topografi. Perhitungan koreksi Bouger menggunakan persamaan (2.21) dan didapatkan anomali Bouger sederhana dengan persamaan (2.22) serta didapatkan anomali Bouger lengkap dengan persamaan (2.23).

j. Reduksi ke Bidang Datar

Nilai anomali yang didapatkan masih terpapar di topografi dan untuk memudahkan pengolahan selanjutnya maka dilakukan reduksi ke bidang datar. Proses ini menggunakan prinsip dampney metode titik massa. Proses perhitungan secara fisis menggunakan persamaan (2.25) dengan bantuan software Matlab R2009a. (lampiran …..)

k. Kontinuasi ke atas (Upward Kontinuation)

(48)

dalam dipilih anomali regional. Proses perhitungan kontinuasi keatas secara fisis mengunakan persamaan (2.29) dengan bantuan software Geosoft Oasis Montaj 7. Target dalam penelitian ini adalah anomali regional yang nantinya akan dimodelkan (lampiran …..)

l. Analisis Derivatif

Analisis derivatif untuk menentukan batas struktur dan jenis sesar dilakukan dengan cara menghitung First Horizontal Derivatif dan Second Vertical Derivatif dari peta anomali regional. Dari penampang

FHD dapat diketahui batas sesar berdasarkan kemenerusan FHD maksimum atau minimum pada penampang FHD. Dari penampang SVD dapat diketahui jenis sesar yang terbentuk berdasarkan perbandingan antara SVD maksimum dan minimum. Reynold (1997) menyatakan untuk menentukan jenis sesar adalah :

2 2

Untuk melihat target berupa struktur dan perlapisan batuan bawah permukaan di area panasbumi dalam penelitian ini dilakukan pemodelan. Dari peta anomali regional yang didapat, diambil tujuh penampang yang mewakili daerah prospek yang dipekirakan merupakan daerah yang dapat

48

(3.1) Untuk sesar normal

(49)

menggambarkan system panasbumi dengan baik. Pemodelan ini menggunakan Grav2dc.

3.3.5. Interpretasi Data

Hasil dari pengolahan data didapatkan peta anomali regional dan residual daerah penelitian. Anomali residual dimodelkan guna memberikan suatu gambaran yang lebih informative mengenai daerah potensi panasbumi parangwedang. Identifikasi struktur dengan menggunakan analisis derivatif FHD dan SVD. Dengan memperhatikan aspek geologi daerah penelitian dan factor-faktor lain dilakukan interpretasi kualitatif dan kuantitatif.

3.5.6. Penulisan Laporan Skripsi

(50)

DAFTAR PUSTAKA

Blakely, Richard J. 1995. Potential Theory In Gravity And Magnetic Applicatons. United States of America : Cambridge University Press.

Idral, A,. Et.al. 2003. Penyelidikan Terpadu geologi, Geokimia, dan Geofisika daerah Panas Bumi Parangtritis, Daerah Istimewa Yogyakarta.

SUBDIT, Panas Bumi.

Meilisa dan Sarkowi, M. 2013. Analisis Data Gravitasi Untuk Menentukan Struktur Bawah Permukaan Daerah Manifestasi Panasbumi di Lereng

Selatan Gunung Ungaran. Seminar Nasional Sains & Teknologi V

Lembaga Penelitian Universitas Lampung

Noor, D. 2009. Pengantar Geologi. Bogor : CV. Graha Ilmu

Nurwidyanto, M. I., dkk. 2011. Study Pendahuluan Sesar Opak dengan Metode Gravity (Studi Kasus Daerah Kecamatan Pleret Bantul). Jurnal Berkala

Fisika Vol. 14, No. 1 Januari 2011, hal 11- 16

Raehanayati, Rachmansyah, A., dan Maryanto, S. 2013. Studi Potensi Energi Geothermal Blawan-Ijen, Jawa Timur Berdasarkan Metode Gravity.

Jurnal Neutrino Vol. 6, No. 1 Oktober 2013. Malang : Universitas Brawijaya

Ridhwan, M. 2010. Interpretasi Struktur Bawah Permukaan Daerah Kretek dan Sekitarnya Kabupaten Bantul Provinsi D.I. Yogyakarta Berdasarkan

Anomali Gravitasi. Jurusan Fisika Fakultas Matematika dan Ilmu

Pengetahuan Alam Universitas Diponegoro Semarang

(51)

Sismanto. 2013. Penyelidikan Geofisika Panas Bumi : Modul 2 Pemetaan Geofisika Daerah Potensi Panas Bumi. Pusat Pendidikan Dan Pelatihan

Geologi Badan Diklat Energi Dan Sumber Daya Mineral Kementerian Energi Dan Sumber Daya Mineral