MODUL RESPONSI MAM 4222 KALKULUS IV

(1)

MAM 4222 KALKULUS IV

Mata Kuliah Wajib 2 sks

untuk mahasiswa Program Studi Matematika

Oleh

Dr. WURYANSARI MUHARINI KUSUMAWINAHYU, M.Si.

PROGRAM STUDI MATEMATIKA

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

(2)

I Barisan Bilangan Real 1

I. 1 Konvergensi Barisan . . . 1

I. 2 Sifat-sifat Barisan Konvergen . . . 6

I. 3 Barisan Monoton dan Terbatas . . . 8

I. 4 Barisan Divergen . . . 12

I. 5 Barisan Cauchy . . . 12

I. 6 Soal-soal Latihan Barisan . . . 13

II Deret Bilangan Real 15 II. 1 Deret Tak Hingga . . . 15

II. 2 Teorema-teorema tentang Deret . . . 16

II. 3 Uji Deret Positif (Tak Negatif) . . . 18

II. 4 Deret Berayun . . . 19

II. 5 Deret Kuasa . . . 21

II. 6 Deret Taylor dan Deret Mac Laurin . . . 22

II. 7 Operasi pada Deret Kuasa . . . 23

II. 8 Soal Latihan Deret . . . 24

(3)

BAB I

Barisan Bilangan Real

I. 1

Konvergensi Barisan

Definisi Barisan Tak Hingga

Barisan bilangan real tak hingga (real infinite sequence) adalah fungsi yang mengaitkan

setiap bilangan asli dengan sekumpulan bilangan real. Selanjutnyabarisan bilangan real tak

hingga dalam modul ini disebut dengan barisan. Jadi barisan adalah

f : N_−→R

f : k _7−→f(k) =ak

Notasi:

{ak}∞k=1 ={ak}= (ak)∞k=1 = (ak) = a1, a2, a3, . . .

Pola suatu barisan dapat diketahui dari penyajiannya. Barisan dapat disajikan dengan

menuliskan suku-sukunya, atau dengan memberikan rumus eksplisitnya atau dengan

mem-berikan rumus rekursifnya. Perhatikan contoh berikut.

1. Bila diberikan rumus eksplisit untuk ak adalah ak = 4k −1 maka barisan {ak} =

3,7,11,15,19. . .

2. Bila diberikan rumus rekursif untuk ak adalah a1 = 3, ak = ak−1 + 4 maka barisan

{ak}= 3,7,11,15,19. . .

(4)

Definisi sub barisan

Misalkan (ak)⊂R adalah barisan bilangan real. Sub barisan dari (ak) adalah hasil

kompo-sisi fungsi f_◦g dengan g :N_−→N _dan _g _{monoton naik. Subbarisan dari (a}_k_{) dinotasikan}

sebagai (aki)⊂(ak).

Berikut ini diberikan rumus eksplisit dan barisan yang dihasilkannya

No. Rumus Eksplisit Barisan i. ak = 1 + 2_k 3,2,5₃,6₄,7₅,8₆,9₇, . . .

Selain mengenali pola barisan, hal menarik yang selalu ditanyakan bila kita menghadapi

barisan adalah pertanyaan mengenai perilaku suku-suku barisan bila k membesar terus

menerus menuju tak hingga. Untuk menjawab pertanyaan tersebut dipelajari konsep

kekon-vergenan barisan.

Definisi Konvergensi Barisan

Barisan _{ak}dikatakan konvergen jika terdapat suatu bilangan realL, sedemikian sehingga

pernyataan berikut ini berlaku: untuk setiap bilangan positif ǫ terdapat bilangan asli n0

sehingga _|ak−L|< ǫ, untuk setiapk ≥n0. Jika hal tersebut terjadi maka dikatakan bahwa

(ak) ke L.

Notasi:

lim

(5)

Barisan yang tidak konvergen menuju suatu bilangan berhingga Ldikatakan divergen.

Be-berapa jenis kedivergenan dibahas secara khusus pada sub bab barisan divergen.

Perhatikan bahwa konsep kekonvergenan barisan serupa dengan konsep limit fungsi f(x)

bila x _{→ ∞}, yang telah dipelajari pada kuliah Kalkulus I. Untuk mengilustrasikan hal

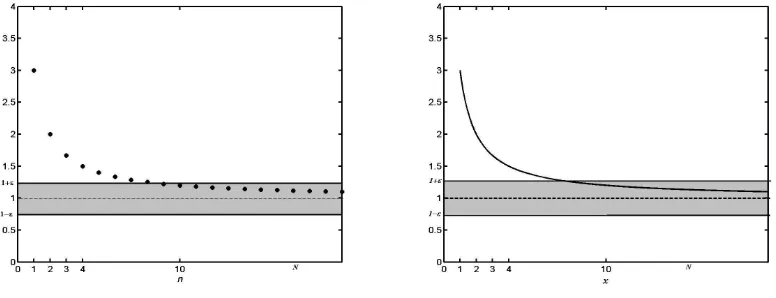
tersebut, perhatikan grafik barisan ak = 1 + 2_k dan grafik fungsi a(x) = 1 + _x2 berikut ini.

Dapatkah saudara melihat perbedaannya? Pada gambar I.1 terlihat bahwa kedua grafik

Gambar I.1: Kaitan ǫdann0dalam definisi kekonvergenan barisan dan fungsi

menuju garis y = 1. Dengan demikian diduga bahwa (ak) konvergen menuju 1. Akan

dibuktikan menggunakan definisi kekonvergenan barisan, bahwa

lim

k→∞ak = limk→∞1 +

2 k = 1.

Menurut definisi, harus dibuktikan bahwa

∀ǫ >0,_∃n0 ∈N∋ |ak−L|< ǫ,∀k ≥n0.

Di siniak = 1 +2_k danL= 1. Karena harus berlaku∀ǫ >0 maka kita ambil sebarangǫ >0.

Selanjutnya, harus ditentukan n0 ∈Nsehingga

1 + 2_k −1

< ǫ,∀k ≥n₀.

Untuk memperoleh nilain0kita lakukan langkah mundur. Yang diinginkan adalah 1 + 2

k −1

=

2_k

= 2_k < ǫ. Pertaksamaan terakhir terpenuhi bila k > 2_ǫ. Dengan demikian harus dipilih

(6)

Jadi telah terbukti bahwa _∀ǫ >0,_∃n0 ∈N dengann0 > 2_ǫ ∋ |ak−L|=

Untuk mengilustrasikan eksistensi nilai n0 pada pembuktian tersebut kita akan mencoba

dengan mengambil sebarang ǫ. Misalkan diambil ǫ = 1, maka n0 ∈ N dengan n0 > 2_ǫ = 2.

misalkan diambil ǫ = 0.01 maka n0 > ₀_.2₀₁ = 200. Artinya, suku-suku barisan ak berada

pada jarak kurang dari 0.01 setelah suku ke-200. Anda dapat mencoba sebarang nilaiǫ >0

yang lain. Apa yang dapat anda simpulkan?

Catatan

Berdasarkan definisi konvergensi barisan tersebut, untuk memeriksa kekonvergenan suatu

barisan terlebih dahulu kita harus mempelajari perilaku suku-suku barisan (ak) bilak

mem-besar menuju tak hingga, sehingga dapat ditebak nilaiL. Hal ini tidak selalu mudah, apalagi

bila ekspresi (ak) cukup rumit. Untuk itu dapat kita gunakan sifat berikut sehingga kita

mungkin dapat menggunakan dalil L’Hospital.

Sifat: Jika lim

Karena harus berlaku _∀ǫ > 0 maka kita ambil sebarang ǫ > 0. Selanjutnya, harus

(7)

Untuk memperoleh nilain0kita lakukan langkah mundur. Yang diinginkan adalah

k < ǫ. Pertaksamaan terakhir terpenuhi

bila k > 64_ǫ2. Dengan demikian harus dipilih n0 ∈N dengan n0 > 64_ǫ2.

3. Buktikan bahwa barisan (ak) dengan ak=k divergen

Jawab:

Andaikan (ak) konvergen maka terdapat suatu bilangan L ∈ R sehingga limk→∞ak =

limk→∞k =L. Berarti∀ǫ >0,∃n0 ∈N∋ |k−L|< ǫ,∀k≥n0.Akibatnya −1< k−L <1,

yang ekivalen dengan₋1 +L < k < L+ 1,_∀k_≥n0.Berarti bahwa himpunan bilangan asli

N _{terbatas. Hal ini tidak benar sehingga pengandaian salah. Jadi seharusnya (a}_k_{) tidak}

konvergen.

4. Buktikan bahwa barisan (ak) dengan ak= (−1)k divergen

Jawab:

Andaikan (ak) konvergen maka terdapat suatu bilangan L ∈ R sehingga limk→∞ak =

limk→∞(−1)k =L . Berarti∀ǫ >0,∃n0 ∈N∋

mustahil. Pengandaian kita tidak benar. Jadi seharusnya (ak) tidak konvergen.

Soal latihan

1. Tentukan n0 agar

Dengan menggunakan definisi kekonvergenan barisan, buktikan bahwa:

(8)

3. limk→∞ k+73kk2 = 0

4. limk→∞ k2+3k = 2

5. limk→∞ _k₊₇3k√_k = 3

I. 2

Sifat-sifat Barisan Konvergen

Teorema: Barisan tak negatif

Jika (ak) barisan tak negatif dan limk→∞ak =Lmaka L≥0

Bukti:

Diketahui ak ≥0,∀k ∈ N. AndaikanL < 0 maka untuk ǫ=−L₂ terdapat n0 ∈ N sehingga

|ak−L|<−L₂,∀k ≥n0.Khususnya untuk k =n0 maka diperoleh |ak0−L|<−L₂.

Akibat-nya ak0 −L < −L₂, sehingga ak0 < L₂ < 0. Dengan demikian ∃n0 ∈ N sehingga ak0 < 0.

Hal ini bertentangan dengan yang diketahui yaitu bahwa ak ≥ 0,∀k ∈ N. Oleh karena itu

pengandaian salah. Jadi haruslah L_≥0. Teorema terbukti

Teorema: Ketunggalan limit

Jika (ak) barisan bilangan real yang konvergen, maka nilai limitnya tunggal. Dengan

perkataan lain, jika limk→∞ak=L dan limk→∞ak=M maka L=M.

Bukti:

Andaikan L ₆= M. Diketahui limk→∞ak = L dan limk→∞ak = M. Berarti ∀ǫ > 0,∃n1 ∈

N_{∋ |}_a_k₋_L_|_{< ǫ,}_∀_k _≥_n₁ _dan _∀_{ǫ >}_0,_∃_n₂ _∈N_{∋ |}_a_k₋_M_|_{< ǫ,}_∀_k _≥_n₂_.

Ambil ǫ = |L−₄M| > 0 maka _∃n1 ∈ N ∋ |ak−L| < |L−₄M|,∀k ≥ n1 dan ∃n2 ∈ N ∋

|ak−M| < |L−₄M|,∀k ≥ n2. Misalkan n0 = max{k1, n2}, maka |ak−L| < |L−₄M| dan

|ak−M| < |L−₄M|,∀k ≥ n0. Khususnya untuk k = n0 maka |ak0 −L| < |L−₄M| dan

|ak0 −M| < |L−₄M|. Perhatikan bahwa |L−M| = |L−ak0 +ak0 −M| ≤ |L−ak0| +

|ak0 −M| = |ak0 −L| +|ak0 −M| < |L−₄M| + |L−₄M| = |L−₂M|. Dengan demikian

diper-oleh _|L₋M_|< |L−₂M|. Mustahil bahwa terdapat bilangan positif yang nilainya kurang dari setengah nilai bilangan tersebut. Berarti pengandaian bahwa L ₆= M tidak benar. Jadi

(9)

Teorema: Ketunggalan limit sub barisan

Jika (ak) barisan bilangan real yang konvergen ke L, maka SETIAP sub barisan (aki) dari

(ak) juga konvergen keL. Akibatnya, semua sub barisan dari suatu barisan yang konvergen

akan konvergen ke nilai limit yang sama.

Memperlihatkan kekonvergenan suatu barisan secara langsung menggunakan definisi

kekon-vergenan barisan tidak selalu mudah, apalagi bila diberikan rumus ak yang rumit. Untuk

mengatasinya, dapat digunakan teorema-teorema berikut.

Teorema: Sifat-sifat Limit Barisan

Misalkan ak dan bk adalah barisan-barisan yang konvergen dan k adalah suatu konstanta,

maka berlaku sifat-sifat berikut.

1. lim

k→∞k =k

2. lim

k→∞kak=kklim→∞ak

3. lim

k→∞(ak±bk) = limk→∞ak±klim→∞bk

4. lim

k→∞(ak·bk) = limk→∞ak·klim→∞bk

5. lim

k→∞ ak

bk =

lim

k→∞

ak

lim

k→∞b

k asalkan lim

k→∞bk6= 0

Coba buktikan kelima sifat tersebut dengan menggunakan definisi kekonvergenan barisan.

Selain menggunakan kelima sifat limit barisan tersebut, kekonvergenan barisan dapat pula

diperiksa dengan menggunakan teorema berikut, yang sering disebut dengan prinsip apit

atau sandwich theorem_.

Teorema: Prinsip APIT

Misalkan ak dan ck adalah barisan-barisan yang konvergen menuju L dan ak ≤ bk ≤ ck

untuk k_≥K, maka bk juga konvergen menujuL.

(10)

ini dapat digunakan untuk memeriksa kekonvergenannya dengan memandang barisan nilai

mutlaknya.

Teorema: konvergensi barisan berubah tanda:

Jika lim

k→∞|ak|= 0 maka limk→∞ak = 0.

Soal latihan

1. Jika (ak) barisan real dengan (ak)≤ M,∀k ∈N dan diketahui lim

k→∞ak =L, buktikan

bahwa L_≤M.

2. Jika L_∈R_{, M} _∈R _dan _L_≤_M ₊_ǫ,_∀_{ǫ >}_{0, buktikan bahwa} _L_≤_M

3. Gunakan sifat _||a_{| − |}b_{|| ≤ |}a₋b_| untuk membuktikan bahwa: Jika (ak) konvergen ke

L maka (_|ak|) konvergen ke|L|.

4. Berikan contoh barisan (ak) yang bersifat (|ak|) konvergen tetapi (ak) tidak konvergen.

5. Tentukan lim

k→∞

√

k√k+ 1₋√k.

6. Jika lim

k→∞ ak−1

ak+1 = 0 buktikan bahwa lim_k

→∞ak = 1.

I. 3

Barisan Monoton dan Terbatas

Pada bagian ini dibahas teorema-teorema yang dapat digunakan untuk memeriksa

kekon-vergenan suatu barisan dengan memanfaatkan sifat kemonotonan dan keterbatasan barisan

tersebut.

Definisi Barisan Monoton

Barisan_{ak}disebut barisan tak turun bilaak≤ak+1,∀k. Sebaliknya, barisan{ak}disebut

barisan tak naik bilaak≥ak+1,∀k. Bila barisan{ak}tak naik atau tak turun maka barisan

(11)

Sebelum membahas barisan terbatas, perlu diperkenalkan terlebih dahulu definisi-definisi,

teorema, dan aksioma mengenai keterbatasan suatu himpunan karena konsep-konsep

terse-but diperlukan dalam pembuktian teorema-teorem mengenai barisan monoton dan terbatas.

Definisi Himpunan Terbatas

Suatu himpunan A_⊂R_{dikatakan Terbatas di Atas jika terdapat bilangan real} _M _sehingga

a _≤M,_∀a_∈A. Sebaliknya, A dikatakan Terbatas di Bawah jika terdapat bilangan real m

sehingga a _≥m,_∀a _∈ A. Dalam hal ini M disebut batas atas dari A dan m disebut batas

bawah dari A. Himpunan A _⊂ R _{dikatakan Terbatas jika} _A _{terbatas di atas dan terbatas}

di bawah. Dengan perkataan lain, himpunan A _⊂R _{terbatas jika dan hanya jika terdapat}

bilangan real m dan M sehingga A _⊂ [m, M]. Perhatikan bahwa batas atas atau batas

bawah suatu himpunan tidak tunggal.

Definisi Supremum

Misalkan A _⊂ R _{adalah himpunan yang terbatas di atas. Bilangan} _α _{disebut Supremum}

atau Batas Atas Terkecil dari A jika

(i)α adalah batas atas dariA

(ii) α _≤M, untuk setiap M batas atas dari A

Notasi: α= supA

Definisi Infimum

Misalkan A _⊂ R _{adalah himpunan yang terbatas di bawah. Bilangan} _β _{disebut Infimum}

atau Batas Bawah Terbesar dari A jika

(i)β adalah batas bawah dari A

(ii) β _≥m, untuk setiap m batas bawah dari A

Notasi: β = infA

Dua teorema berikut dapat digunakan untuk menggantikan definisi supremum dan infimum

(12)

Teorema Supremum

Misalkan A _⊂R _{adalah himpunan yang terbatas di atas. Maka} _α _{= sup}_A _{jika dan hanya}

jika

(i)α adalah batas atas dariA

(ii) _∀ǫ >0_∃a_∈A sehingga a > α₋ǫ

Teorema Infimum

Misalkan A_⊂R _{adalah himpunan yang terbatas di bawah. Maka} _β _{= inf}_A _{jika dan hanya}

jika

(i)β adalah batas bawah dari A

(ii) _∀ǫ >0_∃a_∈A sehingga a < β+ǫ

Aksioma berikut merupakan aksioma yang hanya dimiliki oleh himpunan bilangan real.

Aksioma Eksistensi Supremum Infimum

Misalkan A _⊂ R _{adalah himpunan bilangan real yang terbatas di atas maka} _A _memiliki

supremum di R_{. Sebaliknya, jika} _A _⊂ R _{adalah himpunan bilangan real yang terbatas di}

bawah maka A memiliki infimum di R_.

Definisi Barisan Terbatas

Barisan _{ak}dikatakan terbatas di atas bila terdapat bilanganM ∈Rsedemikian sehingga

ak ≤ M untuk setiap k ∈ N. Barisan {ak} dikatakan terbatas di bawah bila terdapat

bi-langan m _∈ R _{sedemikian sehingga} _a_k _≥ _m _{untuk setiap} _k _∈ N_{. Suatu barisan dikatakan}

terbatas jika barisan tersebut terbatas di atas dan terbatas di bawah. Dengan perkataan lain,

barisan _{ak} ⊂R dikatakan terbatas jika ∃m, M ∈R ∋ ak ∈[m, M],∀k ∈ N. Dapat pula

dikatakan bahwa barisan _{ak} ⊂R dikatakan terbatas jika∃M ∈R∋ |ak| ≤M,∀k ∈N.

Teorema berikut dapat digunakan untuk memperlihatkan bahwa suatu barisan TIDAK

(13)

Teorema: Barisan terbatas

Jika barisan_{ak} konvergen maka {ak} terbatas

Bukti: Diketahui _{ak} konvergen. Misalkan limk→∞ak = L. Berarti ∀ǫ > 0,∃n0 ∈

N _{∋ |}_a_k₋_L_| _{< ǫ,}_∀_k _≥ _n₀_{. Akibatnya} _|_a_k_| ₌ _|_a_k₋_L₊_L_{| ≤ |}_a_k₋_L_| ₊_|_L_| _{< ǫ} ₊

|L_|,_∀k _≥ n0. Jika dimisalkan P = ǫ + |L| maka diperoleh |ak| < P,∀k ≥ n0.

Misal-kan Q = max_{|ak| kk < n0} maka |ak| ≤ Q,∀k < n0. Misalkan M = max{P, Q} maka

|ak| ≤M,∀k ∈N. Jadi telah terbukti bahwa {ak} terbatas.

Perhatikan bahwa menurut teorema tersebut, barisan yang terbatas tidak selalu konvergen.

Sebagai contoh, barisan _{ak} = 1,−1,1,−1,1,−1,1,−1, . . . merupakan barisan terbatas,

namun_{ak} tidak konvergen. Yang dapat disimpulkan dari teorema tersebut adalah bahwa

barisan yang tak terbatas pasti tidak konvergen, sehingga teorema tersebut berguna untuk

memperlihatkan kedivergenan. Namun demikian, Bolzano dan Weierstrass berhasil

menu-runkan suatu teorema yang menyatakan implikasi suatu barisan terbatas, seperti dinyatakan

dalam teorema berikut.

Teorema Bolzano-Weierstrass

Setiap barisan bilangan real yang terbatas pasti memiliki sub barisan yang konvergen.

Teorema berikut menyatakan hubungan antara kemonotonan dan keterbatasan suatu barisan

dengan kekonvergenan, sehingga diperoleh cara lain untuk memperlihatkan kekonvergenan

barisan tanpa menggunakan definisi, melainkan cukup dengan memeriksa kemonotonan dan

keterbatasan barisan saja.

Teorema: barisan monoton

Jika barisan _{ak} terbatas di atas dan monoton tak turun maka barisan {ak} konvergen.

Demikian pula, jika barisan _{ak} terbatas di bawah dan monoton tak naik maka barisan

(14)

I. 4

Barisan Divergen

Definisi Barisan divergen menuju ke tak hingga

Barisan bilangan real (ak) dikatakan divergen menuju tak hingga jika∀M >0, M ∈R∃n0 ∈

N_∋_a_k _≥_M,_∀_k _≥_n₀_{. Notasi: lim}

k→∞ak =∞.

Definisi Barisan divergen menuju ke minus tak hingga

Barisan bilangan real (ak) dikatakan divergen menuju minus tak hingga jika ∀M >0, M ∈

R_∃_n₀ _∈N_∋_a_k_{≤ −}_M,_∀_k_≥_n₀_{. Notasi: lim}

k→∞ak =−∞.

Definisi Barisan berosilasi

Jika barisan bilangan real (ak) divergen namun tidak menuju tak hingga maupun minus tak

hingga maka barisan (ak) disebut barisan berosilasi.

I. 5

Barisan Cauchy

Pada bagian ini diperlihatkan bahwa dengan menggunakan suatu kriteria, yang disebut

kri-teria Cauchy, kita dapat menentukan konvergensi suatu barisan bilangan real tanpa perlu

menentukan nilai Lsebagai nilai limitnya terlebih dahulu.

Definisi: Barisan Cauchy

Barisan bilangan real (ak) disebut barisan Cauchy jika ∀ǫ > 0,∃n0 ∈ N ∋ |ak−am| <

ǫ,_∀k, m_≥n0.

Kriteria konvergensi Cauchy

Barisan bilangan real (ak) konvergen jika dan hanya jika (ak) adalah barisan Cauchy

Bukti:

Akan dibuktikan terlebih dahulu bahwa: jika (ak) konvergen maka (ak) adalah barisan

(15)

Akibatnya _|ak−am| = |ak−L+L−am| ≤ |ak−L|+|L−am| < ₂ǫ + ǫ₂ = ǫ,∀k, m ≥ n0.

Terbukti bahwa (ak) adalah barisan Cauchy.

Pembuktian pernyataan sebaliknya, yaitu jika (ak) adalah barisan Cauchy maka (ak)

kon-vergen, dilakukan dengan menggunakan teorema Bolzano-Wierstrass.

I. 6

Soal-soal Latihan Barisan

1. Pada soal-soal berikut, diberikan rumus eksplisit untukak. Tulislah suku-suku barisan

(ak) dan tentukan apakah barisannya konvergen atau divergen. Jika konvergen,

ten-tukan lim

k→∞ak.

a. ak= 4_kk₋+5₁ b. ak = 6k 2₋₂

3k+1

c. ak= √

k2₊₁

4k+3 d. ak =

kcos(kπ) 6k+5

e. ak=e−ksink f. ak = e 2k

4k

g. ak= 1₄

k

+ 3k/2 _h. _a

k= k 100 ek

i. ak= ln(1√₂/k_k) j. ak = (2k)1/2k

2. Pada soal-soal berikut, tentukan rumus eksplisit untuk setiap barisan. Tentukan

apakah barisannya konvergen atau divergen. Jika konvergen, tentukan lim

k→∞ak.

a. (ak) = ₂12,₂23,₂34,₂45, . . .

b. (ak) = 1,₁₋11 2

,₁1

−2 3

,₁1

−3 4

, . . .

c. (ak) = ₂₋11 2

,₃2

−13

,₄3

−14

,₅4

−15

, . . .

d. (ak) = −1₃,₉4,−₂₇9,16₈₁, . . .

e. (ak) = 1− 1₂,1₂ − 1₃,1₃ −1₄,1₄ − 1₅, . . .

3. Pada soal berikut tunjukkan bahwa (ak) konvergen, dengan menggunakan teorema

kemonotonan.

a. ak= _k₊₁k 2−_k12

b. ak= 1 + _2!1 +_3!1 +_4!1 +. . .+ _k1_!

(16)

d. a1 = 2, ak+1 = 1₂

ak+ _a2k

e. ak=

√

k√k+ 1₋√k

f. ak =k 3 2

√

k3_{+ 1}₋√_k3

4. Misalkan (ak) = 1 +1₂+1₃+₄1+1₅+. . .. Buktikan bahwa barisan (ak+1−ak) konvergen

(17)

BAB II

Deret Bilangan Real

II. 1

Deret Tak Hingga

Misalkan diberikan barisan _{an} =a1, a2, a3, . . .. Misalkan S1 =a1, S2 =a1+a2 = 2 P

n=1

an,

S3 =a1+a2+a3 = 3 P

n=1

an,S4 =a1+a2+a3+a4 = 4 P

n=1

an, . . . ,Sk =a1+a2+a3+a4+. . .+ak =

k

P

n=1

anmaka terbentuklah barisan{Sk}=S1, S2, S3, . . .. Di siniSkdisebut jumlah parsial ke

k, dan P∞

n=1

an =a1+a2+a3+a4+. . .disebut DERET TAK HINGGA atau secara singkat

hanya disebut deret.

Definisi Konvergensi Deret

Deret P∞

n=1

an dikatakan konvergen dan mempunyai jumlah S jika barisan jumlah-jumlah

parsial _{Sk} konvergen menuju S. Notasi:

∞

X

n=1

an = lim k→∞

k

X

n=1

an= lim

k→∞Sk =S.

Sebaliknya, bila barisan_{Sk}divergen maka deret ∞

P

n=1

andikatakan divergen dan tidak

mem-punyai jumlah.

(18)

Contoh:

1. Deret geometri adalah deret yang terbentuk dari barisan_{arn−1_}, dengana₆= 0, yaitu

∞

X

n=1

arn−1 =a+ar+ar2+ar3 +. . . .

Dapat diperlihatkan bahwa deret geometri adalah deret yang konvergen dengan jumlah

S = a

1−r bila |r|<1, namun divergen bila |r| ≥1.

2. Dapat diperlihatkan bahwa deret harmonik

∞

adalah deret yang divergen.

II. 2

Teorema-teorema tentang Deret

Teorema Uji DIVERGENSI

Jika deret P∞

n=1

an konvergen maka lim

n→∞an = 0.

Perlu diperhatikan bahwa jika lim

n→∞an = 0, maka belum tentu deret ∞

P

n=1

an konvergen.

Sifat yang ekivalen dengan teorema tersebut adalah jika lim

n→∞an 6= 0, maka deret ∞

P

n=1

an

divergen. Oleh karena itu, teorema tersebut sangat bermanfaat untuk menguji apakah

suatu deret divergen, yaitu cukup dengan memeriksa lim

n→∞an.

Contoh: deret P∞

n=1

Sifat-sifat kelinieran deret konvergen

Jika P∞

bnkonvergen dancadalah suatu konstanta, maka deret ∞

(19)

(i) P∞

Teorema: Jika P∞

n=1

an divergen maka ∞

P

n=1

c an juga divergen.

Teorema

Jika deret P∞

n=1

an konvergen maka suku-suku dalam deret tersebut boleh dikelompokkan

de-ngan sebarang cara dan deret yang dihasilkan dari pengelompokan suku-suku deret tersebut

akan konvergen dengan jumlah yang sama dengan deret semula.

Soal Latihan

1. Buktikan bahwa: jika a1 + a2 + a3 +a4. . . konvergen ke s maka a2 +a3 +a4. . .

konvergen ke s₋a1

2. Buktikan bahwa deret P∞

n=1

5. Buktikan bahwa: deret P∞

n=1

6. Apakah deret berikut konvergen?

a. P∞

7. Buktikan bahwa: jika P∞

n=1

ankonvergen keAmaka 1₂(a1+a2)+₂1(a2+a3)+1₂(a3+a4)+. . .

(20)

8. Berikan contoh deret P∞

n=1

anyang bersifat: (a1+a2)+(a3+a4)+(a5+a6)+(a7+a8)+. . .

konvergen tetapi a1+a2+a3+a4+. . .divergen

II. 3

Uji Deret Positif (Tak Negatif )

Dalam sub bab ini dibahas mengenai beberapa uji yang dapat digunakan untuk menentukan

kekonvergenan suatu deret dengan suku-suku tak negatif atau positif.

Teorema

Deret P∞

n=1

an, dengan an ≥0 akan konvergen jika dan hanya jika jumlah-jumlah parsialnya

terbatas di atas, yaitu Sn≤M untuk suatu bilangan positifM.

Teorema: uji integral

Misalkan f(x) adalah fungsi yang kontinu, bernilai positif, dan monoton tak naik pada

se-lang [1,_∞], dan andaikan an =f(n),∀k ∈ N. Maka deret tak hingga ∞

P

n=1

an konvergen jika

dan hanya jika integral tak wajar R∞ 1

f(x)dx konvergen .

Teorema tersebut sering dinyatakan pula sebagai berikut. Deret P∞

n=1

f(n) dan integral tak

wajar R∞ 1

f(x)dx konvergen atau divergen secara bersamaan.

Teorema: uji banding biasa

Misalkan 0_≤an ≤bn,∀n ≥N, untuk suatu N.

(i) Jika P∞

n=1

bn konvergen, maka demikian pula halnya dengan ∞

P

n=1

an

(ii) Jika P∞

n=1

an divergen, maka demikian pula halnya dengan ∞

P

n=1

bn.

Teorema: uji banding limit

Misalkan an ≥0, bn≥0, dan

lim

n→∞

an

bn

(21)

(i) Jika 0< L <_∞maka P∞

n=1

an dan ∞

P

n=1

bn sama-sama divergen atau sama-sama konvergen

(ii) Jika L= 0 dan P∞

n=1

bn konvergen, maka ∞

P

n=1

an konvergen.

Teorema: uji rasio

Misalkan P∞

n=1

an adalah deret dengan suku-suku positif dan

ρ= lim

n→∞

an+1

an

.

(i) Jika ρ <1 maka deret tersebut konvergen

(ii) Jika ρ >1 maka deret tersebut divergen

(iii) Jika ρ= 1 maka kekonvergenan deret tersebut tak dapat ditentukan.

Teorema: uji akar

Misalkan P∞

n=1

an adalah deret dengan suku-suku positif dan

ρ= lim

n→∞

n √_a

n.

(i) Jika ρ <1 maka deret tersebut konvergen

II. 4

Deret Berayun

Dalam sub bab ini dipelajari deret berayun, yaitu deret yang nilainya berubah-ubah dari

negatif ke positif dan sebaliknya. Deret berayun sering pula disebut deret berganti tanda.

Bentuk umum deret berganti tanda adalah

∞

X

n=1

(22)

Teorema: uji deret berayun

Misalkan P∞

n=1

(₋1)n+1_a

nadalah deret berayun dengan an> an+1 >0. Jika lim

n→∞an = 0,maka

deret berayun P∞

n=1

(₋1)n+1_a

n konvergen.

Definisi Konvergen Mutlak

Deret P∞

n=1

un disebutkonvergen mutlak jika ∞

P

n=1|

un|konvergen.

Teorema: uji konvergensi mutlak: Jika P∞

n=1|

un| konvergen maka ∞

P

n=1

un konvergen.

Dengan perkataan lain, teorema tersebut menyatakan bahwa deret yang konvergen mutlak

pasti konvergen.

Teorema: uji rasio mutlak

Misalkan P∞

n=1

un adalah deret dengan suku-suku tak nol dan

ρ= lim

n→∞

|un+1|

|un|

.

(i) Jika ρ <1 maka deret tersebut konvergen mutlak (sehingga konvergen)

Definisi Konvergen Bersyarat

Deret P∞

n=1

un disebutkonvergen bersyarat jika ∞

P

n=1

unkonvergen namun ∞

P

n=1|

un|divergen.

Contoh: deret harmonik berayun merupakan contoh deret yang konvergen bersyarat.

Teorema:Jika deret P∞

n=1

un konvergen mutlak maka suku-suku dalam deret tersebut boleh

(23)

II. 5

Deret Kuasa

Pada sub bab - sub bab sebelumnya, deret yang kita bahas adalah deret dengan suku-suku

konstan, yaitu P∞

n=1

un, dengan un berupa konstanta. Kini akan dibahas deret dengan

suku-suku berupa fungsi, yaitu deret berbentuk P∞

n=1

un(x). Lebih khusus lagi, dalam sub bab ini

dibahas deret fungsi P∞

n=1

un(x), dengan un(x) berupa fungsi pangkat dalam x. Deret yang

demikian disebut deret pangkat atau deret kuasa (power series). Bentuk umum deret kuasa

dalam x adalah

∞

X

n=1

an(x−c)n=a0+a1(x−c) +a2(x−c)2+a3(x−c)3+. . . ,

denganc adalah suatu konstanta tertentu yang disebut pusat deret kuasa.

Bila c= 0 maka diperoleh deret kuasa yang sederhana yaitu

∞

X

n=1

anxn=a0+a1x+a2x2+a3x3+. . . .

Bila kita ganti x dengan suatu bilangan, maka akan diperoleh deret konstanta yang dapat

dikaji kekonvergenannya. Dengan demikian sangat masuk akal bila muncul dua pertanyaan

berikut.

1. Untuk nilai xberapakah deret kuasa akan konvergen?

2. Bila deret kuasa tersebut konvergen, akan menuju ke fungsi S(x) yang bagaimanakah?

Definisi: himpunan semua nilai x yang membuat suatu deret kuasa menjadi konvergen

disebut himpunan konvergensi atau daerah kekonvergenan atau selang kekonvergenan deret

kuasa tersebut.

Teorema: Daerah kekonvergenan deret kuasa P∞

n=1

an(x−c)n pasti merupakan salah satu

dari tiga kemungkinan berikut.

(24)

(ii) Selang (c₋R, c+R), ditambah kemungkinan salah satu atau kedua titik ujungnya.

Pada kasus ini dikatakan bahwa jari-jari konvergensinya adalah R

(iii) Seluruh garis bilangan real. Pada kasus ini dikatakan bahwa jari-jari konvergensinya

adalah _∞.

Untuk menentukan daerah kekonvergenan dan jari-jari konvergensi, digunakan uji rasio

mut-lak, yaitu P∞

1. Pertaksamaan terakhir akan terpenuhi jika_|x₋c_|< lim

n→∞

dapat disimpulkan bahwa deret kuasa berpusat di x = c konvergen bila _|x₋c_| < R yang

ekivalen dengan mengatakanx_∈(c₋R, c+R). Dalam hal iniRdisebut JARI-JARI

KON-VERGENSI dan selang (c₋R, c+R) disebut SELANG KONVERGENSI atau DAERAH

KONVERGENSI deret kuasa. PERLU DIINGAT bahwa boleh jadi, pada ujung-ujung

se-lang, yaitu untukx=c₋Rdan x=c+R deret kuasa P∞

n=1

an(x−c)n juga konvergen. Oleh

karena itu, harus selalu diperiksa apakah deret kuasa konvergen di kedua titik tersebut.

PEMERIKSAAN DI KEDUA TITIK UJUNG PASTI GAGAL BILA MENGGUNAKAN

UJI RASIO, SEHINGGA HARUS DIGUNAKAN UJI DERET YANG LAIN.

Untuk menentukan jari-jari konvergensi, dapat pula digunakan uji akar, yaitu P∞

n=1

. Jadi, dengan menggunakan uji akar

diperoleh cara lain menentukan jari-jari konvergensi, yaitu R= lim

n→∞

II. 6

Deret Taylor dan Deret Mac Laurin

Deret Taylor dan Deret Mac Laurin merupakan contoh deret kuasa. Pada kuliah Kalkulus

I telah dipelajari teorema Taylor yang menyatakan suatu fungsi sebagai deret kuasa.

Teorema Taylor

(25)

domainf(x) maka Deret Taylor dari f(x) di sekitar x=cadalah

Sebagai contoh, telah kita pelajari deret Taylor atau Mac Laurin dari fungsi-fungsi berikut.

1. sinx= P∞

Tugas: tentukan jari-jari dan selang konvergensi ketujuh deret kuasa tersebut.

II. 7

Operasi pada Deret Kuasa

Teorema: penjumlahan deret kuasa

Pada daerah konvergensinya, dua deret kuasa dapat dijumlahkan atau dikurangkan suku

(26)

Teorema: turunan deret kuasa

Pada daerah konvergensinya, turunan dari deret kuasa dapat ditentukan dengan

menurun-kannya suku demi suku.

Contoh:

Deret Mac Laurin untuk cosinus dapat diperoleh dengan menurunkan deret Mac Laurin

untuk sinus suku demi suku.

cos(x) = d

Teorema: integral deret kuasa

Pada daerah konvergensinya, integral dari deret kuasa dapat ditentukan dengan

menginte-gralkannya suku demi suku.

Contoh Deret Mac Laurin untuk sin(x) dapat diperoleh dengan mengintegralkan deret Mac

Laurin untuk cos(x) suku demi suku.

cos(x) =

II. 8

Soal Latihan Deret

1. Dengan menentukan rumus untuk an, tentukan kekonvergenan deret berikut.

(27)

b. ₁1_·₂ + ₂1_·₃ +₃1_·₄ +₄1_·₅ +. . .

2. Dengan menggunakan sifat-sifat deret yang telah dipelajari, periksalah apakah

deret-deret berikut konvergen

3. Periksalah apakah deret berikut konvergen, atau konvergen mutlak, atau divergen

(28)

h. P∞

n=1

(₋1)n+1 n

2n−1

i. P∞

n=1 1

√ n+