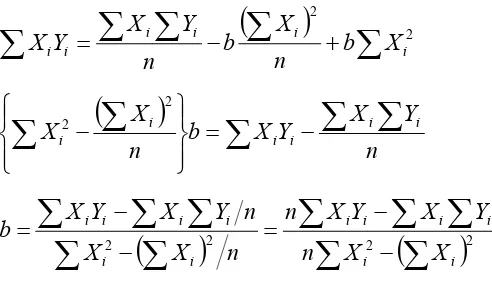Penentuan Koefisien Multiple Regresi Dengan Menggunakan Metode Linier Programming

PENENTUAN KOEFISIEN MULTIPLE REGRESI

DENGAN MENGGUNAKAN METODE LINIER

PROGRAMMING

SKRIPSI

RINA ASTRY GINTING

060823031

PROGRAM STUDI SARJANA MATEMATIKA DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

PERSETUJUAN

Judul : PENENTUAN KOEFISIEN MULTIPLE REGRESI DENGAN METODE LINIER PROGRAMMING

Kategori : SKRIPSI

Nama : RINA ASTRY GINTING

Nomor induk Mahasiswa : 060823031

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di

Medan, Oktober 2008

Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Drs. H. Haluddin Panjaitan Drs. Marwan Harahap, M.Eng

NIP. 130 701 888 NIP. 130 422 443

Diketahui oleh

Departemen Matematika FMIPA USU Ketua,

PERNYATAAN

MENENTUKAN KOEFISIEN MULTIPLE REGRESI DENGAN METODE LINIER PROGRAMMING

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Oktober 2008

PENGHARGAAN

Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Pemurah dan Maha Penyayang, dengan limpah kurnia-Nya skripsi ini berhasil diselesaikan dalam waktu yang telah ditetapkan.

Abstrak

Didalam upaya penentuan persamaan estimasi linier dengan metode garis lurus akan menghasilkan persamaan yang baik, jika semua titik yang mencerminkan pasangan data berada di sekitar garis lurus tersebut. Namun, jika titik-titik pasangan data tersebar satu sama lain, maka persamaan linier yang baik untuk mengestimasi nilai variabel dependen adalah persamaan linier yang yang kurvanya mempunyai kesalahan yang minimum antara titik estimasi dengan titik sebenarnya. Maka dari pada itu, penelitian ini menerangkan bagaimana cara untuk mendekati garis regresi dengan teknik linier programming.

Bentuk umum persamaan multiple regresi linier yang menunjukkan hubungan antara lebih dari satu variabel X sebagai variabel bebas dengan variabel Y sebagai variabel tak bebas adalah :

                 



1 1 2 2 1 1 0 0 0

... _{n n} n i i i X X X Y X Y dengan :

Y = variabel tidak bebas ke-i

Xi = variabel bebas ke-i

β0 = intersep (titik potong kurva terhadap sumbu Y)

βi = kemiringan (slope) kurva linier

dari data yang diperoleh, maka dapat ditentukan . Yang diharapkan sebagaimana mestinya.

i i i Y Y

e   ˆ

DETERMINING MULTIPLE REGRESSION COEFFICIENT BY USING LINEAR PROGRAMMING METHOD

Abstract

In the effort determination of linear estimation with straight line method will yield good equation, if all points expressing data couple to reside in around the straight line. But, if point of data couples spread over one another, hence equation of linear which good to estimating variable value dependent is equation of linear which is the curve having mistake which a minimum of between point of estimations with pointactually. Hence from at that, this research explains how to come near regression line with linear programming technique.

Form of equation public of simple linear regression showing relation between two variables, that is variable X as independent variable and variable Y as non free variable is

 

 



 

 

 

 

 

  



1 1 2

2 1 1 0

0 0

... _{n n}

n

i i i

X X

X Y

X Y

Where

Yi= variable is not free of ke-i

Xi = independent variable ke-i

a is intercept (curve cut point to axis Y) b is inclination (slope) linear curve.

From data obtained, hence determinable ei Yi Yˆi. What expected properly.

DAFTAR ISI

Halaman

Persetujuan ii

Pernyataan iii Penghargaan iv

Abstrak v

Abstract vi

Daftar Isi vii

Daftar Tabel ix

Daftar Gambar x

Bab I Pendahuluan 1

1.1 Latar Belakang 1

1.2 Perumusan Masalah 3

1.3 Tujuan Penelitian 3

1.4 Kontribusi Penelitian 3

1.5 Tinjauan Pustaka 4

1.6 Metode Penelitian

Bab II Landasan Teori 6

2.1 Analisis Regresi 6

2.1.1 Regresi Linier Sederhana 6

2.1.2 Regresi Linier Ganda 10

2.1.3 Ketepatan Garis Estimasi dengan Menggunakan Metode Kuadrat

Terkecil 12 2.1.4 Meminimumkan Rata-rata Deviasi Absolute 13

2.2 Linier Programming 14

2.2.1 Model Linier Programming 14

2.2.2 Asumsi-Asumsi Dasar Linier Programming 20 2.2.3 Terminologi Linier Programming 21 2.2.4 Unsur-Unsur Linier Programming 22 2.3 Dualitas

Bab III Pembahasan 25

3.1 Pengunaan Teknik Linear Programming dengan Metode Simpleks 25 3.2 Komputasi Linear Programming dengan Sistem-QM 32

3.2.1 Pendahuluan 32

3.2.2 Langkah-Langkah Pengerjaan Program QM 33

3.2.3 Dualitas 41

Bab IV Kesimpulan dan Saran 45

4.1 Kesimpulan 45

4.2 Saran 45

DAFTAR TABEL

Halaman

Tabel 2.1 Tabel awal linier programming 17

Tabel 3.1 Tabel awal simpleks 27

Tabel 3.2 Simpleks 28

Tabel 3.3 Simpleks 30

DAFTAR GAMBAR

Halaman

Gambar 2.1 Diagram Pencar 7

Gambar 2.2 Suatu pengamatan (data) yang tidak tepat pada garis regresi 9 Gambar 2.3 Langkah-langkah dalam analisis PL dengan metode simpleks 19 Gambar 3.1 Tampilan sementara (splash)dari program QM for windows 33 Gambar 3.2 Pilihan modul yang tersedia pada program QM for windows 34 Gambar 3.3 Tampilan awal modul linear programming 34 Gambar 3.4 Tampilan untuk mengisi angka-angka sesuai dengan soal 35 Gambar 3.5 Langkah-langkah pengerjaan linear programming 38 Gambar 3.6 Output dari penyelesaian contoh soal linear programming 40

Gambar 3.7 Bentuk dual dari primal 41

Abstrak

Didalam upaya penentuan persamaan estimasi linier dengan metode garis lurus akan menghasilkan persamaan yang baik, jika semua titik yang mencerminkan pasangan data berada di sekitar garis lurus tersebut. Namun, jika titik-titik pasangan data tersebar satu sama lain, maka persamaan linier yang baik untuk mengestimasi nilai variabel dependen adalah persamaan linier yang yang kurvanya mempunyai kesalahan yang minimum antara titik estimasi dengan titik sebenarnya. Maka dari pada itu, penelitian ini menerangkan bagaimana cara untuk mendekati garis regresi dengan teknik linier programming.

Bentuk umum persamaan multiple regresi linier yang menunjukkan hubungan antara lebih dari satu variabel X sebagai variabel bebas dengan variabel Y sebagai variabel tak bebas adalah :

                 



1 1 2 2 1 1 0 0 0

... _{n n} n i i i X X X Y X Y dengan :

Y = variabel tidak bebas ke-i

Xi = variabel bebas ke-i

β0 = intersep (titik potong kurva terhadap sumbu Y)

βi = kemiringan (slope) kurva linier

dari data yang diperoleh, maka dapat ditentukan . Yang diharapkan sebagaimana mestinya.

i i i Y Y

e   ˆ

DETERMINING MULTIPLE REGRESSION COEFFICIENT BY USING LINEAR PROGRAMMING METHOD

Abstract

In the effort determination of linear estimation with straight line method will yield good equation, if all points expressing data couple to reside in around the straight line. But, if point of data couples spread over one another, hence equation of linear which good to estimating variable value dependent is equation of linear which is the curve having mistake which a minimum of between point of estimations with pointactually. Hence from at that, this research explains how to come near regression line with linear programming technique.

Form of equation public of simple linear regression showing relation between two variables, that is variable X as independent variable and variable Y as non free variable is

 

 



 

 

 

 

 

  



1 1 2

2 1 1 0

0 0

... _{n n}

n

i i i

X X

X Y

X Y

Where

Yi= variable is not free of ke-i

Xi = independent variable ke-i

a is intercept (curve cut point to axis Y) b is inclination (slope) linear curve.

From data obtained, hence determinable ei Yi Yˆi. What expected properly.

BAB 1

PENDAHULUAN

1.1Latar Belakang

Dalam kehidupan sehari-hari, seringkali dijumpai hubungan antara suatu variabel

dengan satu atau lebih variabel lain. Di dalam bidang pertanian sebagai contoh, dosis

dan jenis pupuk yang diberikan berhubungan dengan hasil pertanian yang diperoleh,

jumlah makanan yang diberikan pada ternak berhubungan dengan berat badannya, dan

sebagainya. Secara umum ada dua macam hubungan antara dua atau lebih variabel,

yaitu bentuk hubungan dan keeratan hubungan. Bila ingin mengetahui bentuk hubungan dua variabel atau lebih, digunakan analisis regresi. Bila ingin melihat

keeratan hubungan, digunakan analisis korelasi.

Kata regresi diperkenalkan pertama kali oleh Sir Francis Galton tahun 1877

pada bukunya tentang hereditas. Ia menemukan bahwa tinggi badan anak dari orang

tua yang tinggi cenderung memendek menuju tinggi rata-rata populasi. Garis

matematis yang ia kembangkan dikenal sebagai garis regresi. Istilah garis regresi (line of regression) lebih sering digunakan walaupun sebenarnya yang lebih tepat adalah istilah persamaan prediksi (predictive equation) atau persamaan penduga (estimating equation).

Di dalam statistik, pendugaaan pada umumnya bersinonim dengan regresi di

beberapa format. Ada berbagai jenis regresi yang berbeda di dalam statistik tetapi ide

dasarnya adalah bahwa suatu peta model yang diciptakan oleh nilai-nilai penduga itu,

yang sedemikian sehingga kesalahan yang terjadi paling rendah membuat suatu

ramalan. Format regresi yang paling sederhana adalah regresi linier sederhana yang

Analisis regresi dikelompokkan dari mulai yang paling sederhana sampai yang

paling rumit, tergantung tujuan yang berlandaskan pengetahuan atau teori sementara,

bukan asal ditentukan saja.

Masalah (Problem) adalah sesuatu yang terjadi tidak sesuai dengan keinginan

atau harapan setiap yang timbul, pasti ada faktor penyebabnya dan umumnya lebih

dari satu. Kalau masalah kita sebut sebagai ada lebih dari satu X, katakan oleh x1, x2…

xk. Misalnya penjual menurun disebabkan karena biaya promosi, harga, mutu

pelayanan , saingan produk impor, produktivitas rendah mungkin karena upah, gaya

kepemimpinan, masa kerja (pengalaman) motivasi, lingkungan kerja. Masing-masing

faktor akan mempunyai pengaruh positif (menaik) atau negatif (menurunkan) dengan

berbagai besaran yang berbeda. Untuk mempelajari pengaruh dari beberapa variabel

bebas (X) terhadap variabel tak bebas (Y) kita menggunakan metode

ketergantungan/depensi (depency method).

Berdasarkan contoh di atas, maka tampaklah mana variabel bebas (yang

mempengaruhi) dan mana variabel terikat atau tergantung (yang dipengaruhi).

Variabel yang mempengaruhi ini dalam analisis regresi disebut sebagai variabel prediktor, dengan lambang X, sedangkan variabel yang dipengaruhi disebut veriabel kriterium dengan lambang Y.

Mengapa analisis regresi diperlukan? Jawabanya ialah karena kita sebagai

peneliti dituntut untuk mencari kebenaran secara ilmiah atau berdasarkan ilmu. Dan

salah satu fungsi ilmu ialah meramalkan (to predict). Fungsi ilmu yang lainnya adalah

menggambarkan (to describe), mengontrol (to control) dan menerangkan (to explain).

Berdasarkan fungsi ilmu tersebut, maka jika kita mempunyai dua buah

variabel atau lebih, maka sudah sewajarnyalah kalau kita ingin mempelajari

bagaimana variabel-variabel itu berhubungan atau dapat diramalkan. Hubungan yang

diperoleh biasanya dinyatakan dalam persamaan matematika yang menyatakan

hubungan fingsional antara variabel-variabel. Pelajaran yang menyangkut masalah ini

Pendekatan klasik untuk masalah regresi, tujuannya adalah untuk

meminimisasikan jumlah dari kuadrat simpangan baku dari permasalahan yang telah

diteliti dan nilai-nilai yang telah diprediksikan dari variabel yang terikat. Metode ini

lebih dikenal dengan sebutan metode kuadrat terkecil (least-squares method) yang digunakan untuk metode mathematical programming.

Pemrograman linier memakai suatu model matematis untuk menggambarkan

masalah yang dihadapi. Kata sifat ‘linier’ berarti bahwa semua fungsi matematis dalam model ini harus merupakan fungsi-fungsi linier. Kata ‘pemrograman’ disini merupakan sinonim untuk kata perencanaan. Maka membuat pemrograman linier

adalah membuat rencana kegiatan-kegiatan untuk memperoleh hasil yang optimal,

ialah suatu hasil yang mencapai tujuan yang ditentukan dengan cara yang paling baik

(sesuai model matematis) diantara semua alternatif yang mungkin.

1.2Perumusan Masalah

Menentukan model koefisien regresi multiple variabel dengan menggunakan linier

programming.

1.3Tujuan Penelitian

Tujuan penelitian ini untuk menguraikan cara untuk mendekati garis regresi dengan

meminimumkan jarak atau deviasi dengan menggunakan model linier programming.

1.4Kontribusi Penelitian

a. Dengan diketahuinya bagaimana cara mendekati regresi linier dengan

menggunakan linier programming diharapkan dengan meminimumkan jarak

b. Menambah wawasan dan memperkaya literatur dalam bidang statistika yang

berhubungan dengan multiple regresi melalui pendekatan metode linier

programming.

c. Untuk mengetahui besarnya pengaruh dari setiap variabel bebas (yang

tercakup dalam persamaan) terhadap variabel tak bebas.

1.5Tinjauan Pustaka

Selain penulis mendapatkan pelajaran dari bangku kuliah, penulis juga menggunakan

buku-buku berikut sebagai sumber utama, diantaranya yaitu :

1 Supranto, J. 2004, Analisis Multivariat : Arti dan Interpretasi, Jakarta: Penerbit Rineka Cipta

Apabila variabel Y mempunyai hubungan linier dengan n buah variabel X, maka model matematika multiple regresinya adalah :

                 



1 1 2 2 1 1 0 0 0

... _{n n}

n i i i X X X Y X Y

dengan : Y = variabel dependen atau respons

X = variabel independen atau prediktor

ß0 = konstanta yang merupakan titik potong kurva terhadap

sumbu Y

ßi = kemiringan kurva linier

ε = nilai kesalahan

2 Arthanari, T.S. Dodge Yadolah, Mathematical Programming in Statistic, New York : Wiley.

Meminimumkan jumlah dari selisih nilai absolut diantara deviasi yaitu :

Minimumkan :



  j i j i d d





 

j i

j i d

d













   



j i

j j

i

i X Y X

Y ₀ ₁ ₀ ₁



 







 



j i

j i j

i Y X X

Y ₁

misalkan : Y_ij Y_iY_j dan X_ij  X_i X_j ; i<j

maka diperoleh,





 

 



j i

ij ij

j i

j

i d Y X

d ₁

1.6Metode Penelitian

Uraian metode yang digunakan dalam penelitian secara rinci meliputi :

1. membentuk persamaan dari jumlah deviasi kuadrat (regresi kuadrat

terkecil)

2. menganalisis persamaan dengan menggunakan linier programming

BAB 2

LANDASAN TEORI

2.1Analisis Regresi

Analisis regresi adalah teknik statistika yang berguna untuk memeriksa dan

memodelkan hubungan diantara variabel-variabel. Penerapannya dapat dijumpai

secara luas di banyak bidang seperti teknik, ekonomi, manajemen, ilmu-ilmu biologi,

ilmu-ilmu sosial, dan ilmu-ilmu pertanian. Pada saat ini, analisis regresi berguna

dalam menelaah hubungan dua variabel atau lebih, dan terutama untuk menelusuri

pola hubungan yang modelnya belum diketahui dengan sempurna, sehingga dalam

penerapannya lebih bersifat eksploratif.

2.1.1 Regresi Linier Sederhana

Regresi linier sederhana adalah merupakan suatu alat analisis yang digunakan untuk

mengestimasi atau mempresiksi nilai suatu variabel berdasarkan nilai variabel lain

yang diketahui. H_{ubungan linier antara dua variabel, dua variabel ini dibedakan}

menjadi variabel bebas yang dinotasikan X dan variabel terikat yang dinotasikan Y.

Variabel tak bebas adalah variabel yang nilainya selalu bergantung dengan nilai

variabel lain dalam hal ini variabel tak bebas nilainya selalu dipengaruhi oleh variabel

bebas, sehingga sering disebut dengan variabel terikat sedangkan variabel bebas

adalah variabel yang nilainya tidak tergantung dengan nilai variabel lain.

Hubungan-hubungan ini bila dinyatakan dalam model matematis akan memberikan

Pembahasan kita akan terbatas pada regresi garis sederhana yaitu pada

pembahasan mengenai hubungan antara dua variabel yang biasanya cukup tepat

dinyatakan dalam suatu garis lurus.

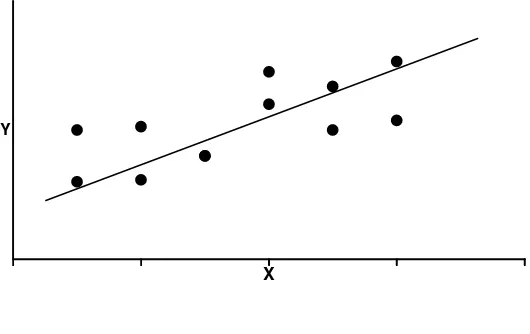
X

Y

Gambar 2.1 Diagram Pencar

Garis lurus yang terdapat pada diagram pencar pada gambar 2.1 yang

memperlihatkan adanya hubungan antara kedua variabel disebut garis regresi atau

garis perkiraan, dan yang seperti kita ketahui, persamaan yang digunakan untuk

mendapatkan garis regresi pada data diagram pencar disebut persamaan regresi yang

merupakan suatu persamaan matematika yang mendefinisikan hubungan antara dua

variabel.

Persamaan umum garis lurus yang diperlihatkan, akan digunakan untuk

menempatkan garis regresi pada data yang diperoleh. Oleh karena itu, metode kuadrat

terkecil sekali lagi akan kita gunakan untuk menempatkan garis pada data yang

diamati. Sehingga bentuk umum dari persamaan regresi adalah sebagai berikut :

i i a bX

Y   , untuk i = 1,2,...n

dengan : Yi = variabel terikat ke-i

Xi = variabel bebas ke-i

a = intersep (titik potong kurva terhadap sumbu Y)

Untuk memperkirakan A dan B, maka dipergunakan metode kuadrat terkecil

Model sebenarnya : Y = A + BX + ε Model perkiraan : Y = a + bX + e

A, b dan e merupakan perkiraan/taksiran atas A, B, dan ε

Metode kuadrat terkecil adalah suatu metode untuk menghitung a dan b

sebagai perkiraan A dan B, sedemikian rupa sehingga jumlah kesalahan kuadrat memiliki nilai terkecil. Dengan bahasa matematik, dapat dinyatakan sebagai berikut :

i i i a bX e

Y    , i = 1,2,...,n



i

i

i Y a bX

e   



kesalahan (error) i







₂ 



 





2

i i

i Y a bX

 = jumlah kesalahan kuadrat

Jadi, metode kuadrat terkecil adalah metode untuk menghitung a dan b

sedemikian rupa sehingga



e_i2 = terkecil (minimum). Caranya ialah dengan

membuat turunan parsial (partial differential) dari



e_i2 mula-mula terhadap a

kemudian terhadap b dan menyamakannya dengan nol.









 









_{       }   i i i i i X b an Y bX a Y a e 0 1 2 2 ... (2.1)























_{       } 

 2 ₂

0

2 _{i i i i i i i}

i X b X a Y X X bX a Y b e ... (2.2)

Persamaan (2.1) dibagi dengan

n X n an n Y

n



i  



i

Y abX

sehingga ; aY bX

masukkan a ke persamaan (2.2)

















_







          

 2 2

i i i i i i i i i

i X b X









 









2

2 i i i i i

i b X

n X b n Y X Y X







 





           n Y X Y X b n X

X_i i _{i i} i i

2 2









 













 

      ₂ 2 2 2 i i i i i i i i i i i i X X n Y X Y X n n X X n Y X Y X b

meminimalkan jumlah deviasi kuadrat (Regresi Kuadrat-Terkecil)

metode ini didasarkan pada pemilihan β0 dan β1 sehingga meminimalkan jumlah

kuadrat deviasi titik-titik data dari garis yang dicocokkan.

Jumlah dari kuadrat deviasi (SSD) dari garis adalah







      n i i i n i

i Y X

e SSD 1 2 1 0 1

2  



... (2.3)

ε

Gambar 2.2 suatu pengamatan (data) yang tidak tepat pada garis regresi

Kemudian akan dipilih taksir ₀ dan 1 sehingga jika taksiran ini disubstitusikan ke dalam persamaan (2.3) maka jumlah deviasi kuadrat menjadi







i i



n i i n i i i X Y X SSD X Y SSD 1 0 1 1 1 1 0 0 2 2                  





 

... (2.4)

Dan karenanya

... (2.5)













        n i i i i n i i i X Y X X Y 1 1 0 1 1 0 0 0    

dari persamaan (2.5), diperoleh











         n i n i n i i i i i n i i n i i Y X X X Y X n

1 1 1

2 1 0 1 1 1 0    

persamaan (2.6) disebut dengan persamaan normal. Dari persamaan (2.6) diperoleh,





















   n X X n Y X Y X i i i i i i 2 2 1 ˆ

 ... (2.6)

dan ˆ₀ Y ˆ₁X, dimana Y dan X adalah



n_

i1Yi n dan



 n

i 1Xi n. dan yang diperoleh dengan cara ini disebut taksiran kuadrat terkecil masing-masing dari

0

ˆ

 _ˆ₁

0

 dan ₁. Dengan demikian, taksiran persamaan regresi dapat ditulis sebagai,

, yang disebut persamaan prediksi.

X 1

ˆ



Yˆˆ₀

2.1.2 Regresi Linier Ganda

Regresi linier ganda adalah analisis regresi yang meramalkan pengaruh dua variabel

tidaknya hubungan fungsional antara dua buah variabel bebas X atau lebih dengan

sebuah variabel terikat Y.

Mengingat model itu :

 



    

 _{0 1}X₁ ... _p1X_p1

Y … (2.7)

dengan : X1,X2, …, Xp-1 diketahui konstan

βj tidak diketahi parameter untuk diestimasi

ε adalah batas error

Seperti dibagian 2.2, metode kuadrat terkecil dari estimasi β terdiri dari

minimize



_i2 dengan respect ke β; bahwa, kita minimize '  YX 2 dengan respect ke β. Sekarang



' 



YX

 

' YX



 

 X Y X X

Y

Y' 2 ' '  ' ' 

Perbedaan ' dengan respect ke β dan persamaan ' 0  

  

, kita dapatkan

-2X’Y + 2X’Xβ = 0 atau X’Xβ = X’Y … (2.8)

… (2.9)



X'X



X'Y

ˆ_ 1



Kemudian untuk β,

(Y – Xβ)’ (Y-Xβ) 



Y XX

 

ˆ-ˆ



'



YXX



ˆˆ







 



 

 

 

 

 

 _{Y X}ˆ ' _{Y X}ˆ ˆ '_X'_X ˆ





_YXˆ



'_{Y X}ˆ





Minimum dari



YX



'



YX



adalah



Y Xˆ



' YXˆ



dicapai pada . Solusi ini untuk melihat minimize



 _ ˆ

2.1.3 Ketepatan Garis Estimasi dengan Menggunakan Metode Kuadrat Terkecil.

Penentuan persamaan estimasi linier dengan menggunakan metode garis lurus akan

menghasilkan persamaan yang baik, jika semua titik yang mencerminkan pasangan

data berada di sekitar garis lurus tersebut. Namun, jika titik-titik pasangan data

tersebar satu sama lain, maka persamaan linier yang baik untuk mengestimasi nilai

variabel dependen adalah persamaan linier yang kurvanya mempunyai kesalahan yang

minimum (minimized the error) antara titik estimasi dengan titik yang sebenarnya.

Metode kuadrat terkecil (least-squares method) untuk menentukan persamaan

linier estimasi, berarti memiliki satu kurva linier dari beberapa kemungkinan kurva

linier yang dibuat dari data yang ada yang mempunyai kesalahan (error) paling kecil

(selisih antara nilai aktual dan nilai taksiran adalah paling kecil). Kriteria ini dikenal

dengan istilah prinsip kuadrat terkecil (principle of least square). Prinsip pemilihan garis regresi ini adalah sebagai berikut :

‘pilih garis yang mempunyai jumlah kuadrat deviasi nilai observasi Y terhadap

nilai Y prediksinya yang minimum sebagai garis regresi yang paling baik’.

Prinsip pemilihan garis yang mempunyai nilai a dan nilai b yang dapat meminimumkan :







   n

i

i i Y

Y SSE

1

2 ˆ

Simbol SSE menunjukkan jumlah kuadrat deviasi, atau sering disebut jumlah

kuadrat untuk kesalahan (sum of square for error). Jika suatu persamaan regresi diperoleh dari mensubstitusikan nilai a dan nilai b yang meminimumkan SSE, maka

akan dihasilkan persamaan garis regresi prediksi kuadrat terkecil (least-squares prediction line) sebagai berikut :

bX a Yˆ 

yang menyatakan bahwa :

Ŷ : taksiran nilai Y

b : taksiran nilai slope populasi

X : nilai tertentu X

Garis estimasi yang tepat (best fitting) adalah garis yang menghasilkan penyimpangan

nilai dalam garis estimasi dengan nilai data observasi sekecil mungkin. Untuk dapat

memperoleh garis estimasi yang tepat, harus dapat diperoleh penduga nilai β0 dan β1

sedemikian rupa sehingga tujuan di atas dapat dicapai. Permasalah tersebut dapat

diatasi dengan menggunakan metode kuadrat terkecil.

Metode kuadrat terkecil merupakan metode yang digunakan untuk menentukan garis estimasi yang terbaik berdasarkan kriteria menghasilkan nilai



e_i2

yang sekecil mungkin.

2.1.4 Meminimumkan Rata-rata Deviasi Absolute

Mengingat masalah meminimumkan



d_i dengan pengaruh β,

dengan : di = deviasi dari pengamatan

Yi = nilai perkiraan

Minimimum Z =



d_i … (2.10.)

kendala Xβ + d = Y

d, β tanda takterbatas

Penting diperhatikan bahwa



d_i d_i

Minimimum Z =



d_1id_2i

kendala Xβ + d1 – d2 = Y

β tanda takterbatas

d1, d2 ≥ 0

2.2LINIER PROGRAMMING

2.2.1 Model Linier Programming

Linier programming merupakan suatu model umum yang dapat digunakan dalam

pemecahan masalah pengalokasian sumber-sumber yang terbatas secara optimal.

Linier programming memakai suatu model matematis yang menggambarkan masalah

yang dihadapi. Linier memiliki arti bahwa semua fungsi matematis dalam model harus

merupakan fungsi-fungsi linier, sedangkan programming/pemrograman dapat

diartikan sebagai perencanaan. Dengan demikian linier programming dapat

didefenisikan sebagai membuat rencana kegiatan-kegiatan dengan menggunakan suatu

model umum dalam pemecahan masalah pengalokasian sumber daya-sumber daya

yang terbatas secara optimal.

Model dasar atau Persamaan linier dapat dirumuskan sebagai berikut :

Cari nilai-nilai yang dapat menghasilkan berbagai kombinasi

optimum (maksimum atau minimum) dari : n

X X X₁, ₂,...,

n nX C X C X C

Z  _{1 1} _{2 2} ...

(fungsi tujuan)

Dengan syarat bahwa fungsi tujuan tersebut memenuhi kendala-kendala atau

syarat-syarat ikatan sebagai berikut :

2 2 2 22 2 21 1 1 2 12 1 11 ... ... b atau X a X a X a b atau X a X a X a n n n n           . . . . . . . . . . . . m n mn m

m X a X a X atau b

a _{1 1} _{2 2} ...  

atau dalam bentuk kompaknya :

optimumkan (maksimumkan atau minimumkan) :





 n

j i iX

C Z

1

untuk j = 1, 2, …n

dengan syarat ikatan :





 

n

i

i j

ijX atau b

a

1

, untuk i = 1, 2, … m

Konsep linier programming ditemukan dan diperkenalkan pertama kali oleh

George Dantzig yang berupa metode mencari solusi masalah linier programming dengan banyak variabel keputusan. Kemudian banyak ahli yang bergabung dengan

Dantzig dalam konsep pengembangan linier programming. Paper pertamanya adalah

metode solusi yang bernama metode simplex. Dalam pengembangan linier programming, Dantzig bekerjasama dengan Marshal Wood dan Alex O, dan masih

banyak para ahli yang lainnya ikut. Kemudian, setelah berhasil diterapkan pada sektor

pemerintah dan swasta, akhirnya disadari bahwa linier programming merupakan

masalah yang sangat membantu dalam analisis bidang bisnis.

Model Linier Programming ini merupakan bentuk dan susunan dari dalam

menyajikan masalah-masalah yang akan dipecahkan dengan teknik linier

programming. Dalam model linier programming dikenal 2 (dua) macam fungsi, yaitu :

1. fungsi tujuan (objective function) adalah fungsi yang menggambarkan tujuan/sasaran di dalam permasalahan linier programming yang berkaitan

dengan pengaturan secara optimal, untuk memperoleh keuntungan maksimal

atau biaya minimal. Pada umumnya nilai yang akan dioptimalkan dinyatakan

sebagai Z.

2. fungsi batasan (constraint function) adalah bentuk penyajian secara matematis batasan-batasan kapasitas yang tersedia yang akan dialokasikan secara optimal

Tabel 2.1 Tabel Awal Linier Programming

1 2 3 4 5

1

Cj X1 X2 … Xk … Xn d1 … dl … dn B

C VB WB 0 0 … 0 … 0 w1 … wl … wn 

1

d X₁ b₁ a₁₁ a₁₂

2

… a_1k … a_1n 1 … 0 … 0 

2

d X₂ b₂ a₂₁ a₂₂ … a_2k … a_2n 0 … 0 … 0 … … … ……… 3

Baris 1  l

d Xl bl al1 al2 … alk … aln 0 … 1 … 0

… … … ………

 n

d Xn bn anl an2 … ank … an 0 … 0 … 1



bidi

: Variabel keputusan dan variabel deviasi

Kolom 5 : Nilai sebelah kanan

putusan

Kolom 4 : Matriks identitas menunjukkan pemasukan variabel deviasi negatif

Kolom 1 : Faktor prioritas dan bobot untuk setiap variabel deviasi positif

(yakni variabel basis) dan memasukkan variabel deviasi artificial

Kolom 2 : wakili jumlah total deviasi dari

Baris 2 :

fungsi objektif.

j

X d_i.

Kolom 3 : Koefisien variabel ke a_ij.

 . i

d

i

P W_i

seperti ditampilkan dalam kolom 2.

Nilai total deviasi absolut, yang me

semua tujuan untuk tiap tabel sebagai interasi proses pendapatan.

Vektor baris dari penunjuk nol pada proses perhitungan

Baris 3 : Bobot W_i untuk setiap variabel deviasi yang dimasukkan dalam

Zj

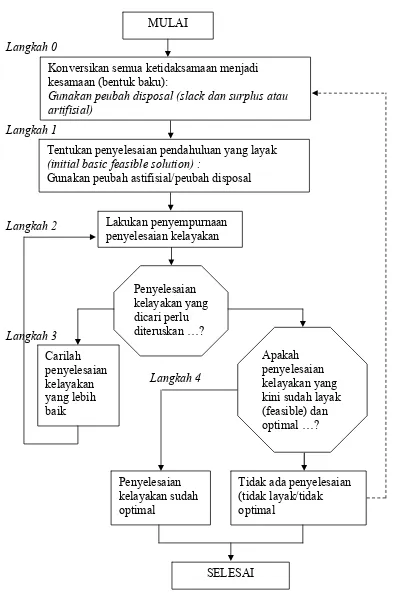
Pada garis besarnya langkah-langkah dalam analisis persoalan linier programming dengan metode simpleks adalah seperti terlihat dalam Gambar 2.3.

Langkah 0

Langkah 1

Langkah 1

Langkah 2

Langkah 3

Langkah 4

Konversikan semua ketidaksamaan menjadi kesamaan (bentuk baku):

Gunakan peubah disposal (slack dan surplus atau artifisial)

Tentukan penyelesaian pendahuluan yang layak

(initial basic feasible solution) :

Gunakan peubah astifisial/peubah disposal

Lakukan penyempurnaan penyelesaian kelayakan

Penyelesaian kelayakan yang dicari perlu diteruskan …?

Apakah penyelesaian kelayakan yang kini sudah layak (feasible) dan optimal …? Carilah

penyelesaian kelayakan yang lebih baik

Penyelesaian kelayakan sudah optimal

Tidak ada penyelesaian (tidak layak/tidak optimal

MULAI

SELESAI

2.2.2 Asumsi-Asumsi Dasar Linier Programming

Dalam model linier programming terdapat asumsi-asumsi yang harus dipenuhi agar

permasalahan linier programming menjadi absah, adapun asumsi linier programming

adalah sebagai berikut :

1. Proportionality

Asumsi ini berarti bahwa naik turunnya nilai Z dan penggunaan sumber atau

fasilitas yang tersedia akan berubah secara sebanding (propotional) dengan perubahan tingkat kegiatan.

contoh :

a. Z C₁X₁C₂X₂C₃X₃ ...C_nX_n

Setiap pertambahan 1 unit X1 akan menaikkan Z sebesar C1

b. a₁₁X₁a₁₂X₂a₁₃X₃ ...a_nX_n b₁

Setiap pertambahan 1 unit X1 akan menaikkan penggunaan sumber

sebesar a11

2. Additivity

Asumsi ini berarti bahwa nilai tujuan setiap kegiatan bersifat independent

(bebas/tidak saling bergantung) dan dalam linier programming dianggap

bahwa kenaikan nilai tujuan (Z) yang diakibatkan oleh suatu kegiatan dapat

langsung ditambahkan tanpa mempengaruhi bagian nilai kegiatan lain.

misalnya :

Z = 3X1 + 5X2

dengan X1 = 10 ; X2 = 2

sehingga Z = 30 + 10 = 40

Andaikan X1 bertambah 1 unit, maka sesuai dengan asumsi pertama, nilai Z

menjadi 40 + 3 = 43. Jadi nilai 3 karena kenaikan X1 dapat langsung

ditambahkan pada nilai Z mula-mula tanpa mengurangi bagian Z yang

diperoleh dari kegiatan 2 (X2). Dengan kata lain, tidak ada korelasi antara X1

3. Divisibility

Dalam linier programming diperbolehkan menggunakan angka pecahan.

misalnya :

dari hasil perhitungan didapat nilai X1 = 4,5 ; X2 = 7,25 dan Z =

85.000,25

Dalam hal tertentu nilai pecahan ini harus dibulatkan dengan menggunakan

integer, misalnya : jumlah mahasiswa diperguruan tinggi tidak mungkin dalam

bentuk pecahan.

4. Deterministik

Asumsi ini menyatakan bahwa semua parameter yang terdapat dalam model

linier programming yang berupa aij, bi dan Cj dapat diketahui secara pasti.

2.2.3 Terminologi Linier Programming

Agar memahami dengan baik bidang yang dipelajari , pembaca selalu harus mengerti

istilah-istilah dan lambang-lambang khusus yang digunakan orang dalam bidang studi

itu. Berikut ini adalah defenisi dari beberapa istilah dan lambang yang biasa

digunakan dalam Linier Programming.

1. Decision variabel adalah seperangkat variabel yang tidak diketahui (dilambangkan x_j, dengan j =1, 2, … n) yang akan dicari nilainya (variabel

keputusan).

2. Right hand side value (RHS) adalah nilai-nilai yang biasanya menunjukkan ketersediaan sumber daya (dilambangkan dengan b_i ) yang akan ditentukan kekurangan atau kelebihan penggunaannya (nilai sisi kanan).

3. Variabel Dasar adalah variabel yang nilainya sama dengan sisi kanan dari persamaan.

4. Kolom Kunci adalah kolom yang merupakan dasar untuk mengubah tabel. Pilih kolom yang mempunyai nilai pada garis fungsi tujuan yang bernilai

5. Baris Kunci adalah baris yang merupakan dasar untuk mengubah tabel tersebut. Untuk itu terlebih dahulu carilah indeks tiap-tiap baris dengan cara

membagi nilai-nilai pada kolom RHS dengan nilai yang sebaris pada kolom

kunci.

6. Angka Kunci (Pivot) merupakan perpotongan antara kolom kunci dengan baris kunci.

2.2.4 Unsur-Unsur Linier Programming

Setiap model Linier Programming paling sedikit terdiri dari dua komponen

yaitu : fungsi tujuan, dan kendala-kendala tujuan.

Fungsi Tujuan

Adapun fungsi tujuan dalam linier programming, yaitu :

Minimumkan





  _  m

i

i i d

d Z

1

Dalam hal ini peubah deviasi positif dan deviasi negatif adalah tidak lain

daripada peubah-peubah slek dan surplus.

Model Linier Programming, nilai yang tidak diketahui, tetapi akan

melakukannya secara tidak langsung melalui minimisasi simpangan negatif dan positif

dari nilai RHS kendala tujuan. Linier Programming mencari nilai solusi secara

langsung melalui minimisasi penyimpangan-penyimpangan dari nilai RHSnya. j

x

j

x

Kendala Tujuan

Ada empat jenis kendala tujuan yang berlainan. Maksud setiap jenis kendala itu

ditentukan oleh hubungannya dengan fungsi tujuan. Pada Tabel 2.1 disajikan keempat

jenis kendala itu. Terlihat bahwa setiap jenis kendala tujuan harus punya satu atau dua

variabel simpangan yang ditempatkan pada fungsi tujuan. Dimungkinkan adanya

kendala-kendala yang tidak memiliki variabel simpangan. Kendala-kendala ini sama

seperti kendala-kendala persamaan linier. Persamaan pertama pada Tabel 2.1

maknanya serupa dengan kendala pertidaksamaan ≤ dalam masalah program linier maksimasi. Persamaan kedua maknanya serupa dengan kendala pertidaksamaan ≥ pada masalah program linier minimisasi. Persamaan ketiga memperbolehkan

diinginkan sama dengan . Jika kendala persamaan dianggap perlu dalam perumusan

model linier programming, ia dapat dimasukkan dengan menempatkan sebuah

artificial variabel , seperti pada persamaan keempat. i

b

 i

d

2.3 Analisis Dualitas

Setiap persoalan program linier selalu memiliki dua macam analisis, atau katakanlah

dua pakar yang menjadi satu, yaitu (1) analisis primal dan (2) analisis dual yang

biasanya disebut analisis primal-dual.

Untuk persoalan maksimisasi, maka semua rumusan fungsi kendalanya

mempunyai tanda “lebih kecil daripada atau sama dengan”. Jika persoalannya adalah

minimisasi maka tanda fungsi syarat ikatanya harus “lebih besar daripada atau sama

dengan”, ingat bahwa tidak perlu semua konstanta atau nilai sebelah kanan (disingkat

nsk)

Jika suatu persoalan dalam rumusan program liniernya memiliki fungsi

kendala kesamaan (nilai nsk-nya bertanda sama dengan), maka fungsi kendala

tersebut dapat ditukar atau diganti dengan dua fungsi lainnya yaitu :

Pertama, bertanda “lebih kecil daripada atau sama dengan”

Kedua, bertanda “lebih besar daripada atau sama dengan”,

Salah satu diantara kedua fungsi kendala lain tersebut (pilih mana saja),

kemudian diambil, dan kalikan dengan -1 unutk mendapatkan fungsi kendala baru

yang sesuai dengan aturan yang diminta.

Model Umum

Masalah primal Masalah dual

Maksimumkan 



_ n

j i iX

C Z

1

dengan kendala : _i, n

j

j ijX b

a 



1

Minimumkan



  n i

i iY

b G

1

dengan kendala : _i, m

i j ijY C

a 



Apabila bentuk persamaan diatas dinyatakan dalam bentuk notasi matriks, maka kita peroleh rumusannya seperti terlihat dalam persamaan berikut :

Masalah primal Masalah dual

Minimum : Gb'Y

dengan kendala : AY ≤ C

Y ≥ 0

Maksimum : Z C'X dengan kendala : AX ≤ b

X ≥ 0

PEMBAHASAN

3.1. Penggunaan Teknik Linear Programming dengan Metode Simpleks

Andaikan suatu persoalan penentuan model multiple regresi yaitu diberikan data

sebagai berikut :

, 3 5 1 2 4 1 1 3 1 2 2 1 3 1 1                  X                  5 5 4 3 4 Y

dengan menentukan regresi MINMAD yang terdiri dari ,

estimasi

2 2 1 1

0 ˆ ˆ

ˆ

ˆ _{X X}

Y    2

1 0, ,

 .

i i i d d

d  ₁  ₂

i i i d d

d  ₁  ₂

bentuk umum

minimum : Z =



d_1i 



d_2i

kendala : Xd₁d₂ Y

bentuk standart

minimum : Z = d₁₁ d₁₂ d₁₃ d₁₄ d₁₅ d₂₁ d₂₂ d₂₃ d₂₄ d₂₅

kendala : ₀ ₁3₂ d₁₁ d₂₁ 4

0  ij

d

misalkan : ₀  X₁ d₁₁  X₄ d₂₁  X₉

3 2 2 1 X X     6 13 5 12 X d X d   11 23 10 22 X d X d   8 15 7 14 X d X d   13 25 12 24 X d X d   fungsi tujuan

minimum : Z  X₄ X₅ X₆ X₇ X₈ X₉  X₁₀ X₁₁X₁₂  X₁₃

kendala : X₁ X₂ 3X₃ X₄ X₉ 4

5 3 5 5 2 4 4 3 3 2 2 13 8 3 2 1 12 7 3 2 1 11 6 3 2 1 10 5 3 2 1                     X X X X X X X X X X X X X X X X X X X X 0  i X

selanjutnya, persamaan fungsi tujuan dan kendala dimasukkan ke dalam tabel awal

[image:36.595.106.483.75.423.2]

simpleks sebagai berikut :

Tabel 3.1 Tabel Awal Simpleks

Cj 0 0 0 1 1 1 1 1 1 1 1 1 1

B

C

B

1 X₄ 4 1 1 3 1 0 0 0 0 -1 0 0 0 0

1 X₅ 3 1 2 2 0 1 0 0 0 0 -1 0 0 0

1 X₆ 4 1 3 1 0 0 1 0 0 0 0 -1 0 0

1 X₇ 5 1 4 2 0 0 0 1 0 0 0 0 -1 0

1 8

X 5 1 5 3 0 0 0 0 1 0 0 0 0 -1

Zj 21 5 15 11 1 1 1 1 1 -1 -1 -1 -1 -1

(Cj– Zj) -5 -15 -11 0 0 0 0 0 2 2 2 2 2

Kolom kunci Baris kunci

Pada tabel dapat dilihat bahwa nilai



C_j Z_j



yang negatif terbesar adalah (-15), maka kolom kuncinya adalah X2 , dan rasio yang positif paling kecil dari X2 yaitu :

4/1, 3/2, 4/3, 5/4, 5/5 adalah 5/5 maka baris kunci adalah X8.

Dengan demikian X2 mengganti X8 di variabel dasar.

Baris kunci baru =

pivot

1 _{(baris kunci lama)}

=

5

1 ( 5 1 5 3 0 0 0 0 1 0 0 0 0 -1)

= ( 1 1/5 1 3/5 0 0 0 0 1/5 0 0 0 0 -1/5)

Baris-I baru = baris-I lama - 5

1 (baris kunci lama)

= ( 4 1 1 3 1 0 0 0 0 -1 0 0 0 0 )

= 5

1 ( 5 1 5 3 0 0 0 0 1 0 0 0 0 -1 )

= 3 4/5 0 12/5 1 0 0 0 -1/5 -1 0 0 0 1/5

Baris-II baru = baris-II lama - 5

2 (baris kunci lama)

= ( 3 1 2 2 0 1 0 0 0 0 -1 0 0 0 ) =

5

2 _{( 5 1 5 3 0 0 0 0 1 0 0 0 0 -1)}

Baris-III baru = baris-III lama - 5

3 (baris kunci lama)

= ( 4 1 3 1 0 0 1 0 0 0 0 -1 0 0 ) =

5

3 _{( 5 1 5 3 0 0 0 0 1 0 0 0 0 -1 )}

= 1 2/5 0 -4/5 0 0 1 0 -3/5 0 0 -1 0 3/5

Baris-IV baru = baris-IV lama - 5

4 (baris kunci lama)

= ( 5 1 4 2 0 0 0 1 0 0 0 0 -1 0 ) =

5

4 _{( 5 1 5 3 0 0 0 0 1 0 0 0 0 -1 )}

= 1 1/5 0 -2/5 0 0 0 1 -4/5 0 0 0 -1 4/5

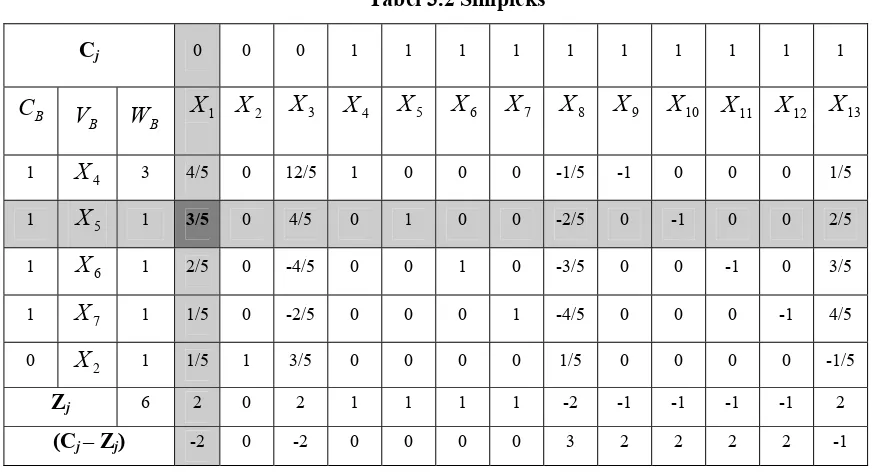
[image:38.595.106.542.402.638.2]

Dengan demikian diperoleh tabel simpleks yang baru :

Tabel 3.2 Simpleks

Cj 0 0 0 1 1 1 1 1 1 1 1 1 1

B

C

B

V W_B X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X12 X13

1 X₄ 3 4/5 0 12/5 1 0 0 0 -1/5 -1 0 0 0 1/5

1 X₅ 1 3/5 0 4/5 0 1 0 0 -2/5 0 -1 0 0 2/5

1 X₆ 1 2/5 0 -4/5 0 0 1 0 -3/5 0 0 -1 0 3/5

1 X₇ 1 1/5 0 -2/5 0 0 0 1 -4/5 0 0 0 -1 4/5

0

2

X 1 1/5 1 3/5 0 0 0 0 1/5 0 0 0 0 -1/5

Zj 6 2 0 2 1 1 1 1 -2 -1 -1 -1 -1 2

(Cj– Zj) -2 0 -2 0 0 0 0 3 2 2 2 2 -1

Karena pada tabel 3.2 ini masih ada nilai



C_j Z_j



yang negatif maka solusi belum optimum, nilai negatif terbesar adalah (-2) yaitu pada kolom , dengan demikian

kolom kuncinya adalah dan rasio yang memiliki nilai positif terkecil yaitu 3/5

pada baris (baris kunci).

1 X

1 X

5

Sehingga X₁ mengganti X₅ di variabel dasar.

Baris kunci baru =

pivot

1 _{(baris kunci lama)}

= 5 / 3

1 _{( 1 3/5 0 4/5 0 1 0 0 -2/5 0 -1 0 0 2/5 )}

= 5/3 1 0 4/3 0 5/3 0 0 -2/3 0 -5/3 0 0 2/3

Baris-I baru = baris-I lama –

5 / 3 5 /

4 _{(baris kunci lama)}

= ( 3 4/5 0 12/5 1 0 0 0 -1/5 -1 0 0 0 1/5 ) =

3

4 _{( 1 3/5 0 4/5 0 1 0 0 -2/5 0 -1 0 0 2/5 )}

= 5/3 1 0 4/3 1 -4/3 0 0 1/3 -1 4/3 0 0 -1/3

Baris-III baru = baris-III lama -

5 / 3 5 /

2 _{(baris kunci lama)}

= ( 1 2/5 0 -4/5 0 0 1 0 -3/5 0 0 -1 0 3/5 ) =

3

2 _{( 1 3/5 0 4/5 0 1 0 0 -2/5 0 -1 0 0 2/5 )}

= 1/3 0 0 -4/3 0 -2/3 1 0 -1/3 0 2/3 -1 0 1/3

Baris-IV baru = baris-IV lama –

5 / 3 5 /

1 _{(baris kunci lama)}

= ( 1 1/5 0 -2/5 0 0 0 1 -4/5 0 0 0 -1 4/5 ) =

3

1 _{( 1 3/5 0 4/5 0 1 0 0 -2/5 0 -1 0 0 2/5 )} = 2/3 0 0 -2/3 0 -1/3 0 1 -2/3 0 1/3 0 -1 2/3

Baris-V baru = baris-V lama -

5 / 3 5 /

1 _{(baris kunci lama)}

= ( 1 1/5 1 3/5 0 0 0 0 1/5 0 0 0 0 -1/5 ) =

3

1 _{( 1 3/5 0 4/5 0 1 0 0 -2/5 0 -1 0 0 2/5 )}

Maka dibentuk tabel 3.3 Simpleks dan substitusikan nilai baris barunya dan masukkan

dan keluarkan X5. Dengan demikian tabel 3.3 simpleks yang baru yaitu :

[image:40.595.107.551.185.450.2]

1 X

Tabel 3.3 Simpleks

Cj 0 0 0 1 1 1 1 1 1 1 1 1 1

B

C

B

V WB 1

X X2 X3 X4 5

X X6 X7 X8 X9 X10 X11 X12 X13

1 X4 _{5/3 0 0 4/3 1 -4/3 0 0 1/3 -1 4/3 0 0 -1/3}

0 X₁ 5/3 1 0 4/3 0 5/3 0 0 -2/3 0 -5/3 0 0 2/3

1 X6 _{1/3 0 0 -4/3 0 -2/3 1 0 -1/3 0 2/3 -1 0 1/3} 1 X7 _{2/3 0 0 -2/3 0 -1/3 0 1 -2/3 0 1/3 0 -1 2/3}

0 X2 _{2/3 0 1 1/3 0 -1/3 0 0 1/3 0 1/3 0 0 -1/3}

Zj 8/3 0 0 -2/3 1 -7/3 1 1 -2/3 -1 7/3 -1 -1 2/3

(Cj– Zj) 0 0 2/3 0 10/3 0 0 5/3 2 -4/3 2 2 1/3

Pada tabel 3.3 masih ditemukan nilai



C_j Z_j



yang negatif sehingga belum ditemukannya solusi yang optimum, maka proses harus dilanjutkan lagi. Kolom kunci

adalah -4/3 yaitu pada kolom . Dan rasio yang memiliki nilai positif terkecil adalah 2/3 yaitu pada baris sebagai baris kunci.

10

X

6

X

Maka X₁₀ mengganti X₆ pada variabel dasar.

Baris kunci baru =

pivot

1 _{(baris kunci lama)}

= 3 / 2

Baris-I baru = baris-I lama -

3 / 2 3 /

4 _{(baris kunci lama)}

= ( 5/3 0 0 4/3 1 -4/3 0 0 1/3 -1 4/3 0 0 -1/3 ) = 2 ( 1/3 0 0 -4/3 0 -2/3 1 0 -1/3 0 2/3 -1 0 1/3 ) = 1 0 0 4 1 0 -2 0 1 -1 0 2 0 -1

Baris-II baru = baris-II lama -

3 / 2 3 / 5

 _{(baris kunci lama)}

= ( 5/3 1 0 4/3 0 5/3 0 0 -2/3 0 -5/3 0 0 2/3 ) =

2 5

 ( 1/3 0 0 -4/3 0 -2/3 1 0 -1/3 0 2/3 -1 0 1/3 ) = 5/2 1 0 -2 0 0 5/2 0 -3/2 0 0 5/2 0 3/2

Baris-III baru = baris-III lama - 4 2

 (baris kunci lama)

= ( 1/2 0 0 -2 0 -1 3/2 0 -1/2 0 1 -3/2 0 1/2 ) =

2 1

 ( 1 0 0 4 1 0 -2 0 1 -1 0 2 0 -1 ) = 1 0 0 0 1/2 -1 1/2 0 0 -1/2 1 -1/2 0 0

Baris-IV baru = baris-IV lama - 4

0 (baris kunci lama)

= ( 1/2 0 0 0 0 0 -1/2 1 -1/2 0 0 1/2 -1 1/2 ) = 0 ( 1 0 0 4 1 0 -2 0 1 -1 0 2 0 -1 ) = 1/2 0 0 0 0 0 -1/2 1 -1/2 0 0 1/2 -1 1/2

Baris-V baru = baris-V lama - 4

1 (baris kunci lama)

= ( 1/2 0 1 1 0 0 -1/2 0 1/2 0 0 1/2 0 -1/2 ) =

4

1 _{( 1 0 0 4 1 0 -2 0 1 -1 0 2 0 -1 )}

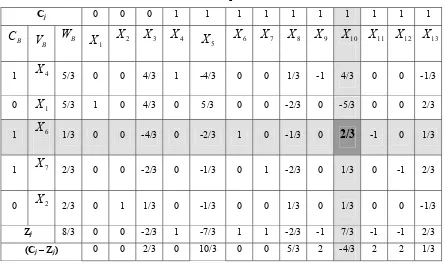
[image:41.595.101.534.97.781.2]

= 1/4 0 1 0 -1/4 0 0 0 1/4 1/4 0 0 0 -1/4

Tabel 3.4 Simpleks

Cj 0 0 0 1 1 1 1 1 1 1 1 1 1

B

C

B

V W_B X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X12 X13

0 X₁ 3 1 0 0 1/2 0 3/2 0 -1 -1/2 0 7/2 0 1

1 X₁₀ 1 0 0 0 1/2 -1 1/2 0 0 -1/2 1 -1/2 0 0

1 X₇ 1/2 0 0 0 0 0 -1/2 1 -1/2 0 0 1/2 -1 1/2

2 X

0 1/4 0 1 0 -1/4 0 0 0 1/4 1/4 0 0 0 -1/4

Z j 3/2 0 0 0 1/2 -1 0 1 -1/2 -1/2 1 0 -1 1/2

(Cj– Z ) j 0 0 0 1/2 2 1 0 3/2 3/2 0 1 2 1/2

(C – Z ) tidak ada lagi yang bernilai negatif maka proses dihentikan, sehingga nilai yang didapat adalah =

Karena nilai j j

1

X ₀= 3 ; X₂=₁= 1/4 danX₃=₂= 1/4. Sehingga didapat model multiple regresinya adalah : _{1 2}

4 1

X X 

rogramming dengan Sistem-QM

putasi persoalan linier programming yang ukurannya

Guna dapat melakukan komputasi dengan komputer, maka diperlukan

program komputer.

QM for windows merupakan paket program komputer untuk

menyelasaikan persoalan-persoalan m

4 1 3 ˆ

Y 

3.2 Komputasi Linier P

3.2.1 Pendahuluan

Analisis perhitungan atau kom

kecil-kecil dapat dilakukan dengan tangan atau kalkulator biasa. Semakin besar suatu

persoalan linier programming maka kita memerlukan bantuan komputer digital karena

cara manual sudah tidak efisien dan tidak layak lagi untuk dilakukan.

Program komputer berguna untuk memberikan instruksi kepada

komputer dengan bahasa komputer tertentu tentang apa yang harus dikerjakan dan

dilakukan oleh komputer. Dalam dunia teknologi tinggi dewasa ini, pada umumnya

telah disusun program-program komputer dalam bentuk paket sesuai dengan jenis dan

sistem komputer yang ada dan dapat dipergunakan sewaktu-waktu bila diperlukan.

Salah satu diantaranya adalah sistem-QM (Quantitative Methods).

Program

etode kuantitatif, manajemen sains atau riset

adalah program ini sangat fleksibel dalam arti bahwa tersedia banyak pilihan dari

modul yang dapat dipergunakan untuk menganalisis berbagai jawaban daripada suatu

persoalan linier programming yang kita hadapi.

3.2.2 Langkah-Langkah Pengerjaan Program QM

ampilan sementara (splash) setelah program QM for windows dijalankan tampak T

[image:43.595.181.474.274.430.2]

pada gambar 3.1.

Gambar 3.1 tampilan sementara (splash) dari program QM for windows

Setelah tampilan sementara (splash) berakhir, akan muncul tampilan awal

seperti gambar 3.2 yang berarti program sudah siap untuk menjalankan modul-modul

[image:44.595.141.526.90.373.2]

Gambar 3.2 Pilihan modul yang tersedia pada program QM for windows

Pilih menu File-New, sehingga muncul tampilan seperti gambar 3.3

[image:44.595.111.524.457.693.2]

55

[image:45.595.108.522.129.256.2]

Lalu mengisi angka-angka pada kotak sesuai dengan persoalan yang akan dikerjakan

Gambar 3.4 Tampilan untuk mengisi angka-angka sesuai dengan soal

Selesaikan persoalan dengan mengklik tombol pada toolbar maka akan

[image:48.842.81.772.74.262.2]

58

Gambar 3.5 Langkah-langkah pengerjaan linier programming

Dari hasil pengerjaan program QM for Windows didapat yaitu : X1 =3 ; X2 = 0,25 ; X3 = 0,25 sehingga dari perhitungan ini didapat suatu

Ada 3 output (tampilan) yang dihasilkan dari penyelesaian soal, dapat dipilih

untuk ditampilkan dari menu Windows yaitu :

1. Linear Programming Results 2. Ranging

[image:50.595.205.428.80.359.2]

Gambar 3.6 Output dari penyelesaian contoh soal linear programming

1. Tampilan linear programming results menunjukkan hasil perhitungan solution X1

= 3,6667 ; X2 = 0,3333 sehingga RHS = 0. Dari hasil perhitungan ini menunjukkan

nilai jumlah optimum.

2. Tampilan ranging khususnya pada kolom lower bond dan upper bond menunjukkan batas maksimal (minimum dan maksimum) pada koefisien variabel

dan pada nilai kendala, dimana pada rentang nilai antara lower bond dan upper

bond.

Dari tabel solution list didapat bahwa nilai optimal (Z) minimum adalah 0.

3.2.3 Pengujian Hipotesis

1) Hipotesis

Ha : terdapat hubungan fungsional linier & signifikan antara variabel

X1, X2, X3 dengan Y

H0 : tidak terdapat hubungan fungsional yang linier dan signifikan

2) Uji signifikansi

 Cari Rhit dengan rumus :













 1 1 2 ₂2 3 3

) 3 , 2 , 1 ( y y x b y x b y x b R_y

 

 

91 0 67 25 , 0 21 25 ,

0  

 24 , 0 91 22 91 75 , 16 25 , 5    

R = 0,49

 Kuadratkan nilai R tersebut menjasi R2 = (0,49)2 = 0,24

 Hitung Fsign hitung dengan menggunakan rumus :

Freg









2 2 1 1 R m m n R    









 

107 , 0 24 , 2 1 24 , 0 24 , 0 1 3 1 3 5 24 , 0      

 Taraf signifikansinya (α) = 0,05

 Ftabel _{ } 

penyebut pembilangdk

dk

F_{1 ,}



= F(1-0,05)(3,1)

= F(0,95)(3,1)

Ftabel = 216

 Tentukan kriteria pengujian H0 yaitu :

Ha : tidak signifikan

H0 : signifikan

Ternyata 0,107 < 216 atau Fhit < Ftab, sehingga H0 diterima atau

signifikan.

3) Kesimpulan

Hipotesis nol yang berbunyi : “terdapat hubungan fungsional yang signifikan

antara variabel X1, X2 dan X3 dengan variabel Y”, diterima. Dan sebaliknya

hipotesis alternatif yang berbunyi : “tidak terdapat hubungan fungsional yang

signifikan antara variabel X1, X2, dan X3 dengan variabel Y”, ditolak.

[image:52.595.108.523.314.606.2]

3.2.3 Dualitas

Gambar 3.7 Bentuk dual dari primal

fungsi tujuan

maximum : G4Y₁3Y₂ 4Y₃5Y₄ 5Y₅

kendala : Y₁Y₂ Y₃ Y₄ Y₅ 0

0 3 2 2

3

0 5 4 3 2

5 4 3 2 1

5 4 3 2 1

    

    

Y Y Y Y Y

1 1 1 1 1

5 4 3 2 1

    

Y Y Y Y Y

1 1 1 1 1

5 4 3 2 1

 

 

 

 

 

Y Y Y Y Y

0  i

Y

Dalam hal ini kita akan menggunakan sistem perhitungan komputasi dengan

menggunakan program-QM. Dengan sistem pengerjaan sebagai berikut :

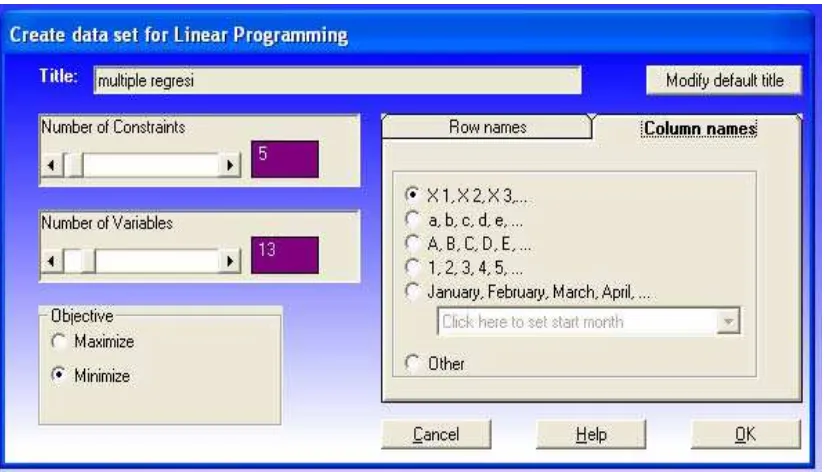
[image:53.595.109.522.380.578.2]

mengisi angka-angka pada kotak sesuai dengan persoalan yang akan dikerjakan

Gambar 3.8 Tampilan untuk mengisi angka-angka sesuai dengan soal

Ada 3 output (tampilan) yang dihasilkan dari penyelesaian soal, dapat dipilih

untuk ditampilkan dari menu Windows yaitu :

1. Linear Programming Results 2. Ranging

[image:55.595.110.522.97.466.2]

1. Tampilan linear programming results menunjukkan hasil perhitungan solution Y1

= 0 ; Y2 = 0; Y3= 0; Y4= 0; dan Y5=0 sehingga RHS = 0. Dari hasil perhitungan ini

menunjukkan nilai jumlah optimum.

2. Tampilan ranging khususnya pada kolom lower bond dan upper bond menunjukkan batas maksimal (minimum dan maksimum) pada koefisien variabel

dan pada nilai kendala, dimana pada rentang nilai antara lower bond dan upper

bond.

67

BAB 4

KESIMPULAN DAN SARAN

4.1 Kesimpulan

Berdasarkan hasil perhitungan dan penganalisaan data yang telah dilakukan, maka

dapat diambil kesimpulan sebagai berikut :

1. Persamaan multiple regresi linier dengan menggunakan teknik linier

programming :

2 1

4 1 4 1 3

ˆ _{X X}

Y   

2. Nilai optimal (Z) dari minimum adalah 0 dan nilai optimal (G) dari maximum

adalah 0. Ini berarti bahwa jarak deviasi dari garis regresi linier adalah 0,

sehingga titik ini tepat berada di garis regresi linier tersebut.

3. Linier programming merupakan alat analisis yang tepat dalam menentukan

model koefisien multiple regresi.

4. Analisis linier programming bertujuan untuk meminimumkan jarak antara titik

estimasi dengan titik sebenarnya.

4.2 Saran

Untuk dapat lebih menghemat waktu dan mempermudah penyelesaian, maka didalam

menyelesaikan masalah dengan menggunakan metode linier programming dapat

DAFTAR PUSTAKA

Algifari. 2003. Statistika Induktif untuk Ekonomi dan Bisnis. Yogyakarta: Akademi Manajemen Perusa