OPTIMISASI MANAJEMEN PRODUKSI BERBASIS
FUZZY GOAL PROGRAMMING
(STUDI KASUS PADA PERUSAHAAN MINUMAN RINGAN)
ALTIEN JONATHAN RINDENGAN
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
Dengan ini saya menyatakan bahwa tesis Optimisasi Manajemen Produksi
Berbasis Fuzzy Goal Programming (Studi Kasus pada Perusahaan Minuman
Ringan) adalah karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam daftar pustaka di bagian akhir tesis ini.
Bogor, Juli 2012
Altien J Rindengan
ABSTRACT
ALTIEN J RINDENGAN. Production Management Optimization Based Fuzzy Goal Programming (Case Study on Soft Drink Companies). Under direction of PRAPTO TRI SUPRIYO and AZIZ KUSTIYO.
Every company wants to regulate the production of each product in order to provide optimum benefit for the company. To optimize the benefits need to consider the cost and used production equipment. So that the objectives are not limited to optimization of profits but also consider the desire of decision makers in the company. This research will analyze production management optimization-based fuzzy goal programming (FGP). By reason of FGP consider the decision maker wishes to determine any restrictions on the objective function value that exists. Companies to be analyzed is the PT. Bangun Wenang Baverages Company (BWBC) which is a soft drink company. The objective function to be analyzed is profit maximization, minimization of working time machine, minimization the cost of raw materials, and minimization the cost of labor. In FGP models, each of the objective function is converted into the form of constraints with fuzzy membership functions respectively. For analysis of the optimal solution, FGP formed into a model such as linear programming. Further sensitivity analysis was performed after the optimal solution is obtained, to see the changes in each interval availability of resources to maintain optimal conditions. Model optimization and sensitivity analysis is a part in the decision support system for the company in its production planning. This study provides the results of the FGP can accommodate the decision-makers desires in each objective function. This model provides an optimal solution for the company based on the decision-makers desire. For PT. BWBC, the model established in this study provide an optimal solution for the company in its production planning based on the decision-maker wishes fourth objective function that is it.
Goal Programming (Studi Kasus pada Perusahaan Minuman Ringan). Dibimbing oleh PRAPTO TRI SUPRIYO dan AZIZ KUSTIYO.
Suatu perusahaan dalam menjalankan kegiatan usahanya, berhubungan dengan jenis produk yang akan dibuat dan jumlah keuntungan yang akan diperoleh dari proses usaha tersebut. Dalam rangkaian proses produksi sampai diperoleh keuntungan, ada banyak faktor yang harus diperhatikan yaitu jenis produk yang akan dibuat, bahan baku atau sumber daya yang diperlukan untuk menghasilkan tiap produk dan ketersediaanya, mesin yang digunakan, dan tenaga kerja yang diperlukan. Sebagai suatu tujuan memperoleh keuntungan yang optimal, di dalamnya mempertimbangkan biaya-biaya yang berhubungan dengan proses produksi tersebut, misalnya biaya bahan baku dan biaya tenaga kerja.
Penelitian ini bertujuan untuk menganalisa dan mencari solusi optimal jumlah tiap-tiap produk yang akan diproduksi dalam perencanaan produksi perusahaan minuman ringan dengan metode fuzzy goal programming (FGP) yang dapat memenuhi beberapa tujuan yang ingin dicapai yaitu keuntungan, biaya tenaga kerja, biaya bahan baku, dan waktu kerja mesin yang memberikan tingkat kepuasan yang terbaik bagi pengambil keputusan dari hasil solusi yang diperoleh berdasarkan preferensi terhadap tujuan-tujuan yang akan dicapai tersebut. Selanjutnya dilakukan analisis sensitivitas dari solusi optimal yang diperoleh untuk melihat pengaruh perubahan paramater faktor produksi terhadap solusi optimal tersebut, yang juga dapat mendukung pengambil keputusan dalam perencanaan produksinya.
Metode optimasi yang dilanjutkan dengan analisis sensitivitas tersebut merupakan bagian dari sistem pengambilan keputusan (decision support system -DSS) yang merupakan analisis berbasis model untuk pemrosesan data dan pengambilan keputusan. Solusi optimal yang diperoleh menjadi dasar pengambil keputusan menentukan produk-produk yang akan diproduksi dan analisis sensitivitas memungkinkan pengambil keputusan mengatur jumlah bahan baku atau sumber daya yang akan disediakan berdasarkan hasil optimal yang diinginkan. Metode FGP dalam penelitian ini memungkinkan pengambil keputusan (decision maker) untuk menentukan batasan keinginannya terhadap tujuan-tujuan yang akan dicapai dari model yang dibangun tersebut.
Penelitian ini mengikuti langkah-langkah kerangka pemikiran yaitu: identifikasi masalah, perumusan tujuan, studi literature, pengumpulan data, dan pembentukan dan analisis model. Dalam pembentukan dan analisis model terdiri dari: penetapan variabel-variabel keputusan, penetapan fungsi-fungsi tujuan, penetapan bentuk-bentuk kendala, membentuk model-model linear programming
Pembentukan dan analisis model menggunakan data perusahaan minuman ringan sebagai studi kasusnya. Dalam penelitian ini menggunakan data dari PT. Bangun Wenang Baverages Company (PT. BWBC) yang berkedudukan di Manado, Sulawesi Utara. Model-model LP dan solusi optimalnya berdasarkan fungsi tujuan maksimisasi keuntungan, minimisasi waktu kerja mesin, minimisasi biaya bahan baku, dan minimisasi biaya tenaga kerja. Fungsi-fungsi tujuan ini berdasarkan solusi optimalnya dan batasan keinginan pengambil keputusan akan diubah menjadi bentuk-bentuk kendala yang akan ditambahkan dalam model menjadi model FGP yang dapat dianalisa sebagai model LP. Analisis sensitivitas yang dilakukan adalah perubahan ketersediaan sumber daya atau bahan baku. Selang dimana kondisi optimal tetap dipertahankan artinya jenis produk yang dihasilkan tetap tapi jumlah dan solusi optimalnya bisa berubah.
Model optimalisasi dan analisis sensitivitas ini merupakan bagian dalam
decision support system (DSS) yang diklasifikasikan dalam analisis model dan berorientasi solver. Analisis sensitivitas membantu dalam DSS untuk melihat dampak perubahan parameter setelah solusi optimal diperoleh.
Penelitian ini memberikan hasil yaitu FGP dapat diterapkan dalam optimisasi manajemen produksi untuk kasus perusahaan minuman ringan. Untuk PT. BWBC, dengan memperhatikan fungsi tujuan yaitu keuntungan, biaya tenaga kerja, biaya bahan baku, dan waktu kerja mesin, dapat ditentukan solusi optimal bagi perusahaan.
Pada kasus keinginan pengambil keputusan yaitu: besarnya keuntungan paling sedikit 80% dari keuntungan maksimal, Rp4926425600.00; waktu kerja mesin paling banyak 1.25 kali waktu kerja mesin minimal, 8145 menit; biaya
bahan baku paling banyak 1.25 kali biaya bahan baku maksimal, Rp3390380000.00; dan biaya tenaga kerja paling banyak 1.25 kali biaya tenaga
kerja maksimal Rp137779875.00; diperoleh solusi optimal yaitu jenis produk
Pada kasus keinginan pengambil keputusan yaitu: pendapatan sekurang-kurangnya Rp4500000000.00; waktu kerja mesin setinggi-tingginya
000
9 menit; biaya bahan baku setinggi-tingginya Rp3000000000.00; biaya tenaga kerja setinggi-tingginya Rp150000000.00; diperoleh solusi optimal yaitu jenis produk yang harus diproduksi adalah cocacola 295 ml sebanyak krat;
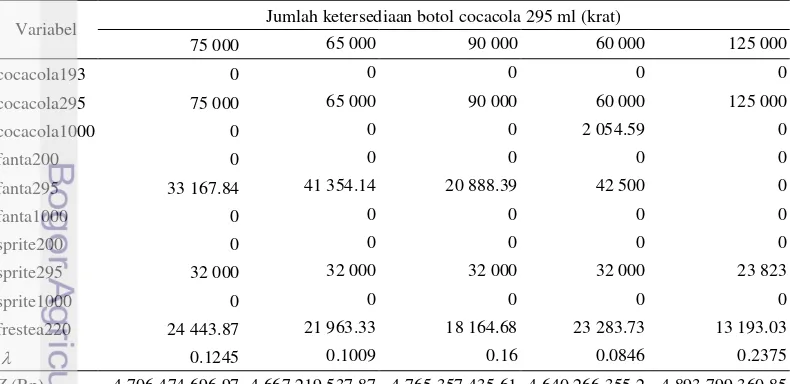
diubah diluar selang ini makan kondisi optimalnya juga akan berubah. Misalkan ketersediaan botol cocacola 295 diubah menjadi 90000krat (masih dalam selang kondisi optimal tetap) maka jika dicari solusi optimalnya diperoleh variabel keputusan sebagai variabel basis solusi tetap (nilainya yang berubah) yaitu cocacola 295 ml sebanyak 90000krat; fanta 295 ml sebanyak 20888.39 krat; sprite 295 ml sebanyak 32000krat; frestea sebanyak 18164.68 krat; dengan nilai keuntungan sebesar Rp4765357435.61.
© Hak Cipta milik IPB, tahun 2012 Hak Cipta dilindungi Undang-Undang
1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumber
a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik atau tinjauan suatu masalah
b. Penelitian tidak merugikan kepentingan yang wajar IPB
2. Dilarang mengumumkan dan memperbanyak sebagian atau seluruh karya tulis dalam bentuk apapun tanpa izin IPB
OPTIMISASI MANAJEMEN PRODUKSI BERBASIS
FUZZY GOAL PROGRAMMING
(STUDI KASUS PADA PERUSAHAAN MINUMAN RINGAN)
ALTIEN JONATHAN RINDENGAN
Tesis
sebagai salah satu syarat untuk memperoleh gelar Magister Komputer pada
Program Studi Ilmu Komputer
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
Nama : Altien Jonathan Rindengan
NIM : G651080041
Disetujui
Komisi Pembimbing
Drs. Prapto Tri Supriyo, M.Kom. Aziz Kustiyo, S.Si., M.Kom.
Ketua Anggota
Diketahui
Ketua Program Studi Dekan Sekolah Pascasarjana
Ilmu Komputer
Dr. Yani Nurhadryani, S.Si., M.T. Dr. Ir. Dahrul Syah, M.Sc.Agr.
PRAKATA
Puji dan syukur dipanjatkan kepada Tuhan Allah Yang Maha Kuasa atas berkat dan karuniaNya sehingga penulis dapat menyelesaikan tesis ini. Tema yang dipilih dalam penelitian ini adalah Optimisasi Manajemen Produksi Berbasis Fuzzy Goal Programming (Studi Kasus pada Perusahaan Minuman Ringan).
Penyelesaian tesis ini melibatkan banyak pihak yang tentunya sangat membantu dalam proses penelitian dan penulisan tesis ini. Oleh karena itu,pada kesempatan ini penulis mengucapkan banyak terima kasih kepada:
1. Bapak Drs. Prapto Tri Supriyo, M.Kom sebagai komisi pembimbing (ketua) atas segala motivasi, bimbingan dan arahan yang diberikan.
2. Bapak Aziz Kustiyo, S.Si., M.Kom sebagai komisi pembimbing atas segala motivasi, bimbingan dan arahan yang diberikan.
3. Bapak Dr. Sugi Guritman sebagai dosen penguji yang telah menguji dan memberikan saran dan masukannya.
4. Ketua dan Sekretaris Program Studi Ilmu Komputer IPB, staf dosen dan staf administrasi.
5. Pimpinan Universitas Sam Ratulangi, Fakultas MIPA dan Jurusan Matematika yang telah memberikan izin dan rekomendasi tugas belajar. 6. Rekan-rekan staf pengajar di Jurusan Matematika FMIPA Unsrat Manado. 7. Pimpinan PT BWBC Manado, Pak Jantje T, Pak Thonce T, Pak Vecky T,
dr. Sem M (alm), atas izin kepada penulis untuk melakukan penelitian dan mengumpulkan data dari perusahaan ini.
8. Rekan-rekan mahasiswa KOM08 (Pak Toto, Pak Aziz, Aris, Rosi, dan Deff) yang sama-sama berjuang, saling memberi dorongan sejak masa kuliah sampai penyusunan tesis.
9. Rekan-rekan mahasiswa Manado di asrama Sempur (E’Itje, Pak Noli, M’Sukma, E’Ratna, Chae, Nando, Bun, Arthus, Bill, Nelda, Onong, Iqbal) dan asrama Bogor Baru I dan II, yang memberikan bantuan saran dan doanya. Karya ini dipersembahkan untuk istri dan anak yang aku cintai dan kasihi,
Grace dan Galnoel, yang sangat banyak memberikan dukungan moril, semangat, doa, dan kesabaran selama penulis kuliah dan menyelesaikan tesis ini.
Sebagai hasil dari suatu proses belajar, penulis menyadari bahwa karya ilmiah ini tidak lepas dari kekurangan. Tetapi, semoga karya kecil ini dapat memberikan manfaat bagi perkembangan ilmu dan pengetahuan.
Bogor Juli 2012
ayah Friets Pieter Rindengan (alm) dan ibu Katrin Agustina Pangkey. Penulis merupakan putra keempat dari empat bersaudara. Pada tahun 2004 menikah dengan Grace Ritny Gladys Sondakh, S.P., dan telah dikaruniai satu orang putra bernama Galnoel Peter Rindengan (7 tahun).
Pendidikan di tingkat SD, SMP, dan SMA diselesaikan di Tomohon. Pada tahun 1999 penulis menyelesaikan pendidikan S1 di Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam-Institut Pertanian Bogor dengan beasiswa EUIDP (Eastern Indonesia University Development Project) yang di sponsori oleh CIDA (Canadian International Development Agency). Pada tahun 2008 penulis melanjutkan pendidikan S2 pada Program Studi Ilmu Komputer, Sekolah Pascasarjana Institut Pertanian Bogor dengan beasiswa BPPS Dikti, Kementerian Pendidikan dan Kebudayaan Indonesia.
Penulis bekerja sebagai staf pengajar di Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sam Ratulangi Manado mulai tahun 2001 sampai sekarang.
xiii
xiv
V SIMPULAN DAN SARAN
5.1 Simpulan ... 45
5.2 Saran ... 45
DAFTAR PUSTAKA ... 47
xv
DAFTAR TABEL
Halaman
1 Bahan baku syrup untuk memproduksi satu krat produk ... 28
2 Biaya bahan baku per krat ... 28
3 Solusi LP model maksimisasi keuntungan ... 32
4 Solusi LP model minimisasi waktu kerja mesin ... 33
5 Solusi LP model minimisasi biaya bahan baku ... 33
6 Solusi LP model minimisasi biaya tenaga kerja ... 34
7 Solusi FGP untuk ... 39
8 Solusi FGP untuk ... 41
xvi
DAFTAR GAMBAR
Halaman
1 Reperesentasi linear naik ... 9
2 Reperesentasi linear turun ... 9
3 Representasi kurva segitiga ... 10
4 Reperesentasi kurva trapezium ... 10
5 Fungsi keanggotaan fuzzy fungsi tujuan model FGP ... 16
6 Langkah-langkah penelitian ... 19
7 Bentuk umum keanggotaan fuzzy dari tiap fungsi tujuan model FGP .... 26
8 Fungsi keanggotaan fuzzy untuk fungsi tujuan maksimisasi keuntungan ... 34
9 Fungsi keanggotaan fuzzy untuk fungsi tujuan minimisasi waktu kerja mesin ... 35
10 Fungsi keanggotaan fuzzy untuk fungsi tujuan minimisasi biaya bahan baku ... 35
xvii
DAFTAR LAMPIRAN
Halaman
1 Produk yang dihasilkan PT. Bangun Wenang Baverages Company ... 49
2 Bahan baku syrup dan hasil produksi ... 49
3 Harga bahan baku ... 49
4 Jumlah bahan baku yang tersedia setiap bulan ... 50
5 Harga jual tiap produk ... 50
6 Biaya tenaga kerja untuk tiap produk ... 51
7 Solusi model maksimisasi keuntungan dengan POM/QM Win ... 52
8 Solusi model minimisasi waktu kerja mesin dengan POM/QM Win ... 53
9 Solusi model minimisasi biaya bahan baku dengan POM/QM Win ... 54
10 Solusi model minimisasi biaya tenaga kerja dengan POM/QM Win ... 55
11 Solusi model FGP untuk dengan POM/QM Win ... 56
12 Solusi model FGP untuk dengan POM/QM Win ... 57
I PENDAHULUAN
1.1 Latar Belakang
Manajemen produksi merupakan perencanaan tentang jenis dan jumlah produk yang akan diproduksi oleh suatu perusahaan dalam satu periode waktu yang akan datang. Perencanaan produksi merupakan bagian dari perencanaan operasional di dalam perusahaan. Dalam penyusunan perencanaan produksi, hal yang perlu dipertimbangkan adalah adanya optimasi produksi sehingga akan dapat dicapai produksi optimal dengan tingkat biaya yang paling rendah untuk pelaksanaan proses produksi tersebut. Perencanaan produksi juga dapat didefinisikan sebagai proses untuk memproduksi barang-barang pada suatu periode tertentu sesuai dengan yang diramalkan atau dijadwalkan melalui pengorganisasian sumber daya seperti tenaga kerja, bahan baku, mesin dan peralatan lainnya. Perencanaan produksi menuntut penaksiran atas permintaan produk atau jasa yang diharapkan akan disediakan perusahaan di masa yang akan datang. Dengan demikian, peramalan merupakan bagian integral dari perencanaan produksi (Buffa & Sarin 1996).
Banyak masalah dalam kehidupan nyata yang dinyatakan dalam bentuk pemrograman matematis. Seperti bentuk pengotimuman fungsi tujuan/objektif dengan kendala tertentu dimana metode pengembangan solusi diarahkan ke tujuan
tunggal seperti metode simpleks untuk linear programming (LP). Dalam menerapkan pemrograman matematika untuk pengambil keputusan, disadari bahwa ada masalah dalam kehidupan nyata yang memiliki beberapa tujuan. Demikian juga dalam masalah manajemen produksi yang tidak bisa hanya dilihat dari sisi memproduksi barang semaksimal mungkin, tapi perlu mempertimbangkan batasan-batasan yang mempengaruhinya. Misalkan ketersediaan bahan baku yang terbatas atau ada tujuan lain yang juga harus dicapai.
deviasinya, GP secara otomatis menangkap informasi tentang pencapaian relatif dari tujuan-tujuan yang ada. Oleh karena itu, solusi optimal yang diberikan dapat dibatasi pada solusi fisibel yang menggabungkan ukuran-ukuran performansi yang diinginkan. Chodary dan Slomp (2002) memaparkan bahwa GP dapat diterapkan secara efektif dalam perencanaan produksi, karena metode GP potensial untuk menyelesaikan aspek-aspek yang bertentangan antara elemen-elemen dalam perencanaan produksi, yaitu konsumen, produk, dan proses manufaktur.
Selain itu, dilihat dari pembuat keputusan, maka tingkat aspirasi pembuat keputusan harus dipertimbangkan untuk memecahkan masalah dari perspektif strategi kepuasan. Oleh karena itu, ketidakjelasan dalam sistem fuzzy
dilambangkan dengan angka oleh pembuat keputusan perlu dipertimbangkan. Menurut Chankong dan Haimes (1993), unsur penilaian manusia adalah di bidang preferensi didefinisikan oleh pembuat keputusan. Menurut Cunkas (2008), proses keputusan dengan beberapa kriteria dalam bisnis dan teknik mengarah pada konsep fuzzy multiobjective linear programming. Model ini juga dikenal dengan
fuzzy goal programming (FGP). Dalam pendekatan ini mendukung pembuat keputusan masing-masing tujuan dengan jumlah tujuan yang harus terpenuhi dengan keyakinan bahwa solusi terbaik yang ditemukan solusi ideal dengan pertimbangan keanggotaan fuzzy (Li et al. 2004). Jenis fungsi keanggotaan fuzzy
yang telah digunakan dalam masalah pemrograman linear dan aplikasinya dalam mengatasi data fuzzy, seperti fungsi keanggotaan linier piecewise (Lopez 2005).
Dilihat dari fungsi tujuan yang harus dicapai, pada GP mengharuskan dilakukan pembobotan atau derajat kepentingan dari setiap fungsi tujuan secara diskrit. Mana yang dianggap mempunyai bobot atau derajat kepentingan lebih besar dari yang lain untuk dianalisa. Sedangkan pada FGP, tidak perlu dilakukan pembobotan. Setiap fungsi tujuannya dinyatakan dalam derajat keanggotaan fuzzy
sesuai preferensi perusahaan atau pengambil keputusan. Dilihat dari keunggulan ini maka analisis dalam penelitian ini akan menggunakan FGP.
multi-objektif (multi objective decision making-MODM). Metode FGP masuk dalam pendekatan MODM (Kahraman 2008).
Sistem pendukung keputusan (decision support system-DSS) yang merupakan prosedur berbasis model untuk pemrosesan data dan penilaian untuk membantu para manajer mengambil keputusan, mempunyai karakteristik dan kapabilitas yang salah satunya adalah pemodelan dan analisis. Kapabilitas pemodelan ini memungkinkan penerapan berbagai strategi yang berbeda dengan konfigurasi yang berbeda pula. Dari sisi klasifikasi DSS, dapat berorientasi data dan model. Salah satu yang berorientasi model adalah model optimisasi (Turban et al. 2005).
PT. Bangun Wenang Baverages Company (BWBC) adalah perusahaan minuman ringan yang berada di kota Manado, Sulawesi Utara dengan pabrik berkedudukan di kota Bitung. Perusahaan ini memproduksi minuman ringan cocacola, fanta, sprite, dan frestea dengan hak distribusi yang diberikan oleh PT. Cocacola Indonesia meliputi wilayah Sulawesi Utara, Gorontalo, Sulawesi Tengah dan Kota Ternate. Selama ini, untuk menentukan jumlah produk yang akan diproduksi setiap bulan, hanya berdasarkan produksi pada tahun sebelumnya dan permintaan konsumen pada bulan berjalan. Perusahaan belum melakukan analisa jumlah produk yang harus diproduksi setiap bulan agar memberikan keuntungan yang optimal, dengan mempertimbangkan jumlah sumber daya yang ada dan tujuan yang ingin dicapai dari sisi keuntungan, penggunaan mesin produksi, dan biaya produksi. Penelitian yang pernah dilakukan berhubungan dengan masalah optimisasi pada perusahaan adalah oleh Wowor (2009), tetapi hanya masalah maksimisasi keuntungan.
1.2 Perumusan Masalah
mesin maka yang menjadi pertanyaan adalah “berapakah jumlah produksi dari setiap produk yang harus dihasilkan agar memberikan hasil yang optimal dan memenuhi tujuan-tujuan yang tersebut?”.
Dilihat dari sisi metode yang ada maka GP dapat digunakan dalam manajemen perencanaan produksi karena adanya beberapa tujuan yang harus dipenuhi dalam proses produksi. Tetapi jika dilanjutkan pada analisis yang lebih dalam dengan melihat bahwa preferensi kepuasan pelaku usaha berbeda-beda terhadap tujuan-tujuan yang akan dicapai tersebut, maka hal ini dapat diatasi dengan mempertimbangkan keanggotaan fuzzy dari solusi yang telah diperoleh secara parsial untuk memperoleh solusi terbaik yang menjadi solusi ideal proses produksi yang paling diinginkan. Metode yang dapat digunakan adalah FGP yang merupakan salah satu metode model optimisasi multi-objektif untuk pengambilan keputusan yang merupakan bagian dalam DSS. Dimana dalam peneltian ini difokuskan pada kasus manajemen produksi perusahaan minuman ringan.
Berdasarkan masalah-masalah ini, maka rumusan masalah dalam penelitian ini adalah bagaimana mencari jumlah produksi yang optimal dari masing-masing produk dalam perencanaan produksi pada perusahaan minuman ringan yang akan memenuhi tujuan yang diharapkan yaitu antara lain memaksimalkan pendapatan, meminimalkan pengunaan tenaga kerja dan meminimalkan waktu kerja mesin, dan juga harus memenuhi batasan kendala atau sumber daya yang tersedia. Kemudian bagaimana memberikan tingkat kepuasan yang baik dari hasil solusi yang diperoleh dengan memperhatikan preferensi manajemen perusahaan atau pengambil keputusan terhadap tujuan-tujuan yang akan dicapai.
1.3 Tujuan Penelitian
solusi optimal yang diperoleh untuk melihat pengaruh perubahan paramater faktor produksi terhadap solusi optimal tersebut, yang juga dapat mendukung pengambil keputusan dalam perencanaan produksinya.
1.4 Manfaat Penelitian
II TINJAUAN PUSTAKA
2.1 Sistem Fuzzy
Sistem fuzzy merupakan penduga numerik yang terstruktur dan dinamik. Sistem ini mempunyai kemampuan untuk mengembangkan sistem cerdas dalam lingkungan yang tidak pasti dan tidak tepat. Sistem ini menduga suatu fungsi dengan logika fuzzy, dimana logika ini merupakan bagian dari logika boolean. Logika fuzzy pada dasarnya digunakan untuk menangani konsep derajat kebenaran yang berkisar antara benar dan salah (Marimin 2009).
Menurut Kusumadewi dan Purnomo (2004), beberapa alasan mengapa logika fuzzy banyak digunakan, antara lain:
Mudah dimengerti, karena menggunakan konsep matematis yang sederhana. Logika yang sangat fleksibel.
Toleransi terhadap data-data yang tidak tepat.
Dapat membangun dan mengaplikasikan suatu keahlian, tanpa harus melalui proses pelatihan.
Didasarkan pada bahasa alami.
Ada beberapa hal yang perlu diketahui dalam memahami sistem fuzzy
(Kusumadewi & Purnomo 2004), yaitu: - Variabel Fuzzy
Variabel fuzzy merupakan variabel yang hendak dibahas dalam suatu sistem
fuzzy. Contoh: umur, temperatur, permintaan. - Himpunan Fuzzy
Himpunan fuzzy merupakan suatu grup yang mewakili suatu kondisi atau
keadaan tertentu dalam suatu variabel fuzzy. Himpunan fuzzy memiliki 2 atribut, yaitu:
1. Linguistik, yaitu penamaan grup yang mewakili suatu keadaan atau kondisi tertentu dengan menggunakan bahasa alami, seperti: Muda, Dewasa, Tua. 2. Numeris, yaitu suatu nilai (angka) yang menunjukkan ukuran dari suatu
- Semesta Pembicaraan
Semesta pembicaraan adalah keseluruhan nilai yang diperbolehkan untuk dioperasikan dalam suatu variabel fuzzy. Semesta pembicaraan merupakan himpunan bilangan real yang senantiasa naik (bertambah) secara monoton dari kiri ke kanan. Nilai semesta pembicaraan dapat berupa bilangan positif maupun negatif. Adakalanya nilai semesta pembicaraan ini tidak dibatasi batas atasnya Contoh:
1. Semesta pembicaraan untuk variabel umur: [0, +∞]. 2. Semesta pembicaraan untuk variabel temperatur: [0, 100]. - Domain
Domain himpunan fuzzy adalah keseluruhan nilai yang diijinkan dalam semesta pembicaraan dan boleh dioperasikan dalam suatu himpunan fuzzy. Seperti halnya dengan semesta pembicaraan, domain merupakan himpunan bilangan real yang senantiasa naik (bertambah) secara monoton dari kiri ke kanan. Nilai domain dapat berupa bilangan positif maupun negatif.
Contoh domain himpunan fuzzy :
Muda = [0, 35]; Dewasa=[35,55]; Tua=[45, +∞].
2.2 Fungsi Keanggotaan Fuzzy
Fungsi keanggotaan (membership function) adalah suatu kurva yang menunjukkan pemetaan titik-titik input data ke dalam nilai keanggotaannya (sering juga disebut dengan derajat keanggotaan) yang memiliki interval antara 0 sampai 1. Salah satu cara yang dapat digunakan untuk mendapatkan nilai keanggotaan adalah dengan melalui pendekatan fungsi. Ada beberapa fungsi yang dapat digunakan (Kusumadewi et al. 2006):
a. Representasi linier
1. Representasi linier naik
Kenaikan himpunan dimulai pada nilai domain yang memiliki derajat keanggotaan nol (0) bergerak ke kanan menuju ke nilai domain yang memiliki
Representasi linier turun merupakan kebalikan dari linier naik. Garis lurus dimulai dari nilai domain dengan derajat keanggotaan tertinggi pada sisi kiri, kemudian bergerak menurun ke nilai domain yang memiliki derajat keanggotaan lebih rendah (Gambar 2).
Gambar 3 Representasi Kurva Segitiga. beberapa titik yang memiliki nilai keanggotaan 1 (Gambar 4).
Gambar 4 Representasi Kurva Trapesium.
Secara umum, model program linear terdiri dari persamaan tujuan/objektif, persamaan atau pertidaksamaan kendala yang berhubungan dengan keterbatasan sumber daya, dan variabel keputusan yang menyusun persamaan dan pertidaksamaan tersebut. Tujuan dari analisis model LP adalah mencari nilai-nilai variabel keputusan optimal yang memberikan nilai fungsi tujuan maksimal/minimal dengan tetap memenuhi kendala yang ada.
Bentuk dasar model linear programming adalah (Taylor 2005):
2.4 Goal Programming
Goal programming (GP) merupakan pengembangan dari model LP. Perbedaan utama antara GP dan LP terletak pada struktur dan penggunaan fungsi tujuan. Dalam LP fungsi tujuannya hanya mengandung satu tujuan, sementara dalam GP dengan beberapa fungsi tujuan digabungkan menjadi sebuah fungsi tujuan. Ini dapat dilakukan dengan mengekspresikan tujuan itu dalam bentuk sebuah kendala (goal constraint), memasukkan suatu variabel simpangan
(deviational variabel) dalam kendala itu untuk mencerminkan seberapa jauh tujuan itu dicapai, dan menggabungkan variabel simpangan dalam fungsi tujuan. Dalam LP tujuannya bisa maksimisasi atau minimisasi, sementara dalam GP tujuannya adalah meminimumkan penyimpangan-penyimpangan dan tujuan-tujuan tertentu. Ini berarti semua masalah GP adalah masalah minimisasi.
Karena penyimpangan-penyimpangan dan tujuan-tujuan itu diminimumkan, sebuah model GP dapat menangani aneka ragam tujuan dengan dimensi atau satuan ukuran yang berbeda. Tujuan-tujuan yang saling bentrok juga dapat diselesaikan. Jika terdapat banyak tujuan, prioritas atau urutan ordinalnya dapat ditentukan, dan proses penyelesaian GP itu akan berjalan sedemikian rupa sehingga tujuan dengan prioritas tertinggi dipenuhi sedekat mungkin sebelum memikirkan tujuan-tujuan dengan prioritas lebih rendah. Jika LP berusaha mengidentifikasi solusi optimum dan suatu himpunan solusi fisibel, GP mencari titik yang paling memuaskan dari sebuah persoalan dengan beberapa tujuan dengan mempertimbangkan hirarki prioritas tujuan-tujuan tersebut.
Ravindran (2009) mengatakan bahwa pada model GP akan dilakukan minimisasi variabel simpangan dari setiap fungsi tujuan. Jika setiap fungsi tujuan ada bobot atau prioritas yang ditetapkan maka model GP menjadi kasus minimisasi variabel simpangan dengan pembobotan atau skala priorotas yang ada.
Ada tiga jenis fungsi tujuan dalam GP, yaitu:
Minimumkan
prioritas setiap variabel simpangan, m adalah banyaknya kendala tujuan dalam model, dan n banyaknya tujuan dalam model.Fungsi tujuan persamaan (2.7), digunakan jika variabel simpangan dalam suatu masalah tidak dibedakan menurut prioritas atau bobot. Fungsi tujuan persamaan (2.8), digunakan dalam suatu masalah dimana urutan tujuan-tujuan diperlukan, tetapi variabel simpangan dalam setiap tingkat prioritas memiliki kepentingan yang sama. Dalam fungsi tujuan persamaan (2.9), tujuan-tujuan diurutkan dan variabel simpangan pada setiap tingkat prioritas dibedakan dengan menggunakan bobot yang berlainan wki. Jadi fungsi tujuan yang akan digunakan
tergantung pada situasi masalahnya.
2.5 Fuzzy Goal Programming
Jika pada GP, dalam melakukan optimasi pada masalah multi objective
harus melakukan penjumlahan terbobot fungsi-fungsi tujuannya menjadi satu fungus tujuan. Atau fungsi-fungsi tujuan tersebut diurutkan berdasarkan kepentingannya dimana fungsi tujuan yang lebih penting diselesaikan dulu dan selanjutnya untuk fungsi tujuan berikutnya. Ini cocok pada kasus dimana derajat kepentingan tiap-tiap fungsi tujuan telah diketahui.
Menurut Li et al. (2004), FGP dapat diformulasikan sebagai berikut: Jika didefinisikan x = [x1, x2,…, xn]T Rn sebagai vektor variabel keputusan dan
f(x)=(f1(x),…,fm(x)) adalah fungsi-fungsi tujuan dengan sistem bentuk kendala
G(x). Pengambil keputusan menginginkan batasan fi* ,(i = 1,2,…m) untuk setiap
fungsi tujuan yang memenuhi kendala linear G(x). Dengan menggunakan konsep himpunan fuzzy, fungsi keanggotaan dapat didefinisikan berdasarkan langkah-langkah berikut:
Model (2.10) ini telah menjadi model LP yang dapat diselesaikan dengan metode simpleks.
Karena fungsi tujuan dalam model yang akan dibahas adalah masalah maksimisasi dan minimisasi, menurut Singh et al. (2011), FGP dapat dinyatakan :
Tentukan x (2.12)
Sedemikian sehingga
dengan kendala
dimana adalah fungsi tujuan ke-i, adalah level aspirasi dari fungsi tujuan
, A adalah matriks koefisien penggunaan setiap sumberdaya untuk menghasilkan satu satuan nilai variabel keputusan xj, dan b adalah vektor kolom
sisi kanan kendala yang menyatakan ketersediaan tiap sumberdaya.
Fungsi keanggotaan dari setiap untuk setiap tujuan fuzzy dapat dinyatakan yang diinginkan, adalah batasan optimal (max/min) dari model.
Model FGP (2.11) dan (2.12) dapat dinyatakan dalam bentuk : Tentukan x* yang memenuhi,
Max (2.15)
dengan kendala
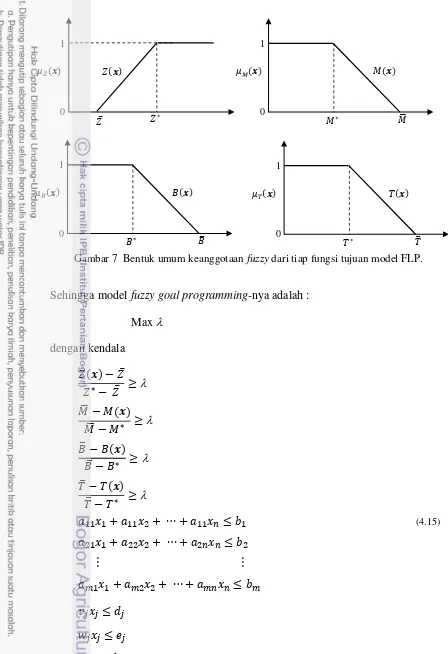
Selanjutnya fungsi keanggotaan fuzzy tiap fungsi tujuan adalah:
Bentuk fungsi keanggotaan (2.16) dan (2.17) dapat digambarkan sebagai berikut :
Gambar 5 Fungsi keanggotaan fuzzy fungsi tujuan model FGP.
Semakin besar nilai yang diperoleh, akan mengakibatkan nilai keanggotaan
fuzzy untuk setiap fungsi tujuan akan makin besar yang artinya solusi yang diperoleh mendekati nilai optimal (max/min).
2.6 Analisis Sensitivitas
Analisis sensitivitas adalah sebuah analisis yang dilakukan setelah solusi optimal diperoleh. Akan dilihat pengaruh perubahan parameter yang ada terhadap solusi yang telah diperoleh. Pada selang berapa perubahan parameter variabel tujuan akan mempengaruhi solusi optimal dan pada selang berapa perubahan pada ketersediaan sumber daya akan mempengaruhi kelayakan solusi (Taha 1997).
Pada pembuatan model untuk prediksi dan asumsi berkenaan dengan data input, ini banyak berkaitan dengan penilaian terhadap perencanaan pada waktu yang akan datang. Ketika model diselesaikan, hasilnya tergantung pada data. Analisis sensitivitas mencoba menilai dampak suatu perubahan pada data input atau parameter pada solusi yang diusulkan atau variabel keputusan.
Dalam penelitian ini, analisis sensitivitas yang dilakukan adalah pada ketersediaan sumberdaya yang dapat berubah. Berapakah selang perubahan masing-masing sumberdaya yang tetap mempertahankan kondisi optimal, nilai diluar selang itu akan membuat kondisi optimal akan berubah. Taha (1997), kondisi optimal yang dipertahankan jika terjadi perubahan ketersediaan sumberdaya atau konstan sisi kanan kendala adalah variabel keputusan tetap sama dengan solusi optimal sebelumnya. Nilai variabel keputusan bisa berubah sesuai perubahan konstan sisi kanan kendala, demikian juga nilai fungsi tujuannya.
2.7 Decision Support System (DSS) Berdasarkan Model Optimasi dan Analisis Sensitivitas
Klasifikasi DSS berdasarkan tingkat dimana output sistem dapat langsung mendukung atau menentukan keputusan dapat dibagi menjadi beberapa kategori dalam dua kelompok klasifikasi data dan model yaitu sistem analisis data, sistem analisis informasi, model akuntansi, model representasional, model optimalisasi dan model saran. Sedangkan berdasarkan orientasi DSS dapat dibagi menjadi berorientasi-teks, berorientasi-database, berorientasi-spreadsheet,
berorientasi-solver, berorientasi-aturan, dan gabungan (Turban et al. 2005). FGP adalah model optimalisasi multi-tujuan yang berorientasi solver merupakan bagian dalam DSS dalam menunjang pengambilan keputusan.
Sebagai model optimalisasi, tipe operasinya ingin mengkalkulasi solusi optimal untuk masalah kombinasi dengan tipe tugas adalah perencanaan dan alokasi sumberdaya. Sedangkan sebagai DSS berorientasi-solver adalah program komputasi untuk memecahkan suatu tipe masalah tertentu.
III METODOLOGI PENELITIAN
3.1 Kerangka Penelitian
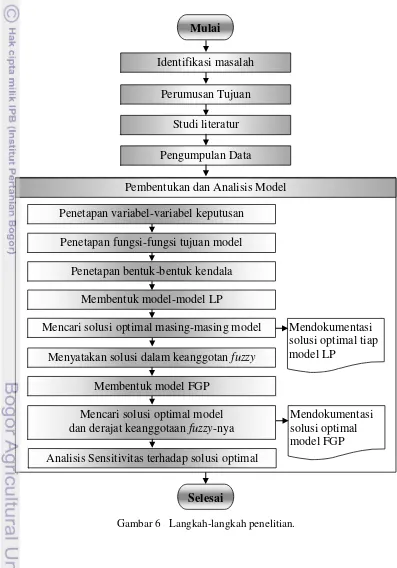
Metodologi dalam penelitian ini mengikuti langkah-langkah kerangka pemikiran pada Gambar 6.
Gambar 6 Langkah-langkah penelitian. Identifikasi masalah
Perumusan Tujuan Studi literatur Pengumpulan Data
Mulai
Penetapan variabel-variabel keputusan Penetapan fungsi-fungsi tujuan model
Penetapan bentuk-bentuk kendala Membentuk model-model LP
Membentuk model FGP Mencari solusi optimal model dan derajat keanggotaan fuzzy-nya Mencari solusi optimal masing-masing model
Menyatakan solusi dalam keanggotan fuzzy
Analisis Sensitivitas terhadap solusi optimal
Selesai
Pembentukan dan Analisis Model
Mendokumentasi solusi optimal tiap model LP
Penelitian ini dilakukan dalam beberapa langkah yaitu: identifikasi masalah, perumusan tujuan, studi literatur dan pengumpulan data yang menunjang tercapainya tujuan, pembentukan dan analisis model dengan metode yang akan digunakan.
Identifikasi Masalah
Identifikasi masalah dilakukan untuk melihat masalah dalam manajemen produksi untuk diterapkan suatu metode yang diharapkan dapat memberikan hasil yang lebih baik dalam optimalisasi.
Perumusan Tujuan
Setelah masalah teridentifikasi, selanjutnya dirumuskan tujuan penelitian dalam mencari kombinasi produk yang optimal yang mempertimbangkan ketersediaan sumberdaya dalam proses produksi yang mengandung ketidakpastian dan solusi masing-masing fungsi tujuan (multi objective) yang akan dinyatakan dalam fungsi keanggotaan fuzzy. Solusi masing-masing fungsi tujuan ini akan saling mempertimbangkan optimalitasnya satu dengan yang lain.
Studi Literatur
Studi literatur dilakukan untuk memahami lingkup penelitian yang akan dilakukan dengan mempelajari teori-teori yang mendasari metode yang akan digunakan dan penelitian-penelitian terkait yang telah dilakukan orang lain sebelumnya.
Pengumpulan Data
Pembentukan dan Analisis Model
Tahap pembentukan dan analisis model dilakukan dalam tahapan: Menetapkan variabel-variabel keputusan
Variabel-variabel keputusan adalah jenis-jenis produk yang dihasilkan perusahaan, dalam hal ini jenis minuman ringan yang diproduksi.
Menetapkan fungsi-fungsi tujuan model
Fungsi tujuan yang akan dianalisa adalah maksimisasi pendapatan, minimisasi penggunaan tenaga kerja, minimisasi biaya transportasi.
Menetapkan bentuk-bentuk kendala.
Bentuk-bentuk kendala berhubungan dengan bahan baku yang diperlukan untuk setiap satuan produk yang akan diproduksi dan batasan ketersediaan bahan baku. Dari sisi tenaga kerja adalah jumlah jam kerja yang diperlukan untuk memproduksi satu satuan produk. Dari biaya transportasi adalah besar biaya per satuan produk.
Membentuk model-model LP berdasarkan fungsi tujuan dan kendala masing-masing
Berdasaarkan fungsi tujuan masing-masing dibentuk model LP yang memenuhi kendala masing-masing yang ada.
Mencari solusi optimal masing-masing model
Solusi optimal dicari dengan metode simpleks menggunakan program
POM/QM Win. Solusi optimal ini didokumentasi sebagai dasar untuk membentuk fungsi keanggotaan fuzzy masing-masing fungsi tujuan.
Membentuk fungsi keanggotaan dari solusi optimalnya menurut fungsi keanggotan fuzzy.
Fungsi keanggotaan fuzzy ini berdasarkan preferensi pengambil keputusan. Fungsi keanggotaan ini bisa terhadap semua tujuan atau sebagian tergantung pengambil keputusan.
Membentuk model FGP
Mencari solusi optimal model dan derajat keanggotaan fuzzy-nya dengan menggunakan POM/QM Win.
Solusi optimal dihasilkan menyatakan jumlah tiap produk yang dihasilkan dan nilai setiap fungsi tujuan yang ingin dicapai berdasarkan preferensi pengambil keputusan yang telah dinyatakan dalam keanggotaan fuzzy. Diperoleh juga derajat keanggotaan setiap fungsi tujuan tersebut. Solusi optimal ini didokumentasi sebagai dasar untuk melakukan analisis sensitivitas.
Analisis sensitivitas terhadap solusi optimal
Berdasarkan solusi optimal yang diperoleh dari model FGP tersebut, dianalisa pengaruh terhadap solusi optimal jika terjadi perubahan terhadap ketersediaan sumber daya atau bahan baku.
3.2 Tempat dan Waktu Penelitian
IV HASIL DAN PEMBAHASAN
4.1 Model FGP untuk Perusahaan Minuman Ringan
Suatu perusahaan pada umumnya ingin memaksimalkan pendapatan dengan memperhatikan biaya-biaya yang harus dikeluarkan dan alat/mesin yang digunakan dalam memproduksi produknya yang akan memberikan hasil yang sesuai dengan keinginan manajemen. Karena adanya pertentangan tujuan maksimisasi pendapatan dan minimisasi biaya maka perlu dilakukan kajian fuzzy goal programming.
4.1.1 Variabel Keputusan
Variabel keputusan adalah jenis-jenis produk minuman ringan yang akan diproduksi yaitu x = ( atau produk ke-j ( )
4.1.2 Fungsi Tujuan
Fungsi tujuan yang dalam model ini adalah : Fungsi pendapatan yang akan dimaksimalkan
(4.1)
dengan adalah harga satu satuan produk ke-j, untuk . Fungsi waktu kerja mesin yang akan diminimalkan
(4.2)
dengan adalah waktu yang diperlukan mesin untuk memproduksi satu satuan produk ke-j, untuk .
Fungsi biaya bahan baku yang akan diminimalkan
(4.3)
dengan adalah biaya bahan baku yang diperlukan untuk memproduksi satu satuan produk ke-j, untuk .
Fungsi biaya tenaga kerja yang akan diminimalkan
(4.4)
Fungi keuntungan yang akan dimaksimalkan. Fungsi keuntungan ini adalah fungsi pendapatan dikurangi fungsi biaya bahan baku dan biaya tenaga kerja. (4.5) 4.1.3 Bentuk Kendala
Bentuk kendala berhubungan dengan ketersediaan sumber daya atau bahan baku. Untuk minuman ringan, bahan bakunya adalah:
Bahan baku untuk membuat sirup minuman
Misalkan total bahan baku ke-i yang tersedia adalah dan jumlah bahan baku ke-i yang diperlukan untuk menghasilkan satu satuan produk ke-j adalah , maka
(4.6)
Bahan baku kemasan dalam hal ini botol dan tutup botol
Misalkantotal botol produk ke-j yang tersedia adalah dan jumlah botol produk ke-j yang diperlukan untuk menghasilkan satu satuan produk ke-j adalah , maka
(4.7)
Misalkantotal tutup botol produk ke-j yang tersedia adalah dan jumlah tutup botol produk ke-j yang diperlukan untuk menghasilkan satu satuan produk ke-j adalah , maka
(4.8)
Packaging atau krat
Misalkantotal krat untuk produk ke-j yang tersedia adalah dan jumlah produk ke-j yang dapat di packing di krat tersebut adalah
produk, maka
(4.9)
Ditambah dengan kendala standar dalam model yaitu kendala nonnegatif yaitu
4.1.4 Model FGP
Untuk membentuk model FGP, perlu dicari terlebih dahulu solusi LP untuk masing-masing fungsi tujuan. keanggotaan fuzzy dari masing-masing fungsi tujuan. Selanjutnya manajerial pengambil keputusan perusahaan dapat menentukan tingkat keuntungan terendah dengan tingkat biaya dan waktu kerja mesin tertinggi yang diinginkan.
Misalkan yang diinginkan adalah:
Serendah-rendahnya keuntungan yang harus diperoleh adalah Setinggi-tingginya waktu kerja mesin yang digunakan adalah Setinggi-tingginya biaya bahan baku adalah
Setinggi-tingginya biaya tenaga kerja adalah
Maka fungsi keanggotaan fuzzy dari setiap fungsi tujuan adalah :
Gambar 7 Bentuk umum keanggotaan fuzzy dari tiap fungsi tujuan model FLP.
4.2 Bentuk dan Analisis Model untuk PT. BWBC
4.2.1 Variabel Keputusan
Variabel keputusan untuk model pada PT. BWBC adalah jenis produk yang dihasilkan perusahaan tersebut yaitu : dibentuk fungsi pendapatan yang akan dimaksimumkan yaitu :
Minimisasi waktu kerja mesin
Min M =
(4.17)
Berdasarkan data Lampiran 2 untuk bahan baku syrup dan hasil produksi maka dapat dihitung bahan baku yang dibutuhkan untuk membuat 1 krat produk seperti pada Tabel 1.
Tabel 1 Bahan baku syrup untuk menghasilkan 1 krat produk
x1 x2 x3 x4 x5 x6 x7 x8 x9 x10
Concentrate
(unit) 0.0024 0.0037 0.0063 0.0024 0.0036 0.0060 0.0024 0.0036 0.0060 0.0026
Gula (kg) 0.4885 0.7527 1.2702 0.6998 1.0384 1.7578 0.6460 0.9587 1.6229 0.5140 CO2 (kg) 0.0343 0.0528 0.0891 0.0237 0.0352 0.0596 0.0351 0.0521 0.0883 0
Selanjutnya berdasarkan harga bahan baku pada Lampiran 3 dan data di Tabel 1, dapat dihitung biaya bahan baku per krat produk seperti pada Tabel 2.
Tabel 2 Biaya bahan baku per krat produk
Produk Ukuran (ml) Biaya per krat (Rp)
Minimisasi biaya tenaga kerja
Min T =
(4.19)
Berdasarkan fungsi pendapatan, biaya bahan baku, dan biaya tenaga kerja, dapat dibentuk fungsi keuntungan yang merupakan pendapatan dikurangi biaya bahan baku dan biaya tenaga kerja sehingga dapat dibentuk fungsi tujuan adalah fungsi maksimisasi keuntungan, minimsasi waktu kerja mesin, minimisasi biaya bahan baku, dan minimisasi biaya tenaga kerja.
4.2.3 Bentuk Kendala
Berdasarkan Tabel 1 dan ketersediaan bahan baku setiap bulan pada Lampiran 4 maka dapat diperoleh bentuk-bentuk kendala :
Fanta 1000 ml : (4.30)
Sprite 200/295 ml : (4.31)
Sprite 1000 ml : (4.32)
Frestea 220 ml : (4.33)
(5) Botol
Cocacola 193 ml : (4.34)
Cocacola 295 ml : (4.35)
Cocacola 1000 ml : (4.36)
Fanta 200 ml : (4.37)
Fanta 295 ml : (4.38)
Fanta 1000 ml : (4.39)
Sprite 200 ml : (4.40)
Sprite 295 ml : (4.41)
Sprite 1000 ml : (4.42)
Frestea 220 ml : (4.43)(6) Krat
Ukuran 193/200/220/295 ml
(4.44)
Ukuran 1000 ml
(4.45)
(7) Waktu kerja mesin
Karena Line 1 dan 2 tidak digunakan secara bersama (salah satu line digunakan maka yang lain tidak), dengan waktu kerja mesin per hari adalah 14 jam (16 jam kerja – 2 jam persiapan) maka dalam 1 bulan (22 hari) waktu kerja mesin adalah 14 × 22 = 308 jam = 308 × 60 menit = 18 480 menit. Bentuk kendalanya dapat dinyatakan :
(4.46)
(8) Jumlah concentrate minimum yang harus diolah
dijadikan batas minimum, sebagai jaminan bahwa produksi yang akan dihasilkan minimal sama dengan produksi real yang dihasilkan perusahaan selama ini.
4.2.4 Model dan Solusi LP untuk Setiap Fungsi Tujuan
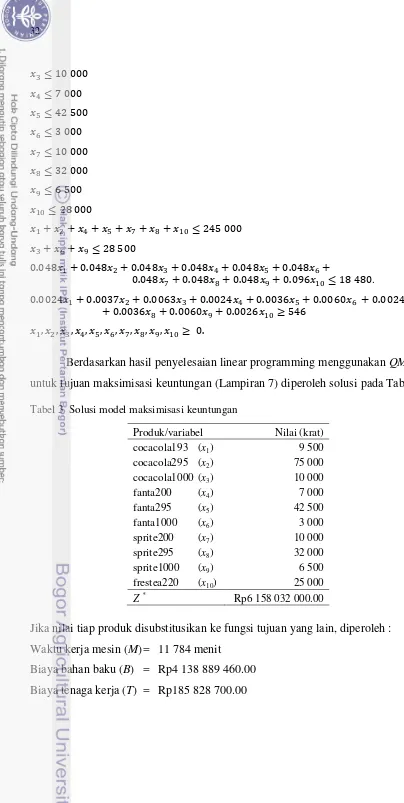
untuk tujuan maksimisasi keuntungan (Lampiran 7) diperoleh solusi pada Tabel 3. Tabel 3 Solusi model maksimisasi keuntungan
Jika nilai tiap produk disubstitusikan ke fungsi tujuan yang lain, diperoleh : Waktu kerja mesin (M) = 11 784 menit
Biaya bahan baku (B) = Rp4 138 889 460.00
Dengan cara yang sama untuk menentukan solusi model LP pada fungsi tujuan yang lain dilakukan dengan mengubah fungsi tujuan maksimisasi keuntungan pada model (4.49) dengan tujuan masing-masing yaitu minimisasi waktu kerja mesin (Lampiran 8), minimisasi biaya bahan baku (Lampiran 9), dan minimisasi biaya tenaga kerja (Lampiran 10), selanjutnya mensubstitusi nilai-nilai tiap produk ke fungsi keuntungan, diperoleh solusi seperti pada Tabel 4, Tabel 5, dan Tabel 6.
Tabel 4 Solusi model minimisasi waktu kerja mesin
Produk/variabel Nilai (krat)
Tabel 5 Solusi model minimisasi biaya bahan baku
Tabel 6 Solusi model minimisasi biaya tenaga kerja
4.2.5 Fungsi Keanggotaan Fuzzy dari Setiap Fungsi Tujuan
Jika pengambil keputusan ingin menentukan kebijakan tertentu yang berhubungan dengan keempat tujuan yang akan dicapai tersebut, maka selang nilai yang dimungkinkan sebagai batasan pada fungsi keanggotaan fuzzy adalah dibatasi oleh solusi optimal untuk masing-masing fungsi tujuan tersebut, dapat dinyatakan dalam bentuk:
≤ 6 158 032 000 ≥ 6 516
≥ 2 712 304 000 ≥ 110 223 900
sehingga berdasarkan bentuk fungsi keanggotaan fuzzy pada (4.11) – (4.14), dapat dinyatakan:
Gambar 8 Fungsi keanggotaan fuzzy untuk fungsi maksimisasi keuntungan.
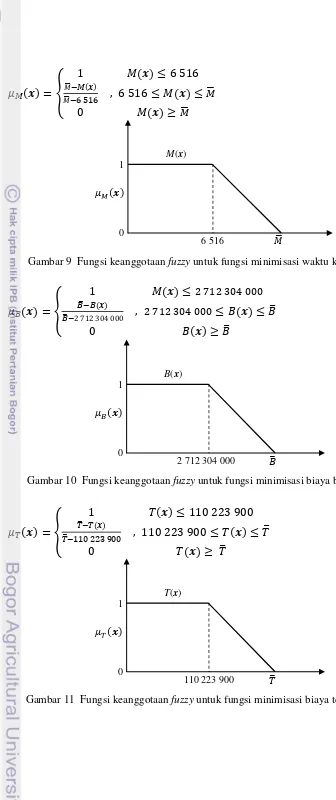
Gambar 9 Fungsi keanggotaan fuzzy untuk fungsi minimisasi waktu kerja mesin.
Gambar 10 Fungsi keanggotaan fuzzy untuk fungsi minimisasi biaya bahan baku.
Gambar 11 Fungsi keanggotaan fuzzy untuk fungsi minimisasi biaya tenaga kerja.
4.2.6 Decision Support System berdasarkan model FGP
Pada bagian ini, pengambil keputusan dapat menentukan preferensi atau batasan keinginannya terhadap setiap fungsi tujuan, sebagai bagian dari sistem penunjang keputusan (decision support system-DSS) dalam keputusan produksi yang akan diambil. Dalam model FGP ini yang merupakan analisis model optimasi berorientasi solver dalam DSS, pengambil keputusan dapat menentukan berapa besar keuntungan yang ingin dicapai dan berapa banyak waktu kerja mesin, biaya bahan baku, biaya tenaga kerja yang dapat digunakan, untuk selanjutnya dapat diperoleh solusi model yang diinginkan. Selanjutnya dilakukan analisis sensitivitas yang juga bagian dalam DSS untuk melihat perubahan ketersediaan sumberdaya dalam hubungannya dengan kondisi optimal yang diinginkan.
4.2.6.1 Solusi Model FGP
Awalnya diberi kesempatan pada pengambil keputusan untuk menentukan keinginannya untuk mencapai semua fungsi tujuan yang ada. Dalam analisa ini, diambil 2 kasus yang menggambarkan keinginan pengambil keputusan.
Kasus 1
Besarnya keuntungan paling sedikit 80% dari keuntungan maksimal maka,
Waktu kerja mesin paling banyak 1.25 kali waktu kerja mesin minimal maka,
Biaya bahan baku paling banyak 1.25 kali biaya bahan baku maksimal maka,
Biaya tenaga kerja paling banyak 1.25 kali biaya tenaga kerja maksimal maka,
Maka bentuk kendala yang ada pada model LP bertambah kendala dari fungsi tujuan yaitu :
Bentuk kendala dari fungsi tujuan maksimisasi keuntungan
(4.54)
Bentuk kendala dari fungsi tujuan minimisasi waktu kerja mesin
Bentuk kendala dari fungsi tujuan minimisasi biaya bahan baku
Bentuk kendala dari fungsi tujuan minimisasi biaya tenaga kerja
Model (4.58) ini dapat diselesaikan dengan metode linear programming (Lampiran 11) yang memberikan solusi pada Tabel 7.
Tabel 7 Solusi FGP untuk
Keinginan pengambil keputusan tercapai dengan hasil yang diberikan adalah berada pada nilai yang diinginkannya. Keuntungan paling sedikit yang
diinginkan adalah Rp4926425600.00, dan diperoleh adalah Rp4963458811.45. Waktu kerja mesin paling banyak yang bisa digunakan
adalah 8145 menit, ternyata yang digunakan hanya 8096.02 menit. Biaya bahan baku paling banyak yang bisa digunakan adalah Rp3390380000.00, ternyata yang digunakan hanya Rp3245727540.16. Biaya tenaga kerja paling banyak yang bisa digunakan adalah Rp137779875.00, ternyata yang digunakan hanya Rp136951289.39.
Kasus 2
Jika pengambil keputusan menginginkan :
keuntungan sekurang-kurangnya Rp4 500 000 000.00 = waktu kerja mesin setinggi-tingginya 9 000 menit =
biaya bahan baku setinggi-tingginya Rp3 000 000 000.00 = biaya tenaga kerja setinggi-tingginya Rp150 000 000.00 = akan membentuk kendala dari tiap fungsi tujuan yaitu :
Tabel 8 Solusi FGP untuk
tujuan akan diperoleh besarnya keuntungan, waktu kerja mesin, biaya bahan baku, dan biaya tenaga kerja:
Rp2964173422.56. Biaya tenaga kerja paling banyak yang bisa digunakan adalah Rp150000000.00, ternyata yang digunakan hanya Rp114610940.47.
4.2.6.2 Analisis Sensitivitas
Analisis sensitivitas dalam penelitian dilakukan pada aspek ketersediaan sumber daya yang tersedia. Ingin melihat selang nilai pada ketersediaan tiap sumber daya yang mempertahankan kondisi optimal. Pada kasus 2 yang dibahas, selang nilai ketersediaan sumberdaya yang mempertahankan kondisi optimal ditunjukkan pada Lampiran 13.
Perhatikan pada ketersediaan botol cocacola 295 ml, kondisi optimalnya pada selang nilai 63600.27115516.30 krat. Artinya, jika ketersediaannya diubah tetap pada selang ini, maka kondisi optimal tetap dipertahankan. Produk yang akan diproduksi tetap sama dengan solusi sebelumnya, yang mungkin berubah adalah jumlah produknya dan besarnya nilai masing-masing fungsi tujuannya. Jika ketersediaannya diubah diluar selang ini, maka kondisi optimal juga akan berubah.
Beberapa contoh perubahan ketersediaan botol cocacola 295 ml, dan hasil solusinya disajikan pada Tabel 9.
Tabel 9 Beberapa perubahan ketersediaan botol cocacola 295 ml dan solusinya
Variabel Jumlah ketersediaan botol cocacola 295 ml (krat)
Perubahan ketersediaan botol cocacola 295 ml yang masih dalam selang
30 . 516 115 27 . 600
63 krat, yaitu 65000 dan 90000krat memberikan solusi jenis produk yang sama seperti solusi awal pada ketersediaan 75000 krat yaitu cocacola295, fanta295, sprite295, dan frestea220. Sedangkan pada perubahan ketersediaan botol cocacola 295 ml diluar selang tersebut, memberikan solusi jenis produk yang berbeda yaitu cocacola295, cocacola1000, fanta295, sprite295, dan frestea220 pada ketersediaan 60000 krat. Kemudian pada ketersediaan
000
V SIMPULAN DAN SARAN
5.1 SIMPULAN
Berdasarkan hasil dari penelitian ini dapat diambil beberapa kesimpulan: Fuzzy Goal Programming (FGP) dapat digunakan untuk menentukan solusi
optimal dalam manajemen produksi yang memiliki beberapa fungsi tujuan dengan memperhatikan batasan keinginan manajerial pada setiap fungsi tujuan yang ada.
Pada PT. Bangun Wenang Baverages Company (BWBC), dengan memperhatikan fungsi tujuan maksimisasi keuntungan, minimisasi waktu kerja mesin, minimisasi biaya bahan baku, dan minimisasi biaya tenaga kerja dapat diperoleh solusi optimal yang sesuai dengan keinginan manajerial pada tiap fungsi tujuan tersebut,
Dalam analisis sensitivitas memberikan batasan selang perubahan tiap ketersediaan sumberdaya yang mempertahankan solusi optimal.
5.2 SARAN
DAFTAR PUSTAKA
Buffa E, Sarin R. 1996. Manajemen Operasi dan Produksi Modern, Jilid 1 Edisi Kedelapan. Binarupa Aksara, Jakarta.
Environment: A Multi-objective Goal Programming Approach.
http://www.ub.rug.nl/eldoc/som/a/02A12/02A12.pdf [15 Des 2009].
Cunkas M. 2008. Design Optimization of Electric Motor by Multiobjective Fuzzy Genetic Algoritms. Mathematics and Computational Application Vol. 13. Kahraman C. 2008. Multi-Criteria Decision Making Methods and Fuzzy Sets.
Di dalam: Kahraman C, editor. Fuzzy Multi-Criteria Decision Making. Theory and Application with Recent Development. New York : Springer Optimization and Its Applications Vol. 16. hlm 1 – 18.
Kusumadewi S, Hartarti S, Harjoko A, Wardoyo R. 2006. Fuzzy Multi-Attribut Decision Making. Penerbit Graha Ilmu. Yogyakarta.
Kusumadewi S, Purnomo H. 2004. Aplikasi Logika Fuzzy untuk Pendukung Keputusan. Penerbit Graha Ilmu. Yogyakarta.
Li S, Yang Y, Teng C. 2004. Fuzzy Goal Programming With Multiple Priorities via Generalized Verying-Domain Optimization Method. IEEE Transactions on Fuzzy System 12(5):597-605. Multiobjective Linear Plus Linaer Fractional Programming Problem.
WSEAS Proceedings of American Conference on Applied Mathematics
Taylor BW. 2005. Sains Manajemen. Edisi 8. Vita Silvira,penerjemah. Jakarta: Penerbit Salemba Empat. Terjemahan dari: Introduction to Management Science.
Turban E, Aronson J E, Liang T P. 2005. Decision Support System and Intelligent System. Seventh Edition. Pearson Prentice Hall. USA.
Lampiran 1 Produk yang dihasilkan PT. Bangun Wenang Baverages
Lampiran 2 Bahan baku syrup dan hasil produksi
* Sumber : PT. Bangun Wenang Baverages Company per bulan Oktober 2011.
Lampiran 3 Harga bahan baku
* Sumber : PT. Bangun Wenang Baverages Company per bulan Oktober 2011.
Lampiran 4 Jumlah bahan baku yang tersedia setiap bulan Bahan baku Jumlah
Concentrate (unit) Cocacola 870 unit
Fanta 370 unit
* Sumber : PT. Bangun Wenang Baverages Company per bulan Oktober 2011.
Lampiran 5 Harga jual tiap produk
Produk Ukuran Satuan Harga jual (Rp)
Lampiran 6 Biaya tenaga kerja untuk tiap produk
Produk Ukuran (ml) Biaya per krat (Rp)
Cocacola 193 482.47
295 737.45
1000 2 499.84
Fanta 200 499.97
295 737.46
1000 2 499.85
Sprite 200 499.97
295 737.46
1000 2 499.85
Frestea 220 549.97
Lampiran 7 Solusi model maksimisasi keuntungan dengan POM/QM Win
X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 RHS
Maximize 19,969.57 31,038.68 31,077.09 17,991.69 28,690.12 27,064.59 18,432.99 29,345.01 28,173.17 23,867.50
(1) Concentrate cocacola 0.0024 0.0037 0.0063 0 0 0 0 0 0 0 <= 870
(2) Concentrate fanta 0 0 0 0.0024 0.0036 0.006 0 0 0 0 <= 370
(3) Concentrate sprite 0 0 0 0 0 0 0.0024 0.0036 0.006 0 <= 345
(4) Concentrate frestea 0 0 0 0 0 0 0 0 0 0.0026 <= 65
(5) Gula 0.4885 0.7527 1.2702 0.6998 1.0384 1.7578 0.646 0.9587 1.6229 0.514 <= 200,000 (6) CO2 0.0343 0.0528 0.0891 0.0237 0.0352 0.0596 0.0351 0.0521 0.0883 0 <= 25,000
(7) Tutup btl cocacola 193/295 24 24 0 0 0 0 0 0 0 0 <= 5,500,000
(8) Tutup btl cocacola 1000 0 0 12 0 0 0 0 0 0 0 <= 1,000,000
(9) Tutup btl fanta 200/295 0 0 0 24 24 0 0 0 0 0 <= 3,500,000
(10) Tutup btl fanta 1000 0 0 0 0 0 12 0 0 0 0 <= 750,000
(11) Tutup btl sprite 200/295 0 0 0 0 0 0 24 24 0 0 <= 3,400,000
(12) Tutup btl sprite 1000 0 0 0 0 0 0 0 0 12 0 <= 750,000
(13) Tutup btl frestea 220 0 0 0 0 0 0 0 0 0 24 <= 2,500,000
(14) Botol cocacola 193 1 0 0 0 0 0 0 0 0 0 <= 9,500
(15) Botol cocacola 295 0 1 0 0 0 0 0 0 0 0 <= 75,000
(16) Botol cocacola 1000 0 0 1 0 0 0 0 0 0 0 <= 10,000
(17) Botol fanta 200 0 0 0 1 0 0 0 0 0 0 <= 7,000
(18) Botol fanta 295 0 0 0 0 1 0 0 0 0 0 <= 42,500
(18) Botol fanta 1000 0 0 0 0 0 1 0 0 0 0 <= 3,000
(20) Botol sprite 200 0 0 0 0 0 0 1 0 0 0 <= 10,000
(21) Botol sprite 295 0 0 0 0 0 0 0 1 0 0 <= 32,000
(22) Botol sprite 1000 0 0 0 0 0 0 0 0 1 0 <= 6,500
(23) Botol frestea 220 0 0 0 0 0 0 0 0 0 1 <= 28,000
(24) Krat 193/200/220/295 1 1 0 1 1 0 1 1 0 1 <= 245,000
(25) Krat 1000 0 0 1 0 0 1 0 0 1 0 <= 28,500
Lampiran 8 Solusi model minimisasi waktu kerja mesin dengan POM/QM Win
X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 RHS
Minimize 0.048 0.048 0.048 0.048 0.048 0.048 0.048 0.048 0.048 0.096
(1) Concentrate cocacola 0.0024 0.0037 0.0063 0 0 0 0 0 0 0 <= 870
(2) Concentrate fanta 0 0 0 0.0024 0.0036 0.006 0 0 0 0 <= 370
(3) Concentrate sprite 0 0 0 0 0 0 0.0024 0.0036 0.006 0 <= 345
(4) Concentrate frestea 0 0 0 0 0 0 0 0 0 0.0026 <= 65
(5) Gula 0.4885 0.7527 1.2702 0.6998 1.0384 1.7578 0.646 0.9587 1.6229 0.514 <= 200,000 (6) CO2 0.0343 0.0528 0.0891 0.0237 0.0352 0.0596 0.0351 0.0521 0.0883 0 <= 25,000
(7) Tutup btl cocacola 193/295 24 24 0 0 0 0 0 0 0 0 <= 5,500,000
(8) Tutup btl cocacola 1000 0 0 12 0 0 0 0 0 0 0 <= 1,000,000
(9) Tutup btl fanta 200/295 0 0 0 24 24 0 0 0 0 0 <= 3,500,000
(10) Tutup btl fanta 1000 0 0 0 0 0 12 0 0 0 0 <= 750,000
(11) Tutup btl sprite 200/295 0 0 0 0 0 0 24 24 0 0 <= 3,400,000
(12) Tutup btl sprite 1000 0 0 0 0 0 0 0 0 12 0 <= 750,000
(13) Tutup btl frestea 220 0 0 0 0 0 0 0 0 0 24 <= 2,500,000
(14) Botol cocacola 193 1 0 0 0 0 0 0 0 0 0 <= 9,500
(15) Botol cocacola 295 0 1 0 0 0 0 0 0 0 0 <= 75,000
(16) Botol cocacola 1000 0 0 1 0 0 0 0 0 0 0 <= 10,000
(17) Botol fanta 200 0 0 0 1 0 0 0 0 0 0 <= 7,000
(18) Botol fanta 295 0 0 0 0 1 0 0 0 0 0 <= 42,500
(18) Botol fanta 1000 0 0 0 0 0 1 0 0 0 0 <= 3,000
(20) Botol sprite 200 0 0 0 0 0 0 1 0 0 0 <= 10,000
(21) Botol sprite 295 0 0 0 0 0 0 0 1 0 0 <= 32,000
(22) Botol sprite 1000 0 0 0 0 0 0 0 0 1 0 <= 6,500
(23) Botol frestea 220 0 0 0 0 0 0 0 0 0 1 <= 28,000
(24) Krat 193/200/220/295 1 1 0 1 1 0 1 1 0 1 <= 245,000
(25) Krat 1000 0 0 1 0 0 1 0 0 1 0 <= 28,500
(26) Waktu kerja mesin/line 0.048 0.048 0.048 0.048 0.048 0.048 0.048 0.048 0.048 0.096 <= 18,480 (27) Concentrate min 0.0024 0.0037 0.0063 0.0024 0.0036 0.006 0.0024 0.0036 0.006 0.0026 >= 546
Lampiran 9 Solusi model minimisasi biaya bahan baku dengan POM/QM Win
X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 RHS
Minimize 13,047.96 18,223.87 26,423.07 15,008.34 20,572.42 30,435.56 14,567.04 19,917.53 29,326.98 13,582.53
(1) Concentrate cocacola 0.0024 0.0037 0.0063 0 0 0 0 0 0 0 <= 870
(2) Concentrate fanta 0 0 0 0.0024 0.0036 0.006 0 0 0 0 <= 370
(3) Concentrate sprite 0 0 0 0 0 0 0.0024 0.0036 0.006 0 <= 345
(4) Concentrate frestea 0 0 0 0 0 0 0 0 0 0.0026 <= 65
(5) Gula 0.4885 0.7527 1.2702 0.6998 1.0384 1.7578 0.646 0.9587 1.6229 0.514 <= 200,000 (6) CO2 0.0343 0.0528 0.0891 0.0237 0.0352 0.0596 0.0351 0.0521 0.0883 0 <= 25,000
(7) Tutup btl cocacola 193/295 24 24 0 0 0 0 0 0 0 0 <= 5,500,000
(8) Tutup btl cocacola 1000 0 0 12 0 0 0 0 0 0 0 <= 1,000,000
(9) Tutup btl fanta 200/295 0 0 0 24 24 0 0 0 0 0 <= 3,500,000
(10) Tutup btl fanta 1000 0 0 0 0 0 12 0 0 0 0 <= 750,000
(11) Tutup btl sprite 200/295 0 0 0 0 0 0 24 24 0 0 <= 3,400,000
(12) Tutup btl sprite 1000 0 0 0 0 0 0 0 0 12 0 <= 750,000
(13) Tutup btl frestea 220 0 0 0 0 0 0 0 0 0 24 <= 2,500,000
(14) Botol cocacola 193 1 0 0 0 0 0 0 0 0 0 <= 9,500
(15) Botol cocacola 295 0 1 0 0 0 0 0 0 0 0 <= 75,000
(16) Botol cocacola 1000 0 0 1 0 0 0 0 0 0 0 <= 10,000
(17) Botol fanta 200 0 0 0 1 0 0 0 0 0 0 <= 7,000
(18) Botol fanta 295 0 0 0 0 1 0 0 0 0 0 <= 42,500
(18) Botol fanta 1000 0 0 0 0 0 1 0 0 0 0 <= 3,000
(20) Botol sprite 200 0 0 0 0 0 0 1 0 0 0 <= 10,000
(21) Botol sprite 295 0 0 0 0 0 0 0 1 0 0 <= 32,000
(22) Botol sprite 1000 0 0 0 0 0 0 0 0 1 0 <= 6,500
(23) Botol frestea 220 0 0 0 0 0 0 0 0 0 1 <= 28,000
(24) Krat 193/200/220/295 1 1 0 1 1 0 1 1 0 1 <= 245,000
(25) Krat 1000 0 0 1 0 0 1 0 0 1 0 <= 28,500