Eksplorasi Masalah Logaritma Diskret pada Finite Field GF(3m)

(1)

AI TUSI FATIMAH

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

(2)

Dengan ini saya menyatakan bahwa tesis dengan judul Eksplorasi Masalah Logaritma Diskret pada Finite Field GF(3m) adalah karya saya sendiri dengan arahan dari komisi pembimbing, dan belum diajukan dalarn bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Bogor, Juni 2009

(3)

AI TUSI FA TIMAH. The Exploration of Discrete Logarithm over Finite Field GF(3m). Under supervision of SUGI GURITMAN and NUR ALIATININGTYAS.

The security of many ｰｵ｢ｬｩ｣ｾｫ･ｹ＠ algorithms is based on the problem of finding discrete logarithms. The generalized discrete logarithm problem is the following: given a finite cyclic group G of order

n,

a generator

a

of G, and an element

fl

E G, find the integer x, 0 ｾ＠ x ｾ＠ n - 1, such that

0:

=

fl.

Algorithm for discrete logarithm problem focused on Menezes et al. (1997) that consist of exhaustive search algorithm, the baby-step giant-step algorithm, Pollard's rho algorithm, Pohlig-Hellman algorithm, and index-calculus algorithm. These algorithms are explorated to be used in discrete logarithm problem over finite field GF(3m). The exploration also produces some algorithms, i.e. naif negative

algorithm, baby-step mother-step algorithm, baby-step mother free-step algorithm, and baby-step free-step algorithm. All algorithms implemented using Maple 11. The Pohlig-Hellman and baby-step giant-step algorithms are efficient enough to be used in discrete logarithm problem over finite field GF(3m) for m ｾ＠ 20.

(4)

AI TUSI FA TIMAH. Eksplorasi Masalah Logaritma Diskret pada Finite Field GF(3m). Dibimbing oleh SUGI GURITMAN dan NUR ALIATININGTYAS.

Banyak algoritme kriptografi yang tumpuan keamanannya menggunakan masalah logaritma diskret pada suatu grup siklik. Misal G adalah grup siklik hingga berorder

n,

a adalah generator dari G, dan j3 E G. Logaritma diskret dari j3, dengan basis a, dinotasikan loga j3 adalah integer tunggal x, O:S x:S n - 1, sedemikian sehingga j3 =

0:

(Menezes et al. 1997). Jika n besar, maka logaritma diskret menjadi tak layak hitung. Masalah logaritma diskret didefinisikan sebagai berikut : diberikan grup siklik hingga G berorder n, suatu generator a dari G, dan j3 E G, bagaimana menentukan integer x, 0

:s

x

:s

n - 1 sedemikian sehingga of == j3.

Algoritme untuk menyelesaikan masalah logaritma diskret adalah exhaustive search, baby-step giant-step, Pollard-rho, Pohlig-Hellman, dan index-calculus (Menezes et al. 1997). Algoritme-algoritme tersebut dieksplorasi sehingga dapat digunakan padafinite field GF(3m). Eksplorasi masalah logaritma

diskret padafinite field GF(3m) juga menghasilkan algoritme yakni algoritme naif negatif, baby-step mother-step, baby-step mother free-step dan baby-step free-step.

GF(3m) =

a:

₃[x]/(f(x)} adalah finite field berorder 3m di mana operasi penjumlahan dan perkalian dalam modulof{x).f{x) E

a:

₃[x] merupakan polinomial irreducible atas

a:

3 berderajat m. GF(3

m

)*

=

GF(3m) - {O} merupakan grup siklik

perkalian yang berorder n

=

3 m - 1.

Algoritme exhaustive search (pelacakan lengkap) merupakan algoritme yang berdasarkan definisi masalah logaritma diskret. Pe1acakan untuk mendapatkan solusi masalah logaritma diskret dilakukan dengan cara mencoba semua kemungkinan solusi. Untuk order n yang besar, komputasi dengan algoritme ini kurang efisien. Eksplorasi dilakukan untuk efisiensi komputasi dengan menggunakan sifat order GF(3m)* yang se1alu bemilai genap. Akibatnya komputasi dapat dilakukan pad a setengah order GF(3m)*. Eksplorasi menghasilkan algoritme naif negatif dengan kompleksitas komputasi O(nI2).

Terdapat dua fase pada algoritme baby-step giant-step (Hoffstein et al. 2008). Fase baby-step digunakan untuk mengurangi beban komputasi dengan menggunakan memori komputer. Fase giant-step digunakan untuk memperoleh solusi. Untuk order n yang besar, diperlukan memori yang besar juga. Eksplorasi dilakukan sehingga tidak diperlukan memori yang besar untuk order n yang besar. Eksplorasi menghasilkan algoritme baby-step mother-step, baby-step mother-free step, dan baby-step free-step dengan kompleksitas komputasi masing-masing O(n).

Ide dasar algoritme Pollard-rho adalah Floyd's Cycle-finding dan Teori Birthday Paradox. Barisan dari suatu fungsi yang dipartisi menjadi tiga bagian dibangkitkan untuk memperoleh solusi. Floyd's cycle-finding digunakan untuk menemukan cycle dalam barisan {Xl, X2, X3, ... , Xk} dengan membandingkan

unsur-unsur Xi dengan X2i sehingga diperoleh pasangan Xi = X2i. Birthday paradox

(5)

dalam barisan dengan pe1uang lebih dari setengah sedikitnya setelah langkah ke '/rI'V2

In

2 (Hoff stein et al. 2008).

Algoritme Pollard-rho biasanya digunakan pada grup siklik berorder prima. GF(3m)* berorder komposit. Eksplorasi dilakukan dalam pemilihan basis, misalkan

o?,

di mana gcd(n,p)

=

1, sehingga diperoleh algoritme yang dapat digunakan padafinite field GF(3m).

Algoritme Pohlig-Hellman pada Menezes et al. (1997) hanya berlaku untuk m ganjil. Algoritme ini dieksplorasi menggunakan sifat-sifat grup siklik sehingga dapat digunakan untuk sembarang m padafinite field GF(3m). Algoritme index-calculus pada Menezes et al. (1997) dapat digunakan untuk masalah logaritma diskret padafinite field GF(3m).

Algoritme-algoritme yang dihasilkan diimplementasikan menggunakan sofware Maple 11. Komputasi masalah logaritma diskret padafinite field GF(3m) dapat dilakukan kasus per kasus berdasarkan nilai m. Algoritme Pohlig-Hellman dan algoritme baby-step giant-step cukup efisien untuk masalah logaritma diskret padafinite field GF(3m) dengan m

:s

20.

(6)

mencantumkan atau menyebutkan sumber

a. Pengutipan hanya boleh untuk kepentingan pendidikan penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik atau tinjauan suatu masalah,

b. Pengutipan tidak merugikan kepentingan yang wajar IPB

(7)

AI TUSI FATIMAH

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Program Studi Matematika Terapan

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

BOGOR

(8)

NIM : 0551070331

Disetujui

Komisi Pembimbing

Dra. Nur Aliatiningtyas, M.Si.

Ketua Program Studi Matematika Terapan

Tanggal Ujian: 19 Juni 2009

Diketahui

Tanggal Lulus:

Anggota

airil A. Notodi utro M.S.

(9)

Puji dan syukur penulis panjatkan kepada Allah SWT atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Desember 2008 ini adalah logaritma diskret, dengan judul Eksplorasi Masalah Logaritma Diskret pada Finite Field GF(3m).

Terima kasih penulis ucapkan kepada Bapak Dr. Sugi Guritman dan Ibu Dra. Nur Aliatiningtyas, M.Si. yang telah membimbing dan banyak memberikan saran. Ucapan terima kasih juga disampaikan kepada Departemen Agama Republik Indonesia yang telah memberikan beasiswa kepada penulis selama menempuh pendidikan di IPB. Ucapan terima kasih yang tiada hingga kepada ayah, ibu, serta seluruh keluarga, atas segala do'a dan kasih sayangnya.

Semoga karya ilmiah ini bermanfaat.

Bogor, Juni 2009

(10)

Penulis dilahirkan di Ciamis pada tanggal 14 Januari 1981 dari Bapak Eman Sulaeman dan Ibu Encun Sutiamah. Penulis merupakan putri bungsu dari empat bersaudara.

Tahun 2000 penulis lulus dari SMA Negeri 1 Ciamis dan pada tahun yang sama masuk Universitas Siliwangi Tasikmalaya. Penulis memilih Program Studi Pendidikan Matematika, Fakultas Keguruan dan Ilmu Pendidikan, lulus tahun 2004. Kesempatan untuk melanjutkan ke program magister pada Program Studi Matematika Terapan pada tahun 2007. Beasiswa pendidikan pascasarjana diperoleh dari Departemen Agama Republik Indonesia.

(11)

Halaman

DAFTAR TABEL Xlll

DAFT AR GAMBAR .... ... ... ... ... ... ... XIV

DAFTAR LAMPIRAN ... XV

BAB 1 PENDAHULUAN ... 1

1.1 Latar Belakang ... 1

1.2 Tujuan Penelitian ... ... ... ... ... 3

1.3 Manfaat Penelitian ... ... ... 3

BAB 2 TINJAUAN PUSTAKA ... 4

2.1 Teori Bilangan ... 4

2.2 Teori Peluang ... 7

2.3 Struktur Aljabar ... .... 7

2.4 Masalah Logaritma Diskret ... 17

2.5 Kompleksitas Algoritme ... 18

BAB 3 BASIL DAN PEMBAHASAN ... 19

3.1 Masalah Logaritma Diskret padafinitefield GF(3m) 19 3.2 Analisis Solusi Masalah Logaritma diskret pada finite field GF(3m) ... 21

3.3 Komputasi Masalah Logaritma diskret pada finite field GF(3m) ... 67

BAB 4 KESIMPULAN DAN SARAN ... 72

DAFTAR PUSTAKA ... 74

(12)

1

2

3 4 5 6 Oh-Besar

Representasi solusi GF(32)* untuk

fJ

= 2a ... .

Representasi solusi GF(35)* untuk

fJ

= 2a4 + a3 + 2a2 + a + 2 ... . Representasi Polinomial GF(33)* ... .

Baby-step untuk solusi GF(35)* dengan

fJ

= 20.4 + 0.3 + 20.2 + a + 2 Giant-step untuk solusi GF(35)* dengan

fJ

= 20.4 + 0.3 + 20.2 + a + 2

18 23 24 27 32 32

7 Fase mother-step: menghitungfJo.-im (modj{o.)) ... 35

8 fJo.-2mi _{(modj{o.)) pada}_fJ = 2a4 + 0.3 + 20.2 + a + 2 ... 38

9 Fase Baby-step pada algoritme baby-step free-step ... 40

10 Free-step untuk solusi GF(35)* dengan.8 = 2a4 + 0.3 + 20.2 + 0. +2 40 11 Perhitungan Birthday Paradox ... 43

12 Definisi Un sur x dalam G ... 47

13 14 15 16 17 18 19

20

21

22

Iterasi metode Po llar- rho cara 1 Iterasi metode Po llar- rho cara 2 Iterasi metode Pollar- rho cara 3 Iterasi metode Pollard-rho pada contoh 3.2.3.4 ... . Faktorisasi prima order GF(3m)* ... . Masalah logaritma dengan Pohlig-Hellman ... . Waktu komputasi solusi dengan algoritme naif dan naifnegatif .... . Waktu komputasi solusi dengan algoritme baby-step giant-step ... . Waktu komputasi solusi dengan algoritme baby-step mother-step Waktu komputasi solusi dengan algoritme baby-step mother-free 49 50 50 52

57

58 67

68

69 step ... 69

23 Waktu komputasi solusi dengan algoritme baby-step free-step ... 69

24 Waktu komputasi solusi dengan algoritme Pllard-rho ... 70

25 Waktu komputasi solusi dengan algoritme Pohlig-Hellman ... 70

26 Waktu komputasi solusi dengan algoritme index-calculus ... 71

27 Daftar polinomial primitif GF(3m) ... 76

(13)

Halaman

1 Baby-step giant-step ... 30

2 Baby-step mother-step ... ... ... ... ... ... 33

3 Baby-step mother-free step ... ... 35

4 Baby-step mother-free step denganp = am+l ...••...•... 38

5 Pollard-rho... ... ... .... 45

(14)

Halaman

1 Daftar Polinomial Primitif ... 76

2 Program Aritmetika Finite field GF(3m) ... 77

3 Program Masalah Logaritma Diskret pada Finite Field GF(3m) ... 91

4 Faktorisasi Prima ... 104

(15)

1.1 Latar Belakang

Banyak sistem kriptografi yang tumpuan keamanannya menggunakan

masalah logaritma diskret pada suatu grup siklik G. Contohnya pada pertukaran

kunci Diffie-Hellman dan enskripsi EIGamal. Grup G yang dapat dipilih di

antaranya grup perkalian 71.; dan grup perkalian GF(q)

* ,

di mana q = pm, p

bilangan prima.

Misal G adalah grup siklik hingga berorder

n, a

adalah generator dari G,

dan

/3

E G. Logaritma diskret dari

/3,

dengan basis a, dinotasikan loga

/3

adalah integer tunggal x, O:S x:S n - 1, sedemikian sehingga

p

= aX (Menezes et al.

1997). Jika n besar, maka logaritma diskret menjadi tak layak hitung. Masalah

logaritma diskret didefinisikan sebagai berikut : diberikan grup siklik hingga G

berorder n, suatu generator a dari G, dan

/3

E G, bagaimana menentukan integer x,

dengan O:S x:S n - 1 sedemikian sehingga ｾ＠ ==

/3.

Dalam Menezes et al. (1997) dijelaskan algoritme solusi masalah

logaritma diskret untuk grup siklik hingga G secara umum. Algoritme yang

digunakan pada masalah logaritme diskret terse but adalah exhaustive search

(pelacakan lengkap), baby-step giant-step, Pollard-rho, Pohlig-Hellman, dan

index-calculus. Pada Menezes et al. (1997) diberikan contoh penerapan

algoritme-algoritme tersebut pada grup perkalian 71.; berorder p - 1 di mana operasi grup di bawah perkalian modulo p. Aritmetika

7l.;

sudah umum diterapkan untuk

algoritme-algoritme kriptografi, sebagai aIternatif dapat dipilih aritmetika grup

siklik GF(pm) di mana p adalah bilangan prima.

Tulisan ini membahas masalah logaritma diskret padafinite field GF(3m).

GF(3m) = 71.3 [x]/(f(x) adalahfinitefieldberorder 3m di mana operasi penjumlahan dan perkalian dalam modulo fix). fix) E 71.3 [x] merupakan polinomial irreducible

atas 71.3 berderajat m. GF(3m)* = GF(3m) - {O} merupakan grup siklik perkalian

berorder n = 3m - 1. Aritmetika parla finite field GF(3m) mengacu pada tulisan

(16)

Algoritme solusi masalah logaritma diskret pada finite field GF(3m) mengacu pada Menezes et al. (1997). Algoritme-algoritme tersebut dieksplorasi menggunakan sifat-sifat finite field GF(3m). Eksplorasi menghasilkan algoritme yang sesuai untuk solusi masalah logaritma diskret pad a finite field GF(3m).

Algoritme exhaustive search (pelacakan lengkap) merupakan algoritme yang berdasarkan definisi masalah logaritma diskret. Pelacakan untuk

mendapatkan solusi masalah logaritma diskret dilakukan dengan cara mencoba

semua kemungkinan solusi. Untuk order n yang besar, komputasi dengan algoritme ini kurang efisien. Eksplorasi dilakukan untuk efisiensi komputasi

dengan menggunakan sifat order GF(3m)* yang selalu bernilai genap. Akibatnya komputasi dapat dilakukan pada setengah order GF(3m)

* .

Algoritme hasil

eksplorasi adalah algoritme naif negatif.

Ide dasar algoritme baby-step giant-step adalah space-time tradeoff. Dalam sains komputer, space-time tradeoff adalah situasi di mana memori komputer digunakan untuk mengurangi biaya dan waktu eksekusi program

(Hellman 1980). Untuk order n yang besar diperlukan memori komputer yang besar juga. Eksplorasi dilakukan sehingga tidak diperlukan memori yang besar

untuk order n yang besar. Eksplorasi menghasilkan algoritme baby-step mother-step, baby-step mother-free mother-step, dan baby-step free-step.

Ide dasar algoritme Pollard-rho adalah Floyd's Cycle-finding dan Teori Birthday Paradox. Barisan dari suatu fungsi yang dipartisi menjadi tiga bagian dibangkitkan untuk memperoleh solusi. Floyd's cycle-finding digunakan untuk menemukan cycle dalam barisan {Xl, X2, X3, ••. , Xk} dengan membandingkan unsur-unsur Xi dengan X2i sehingga diperoleh pasangan Xi = X2i. Birthday paradox digunakan untuk menjamin bahwa adanya satu atau lebih bilangan yang sarna

dalam barisan dengan peluang lebih dari setengah sedikitnya setelah Iangkah ke

.. /Yn/2 In 2 (Hoffstein et al. 2008).

Algoritme Pohlig-Hellman pada Menezes et al. (1997) hanya berlaku untuk GF(3m) dengan m ganjil. Algoritme ini dieksplorasi menggunakan sifat-sifat grup siklik sehingga dapat digunakan untuk sembarang m padafinite field GF(3m). Algoritme index-calculus pada Menezes ej- al. (1997) dapat digunakan untuk

(17)

Dalam paper yang ditulis Odlyzko dengan judul Discrete Logarithms in

Finite Fields and their Cryptographic Significance dilakukan penelitian dan

analisis untuk mengetahui algoritme solusi masalah logaritma diskret pada field

GF(2n). Hasil penelitian menyatakan bahwa logaritma diskret pada GF(2n) mudah

dipecahkan. Studholme (2002) menulis paper yang berjudul The Discrete Log

Problem. Masalah logaritma diskret pada paper tersebut menggunakan metode

square-root attacks dan metode index-calculus untuk grup siklik umum. Metode

square-root attacks terdiri dari metode Shanks' baby-step giant-step, Pollard-rho

dan Lambda (Kangaroo). Metode index-calculus diperluas untuk sebarang grup

menggunakan sifat smoothness.

Algoritme yang efisien untuk komputasi logaritma diskret sangat

diperlukan. Algoritme tersebut dapat dimanfaatkan untuk mengukur tingkat

keamanan algoritme kriptografi yang aspek keama..'1annya berbasis pada masalah

logaritma diskret. Oleh karena itu, tulisan ini menjelaskan eksplorasi algoritme

untuk menyelesaikan masalah logaritma diskret pada finite field GF(3m) sehingga

diperoleh algoritme yang efisien .

. 1.2 Tujuan Penelitian

1. Mengkaji secara teoritik masalah logaritma diskret pada finite field

GF(3m).

2. Melakukan eksplorasi algoritme yang berhubungan dengan masalah

logaritma diskret.

3. Mengimplementasikan algoritme-algoritme yang dihasilkan pada sofivare

Maple 11.

1.3 Manfaat Penelitian

Kajian ini dapat digunakan untuk mengukur tingkat keamanan algoritme

(18)

Pada bagian ini dituliskan beberapa aspek teoritis sebagai landasan teori

untuk penulisan tugas akhir ini.

2.1 Teori Bilangan

Himpunan integer { ... , -3, -2, -1, 0, 1,2,3, ... } dinotasikan dengan simbol

ｾＮ＠

Definisi 2.1.1 (Menezes et al. 1997) Misalkan a, b adalah integer. Maka a membagi b jika terdapat integer c sedemikian sehingga b = ac. Jika a membagi b, maka dinotasikan oleh alb.

Definisi 2.1.2 (Menezes et al. 1997). Jika a dan b adalah integer dengan b ｾ＠ 1, maka pembagian a oleh b menghasilkan integer q (hasil pembagian) dan r (sisa pembagian) sehingga a = qb

+

r, di mana 0 ｾ＠ r < b. Sisa pembagian dinotasikan a

mod b dan hasil pembagian dinotasikan a div b.

Definisi 2.1.3 (Menezes et al. 1997) Suatu integer c dikatakan pembagi bersama dari a dan b jika cia dan clb.

Definisi 2.1.4 (Menezes et al. 1997) Suatu integer tak negatif d disebut pembagi bersama terbesar (greatest common divisor/gcd) dari integer a dan b, dinotasikan d= gcd(a,b) jika

1. d adalah pembagi bersama a dan b, 2. jika 3c dengan cia dan clb, maka cld.

Definisi 2.1.5 (Menezes et al. 1997) Integer a dan b dikatakan prima relatif atau disebut juga koprima jika gcd(a,b)

=

1.

Teorema 2.1.6 (Menezes et al. 1997) Teorema dasar aritmetika.

Setiap bilangan bulat n ｾ＠ 2 dapat difaktorkan sebagai produk kuasa prima yang khas:

_ el e2 ek

n-p]P2 ···Pk '

(19)

Definisi 2.1.7 (Childs 2009) Untuk sebarang bilangan a ｾ＠ 2, dapat dituliskan

dalam suatu bilangan b menggunakan kuasa a,

b

=

rna +rn-la n n-l + .. . +rla+rO

di mana untuk setiap ro, . . . , r n diantara 0 and a-I, hal ini disebut representasi dari b dalam basis (atau radix) a.

Definisi 2.1.8 (Menezes et a/., 1997) Jika a dan b adalah integer, maka a disebut

kongruen b modulo n, ditulis a

==

b (mod n), jika n membagi (a - b). Integer n

disebut modulus dari kongruensi.

Teorema 2.1.9 Sifat-sifat kongruensi (Koshy 2007).

Misal

a,

b,

e,

d dan

n

adalah integer, maka pernyataan berikut benar :

1. a == b (mod n) j ika dan hanya j ika a

=

b

+

kn untuk suatu integer k.

2. a == a (mod n). (sifat refleksi)

3. Jika a == b (mod n) maka b == e (mod n). (sifat simetri)

4. Jika a == b (mod n) dan b == e (mod n), maka a == e (mod n). (sifat transitif)

5. Jika a == b (mod n) dan e == d (mod n), maka

(i) a + e == b + d (mod n),

(ii) ae == bd (mod n).

6. Jika a == b (mod n) maka

(i) a + e =. b + e (mod n),

(ii) ae == be (mod n).

7. Jika ae == be (mod n) and (e, n)

=

1, maka a == b (mod n).

8. Jika ae == be (mod n) and (e, n)

=

d, maka a == b (mod n/ei).

9. Jika a == b (mod ni), di mana 1 :S i:S k, maka a == b (mod [nl,n2, ... ,nk]).

10. Jika a == b (mod n), maka

i

== bk (mod n) untuk sebarang integer positif k.

Teorema 2.1.10 (Niven ef al. 1991, diacu dalam Lestari 2007) Sistem Residu

Lengkap Modulo n. Jika x == y (mod n) maka y disebut residu dari x modulo n.

Selanjutnya himpunan A

=

{Xl, X2, ... , Xn} dinamakan sistem residu lengkap (SRL)

modulo n jika untuk setiap integer y terdapat satu dan hanya satu Xi sedemikian

sehinggay == Xi (mod n).

Teorema 2.1.11 (Niven

et

al. 1991, diacu dalam Lestari 2007) Sistem Residu

(20)

bilangan bulat Xi, di mana gcd(Xi,n) = 1, Xi $. Xj jika i

*

j. Selanjutnya, setiap y yang prima relatif dengan n kongruen dengan suatu Xi pada himpunan tersebut.

Definisi 2.1.12 (Menezes et al. 1997) Misalkan n integer positif. Himpunan integer modulo n dinotasikan 7l._n adalah himpunan integer {O, 1, 2, ... , n-l}. Operasi penjumlahan, pengurangan, dan perkalian dinyatakan dalam modulo

n.

Definisi 2.1.13 (Menezes et al. 1997) Invers perkalian dari a modulo n adalah

suatu integer X E &::n sedemikian sehingga ax == 1 (mod n). Jika terdapat bilangan X yang demikian, maka X tunggal dan a dikatakan invertibel yang dinotasikan a-I.

Teorema 2.1.14 (Menezes et al. 1997) Misalkan a E 7l._n.Maka a adalah invertibel

jika dan hanyajika gcd(a,n) = 1.

Teorema 2.1.15 (Menezes et al. 1997) Misalkan d = gcd(a, n). Kongruensi

persamaan ax

=

b (mod n) mempunyai solusi X jika dan hanyajika d membagi b, dalam hal ini terdapat solusi eksak d antara 0 dan n - 1.

Teorema 2.1.16 (Munir 2006) Teorema sisa Cina. Misalkan mJ, m2, ... , mn adalah

bilangan bulat positif sedemikian sehingga PBB(m;, m;) = 1 untuk i -:f. j. Maka sistem kongruen lanjar

mempunyai sebuah solusi tunggal modulo m = ml . m2 ... mn.

Algoritme 2.1.17 (Menezes et al. 1997) Algoritme Gauss.

Solusi x pada teorema sisa Cina dihitung sebagai x = ｌｾ］ｉ＠ a; N;M; mod n, di mana N; = nln; dan M; = N;-I mod n;.

Teorema 2.1.18 (Menezes et al. 1997) Grup Perkalian dari 7l._n adalah

ＷｬＮｾ＠ = {a E 7l._n

I

gcd(a, n) = I}. Jika n prima, maka ＷｬＮｾ＠ = {a

11

S: a S: n - I}.

Teorema 2.1.19 (Menezes et al. 1997) Teorema Euler. Misalkan n ｾ＠ 2 adalah

suatu integer. Jika a E ＷｬＮｾ＠ dan gcd(a, n) = 1, maka a¢(n)

==

1 (mod n).

Teorema 2.1.20 (Menezes et al. 1997) Misalkan p adalah prima.

1. (Teorema Fermat) Jika gcd(a,p) =1, maka

d-

I == 1 (mod p).

2. Jika r

==

s (mod p - 1), maka ar

==

as (mod p) untuk setiap integer a.

(21)

2.2 Teori Peluang

Definisi 2.2.1 (Mangku 2005) Suatu percobaan yang dapat diulang dalarn kondisi

yang sarna yang hasilnya tidak dapat ditebak dengan tepat, namun dapat diketahui

setiap kemungkinan hasilnya disebut percobaan acak.

Definisi 2.2.2 (Mangku 2005) Himpunan setiap hasil dari suatu percobaan acak

disebut ruang contoh (ruang sampel). Himpunan bagian dari suatu ruang contoh

disebut kejadian.

Teorema 2.2.3 (Munir 2003) Peluang kejadian E di dalam ruang contoh S adalah

peE) = n(E) n(S) .

Teorema 2.2.4 (Guritman 2005) Jika suatu prosedur dapat dipecah menjadi dua

tahap, dan jika tahap pertama menghasilkan m keluaran yang mungkin dan

masing-masing keluaran dilanjutkan ke tahap kedua dengan n keluaran yang

mungkin, maka prosedur tersebut akan menghasilkan mn keluaran yang mungkin.

Lemma 2.2.5 (Niven 1991, diacu dalam Safaat 2007) Andaikan bahwa 1

:s

k

:s

n,

dan bilangan-bilangan u}, U2, .•. , Uk bebas dipilih dari himpunan {I, 2, ... , n}.

Peluang bahwa setiap bilangan Uj berbeda adalah

2.3 Struktur Aljabar

Definisi 2.3.1 (Aliatiningtyas 2002) Operasi biner

*

pada suatu himpunan S adalah suatu fungsi dari S x S ke S, yang membawa setiap a

*

b E S yang tunggal. Jadi (a,b) ｾ＠ a

*

b. Karena a

*

b juga berada dalam S maka dikatakan S tertutup di bawah operasi

*.

2.3.1 Grup

Definisi 2.3.2 (Aliatiningtyas 2002) Struktur aljabar G dengan operasi biner

*

disebut grup jika memenuhi aksioma-aksioma berikut ini,

(22)

a

*

e = e

*

a = a, Va E G,

3. untuk setiap a E Gada unsur a-I E G, sehingga a

*

a-I

=

a-I

*

a

=

e.

Grup G disebut grup komutatifjika operasi

*

bersifat komutatifyaitu :

a

*

b = b

*

a, Va,b E G.

Definisi 2.3.3 (Menezes, et al. 1997) Suatu grup G dikatakan berhingga jika

kardinalitas G berhingga. Banyaknya unsur dari grup hingga disebut order,

dinotasikan: o(G) atau IGI.

Definisi 2.3.4 (Menezes, et al. 1997) Suatu himpunan bagian tak nol H dari grup

G adalah subgrup dari G jika H adalah grup yang operasinya sarna dengan G. Jika H adalah subgrup dari G dan H

f:

G, maka H disebut proper subgrup dari G.

Definisi 2.3.5 (Guritman 2004) Misal G sembarang grup, a E G, dan n bilangan bulat positif, maka:

an = aa ... a,

---,...-n kali a -n

=

g-Ia-I ... a-I"

n kali

aO =e.

Teorema 2.3.6 (Guritman 2004) Jika G yaitu suatu grup dan a E G, maka untuk setiap bilangan bulat m dan n berlaku hukum eksponen:

2. (am)n.

3. a -n = (a-If = (an)-l.

Definisi 2.3.7 (Menezes, et al. 1997) Misalkan G grup dan a E G. Order dari a

(notasi O(a» didefinisikan sebagai bilangan bulat positif terkecil m sedemikian

sehingga ｾ＠ = e, jika bilangan terse but ada. Jika tidak terdapat bilangan m yang

demikian maka order dari a adalah tak-hingga.

Teorema 2.3.8 (Guritman, 2004) Tiga sifat dasar yang berkaitan dengan

pengertian order.

(23)

2. Jika D(a) tak hingga, maka setiap kuasa dari a berbeda. Artinya, jika r dan

s yaitu dua bilangan bulat yang berbeda, maka ar =I-as.

3. Misalkan a yaitu unsur dari grup G dan D(a) = n. Maka

d

= e jika dan

hanya jika t yaitu kelipatan dari n (t kelipatan n artinya ada bilangan bulat q sehingga t

=

nq).

Teorema 2.3.9 (Fraleigh 2000) Misalkan grup G dan a E G. Maka H={anlnE&::}

merupakan subgrup dari G dan merupakan subgrup terkecil dari G yang memuat

a. Subgrup demikian disebut subgrup siklik yang dihasilkan oleh a dan

dinotasikan (a). Jadi,

Teorema 2.3.10 Sifat-sifat Grup Siklik (Guritman 2004).

1. Jika grup G berorder n, maka G yaitu siklik jika dan hanya jika ada a E G

sehingga D(a) = n.

2. Setiap grup siklik yaitu abelian.

3. Setiap subgrup dari grup siklik yaitu siklik.

4. Jika G = (a) dan bEG, maka O(b)ID(a).

5. Jika G yaitu grup siklik berorder n dan suatu bilangan bulat kin, maka ada

bEG sehingga D(b) = k.

6. Misalkan D yaitu grup abelian berorder mn dengan m dan n prima relatif.

Jika a,b E G dengan D(a) = m dan b dengan D(a) = n, maka G merupakan

grup siklik dengan G = (ab).

7. Unsur ar merupakan generator dari G = (a) dengan IGI = n jika dan hanya

jika r dan n prima relatif.

Lemma 2.3.11 (Guritman 2004) Misalkan G = (a) dengan IGI = n, jika min, maka

Cm

=

{x E G / xm

=

e} merupakan subgrup dari G dan ICml = m.

Definisi 2.3.12 (Aliatiningtyas 2002) Misal

H

adalah subgrup dari grup G dan

(24)

Teorema 2.3.13 Teorema Lagrange (Guritman 2004) Misalkan G yaitu grup

berhingga dan H subgrup dari G. Maka order dari H membagi order G. Akibatnya,

jika a sembarang unsur G, maka O(a) membagi order G.

Definisi 2.3.14 (Guritman 2004) Misal G dan H grup. Suatu homomorfisma (grup) dari G ke H adalah suatu fungsi

J:

G -+ H sehingga untuk sembarang a dan b di dalam G,

j(ab) =j(a)j(b).

Definisi 2.3.15 (Guritman 2004) Misal G1 dan G2 grup. HomomorfismaJ: G1 -+

G2 yang bijektif disebut isomorfisma dari G1 ke G2. Dua grup G1 dan G2

dikatakan isomorfik, dinotasikan G1 ｾ＠ G2, jika ada suatu isomorfisma dari Gl ke

G2•

Bayangan (Imej) dariJ, dinotasikan Im if), yaitu

Im if) = j(G) = (f(x)

I

x E G}.

Kernel dari f, dinotasikan ker if), yaitu

Ker if) = { x E G Ij(x) = e}.

Definisi 2.3.16 (Aliatiningtyas 2002) Misalkan G grup dan N subgrup dari G.

MakaN disebut subgrup normal dari G jika Vg E G, Vn EN, gng-l EN.

Definisi 2.3.17 (Aliatiningtyas 2002) Misalkan G grup, N subgrup normal dari G dan himpunan GIN beserta operasi perkalian pada GIN adalah sebagai berikut:

GIN = { aN

I

a E G}

aN· bN=abN.

Maka GIN merupakan grup dan disebut grup faktor dari G oleh N.

Teorema 2.3.18 (Aliatiningtyas 2002) Teorema Dasar Homomorjisma untuk Grup. Misalkan f1 : G -+ G' epimorfisma (surjektif) grup dengan Ker f1 = H, maka

ｇｉｈｾ＠ G'.

2.3.2 Ring

Definisi 2.3.19 (Aliatiningtyas 2002) Struktur aljabar (R, +, .) dengan operasi + disebut operasi penjumlahan dan operasi . disebut operasi perkalian, disebut ring

(25)

1. (R, +) grup komutatif.

2. Operasi perkalian bersifat asosiatif.

3. Hukum distributifkiri berlaku 'Vx,y,z E R, x(y + z) = xy + xz

Hukum distributifkanan berlaku, 'Vx,y,z E R, (x

+

y) z = xz

+

yz.

Unsur identitas terhadap

+

dinotasikan dengan 0 dan disebut unsur no!.

Selanjutnya,

1. Jika operasi perkalian bersifat komutatif, 'Vx,y,z E R, xy = yz maka R disebut ring komutatif.

2. Jika ada unsur identitas di bawah operasi perkalian (unsur ini disebut

unsur kesatuan, dinotasikan dengan 1 dan disingkat unkes), 'Vx E R, 31 E

R,

X· 1 = 1 . x = x maka R disebut ring dengan unsur kesatuan (unkes).

Definisi 2.3.20 (Aliatiningtyas 2002) Misalkan R ring, I ｾ＠ R, Ii-

0.

Himpunan bagian I disebut ideal jika memenuhi

1. x, y E I ｾ＠ x - Y E I

2. r E R, x E I ｾ＠ rx E I dan xr E 1.

Lemma 2.3.21 (Aliatiningtyas 2002) Misalkan R adalah ring komutatif dengan unkes 1 dan a E R. Himpunan (a) didefinisikan sebagai (a) = {ra IrE R}. (a)

adalah ideal dari R disebut ideal utama yang dibangun oleh a.

Definisi 2.3.22 (Aliatiningtyas 2002) Fungsi <p dari ring R ke ring R' disebut homomorfisma jika 'Va, b E R, berlaku

<pea + b) = <pea) + <pCb)

<p(ab) = <pea) <pCb)

Kernel <p

= {

x E R

I

<p(x)

= O'}, 0' unsur nol dari

R '. Jika ada isomorfisma dari R ke R " maka dikatakan R isomorfik dengan R', dinotasikan: R ::::: R '.

Teorema 2.3.23 (Aliatiningtyas 2002) Misalkan 8: R ｾ＠ R' adalah homomorfisma ring. Maka

1. 8(R) subring dari R' 2. Ker

e

adalah ideal dari R

(26)

Definisi 2.3.24 (Aliatiningtyas 2002) Ring Faktor

Misalkan R ring, N ideal dari R, maka koset-koset aditif dari N adalah a

+

N dengan a E R. Definisikan: RlN = {a + N

I

a E R}. Operasi penjumlahan dan perkalian didefinisikan:

(a + N) + (b + N)

=

(a + b) + N

(a + N) (b + N) = ab + N.

Teorema 2.3.25 (Aliatiningtyas 2002) < RlN, +, . > merupakan ring dan disebut ring faktor dari R oleh N.

Definisi 2.3.26 (Aliatiningtyas 2002) Ideal M dari ring R disebut ideal maksimal jika tidak ada ideal sejati dari R yang memuat M.

Teorema 2.3.27 (Aliatiningtyas 2002) Misalkan R ring dengan unkes 1 dan M

ideal dari R. Ring faktor RlMfieldjika dan hanyajika Mideal maksimal.

2.3.3 Field

Definisi 2.3.28 (Aliatiningtyas 2002) Suatu ring yang komutatif, ada unkes dan setiap unsur tak nolnya mempunyai invers (perkalian) disebutfield.

Definisi 2.3.29 (Weintraub 2006) Karakteristik dari field

F

dinotasikan char(F) adalah bilangan bulat positif terkecil n sedemikian sehingga n . 1 = 0 E F, jika tidak terdapat n seperti di atas dikatakan F berkarakteristik nol.

Teorema 2.3.30 (Menezes, et al. 1997) ｾｮ＠ adalah field jika dan hanya jika n bilangan prima. Jika n adalah prima, maka ｾｮ＠ mempunyai karakteristik n.

2.3.4 Polinomial Ring

Definisi 2.3.31 (Fraleigh 2000) Misalkan R adalah ring. Suatu polinomial j(x) dengan koefisien dalam R adalah penjumlahan formal takhingga

OCJ

I

ai xi

=

ao+ aJx + ... + anJ!i + ... i=O

(27)

terbesar dari i yang demikian disebut derajat darifix) danjika aj = 1 maka disebut

polinomial monik. Jika tidak ada i> 0 yang demikian makafix) berderajat DOl.

Definisi 2.3.32 (Fraleigh 2000) Jikafix)

=

ao+ ajX

+ ... +

anY!'

+ ...

dan g(x)

=

_{bo+ b jX}

+ ... +

bnY!'

+ ... ,

maka penjumlahan polinomial adalah

fix)

+

g(x)

=

co+ CjX

+ ... +

cnY!'

+ ...

di mana Co

=

an

+

bn.

dan perkalian polinomial adalah

fix)g(x) = _{do+ djx}

+ ... +

dnY!'

+ ...

di mana

do

=

I7=o

_{ai bn-}_1•

Teorema 2.3.33 (Fraleigh 2000) R[x] adalah himpunan semua polinomial dalam

peubah x dengan koefisien dalam ring R merupakan sebuah ring di bawah operasi

penjumlahan dan perkalian polinomial. Selanjutnya jika R komutatif maka R[x]

juga komutatif, danjika R memiliki unkes 1 maka 1 juga merupakan unkes dalam

R[x].

Definisi 2.3.34 (Fraleigh 2000) Suatu polinomial yang bukan konstantafix)E F[x]

adalah irreducible atas F atau irreducible F[x] jika fix) tidak dapat dinyatakan

sebagai perkalian g(x)h(x) yakni dua polinomial g(x) dan hex) dalam F[x] yang

keduanya berderajat lebih rendah darifix). Jikafix)E F[x] polinomial yang bukan

konstanta tak irreducible makafix) adalah reducible.

Teorema 2.3.35 (Rosdiana 2009) Misalkan F field, I ideal tak nol di F[x], dan

unsur g(x) E F[x]. Ideal 1= (g(x) jika dan hanya jika g(x) merupakan polinomial

tak nol berderajat terendah di I.

Teorema 2.3.36 (Menezes 1997) Jika fix) adalah irreducible atas F, maka

F[x]/{ftx) adalahfield.

2.3.5 Ruang Vektor

Definisi 2.3.37 (Guritman 2005) Diberikan sembarang himpunan V dan

sembarangfield IF. Pada V didefinisikan aturan jumlah dan aturan perkalian skalar

vektor. V disebut ruang vektor atas IF jika terdapat aturan-aturan tersebut

memenuhi aksioma-aksioma berikut.

1. ('v'u,v E V) (3!wE V) u

+

v

=

w.

(28)

3. (3 fOE V) ('v'u E V) 0

+

U = U

+

0 = u.

4. ('v'u E V) (31vE V) u

+

v = v

+

u = 0, dalam hal ini v = - u. 5. ('v'u,v E V) u

+

v = v

+

u.

6. ('v'k ElF, 'v'u E V) (31v E V) 1m

=

v.

7. ('v'k E IF, 'v'u,v E V) k(u

+

v) = 1m

+

kv.

8. ('v'k,l E IF, 'v'u E V) (k

+

l)u = 1m

+

lu. 9. ('v'k,1 E IF, 'v'u E V) (kl)u = k(lu).

10. ('v'u E V) 1 u = u di mana 1 adalah unsur identitas dari IF terhadap operasi kali

Teorema 2.3.38 (Guritman 2005) Sifat-Sifat Dasar Ruang Vektor. Misal V ruang vektor atas skalar IF, maka sifat-sifat berikut dipenuhi:

1. kO = 0, 'v'k E IF.

2. Ov = 0, ('v'v E V).

3. (kv = 0) ｾ＠ (k = 0 V v = 0), 'v'k E IF, 'Iv E V.

4. k(-v) = - kv , 'v'k E IF, 'Iv E V.

5. (- k)v = -kv , 'v'k E IF, 'Iv E V.

6. (k-l)v = kv -Iv, 'v'k,1 E IF, 'Iv E V.

7. k(v - w) = kv - kw, 'v'k E IF, 'v'v,w E V.

Definisi 2.3.39 (Guritman 2005) Misalkan Vadalah ruang vektor atas skalar IF, dan misalkan A = {VI, V2, ... , v_{n }}adalah himpunan yang terdiri atas n vektor dalam

V. A disebut bebas linear jika

(Lf=l Cj Vj

=

0) ｾ＠ ('Ii E 1= {l,2, ... ,n} Cj

=

0).

Ingkarannya, A disebut terpaut linear jika

(L7=lCjVj = 0) 1\ (3) E 1= {1,2, ... ,n} Cj

*-

0).

Definisi 2.3.40 (Guritman 2005) Misalkan Vadalah ruang vektor atas IF, dan B

adalah himpunan berhingga vektor-vektor di dalam V. Dikatakan B adalah basis

(29)

2.2.6 Perluasan Field

Definisi 2.3.41 (Weintraub 2006) Jika E field yang memuat subfield F, maka E disebut perluasanfield dari F.

Definisi 2.3.42 (Menezes et al. 1997) Finite field adalah field F yang memuat unsur sebanyak berhingga. Order dari F adalah banyaknya unsur dalam F.

Definisi 2.3.43 (Rosdiana 2009) Misal E perluasanfield darifield F dan c E E. c disebut algebraic atas F jikaj(c) = 0 untukj(x) E F[x] yang tak no!.

Definisi 2.3.44 (Rosdiana 2009) Misal E perluasan field dari field F dan c E E algebraic atas F. Polinornial irreducible untuk c atas F dari polinomial monik p(x) dinotasikan dengan irr( c, F) dan derajat dari polinomial irreducible untuk c atas F dinotasikan dengan deg(c, F).

Teorema 2.3.45 (Rosdiana 2009) Misal F subfield darifield E, c E E dan x adalah sebuah indeterminasi. Pemetaan (Jc : F[x] -+ E yang didefinisikan dengan (Jc(j(x))

= j(c) di mana j(x) = ao + a/x + a2x2 + ... + anX", j(x) E F[x] merupakan homomorfisma. Homomorfisrna (Jc disebut homomorfisma evaluasi dan berlaku

(Jc(x) = c serta (Jc(a) = a, a E F.

Teorema 2.3.46 (Rosdiana 2009) Misal F field dan p(x) E F[x]. (P(x) ideal maksimaljika dan hanyajikap(x) irreducible atas F.

Teorema 2.3.47 (Rosdiana 2009) Misal F field dan p(x) polinornial tak konstan di F[x]. Ada suatu perluasanfield E dari F dan unsur c di E sehingga c akar p(x).

Definisi 2.3.48 (Rosdiana 2009) Misal E perluasan field dari field F. lika E berdimensi hingga n sebagai ruang vektor atas F, rnaka E disebut perluasan hingga berderajat n atas F. Derajat E atas F sarna dengan n dinotasikan [E:F] = n.

Definisi 2.3.49 (Rosdiana 2009) Suatu perluasan field E dari field F disebut perluasan tunggal jika E

=

FCc) untuk suatu c E E.

Definisi 2.3.50 (Rosdiana 2009) likafield E dibangun oleh unsur satu c atas field

(30)

Teorema 2.3.51 (Rosdiana 2009) Misal E = F(c) dengan c E E algebraic atas F, dan deg(c,F) = m, m ｾ＠ 1. Setiap unsur

fJ

dari E = F(c) dapat dinyatakan secara

unik dalam bentukp= b_o+ blcl + ... + bm_Icm-l, di mana bi E F.

Teorema 2.3.52 (Rosdiana 2009) Misal E perluasanfield darifield F dan c E E algebraic atas F. Jika deg(c,F) = m, maka F(c) ruang vektor atas F berdimensi-m

dengan basis {1,c ,c2 , ••• ,cm-I } .

Teorema 2.3.53 (Menezes et al. 1997) Eksistensi dan kekhasanfinitefield.

1. Jika F adalahfinite field maka F terdiri dari pm unsur dengan p prima dan

danm ｾ＠ 1.

2. Untuk setiap prima berorder pm, ada finite field yang khas berorder pm.

Field ini dinotasikan dengan IFp"', atau sering juga dinotasikan dengan

GF(pm).

Teorema 2.3.54 (Menezes et al. 1997) Himpunan dengan unsur-unsur tak nol dari GF(pm), merupakan grup di bawah perkalian dinotasikan dengan GF(pm)

* .

Teorema 2.3.55 (Menezes et al. 1997) Grup GF(q)* di mana q = pm adalah siklik berorder q - 1. Karenanya aq = a untuk setiap a E GF(pm).

Teorema 2.3.56 (Menezes et al. 1997) a:p[x] adalahfaktorisasi domain tunggal. Yakni, setiap polinomial tak nol.f{x) E a:p[x] memiliki faktorisasi

.f{x) = ajj(x/1 _h(x/2

.,. fi(x)ek

di manaJi(x) polinomial irreducible dalam

a:

_p[x

L

ei adalah positif integer, dan a E

a:p.

Teorema 2.3.57 (Menezes et al. 1997) Misalkan.f{x) E a:p[x] adalah polinomial irreducible berderajat m, maka F[x]/(f(x)) adalah finite field berorder pm. Penjumlahan dan perkalian polinomial dinyatakan dalam bentuk modulo fix).

Teorema 2.3.58 (Menezes et al. 1997) Polinomial irreducible fix) E a:p[ x] berderajat m adalah polinomial primitif jika dan hanya jika .f{x) membagi xk - 1

(31)

2.4 Masalah Logaritma Diskret

Berikut diberikan definisi logaritma diskret pada grup umum beserta sifat

logaritma diskret. Lebih khusus diberikan pula definisi masalah logaritma diskret

pada ｾ＠ _p* dan definisi yang diperumum untuk sembarang grup siklik.

Definisi 2.4.1 (Menezes et al. 1997) Misal G adalah grup siklik hingga berorder n. Misal

a

adalah suatu generator dari G, dan misal pEG. Logaritma diskret dari

p,

dengan basis a, dinotasikan loga

P

adalah integer tunggal x, 0 S x S n - 1, sedemikian sehingga

P

= 0:.

Teorema 2.4.2 (Menezes et al. 1997) Jika a. adalah generator grup siklik G berorder

n,

p,

y E G dan

s

adalah integer maka

loga (fJa) = (loga

P

+

logaa) mod n dan loga (ff)=s loga

P

mod n .

Definisi 2.4.3 (Menezes et al. 1997) Masalah logaritma diskret adalah sebagai berikut : Diberikan suatu prima p, generator a dari

tz:

*, dan suatu unsur

P

E

tz:

* ,

p p

tentukan integer x, 0 S x S p - 2 sedemikian sehingga a! ==

P

(mod p).

Logaritma diskret pada

tz:

_p* sudah banyak digunakan oleh kriptografer dan

algoritme untuk memecahkan masalah logaritma diskret pada

tz:

_p* sudah banyak

dilakukan, sehingga tingkat keamanannya semakin berkurang. Kriptografer

tertarik pada grup siklik yang lain. Misalnya grup siklik pada IF _q* , dengan q = pm,

p adalah bilangan prima dan grup pada titik dalam suatu kurva eliptik yang

didefinisikan atas finite field. Akibatnya definisi masalah logaritma diskret dapat diperumum sebagai berikut.

(32)

2.5 Kompleksitas Algoritme

Definisi 2.5.1 (Guritman & Supriyo 2004) Misalkanf g : ｾＫ＠ｾ＠ IRL Kita katakan

bahwa g mendominasi

f

(atau

f

didominasi g) jika ada konstanta m E JR{+ dan

konstanta k E ｾＫ＠ sedemikian sehingga

If{n)1

::s

ml(g(n))I, di mana n ｾ＠ k, 'r/ n E ｾ＠ + .

Apabilaf didominasi oleh g, makaf dikatakan berorder (paling banyak) g

dan ditulis denganf E O(g) di mana O(g) dibaca dengan "order g" atau "Oh-besar dari g". O(g) merepresentasikan himpunan semua fungsi dengan domain ｾＫ＠ dan

kodomain JR{+ yang didominasi oleh g.

Dalam tabel berikut diberikan beberapa bentuk Oh-besar, urutan batasan

lebih baik disusun dari atas ke bawah.

Tabel 1 Oh-Besar

Bentuk Oh-Besar

0(1) 0(lOg2 n)

O(n) O(n IOg2 n)

0(n2) 0(n3)

O(nm), m = 0, 1,2, ... O(cn), c> 1

O(n!)

Nama

konstan logaritmik linear

n IOg2 n

kuadratik kubik polinomial eksponensial faktorial

Didefinisikan fungsi kompleksitas waktu j(n) sebagai fungsi yang

mengukur banyaknya operasi dalam suatu algoritme yang mempunyai variabel

input n. Yang dimaksud dengan banyaknya operasi adalah banyaknya operasi

dasar Gumlah, kurang, kali, bagi), ditambahkan dengan assigment, dan

perbandingan (ekspresi logika). Setelah kit a mendefinisikan j(n) untuk suatu

algoritme, kemudian dengan tabel Oh-Besar kita tentukan order darifatau bentuk

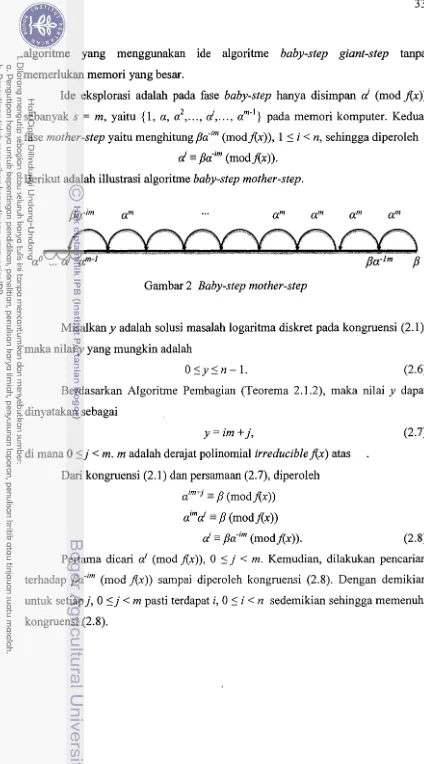
[image:32.567.33.449.0.777.2]

(33)

Bagian ini akan membahas masalah logaritma diskret pada finite field GF(3m), analisis teoritik, analisis efisiensi algoritme dan komputasi solusi masalah

logaritma diskret padafinite field GF(3m).

3.1 Masalah Logaritma Diskret pada Finite Field GF(3m)

Logaritma diskret merupakan invers dari eksponensial diskret dalam grup siklik hingga. Diberikan grup siklik hingga G dengan operasi perkalian . , suatu generator a, dan y adalah integer tunggal. Eksponensial dalam G didefinisikan oleh

sebanyak y kali

y - ' ,

a -

aa ...

a .

Misalkan

f3

=

eX

E G, maka logaritma diskret dari

f3

dengan basis a adalah y dan dituliskan sebagai

(1)

Tulisan ini akan membahas logaritma diskret pada grup siklik GF(3m)* darifinite field GF(3m), di mana m ｾ＠ 2. Berdasarkan Teorema 2.3.53, eksistensi dan kekhasan dari GF(3m) dijamin dan berdasarkan Teorema 2.3.59 Z3[X]/(f(X)

adalahfinite field berorder 3m dengan operasi penjumlahan dan perkalian modulo

j(x). Akibatnya GF(3m)

=

Z3[X]/(f(X».

E perluasanfield darifield F dan c E E,j(c) = 0 untukj(x) E F[x] yang tak nol dan E = F(c). Berdasarkan Teorema 2.3.18 yakni teorema dasar homomorfisma dapat ditunjukkan 23[X]/(f(X» :::::: 23(C). Karena j(x) adalah polinomial irreducible atas 23 maka (f(x» adalah ideal maksimal (Teorema 2.3.46), sehingga berdasarkan Teorema 2.3.27, Ring faktor 23[X]/(f(X» adalah

field. Akibatnya 23 (c) adalahfieldyang merupakan perluasanfield dari F.

(34)

GF(3m)

=

Z3[X]/(f(X)

=

{b

o

+

blx

+

b2x2

+ ... +

bm_Ixm-1

I

bi E {0,1,2}}. (2) Berdasarkan Teorema 2.3.52, GF(3m) dapat dinyatakan sebagai ruang vektor atas Z3 berdimensi m dengan basis standar { 1, X, x2, ... , xm-I}. Polinomial pada persamaan (2) dapat direpresentasikan sebagai

(3)

G = GF(3m)* = GF(3m) - {O} merupakan grup siklik perkalian yang

berorder n = 3m - 1 (Teorema 2.3.54 dan 2.3.55). Misalkan a adalah generator dari

G, berdasarkan Teorema 2.3.10 Bagian 1, jika O(G) = n dan G = (a) maka

O(a) = n. Akibatnya,

G = (a) = { aO, a, a2, ... , an-I}.

Berdasarkan Teorema 2.3.8 Bagian 1, unsur-unsur aO, a, a2, ... , an-I semuanya berbeda.

Berdasarkan definisi logaritma diskret (Definisi 2.4.1), maka nilai y pada persamaan (1) terdapat pada rentang 0 :s y :s n - 1 yang merupakan solusi masalah logaritma uiskret

eX

== fJ pada G. Hal ini dijamin oleh teorema berikut ini.

Teorema 3.1 Misalkan diberikan grup perkalian G

=

GF(3m)* dari finite field

GF(3m). a adalah generator dari G dan fJ E G. fix) E Z3[X] adalah polinomial

irreducible berderajat

m

atas Z3. G berorder n = 3m - 1. Maka terdapat nilai y yang

unik pada rentang O:S y:S n - 1 sedemikian sehingga

eX

== fJ (modf{x».

Bukti:

Diketahui

a

adalah generator dari G berorder

n,

maka berdasarkan Teorema 2.3.8

bagian satu, unsur-unsur 1, a, a2, ... , an-I semuanya berbeda. Karena banyaknya anggota G adalah n, maka terdapat korespondensi 1-1 antara l,a,a2, ••• ,an-1 dengan

anggota G, mengikuti aturan sistem residu tereduksi (Teorema 2.1.11).

Akibatnya fJ E G dipetakan tepat satu ke 1, a, a2, ••• , an-I.

Untuk setiap

fJ

E Gada tepat satu eX E G sehingga eX ==

fJ

(mcdf{x».

(35)

Berdasarkan definisi perumuman masalah logaritma diskret (Definisi

2.4.4) masalah logaritma diskret padafinite field GF(3m) adalah sebagai berikut : diberikan grup siklik hingga G = GF(3m)* berorder n = 3m - 1, suatu generator a

dari G, dan pEG, bagaimana menentukan integer y, 0 :S y:S n - 1 sedemikian sehingga aY ₌₌

p.

Untuk order n yang besar, komputasi logaritma diskret pada G menjadi tak

layak hitung. Oleh karena itu, diperlukan algoritme untuk menyelesaikan masalah

logaritma diskretfinite field GF(3m). Subbab 3.2 menjelaskan algoritme masalah logaritma diskretfinite field GF(3m).

3.2 Analisis Solusi Masalah Logaritma Diskret pada Finite Field GF(3j

Algoritme untuk menyelesaikan masalah logaritma diskret yang sudah

dikenal adalah metode naif, baby-step giant step, Pollard-rho, Pohlig-Hellman, dan index-calculus. Tulisan ini membahas rekonstruksi dan eksplorasi algoritme-algoritme terse but sehingga dapat digunakan untuk menyelesaikan masalah

logaritma diskret padafinite field GF(3m).

3.2.1 Metode Naif

Metode exhausetive search (pelacakan lengkap) disebut juga pelacakan naif atau bruce force. Metode ini merupakan metode yang sederhana. Pelacakan dilakukan pada ruang pelacakan. Himpunan semua kemungkinan solusi dari

sebuah masalah disebut ruang pelacakan.

Algoritme naif adalah algoritme yang ｢･ｲ､ｾｳ｡ｲ＠ pada definisi logaritma diskret. Misalkan G

=

(a)

= { 1,

a, a2, ... ,

p,

...

an-I}, untuk menentukan nilai y sedemikian sehingga aY

==

P

(mod j(x» , dilakukan dengan mencoba semua kemungkinan nilai y = 0, 1, 2, 3, ... , n - 1. Berikut adalah algoritme untuk

(36)

Algoritme 3.2.1.1

Algoritme naifuntuk menentukan solusi masalah logaritma diskret Input : generator a dari grup siklik G = GF(3m)*, fJ E G,

fix) E 7l3[x] adalah polinomial irreducible atas 713 berderajat m.

Output : y

=

logafJ (modf{x)). 1. Hitung: n = 3m - 1.

2. Untuk setiap k,

o:s k:s

n - 1, hitung nilai ak (modf{x)).

3. Setelah langkah ke-k di mana ak

==

fJ (modf{x)) maka proses berhenti. 4. Solusi dari

d'

=

fJ (modf{x)) adalahy

=

k (mod n).

Untuk mendapatkan ak

==

fJ (modf{x)) dilakukan pengulangan sebanyak n

kali. Jadi, kompleksitas waktu komputasi algoritme naif adalah O(n) (Menezes et al. 1997). Untuk n besar, algoritme ini tidak efisien, sehingga logaritma diskret menjadi tak layak hitung. Algoritme naif diimplementasikan pada sofware Maple 11 dapat dilihat pada Lampiran 3.

Contoh 3.2.1.2

Diketahui grup silkik G = GF(32)

* ,

a adalah generator dari G, fJ = 2a E G. Tentukan y = loga f3 dengan menggunakan algoritme naif.

Solusi:

Berdasarkan persamaan (2), grup G dapat direpresentasikan sebagai himpunan

setiap polinomial dalam 7l3[a] berderajat paling banyak 1,

GF(32) = 7l3[a]/ (j{a)

= {

cIa +co

I

Cj E {0,1,2} },

atau berdasarkan persamaan (3), dapat juga direpresentasikan sebagai vektor

temer,

GF(32)

=

{(CI,CO)

I

aj E {0,1,2}}. dengan perkalian dibentuk oleh modulof{a).

Pilih polinomial irreducible atas 713 yaituf{a) = a2

+

a

+

2.

Order dari G adalah n = 32 - 1 = 8, artinya terdapat delapan kemungkinan nilai y.

Pelacakan dilakukan dengan mencoba setiap kemungkinan nilai y sampai dipeoleh

rI

=: 2a (modf{a)).

(37)

aO = 1

a1

=a

a 2

+

a

+

2 = 0

<=>

a 2 = -a - 2 = 2a

+

1

a3 = a2 a = (2a

+

1) a = 2a 2

+

a = 2 (2a

+

1)

+

a = 2a

+

2 a4 = a3 a = (2a

+

2) a

=

2a2

+

2a = 2 (2a

+

1)

+

2a

=

2

as = a4 a = 2a

Setelah di peroleh as = 2a pada langkah keenam berhenti, karena memenuhi

d'

= 2a (modf{a)), sehingga diperolehy = loga 2a = 5.

Lebih jelasnya, tabel berikut memperlihatkan pelacakan yang direpresentasikan

dengan basis, polinomial basis, dan vektor temer.

Tabel2 Representasi solusi GF(32)* untuk

fJ

= 2a

No. Representasi Representasi Representasi Basis Polinomial Basis Vektor Terner

1 aU 1 01

2 a1 a 10

3 a2 2a

+

1 21

4 a3 2a+2 22

5 a4 2 02

6 a5 2a 20

0

Contoh 3.2.1.3

Diketahui G = GF(3s)*, a adalah generator dari G,

fJ

= 2a4 +a3

+

2a2

+

a

+

2 E G. Tentukan y = loga

fJ

dengan menggunakan algoritme naif.

Solusi:

Pilih polinomial irreducible atas ｾＳ＠ yaitu f{a) = a5

+

2a

+

1. Grup G dapat

direpresentasikan sebagai himpunan untuk setiap polinomial dalam ｾＳ＠ [a] berderajat paling banyak 4,

GF(35) = ｾＳ｛｡｝Ｏ＠ if(a)

= {

C4a4

+

C3 a3

+

c2a2

+

cIa +co

I

Ci E {0,1,2}},

atau dapat juga direprentasikan sebagai vektor temer.

GF(3s) = {(C4, C3, C2, Cl,CO)

I

ai E {0,1,2}}.

Perkalian dibentuk oleh modulof{a). Order dari G adalah n = 35 - 1 = 242, artinya

[image:37.561.30.459.37.723.2]

(38)

Misalkanj{a) = as

+

2a

+

Idanj{a) = 0, Sehingga

as

+

2a

+

1

=

0 ｾ＠ as

= -

2a - 1

=

a

+

2.

Berikut adalah Tabel yang memperlihatkan solusi Contoh 3.2.1.3 yang

direpresentasikan dengan basis, polinomial basis, dan vektor temer.

Tabel3 Representasi solusi GF(35)* untuk

fJ

= 2a4

+

a3

+

2a2

+

a

+

2 Representasi

No. Basis

1 aU

2 al

3 a2

4

a3

5

a

4

6 as

7 a6

8

a

7

9 as

10 a9

11 alO

12 all

13 al2

14 a13

15 al4

16 al5

17 al6

18 al7

19 all:!

20

al9

21 a20

22 a21

23 a22

24 a23

25 a24

26 0..25

27 a26

28 a27

29 a2S "

30 a29

31 a30

32 a31

33 a32

34 a33

35 a34

36 a35

37 a36

1

a

Representasi Polinomial Basis a2 a3 a4 a+2 a2+2a a3

+

2a2 a4

+

2a3 2a4

+

a

+

2 a2+a+l a3 + a2 + a a4 + a3 _{+ a}2 a4

+

a3

+

a

+

2

a4

+

a2

+

2 a3 +2 a4 +2a 2a2

+

a

+

2 2a3

+

a2

+

2a 2a4

+

a3

+

2a2

a 4 + 2a3 + 2a

+

1

2a 4

+

2a2

+

2a

+

2 2a3

+

2a2

+

a

+

1

2a 4

+

2a3

+

a2

+

a 2a 4

+

a3

+

a2

+

2a

+

1 a 4

+

a3

+

2a2

+

1 a 4

+

2a3

+

2a

+

2

2a4

+

2a2

+

2 2a3

+

a

+

1

2a4 + a2 + a a3

+

a2

+

2a

+

1 a 4

+

a3

+

2a2

+

a a4

+

2a3

+

a2

+

a

+

2 2a 4

+

a3

+

a2

+

2 a4

+

a3

+

a

+

1 -a4

+

a2

+

2a

+

2

a3

+

2a2

+

2 [image:38.559.64.435.161.747.2]

(39)

Representasi No. Basis

38 a37

39 a38

40 a39

41 a40

42

a

41

43 a42

44 a43

45

a

44

46 a45

47 a46

48 a47

49

a

48

50 a49

51 aSo

52 aSl

53 aS2

54 aS3

Representasi Polinomial Basis a4

+

2a3

+

2a 2a4 +2i

+

a +2 2a3

+

a2

+

a

+

1 2a 4

+

a3

+

a2

+

a a4

+

a3

+

a2

+

2a

+

1

a4

+

a3

+

2a2

+

2a

+

2 a 4

+

2a3

+

2a2

+

2

2a4

+

2a3

+

2 2a4

+

a

+

1 a2

+

1

a3 +a a4+a2 a3+a+2 a4

+

a2

+

2a a3

+

2a2

+

a

+

2 a 4

+

2a3

+

a2

+

2a 2a 4

+

a3

+

2a2

+

a

+

2

Representasi Vektor Terner

12020

20212

02111

21110

11121

11222

12202

22002

20011

00101

01010

10100

01012

10120

01212

12120

21212

Setelah langkah ke 54 berhenti karena memenuhi

o!'

=

j3 (mod j(a)), sehingga diperoleh aS3

==

2a4

+

a3

+

2a2

+

a + 2 (modj(a)).

Jadi, solusiy = loga (2a4

+

a?

+

2a2

+

a

+

2) (modj(a)) = 53. o

Semakin besar nilai m pada finite field GF(3m), semakin banyak kemungkinan nilai y yang memenuhi

o!'

= j3 pada G. Algoritme ini tidak efisien untuk n yang besar. Oleh karena itu, algoritme naif dapat dieksplorasi lebih lanjut dengan menggunakan sifat grup siklik GF(3m)* yang selalu berorder genap. Grup ini mempunyai karakteristik khusus. Berikut kekhususan grup GF(3m)*.

Lemma 3.2.1.4

Misal G adalah grup siklik berorder genap n, G = (a)

= { 1,

a, a2, ••• , j3, ... an-I},

maka dalam G berlaku X2

=

1 ｾ＠ X

=

an12•

Bukti:

Misalkan X E G, maka ada k, 0

:s

k:S n - 1.

Akibatnya

x

= a\ sehingga

x

2 = 1 ｾ＠ (i)2 =

an

ｾ＠

a

2k =

an

ｾ＠

2k

=

n (mod n).

Karena n genap, maka k

=

n12.

(40)

Berdasarkan Teorema 2.3.58, polinomial irreducible fix) E ｾＳ｛ｘ｝＠

berderajat m atas ｾＳ＠ adalah primitifjika dan hanyajikaf{x) membagi Xk - 1 untuk

k = pm - 1 dan bukan untuk integer positif terkecil k. Akibatnya diperoleh sifat berikut ini.

Akibat 3.2.1.5 Grup G = GF(3m)*, m ｾ＠ 2, a adalah generator dari G dan

fJ

E G.

fix) E ｾＳ｛ｘ｝＠ adalah polinomial primitifberderajat m atas ｾＳＧ＠ G berorder n = 3m - 1.

Nilai y unik pada rentang 0

:s

y:S n - 1 sedemikian sehingga a!

==

fJ

(modf{x)), berlaku:

n 1. 0.2 = 2.

2.

a

nl2 (-

fJ)

=

fJ·

3.

fJ

=

-fJ

ｾ＠ a

i

= -

fJ,

1

:s

i:S n - 1.

Bukti:

1. Diketahui G adalah grup siklik. Dari Lemma 3.2.1.4 berlaku x2 = 1 ｾ＠ x = an12•

Diketahui 2 E G, sehingga berlaku 22 = 1 ｾ＠ 2 = an12•

2. Akan dibuktikan: anl2 (-

fJ)

=

fJ

a

nl2

(-

fJ)

= 2 (-

fJ)

=-1

(-fJ)

=

fJ·

3. Akan dibuktikan: ai = -

fJ,

0

:s

i:S n - 1.

-1 = 2 mod 3

Solusi logaritma diskret pada grup G yaitu y merentang pada 0

:s

y

:s

n - 1.

Dengan demikian, solusi berada pada dua rentang yang memenuhi,

o

ai=fJ

_{' - - 2 '}O<i< ｾ＠ -1 danai=fJ _{' 2 - -}ｾ＼ｩ＼ｮＭＱＮ＠ (2.1)

(i) Jika ai =

fJ

_,0 < _- i < _- ｾ＠₂- 1 maka

n

(0.) = {I, 0., 0.2, ...

,fJ,

... ,

ai -1}. (2.2)

n n n

(") J'k ₁₁ ₁_a_ai ₌

fJ

_'2.:Sn ₁. < _{_} _n_- 1 _{rna a}k () {-_0. ₌ _0.2,_0.-+1 2 _,0.2 -+2 _{, ... ,}

fJ

_{, ... ,}_0.n-l} _. n

(41)

(a) = {-I, -a, _a2, ••• ,

-/3, ... ,

_an-I}. (2.3)

Berdasarkan Teorema 2.1.11, terdapat korespondensi satu-satu antara

persamaan (2.1) dan (2.2),

n

ao -_{- - , - -}1 a I - _a,a2 -_{- -} _a2 _{, ... , - - , ... , - -}

/3 -

fJ

ai - _ai _{, ... ,}_a"2-1 -_- _{a .}n-l

Jadi, persamaan (2.1) menjadi

/3

=

-/3

ｾ＠ ai = -

/3,

0 SiS n - 1.

o

Contoh 3.2.1.6

Akan dibangun grup G

=

GF(33)

* .

Order G adalah n

=

33 - 1

=

26. Dipilih

polinomial primitifatas Z3 yaitu!{a) = a3

+

2a

+

1. Tabel berikut memperlihatkan

G

=

(a).

Tabel 4 Representasi Polinomial GF(33)*

No i ｒ･ｾｲ･ｳ･ｮｴ｡ｳｩ＠ Basis No i ｒ･ｾｲ･ｳ･ｮｴ｡ｳｩ＠ Basis

1 0 aU 1 14 13 a13 2

2 1 al a 15 14 al4 2a

3 2 a2 a2 16 15 al5 2a2

4 3 a3 a+2 17 16 al6 2a + 1 5 4 a4 a2+2a 18 17 al7 2a2+ a