Eksplorasi Masalah Logaritma Diskret pada Finite Field G P(2m)

(1)

EKSPLORASI MASALAH LOGARITMA DISKRET

PADA FINITE FIELD

Y A N A

SEKOLAH PASCA SARJANA INSTITUT PERTANIAN BOGOR

(2)

PERNYATAAN MENGENAI TUGAS AKHIR DAN SUMBER INFORMASI

Dengan ini saya menyatakan bahwa tesis dengan judul “Eksplorasi Masalah Logaritma Diskret pada Finite Field ” adalah karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Bogor, Agustus 2009

Yana

(3)

ABSTRACT

YANA. The Exploration of Discrete Logarithm Problem over Finite Field . Under direction of SUGI GURITMAN and NUR ALIATININGTYAS.

Discrete logarithm problem represents a problem which is defined as modular arithmetic. It is often used to generate a key pair on public key cryptography as security object. Given cyclic group Gof order n, generator of G, and ∈ , then,

in general, discrete logarithm problem is determined as the integer , −, such that mod . In Menezes et al.(1997) the algorithm to

solve the discrete logarithm problem in common cyclic group G are Exhaustive Search algorithm, Baby-Step Giant-Step, Pollard's rho, Pohlig Hellman and Index Calculus. Furthermore, these algorithms are explored to determine the solution of discrete logarithm problem on . The reconstructed algorithms are implemented using Maple 11 software. These implementation can be used to measure security level of cryptography algorithm, which is based on security aspects of discrete logarithm problem.

(4)

RINGKASAN

YANA. Eksplorasi Masalah Logaritma Diskret Pada Finite Field . Dibimbing oleh SUGI GURITMAN dan NUR ALIATININGTYAS.

= ℤ [ ]/ adalah field berorder dengan adalah polinomial irredusibel atas ℤ berderajad . Setiap ∈ dapat dinyatakan secara unik dalam bentuk = + + + + , dimana ∈ ℤ , −. ∗= \{ }adalah grup di bawah operasi penjumlahan dan perkalian modulo 2.

Jika diberikan grup siklik ∗ berorder , generator ∗, ∈ ∗_{, dan} _{adalah polinomial irredusibel atas}_ℤ _{. Logaritma diskret} dengan basis adalah integer unik , −, sedemikian sehingga mod , dan bagaimana menentukan disebut masalah logaritma diskret.

Dalam Menezes et al. (1997) lima algoritme untuk menyelesaikan masalah logaritma diskret pada grup siklik umum adalah Algoritme Exhaustive Search,

Baby-Step Giant-Step, Pollard’s rho, Pohlig Hellmandan Index Calculus. Kelima algoritme ini dieksplorasi untuk menentukan masalah logaritma diskret pada

∗_.

Ide dasar Algoritme Exhaustive Search untuk menentukan logaritma diskret adalah Definisi Masalah Logaritma Diskret, yaitu dengan mencoba setiap kemungkinan nilai , − , sampai ditemukan yang benar.

Baby-Step Giant-Step adalah merupakan time-memory trade-off dari Algoritme Exhaustive Search yakni situasi dimana memori komputer digunakan untuk mengurangi biaya dan waktu eksekusi program. Representasi polinomial akan disimpan di memori komputer sebanyak √ , adalah order ∗. Semakin besar maka representasi polinomial yang disimpan di memori komputer semakin banyak juga. Ide dasar algoritme ini adalah membagi dengan suatu representasi polinomial , =√ , hingga ditemukan salah satu representasi polinomial yang disimpan di memori komputer.

Ide dasar Algoritme Pollard’s rhoadalah menemukan cycle dalam barisan { , , , … , }. Untuk menemukan cycle dalam barisan { , , , … , } digunakan Algoritme Floyd’s Cycle-Finding dengan membandingkan elemen-elemen sampai sehingga pasangan = ditemukan. Selanjutnya Birthday Paradox digunakan untuk menjamin bahwa mulai adanya satu atau lebih bilangan yang sama dalam barisan bilangan sedikitnya setelah langkah ke-√ √ ln dengan peluang lebih dari setengah.

Misalkan ∗ adalah grup siklik dibawah operasi perkalian berorder = − , =∏ , adalah bilangan prima berbeda dan . Ide dari Algoritme Pohlig Hellman untuk menentukan masalah logaritma diskret

(5)

Kekuatan Algoritme Index Calculus terletak pada faktorisasi polinomial. Faktorisasi polinomial dapat dilakukan dalam 4 tahap. Tahap pertama adalah faktorisasi bebas kuadrat, kedua faktorisasi bebas kuadrat berderajad , ketiga faktorisasi berderajad , dan terakhir faktorisasi lengkap

= … . Ide dasar Algoritme Index Calculus adalah dengan memilih subset dari ∗ sebagai faktor basis sedemikian sehingga elemen-elemen ∗ secara efisien dapat dinyatakan sebagai produk elemen-elemen .

(6)

© Hak Cipta milik IPB, tahun 2009

Hak Cipta dilindungi Undang-Undang

1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumber.

a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah

b. Pengutipan tidak merugikan kepentingan yang wajar IPB

(7)

EKSPLORASI MASALAH LOGARITMA DISKRET

PADA FINITE FIELD

Y A N A

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Program Studi Matematika Terapan

(8)

(9)

Judul Tesis : Eksplorasi Masalah Logaritma Diskret pada Finite Field

Nama : Yana

NRP : G551070411

Disetujui Komisi Pembimbing

Dr. Sugi Guritman Dra. Nur Aliatiningtyas, M.Si.

Ketua Anggota

Diketahui

Ketua Progam Studi Dekan Sekolah Pascasarjana Matematika Terapan

Dr. Ir. Endar H. Nugrahani, M.S. Prof. Dr. Ir. Khairil A. Notodiputro, M.S.

(10)

PRAKATA

Puji dan syukur penulis panjatkan ke hadirat Allah SWT atas segala rahmat dan karuniaNya tugas akhir yang berjudul “Eksplorasi Masalah Logaritma Diskret pada Finite Field ” ini bisa terselesaikan sebagai salah satu syarat untuk menyelesaikan pendidikan pada Program Studi Matematika, Sekolah Pascasarjana Institut Pertanian Bogor.

Terimakasih yang mendalam penulis sampaikan kepada Abah dan Mama atas segala doa dan kasih sayangnya. Terimakasih juga penulis sampaikan kepada Dr. Sugi Guritman dan Dra. Nur Aliatiningtyas, M.Si selaku pembimbing yang telah membantu dan mengarahkan penulis selama penyusunan tugas akhir ini, serta Drs. Prapto Tri Supriyo, M.Kom. selaku dosen penguji. Ucapan terima kasih juga penulis sampaikan kepada Departemen Agama Republik Indonesia yang telah memberikan beasiswa kepada penulis selama menempuh pendidikan di IPB. Terimakasih juga penulis sampaikan kepada Ai Tusi Fatimah, Salamia, Lathifaturrahmah dan semua pihak yang tidak dapat dituliskan namanya satu persatu atas segala bantuannya selama penelitian. Tentu saja dari awal hingga selesainya tulisan ini tidak terlepas dari dukungan, motivasi dan doa dari suami tercinta dan semua keluarga.

Akhirnya penulis menyadari bahwa tugas akhir ini masih begitu banyak kekurangan. Dengan segala keterbatasan yang ada, semoga tugas akhir ini bermanfaat.

Bogor, Agustus 2009

(11)

EKSPLORASI MASALAH LOGARITMA DISKRET

PADA FINITE FIELD

Y A N A

(12)

PERNYATAAN MENGENAI TUGAS AKHIR DAN SUMBER INFORMASI

Dengan ini saya menyatakan bahwa tesis dengan judul “Eksplorasi Masalah Logaritma Diskret pada Finite Field ” adalah karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Bogor, Agustus 2009

Yana

(13)

ABSTRACT

YANA. The Exploration of Discrete Logarithm Problem over Finite Field . Under direction of SUGI GURITMAN and NUR ALIATININGTYAS.

Discrete logarithm problem represents a problem which is defined as modular arithmetic. It is often used to generate a key pair on public key cryptography as security object. Given cyclic group Gof order n, generator of G, and ∈ , then,

in general, discrete logarithm problem is determined as the integer , −, such that mod . In Menezes et al.(1997) the algorithm to

solve the discrete logarithm problem in common cyclic group G are Exhaustive Search algorithm, Baby-Step Giant-Step, Pollard's rho, Pohlig Hellman and Index Calculus. Furthermore, these algorithms are explored to determine the solution of discrete logarithm problem on . The reconstructed algorithms are implemented using Maple 11 software. These implementation can be used to measure security level of cryptography algorithm, which is based on security aspects of discrete logarithm problem.

(14)

RINGKASAN

YANA. Eksplorasi Masalah Logaritma Diskret Pada Finite Field . Dibimbing oleh SUGI GURITMAN dan NUR ALIATININGTYAS.

= ℤ [ ]/ adalah field berorder dengan adalah polinomial irredusibel atas ℤ berderajad . Setiap ∈ dapat dinyatakan secara unik dalam bentuk = + + + + , dimana ∈ ℤ , −. ∗= \{ }adalah grup di bawah operasi penjumlahan dan perkalian modulo 2.

Jika diberikan grup siklik ∗ berorder , generator ∗, ∈ ∗_{, dan} _{adalah polinomial irredusibel atas}_ℤ _{. Logaritma diskret} dengan basis adalah integer unik , −, sedemikian sehingga mod , dan bagaimana menentukan disebut masalah logaritma diskret.

Dalam Menezes et al. (1997) lima algoritme untuk menyelesaikan masalah logaritma diskret pada grup siklik umum adalah Algoritme Exhaustive Search,

Baby-Step Giant-Step, Pollard’s rho, Pohlig Hellmandan Index Calculus. Kelima algoritme ini dieksplorasi untuk menentukan masalah logaritma diskret pada

∗_.

Ide dasar Algoritme Exhaustive Search untuk menentukan logaritma diskret adalah Definisi Masalah Logaritma Diskret, yaitu dengan mencoba setiap kemungkinan nilai , − , sampai ditemukan yang benar.

Ide dasar Algoritme Pollard’s rhoadalah menemukan cycle dalam barisan { , , , … , }. Untuk menemukan cycle dalam barisan { , , , … , } digunakan Algoritme Floyd’s Cycle-Finding dengan membandingkan elemen-elemen sampai sehingga pasangan = ditemukan. Selanjutnya Birthday Paradox digunakan untuk menjamin bahwa mulai adanya satu atau lebih bilangan yang sama dalam barisan bilangan sedikitnya setelah langkah ke-√ √ ln dengan peluang lebih dari setengah.

(15)

Kekuatan Algoritme Index Calculus terletak pada faktorisasi polinomial. Faktorisasi polinomial dapat dilakukan dalam 4 tahap. Tahap pertama adalah faktorisasi bebas kuadrat, kedua faktorisasi bebas kuadrat berderajad , ketiga faktorisasi berderajad , dan terakhir faktorisasi lengkap

= … . Ide dasar Algoritme Index Calculus adalah dengan memilih subset dari ∗ sebagai faktor basis sedemikian sehingga elemen-elemen ∗ secara efisien dapat dinyatakan sebagai produk elemen-elemen .

(16)

© Hak Cipta milik IPB, tahun 2009

Hak Cipta dilindungi Undang-Undang

1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumber.

a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah

b. Pengutipan tidak merugikan kepentingan yang wajar IPB

(17)

EKSPLORASI MASALAH LOGARITMA DISKRET

PADA FINITE FIELD

Y A N A

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Program Studi Matematika Terapan

(18)

(19)

Judul Tesis : Eksplorasi Masalah Logaritma Diskret pada Finite Field

Nama : Yana

NRP : G551070411

Disetujui Komisi Pembimbing

Dr. Sugi Guritman Dra. Nur Aliatiningtyas, M.Si.

Ketua Anggota

Diketahui

Ketua Progam Studi Dekan Sekolah Pascasarjana Matematika Terapan

Dr. Ir. Endar H. Nugrahani, M.S. Prof. Dr. Ir. Khairil A. Notodiputro, M.S.

(20)

PRAKATA

Puji dan syukur penulis panjatkan ke hadirat Allah SWT atas segala rahmat dan karuniaNya tugas akhir yang berjudul “Eksplorasi Masalah Logaritma Diskret pada Finite Field ” ini bisa terselesaikan sebagai salah satu syarat untuk menyelesaikan pendidikan pada Program Studi Matematika, Sekolah Pascasarjana Institut Pertanian Bogor.

Terimakasih yang mendalam penulis sampaikan kepada Abah dan Mama atas segala doa dan kasih sayangnya. Terimakasih juga penulis sampaikan kepada Dr. Sugi Guritman dan Dra. Nur Aliatiningtyas, M.Si selaku pembimbing yang telah membantu dan mengarahkan penulis selama penyusunan tugas akhir ini, serta Drs. Prapto Tri Supriyo, M.Kom. selaku dosen penguji. Ucapan terima kasih juga penulis sampaikan kepada Departemen Agama Republik Indonesia yang telah memberikan beasiswa kepada penulis selama menempuh pendidikan di IPB. Terimakasih juga penulis sampaikan kepada Ai Tusi Fatimah, Salamia, Lathifaturrahmah dan semua pihak yang tidak dapat dituliskan namanya satu persatu atas segala bantuannya selama penelitian. Tentu saja dari awal hingga selesainya tulisan ini tidak terlepas dari dukungan, motivasi dan doa dari suami tercinta dan semua keluarga.

Akhirnya penulis menyadari bahwa tugas akhir ini masih begitu banyak kekurangan. Dengan segala keterbatasan yang ada, semoga tugas akhir ini bermanfaat.

Bogor, Agustus 2009

(21)

RIWAYAT HIDUP

Penulis dilahirkan di Tambarangan, Banjarmasin pada tanggal 13 Juni 1977 sebagai anak pertama dari tiga bersaudara.

Pada tahun 2001 penulis menyelesaikan pendidikan strata satu di Program Studi Pendidikan Matematika, FKIP UNLAM Banjarmasin, dan langsung bekerja sebagai tenaga pengajar pada Madrasah Tsanawiyah Negeri Binuang sampai sekarang.

(22)

(23)

3.2.8.2 Solusi Masalah Logaritma Diskret pada

(24)

DAFTAR TABEL

Halaman 2.7.1 Oh-Besar ... 18 3.1.1 Elemen-elemen ... 21 3.2.1 Representasi Polinomial ( mod untuk ∗dengan

= + + + ... 25 3.2.2 Representasi Polinomial ( mod untuk ∗dengan

= + + + + ……….. 30

3.2.3 Hasil Perhitungan _{, :} _mod , untuk ∗

dengan = + + + + ………..… 31

dengan = + + + + ………..… 34

dengan = + + + + ……….. 38

3.2.6 Hasil Perhitungan , mod , untuk ∗

dengan = + + + + ……….. 41

3.2.7 Hasil Perhitungan Birthday Paradox ………... 44 3.2.8 Beberapa Kemungkinan Pendefinisian Keanggotaan Himpunan

⊆ ∗_, _{= , ,} _{untuk Algoritme}_{Pollard’s rho}_... ₄₆ 3.2.9 Hasil Perhitungan , , , , , , pada ∗dengan

= + + dan = ………... 49

3.2.10 Hasil Perhitungan , , , , , , pada ∗dengan

= + + dan = = + ……… 50

= + + dan = = + + + + ……. 51

= + dan = = + ………. 52

= + dan = = + + ……… 53

(25)

= + dan = ……… 53 3.2.15 Hasil Perhitungan , ℎ , dan , dengan

= + + + ………... 69

(26)

DAFTAR ALGORITME

(27)

DAFTAR LAMPIRAN

(28)

BAB I

PENDAHULUAN

1.1 Latar Belakang

Logaritma adalah suatu operasi matematika kebalikan dari eksponen atau pemangkatan. Logaritma sering digunakan untuk memecahkan persamaan yang pangkatnya tidak diketahui. Dalam persamaan = , dapat dicari dengan

pengakaran, dengan logaritma, dan dengan pemangkatan. Contoh, berapakah pada persamaan = . dapat dihitung atau dicari dengan menggunakan tabel atau kalkulator yang sudah dilengkapi fitur , hasilnya adalah = . Bentuk persamaan = ini adalah suatu sistem aritmetik bilangan nyata (ℝ), sistem aritmetik umum lainnya adalah grup siklik.

Struktur aljabar dengan operasi biner ∗ yang memenuhi sifat assosiatif, terdapat unsur identitas dan setiap unsurnya memiliki invers disebut grup. Suatu grup yang mempunyai generator disebut grup siklik. Generator ini berperan dalam membangkitkan unsur-unsur grup siklik . Misalkan adalah generator grup siklik , berorder , maka = = { , , , … , = , … , }. Pada kasus = , disebut logaritma diskret. Jika diketahui dan , maka masalah bagaimana menentukan dikenal dengan istilah masalah logaritma diskret.

Masalah logaritma diskret merupakan masalah yang didefinisikan pada aritmetika modular, sering dijadikan dasar pembangkitan sepasang kunci pada kriptografi kunci publik sebagai tumpuan keamanan. Contohnya pada pertukaran kunci Diffie-Hellman dan enkripsi Elgamal. Logaritma umum pasti akan tuntas secara komputasi, tetapi untuk logaritma diskret khusus berorder besar menentukannya tidak akan layak hitung (sulit dihitung) walaupun menggunakan kalkulator yang canggih. Tidak layak hitung itulah yang menyebabkan masalah logaritma diskret layak digunakan sebagai tumpuan keamanan dalam kriptogafi. Masalah logaritma diskret sering diterapkan pada grup siklik ℤ ∗, prima.

(29)

generator dari ∗, maka untuk sembarang ∈ ∗terdapat suatu yang khas pada rentang − sedemikian sehingga :

mod = ℤ [ ]/ adalah field dibawah operasi penjumlahan dan perkalian dalam modulo berorder , dengan polinomial irredusibel atas ℤ . ∗ _{adalah field} _{tanpa elemen {0} membentuk grup dibawah} operasi perkalian berorder − (Menezes et al. 1997). Elemen-elemen grup multiplikatif ∗ dengan generator dalam bentuk representasi grup siklik adalah , , , … , = , … , .

Menentukan masalah logaritma diskret menjadi sulit apabila digunakan grup ∗ dengan order besar. Karena itu diperlukan suatu teknik tertentu untuk menyelesaikannya. Beberapa teknik yang dapat digunakan untuk menentukan masalah logaritma diskret ini adalah Algoritme Exhaustive Search,

Baby-Step Giant-Step, Pollard’s rho,Pohlig Hellman, dan Index Calculus. Dalam Menezes et al. (1997) kelima algoritme tersebut dikenakan pada grup siklik umum. sedangkan pada tulisan ini dikenakan pada sistem aritmatik grup multiplikatif ∗.

Ide dasar Algoritme Exhaustive Search untuk menentukan logaritma diskret adalah Definisi Masalah Logaritma Diskret, yaitu dengan mencoba setiap kemungkinan nilai , − , sampai ditemukan yang benar. Algoritme ini tidak efisien digunakan untuk grup multiplikatif ∗ berorder besar.

(30)

digunakan Algoritme Floyd’s Cycle-Finding dengan membandingkan elemen-elemen sampai sehingga pasangan = ditemukan. Selanjutnya

Birthday Paradox digunakan untuk menjamin bahwa mulai adanya satu atau lebih bilangan yang sama dalam barisan bilangan sedikitnya setelah langkah ke-√ ke-√ ln dengan peluang lebih dari setengah.

log mod adalah menemukan mod , dengan terlebih dahulu menentukan mod ,untuk setiap , , menggunakan Teorema Sisa Cina. Artinya komputasi dilakukan pada subgrup berorder prima berpangkat integer positif ( .

Kekuatan Algoritme Index Calculus terletak pada faktorisasi polinomial, idenya adalah dengan memilih subset dari ∗ sebagai faktor basis sedemikian sehingga elemen-elemen ∗ secara efisien dapat dinyatakan sebagai produk elemen-elemen .

Algoritme Exhaustive Search, Baby-Step Giant-Step, Pollard’s rho, Pohlig Hellman, dan Index Calculus dieksplorasi untuk menentukan masalah logaritma diskret pada grup multiplikatif ∗ dan diimplementasikan dengan bantuan sofware Maple 11.

1.2 Tujuan Penelitian

Tujuan penelitian ini adalah :

1. Mengkaji secara teoritik masalah logaritma diskret pada finite field . 2. Merekonstruksi algoritme-algoritme yang berhubungan dengan masalah

logaritma diskret pada finite field .

(31)

1.3 Manfaat Penelitian

(32)

BAB II

TINJAUAN PUSTAKA

Pada bab ini dituliskan beberapa aspek teoritis berupa definisi, teorema dan sifat-sifat yang berhubungan dengan teori bilangan, integer modulo , aljabar abstrak, masalah logaritma diskret, sistem persamaan linear, dan kompleksitas waktu asimptotik sebagai landasan teori untuk penulisan tugas akhir ini.

2.1 Teori Bilangan

Definisi 2.1.1 Misalkan , integer. membagi (notasi | jika terdapat integer sedemikian sehingga = .

Definisi 2.1.2Jika dan adalah integer dengan , maka pembagian oleh menghasilkan integer (hasil pembagian) dan (sisa pembagian) sehingga = +, dimana . Sisa pembagian dinotasikan mod dan hasil pembagian dinotasikan div (Menezes et al. 1997).

Definisi 2.1.3 Suatu integer dikatakan sebagai pembagi bersama dari dan , jika | dan | (Menezes et al. 1997).

Definisi 2.1.4 Suatu integer non-negatif disebut pembagi bersama terbesar

(gcd) dari integer dan , dinotasikan = gcd , , jika : 1. adalah pembagi bersama dari dan

2. jika | dan |, maka | (Menezes et al. 1997).

Teorema 2.1.5 (Algoritme Euclidean) Diberikan integer , >. Berdasarkan algoritme pembagian, dapat dibentuk barisan persamaan berikut :

= + , < < = + , < <

= + , < <

(33)

dengan = gcd , , yang merupakan sisa terakhir tak nol dari proses pembagian. Nilai dari dan dari , = + dapat diperoleh dengan menuliskan setiap sebagai kombinasi linear dari dan (Lestari 2007).

Definisi 2.1.6 Integer dan dikatakan prima relatif atau koprima jika gcd , = (Lestari 2007).

Definisi 2.1.7 (Fungsi-∅ Euler) Untuk , didefinisikan ∅ adalah banyaknya integer pada selang [ , ]yang prima relatif dengan . Fungsi ∅ disebut fungsi-∅Euler (Menezes et al. 1997).

Teorema 2.1.8 (Sifat-sifat fungsi-∅Euler) 1. Jika prima, maka ∅ = − .

2. Fungsi-∅ Euler bersifat multiplikatif. Artinya, jika gcd , = maka

∅ = ∅ ∅

3. Jika = … adalah faktorisasi prima dari , maka ∅ = − − − (Menezes et al. 1997).

Fakta 2.1.9 (Teorema Dasar Aritmetika)Setiap integer dapat difaktorkan sebagai produk dari kuasa prima yang khas: = … , dimana

adalah bilangan prima yang berbeda dan adalah integer positif (Menezes et al. 1997).

2.2 Integer Modulo

Definisi 2.2.1 (Kongruensi) dan adalah integer. dikatakan kongruendengan modulo , ditulis mod , jika membagi habis − . Selanjutnya disebut modulus kongruensi(Menezes et al. 1997).

Teorema 2.2.2 (Syarat-syarat Kekongruenan)Untuk semua , , , , ∈ ℤ, hal-hal di bawah ini adalah benar.

1) mod jika dan hanya jika dan mempunyai sisa yang sama jika dibagi dengan .

(34)

3) (simetri) Jika mod maka mod .

4) (transitif) Jika mod dan mod , maka mod .

5) Jika mod dan mod , maka + + mod

dan mod (Guritman et al. 2004).

Definisi 2.2.3 Integer modulo , dinotasikan ℤ , adalah himpunan (kelas ekuivalensi) integer { , , , … , − }yang dikenai operasi penjumlahan dan perkalian diperlakukan dalam modulo . Untuk , , ∈ ℤ,

+ = ⇔ + mod

= ⇔ mod (Guritman et al. 2004). Definisi 2.2.4 (Sistem Residu Lengkap Modulo )Jika mod , maka disebut residu dari modulo . Selanjutnya himpunan = { , , … , } dinamakan sistem residu lengkap modulo jika untuk setiap integer terdapat satu dan hanya satu sedemikian sehingga mod (Lestari 2007).

Definisi 2.2.5 (Sistem Residu Tereduksi Modulo ) Sistem residu tereduksi modulo adalah himpunan integer , dimanagcd , = , , jika ≠. Selanjutnya setiap yang prima relatif dengan , kongruen dengan suatu pada himpunan tersebut (Lestari 2007).

Fakta 2.2.6 (Invers) Misalkan ∈ ℤ. memiliki invers jika dan hanya jika gcd , = (Menezes et al. 1997).

Definisi 2.2.7 (Invers Multiplikatif)Misalkan ∈ ℤ, Invers multiplikatifdari modulo adalah suatu integer ∈ ℤ sehingga mod . Faktanya tidak semua anggota ℤ mempunyai invers ( belum tentu ada). Dalam hal yang bersangkutan ada, maka disebut invertibel dan disebut invers dari , dinotasikan = (Guritman et al. 1997).

(35)

Definisi 2.2.9Grup multiplikatif ℤ adalah ℤ ∗= { ∈ ℤ | gcd , = }. Jika bilangan prima, maka ℤ ∗= { | − }(Menezes et al. 1997).

Teorema 2.2.10 (Solusi Persamaan kongruen) Misal = gcd , . Persamaan kongruen mod mempunyai solusi jika dan hanya jika membagi , dalam hal ini terdapat tepat solusi antara 0 dan − ; solusi ini semua kongruen modulo / (Menezes et al. 1997).

Teorema 2.2.11 (Teorema Sisa Cina)Jika , , … , merupakan integer yang prima relatif satu sama lain, , , … , adalah sembarang integer, maka sistem kongruensi

mod mod

mod

… … ∗

mempunyai solusi unik modulo , = … (Menezes et al. 1997).

Algoritme 2.2.12 (Algoritme Gauss’s)Solusi dari sistem kongruensi Teorema 2.2.11 dapat dihitung sebagai =∑ mod , dimana = ⁄ dan

= mod (Menezes et al. 1997).

Teorema 2.2.13Misalkan adalah integer.

(i) (Teorema Euler)Jika ∈ ℤ∗, maka ∅ mod .

(ii) Jika adalah produk bilangan prima berbeda, dan jika mod ∅ , maka mod , untuk semua integer (Menezes et al. 1997).

Teorema 2.2.14Misalkan prima,

1. (Teorema Fermat)Jika gcd , = , maka mod . 2. Jika mod −, maka mod , untuk semua integer . 3. Untuk setiap integer , mod (Menezeset al.1997).

2.3 Struktur Aljabar

(36)

, → ∗. Karena ∗ juga berada dalam maka dikatakan tertutup di bawah operasi ∗(Aliatiningtyas 2002).

Definisi 2.3.2 (Grup)Struktur aljabar dengan operasi biner ∗disebut grupjika memenuhi aksioma-aksioma berikut ini,

1. operasi ∗bersifat assosiatif ∗ ∗ = ∗ ∗ , ∀ , , ∈.

2. ada unsur identitas ∈ , untuk ∗ pada sehingga berlaku

∗ = ∗ =, ∀ ∈ .

3. untuk setiap ∈ ada unsur ∈ sehingga ∗ = ∗ = (Aliatiningtyas 2002).

Definisi 2.3.3 Grup disebut grup komutatif jika operasi ∗ bersifat komutatif yaitu ∀ , ∈, ∗ = ∗(Aliatiningtyas 2002).

Definisi 2.3.4 (Grup Hingga dan Order)Suatu grup dikatakan berhingga jika banyaknya unsur berhingga. Banyaknya unsur dari grup hingga dinamakan order dari , dinotasikan ℴ (Aliatiningtyas 2002).

Definisi 2.3.5 (Order dari Unsur Grup)Misalkan grup, dan ∈ . Order (notasi ℴ adalah integer positif minimal sehingga = . Jika tidak ada bilangan yang demikian, maka dikatakan order dari tak hingga atau nol (Aliatiningtyas 2002).

Toerema 2.3.6Berikut ini 3 sifat dasar yang berkaitan dengan pengertian order. 1. Misalkan grup, ∈ dan ℴ = , maka ada tepat kuasa dari yaitu

= , , , … , yang semuanya berbeda.

2. Misalkan grup, ∈ . Jika ℴ tak hingga, maka semua kuasa dari berbeda. Artinya, jika dan adalah dua integer yang berbeda, maka

≠ .

(37)

Definisi 2.3.7 (Subgrup)Misalkan grup dan ⊆ . Maka disebut subgrup

dari jika grup dibawah operasi biner yang sama dengan operasi biner pada . (Notasi : ⊴ ) (Aliatiningtyas 2002).

Definisi 2.3.8 (Grup Siklik) Suatu grup dikatakan siklik jika dan hanya jika ada unsur ∈ ( disebut generator) sedemikian sehingga

= = ∈ ℤ}(Guritman 2004).

Teorema 2.3.9Jika grup berorder , maka adalah siklik jika dan hanya jika ada ∈ sehingga ℴ = (Guritman 2004).

Teorema 2.3.10 (Teorema Lagrange’s) Jika grup hingga dan adalah subgrup , maka order dari membagi order dari (Menezes et al. 1997; Aliatiningtyas 2002).

Definisi 2.3.11 (Ring)Struktur aljabar , +,∙ dengan operasi + disebut operasi penjumlahan dan operasi ∙disebut operasi perkalian, disebut ring jika memenuhi aksioma-aksioma berikut ini.

1. , +grup komutatif.

2. Operasi perkalian bersifat assosiatif.

3. Hukum distributif kiri berlaku : ∀ , , ∈ , + = + . Hukum distributif kanan berlaku : ∀ , , ∈ , + = +.

Unsur identitas terhadap + dinotasikan dengan 0 dan disebut unsur nol. Selanjutnya,

1. Jika operasi perkalian bersifat komutatif, ∀ , ∈, = maka disebut

ring komutatif.

2. Jika ada unsur identitas dibawah operasi perkalian (unsur ini disebut unsur

kesatuan, dinotasikan dengan 1 dan disingkat unkes) ∀ ∈ , ∃ ∈ , ∙ = ∙ = maka disebut ring dengan unsur kesatuan

(Aliatiningtyas 2002).

Definisi 2.3.12 Misalkan ring. Himpunan bagian dari ring disebut subring

(38)

Definisi 2.3.13 (Ideal)Misal ring, ⊆ , tidak kosong. Himpunan bagian disebut idealjika memenuhi :

a. , ∈ − .∈

b. ∈ dan ∈ ∈dan ∈(Aliatiningtyas 2002).

Teorema 2.3.14 (Ideal Utama) Misalkan ring komutatif dengan unsur kesatuan 1 dan ∈ . Suatu himpunan dilambangkan , yang didefinisikan sebagai = { | ∈ }merupakan ideal. Ideal yang demikian disebut ideal utama yang dibangun oleh (Rosdiana 2009).

Definisi 2.3.15 Misalkan ring, ideal dari , maka koset-koset aditif dari adalah + dengan ∈ . Definisikan / = { + | ∈ }. Operasi penjumlahan dan perkalian didefinisikan :

+ + + = + +

+ + = + (Aliatiningtyas 2002). Teorema 2.3.16 / , +,∙merupakan ring dan disebut ring faktor dari oleh (Aliatiningtyas 2002).

Definisi 2.3.17Fungsi dari ring Rke ring R’disebut homomorfisma jika ∀a,b

∈R, berlaku

(a + b) = (a) + (b) (ab) = (a) (b)

Kernel = { x∈ R | (x) = 0’}, 0’unsur nol dari . Jika ada homomorfisma ’ yang bijektif dari Rke R’, maka dikatakan Risomorfik dengan R’, dinotasikan : R

≃R’(Aliatiningtyas 2002).

Teorema 2.3.18Misalkan θ:R → R’adalah homomorfisma ring. Maka 1. θ(R) subring dari R’

2. Ker θadalah ideal dari R

3. Jika Nideal dari R, maka θ(N) juga ideal dari R’(Aliatiningtyas 2002). Definisi 2.3.19 (Polinomial) Jika ring komutatif, maka polinomial dengan parameter atas diekspresikan dalam bentuk :

(39)

dimana ∈ dan . disebut koefisien dari dalam . Integer terbesar pada ≠ disebut derajad , dinotasikan deg dan disebut koefisien utama (leading coeffisien) dari . Jika = (polinomial konstan) dan ≠ , maka mempunyai derajad 0. Jika semua koefisien adalah 0, maka disebut polinomial nol dan derajadnya dinotasikan −∞.

Polinomial dikatakan monik jika koefisien utamanya 1 (Menezes et al. 1997).

Definisi 2.3.20ℤ [x] adalah himpunan semua polinomial dalam peubah xdengan koefisien dalam ring ℤ merupakan sebuah ring di bawah operasi penjumlahan dan perkalian polinomial (Fraleigh 2000).

Definisi 2.3.21 (Polinomial Irredusibel) Misal ∈ ℤ[ ]adalah polinomial berderajad paling kecil 1. dikatakan irredusibel atas ℤ jika f(x) tidak dapat dinyatakan sebagai produk dari dua polinomial berderajad lebih kecil dari f(x)

dalam ℤ [ ]. Dan dikatakan redusibel jika faktorisasinya ada (Menezes et al. 1997).

Definisi 2.3.22 Misal polinomial tak-nol , ℎ ∈ ℤ [ ]. Maka dari dan ℎ , dinotasikan gcd , ℎ , adalah polinomial monik berderajad terbesar dalam ℤ [ ]yang membagi dan ℎ (Menezes et al.

1997).

Teorema 2.3.23 (Teorema Faktor) Jika ℤ adalah ring komutatif dengan unsur kesatuan dan ∈ ℤ[ ] berderajad , maka = jika dan hanya jika

− adalah faktor dari (Michaels 2000).

Definisi 2.3.24 (Field)Suatu ring yang komutatif, ada unkes dan setiap unsur tak nolnya mempunyai invers (multiplikatif) disebut lapangan (field) (Aliatiningtyas 2002).

Definisi 2.3.25 (Subfield) Jika field memuat field (sedemikian sehingga operasi penjumlahan dan perkalian di sama dengan di ), maka disebut

(40)

Definisi 2.3.26 (Finite Field)Suatu field dikatakan berhingga (finite field) jika himpunannya memiliki banyak elemen yang berhingga. Order adalah banyaknya anggota (Menezes et al. 1997).

Teorema 2.3.27Eksistensi dan kekhasan finite field.

1. Jika F adalah finite field maka F terdiri dari unsur dengan p prima dan .

2. Untuk setiap prima berorder pm, ada finite fieldyang khas berorder pm. Field

ini dinotasikan dengan GF(pm) (Menezes et al. 1997).

Teorema 2.3.28Misal bilangan prima. Himpunan integer modulo berbentuk field berorder dinotasikan dengan atau ℤ (Rosdiana 2009).

Teorema 2.3.29 Unsur tak-nol membentuk sebuah grup di bawah operasi perkalian disebut grup perkalian dari , dinotasikan dengan

∗_(Menezes_{et al}_{. 1997).}

Teorema 2.3.30 ∗ adalah grup siklik yang berorder − dan berlaku = , untuk setiap ∈ (Menezes et al. 1997).

Teorema 2.3.31 Finite field adalah perluasan field ℤ berderajad , dan setiap elemen adalah akar polinomial − atas ℤ (Saeki 1997).

Teorema 2.3.32 Misalkan ℤ adalah field dan misalkan adalah polinomial tak-konstan di ℤ [ ]. Maka ada perluasan field dari ℤ dan ada ∈ sedemikian sehingga = (Fraleigh 2000).

Definisi 2.3.33 adalah perluasan field ℤ . ∈ disebut algebraicatas ℤ jika = untuk beberapa polinomial tak-nol ∈ ℤ[ ]. Jika tidak algebraic

atas ℤ , maka transcendental atas ℤ (Fraleigh 2000).

(41)

Definisi 2.3.35 Suatu polinomial irredusibel ∈ ℤ[ ]berderajad disebut polinomial primitif jika adalah generator dari ∗(Menezes et al. 1997). Definisi 2.3.36Misal Eperluasan fielddari field ℤ dan c ∈E algebraicatas ℤ . Polinomial irreducible untuk c atas ℤ dari polinomial monik ( ) dinotasikan dengan irr(c, ℤ ) dan derajad dari polinomial irreducible untuk c atas ℤ dinotasikan dengan deg(c, ℤ ) (Rosdiana 2009).

Teorema 2.3.37 Misal = ℤ dengan ∈ algebraic atas ℤ , dan deg , ℤ = , . Setiap unsur dari = ℤ dapat dinyatakan secara unik dalam bentuk = + + + , dimana ∈ ℤ (Rosdiana 2009).

Teorema 2.3.38 Diberikan polinomial irredusibel ∈ ℤ [ ]

berderajad dan = , ≅ ℤ [ ]/ ≅ ℤ ≅ { +

+ + | ∈ ℤ untuk semua }(Michaels 2000).

Definisi 2.3.39 (Ruang Vektor) Misal di bawah operasi penjumlahan abelian grup, field. Pada V didefinisikan aturan penjumlahan dan aturan perkalian skalar. disebut ruang vektor atas jika memenuhi aksioma berikut.

1. Untuk setiap ∈ dan setiap ⃗ ∈ terdapat tunggal ⃗ ∈ sehingga tertutup terhadap perkalian : ⃗ =⃗.

2. Untuk setiap ∈ dan setiap ⃗,⃗ ∈ , ⃗ +⃗ = ⃗ +⃗. 3. Untuk setiap , ∈ dan setiap ⃗ ∈ , + ⃗ = ⃗ +. ⃗ 4. Untuk setiap , ∈ dan setiap ⃗ ∈ , ⃗ = ⃗.

5. Untuk setiap ⃗ ∈ , ⃗ = ⃗; 1 unsur identitas di ,∙(Rosdiana 2009).

Definisi 2.3.40 Misalkan V adalah ruang vektor atas skalar , dan misalkan

A= {v1, v2, ..., vn} adalah himpunan yang terdiri atas nvektor dalam V. Adisebut

bebas linearjika

∑n c_i

i vi = ⇒ ∀i∈I= {1,2,…,n} ci = .

Ingkarannya, Adisebut terpaut linear jika ∑n c_i

(42)

Definisi 2.3.41 Misalkan V adalah ruang vektor atas , dan = { , , … , } adalah himpunan berhingga vektor-vektor di dalam V. Untuk menyatakan bahwa

V adalah ruang yang direntang oleh vektor-vektor pada himpunan B dituliskan = .Artinya ∀ ∈ , =∑ , adalah integer.

Definisi 2.3.42 Misalkan V adalah ruang vektor atas , dan B adalah himpunan berhingga vektor-vektor di dalam V. Dikatakan B adalah basis untuk V jika B

bebas linear dan V=B (Guritman 2005).

Teorema 2.3.43 Misal perluasan field dari field ℤ dan ∈ algebraic atas ℤ . Jika deg , ℤ = , maka ℤ ruang vektor atas ℤ berdimensi- dengan

basis{ , , , … , }(Rosdiana 2009). 2.4 Masalah Logaritma Diskret

Definisi 2.4.1 (Logaritma Diskret) Misalkan grup siklik berorder . generator , dan ∈ . Logaritma diskret dengan basis , dinotasikan log , adalah integer unik , −, sedemikian hingga = (Menezes et al. 1997).

Teorema 2.4.2 Misalkan generator grup siklik berorder , dan , ∈. Misal adalah sebuah integer. Maka log =log + log mod , dan log = log mod (Menezes et al. 1997).

Definisi 2.4.3 (Masalah Logaritma Diskret) Diberikan bilangan prima , generator dari ℤ ∗, dan ∈ ℤ∗. Masalah logaritma diskret adalah menentukan ,

−sehingga mod (Menezes et al. 1997).

Definisi 2.4.4 (Masalah Logaritma Diskret diperumum)Diberikan grup siklik berorder , generator , dan ∈ . Masalah logaritma diskret adalah menentukan , −, sehingga = (Menezes et al. 1997).

(43)

Teorema 2.4.6 Misalkan generator dari ℤ ∗, maka untuk setiap ∈ ℤ∗ terdapat integer yang khas pada rentang ∅ − sedemikian sehingga mod (Lestari 2007).

Teorema 2.4.7 Setiap unsur ∈ , prima, memenuhi = atau ekivalen dengan akar dari persamaan = sehingga − =∏ _∈ − (Rosdiana 2009).

Lemma 2.4.8 Andaikan adalah himpunan hingga dan diketahui ada fungsi : → . Dipilih ∈ untuk membangkitkan barisan , , , …, dengan menggunakan iterasi = untuk . Ada , ∈ sehingga = untuk ≠ dan ada > sehingga = . Jika barisan , , , … dibangkitkan oleh = menggunakan iterasi = untuk maka hasilnya akan sama dengan barisan , , , …(Safaat 2007).

Lemma 2.4.9 Andaikan bahwa , dan bilangan-bilangan , , … , bebas dipilih dari himpunan {1, 2, …, }. Peluang bahwa setiap bilangan berbeda adalah − − … − (Safaat 2007).

2.5 Sistem Persamaan Linear

Definisi 2.5.1 Suatu persamaan linear dalam peubah (variabel) adalah persamaan dengan bentuk

+ + + =

dimana , , …, dan adalah bilangan-bilangan real dan , , …, adalah peubah. Dengan demikian maka suatu sistem linear dari persamaan dalam peubah adalah satu sistem berbentuk :

+ + + =

(44)

Definisi 2.5.2 Suatu sistem persamaan linear dikatakan homogen jika konstanta-konstanta di ruas kanan semuanya nol. Sistem-sistem homogen selalu konsisten (Leon 1998).

Teorema 2.5.3 Sistem persamaan linear homogen × memiliki penyelesaian

taktrivialjika > (Leon 1998).

2.6 Algoritme Berlekamp’s Q-matrix

Algoritme 2.6.1 AlgoritmeBerlekamp’s Q-Matrix

Input : Polinomial monik bebas kuadrat berderajad dalam [ ]. Output : Faktorisasi dalam polinomial irredusibel monik.

1. Untuk setiap , −, hitung polinomial mod =

∑ , ∈ .

2. Bentuk matriks ×

3. Tentukan basis , , … , untuk ruang null pada matriks − , dengan matriks identitas × . Banyaknya faktor irredusibel pada adalah . 4. ← { }.

5. Untuk , lakukan langkah berikut :

5.1 Untuk setiap polinomial ℎ ∈ , degℎ > , lakukan langkah berikut Hitung gcd ℎ , − , untuk setiap ∈ , dan ganti ℎ pada

dengan semua polinomial hasil perhitungan gcd yang berderajad . 6. Hasilnya adalah polinomial-polinomial F yang berupa faktor-faktor

irredusibel (Menezes et al.1997).

2.7 Kompleksitas Waktu Asimptotik

(45)

untuk mengetahui kinerja algoritme. Kinerja algoritme akan tampak untuk besar, bukan pada kecil.

Langkah pertama dalam pengukuran kinerja algoritme adalah membuat makna sebanding. Gagasannya adalah dengan menghilangkan faktor koefisien di dalam ekspresi . Sebagai contoh, andaikan bahwa kompleksitas waktu terburuk dari sebuah algoritme adalah = + + . Untuk besar, pertumbuhan sebanding dengan , suku + menjadi tidak berarti dibandingkan . Suku-suku yang tidak mendominasi perhitungan pada rumus dapat diabaikan, sehingga kompleksitas waktu adalah (dengan mengabaikan koefisien 2), ditulis = .

Definisi 2.7.1 = (dibaca ” adalah ” artinya berorder paling besar ) bila terdapat konstanta C dan sedemikian sehingga

, untuk (Munir 2001).

Teorema 2.7.2 Bila = + + + + adalah

polinom derajad maka = (Munir 2001).

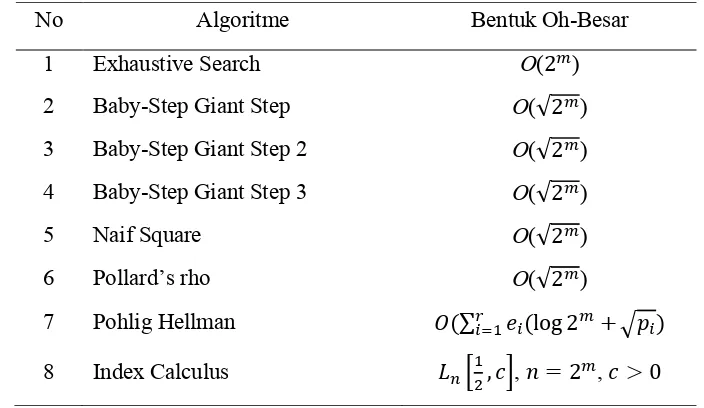
Setelah mendefinisikan fungsi untuk suatu algoritme, kemudian dengan Tabel Oh-Besar (Menezeset al. 1997) kita tentukan order dari sebagai ukuran efisiensi algoritme yang bersangkutan.

Dalam tabel berikut diberikan beberapa bentuk Oh-Besar yang sering muncul dalam aplikasi analisis algoritme (Guritman 2004). Urutan batasan lebih baik disusun dari atas ke bawah.

(46)

(47)

BAB III

HASIL DAN PEMBAHASAN

Pada bab ini akan dijelaskan hal-hal yang berhubungan dengan masalah logaritma diskret pada dan bagaimana mengeksplorasinya dengan menggunakan algoritme Exhaustive Search, Baby-Step Giant-Step, Pollard’s rho,

Pohlig-Hellman, dan Index Calculus.

3.1

MASALAH LOGARITMA DISKRET PADA FINITE FIELD

3.1.1 FINITE FIELD

Galois Field adalah nama populer untuk field dengan jumlah elemen terbatas (finite). Disebut Galois Field, sebagai penghargaan terhadap Evariste Galois yang menemukan hubungan antara grup dan persamaan polinomial. Galois Field dinotasikan , berorder , dengan prima dan integer positif. Jika = , maka menurut Teorema 2.3.28 (atau bisa juga dinotasikan ℤ adalah integer modulop berbentuk field berorder . Setiap operasi aritmetikanya dilakukan dalam modulo agar hasilnya tetap berada dalam daerah . Selanjutnya pembahasan akan difokuskan pada .

Berdasarkan Teorema 2.3.31 adalah perluasan field ℤ . Berdasarkan Definisi 2.3.20 ℤ [x] adalah himpunan semua polinomial dalam peubah x dengan koefisien dalam ℤ merupakan sebuah ring di bawah operasi penjumlahan dan perkalian polinomial. Misalkan polinomial tak konstan atas ℤ [ ], maka berdasarkan Teorema 2.3.32 ada ∈ sedemikian sehingga = . Jika ada seperti ini, maka disebut algebraic atas ℤ (Definisi 2.3.33). Selanjutnya berdasarkan Teorema 2.3.43, jika deg , ℤ = , maka ℤ merupakan ruang vektor atas ℤ berdimensi- dengan basis

{ , , , … . , , }.

(48)

dengan = { | ∈ ℤ[ ]}. Selanjutnya, berdasarkan Teorema 2.3.34ℤ [ ]/ adalah finite field berorder , dengan operasi penjumlahan dan perkalian polinomial dilakukan dalam modulo .

Dari uraian di atas dan berdasarkan Teorema 2.3.37 dan Teorema 2.3.38, jika diberikan polinomial irredusibel ∈ ℤ[ ]berderajad dan = ,

maka setiap ∈ ℤ dapat dinyatakan secara unik dalam bentuk

= + + + + , dimana ∈ ℤ , −, dan

≅ ℤ [ ]/ ≅ ℤ ≅{ + + + | ∈ ℤ

untuk semua }.

Contoh 1 (Finite Field )

= + + adalah polinomial irredusibel berderajad 4 atas ℤ , dan

= + + = = + , maka

= ℤ [ ]/

= { , , , , , , , , , , , , , , , }

= { , , , , , + , + , + , + + , + , + ,

+ + , + + , + + + , + + , + }

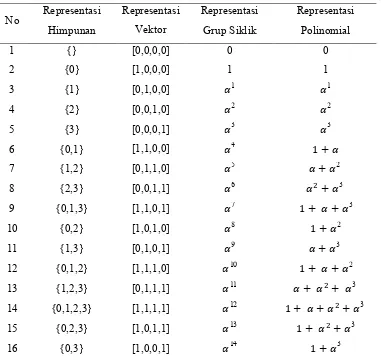
Dari uraian di atas, ada beberapa cara yang dapat dilakukan untuk merepresentasikan elemen-elemen , diantaranya adalah dengan representasi grup siklik, representasi polinomial, representasi vektor dan representasi himpunan.

1) Representasi grup siklik : 0, 0, 1, ..., , dengan adalah generator ∗_{, dimana} ∗₌ _{− { }}_.

2) Representasi polinomial dalam peubah : + + + + , dimana ∈ ℤ , −.

3) Representasi vektor : [ , , , ...], dengan ∈ ℤ 4) Representasi himpunan : { , , , ...}, dengan .

(49)

dengan representasi grup siklik dan representasi polinomial. Tabel 3.1.1 berikut memperlihatkan elemen-elemen dalam beberapa representasi.

Tabel 3.1.1 Elemen-elemen

(50)

Jika = + + + + , = + + + +

∈ . Maka . =, dimana s= + + + +

dengan = ∑ mod , −.

Penjumlahan dan perkalian dalam ini dihitung dengan menggunakan algoritme standar untuk integer dan aritmetika polinomial. Unsur identitas penjumlahannya adalah polinomial 0, dan unsur identitas perkaliannya

adalah polinomial 1. Pengurangan adalah invers dari penjumlahan; jika ∈ maka invers penjumlahan dari (dinotasikan − pada

adalah solusi unik untuk persamaan + = dalam . Selanjutnya, pembagian adalah invers dari perkalian; jika ∈ maka invers perkalian dari (dinotasikan pada adalah solusi unik untuk persamaan . = pada . Invers perkalian dalam dapat dihitung secara efisien dengan menggunakan Algoritme Euclidean yang Diperluas.

Dalam pembahasan selanjutnya akan dibahas tanpa elemen {0}, dinotasikan dengan ∗, membentuk grup di bawah operasi perkalian (Definisi 2.3.29).

3.1.2 MASALAH LOGARITMA DISKRET PADA ∗

Berdasarkan Teorema 2.3.30, ∗ adalah grup siklik yang berorder = − . Karena ∗ merupakan grup siklik maka terdapat suatu generator yang membangun ∗ yang disebut elemen primitif. Jika diberikan elemen primitif dari ∗ dan diketahui order dari ∗ adalah , maka ℴ = (Teorema 2.3.9), sehingga :

∗₌ _{= { , , , … ,} _}

dan berdasarkan Teorema 2.3.6 , , , … , semuanya berbeda.

Berdasarkan Definisi 2.4.1 dan Definisi 2.4.4, jika diberikan grup siklik ∗ _{berorder ,} _generator ∗_, _∈ ∗_{, dan} _adalah polinomial irredusibel atas ℤ . Logaritma diskret dengan basis adalah integer unik , −, sedemikian sehingga :

(51)

dan bagaimana menentukan disebut masalah logaritma diskret. Nilai pada rentang − yang merupakan solusi masalah logaritma diskret

mod dijamin ada (Teorema 2.4.6).

Menentukan masalah logaritma diskret menjadi sulit apabila order grup multiplikatif ∗ besar. Karena itu diperlukan suatu teknik tertentu untuk menyelesaikannya. Beberapa teknik yang dapat digunakan untuk menentukan masalah logaritma diskret ini adalah Algoritme Exhaustive Search, Baby-Step Giant-Step, Pollard’s rho, Pohlig Hellman, dan Index Calculus. Dalam Menezes

et el. (1997) kelima algoritme tersebut dikenakan pada grup siklik G umum, sedangkan pada tulisan ini dikenakan pada sistem aritmatik grup multiplikatif

∗_.

3.2 SOLUSI MASALAH LOGARITME DISKRET PADA ∗

Untuk menentukan masalah logaritma diskret diatas ada beberapa algoritme yang bisa digunakan, diantaranya adalah Algoritme Exhaustive Search,

Baby-Step Giant-Step, Pollard’s rho, Pohlig-Hellman dan Index Calculus. Algoritme untuk menentukan masalah logaritma diskret dalam Menezes et al.

(1997) dijelaskan secara umum dalam grup siklik berhingga berorder dengan generator , dan untuk pendekatan yang lebih konkrit dipilih grup multiplikatif ℤ ∗ berorder − dimana operasi grupnya adalah operasi perkalian modulo . Pada tulisan ini algoritme-algoritme tersebut dieksplorasi untuk menentukan masalah logaritma diskret pada ∗.

3.2.1 Solusi Masalah Logaritma Diskret pada ∗ dengan Algoritme Exhaustive Search

Ide dasar Algoritme Exhaustive Searchadalah Definisi Masalah Logaritma Diskret (Definisi 2.4.4).Misalkan adalah polinomial irredusibel atas ℤ dan

(52)

akan sama dengan dalam mod dinotasikan mod . Atau dengan bahasa sederhana untuk menentukan masalah logaritma diskret , kalikan dengan sampai ditemukan . Banyaknya langkah dalam proses perkalian ini

adalah , − .

. =

. = = Selama proses perkalian jika ditemukan , maka direduksi ke mod dan dalam proses reduksi berlaku aturan penjumlahan dan perkalian dalam

. Selanjutnya dari dan diperoleh : =

=

log = log

=

Jadi = mod .

Berikut Algoritme Exhaustive Search yang dieksplorasi dari Definisi Masalah Logaritma Diskret secara umum (Definisi 2.4.4)

Algoritme 3.2.1

Algoritme Exhaustive Search untuk menentukan masalah logaritma diskret pada

∗

Input : generator grup multiplikatif ∗berorder = − , ∈ ∗_{, dan} _{polinomial irredusibel atas}_ℤ _{berderajad .} Output : logaritma diskret log mod .

1) Untuk setiap , −, hitung nilai mod .

(53)

Dalam Menezes et al.(1997) nilai harapan kompleksitas waktu Algoritme

Exhaustive Search adalah . Algoritme Exhaustive Search ini diimplementasikan dengan bantuan sofware Maple 11, dapat dilihat pada Lampiran 3.1

Contoh 2 (Menentukan masalah logaritma diskret pada grup multiplikatif ∗_{dengan Algoritme}_{Exhaustive Search}₎

Diketahui : adalah generator grup multiplikatif ∗,

= + + + ∈ ∗_{, dan}

= + + .

Tentukan log mod . Solusi :

Grup multiplikatif ∗ dibangun oleh suatu polinomial berderajad 7 irredusibel atas ℤ . Diketahui adalah generator grup multiplikatif ∗. Perkalian dari elemen-elemen ∗ adalah perkalian dalam modulo , sehingga

mod

+ + mod

− − + mod ,

sebab − dalam ℤ .

Grup multiplikatif ∗ berorder = − = , artinya ada 127 kemungkinan nilai , , yang memenuhi mod .

Dengan Algoritme Exhaustive Search, akan dicari nilai sedemikian sehingga

+ + + mod .

Kita akan coba untuk setiap kemungkinan nilai , , sampai ditemukan nilai yang benar yang memenuhi mod .

Tabel 3.2.1 Representasi Polinomial ( mod untuk ∗dengan = + + +

mod 0

(54)

mod 2

3 4 5 6

7 ₊

8 ₊

9 +

10 +

11 ₊

12 ₊

13 + +

14 +

15 ₊

16 ₊

17 +

18 +

19 _{+ +}

20 ₊ ₊

21 ₊ _{+ +}

Pada saat = , diperoleh kongruensi + + + mod .

Dengan demikian diperoleh solusi dari log mod adalah (mod ) mod 127).

(55)

3.2.2 Solusi Masalah Logaritma Diskret pada ∗ dengan Algoritme Baby-Step Giant-Step

AlgoritmeBaby-Step Giant-Step pertama kali dipublikasikan oleh Shanks pada tahun 1971. Algoritme ini merupakan time-memory trade-off dari Algoritme

Exhaustive Search yakni situasi dimana memori komputer digunakan untuk mengurangi biaya dan waktu eksekusi program (Menezes et al.1997).

Berikut analisis Algoritme Baby-Step Giant-Step untuk ∗ yang dieksplorasi dari Algoritme Baby-Step Giant-Stepuntuk grup siklik umum.

Misalkan adalah sebuah generator grup siklik ∗, dengan order ∗ _{adalah ,} _∈ ∗ _dan _{polinomial irredusibel berderajad} atas ℤ . Masalah logaritma diskret adalah menentukan , −,

sedemikian sehingga log mod . Untuk menentukan log mod , dengan Algoritme Baby-Step Giant-Step ada dua fase

yang harus dilewati yaitu fase baby-step dan fase giant-step. Ide dasarnya adalah membagi dengan , = √ , sampai ditemukan dalam himpunan { , , , … , }.

Langkah pertama menentukan nilai = √ dimaksudkan untuk menentukan batas minimal banyaknya representasi polinomial yang akan disimpan dalam memori komputer.

Langkah kedua adalah membentuk tabel dengan pasangan , (mod ), < −, dimaksudkan untuk menentukan representasi polinomial sebanyak yang akan disimpan di memori komputer, yakni { , , , … , }. Untuk membentuk tabel pasangan , (mod ) dapat digunakan Algoritme Exhaustive Search. Selanjutnya representasi polinomial– polinomial disimpan dalam memori komputer. Penyimpanan representasi polinomial–polinomial ini disebut fase baby-step.

(56)

langkah dalam proses pembagian ini adalah . Dalam proses pembagian ini berlaku aturan penjumlahan dan perkalian polinomial dalam .

∶ =

: =

∶ =

∶ = = Untuk menentukan nilai dan dengan cara membagi dengan representasi polinomial sama artinya dengan mengalikan dengan polinomial . Kalau cara kedua ini yang digunakan maka langkah pertama adalah menentukan dengan menggunakan Algoritme Euclidean yang Diperluas. Selanjutnya kalikan dengan representasi polinomial sampai diperoleh = . Proses menghitung nilai ini disebut fase giant-step.

Jika sudah ditemukan nilai dan , maka selanjutnya dapat ditentukan nilai logaritma diskret . Berdasarkan Definisi Logaritma Diskret :

log mod ⇔ mod Sehingga dari (1) dan (2) diperoleh :

= =

= log = log

− = = +

Jadi solusi dari mod adalah = + log mod .

Algoritme 3.2.2

Algoritme Baby-Step Giant-Step untuk menentukan masalah logaritma diskret

pada ∗

Input : generator grup siklik ∗ berorder = − , dan ∈ ∗_{, dan} _{polinomial irredusibel atas}_ℤ _{berderajad .}

(57)

1) Menetapkan nilai = √

2) Bentuk tabel dengan pasangan , mod , dimana −. 3) Hitung , kemudian tetapkan nilai = .

Bentuk tabel dengan pasangan , mod , , sampai diperoleh nilai dari = .

4) Solusi dari mod adalah + mod .

Baby-Step Giant-Stepadalah √ . Implementasinya dengan bantuan sofware Maple 11 dapat dilihat pada Lampiran 3.3.

Contoh 3 (Menentukan masalah logaritma diskret pada grup multiplikatif ∗_dengan_{Baby-Step Giant-Step}₎

= + + + + ∈ ∗_{, dan}

= + + . Tentukan log mod . Penyelesaian :

1. Order dari ∗adalah = − =

Jadi = √ = . Artinya banyaknya representasi polinomial yang akan disimpan di memori komputer minimal adalah 12, , yakni

{ , , , … , }

2. = + + polinomial irredusibel atas ℤ , dengan generator ∗_{sehingga :}

mod + + mod

(58)

Tabel 3.2.2 Representasi Polinomial ( mod untuk ∗dengan = + + + +

Representasi polinomial mod

0 1

1 2 3 4 5 6

7 +

8 +

9 +

10 ₊

11 ₊

Pada Tabel 3.2.2 ini terlihat jika , maka polinomial direduksi ke

mod .

3. Menentukan nilai , = , , , … yang memenuhi kongruensi mod . Agar mudah tentukan terlebih dahulu mod . Untuk menentukan gunakan Algoritme Euclidean

Diperluas :

+ +

+ + + +

+ +

+ + + +

(59)

Tabel 3.2.3Hasil Perhitungan , : mod , untuk ∗

dengan = + + + + .

Representasi Polinomial

: mod

0 + + + +

1 + + +

2 + + +

3 +

Pada saat = , diperoleh nilai = = + , dengan = .

4. Jadi solusi = log mod = + = . + =

Tiga algoritme berikut (Algoritme Baby-Step Giant-Step 2, Algoritme

Baby-Step Giant-Step 3, AlgoritmeNaif Square) juga dieksplorasi dari Algoritme

Baby-Step Giant-Stepuntuk grup siklik umum.

3.2.3 Solusi Masalah Logaritma Diskret pada ∗ dengan Algoritme Baby-Step Giant-Step 2

Misalkan adalah sebuah generator grup siklik ∗, dengan order ∗_{adalah ,} _∈ ∗_dan _{polinomial irredusibel berderajad} atas ℤ . Masalah logaritma diskret adalah menentukan , −,

sedemikian sehingga log mod . Untuk menentukan log mod , dengan Algoritme Baby-Step Giant-Step2 juga ada dua

fase yang harus dilewati yaitu fase baby-step dan fase giant-step. Ide dasarnya adalah membagi dengan , sampai ditemukan dalam himpunan { , , , … , }.

Langkah pertama menentukan nilai = √ dimaksudkan untuk menentukan batas minimal banyaknya representasi polinomial yang akan disimpan dalam memori komputer. Sebenarnya tidak harus sama dengan √ ,

(60)

Langkah kedua adalah membentuk tabel dengan pasangan , (mod ), < −, dimaksudkan untuk menentukan polinomial sebanyak yang akan disimpan di memori komputer, yakni { , , , … , }. Untuk membentuk tabel pasangan , (mod ) dapat digunakan Algoritme

Exhaustive Search. Selanjutnya representasi polinomial–polinomial disimpan dalam memori komputer. Penyimpanan polinomial–polinomial ini disebut fase baby-step.

Langkah ketiga Algoritme Baby-Step Giant-Stepadalah menentukan nilai dan sedemikian sehingga (mod ), untuk suatu . Caranya adalah dengan membagi dengan representasi polinomial sampai ditemukan yang merupakan salah satu anggota { , , , … , }. Banyak langkah dalam proses pembagian ini adalah . Dalam proses pembagian ini berlaku aturan penjumlahan dan perkalian polinomial dalam .

∶ =

: =

∶ =

∶ = = Proses menghitung nilai ini disebut fase giant-step.

Jika sudah ditemukan nilai dan , maka selanjutnya dapat ditentukan nilai logaritma diskret . Berdasarkan Definisi Logaritma Diskret :

=

= log = log

− = = +

(61)

Algoritme 3.2.3

Algoritme Baby-Step Giant-Step 2 untuk menentukan masalah logaritma diskret

pada ∗

Input : generator grup multiplikatif ∗ berorder = − , ∈ ∗_{, dan} _{polinomial irredusibel atas}_ℤ _{berderajad .}

Output : logaritma diskret log mod 1) Menetapkan nilai = √

2) Bentuk tabel dengan pasangan , mod , dimana −. 3) Hitung , kemudian tetapkan nilai = .

Bentuk tabel dengan pasangan , mod , , sampai diperoleh nilai dari = .

4) Solusi dari mod adalah + mod .

Baby-Step Giant-Stepadalah √ . Implementasinya dengan bantuan sofware Maple 11 dapat dilihat pada Lampiran 3.4.

Contoh 4 (Menentukan masalah logaritma diskret pada grup multiplikatif ∗_dengan_{Baby-Step Giant-Step}₂₎

= + + + + ∈ ∗_{, dan}

1) Order dari ∗adalah = − =

Jadi = √ = . Artinya banyaknya representasi polinomial yang akan disimpan di memori komputer minimal adalah 12, −, yakni

{ , , , … , }

2) = + + polinomial irredusibel atas ℤ , dengan generator ∗_{sehingga :}

(62)

+ mod

Representasi polinomial yang akan disimpan di memori komputer dapat dilihat pada Tabel 3.2.2 hal 30.

3) Menentukan nilai , = , , , … yang memenuhi kongruensi mod . Agar mudah menentukan terlebih dahulu tentukan

mod dengan menggunakan Algoritme Euclidean yang Diperluas :

Jadi + + + + + mod .

Tabel 3.2.4 Hasil Perhitungan , : mod , untuk ∗

dengan = + + + + .

Representasi Polinomial

: mod

0 + + + +

1 + + +

2 + +

3 + + +

4 + +

5 +

6

Pada saat = , diperoleh nilai = = , dengan = . 4) Jadi solusi = log mod = + = . + =.

+ +

+ + + + + = +

+ + + + + +

(63)

3.2.4 Solusi Masalah Logaritma Diskret pada ∗ dengan Algoritme Baby-Step Giant-Step 3

Misalkan adalah sebuah generator grup multiplikatif ∗, dengan order ∗ adalah , ∈ ∗ dan polinomial irredusibel berderajad atas ℤ . Masalah logaritma diskret adalah menentukan , −, sedemikian sehingga log mod . Untuk menentukan log mod seperti halnya pada Algoritme

Baby-Step Giant-Step dan Algoritme Baby-Step Giant-Step 2, Algoritme Baby-Step Giant-Baby-Step 3 juga harus melewati fase baby-step dan fase giant-step. Ide dasarnya adalah membagi dengan sampai ditemukan ; = ,

< , −, integer positif, < , dengan adalah salah satu anggota himpunan { , , , … , , … , }.

Langkah pertama menentukan nilai = , < , dimaksudkan untuk menentukan batas minimal banyaknya representasi polinomial ,

−. yang akan disimpan di memori komputer.

Langkah kedua adalah membentuk tabel dengan pasangan , mod , ∀ , dimana −, dimaksudkan untuk menentukan representasi polinomial yang akan disimpan di memori komputer, yakni { , , , … , }. Sama seperti pada algoritme Baby-Step Giant-Step, untuk membentuk tabel pasangan , (mod )) juga dapat digunakan Algoritme

Exhaustive Search. Fase ini disebut fase baby-step.

Langkah ketiga Algoritme Baby-Step Giant-Step 3 adalah menentukan nilai , dan sedemikian sehingga (mod ), untuk suatu

< , . Caranya adalah membagi dengan representasi polinomial sampai ditemukan , dimana merupakan salah satu anggota { , , , … , }. Dalam proses pembagian ini berlaku aturan penjumlahan dan perkalian polinomial dalam . Banyak langkah dalam proses pembagian ini adalah .

∶ =

(64)

∶ =

∶ = = Proses menghitung nilai ini disebut fase giant-step.

Jika sudah ditemukan nilai , dan , maka selanjutnya dapat ditentukan nilai logaritma diskret . Berdasarkan Definisi Logaritma Diskret :

=

log = log

− = + = + +

Jadi solusi dari mod adalah = + +

log mod .

Algoritme 3.2.4

Algoritme Baby-Step Giant-Step 3 untuk menentukan masalah logaritma diskret

pada ∗

Input : generator grup multiplikatif ∗berorder = − , ∈ ∗_{, dan} _{polinomial irredusibel atas}_ℤ _{berderajad .} Output : logaritma diskret log mod .

1) Tetapkan nilai = , < .

2) Bentuk tabel dengan pasangan , mod , ∀ , dimana −.

3) Mencari nilai , dan , sedemikian sehingga mod , untuk suatu < dan .

(65)

Nilai harapan kompleksitas waktu Algoritme Baby-Step Giant-Step 2 adalah √ (Menezes et al. 1997). Implementasinya dengan bantuan sofware Maple 11 dapat dilihat pada Lampiran 3.5.

Contoh 5 (Menentukan masalah logaritma diskret pada grup siklik = ∗ denganBaby-Step Giant-Step3)

= + + + + ∈ ∗_{, dan}

= + + irredusibel atas ℤ . Ambil = √ = √ − = . Jadi banyaknya representasi polinomial yang akan disimpan di memori komputer sebanyak =12 yaitu { , , … , }, generator, maka

= + + = = +

Representasi polinomial yang akan disimpan di memori komputer dapat dilihat pada Tabel 3.2.2 hal 30.

Selanjutnya menentukan nilai dan , yang memenuhi kongruensi

mod . Agar mudah menentukan dan terlebih dahulu tentukan

mod . Ambil = , Sehingga diperoleh = = . Untuk

menentukan gunakan Algoritme Euclidean yang Diperluas :

Jadi mod = + + + + +

Selanjutnya tentukan terlebih dahulu mod , untuk .

+ +

+ + + + + = +