Rute Dan Jadwal Pesawat Untuk Memenuhi Permintaan Penumpang : Kasus Airasia

RUTE DAN JADWAL PESAWAT UNTUK MEMENUHI

PERMINTAAN PENUMPANG : KASUS AIRASIA

AVFITRIYANA

G54102034

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

ABSTRACT

AVFITRIYANA. Routing and Scheduling Aircraft to Fulfill Passenger Demand : AirAsia Case. Directed by AMRIL AMAN and PRAPTO TRI SUPRIYO.

An operation of flight industry is a complex management problem. Commonly, the carrier faces problems to fulfill passenger demand and this should be done in order to maximize profit. One of problem is how the carrier solve fleet routing and flight scheduling problem with minimum aircraft quantity usage.

Fleet routing and flight scheduling are critical activities in airline operations because both of them extremely affect aircraft usage efficiency, establishment of timetables, aircraft maintenance and crew scheduling. All of these will determine carrier’s profitability, its level of service and its competitive capability in the market.

The flight scheduling process consists of two dependent phases, 1) the schedule construction phase and 2) the schedule evaluation phase. In schedule construction phase a timetable is developed based on the projected demand and the market share. Then, the drafted timetable is examined during the schedule evaluation phase for operating feasibility, cost and performance considerations. The feasibility checks in this evaluation phase is conducted to aspects related to fleet route, fleet size, crew scheduling, and maintenance arrangements.

ABSTRAK

AVFITRIYANA. Rute dan Jadwal Pesawat untuk Memenuhi Permintaan Penumpang : Kasus AirAsia. Dibimbing oleh AMRIL AMAN dan PRAPTO TRI SUPRIYO .

Operasi suatu industri penerbangan merupakan suatu permasalahan manajemen yang kompleks. Secara umum, perusahaan dihadapkan pada persoalan dalam memenuhi permintaan calon penumpang dan upaya untuk memaksimumkan keuntungan. Salah satu dari masalahnya adalah bagaimana perusahaan memecahkan menentukan masalah rute armada dan jadwal penerbangan dengan penggunaan jumlah pesawat yang minimum.

Rute armada dan jadwal penerbangan adalah aktifitas penting dalam operasi perusahaan penerbangan karena sangat mempengaruhi efisiensi penggunaan pesawat, pembuatan jadwal penerbangan, perawatan pesawat dan penjadwalan awak. Hal tersebut menentukan keuntungan perusahaan, tingkat pelayanan dan kemampuan bersaing di pasar.

Proses penjadwalan penerbangan terdiri dari dua tahap yang saling bergantung, 1) tahap pembuatan jadwal dan 2) tahap evaluasi jadwal. Pada tahap pembuatan jadwal dikembangkan konsep jadwal berdasarkan perkiraan permintaan dan penguasaan pasar. Konsep jadwal tersebut diuji selama tahap evaluasi untuk kelayakan operasi, pertimbangan biaya dan performa. Pemeriksaan kelayakan pada tahap evaluasi terutama mencakup hal yang berkaitan dengan rute armada, ukuran armada, jadwal awak dan pengaturan perawatan.

Penelitian ini menggunakan teknik jaringan ruang-waktu dalam memformulasikan model untuk masalah rute armada dan jadwal penerbangan. Penyelesaian masalah ini menggunakan software LINGO 8.0 dengan metode Branch and Bound.

RUTE DAN JADWAL PESAWAT UNTUK MEMENUHI

PERMINTAAN PENUMPANG : KASUS AIRASIA

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Oleh :

AVFITRIYANA

G 54102034

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

Judul

:

RUTE DAN JADWAL PESAWAT UNTUK MEMENUHI

PERMINTAAN PENUMPANG : KASUS AIRASIA

Nama : Avfitriyana

NRP : G 54102034

Menyetujui,

Pembimbing I

Pembimbing II

Dr. Ir. Amril Aman, Msc.

Drs. Prapto Tri Supriyo, M.Kom

NIP 130 937 092

NIP 131 878 952

Mengetahui,

Dekan Fakultas Matematika dan Ilmu pengetahuan Alam

Institut Pertanian Bogor

Prof. Dr. Ir. Yonny Koesmaryono, M.S.

NIP 131 473 999

RIWAYAT HIDUP

Penulis dilahirkan di Jakarta pada tanggal 20 April 1984 sebagai anak kedua

dari pasangan bapak Amri Sulaiman dan ibu Maniar Idris.

Pada tahun 1990 penulis mulai bersekolah di SDN Pasar Manggis 03 Pagi,

Jakarta Selatan, dan penulis melanjutkan sekolah ke SLTP 145 Jakarta sampai

tahu 1999. Pada tahun 2002 penulis lulus dari SMUN 3 Setiabudi, Jakarta dan

berhasil menjadi mahasiswa Departemen Matematika, Fakultas Matematika dan

Ilmu pengetahuan Alam, Institut Pertanian Bogor melalui jalur USMI (Undangan

Seleksi Masuk IPB).

PRAKATA

Assalamualaikum, Wr. Wb.,

Alhamdulillahi Rabbil Alamin, segala puji dan syukur penulis panjatkan kepada Allah, Rabb semesta alam, yang atas karunia dan kemurahanNya akhirnya penulis dapat menyelesaikan karya ilmiah ini. Tanpa dukungan, bantuan, dan doa dari berbagai pihak, penulis juga tidak dapat menyelesaikan tugas akhir dan perkuliahan di IPB. Penulis ingin mengucapkan terima kasih yang sedalam-dalamnya kepada :

1 Bapak Dr. Ir. Amril Aman, Msc. selaku dosen pembimbing I, terima kasih atas segala bimbingan, pengarahan, saran dan masukan yang diberikan serta bantuan yang tak terbalaskan sehingga pada akhirnya tugas akhir ini dapat terselesaikan. Bapak Drs. Prapto Tri Supriyo, M.Kom. selaku dosen pembimbing II, yang telah sangat mempermudah penyelesaian tugas akhir ini. Bapak Drs. Siswandi, M.Si. selaku dosen penguji luar, tanpa bapak, ujian tidak akan bisa berjalan.

2 Bapak dan Mama yang telah memberikan kasih sayang yang tak terkira, bantuan dan dorongan serta doa yang tak henti sehingga penulis bisa menjalankan tugas sebagai mahasiswa sampai pada tahap akhr ini.

3 Kakakku, Ria, yang selalu menanyakan sampai mana skripsinya, kapan seminar ? Pertanyaan itulah yang membuat aku terus semangat menyelesaikan tugas akhir, walaupun semangat itu sempat hilang. Adikku, Mei, yang cuek tapi perhatian walaupun sedikit.

4 Anakku Ralvien, yang selalu menghibur dikala sedih dengan kelucuanmu dan yang selalu membuatku ingin cepat pulang ke rumah.

5 Irwan yang telah banyak membantu dalam mengerjakan Lingo. Desi, teman suka dan duka dalam mengerjakan tugas akhir ini, terima kasih atas kebersamaan dan semangatnya ketika keputusasaan mulai datang.

6 Dina, Eryt, Ade, Arif, Febi dan Ardi yang telah memberikan warna dalam hidup. Bagiku kalian tetap sahabat terbaik.

7 Temanku angkatan 39 yang telah pergi mencari cita-citanya masing-masing. Terima kasih atas kebersamaan dalam perjalanan selama 4 tahun.

8 Terima kasih untuk Mayang, Tiwi, dan Mita atas kesediaannya menjadi pembahas, terima kasih juga untuk Desi dan Neli atas konsumsinya.

9 Kepada para dosen Departemen Matematika yang telah banyak memberikan ilmunya hingga penulis lulus dari IPB. Juga kepada staf Departemen Matematika, khususnya Ibu Susi yang telah banyak memberikan masukan, bantuan dan nasehatnya.

10 Kepada pihak-pihak yang telah membantu dalam menyelesaikan tugas akhir ini yang tidak dapat disebutkan satu per satu.

Semoga karya ilmiah ini dapat bermanfaat bagi yang membacanya, khususnya bagi penulis sendiri.

Wassalamualaikum Wr. Wb.

Bogor, Februari 2007

DAFTAR ISI

halaman

DAFTAR TABEL ... ix

DAFTAR GAMBAR ... ix

DAFTAR LAMPIRAN ... ix

I PENDAHULUAN ... 1

1.1 Latar Belakang ... 1

1.2 Tujuan ... 1

II LANDASAN TEORI ... 1

2.1 Linear Programming ... 1

2.2 Integer Linear Programming ... 3

2.3 Graf ... 3

2.4 Metode Branch and Bound umtuk Menyelesaikan Masalah Integer Programming ... 5

III DESKRIPSI DAN FORMULASI MASALAH RUTE DAN JADWAL PESAWAT UNTUK MEMENUHI PERMINTAAN PENUMPANG ... 8

3.1 Jaringan Aliran Ruang-Waktu Armada ... 8

3.2 Jaringan Aliran Ruang-Waktu Penumpang ... 9

3.3 Notasi Simbol ... 10

3.4 Formulasi Model ... 11

IV STUDI KASUS MASALAH RUTE DAN JADWAL PESAWAT UNTUK MEMENUHI PERMINTAAN PENUMPANG ... 12

4.1 Data dari Perusahaan Penerbangan AirAsia ... 12

4.2 Penyelesaian Masalah Rute dan Jadwal Pesawat untuk Memenuhi Permintaan Penumpang pada Perusahaan Penerbangan AirAsia ... 12

V SIMPULAN DAN SARAN ... 16

5.1 Simpulan ... 16

5.2 Saran ... 16

DAFTAR PUSTAKA ... 17

DAFTAR TABEL

halaman

1 Data rute dan biaya penerbangan domestik pada perusahaan AirAsia ... 13

2 Daftar aktifitas penerbangan AirAsia ... 14

DAFTAR GAMBAR

halaman

1 Graf G = (V, E) ... 4

2 Digraf G'=(V,A) ... 4

3 Sisi berarah menjauhi atau mendekati, suksesor dan predesesor ... 5

4 Graf berbobot G=

(

V,A∪L

)

... 5

5 Daerah fisibel untuk LP-relaksasi dari IP(9) ... 6

6 Daerah fisibel untuk subproblem 2 dan subproblem 3 dari IP(9) ... 6

7 Metode branch and bound dengan subproblem yang tidak dicabangkan lagi ... 7

8 Pencabangan keseluruhan pada metode branch and bound ... 8

9 Jaringan aliran ruang-waktu armada ... 9

10 Jaringan aliran ruang-waktu penumpang ... 10

11 Jaringan dari armada tipe B737-300 ... 15

DAFTAR LAMPIRAN

halaman

1 Contoh penyelesaian suatu LP dengan algoritma simpleks ... 19

2 Program LINGO 8.0 untuk formulasi masalah ... 21

I PENDAHULUAN

1.1 Latar Belakang

Manajemen operasi suatu industri penerbangan merupakan suatu permasalahan Operations Research yang kompleks. Secara umum, perusahaan dihadapkan pada berbagai persoalan dalam memenuhi permintaan calon penumpang dan upaya untuk memaksimumkan keuntungan. Misalnya, perusahaan harus memecahkan masalah menentukan rute armada dan jadwal penerbangan.

Rute armada dan jadwal penerbangan adalah aktifitas penting dalam operasi perusahaan penerbangan. Keduanya sangat mempengaruhi efisiensi penggunaan pesawat, pembuatan jadwal, perawatan pesawat dan penjadwalan awak. Hal tersebut sangat penting bagi keuntungan perusahaan, tingkat pelayanan dan kemampuan bersaing di pasar. Untuk peningkatan efisiensi penggunaan pesawat, maka dikembangkan kerangka kerja untuk penjadwalan penerbangan dan rute penerbangan yang jumlahnya besar. Kerangka kerja ini tersusun dari beberapa model strategis yang memberi nilai pada rancangan jadwal, jumlah pesawat yang siap, biaya pesawat dan data lain yang digunakan sebagai masukan sehingga tercapai pemecahan untuk keuntungan maksimum.

Proses penjadwalan penerbangan terdiri dari dua tahap yang saling bergantung, yaitu tahap pembuatan jadwal dan tahap evaluasi jadwal. Pada tahap pembuatan jadwal dikembangkan konsep jadwal berdasarkan perkiraan permintaan dan penguasaan pasar. Konsep jadwal tersebut diuji selama tahap evaluasi untuk kelayakan operasi, pertimbangan biaya dan performa. Pemeriksaan kelayakan pada tahap evaluasi terutama mencakup hal yang berkaitan dengan rute armada, ukuran armada, jadwal awak dan pengaturan perawatan. Proses penjadwalan penerbangan dilaksanakan dengan dua tahap tersebut sampai diperoleh jadwal yang diharapkan.

Ada beberapa jenis model penjadwalan penerbangan yang dikembangkan, seperti model integer linear programming untuk penerbangan dengan waktu keberangkatan tetap (Abara, 1989), model multikriteria untuk menentukan frekuensi penerbangan di bawah kondisi kompetitif (Teodorovic dan Krcmar-Nozic, 1989), model mixed integer programming untuk rute penerbangan jauh (Balakrishnan et al, 1990), model aliran jaringan multikomoditas untuk memecahkan daily aircraft routing and scheduling problem (DARSP) tanpa diketahui waktu keberangkatan (Hane et al, 1995), model set partitioning type dan model aliran jaringan multikomoditas dengan kendala waktu untuk memecahkan masalah DARSP berdasarkan pada serangkaian penerbangan yang diketahui waktu keberangkatannya (Desaulniers et al, 1997).

Lingkup penelitian ini terbatas pada subjek dari rute penerbangan murni operasi jadwal penerbangan dengan Origin-Destination (OD) yang diketahui, berbagai jenis pesawat, ukuran armada dan yang berhubungan dengan biaya data. Walaupun proses penjadwalan dalam prakteknya berhubungan erat dengan pemeliharaan pesawat terbang dan proses penjadwalan awak kapal, proses ini umumnya dipisahkan untuk memudahkan pemecahan masalah.

Model rute armada dan jadwal penerbangan diformulasikan sebagai integer network flow problem with side constraints (NFPWS) yang dikarakteristikan sebagai masalah NP-Complete (Garey dan Johnson, 1979). Penelitian ini menggunakan teknik jaringan ruang-waktu dalam memformulasikan model untuk masalah rute armada dan jadwal penerbangan.

1.2 Tujuan

Tujuan penulisan karya ilmiah ini adalah mempelajari model jaringan terintegrasi untuk membantu perusahaan penerbangan dalam penjadwalan dan rute penerbangan.

II LANDASAN TEORI

Untuk membuat model masalah rute armada dan jadwal penerbangan serta mencari solusinya diperlukan beberapa pemahaman teori seperti linear programming, integer linear programming,

2.1 Linear Programming

Linear programming (LP) adalah suatu model optimasi dimana fungsi tujuannya mempunyai bentuk linear dan kendalanya memiliki bentuk persamaan atau pertidaksamaan linear.

Pada tulisan ini, suatu LP mempunyai bentuk standar seperti yang didefinisikan sebagai berikut :

Definisi 1 (Bentuk Standar Suatu LP) Suatu linear programming didefinisikan mempunyai bentuk standar:

Minimumkan z=cTx

Terhadap Ax=b 0

≥

x (1) dengan x dan c berupa vektor berukuran n, vektor b berukuran m, sedangkan A berupa matriks berukuran m×n, yang disebut juga sebagai matriks kendala.

(Nash & Sofer, 1996)

2.1.1 Solusi suatu Linear Programming

Untuk menyelesaikan suatu masalah Linear Programming (LP), metode simpleks merupakan salah satu metode yang dapat menghasilkan solusi optimum. Metode ini mulai dikembangkan oleh Dantzig tahun 1947. Sejak perkembangannya, metode ini adalah metode yang paling umum digunakan untuk menyelesaikan LP, yaitu berupa metode iteratif untuk menyelesaikan masalah LP dalam bentuk standar.

Pada linear programming (1), vektor x yang memenuhi kendala Ax=bdisebut sebagai solusi LP (1). Misalkan matriks A dapat dinyatakan sebagai A = (B N), dengan B adalah matriks berukuran m×m yang merupakan matriks yang elemennya berupa koefisien variabel basis dan N merupakan matriks yang elemennya berupa koefisien variabel nonbasis pada matriks kendala. Matriks B disebut matriks basis untuk LP. Berikut definisi matriks basis:

Definisi 2 (Matriks Basis)

Matriks B disebut matriks basis untuk LP (1) jika B adalah matriks tak singular, yaitu matriks yang determinannya tidak sama dengan nol.

(Garfinkel & Nemhausher, 1972)

Misalkan x dapat dinyatakan sebagai

vektor _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = N B x x

x , dengan xB adalah vektor

variabel basis dan xN adalah vektor variabel

nonbasis. Maka Ax=b dapat dinyatakan sebagai

(

)

_⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = N B x x N B Ax

=BxB+NxN =b (2) karena B adalah matriks taksingular, maka B memiliki invers, sehingga dari (2) xB dapat dinyatakan sebagai :

xB =B -1

b - B-1 NxN (3)

Definisi 3 ( Solusi Basis )

Solusi dari suatu linear programming disebut solusi basis jika memenuhi :

xB =B -1

b, xN = 0 (4) (Garfinkel & Nemhausher, 1972)

Definisi 4 (Solusi Fisibel Basis)

x disebut solusi fisibel basis jika x merupakan solusi basis dan x≥0

(Nash & Sofer, 1996)

Ilustrasi solusi basis dan solusi fisibel basis dapat dilihat dalam contoh berikut:

Contoh 1

Misalkan diberikan linear programming berikut :

Minimumkan z=−2x1−3x2 terhadap −2x₁+x₂+x₃ =4

11 2 _{2 4}

1+ + =

−x x x

5 5 1+x =

x (5)

0 , , ,

, 2 3 4 5 1 x x x x ≥

x

Dari linear programming tersebut didapatkan : A = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − − 1 0 0 0 1 0 1 0 2 1 0 0 1 1 2

, b = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ 5 11 4 Misalkan dipilih

(

)

T

B x x x

x = 3 4 5 dan

(

)

T N x x x = 1 2 maka matriks basis

⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 1 0 0 0 1 0 0 0 1 B

Dengan menggunakan matriks basis tersebut, diperoleh

(

)

T

B B b

dari kolom yang lain). Solusi (6) juga merupakan solusi fisibel basis, karena nilai-nilai variabelnya lebih dari atau sama dengan nol. ■

LP (1) dapat dinyatakan dalam xB dan xN sebagai berikut:

Minimumkan z=c_BTx_B+c_NTx_N Terhadap Bx_B+Nx_N =b

0 ≥ x

dengan

c

_Badalah koefisien variabel basis

pada fungsi objektif,

c

_N adalah koefisien

variabel nonbasis pada fungsi objektif. Jika persamaan (3) disubstitusikan ke persamaan Z maka akan didapat :

(

)

N

T N n T

B B b B Nx c x c

z= −1 − −1 +

(

)

N

T B T N T

B B b c c B N x c

z= −1 + − −1

Jika didefinisikan

(

)

B

T T T

B B B c

c

y= −1 = − maka z dapat dinyatakan dalam y :

(

)

N

T T N T x N y c b y

z= + − (7) Vektor y disebut vektor simplex multiplier.

Untuk suatu solusi basis x_N =0 dan b B b xB 1 ˆ₌ −

= , maka zˆ=c_B TB−1b. Notasi zˆ adalah notasi untuk z optimal.

Koefisien cˆ disebut reduced cost dari xj j

dengan cˆ adalah elemen dari vektor j

(

c c B b

)

cˆ_NT = _NT − _BT −1 . Reduced cost adalah penambahan nilai fungsi objektif jika suatu variabel nonbasis dijadikan variabel basis (artinya menjadi solusi taknol) pada suatu linear programming. Maka z dapat dinyatakan sebagai z=zˆ+cˆ_NTx_N.

2.1.2 Penyelesaian Linear Programming

dengan algoritma simpleks

Solusi suatu linear programming dapat diketahui optimal atau tidak untuk LP tersebut melalui algoritma sebagai berikut:

• Tes Keoptimalan

Vektor y=cBTB−1 dihitung, kemudian dapat dihitung pula nilai reduced cost

(

c y b

)

cˆ_NT = _NT − T .

Jika cˆ_NT ≥0 maka solusi yang diperoleh adalah solusi optimal.

Jika cˆ_NT <0 , pilih variabel xt yang memenuhi cˆ_t <0sebagai entering variable yaitu variabel xt yang akan masuk ke dalam basis.

• Langkah tertentu (t)

Hitung Aˆ_t =B−1A_t, yaitu koefisien kendala yang berhubungan dengan entering variable ke t. Tentukan indeks s pada kolom kendala yang berhubungan dengan entering variable yang memenuhi

⎭ ⎬ ⎫ > ⎪⎩ ⎪ ⎨ ⎧ ≤ ≤

= :ˆ 0

ˆ ˆ 1 min ˆ ˆ , , , t i t i t s s _a a i b m i a b

. (8)

Memilih indeks dengan cara tersebut disebut dengan minimum ratio test.

Variabel yang menjadi leaving variable (variabel yang akan keluar dari basis, tergantikan oleh entering variable) dan pivot entry adalah variabel yang berhubungan dengan aˆs,t.

Jika aˆ_i,t ≤0, )(1≤i≤m , untuk semua i, maka masalah LP disebut unbounded. • Pivot

Update matriks basis B dan vektor basis xB.

Kembali ke tes keoptimalan.

Berikut contoh penggunaan algoritma simpleks :

Contoh 2

Misalkan diberikan linear programming (5) seperti pada Contoh 1, maka dengan menggunakan algoritma simpleks akan diperoleh solusi :

0 , 6 , 8 ,

5 _{2 3 4 5}

1= x = x = x =x =

x dengan

34 − =

z (lihat Lampiran 1).

2.2 Integer Linear Programming

Model Integer Linear Programming (ILP) atau disebut juga Integer Programming (IP), adalah suatu model linear programming dengan variabel yang digunakan berupa bilangan bulat (integer). Jika semua variabel harus berupa integer, maka masalah tersebut disebut pure integer programming. Jika hanya sebagian yang harus integer, maka disebut mixed integer programming. IP dengan semua variabelnya harus bernilai 0 atau 1 disebut 0-1 IP.

tersebut dengan menghilangkan kendala integer atau kendala 0-1 pada variabelnya. (Winston, 1995)

2.3 Graf Definisi 6 (Graf)

Suatu graf adalah pasangan terurut (V,E), dengan V himpunan takkosong dan hingga dan E adalah himpunan pasangan takterurut yang menghubungkan elemen-elemen V dan dinotasikan dengan G=

(

V,E

)

.

Elemen V dinamakan simpul (vertex/node), dan elemen E dinamakan sisi (edge), dinotasikan sebagai

{ }

i,j , yaitu sisi yang menghubungkan simpul i dengan simpul j, dengan i,j∈V.

(Foulds, 1992)

Ilustrasi graf dapat dilihat pada Contoh 3 berikut:

Contoh 3 G :

Gambar 1. Graf G = (V, E).

Pada Gambar 1, V=

{

v1,v2,v3,v4,v5

}

dan

{

} {

} {

} {

} {

}

{

v1,v2 , v1,v5 , v2,v3 , v2,v5 , v3,v4 E=

{

v3,v5

} {

, v4,v5

}}

.

Definisi 7 (Digraf)

Digraf (directed graf/graf berarah) adalah pasangan terurut (V, A) dengan V adalah himpunan takkosong dan hingga, dan A adalah himpunan pasangan terurut dari elemen-elemen di V.

Elemen dari A disebut sisi berarah (arc) dan dituliskan sebagai

( )

i,j dengan i,j∈V.

(Foulds, 1992)

Ilustrasi digraf dapat dapat dilihat pada Contoh 4 berikut :

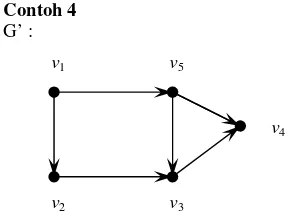
Contoh 4 G’ :

Gambar 2. Digraf G'=(V,A).

Pada Gambar 2, digraf G’ memiliki

{

v1,v2,v3,v4,v5

}

V= dan

(

)

{

v₁,v₂ ,

(

v₁,v₅

) (

, v₂,v₃

) (

, v₂,v₅

) (

, v₃,v₄

)

, A=

(

v3,v5

) (

, v4,v5

)}

.

Definisi 8 (Walk)

Suatu walk pada graf G=

(

V,E

)

adalah suatu barisan simpul dan sisi dari G dengan bentuk

{

v v

} {

v v v

} {

vn vn

}

vn

v₁, ₁, ₂ , ₂, ₂, ₃,..., ₋₁, , , atau

ditulis dengan ringkas : v₁,v₂,...,v_n atau

n v v

v1, 2,..., . Walk tersebut menghubungkan simpul v1denganvn.

(Foulds, 1992)

Definisi 9 (Path)

Path pada suatu graf G adalah suatu walk dengan semua simpulnya berbeda.

(Foulds, 1992)

Berikut diberikan ilustrasi dari walk dan path. Pada graf G yang terdapat pada Gambar 1 salah satu contoh walk adalah

3 4 5 2

1,v ,v ,v ,v

v .

Sedangkan v1,v2,v5,v4 adalah salah satu contoh path.

Definisi 10 (Cycle)

Suatu cycle pada graf G=

(

V,E

)

atau digraf G'=(V,A)adalah suatu path yang dimulai dan diakhiri oleh simpul yang sama dan terdiri atas sedikitnya tiga simpul yang berbeda pada graf G=

(

V,E

)

atau dua simpul yang berbeda pada digraf G'=(V,A). Cycle disebut juga path tertutup.

(Foulds, 1992)

v1 v5

v4

v1 v5

v4

v2 v3

Definisi 11 (Sisi Berarah Menjauhi atau Mendekati, Suksesor dan Predesesor)

Misalkan diberikan digraf D=

(

V,A

)

. Jika a=

(

vi,vj

)

∈A maka sisi berarah ini dikatakan menjauhi vi dan mendekati vj.

Simpul vi disebut predesesor bagi simpul

j

v , simpul vj disebut suksesor bagi simpul i

v .

(Foulds, 1992)

Definisi tersebut dapat digambarkan dalam digraf seperti berikut :

Gambar 3. Sisi berarah menjauhi atau mendekati, suksesor, dan predesesor.

Definisi 12 (Graf Berbobot)

Suatu graf G=

(

V,E

)

atau digraf

(

V A

)

D= , dikatakan berbobot jika terdapat fungsi w:E→ℜatau ϑ:A→ℜ (dengan

ℜ

himpunan bilangan real) yang memberikan bobot pada setiap elemen E atau A.

(Foulds, 1992)

Ilustrasi graf berbobot dapat dilihat pada Contoh 5 berikut:

Contoh 5

Misalkan diberikan w:A→ℜuntuk graf berbobot G=

(

V,A∪L

)

pada Gambar 4, maka w((v4,v5)) atau secara ringkas ditulis

. 3 , 0 , 2 , 1 3 5 3 2 2 1 4 3 5 1 4 5 = = = = = − = v v v v v v v v v v v v w w w w w w G :

Gambar 4. Graf berbobot G=

(

V,A∪L

)

.

Terdapat kasus khusus dari graf berbobot yaitu network. Beberapa konsep dalam network :

Definisi 13 (Source)

Source adalah suatu simpul dengan tidak ada sisi berarah yang mendekati simpul tersebut.

(Foulds, 1992) Definisi 14 (Sink)

Sink adalah suatu simpul sehingga tidak ada sisi berarah yang menjauhi simpul tersebut.

(Foulds, 1992)

Definisi 15 (Network)

Network adalah suatu digraf yang mempunyai tepat satu source dan satu sink.

(Foulds, 1992)

2.4 Metode Branch and Bound umtuk menyelesaikan masalah Integer Programming

Dalam penulisan karya ilmiah ini, untuk memperoleh solusi optimal dari masalah IP digunakan software Lingo 8.0 yaitu sebuah program yang didesain untuk membangun dan menentukan solusi model linear, nonlinear dan optimisasi integer menjadi lebih cepat, mudah dan lebih efisien dengan prinsip pemecahannya berdasarkan metode branch and bound.

Prinsip dasar metode branch and bound adalah memecah daerah fisibel dari masalah LP-relaksasi dengan membuat subproblem-subproblem. Daerah fisibel linear programming adalah daerah yang memenuhi semua kendala linear programming.

• Branch

Membuat partisi daerah solusi kedalam subproblem. Tujuannya untuk menghapus daerah solusi yang tidak fisibel. Hal ini dicapai dengan menentukan kendala yang penting untuk menghasilkan solusi IP, secara tidak langsung titik integer yang tidak fisibel terhapus. Dengan kata lain, hasil pengumpulan dari subproblem-subproblem yang lengkap menunjukkan setiap titik integer yang fisibel dari masalah asli. Karena sifat alami partisi itu, maka dinamakan Branching.

● Bound

Asumsikan masalahnya merupakan tipe maksimisasi, nilai objektif yang optimal untuk setiap subproblem dibuat dengan membatasi percabangan dengan batas atas dari nilai objektif yang dihubungkan dengan sembarang nilai integer yang fisibel. Hal ini sangat penting untuk mengatur dan menempatkan solusi optimum. Operasi ini yang menjadi alasan dinamakan Bounding. (Taha, 1975)

v1 v5

v4

v2 v3

2 -1 3 2 0 0

Metode branch and bound (pencabangan dan pembatasan) dimulai dengan menyelesaikan LP-relaksasi dari integer programmingnya. Jika sudah diperoleh semua variabel keputusan solusi optimal integer, maka solusi tersebut juga merupakan solusi optimal IP. Jika tidak, maka akan dilakukan pencabangan dan penambahan batasan pada LP-relaksasinya, kemudian diselesaikan.

Contoh 6

Misalkan diberikan integer programming berikut :

Maksimumkan z=8x1+5x2

terhadap x1+x2≤6 9x1+5x2≤45

x₁,x₂ ≥0

x₁,x₂integer (9)

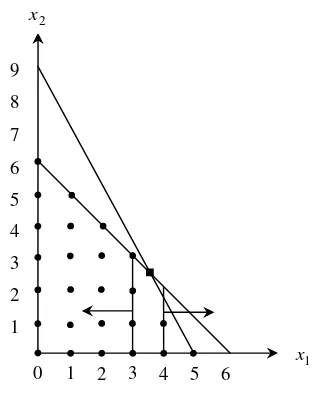
Gambar 5. Daerah fisibel untuk LP-relaksasi dari IP(9).

Ket : ● = solusi fisibel untuk IP

■= solusi optimal untuk LP-relaksasi

Solusi optimal LP-relaksasinya adalah 75

, 3 1=

x , 25x₂ =2, dengan z=41,25. Karena nilai optimal untuk IP ≤ nilai optimal untuk LP-relaksasi (masalah maksimisasi), maka nilai optimal LP-relaksasi merupakan batas atas untuk nilai optimal IP.

Gambar 6. Daerah fisibel untuk subproblem 2 dan subproblem 3 dari IP(9).

Langkah berikutnya adalah mempartisi daerah fisibel LP-relaksasi (lihat Gambar 6) menjadi dua bagian berdasarkan pada variabel yang masih dalam bentuk pecahan. Karena dua variabel diatas bukan integer, maka dipilih salah satu variabel untuk dasar pencabangan. Misalkan disini dipilih x1. Jika masalah LP-relaksasi diberi nama Subproblem 1, maka pencabangan tersebut menghasilkan dua subproblem, yaitu : • Subproblem 2 : Subproblem 1 ditambah

kendala x1≥4.

• Subproblem 3 : Subproblem 1 ditambah kendala x₁≤3.

Dari gambar 6 terlihat bahwa setiap titik (solusi) fisibel dari IP (9) termuat dalam daerah fisibel subproblem 2 atau subproblem 3. Juga setiap subproblem ini saling lepas. Subproblem 2 dan subproblem 3 ini dikatakan dicabangkan atas x1.

Sekarang dipilih subproblem yang belum diselesaikan. Misalkan dipilih subproblem 2, kemudian diselesaikan dengan menggunakan metode simpleks, sehingga diperoleh solusi optimal untuk subproblem 2 ini adalah

4 1=

x , x2 =1,8 dengan z=41.

Karena solusi optimal subproblem 2 bukan solusi integer, maka pilih pencabangan pada subproblem 2 atas x2, sehingga diperoleh dua subproblem lagi.

• Subproblem 4 : Subproblem 2 ditambah kendala x₂≥2.

9

8

7

6

5

4

3

2

1

1

0 2 3 4 5 6 1 x 2

x

9

8

7

6

5

4

3

2

1

1

0 2 3 4 5 6 1 x 2

• Subproblem 5 : subproblem 2 ditambah kendala 1x2≤ .

Sekarang, subproblem yang belum diselesaikan adalah subproblem 3, 4 dan 5. Pilih salah satu subproblem, misalnya dengan aturan LIFO (Last In First Out). Dengan aturan ini berarti pilih subproblem 4 atau subproblem 5. Karena subproblem 4 takfisibel, maka subproblem 4 tidak dapat menghasilkan solusi optimal. Tinggal subproblem 3 dan 5. Aturan LIFO membuat kita memilih subproblem 5 kemudian diperoleh solusi optimalnya x₁=4,44,

1 2 =

x dengan z=40,556.

Demikian seterusnya, sehingga dilakukan pencabangan lagi atas x1, sehingga diperoleh:

• Subproblem 6 : Subproblem 5 ditambah kendala x₁≥5.

• Subproblem 7 : Subproblem 5 ditambah kendala x1≤4.

Misalkan dipilih subproblem 7 dan kemudian diselesaikan sehingga diperoleh solusi optimal x₁=4, x₂=1dengan z=37. Karena solusi ini sudah berupa integer, maka solusi ini merupakan calon solusi (candidate solution) untuk solusi optimal IP (9). Dengan demikian nilai optimal subproblem 7 (yaitu 37) merupakan batas bawah dari nilai optimal IP (9) dan diberi notasi LB = 37.

Subproblem yang belum diselesaikan tinggal subproblem 6 dan 3, sehingga dengan aturan LIFO dipilih subproblem 6 dengan solusi optimalnya x₁=5, x₂ =0dengan z=40. Ini juga merupakan candidate solution untuk IP (9) dan nilai batas bawah (LB) berubah menjadi LB = 40. Tinggal subproblem 3 yang harus diselesaikan dan diperoleh solusi optimalnya adalah x₁=x₂ =3dengan

39 =

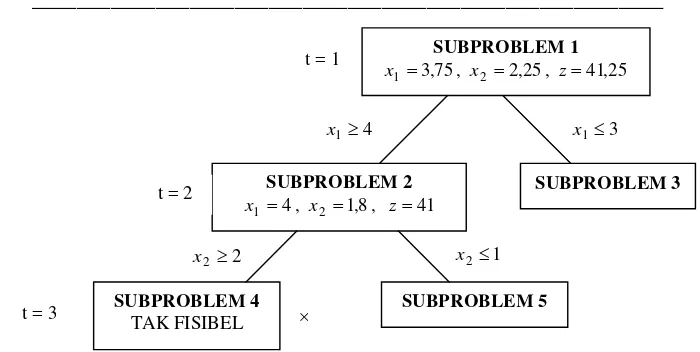
z . Karena subproblem 3 tidak dapat menghasilkan nilai optimal yang lebih baik dari LB = 40, maka subproblem 3 tidak dicabangkan lagi (fathomed) dan disini diberi tanda × (perhatikan Gambar 7).

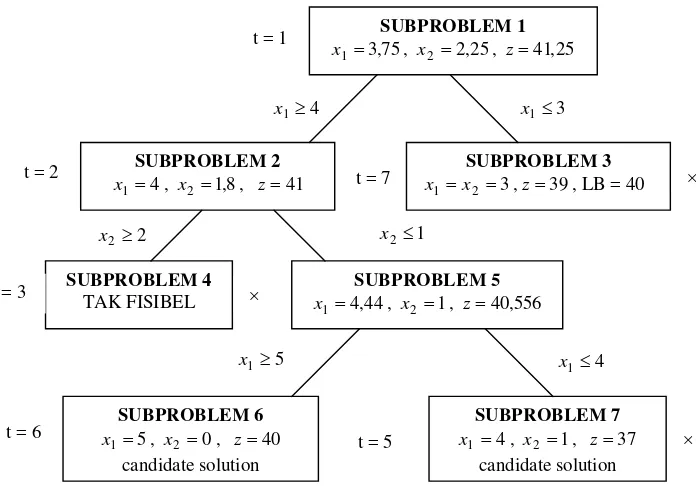
Demikian dilakukan dengan cara serupa sehingga diperoleh pencabangan keseluruhan yang diperlihatkan pada gambar 8. Dengan cara ini diperoleh solusi optimal untuk IP (9) adalah x1=5, x2 =0dengan z=40. Perlu diperhatikan bahwa situasi dimana subproblem dihentikan pencabangannya (fathomed) antara lain adalah : subproblemnya takfisibel (seperti subproblem 4 pada IP (9)), subproblem tersebut menghasilkan solusi optimal dengan semua variabelnya integer, atau nilai optimal subproblem tersebut tidak lebih bagus dari batas bawah (untuk masalah maksimisasi) atau batas atasnya (untuk masalah minimisasi).

________________________________________________________

Gambar 7. Metode branch and bound dengan subproblem yang tidak dicabangkan lagi. SUBPROBLEM 1

75 , 3 1=

x , x₂ =2,25, z=41,25

SUBPROBLEM 3 SUBPROBLEM 2

4 1=

x , x2=1,8, z=41

SUBPROBLEM 5 SUBPROBLEM 4

TAK FISIBEL

t = 1

4 1≥

x x₁≤3

t = 2

2 2≥

x x₂≤1

Gambar 8. Pencabangan keseluruhan pada metode branch and bound. _____________________________________________________________________

III DESKRIPSI DAN FORMULASI MASALAH RUTE DAN JADWAL

PESAWAT UNTUK MEMENUHI PERMINTAAN PENUMPANG

Teknik jaringan ruang-waktu (time-space network) digunakan untuk membuat model penjadwalan dan rute penerbangan dengan tujuan memaksimumkan keuntungan perusahaan penerbangan. Model ini membangun manajemen optimal dari pesawat dan pergerakan penumpang dalam jaringan dari penerbangan langsung dan berbagai penerbangan. Teknik jaringan ini dibagi menjadi dua, yaitu jaringan aliran waktu armada dan jaringan aliran ruang-waktu penumpang. Berikut ini adalah penjelasannya.

3.1 Jaringan Aliran Ruang-Waktu Armada

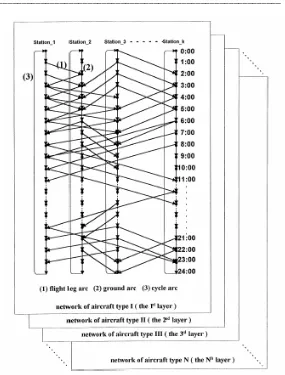
(The fleet-flowtime-space network) Jaringan aliran ruang-waktu armada digunakan untuk memformulasikan masalah berbagai rute penerbangan dan jadwal penerbangan. Tiap jaringan (network) menunjukkan satu tipe khusus pergerakan potensial dengan periode waktu dan lokasi airport tertentu, ditunjukkan pada Gambar 9. Sumbu horizontal menunjukkan lokasi airport; sumbu vertikal menunjukkan durasi waktu. Node dan arc adalah dua komponen

penting pada jaringan. Suatu node menunjukkan suatu airport pada waktu tertentu, sedangkan arc menunjukkan aktivitas, seperti penerbangan, landasan, atau tinggal semalaman (overnight stay). Aliran arc menunjukkan aliran pesawat pada jaringan. Tiga jenis arc dijelaskan sebagai berikut.

3.1.1 Flight leg arc

Flight leg arc menunjukkan suatu penerbangan antara dua airport yang berbeda. Sebagai contoh yaitu pada Gambar 9, flight leg arc ditunjukkan oleh nomor 1. Salah satu contohnya adalah ada penerbangan dari airport 1 pada pukul 01:00 sampai ke airport 2 pada pukul 02:00. Biaya penerbangan adalah biaya arc pada jaringan. Upperbound dari aliran arc adalah satu, artinya bahwa penerbangan dapat dilayani paling banyak sekali. Lowerbound dari aliran arc adalah nol, menunjukkan bahwa tidak ada pesawat yang melayani penerbangan.

SUBPROBLEM 1 75

, 3 1=

x , 25x2=2, , z=41,25

SUBPROBLEM 3 3

2 1=x =

x ,z=39, LB = 40 SUBPROBLEM 2

4 1=

x , 8x2 =1, , z=41

SUBPROBLEM 5 44

, 4 1=

x , x2 =1, z=40,556 SUBPROBLEM 4

TAK FISIBEL

t = 1

4 1≥

x x1≤3

t = 2

2 2≥

x x₂≤1

t = 3 ×

SUBPROBLEM 7 4

1=

x , x₂ =1, z=37 candidate solution SUBPROBLEM 6

5 1=

x , x₂ =0, z=40 candidate solution

t = 5

t = 6 _×

5 1≥

x x₁≤4

3.1.2 Ground arc

Suatu ground arc menggambarkan lamanya pesawat tinggal di airport dalam time window. Time window adalah jangka waktu yang telah ditentukan atau disebut juga dengan kendala waktu. Sebagai contoh yaitu pada Gambar 9, ground arc ditunjukkan oleh nomor 2. Salah satu contohnya adalah ada pesawat yang tinggal di airport 2 dari pukul 02:00 sampai pukul 03:00. Pukul 02:00 sampai pukul 03:00 disebut dengan time window. Biaya arc merupakan biaya yang terjadi untuk menempatkan satu pesawat di airport dalam time window. Upperbound dari aliran arc adalah kapasitas yang sesuai (atau tanpa batas, jika kapasitas besar), menunjukkan jumlah maksimum pesawat yang dapat ditampung di airport selama time window. Lowerbound dari aliran arc adalah nol, menunjukkan bahwa tidak ada pesawat yang ditampung di airport pada time window.

3.1.3 Cycle arc

Sebuah cycle arc berfungsi untuk menunjukkan kontinuitas antara dua periode (jangka waktu) perencanaan berurut. Menghubungkan akhir periode pertama dengan awal periode kedua untuk masing-masing airport. Sebagai contoh yaitu pada Gambar 9, cycle arc ditunjukkan oleh nomor 3. Salah satu contohnya adalah ada pesawat yang tinggal di airport 1 dari pukul 24:00 pada hari pertama sampai pukul 00:00 pada hari berikutnya. Pukul 24:00 pada hari pertama disebut akhir periode pertama. Sedangkan pukul 00:00 pada hari berikutnya disebut awal periode kedua. Aliran arc upperbound dan lowerbound dari aliran arc seperti halnya biaya arc adalah sama pada ground arc.

_____________________________________________________________________

3.2 Jaringan Aliran Ruang-Waktu Penumpang

(The passenger-flow time-space network)

Teknik jaringan ruang-waktu juga digunakan untuk menunjukkan pergerakan penumpang terhadap waktu dan lokasi tertentu, sebagaimana ditunjukkan pada Gambar 10. Masing-masing jaringan menunjukkan pasangan OD spesifik dari tabel asal-tujuan (dikenal dengan tabel OD). Sumbu horizontal dan vertikal adalah sama dengan sumbu pada jaringan aliran ruang-waktu armada. Suatu node disini juga menunjukkan suatu airport pada waktu tertentu. Suatu arc menunjukkan suatu aktivitas pergerakan penumpang. Secara keseluruhan, ada tiga tipe arc dijelaskan berikut ini.

3.2.1 Delivery arc

Suatu delivery arc menunjukkan penumpang yang diberangkatkan dari satu airport ke airport lainnya pada suatu penerbangan. Sebagai contoh yaitu pada Gambar 10, delivery arc ditunjukkan oleh nomor 1. Salah satu contohnya adalah ada penumpang yang diberangkatkan dari airport 3 pada pukul 00:00 sampai ke airport k pada pukul 02:00. Biaya arc adalah biaya variabel untuk melayani penumpang (misalnya biaya catering). Upperbound dari aliran arc adalah kapasitas pesawat (khususnya jenis paling besar), artinya bahwa aliran maksimum dalam arc adalah kapasitas muatan pesawat. Lowerbound dari aliran arc adalah nol, artinya bahwa tidak ada penumpang dari OD yang berhubungan diantarkan pada penerbangan.

3.2.2 Holding arc

Suatu holding arc menunjukkan bahwa penumpang tinggal di airport pada time window. Sebagai contoh yaitu pada Gambar 10, holding arc ditunjukkan oleh nomor 2. Salah satu contohnya adalah ada penumpang yang tinggal di airport 2 dari pukul 02:00 sampai pukul 03:00. Biaya menunggu (atau penalti) adalah biaya arc untuk time window. Upperbound dari aliran arc adalah kapasitas stasiun pelayanan penumpang dengan jaringan interval waktu minimum, menunjukkan bahwa jumlah maksimum penumpang dapat ditampung pada airport ini selama time window. Lowerbound dari aliran arc adalah nol, menunjukkan tidak ada penumpang dari OD bersangkutan tinggal di airport selama time window.

3.2.3 Demand arc

Suatu demand arc menghubungkan stasiun keberangkatan dan stasiun kedatangan dari pasangan OD bersangkutan. Sebagai contoh yaitu pada Gambar 10, demand arc ditunjukkan oleh nomor 3. Salah satu contohnya adalah ada penumpang yang diberangkatkan dari airport 2 pada pukul 06:00 pada hari pertama sampai ke airport 1 pada pukul 00:00 pada hari berikutnya.. Demand arc merupakan permintaan pelayanan untuk pasangan OD yang akan secara nyata dilayani pada jaringan. Biaya arc adalah nilai dari harga rata-rata tiket. Upperbound dari aliran arc adalah permintaan yang sudah diperhitungkan untuk pasangan OD. Lowerbound dari aliran arc adalah nol, artinya bahwa tidak ada pasangan OD penumpang dilayani pada jaringan.

Gambar 10. Jaringan aliran ruang-waktu penumpang.

______________________________________________________________________

3.3 Notasi Simbol

Notasi simbol yang digunakan dalam formulasi model adalah sebagai berikut :

ij

X : Aliran arc (i,j) dalam jaringan armada

ij

Y : Aliran arc (i,j) dalam jaringan

penumpang

ij

C : Biaya arc (i,j) dalam jaringan armada ij

T : Biaya arc (i,j) dalam jaringan

penumpang

NF : Himpunan semua node dalam jaringan armada

NP : Himpunan semua node dalam jaringan penumpang

K : Kapasitas pesawat dalam jaringan armada

ij

U : Upperbound dari aliran arc (i,j) dalam

jaringan armada

ij

V : Upperbound dari aliran arc (i,j)

dalam jaringan penumpang

AF : Jumlah pesawat yang tersedia dalam jaringan armada

3.4 Formulasi Model

Berdasarkan jaringan aliran ruang-waktu armada dan penumpang yang dijelaskan di atas, formulasi modelnya sebagai masalah aliran jaringan integer. Ada beberapa persoalan yang perlu dipertimbangkan secara hati-hati, yaitu :

1. Jumlah pesawat yang diperlukan dalam jaringan seharusnya tidak melebihi jumlah pesawat yang bisa dipakai untuk masing-masing armada.

3. Jumlah penumpang yang diangkut seharusnya tidak pernah melebihi kapasitas pesawat.

Oleh karena itu, tiga jenis kendala dibuat berhubungan dengan formulasi masalah, yaitu :

1. Jumlah siklus aliran arc pada masing-masing jaringan aliran armada tidak akan lebih besar daripada jumlah pesawat yang tersedia.

2. Jumlah seluruh aliran arc berhubungan dengan penerbangan yang sama seharusnya sama dengan satu atau nol.

3. Jumlah seluruh aliran delivery arc berhubungan dengan penerbangan yang sama tidak seharusnya melebihi jumlah masing-masing aliran arc penerbangan dikalikan dengan kapasitas pesawat.

Tujuan model ini adalah maksimalisasi profit sehingga model diformulasikan sebagai berikut.

Maksimalkan

∑ − ∑

=

∈NP ∈

ij ij ij ij NF ij ij X C Y

T

Z

terhadap

1. banyaknya pesawat yang pergi sama dengan banyaknya pesawat yang datang ∑ − ∑ = ∀ ∈

∈NF ∈

ij ij ki NF ki

NF i X

X 0,

2. banyaknya penumpang yang pergi sama dengan banyaknya penumpang yang datang Y Y i NP

NP

ij ij ki NPki

∈ ∀ =

∑ − ∑

∈ ∈ 0,

3. jumlah pesawat yang digunakan pada jaringan armada seharusnya tidak melebihi jumlah pesawat yang tersedia

∑ ≤

∈NF ij ij

AF X

4. masing-masing penerbangan dilakukan paling banyak sekali

Xij ≤1,∀ij∈NF

5. banyaknya pengangkutan penumpang tidak melebihi kapasitas pesawat

Yij ≤KXij,∀ij∈NF

6. jika ada penerbangan ke suatu airport, maka harus ada pesawat yang tinggal di airport tersebut

Xij −Xjk =0,∀ij∈NF,∀ij∈NF

7. menjaga semua aliran arc armada dengan batasannya

0≤X_ij ≤U_ij,∀ij∈NF

8. menjaga semua aliran arc penumpang dengan batasannya

0≤Yij ≤Vij,∀ij∈NP

9. semua aliran arc armada merupakan integer

Xij∈integer,∀ij∈NF

10. semua aliran arc penumpang merupakan integer

Y_ij∈integer,∀ij∈NP

IV STUDI KASUS MASALAH RUTE DAN JADWAL PESAWAT UNTUK

MEMENUHI PERMINTAAN PENUMPANG

4.1 Data dari Perusahaan Penerbangan AirAsia

Studi kasus yang dilakukan penulis untuk karya ilmiah ini yaitu pada perusahaan penerbangan AirAsia, yang datanya diperoleh pada tanggal 7 Agustus 2006. Penerbangan yang dibahas hanya meliputi operasi domestik dengan melayani tujuh kota di Indonesia. Tujuh kota tersebut antara lain adalah Jakarta (CGK), Surabaya (SUB), Medan (MES), Padang (PDG), Batam (BTH), Denpasar (DPS) dan Balikpapan (BPN). Perusahaan penerbangan AirAsia hanya menggunakan satu armada untuk rute penerbangan domestik, yaitu armada Boeing 737-300 dengan kapasitas 148 penumpang dan memiliki persediaan 26 pesawat. Lamanya pesawat tinggal di airport setelah melakukan penerbangan minimal 25 menit. Jadwal penerbangan, waktu keberangkatan dan kedatangan serta biaya diberikan pada Tabel 1. Perusahaan penerbangan ini dihadapkan pada masalah bagaimana menentukan rute armada dari jadwal penerbangan yang tersedia dengan menggunakan jumlah pesawat yang minimum. Hal ini bertujuan agar perusahaan menghasilkan keuntungan yang maksimum. Asumsi yang digunakan dalam permasalahan ini adalah :

1. Biaya flight leg arc dikonversi dari block hours, yaitu lamanya waktu penerbangan, bahwa biaya satu jam block hours sama dengan dua juta rupiah.

2. Biaya ground arc dan cycle arc adalah dua ratus ribu rupiah.

3. Semakin lama waktu penerbangan, maka biaya delivery arc (biaya catering) semakin mahal.

4.2 Penyelesaian Masalah Rute dan Jadwal Pesawat untuk Memenuhi Permintaan Penumpang pada Perusahaan Penerbangan AirAsia

No. Origin -Destination

(OD)

Waktu Harga Tiket (dalam ribuan)

Biaya Catering

(dalam ribuan)

Biaya Penerbangan (dalam ribuan) 1. CGK-SUB 06:50 - 08:10 229 44 2700 2. CGK-SUB 11:15 – 12:35 129 44 2700 3. CGK-SUB 15:25 – 16:45 219 44 2700 4. CGK-SUB 19:30 – 20;50 219 44 2700 5. CGK-SUB 20:35 – 21:55 179 44 2700 6. CGK-MES 06:00 – 08:15 329 47 4500 7. CGK-MES 10:45 – 13:00 329 47 4500 8. CGK-MES 14:40 – 16:55 329 47 4500 9. CGK-MES 16:25 – 18:40 329 47 4500 10. CGK-MES 18:50 – 21:05 299 47 4500 11. CGK-PDG 06:35 – 08:15 199 46 3300 12. CGK-PDG 11:30 – 13:10 199 46 3300 13. CGK-PDG 15:40- 17:20 149 46 3300 14. CGK-BTH 07:15 – 08:50 329 45 3200 15. CGK-BTH 11:25 – 13:00 249 45 3200 16. CGK-BTH 15:30 – 17:05 249 45 3200 17. CGK-DPS 11:15 – 14:00 415 49 5500 18. CGK-DPS 16:10 – 18:55 315 49 5500 19. CGK-DPS 19:50 – 22:35 299 49 5500 20. CGK-BPN 06:40 – 09:40 325 50 6000 21. SUB-CGK 13:00 – 14:15 179 43 2500 22. SUB-CGK 14:45 – 16:00 219 43 2500 23. SUB-CGK 17:10 – 18:25 219 43 2500 24. SUB-CGK 21:15 – 22:30 99 43 2500 25. SUB-CGK 22:20 – 23:35 99 43 2500 26. MES-CGK 08:40 – 11:00 379 48 4700 27. MES-CGK 13:25 – 15:45 369 48 4700 28. MES-CGK 19:05 – 21:25 299 48 4700 29. MES-CGK 20:10 – 22:30 299 48 4700 30. MES-CGK 21:30 – 23:50 199 48 4700 31. PDG-CGK 08:40 – 10:20 329 46 3300 32. PDG-CGK 13:35 – 15:15 219 46 3300 33. PDG-CGK 17:45 – 19:25 199 46 3300 34. BTH-CGK 09:15 – 10:50 99 42 2200 35. BTH-CGK 13:25 – 15:50 219 42 2200 36. BTH-CGK 17:30 – 19:05 199 42 2200 37. DPS-CGK 14:25 – 15:05 315 40 1400 38. DPS-CGK 19:20 – 20:00 315 40 1400 39. DPS-CGK 23:00 – 23:40 199 40 1400 40. BPN-CGK 10:05 – 11:05 345 41 2000

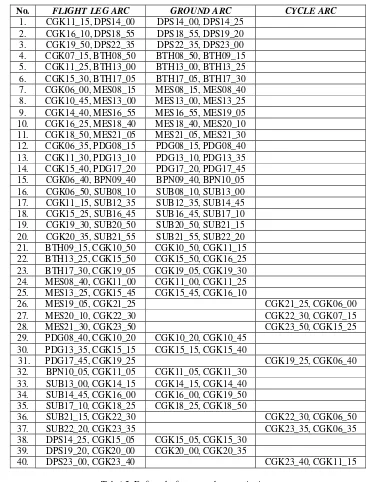
No. FLIGHT LEG ARC GROUND ARC CYCLE ARC

1. CGK11_15, DPS14_00 DPS14_00, DPS14_25 2. CGK16_10, DPS18_55 DPS18_55, DPS19_20 3. CGK19_50, DPS22_35 DPS22_35, DPS23_00 4. CGK07_15, BTH08_50 BTH08_50, BTH09_15 5. CGK11_25, BTH13_00 BTH13_00, BTH13_25 6. CGK15_30, BTH17_05 BTH17_05, BTH17_30 7. CGK06_00, MES08_15 MES08_15, MES08_40 8. CGK10_45, MES13_00 MES13_00, MES13_25 9. CGK14_40, MES16_55 MES16_55, MES19_05 10. CGK16_25, MES18_40 MES18_40, MES20_10 11. CGK18_50, MES21_05 MES21_05, MES21_30 12. CGK06_35, PDG08_15 PDG08_15, PDG08_40 13. CGK11_30, PDG13_10 PDG13_10, PDG13_35 14. CGK15_40, PDG17_20 PDG17_20, PDG17_45 15. CGK06_40, BPN09_40 BPN09_40, BPN10_05 16. CGK06_50, SUB08_10 SUB08_10, SUB13_00 17. CGK11_15, SUB12_35 SUB12_35, SUB14_45 18. CGK15_25, SUB16_45 SUB16_45, SUB17_10 19. CGK19_30, SUB20_50 SUB20_50, SUB21_15 20. CGK20_35, SUB21_55 SUB21_55, SUB22_20 21. BTH09_15, CGK10_50 CGK10_50, CGK11_15 22. BTH13_25, CGK15_50 CGK15_50, CGK16_25 23. BTH17_30, CGK19_05 CGK19_05, CGK19_30 24. MES08_40, CGK11_00 CGK11_00, CGK11_25 25. MES13_25, CGK15_45 CGK15_45, CGK16_10

26. MES19_05, CGK21_25 CGK21_25, CGK06_00 27. MES20_10, CGK22_30 CGK22_30, CGK07_15 28. MES21_30, CGK23_50 CGK23_50, CGK15_25 29. PDG08_40, CGK10_20 CGK10_20, CGK10_45

30. PDG13_35, CGK15_15 CGK15_15, CGK15_40

31. PDG17_45, CGK19_25 CGK19_25, CGK06_40 32. BPN10_05, CGK11_05 CGK11_05, CGK11_30

33. SUB13_00, CGK14_15 CGK14_15, CGK14_40 34. SUB14_45, CGK16_00 CGK16_00, CGK19_50 35. SUB17_10, CGK18_25 CGK18_25, CGK18_50

36. SUB21_15, CGK22_30 CGK22_30, CGK06_50 37. SUB22_20, CGK23_35 CGK23_35, CGK06_35 38. DPS14_25, CGK15_05 CGK15_05, CGK15_30

39. DPS19_20, CGK20_00 CGK20_00, CGK20_35

40. DPS23_00, CGK23_40 CGK23_40, CGK11_15

Gambar 10. Jaringan dari armada tipe B737-300. 13:35

14:45

14:40 14:25

13:25 13:00 08:40

07:15 06:50

06:35 06:00

06:40

09:15

10:05

11:30

11:25 11:15

10:45

15:25

15:30 08:10 08:15

08:50

09:40

10:20 10:50

14:15

15:05

15:15

15:45 15:50

16:00

16:45

16:55 17:05

11:00 11:05

12:35 13:10

14:00

15:40

16:10

16:25

17:10

17:30 17:45

18:50

19:05 19:20

19:30

20:35

19:50

20:10

22:20 21:30

23:00 17:20

18:25 18:40

18:55

19:25

21:25

21:55

21:05 20:50

20:00

22:30

22:35

23:35

23:50 23:40

V SIMPULAN DAN SARAN

5.1 Simpulan

Masalah jadwal penerbangan dan rute armada merupakan hal penting dalam operasi perusahaan penerbangan yang menghasilkan kontribusi besar dalam meminimumkan biaya mengingat biaya penerbangan adalah salah satu biaya terbesar dalam perusahan penerbangan. Perusahaan harus dapat mengalokasikan sejumlah pesawat dengan biaya minimum untuk memenuhi jadwal penerbangan yang tersedia.

Untuk memformulasikan masalah ini digunakan teknik jaringan ruang-waktu, yaitu jaringan ruang-waktu armada dan jaringan ruang-waktu penumpang. Penyelesaian masalah ini menggunakan LINGO 8.0 dengan metode branch and bound. Prinsip dasar metode branch and bound adalah memecah daerah fisibel dari masalah

LP-relaksasi dengan membuat subproblem-subproblem. Daerah fisibel linear programming adalah daerah yang memenuhi semua kendala linear programming. Metode branch and bound menghasilkan banyaknya pesawat yang dibutuhkan dengan jumlah optimal untuk menjalankan jadwal penerbangan yang telah ditentukan.

5.2 Saran

DAFTAR PUSTAKA

Airasia.http://www.airasia.com/site/in/home. jsp 7 Agustus 2006.

Airasia.http://www.airasia.com/skylights/cgi

-bin/skylights.cgi 7 Agustus 2006.

Foulds, L.R. 1992. Graph Theory Applications. Springer-Verlag, New York.

Garfinkel, R.S & G.L. Nemhauser. 1972. Integer Programming. John Wiley & Sons, New York.

Nash, S.G. & A. Sofer. 1996. Linear and Nonlinear Programming. McGraw-Hill, New York.

Taha, H.A. 1975. Integer Programming. Academic Press, New York.

Winston, W.L. 1995. Introduction to Mathematical Programming 2nd ed. Duxbury, New York.

Lampiran 1

Contoh Penyelesaian Suatu LP dengan Algoritma Simpleks

Dari LP pada contoh 2, dapat diketahui

bahwa ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − − = 1 0 0 0 1 0 1 0 2 1 0 0 1 1 2 A , ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 5 11 4 b ,

dan cT =

(

−2 −3 0 0 0

)

. Iterasi 1

Misalkan dipilih sebagai basis adalah

(

)

T

B x x x

x = _{3 4 5} dan xN =

(

x1 x2

)

T, 1

−

= =I B

B ,

(

0 0 0

)

= T B

c , cTN =

(

−2 −3

)

dan

⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − − = 0 1 2 1 1 2 N .

Nilai dari xB bˆ B b

(

4 11 5

)

T 1 ₌

=

= −

. Dengan basis ini nilai simplex multiplier

(

0 0 0

)

1₌

= −

B c y TB

T

dan nilai reduced costnya adalah

(

2 3

)

ˆ =c −y N= − −

cTN TN T .

Keduanya bernilai negatif, jadi basis ini belum optimal.

Nilai

( )

cˆT_{N 2} , yaitu nilai elemen baris

kedua dari cˆ , memiliki nilai negatif yang TN lebih besar, maka pilih x₂ (variabel nonbasis kedua) sebagai entering variable.

Untuk ratio test, hitung

⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = = − 0 2 1 ˆ 2 1 2 B A

A ,

maka perbandingannya adalah :

1 4 ˆ / ˆ 2 , 1 1 a =

b dan

2 11 ˆ / ˆ 2 , 2 2 a =

b .

Perbandingan pertama bernilai lebih kecil, maka x3 (variabel basis pertama) merupakan variabel yang akan meninggalkan basis (leaving variable).

Iterasi 2

Pada iterasi ini, x2 menggantikan x3 dalam basis. Jadi

(

)

T

B x x x

x = _{2 4 5} dan x_N =

(

x₁ x₃

)

T,

⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 1 0 0 0 1 2 0 0 1 B , ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − = − 1 0 0 0 1 2 0 0 1 1 B ,

(

−3 0 0

)

= T B

c , cTN =

(

−2 0

)

dan

⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − − = 0 1 0 1 1 2 N .

Sehingga dapat dihitung

(

)

T

B b B b

x = ˆ= −1 = 4 3 5

(

3 0 0

)

1_{= −} =_{c B}−

yT T_B

(

8 3

)

ˆ =c −y N= −

cT_N T_N T .

Reduced cost pertama bernilai negatif, maka basis ini belum optimal, dan x1 (variabel nonbasis pertama) sebagai entering variable. Kolom yang berpadanan dengan entering variable adalah ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛− = = − 1 3 2 ˆ 1 1 1 B A

A .

Dari minimum ratio test, yaitu hasil dari min

{

bˆ2/aˆ2,1=1,bˆ3/aˆ3,1=5

}

, variabel x4 yang merupakan variabel basis kedua akan menjadi leaving variable.

Iterasi 3

Pada iterasi ini, x₁ menggantikan x₄ dalam basis. Jadi

(

)

T

B x x x

x = 2 1 5 dan

(

)

T N x x x = 4 3 ,

⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − − = 1 1 0 0 1 2 0 2 1 B , ⎟⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎝ ⎛ − − − = − 1 0 0 3 1 3 2 3 1 3 2 3 2 3 1 1 B ,

(

−3 −2 0

)

= T B

c , cTN =

(

0 0

)

dan

⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 0 0 0 1 1 0 N .

Sehingga dapat dihitung

(

)

T

B b B b

x = ˆ= −1 = 6 1 4

(

₃7 ₃8 0

)

1_{= −} =_{c B}−

yT T_B

(

₃7

)

3 8 ˆ =c −y N= −

cT_N T_N T .

⎟⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎝ ⎛ − − = = − 3 2 3 2 3 1 3 1 3 ˆ _{B A}

A .

Calon untuk minimum ratio test hanya

satu, yaitu bˆ3/aˆ3,2 =6, maka x5 sebagai leaving variable.

Iterasi 4

Pada iterasi ini, x₃ menggantikan x₅ dalam basis. Jadi

(

)

T

B x x x

x = 2 1 3 dan

(

)

T N x x x = 4 5 ,

⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − − = 0 1 0 0 1 2 1 2 1 B , ⎟⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎝ ⎛ − = − 2 3 2 1 2 1 2 1 1 1 1 0 0 0 B ,

(

−3 −2 0

)

= T B

c , cT_N =

(

0 0

)

dan

⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 1 0 0 1 0 0 N .

Sehingga dapat dihitung

(

)

T

B b B b

x = ˆ= −1 = 8 5 6

(

₂7

)

2 3 1_{= 0 − −} =_{c B}−

yT T_B

( )

2

7 2 3 ˆ =c −y N= c TN T

T

N .

Nilai reduced cost dengan menggunakan basis ini bernilai positif. Hal ini berarti basis telah optimal.

Jadi solusi optimalnya adalah 0 , 6 , 8 ,

5 _{2 3 4 5}

1= x = x = x =x =

x , dengan

Lampiran 2

Program LINGO 8.0 untuk Formulasi Masalah

MODEL :

TITLE Flight Schedulling;

SETS : AIRPORT1 ;

AIRPORT2 ;

LINKS(AIRPORT1, AIRPORT2) : FLIGHT, GROUND, CYCLE, DEMAND, DELIVERY, BIAYA_F, BIAYA_G, BIAYA_C, BIAYA_DM, BIAYA_DL;

ENDSETS

!FUNGSI OBJEKTIF;

MAX = @SUM(LINKS(I,J) : (DEMAND(I,J) * BIAYA_DM(I,J) +

DELIVERY(I,J) * BIAYA_DL(I,J)) - (FLIGHT(I,J) * BIAYA_F(I,J) + GROUND(I,J) * BIAYA_G(I,J) + CYCLE(I,J) * BIAYA_C(I,J)));

!KENDALA;

!(1) BANYAKNYA PESAWAT YANG DATANG SAMA DENGAN BANYAKNYA PESAWAT YANG PERGI;

@FOR(AIRPORT1(I) : @SUM(LINKS(I,J) : FLIGHT(I,J)) - @SUM(LINKS(K,I) : FLIGHT(K,I)) = 0);

!(2) BANYAKNYA PENUMPANG YANG DATANG SAMA DENGAN BANYAKNYA PENUMPANG YANG PERGI;

@FOR(AIRPORT1(I) : @SUM(LINKS(I,J) : DELIVERY(I,J)) - @SUM(LINKS(K,I) : DELIVERY(K,I)) = 0);

!(3) JUMLAH PESAWAT YANG DIGUNAKAN TIDAK BOLEH MELEBIHI PESAWAT YANG TERSEDIA;

@SUM(LINKS(I,J) : CYCLE(I,J)) <= 26;

!(4) MASING-MASING PENERBANGAN DILAKUKAN PALING BANYAK SEKALI; @FOR(LINKS(I,J) : FLIGHT(I,J) <= 1);

!(5) BANYAKNYA PENUMPANG YANG DIANGKUT TIDAK MELEBIHI KAPASITAS PESAWAT;

@FOR(LINKS(I,J) : DELIVERY(I,J) <= (148 * FLIGHT(I,J)));

@FOR(LINKS(I,J) |I#EQ#24: FLIGHT(I,J) = CYCLE(6,J)); @FOR(LINKS(I,J) |I#EQ#25: FLIGHT(I,J) = CYCLE(11,J)); @FOR(LINKS(I,J) |I#EQ#28: FLIGHT(I,J) = CYCLE(1,J)); @FOR(LINKS(I,J) |I#EQ#29: FLIGHT(I,J) = CYCLE(14,J)); @FOR(LINKS(I,J) |I#EQ#30: FLIGHT(I,J) = CYCLE(3,J)); @FOR(LINKS(I,J) |I#EQ#33: FLIGHT(I,J) = CYCLE(20,J)); @FOR(LINKS(I,J) |I#EQ#39: FLIGHT(I,J) = CYCLE(17,J));

!(7) BATASAN UNTUK SETIAP ALIRAN ARC ARMADA; @FOR(LINKS(I,J) : FLIGHT(I,J) >= 0);

@FOR(LINKS(I,J) : FLIGHT(I,J) <= 1); @FOR(LINKS(I,J) : GROUND(I,J) >= 0); @FOR(LINKS(I,J) : GROUND(I,J) <= 1); @FOR(LINKS(I,J) : CYCLE(I,J) >= 0); @FOR(LINKS(I,J) : CYCLE(I,J) <= 1);

!(8) BATASAN UNTUK SETIAP ALIRAN ARC PENUMPANG; @FOR(LINKS(I,J) : DELIVERY(I,J) >= 0);

@FOR(LINKS(I,J) : DELIVERY(I,J) <= 148); @FOR(LINKS(I,J) : DEMAND(I,J) >= 0); @FOR(LINKS(I,J) : DEMAND(I,J) <= 40);

!(9) ALIRAN ARC ARMADA MERUPAKAN INTEGER; @FOR(LINKS(I,J) : @GIN(FLIGHT(I,J))); @FOR(LINKS(I,J) : @GIN(GROUND(I,J))); @FOR(LINKS(I,J) : @GIN(CYCLE(I,J)));

!(10) ALIRAN ARC PENUMPANG MERUPAKAN INTEGER ; @FOR(LINKS(I,J) : @GIN(DELIVERY(I,J))); @FOR(LINKS(I,J) : @GIN(DEMAND(I,J)));

DATA :

AIRPORT1, AIRPORT2, BIAYA_F, BIAYA_G, BIAYA_C, BIAYA_DM, BIAYA_DL = @OLE('C:\DATA\BIAYA.XLS');

Lampiran 3

Hasil dari Program LINGO 8.0

Global optimal solution found at iteration: 80 Objective value: 527080.0 Model Title: Flight Schedulling

RUTE DAN JADWAL PESAWAT UNTUK MEMENUHI

PERMINTAAN PENUMPANG : KASUS AIRASIA

AVFITRIYANA

G54102034

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

ABSTRACT

AVFITRIYANA. Routing and Scheduling Aircraft to Fulfill Passenger Demand : AirAsia Case. Directed by AMRIL AMAN and PRAPTO TRI SUPRIYO.

An operation of flight industry is a complex management problem. Commonly, the carrier faces problems to fulfill passenger demand and this should be done in order to maximize profit. One of problem is how the carrier solve fleet routing and flight scheduling problem with minimum aircraft quantity usage.

Fleet routing and flight scheduling are critical activities in airline operations because both of them extremely affect aircraft usage efficiency, establishment of timetables, aircraft maintenance and crew scheduling. All of these will determine carrier’s profitability, its level of service and its competitive capability in the market.

The flight scheduling process consists of two dependent phases, 1) the schedule construction phase and 2) the schedule evaluation phase. In schedule construction phase a timetable is developed based on the projected demand and the market share. Then, the drafted timetable is examined during the schedule evaluation phase for operating feasibility, cost and performance considerations. The feasibility checks in this evaluation phase is conducted to aspects related to fleet route, fleet size, crew scheduling, and maintenance arrangements.

ABSTRAK

AVFITRIYANA. Rute dan Jadwal Pesawat untuk Memenuhi Permintaan Penumpang : Kasus AirAsia. Dibimbing oleh AMRIL AMAN dan PRAPTO TRI SUPRIYO .

Operasi suatu industri penerbangan merupakan suatu permasalahan manajemen yang kompleks. Secara umum, perusahaan dihadapkan pada persoalan dalam memenuhi permintaan calon penumpang dan upaya untuk memaksimumkan keuntungan. Salah satu dari masalahnya adalah bagaimana perusahaan memecahkan menentukan masalah rute armada dan jadwal penerbangan dengan penggunaan jumlah pesawat yang minimum.

Rute armada dan jadwal penerbangan adalah aktifitas penting dalam operasi perusahaan penerbangan karena sangat mempengaruhi efisiensi penggunaan pesawat, pembuatan jadwal penerbangan, perawatan pesawat dan penjadwalan awak. Hal tersebut menentukan keuntungan perusahaan, tingkat pelayanan dan kemampuan bersaing di pasar.

Proses penjadwalan penerbangan terdiri dari dua tahap yang saling bergantung, 1) tahap pembuatan jadwal dan 2) tahap evaluasi jadwal. Pada tahap pembuatan jadwal dikembangkan konsep jadwal berdasarkan perkiraan permintaan dan penguasaan pasar. Konsep jadwal tersebut diuji selama tahap evaluasi untuk kelayakan operasi, pertimbangan biaya dan performa. Pemeriksaan kelayakan pada tahap evaluasi terutama mencakup hal yang berkaitan dengan rute armada, ukuran armada, jadwal awak dan pengaturan perawatan.

Penelitian ini menggunakan teknik jaringan ruang-waktu dalam memformulasikan model untuk masalah rute armada dan jadwal penerbangan. Penyelesaian masalah ini menggunakan software LINGO 8.0 dengan metode Branch and Bound.

I PENDAHULUAN

1.1 Latar Belakang

Manajemen operasi suatu industri penerbangan merupakan suatu permasalahan Operations Research yang kompleks. Secara umum, perusahaan dihadapkan pada berbagai persoalan dalam memenuhi permintaan calon penumpang dan upaya untuk memaksimumkan keuntungan. Misalnya, perusahaan harus memecahkan masalah menentukan rute armada dan jadwal penerbangan.

Rute armada dan jadwal penerbangan adalah aktifitas penting dalam operasi perusahaan penerbangan. Keduanya sangat mempengaruhi efisiensi penggunaan pesawat, pembuatan jadwal, perawatan pesawat dan penjadwalan awak. Hal tersebut sangat penting bagi keuntungan perusahaan, tingkat pelayanan dan kemampuan bersaing di pasar. Untuk peningkatan efisiensi penggunaan pesawat, maka dikembangkan kerangka kerja untuk penjadwalan penerbangan dan rute penerbangan yang jumlahnya besar. Kerangka kerja ini tersusun dari beberapa model strategis yang memberi nilai pada rancangan jadwal, jumlah pesawat yang siap, biaya pesawat dan data lain yang digunakan sebagai masukan sehingga tercapai pemecahan untuk keuntungan maksimum.

Proses penjadwalan penerbangan terdiri dari dua tahap yang saling bergantung, yaitu tahap pembuatan jadwal dan tahap evaluasi jadwal. Pada tahap pembuatan jadwal dikembangkan konsep jadwal berdasarkan perkiraan permintaan dan penguasaan pasar. Konsep jadwal tersebut diuji selama tahap evaluasi untuk kelayakan operasi, pertimbangan biaya dan performa. Pemeriksaan kelayakan pada tahap evaluasi terutama mencakup hal yang berkaitan dengan rute armada, ukuran armada, jadwal awak dan pengaturan perawatan. Proses penjadwalan penerbangan dilaksanakan dengan dua tahap tersebut sampai diperoleh jadwal yang diharapkan.

Ada beberapa jenis model penjadwalan penerbangan yang dikembangkan, seperti model integer linear programming untuk penerbangan dengan waktu keberangkatan tetap (Abara, 1989), model multikriteria untuk menentukan frekuensi penerbangan di bawah kondisi kompetitif (Teodorovic dan Krcmar-Nozic, 1989), model mixed integer programming untuk rute penerbangan jauh (Balakrishnan et al, 1990), model aliran jaringan multikomoditas untuk memecahkan daily aircraft routing and scheduling problem (DARSP) tanpa diketahui waktu keberangkatan (Hane et al, 1995), model set partitioning type dan model aliran jaringan multikomoditas dengan kendala waktu untuk memecahkan masalah DARSP berdasarkan pada serangkaian penerbangan yang diketahui waktu keberangkatannya (Desaulniers et al, 1997).

Lingkup penelitian ini terbatas pada subjek dari rute penerbangan murni operasi jadwal penerbangan dengan Origin-Destination (OD) yang diketahui, berbagai jenis pesawat, ukuran armada dan yang berhubungan dengan biaya data. Walaupun proses penjadwalan dalam prakteknya berhubungan erat dengan pemeliharaan pesawat terbang dan proses penjadwalan awak kapal, proses ini umumnya dipisahkan untuk memudahkan pemecahan masalah.

Model rute armada dan jadwal penerbangan diformulasikan sebagai integer network flow problem with side constraints (NFPWS) yang dikarakteristikan sebagai masalah NP-Complete (Garey dan Johnson, 1979). Penelitian in