MODEL MATEMATIKA TIPE SEIRS-SEI UNTUK
TRANSMISI PENYAKIT MALARIA
RESMAWAN
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI TESIS DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA*
Dengan ini saya menyatakan bahwa tesis berjudul Model Matematika Tipe SEIRS-SEI untuk Transmisi Penyakit Malaria adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
RINGKASAN
RESMAWAN. Model Matematika Tipe SEIRS-SEI untuk Transmisi Penyakit Malaria. Dibimbing oleh PAIAN SIANTURI dan ENDAR HASAFAH NUGRAHANI.
Malaria merupakan penyakit yang disebabkan oleh infeksi parasit dari Nyamuk Anopheles betina genus Plasmodium, yang dapat menyerang manusia. Penyakit malaria menular melalui gigitan nyamuk yang dapat membahayakan kesehatan manusia. Pada penelitian ini disajikan sebuah model dalam bentuk sistem persamaan diferensial biasa bagi penyebaran malaria pada populasi manusia dan nyamuk.
Pada model yang telah dirumuskan oleh Chitnis, populasi manusia dibagi menjadi empat subpopulasi, yaitu manusia rentan (susceptible), manusia terpapar (exposed), manusia terinfeksi (infected), dan manusia sembuh (recovered), sedangkan populasi nyamuk dibagi menjadi tiga subpopulasi, yaitu nyamuk rentan (susceptible), nyamuk terpapar (exposed), dan nyamuk terinfeksi (infected). Manusia rentan dapat terinfeksi ketika digigit oleh nyamuk terinfeksi. Setelah itu, manusia rentan dianggap telah terbuka untuk diinfeksi oleh parasit sehingga dikelompokkan kedalam subpopulasi manusia terpapar. Setelah melalui masa inkubasi, sebagaian manusia terpapar akan terinfeksi sehingga dikelompokkan kedalam subpopulasi manusia terinfeksi. Sebagian manusia terinfeksi akan sembuh setelah melalui periode laten sehingga dikelompokkan ke dalam subpopulasi manusia sembuh, atau dapat kembali ke subpopulasi manusia rentan tanpa mengalami kekebalan. Manusia yang telah sembuh akan memiliki kekebalan yang bersifat sementara hingga kembali menjadi rentan pada periode tertentu.
Dalam penelitian ini diperoleh dua titik tetap, yaitu titik tetap tanpa penyakit (disease-free equilibrium) dan titik tetap endemik (endemic equilibrium). Selanjutnya dilakukan analisis kestabilan pada titik tetap dengan mempertimbangkan bilangan reproduksi dasar Bilangan reproduksi dasar merupakan nilai harapan banyaknya infeksi tiap satuan waktu. Bilangan ini menjadi tolok ukur penularan penyakit dalam populasi. Jika < 1, maka rata-rata setiap individu terinfeksi akan menginfeksi kurang dari satu individu baru, sehingga penyakit tidak akan menyebar. Jika > 1, maka rata-rata setiap individu terinfeksi akan menghasilkan lebih dari satu individu baru terinfeksi, sehingga penyakit akan menyebar.
Selanjutnya ditunjukkan bahwa pada populasi manusia, jika laju pemulihan dinaikkan, maka banyaknya manusia rentan menjadi terpapar semakin kecil. Demikian juga pada populasi nyamuk, jika laju pemulihan dinaikkan, maka jumlah nyamuk rentan yang menjadi terpapar semakin sedikit. Akibatnya, penyakit akan semakin cepat hilang dari populasi.
SUMMARY
RESMAWAN. A SEIRS-SEI Mathematical Model for Malaria Disease Transmission. Supervised by PAIAN SIANTURI and ENDAR HASAFAH NUGRAHANI.
Malaria is an infectious disease caused by a parasite of the genus Plasmodium of Anopheles mosquito. The malaria is transmitted to human through mosquito bites which is very dangerous for our health. In this research, a system of ordinary differential equations for the spread of malaria in human and mosquito populations is presented.
In the model formulated by Chitnis, the human population is divided into four classes, namely susceptible, exposed, infected, and recovered. The mosquito population is divided into three classes, namely susceptible, exposed, and infected. Susceptible human can be infected when they are bitten by infectious mosquitos. In this study, the exposed humans considered to have been open to be infected by parasites so they are classified into human exposed class. After a period of incubation elapsed, those in human exposed class might be infected so that they are classified into infected class. Those in infected class might be recovered after a latent period passed on so that they are classified into recovered class, or may return back to the susceptible class when the immunity decreased. Those in recovered class will have temporary immunity so that again be susceptible human in a given period. In this study, this model is a modification of a previous model is proposed and analyzed by adding a recovery rate of infected subclass into susceptible subclass of human.
The simulation study showed the existence of two equilibrium points, i.e. the disease-free equilibrium and the endemic equilibrium points. Next, the stability analysis of the equilibrium points were conducted by considering the basic reproduction number ( ). The basic reproduction number is the expected value of infections per unit of time. The number is considered as a benchmark of disease transmission in the population. If then on average each infected individual will be infecting less than one newly individual, so that the disease will disappear. If , then on average each infected individual will generate more than one newly infected individuals, so that the disease will spread.
rate increase, then the number of susceptible mosquitoes become exposed also decrease. As a consequence, disease will be vanished from population.
© Hak Cipta Milik IPB, Tahun 2013
Hak Cipta Dilindungi Undang-Undang
Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB
Tesis
sebagai salah satu syarat untuk memperoleh gelar Magister Sains
pada
Program Studi Matematika Terapan
MODEL MATEMATIKA TIPE SEIRS-SEI UNTUK
TRANSMISI PENYAKIT MALARIA
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
Judul Tesis : Model Matematika Tipe SEIRS-SEI untuk Transmisi Penyakit Malaria
Nama : Resmawan
NIM : G551110021
Disetujui oleh Komisi Pembimbing
Dr Paian Sianturi Ketua
Dr Ir Endar H Nugrahani, MS Anggota
Diketahui oleh
Ketua Program Studi Matematika Terapan
Dr Ir Endar H Nugrahani, MS
Dekan Sekolah Pascasarjana
Dr Ir Dahrul Syah, MScAgr
Tanggal Ujian: 31 Juli 2013
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah Subhanahu wa ta’ala atas segala nikmat dan karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Februari 2013 ini ialah pemodelan matematika, dengan judul Model Matematika Tipe SEIRS-SEI untuk Transmisi Penyakit Malaria.
Penulisan tesis ini merupakan salah satu syarat memperoleh gelar Magister Sains pada program studi Matematika Terapan Sekolah Pascasarjana Institut Pertanian Bogor. Penulis menyadari bahwa bantuan-bantuan dan arahan-arahan dari kedua pembimbing sangat membantu dalam menyelesaikan karya tulis ini. Terima kasih penulis ucapkan kepada Bapak Dr Paian Sianturi selaku pembimbing I dan Ibu Dr Ir Endar Hasafah Nugrahani MS selaku pembimbing II.
Penulis juga menyampaikan terima kasih kepada:
1. Prof Dr Ir Herry Suhardiyanto, MSc selaku Rektor Institut Pertanian Bogor. 2. Dr Ir Dahrul Syah, MSc Agr selaku Dekan Sekolah Pascasarjana Institut
Pertanian Bogor.
3. Dr Ir Endar H Nugrahani, MS selaku Ketua Program Studi Matematika Terapan sekaligus sebagai Pembimbing II.
4. Dr Ir Hadi Sumarno, MS selaku penguji luar komisi pembimbing. 5. Seluruh dosen dan staf pegawai tata usaha Departemen Matematika.
6. Direktorat Jenderal Pendidikan Tinggi (DIKTI) sebagai sponsor Beasiswa Unggulan.
7. Orang tua, saudara dan seluruh keluarga yang selalu memberikan dorongan dan mendoakan untuk keberhasilan studi bagi penulis.
8. Seluruh mahasiswa Departemen Matematika khususnya teman-teman angkatan tahun 2011 di program studi S2 Matematika Terapan.
9. Sahabat-sahabat yang tak dapat disebutkan satu persatu yang telah banyak membantu penulis dalam penyelesaian tesis ini.
Semoga segala bantuan, bimbingan, dan motivasi yang telah diberikan kepada penulis senantiasa mendapat balasan dari Allah Subhanahu wa ta’ala.
Akhirnya, semoga penulisan tesis ini dapat memperkaya pengalaman belajar serta wawasan kita semua.
DAFTAR ISI
DAFTAR TABEL vi
DAFTAR GAMBAR vi
DAFTAR LAMPIRAN vi
1 PENDAHULUAN 1
Latar Belakang 1
Tujuan Penelitian 2
2 TINJAUAN PUSTAKA 2
Sistem Persamaan Diferensial Biasa 2
Titik Tetap 2
Kestabilan Titik Tetap 3
Nilai Eigen dan Vektor Eigen 3
Pelinearan 3
3 MODEL MATEMATIKA TRANSMISI PENYAKIT MALARIA 4
Penelitian Sebelumnya 4
Modifikasi Model 7
4 HASIL DAN PEMBAHASAN 11
Penentuan Titik Tetap 11
Penentuan Bilangan Reproduksi Dasar 12
Analisis Kestabilan Titik Tetap 14
Simulasi Dinamika Populasi Penularan Malaria 16
5 SIMPULAN DAN SARAN 23
Simpulan 23
Saran 23
DAFTAR PUSTAKA 24
LAMPIRAN 25
DAFTAR TABEL
1 Parameter pada model SEIRS-SEI 9
2 Variabel pada model SEIRS-SEI 10
3 Parameter pada bilangan reproduksi dasar 13
4 Sifat kestabilan titik tetap 16
5 Nilai-nilai parameter pada model untuk kondisi dan 17 6 Hasil Simulasi laju pemulihan manusia terhadap bilangan reproduksi
dasar 21
DAFTAR GAMBAR
1 Skema penyebaran penyakit malaria oleh Chitnis (2005) 5 2 Skema penyebaran penyakit malaria model modifikasi SEIRS-SEI
dari Chitnis (2005) 7
3 Dinamika populasi manusia pada kondisi 18
4 Dinamika populasi nyamuk pada kondisi 18
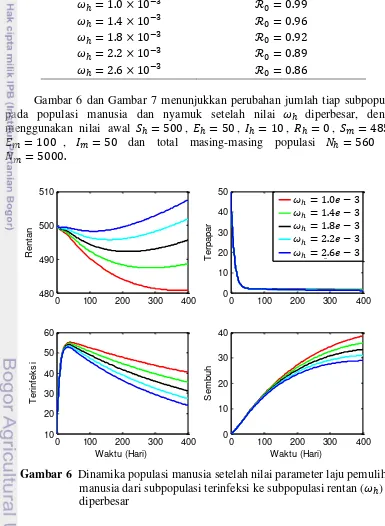
5 Dinamika populasi manusia dan nyamuk pada kondisi 20 6 Dinamika populasi manusia setelah nilai parameter laju pemulihan
manusia dari subpopulasi terinfeksi ke subpopulasi rentan (ωh)
diperbesar 21 7 Dinamika populasi nyamuk setelah nilai parameter laju pemulihan
manusia dari subpopulasi terinfeksi ke subpopulasi rentan (ωh)
diperbesar 22
3 Unsur-unsur matriks Jacobi untuk titik tetap tanpa penyakit 30
4 Penentuan nilai eigen 31
5 Koefisien Persamaan Karakteristik 32
6 Penentuan dan analisis kestabilan titik tetap tanpa penyakit 33 7 Penentuan dan analisis kestabilan titik tetap endemik 35 8 Dinamika populasi manusia dan nyamuk pada kondisi 37 9 Dinamika populasi manusia dan nyamuk pada kondisi 40 10 Dinamika populasi manusia dan nyamuk setelah nilai parameter laju
1
PENDAHULUAN
Latar Belakang
Malaria adalah penyakit yang disebabkan oleh infeksi parasit dari genus Plasmodium. Secara epidemiologi, penyakit malaria dapat menyerang semua orang baik laki-laki maupun perempuan, pada semua golongan usia. Ada empat jenis Plasmodium yang dapat menyebabkan penyakit malaria, yaitu Plasmodium Falciparum, Plasmodium Vivax, Plasmodium Ovale, dan Plasmodium Malariae (Bloland & Williams 2002). Parasit Plasmodium ditularkan melalui gigitan Nyamuk spesies Anopheles betina (anopheles spp.) yang merupakan vektor utama penyebab malaria.
Malaria terjadi terutama di daerah tropis dan beberapa daerah subtropis Afrika, Amerika Tengah dan Selatan, Asia, dan Oseania (Bloland & Williams 2002). Malaria merupakan salah satu penyakit menular yang masih menjadi masalah bagi kesehatan masyarakat baik di dunia maupun di Indonesia. Berdasarkan The World Malaria Report 2011 tentang kasus malaria di dunia, lebih dari 655 ribu orang meninggal pada tahun 2010. Secara keseluruhan terdapat 3,3 milyar penduduk dunia tinggal di daerah endemik malaria yang terdapat di 106 negara (Ditjen PP & PL 2012b).
Indonesia merupakan salah satu negara yang masih berisiko penyakit malaria. Pada tahun 2010, tercatat bahwa sekitar 65% kabupaten di Indonesia merupakan daerah endemik dimana sekitar 45% penduduk di kabupaten tersebut berisiko tertular malaria. Data kasus malaria pada tahun 2010 menunjukkan bahwa terdapat sekitar 229 ribu kasus malaria, sedangkan tahun 2011 menjadi 256 ribu kasus (Ditjen PP & PL 2012a).
Berdasarkan beberapa kasus malaria yang telah terjadi, muncul berbagai penelitian yang mengontruksikan sebuah model matematika untuk malaria. Model matematika telah memainkan peran besar dalam pengembangan epidemiologi penyakit. Pemodelan matematika dapat membantu memahami dan mengidentifikasi hubungan penyebaran penyakit malaria dengan berbagai parameter epidemiologi, membantu dalam perencanaan masa depan dan mempertimbangkan langkah-langkah pengendalian yang tepat.
Pemodelan matematika untuk penyakit malaria pertama kali dilakukan oleh Ross pada tahun 1911 yang dikenal dengan nama Model Ross. Model sederhana ini kemudian dikembangkan oleh MacDonald pada tahun 1957 yang dikenal dengan nama model Ross-MacDonald (Ngwa & Shu 2000). Beberapa penelitian serupa yang mempertimbangkan perubahan dalam ukuran populasi antara lain dilakukan oleh Ngwa & Shu (2000) dan Chitnis (2005). Chitnis melakukan analisis bifurkasi terhadap titik tetap tanpa penyakit dan titik tetap endemik, dengan menggunakan definisi bilangan reproduksi dasar ( ). Hasil analisis menunjukkan terjadinya bifurkasi pada titik tetap endemik saat .
2
malaria akan akan mengalami kekebalan tubuh yang sifatnya sementara dan sebagian lainnya akan kembali menjadi rentan (Ngwa & Shu 2000).
Tujuan Penelitian
Penelitian ini bertujuan untuk:
1. Memodifikasi model matematika penyakit malaria.
2. Menentukan titik tetap dan analisis kestabilan pada model tipe SEIRS-SEI. 3. Melakukan simulasi numerik terhadap model untuk melihat dinamika populasi
manusia dan nyamuk pada kondisi tanpa penyakit dan endemik.
4. Melakukan simulasi numerik untuk menunjukkan pengaruh laju pemulihan manusia dari subpopulasi terinfeksi ke subpopulasi rentan terhadap laju penyebaran penyakit dalam populasi.
2
TINJAUAN PUSTAKA
Sistem Persamaan Diferensial Biasa
Definisi 1 Sistem Persamaan Diferensial Biasa Taklinear
Misalkan suatu sistem persamaan diferensial biasa (SPDB) dinyatakan sebagai: persamaan diferensial biasa taklinear (Braun 1983).
Definisi 2 Sistem Persamaan Diferensial Biasa Mandiri
Misalkan suatu sistem persamaan diferensial biasa (SPDB) dinyatakan sebagai:
̇ (2.3) dengan merupakan fungsi kontinu bernilai real dari . Sistem persamaan (2.3) disebut sistem persamaan diferensial biasa mandiri (autonomous) karena tidak memuat secara eksplisit di dalamnya (Tu 1994).
Titik Tetap
3 kritis atau titik kesetimbangan atau titik ekuilibrium (Tu 1994). Untuk selanjutnya digunakan istilah titik tetap.
Kestabilan Titik Tetap
Misalkan diberikan sistem persamaan diferensial biasa sebarang ̇ dengan ̅ sebagai titik tetap. Kestabilan titik tetap ̅ dapat ditentukan dengan memperhatikan nilai-nilai eigen, yaitu , yang diperoleh dari persamaan karakteristik. Secara umum, kestabilan titik tetap mempunyai perilaku sebagai berikut: Nilai skalar dinamakan nilai eigen dari .
Untuk mencari nilai dari , maka sistem persamaan (2.4) dapat ditulis
(2.5) dengan adalah matriks identitas. Sistem persamaan (2.5) mempunyai solusi taknol jika dan hanya jika
(2.6) Persamaan (2.6) merupakan persamaan karakteristik matriks (Anton & Rorres 1995).
Pelinearan
Misalkan diberikan sistem persamaan diferensial biasa taklinear
̇ (2.7) Dengan menggunakan ekspansi Taylor di sekitar titik tetap ̅, maka sistem persamaan (2.7) dapat ditulis sebagai
4 sistem persamaan (2.8) disebut pelinearan sistem persamaan (2.7) (Tu 1994).
3
MODEL MATEMATIKA TRANSMISI
PENYAKIT MALARIA
Penelitian Sebelumnya
Pemodelan matematika untuk penyakit malaria pertama kali dilakukan oleh Ross pada tahun 1911. Menurut Ross, jika populasi nyamuk dapat dikurangi hingga di bawah ambang batas tertentu, maka malaria dapat diberantas. Model sederhana yang dibangun dikenal sebagai Model Ross dan telah dikembangkan selama bertahun-tahun. MacDonald pada tahun 1957 mengembangkan lebih lanjut dengan mempertimbangkan populasi manusia dan nyamuk pada suatu daerah dan tanpa memperhitungkan pola mobilitas manusia dan nyamuk. Perumusan model ini kemudian dikenal dengan nama Model Ross-MacDonald.
Beberapa penelitian serupa mulai mempertimbangkan perubahan dalam ukuran populasi antara lain yang dilakukan oleh Chitnis (2005) dengan menambahkan parameter imigrasi pada populasi manusia. Adanya imigrasi manusia memainkan peran besar dalam epidemiologi penyakit, termasuk malaria. Pada model ini, populasi manusia, dibagi menjadi empat subpopulasi, yaitu manusia rentan (susceptible), , manusia terpapar (exposed), , manusia terinfeksi (infected), , dan manusia sembuh (recovered), , sedangkan populasi nyamuk, , dibagi menjadi tiga subpopulasi, yaitu nyamuk rentan (susceptible),
, nyamuk terpapar (exposed), , dan nyamuk terinfeksi (infected), .
5 (Chitnis 2005). Setiap subpopulasi pada populasi manusia akan berkurang karena adanya kematian secara alami dan emigrasi kecuali untuk subpopulasi terinfeksi yang juga berkurang karena kematian yang disebabkan oleh penyakit.
Adapun penularan sporozoid dari manusia terinfeksi ( ) atau manusia sembuh ( ) ke nyamuk hanya dapat terjadi jika nyamuk rentan ( ) menggigit manusia terinfeksi atau manusia sembuh, yaitu kondisi dimana darah manusia mengandung gametosid. Di dalam tubuh nyamuk, gamet betina dan gamet jantan melakukan pembuahan menjadi zigot sampai pada akhirnya terbentuklah menjadi sporozoid yang bersifat infektif dan siap ditularkan ke manusia. Masa ini disebut dengan masa inkubasi ekstrinsik. Pada masa inkubasi ini, nyamuk rentan ( ) dianggap telah terbuka untuk diinfeksi oleh sporozoid, sehingga dikelompokkan ke dalam subpopulasi nyamuk terpapar ( ). Setelah melalui masa inkubasi, maka nyamuk akan segera terinfeksi sehingga dikelompokkan ke dalam subpopulasi nyamuk terinfeksi ( ).
Beberapa asumsi yang digunakan antara lain: a. Semua bayi yang baru lahir rentan terhadap penyakit. b. Kematian nyamuk tidak bergantung pada infeksi parasit.
c. Manusia sembuh masih dapat menularkan penyakit tetapi pada tingkat yang lebih rendah.
d. Laju kelahiran nyamuk lebih besar dari laju kematian nyamuk
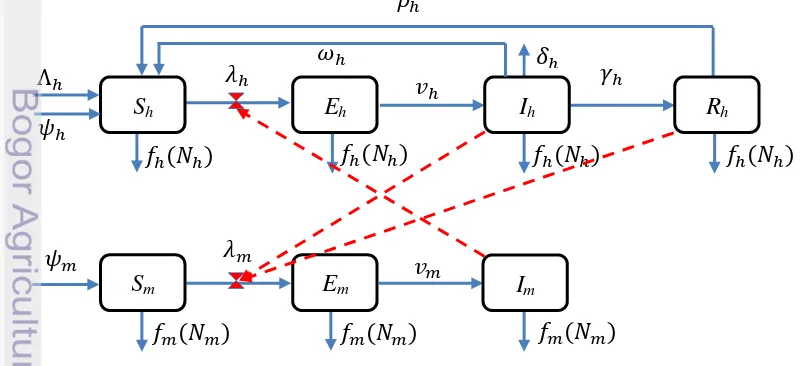
Secara skematis, pola penyebaran penyakit malaria pada model ini dapat digambarkan dalam diagram kompartemen berikut:
Gambar 1 Skema penyebaran penyakit malaria oleh Chitnis (2005)
6
Keterangan parameter disajikan pada Tabel 1. Laju kematian alami mengikuti fungsi
dan laju infeksi
( ̃ )
Laju infeksi dari nyamuk ke manusia ( ) didefinisikan sebagai perkalian antara proporsi gigitan nyamuk pada satu manusia tiap satuan waktu ( , peluang terjadinya penularan penyakit dari nyamuk ke manusia ( ), dan peluang bahwa nyamuk akan terinfeksi . Laju infeksi dari manusia ke nyamuk ( ) didefinisikan sebagai perkalian antara proporsi gigitan pada manusia dari satu nyamuk tiap satuan waktu ( ), jumlah peluang terjadinya penularan penyakit dari manusia terinfeksi ke nyamuk dengan peluang terjadinya penularan penyakit dari manusia sembuh ke nyamuk ̃ dimana ̃ , dan jumlah peluang bahwa manusia akan terinfeksi dengan peluang bahwa manusia akan sembuh Adapun proporsi gigitan nyamuk pada manusia didefinisikan sebagai
sehingga jumlah kontak nyamuk-manusia tergantung pada populasi kedua spesies. Didefinisikan,
sebagai jumlah gigitan pada tiap manusia per satuan waktu, dan
7 sebagai jumlah gigitan tiap nyamuk per satuan waktu.
Total populasi dirumuskan dengan
dan laju perubahan populasi manusia dan populasi nyamuk mengikuti persamaan, yang diperoleh dari sistem (3.1), yaitu
Pada model yang dirumuskan oleh Chitnis ini dilakukan analisis bifurkasi terhadap titik tetap tanpa penyakit dan titik tetap endemik. Analisis dilakukan dengan melibatkan definisi bilangan reproduksi dasar ( ). Hasil analisis menunjukkan terjadinya bifurkasi pada titik tetap endemik saat (Chitnis 2005). Disisi lain, Ngwa & Shu (2000) mengungkapkan bahwa sebagian manusia yang pulih dari penyakit malaria akan mengalami kekebalan tubuh yang sifatnya sementara dan sebagian lainnya akan kembali menjadi rentan. Oleh karena itu, perlu dilakukan modifikasi model dengan menambahkan parameter laju pemulihan manusia dari subpopulasi terinfeksi ke subpopulasi rentan. Parameter ini dianggap berpengaruh untuk menurunkan nilai bilangan reproduksi dasar ( ).
Modifikasi Model
Pada penelitian ini dilakukan modifikasi terhadap model SEIRS-SEI yang dirumuskan oleh Chitnis (2005) dengan menambahkan laju pemulihan manusia dari subpopulasi terinfeksi ke subpopulasi rentan. Parameter ini selanjutnya dilambangkan dengan
Secara skematis, pola penyebaran penyakit malaria dapat digambarkan dalam diagram kompartemen berikut:
8
Dengan demikian, persamaan dinamika sistem tersebut diformulasikan sebagai berikut:
dimana laju kematian alami mengikuti fungsi
dan laju infeksi mengikuti persamaan
( ̃ )
Laju perubahan populasi manusia dan populasi nyamuk mengikuti persamaan yang diperoleh dari sistem (3.9), yaitu
{
9 Tabel 1 Parameter pada model SEIRS-SEI
Variabel Keterangan Satuan
Laju perpindahan manusia terpapar ke manusia terinfeksi perkapita.
Laju perpindahan nyamuk terpapar ke nyamuk terinfeksi perkapita.
Laju pembentukan kekebalan efektif perkapita dari manusia terinfeksi ke manusia sembuh.
Laju pemulihan manusia perkapita dari manusia terinfeksi ke manusia rentan. Laju kematian manusia yang disebabkan oleh infeksi malaria.
Laju konstan hilangnya kekebalan tubuh pada manusia setelah sembuh.
Laju kematian manusia yang tidak bergantung pada kepadatan populasi. Laju kematian manusia yang bergantung pada kepadatan populasi.
10
11
4
HASIL DAN PEMBAHASAN
Penentuan Titik Tetap
Pada sub-bab ini akan dicari titik tetap dari sistem (3.12), yang dapat diperoleh dengan menyelesaikan sistem tersebut. Solusinya merupakan suatu kondisi yang diperoleh pada saat Sistem tersebut memiliki dua jenis titik tetap, yaitu titik tetap tanpa penyakit (disease-free equilibrium), , yang memuat nilai
dan titik tetap endemik (endemic equilibrium), yang memuat nilai .
12 Penentuan titik tetap dapat dilihat pada Lampiran 1.
Selanjutnya akan dilakukan analisis kestabilan pada titik tetap. Untuk itu, diperlukan bilangan reproduksi dasar.
Penentuan Bilangan Reproduksi Dasar
Bilangan reproduksi dasar dinotasikan dengan adalah nilai harapan banyaknya infeksi tiap satuan waktu. Infeksi ini terjadi pada suatu populasi rentan yang dihasilkan oleh satu individu terinfeksi.
Untuk menentukan bilangan reproduksi dasar digunakan pendekatan the next generation matrix seperti yang dijelaskan oleh Diekmann et al. (1990). The next generation matrix, , didefinisikan sebagai
(
Berdasarkan van den Driessche & Watmough (2008), bilangan reproduksi dasar merupakan nilai eigen dengan modulus terbesar matriks Untuk menentukan nilai eigen dari matriks maka dapat dituliskan persamaan karakteristik
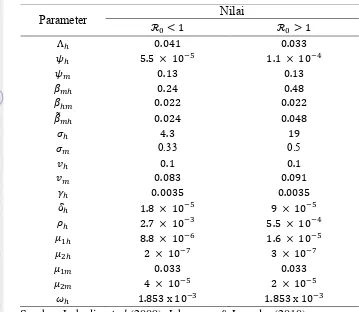
13 Tabel 3 Parameter pada bilangan reproduksi dasar
Formula Keterangan
Peluang nyamuk bertahan hidup dari keadaan terpapar
hingga terinfeksi
Peluang manusia akan bertahan hidup dari keadaan
terpapar hingga terinfeksi
Banyaknya kontak antara seekor nyamuk dengan manusia tiap satuan waktu
Banyaknya kontak antara satu orang manusia dengan
nyamuk tiap satuan waktu
Peluang terjadinya penularan dari nyamuk terinfeksi
ke manusia rentan
Peluang terjadinya penularan dari manusia terinfeksi
ke nyamuk rentan
̃ Peluang terjadinya penularan dari manusia sembuh ke
nyamuk rentan
Rata-rata masa hidup nyamuk terinfeksi Rata-rata jangka waktu infeksi pada manusia ̃ Rata-rata jangka waktu sembuh pada manusia
Peluang manusia akan bertahan hidup dari keadaan
terinfeksi hingga sembuh
Dengan demikian, dapat ditentukan nilai eigen dengan modulus terbesar matriks yaitu
| | sehingga diperoleh bilangan reproduksi dasar
√ (4.6) Kondisi yang memungkinkan dari bilangan reproduksi dasar menurut van den Driessche & Watmough (2008) adalah:
1. Jika < 1, maka jumlah individu yang terinfeksi akan menurun pada setiap generasi, sehingga penyakit tidak akan menyebar.
14
Analisis Kestabilan Titik Tetap
Pada bagian ini, akan dilakukan analisis untuk melihat sifat kestabilan pada titik tetap tanpa penyakit. Sifat kestabilan titik tetap, selanjutnya dapat dilihat pada Tabel 4. Pada bagian ini tidak dilakukan analisis kestabilan pada titik tetap endemik karena bentuknya yang sangat kompleks, namun keberadaan dan prilaku sistem disekitar titik tetap endemik akan ditunjukkan pada bagian simulasi.
Penentuan Matriks Jacobi
Misalkan sistem (3.12) didefinisikan sebagai fungsi sebagai berikut
̇ (4.7) dengan adalah variabel-variabel yang terdapat pada sistem (3.12).
Matriks Jacobi dari sistem (3.12) didefinisikan sebagai
Penentuan Matriks Jacobi untuk Titik Tetap Tanpa Penyakit
Sifat kestabilan titik tetap tanpa penyakit
Menurut Tu (1994), titik tetap bersifat stabil jika dan hanya jika setiap nilai eigen dari matriks bernilai negatif, dan tidak stabil jika dan hanya jika ada minimal satu nilai eigen dari matriks yang taknegatif.
15 √
(Lihat Lampiran 4).
Nilai eigen dan negatif, karena semua parameter yang digunakan positif. Lima nilai eigen lainnya merupakan akar-akar dari persamaan karakteristik
(4.10) dimana dapat dilihat pada Lampiran 5.
Untuk mengevaluasi tanda dari kelima nilai eigen pada persamaan karakteristik (4.10), digunakan kriteria Routh-Horwitz dan aturan Descartes.
1. Kriteria Routh-Horwitz digunakan untuk menunjukkan bahwa semua nilai eigen adalah real negatif jika dan semua adalah positif.
2. Aturan Descartes digunakan untuk menunjukkan bahwa terdapat satu nilai eigen taknegatif ketika dan terdapat satu perubahan tanda pada (Chitnis, 2005).
Untuk membuktikan hal tersebut, diperlukan bilangan reproduksi dasar ( ). Formulasi (4.6) dapat ditulis kembali dalam bentuk sebagai
sehingga titik tetap tanpa penyakit ( )dinyatakan tidak stabil.
16
yang diperoleh pada titik tetap tanpa penyakit. Hal ini memungkinkan karena kondisi sistem tidak mungkin stabil pada dua kondisi dalam waktu yang bersamaan. Akibatnya, jika sistem stabil pada titik tetanp tanpa penyakit , maka tidak stabil pada titik tetap endemik demikian sebaliknya. Selanjutnya, sifat kestabilan dari titik tetap yang diperoleh diberikan pada Tabel 4.
Tabel 4 Sifat kestabilan titik tetap
Kondisi
Stabil Tidak Stabil
Tidak Stabil Stabil
Pada tahap selanjutnya dilakukan pengamatan terhadap dinamika populasi melalui simulasi numerik untuk menunjukkan perilaku populasi dalam keadaan tanpa penyakit maupun dalam keadaan endemik. Kita akan menunjukkan bahwa sistem akan stabil menuju titik tetap tanpa penyakit saat dan stabil menuju titik tetap endemik saat . Disamping itu, akan ditunjukkan melalui simulasi bahwa laju pemulihan manusia dari subpopulasi terinfeksi ke subpopulasi rentan memiliki kontribusi terhdapa perubahan nilai bilangan reproduksi dasar ( ), yang menjadi tolak ukur penyebaran penyakit malaria dalam populasi.
Simulasi Dinamika Populasi Penularan Malaria
Pada bagian simulasi ini, diamati dinamika populasi dalam dua kondisi, yaitu kondisi ketika dan . Dalam hal ini, merupakan bilangan reproduksi yang didefinisikan pada persamaan (4.6). Simulasi ini diperlukan untuk menunjukkan bahwa sistem akan stabil menuju titik tetap tanpa penyakit saat dan stabil menuju titik tetap endemik saat . Simulasi juga diperlukan untuk menunjukkan adanya pengaruh laju pemulihan manusia dari subpopulasi terinfeksi ke subpopulasi rentan terhadap laju penularan penyakit dalam populasi.
Nilai Parameter
Pemilihan parameter didasarkan pada studi yang dilakukan oleh berbagai sumber terpercaya. Beberapa nilai parameter seperti yang menyangkut populasi manusia, didasarkan pada asumsi tentang situasi penyakit yang paling umum. Nilai-nilai parameter yang diambil mewakili dua kondisi seperti yang ditunjukkan pada Tabel 5.
Dinamika Populasi untuk Kondisi
Sistem (3.12) pada kondisi memiliki satu titik tetap tanpa penyakit yang dapat ditunjukkan dengan solusi numerik menggunakan software Mathematica. Titik tetap diperoleh dengan menggunakan nilai parameter pada Tabel 5 dengan nilai bilangan reproduksi dasar sebesar Titik tetap tanpa penyakit adalah
17 Tabel 5 Nilai-nilai parameter pada model untuk kondisi
dan Sumber: Labadin et.al (2009), Johansson & Leander (2010)
Dengan linearisasi dan perhitungan terhadap sistem (3.12) disekitar titik tetap, diperoleh matriks jacobian dan nilai eigen untuk titik tetap tanpa penyakit. Selanjutnya dapat disimpulkan bahwa titik tetap tanpa penyakit memiliki sifat stabil karena semua nilai eigen bernilai negatif. Penentuan dan analisis kestabilan titik tetap dapat dilihat pada Lampiran 6.
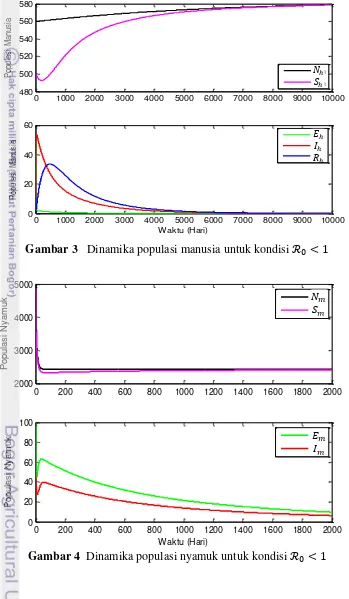
Jika digunakan beberapa nilai awal dan mensimulasikan sistem (3.9) untuk jangka waktu yang cukup, maka kita akan menemukan bahwa solusi mendekti titik tetap tanpa penyakit. Hal ini ditunjukkan pada Gambar 3 dan Gambar 4.
Gambar 3 dan Gambar 4 menunjukkan dinamika subpopulasi manusia dan nyamuk pada kondisi dengan menggunakan nilai awal , , , , , , dan total masing-masing populasi dan . Dalam hal ini .
18
titik . Adapun manusia terinfeksi ( ), dan manusia sembuh ( ), masing-masing mengalami peningkatan jumlah populasi dari titik awal kemudian kembali muenurun hingga mencapai kondisi stabil di sekitar titik yaitu kondisi dimana penyakit akan menghilang dari populasi.
Gambar 3 Dinamika populasi manusia untuk kondisi
Gambar 4 Dinamika populasi nyamuk untuk kondisi
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000 480
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000 0
0 200 400 600 800 1000 1200 1400 1600 1800 2000
2000
0 200 400 600 800 1000 1200 1400 1600 1800 2000
19 Gambar 4 menunjukkan dinamika subpopulasi pada nyamuk. Dinamika populasi menunjukkan bahwa sub-subpopulasi nyamuk menuju titik tetap tanpa penyakit atau stabil di sekitar titik tetap tanpa penyakit. Subpopulasi nyamuk rentan ( ) mengalami penurunan dari titik awal kemudian stabil di sekitar titik atau sekitar 2425 ekor nyamuk. Subpopulasi nyamuk rentan sebanyak 2425 ekor diperoleh dari perkalian proporsi 1 dengan total populasi nyamuk sebanyak 2425 ekor. Hal sama berlaku pada subpopulasi nyamuk yang lain. Subpopulasi nyamuk terpapar ( ) dan subpopulasi nyamuk terinfeksi ( ) mengalami fluktuasi perubahan jumlah populasi berupa penurunan dan peningkatan jumlah populasi dari nilai awal kemudian konsisten mengalami penurunan hingga mencapai kondisi stabil di sekitar titik , yaitu kondisi dimana penyakit akan menghilang dari populasi.
Dengan demikian, dapat dikatakan bahwa jumlah tiap subpopulasi manusia dan nyamuk stabil ke titik tetap tanpa penyakit .
Dinamika Populasi untuk Kondisi
Sistem (3.12) pada kondisi memiliki satu titik tetap endemik yang dapat ditunjukkan dengan solusi numerik menggunakan software Mathematica. Titik tetap diperoleh dengan menggunakan nilai parameter pada Tabel 5 dengan nilai bilangan reproduksi dasar sebesar Titik tetap endemik adalah
Dengan linearisasi dan perhitungan terhadap sistem (3.12) disekitar titik tetap, diperoleh matriks jacobian dan nilai eigen untuk titik tetap endemik. Selanjutnya dapat disimpulkan bahwa titik tetap endemik memiliki sifat stabil karena semua nilai eigen bernilai negatif. Penentuan dan analisis kestabilan titik tetap endemik dapat dilihat pada Lampiran 7.
Jika digunakan beberapa nilai awal endemik dan mensimulasikan sistem (3.9) untuk jangka waktu yang cukup, maka kita akan menemukan bahwa solusi mendekati titik tetap endemik. Hal ini ditunjukkan pada Gambar 5.
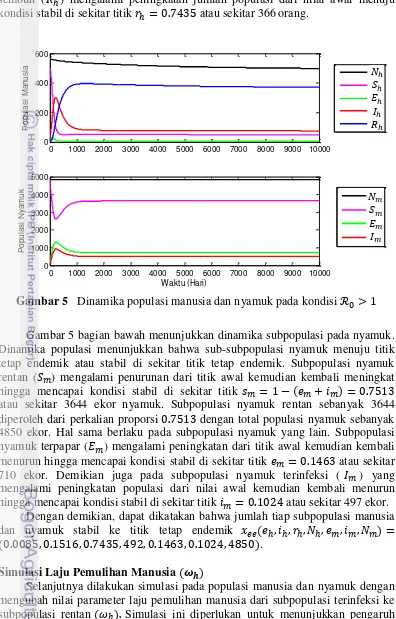
Gambar 5 menunjukkan dinamika subpopulasi manusia dan nyamuk pada kondisi dengan menggunakan nilai awal , , , , , , dan total masing-masing populasi dan . Dalam hal ini
20
sembuh ( ) mengalami peningkatan jumlah populasi dari nilai awal menuju kondisi stabil di sekitar titik atau sekitar 366 orang.
Gambar 5 Dinamika populasi manusia dan nyamuk pada kondisi Gambar 5 bagian bawah menunjukkan dinamika subpopulasi pada nyamuk. Dinamika populasi menunjukkan bahwa sub-subpopulasi nyamuk menuju titik tetap endemik atau stabil di sekitar titik tetap endemik. Subpopulasi nyamuk rentan ( ) mengalami penurunan dari titik awal kemudian kembali meningkat hingga mencapai kondisi stabil di sekitar titik atau sekitar 3644 ekor nyamuk. Subpopulasi nyamuk rentan sebanyak 3644 diperoleh dari perkalian proporsi dengan total populasi nyamuk sebanyak 4850 ekor. Hal sama berlaku pada subpopulasi nyamuk yang lain. Subpopulasi nyamuk terpapar ( ) mengalami peningkatan dari titik awal kemudian kembali menurun hingga mencapai kondisi stabil di sekitar titik atau sekitar 710 ekor. Demikian juga pada subpopulasi nyamuk terinfeksi ( ) yang mengalami peningkatan populasi dari nilai awal kemudian kembali menurun hingga mencapai kondisi stabil di sekitar titik atau sekitar 497 ekor.
Dengan demikian, dapat dikatakan bahwa jumlah tiap subpopulasi manusia dan nyamuk stabil ke titik tetap endemik .
Simulasi Laju Pemulihan Manusia ��
Selanjutnya dilakukan simulasi pada populasi manusia dan nyamuk dengan mengubah nilai parameter laju pemulihan manusia dari subpopulasi terinfeksi ke subpopulasi rentan Simulasi ini diperlukan untuk menunjukkan pengaruh parameter terhadap laju penyebaran penyakit. Dalam hal ini, akan ditunjukkan bahwa peningkatan atau penurunan nilai parameter dapat mengubah nilai bilangan reproduksi dasar ( ) yang didefinisikan pada (4.6). Terdapat 5 nilai
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000 0
21 yang diamati, diambil pada [ − − ] dengan langkah − . Nilai-nilai parameter lain dapat dilihat pada Tabel 5 untuk kondisi , kecuali nilai parameter yang dibuat bervariasi mengikuti simulasi. Adapun perubahan nilai parameter yang menyebabkan terjadinya perubahan pada nilai bilangan reproduksi dasar ( ), dapat dilihat pada Tabel 6.
Tabel 6 Hasil simulasi laju pemulihan manusia terhadap bilangan reproduksi dasar
22
Pada populasi manusia sebagaimana ditunjukkan pada Gambar 6, jika laju pemulihan manusia dari subpopulasi terinfeksi ke subpopulasi rentan diperbesar dan nilai parameter lain tetap, maka jumlah subpopulasi manusia rentan semakin bertambah sedangkan jumlah subpopulasi manusia lainnya semakin berkurang. Hal ini dikarenakan peningkatan laju pemulihan manusia menyebabkan penurunan pada jumlah subpopulasi manusia terinfeksi. Hal ini secara tidak langsung akan menyebabkan penurunan jumlah populasi pada subpopulasi nyamuk terinfeksi. Akibatnya, proporsi perpindahan manusia rentan ke manusia terpapar semakin berkurang sehingga jumlah manusia rentan semakin bertambah.
Gambar 7 Dinamika populasi nyamuk setelah nilai parameter laju pemulihan manusia dari subpopulasi terinfeksi ke subpopulasi rentan ( ) diperbesar
Pada populasi nyamuk sebagaimana ditunjukkan pada Gambar 7, jika laju pemulihan manusia dari subpopulasi terinfeksi ke subpopulasi rentan diperbesar dan nilai parameter lainnya tetap, maka jumlah subpopulasi nyamuk rentan semakin bertambah sedangkan jumlah subpopulasi nyamuk lainnya semakin berkurang. Peningkatan laju pemulihan manusia dari subpopulasi terinfeksi ke subpopulasi rentan ini menyebabkan terjadinya penurunan pada jumlah nyamuk terinfeksi sehingga jumlah manusia terinfeksi pun semakin berkurang. Akibatnya, proporsi perpindahan nyamuk rentan ke nyamuk terpapar semakin berkurang sehingga jumlah nyamuk rentan semakin bertambah.
23
Secara umum model yang dihasilkan dapat menunjukkan adanya endemik di suatu daerah untuk nilai parameter tertentu. Hal ini dapat dilihat dari perhitungan titik tetap model SEIRS-SEI. Dari model tersebut diperoleh dua titik tetap, yaitu titik tetap tanpa penyakit dan titik tetap endemik. Rincian hasil-hasil utama dalam tesis ini disimpulkan pada uraian berikut:
1. Simulasi numerik menunjukkan bahwa jumlah tiap subpopulasi manusia dan nyamuk mencapai kondisi stabil di sekitar titik tetap tanpa penyakit pada kondisi dan stabil di sekitar titik tetap endemik pada kondisi 2. Simulasi juga menunjukkan adanya kontribusi parameter laju pemulihan
manusia dari subpopulasi terinfeksi ke subpopulasi rentan terhadap perubahan nilai bilangan reproduksi dasar ( ). Jika laju pemulihan manusia ditingkatkan, maka bilangan reproduksi dasar akan semakin kecil. Dengan demikian, peningkatan nilai parameter ini dapat membantu menekan laju penularan penyakit dalam populasi.
3. Pada populasi manusia, semakin besar laju pemulihan manusia dari keadaan terinfeksi menjadi rentan, maka jumlah manusia rentan yang menjadi terpapar semakin sedikit. Pada populasi nyamuk, semakin besar laju pemulihan manusia dari keadaan terinfeksi menjadi rentan, maka jumlah manusia rentan yang menjadi terpapar semakin sedikit. Demikian juga pada populasi nyamuk, semakin besar laju pemulihan manusia dari keadaan terinfeksi menjadi rentan, maka jumlah nyamuk rentan yang menjadi terpapar semakin sedikit. Akibatnya, penyakit akan semakin cepat hilang dari populasi.
Saran
24
DAFTAR PUSTAKA
Anton H & Rorres C. 1995. Elementary Linear Algebra (Ninth Edition). John Wiley and Sons, Inc
Bloland PB & Williams HA. 2002. Malaria Control During Mass Population Movements and Natural Disasters. Washington: The National Academies Press
Braun M. 1983. Differential Equations and Their Applications. New York: Springer-Verlag
Chitnis N. 2005. Using Mathematical Models in Controlling the Spread of Malaria, Ph.D. thesis, Program in Applied Mathematics. University of Arizona, Tucson, AZ
Chitnis N, Chussing JM, Hyman JM. 2006. Bifurcation Analysis of A Mathematical Model for Malaria Transmission. Siam J. Appl. Math. Vol. 67, No. 1, pp. 24–45
Diekmann O, Heesterbeek JAP, Metz JAJ. 1990. On the Definition and the Computation of the Basic Reproduction Ratio in Models for Infectious Diseases in Heterogeneous Populations. J. Math. Biol., 28, pp. 365-382 [Ditjen PP & PL] Direktorat Jenderal Pengendalian Penyakit dan Penyehatan
Lingkungan. 2012a. Pedoman Tata Laksana Malaria. Jakarta: Departemen Kesehatan RI
[Ditjen PP & PL] Direktorat Jenderal Pengendalian Penyakit dan Penyehatan Lingkungan. 2012b. Profil Pengendalian Penyakit dan Penyehatan Lingkungan Tahun 2011. Jakarta: Departemen Kesehatan RI
Johansson P & Leander J. 2010. Mathematical Modeling of Malaria: Methods for Simulation of Epidemics. Gothenburg: Chalmers University of Technology Labadin C, Kon ML, Juan SFS. 2009. Deterministic Malaria Transmission Model with Acquired Immunity. Proceedings of the World Congress on Engineering and Computer Science 2009 Vol II. San Francisco, USA Ngwa GA & Shu WS. 2000. A Mathematical Model for Endemic Malaria with
Variable Human and Mosquito Populations. Math. Comput. Modelling, 32, pp. 747–763
Tu PNV. 1994. Dynamical System: An Introduction with Applications in Economics and Biology. New York: Springer-Verlag
25
LAMPIRAN
27
28
Lampiran 2 Penentuan matriks jacobi
Diperoleh
( )
( )
( )
29
̃
( ̃ )
( ̃ )
( ( ̃ ) )
( ̃ )
( ̃ )
30
Lampiran 3 Unsur-unsur matriks jacobi untuk titik tetap tanpa penyakit
Diperoleh
√
√
√
√
√
√
√
√
√
√
31
32
Lampiran 5 Koefisien Persamaan Karakteristik
Persamaan Karakteristik
Koefisien Karakteristik
dimana
√
( √ )
( √ )
33
35
Lampiran 7 Penentuan dan analisis kestabilan titik tetap endemik
37
Lampiran 8 Dinamika populasi manusia dan nyamuk pada kondisi gh=0.0035; dh=1.8e-5; roh=2.7e-3; m1h=8.8e-6;
m2h=2e-7; m1m=0.033; m2m=4e-5; omg=1.853e-3;
%Nilai-nilai Parameter u ntuk R0>1 (R0=3.63)
38
Syntax program untuk Gambar 3 dan Gambar 4
%Batas Toleransi
options = odeset('RelTol',1e-5,'AbsTol',1e-7);
39 set(h3,{'Color'},{'k';'m'})
ylabel('Populasi Nyamuk') legend(h3,'Nm','Sm')
subplot(2,1,2)
h4=plot(T1,Y1(:,6),T1,Y1(:,7));
set(h4,'LineWidth',2,{'LineStyle'},{'-';'-'}) set(h4,{'Color'},{'g';'r'})
40
Lampiran 9 Dinamika populasi manusia dan nyamuk pada kondisi
Syntax program untuk Gambar 5
%Batas Toleransi
options = odeset('RelTol',1e-5,'AbsTol',1e-7);
[T1,Y1] = ode45(@malaria,[0 1000],[500 50 10 0 4850 100 50 560 5000],options);
%Kondisi R0>1 %Manusia
subplot(2,1,1)
h2=plot(T1,Y1(:,8),T1,Y1(:,1),T1,Y1(:,2),T1,Y1(:,3),T1, Y1(:,4));
set(h2,'LineWidth',2,{'LineStyle'},{'-';'-';'-';'-';'-'})
set(h2,{'Color'},{'k';'m';'g';'r';'b';}) ylabel('Populasi Manusia')
legend(h2,'Nh','Sh','Eh','Ih','Rh')
%Nyamuk
subplot(2,1,2)
h3=plot(T1,Y1(:,9),T1,Y1(:,5),T1,Y1(:,6),T1,Y1(:,7)); set(h3,'LineWidth',2,{'LineStyle'},{'-';'-';'-';'-'}) set(h3,{'Color'},{'k';'m';'g';'r'})
xlabel('Waktu (hari)') ylabel('Populasi Nyamuk')
41
Lampiran 10 Dinamika populasi manusia dan nyamuk setelah nilai parameter laju pemulihan manusia ditingkatkan
42
Syntax Program untuk Gambar 6 dan Gambar 7 %Batas Toleransi
43 [T1,Y1] = ode45(@kasus1,[0 400],[500 50 10 0 4850 100 50 560 5000]);
[T2,Y2] = ode45(@kasus2,[0 400],[500 50 10 0 4850 100 50 560 5000]);
[T3,Y3] = ode45(@kasus3,[0 400],[500 50 10 0 4850 100 50 560 5000]);
[T4,Y4] = ode45(@kasus4,[0 400],[500 50 10 0 4850 100 50 560 5000]);
45
RIWAYAT HIDUP
Penulis dilahirkan di Toasae, Kabupaten Bone Provinsi Sulawesi Selatan pada tanggal 13 April 1988 sebagai anak ketiga dari lima bersaudara, dari pasangan Bapak Jempo dan Ibu Amisah.
Penulis menamatkan pendidikan dasar dan menengah di Kabupaten Bone, yaitu di SDN 290 Bulu’Sirua (2001), SMPN 1 Kahu (2004) dan SMAN 1 Kahu (2007). Setelah lulus dari SMA, penulis melanjutkan studi S1 pada Jurusan Pendidikan Matematika FMIPA Universitas Negeri Gorontalo dan lulus pada tahun 2011. Pada tahun yang sama penulis melanjutkan S2 Program Magister Sains pada Sekolah Pascasarjana Institut Pertanian Bogor (IPB), Program Studi Matematika Terapan dengan sponsor Beasiswa Unggulan Direktorat Jenderal Pendidikan Tinggi (BU DIKTI).