Analisi Torsi pada Tambang Persegi Panjang dan Aplikasi pada Komponen Struktur Beton Bertulang dengan Menggunakan Elemen Grid

ANALISIS TORSI PADA TAMPANG PERSEGI PANJANG DAN

APLIKASI PADA KOMPONEN STRUKTUR BETON

BERTULANG DENGAN MENGGUNAKAN

ELEMEN GRID

Tugas Akhir

Diajukan untuk melengkapi tugas-tugas dan memenuhi Syarat untuk menempuh ujian sarjana Teknik Sipil

Disusun oleh:

ERWIN 04 0404 009

SUB JURUSAN STRUKTUR DEPARTEMEN TEKNIK SIPIL

FAKULTAS TEKNIK

UNIVERSITAS SUMATERA UTARA MEDAN

LEMBAR PENGESAHAN

ANALISIS TORSI PADA TAMPANG PERSEGI PANJANG DAN APLIKASI PADA KOMPONEN STRUKTUR BETON

BERTULANG DENGAN MENGGUNAKAN ELEMEN GRID

Tugas Akhir

Diajukan untuk melengkapi tugas-tugas dan memenuhi Syarat untuk menempuh ujian sarjana Teknik Sipil

Disusun oleh:

ERWIN 04 0404 009

Disetujui oleh : Dosen Pembimbing

Prof.Dr.Ing.Johannes Tarigan NIP.130 905 362

SUB JURUSAN STRUKTUR DEPARTEMEN TEKNIK SIPIL

FAKULTAS TEKNIK

UNIVERSITAS SUMATERA UTARA MEDAN

ABSTRAK

Penyusunan tugas akhir ini, merupakan penjabaran beberapa besaran yang berhubungan dengan torsi untuk memperoleh tabel-tabel praktis yang dapat digunakan untuk tampang persegi. Penjabaran ini dimulai dengan penurunan fungsi torsi dengan berdasarkan pada metode semi-invers Saint-Venant dengan bantuan Soap Film Analogy dari Prandtl. Dari fungsi torsi yang diperoleh, beberapa besaran yang berhubungan dengan torsi pada tampang persegi dapat diturunkan.

Alasan memilih tampang persegi sebagai pembahasan dalam tugas akhir ini adalah karena tampang persegi ini banyak dijumpai pada komponen-komponen struktur di sekitar khususnya bangunan dari beton. Sedangkan di beberapa literatur, masih jarang ditemukan pembahasan tentang tampang ini secara lengkap.

Pembahasan dalam tugas akhir ini, memberikan penjabaran rumus-rumus untuk menentukan tegangan geser maksimum akibat torsi dan hubungan dari beberapa besaran seperti momen torsi dan inersia torsi dengan tegangan geser maksimum ini. Hasil dari pembahasan tugas akhir ini akan disajikan dalam bentuk tabel yang memberikan hubungan antara koefisien untuk beberapa besaran yang berhubungan dengan pembahasan dan disertai dengan penjalasan singkat mengenai cara penggunaan tabel-tabel yang dihasilkan.

KATA PENGANTAR

Puji syukur penulis ucapkan atas kehadirat Tuhan Yang Maha Esa yang telah memberikan anugrah, berkat dan karunia-Nya hingga terselesaikannya tugas akhir ini dengan judul “Analisis Torsi Pada Tampang Persegi Dan Aplikasi Pada Komponen Struktur Beton Bertulang Dengan Menggunakan Elemen Grid”.

Tugas akhir ini disusun untuk diajukan sebagai syarat dalam ujian sarjana teknik sipil bidang studi struktur pada fakultas teknik Universitas Sumatera Utara Medan. Penulis menyadari bahwa isi dari tugas akhir ini masih banyak kekurangannya. Hal ini disebabkan keterbatasan pengetahuan dan kurangnya pemahaman penulis. Untuk penyempurnaannya, saran dan kritik dari bapak dan ibu dosen serta rekan mahasiswa sangatlah penulis harapkan.

Penulis juga menyadari bahwa tanpa bimbingan, bantuan dan dorongan dari berbagai pihak, tugas akhir ini tidak mungkin dapat diselesaikan dengan baik. Oleh karena itu pada kesempatan ini penulis menyampaikan rasa terima kasih yang sebesar-besarnya kepada kedua orang tua yang senantiasa penulis cintai yang dalam keadaan sulit telah memperjuangkan hingga penulis dapat menyelesaikan perkuliahan ini.

Ucapan terima kasih juga penulis ucapkan kepada :

1. Bapak Dr.Ing.Johannes Tarigan. Selaku dosen pembimbing dan juga selaku Ketua Departemen Teknik Sipil Universitas Sumatera Utara yang telah banyak meluangkan waktu, tenaga dan pikiran untuk memberikan bimbingan dalam menyelesaikan tugas akhir ini

3. Bapak/Ibu staf pengajar jurusan teknik sipil Universitas Sumatera Utara.

4. Seluruh pegawai administrasi yang telah memberikan bantuan dan kemudahan dalam penyelesaian administrasi

5. Untuk sahabat-sahabat terbaikku Mayjen, Nuel, Robby, Perdi, Erwin FS, Leo, Roy, Samuella, Andrew, Nando, Benny, Budiman, Syawal, Rizky, Ica, Sheila, Syafirah, Dian, Dini, Nova, Joko, Erick, Ari Gelap, Wija, Welling, Mike, Meijer, Emir, Topan, Suryo, Ary, Dody, Acca, Verik, Novrizal, Mario, Freddi, Juntriman, Egy, Daniel, Joseph, Jaka, Kingson, para Spice (Muti, Agustina, Siska, Indah, Grace), Orry, Gafur, Andi, Aswin, Nailul, dan teman-teman stambuk 04 lainnya, buat doa, semangat dan dukungan kalian. May our friendship will be everlasting no matter where we are tomorrow

6. Seluruh rekan-rekan mahasiswa-mahasiswi jurusan teknik sipil.

Akhir kata penulis mengharapkan tugas akhir ini dapat bermanfaat bagi kita semua.

Medan, Juni 2008

DAFTAR ISI

Abstrak ... i

Kata Pengantar ... ii

Daftar Isi ... iv

Daftar Notasi ... vi

Daftar Tabel ... x

Daftar Gambar ... xi

BAB I Pendahuluan ... 1

I.1. Latar Belakang Masalah ... 1

I.2. Permasalahan ... 3

I.3. Maksud dan Tujuan ... 3

I.4. Pembatasan Masalah ... 4

I.5. Metodologi Pembahasan ... 5

BAB II Tinjauan Pustaka ... 8

II.1. Dasar-Dasar Teori ... 8

II.1.1. Pengantar Torsi ... 8

II.1.2. Elastisitas ... 10

II.1.3. Tegangan ... 10

II.1.4. Regangan ... 15

II.1.5. Hukum Hooke ... 18

II.1.6. Analogi Membrane Elastic oleh Prandtl (Soap Film Analogy) ... 21

II.2. Analisis Torsi Pada Tampang Sembarang ... 27

II.2.1. Metode Semi-Invers Saint-Venant ... 27

II.2.2. Hubungan Antara Momen Torsi Dengan Fungsi Torsi .... 33

II.3. Torsi Pada Beton Bertulang ... 34

BAB III Torsi Pada Tampang Persegi ... 36

III.1. Fungsi Torsi ... 36

III.2. Tegangan Torsi ... 40

III.3. Inersia Torsi ... 46

III.4. Hubungan Antara Momen Torsi Dengan Tegangan Torsi Maksimum ... 48

BAB IV Cara Penggunaan Tabel ... 50

IV.1.Penggunaan Tabel III.1, Tabel.III.2, dan Tabel.III.3 Untuk Menghitung Besarnya Tegangan Geser Maksimum Pada Suatu Tampang Persegi ... 50

IV.2.Penggunaan Tabel III.4 Untuk Menghitung Besarnya Inersia Torsi Pada Suatu Tampang Persegi ... 51

IV.3.Penggunaan Tabel III.5 Untuk Menghitung Besarnya Tegangan Geser Maksimum Arah zy Pada Suatu Tampang Persegi Jika Besarnya Momen Torsi yang Telah Diperoleh ... 51

BAB V Aplikasi Analisis Torsi Pada Tampang Persegi dan Pembahasan ... 52

V.1. Aplikasi Besaran Inersia Torsi Dalam Menghitung Gaya Dalam Pada Sistem Balok Bersilang dari Beton Bertulang ... 52

V.3. Pembahasan ... 79

BAB VI Penutup ... 80

VI.1.Kesimpulan ... 80

VI.2.Saran ... 82 Daftar Pustaka

DAFTAR NOTASI

A = Luas potongan penampang

Ao = Luas bruto yang dibatasi oleh lintasan aliran geser

Aoh = Luas daerah yang dibatasi oleh garis pusat tulangan sengkang torsi

terluar

Al = Luas tulangan torsi longitudinal

At = Luas satu kaki sengkang tertutup yang menahan puntir dalam daerah

sejarak s

E = Modulus elastisitas Fx = Gaya sejajar sumbu x

Fy = Gaya sejajar sumbu y

G = Modulus geser

MT = Momen torsi per satuan panjang

P = Gaya Luar Total

Ph = Keliling dari garus pusat tulangan sengkang torsi terluar

Pn = Gaya luar yang bekerja pada elemen

S = Gaya inisial dalam gaya per satuan panjang T = Momen torsi

Tu = Momen torsi ultimate

Tn = Momen torsi rencana

Vc = Kuat geser nominal yang disumbangkan oleh beton

Vu = Gaya geser ultimate

Yn = Fungsi y yang tidak bergantung pada x

Z = Komponen gaya per satuan volume sejajar sumbu z bn = Koefisien konstanta

bw = Lebar badan balok

d = Jarak dari serat tekan terluar ke titik berat tulangan tarik longitudinal ds = Panjang sisi elemen kecil

dx = Panjang sisi elemen kecil yang sejajar sumbu x dy = Panjang sisi elemen kecil yang sejajar sumbu y dz = Panjang sisi elemen kecil yang sejajar sumbu z f’c = Kuat tekan beton yang disyaratkan

fy = Kuat leleh yang disyaratkan untuk tulangan non-prategang

fyt = Kuat leleh tulangan torsi longitudinal

fyv = Kuat leleh tulangan sengkang torsi

k1 = Konstanta tegangan maksimum arah zy untuk tampang persegi

k2 = Konstanta tegangan maksimum arah zx untuk tampang persegi

k3 = Konstanta rasio tegangan maksimum arah zx terhadap arah zy untuk

tampang persegi

k4 = Konstanta inersia torsi untuk tampang persegi

k5 = Konstanta hubungan antara momen torsi dengan tegangan maksimum

arah zy

p = Tekanan lateral dalam gaya per satuan luas q = Beban per satuan panjang

u = komponen perpindahan elemen dalam arah x v = komponen perpindahan elemen dalam arah y w = komponen perpindahan elemen dalam arah z x, y, z = Sumbu koordinat utama

Φ = Koefisien reduksi untuk geser dan torsi

Θ = Sudut diagonal tekan pada penerapan analogi rangka untuk torsi

β = Sudut puntir

γ = Regangan geser

γxy , γyx = Regangan geser sejajar bidang xy

γxz , γzx = Regangan geser sejajar bidang xz

γyz , γzy = Regangan geser sejajar bidang yz

δA = Luasan kecil pada potongan penampang

δP = Resultan gaya yang bekerja pada potongan kecil δA

Є = Perpanjangan elemen

Єx = Perpanjangan elemen dalam arah x

Єy = Perpanjangan elemen dalam arah y

Єz = Perpanjangan elemen dalam arah z

= Laju puntir per satuan panjang = Angka perbandingan Poisson

σ = Tegangan normal

σy = Tegangan normal yang sejajar sumbu x

σx = Tegangan normal yang sejajar sumbu y

σz = Tegangan normal yang sejajar sumbu z

τxy = Tegangan geser yang sejajar sumbu y dan tegak lurus sumbu x

τxz = Tegangan geser yang sejajar sumbu z dan tegak lurus sumbu x

τyx = Tegangan geser yang sejajar sumbu x dan tegak lurus sumbu y

τyz = Tegangan geser yang sejajar sumbu z dan tegak lurus sumbu y

τzx = Tegangan geser yang sejajar sumbu x dan tegak lurus sumbu z

τzy = Tegangan geser yang sejajar sumbu y dan tegak lurus sumbu z

= Fungsi torsi

DAFTAR TABEL

Tabel.III.1 : Nilai Konstanta Tegangan Maksimum Arah zy (k1) Untuk Tampang Persegi ... 43 Tabel.III.2 : Nilai Konstanta Tegangan Maksimum Arah zx (k2) Untuk

Tampang Persegi ... 44 Tabel.III.3 : Nilai Konstanta Perbandingan Antara τ_{zx max Terhadap} τ_{zy max}

(k3) Untuk Tampang Persegi ... 46 Tabel.III.4 : Nilai Konstanta Inersia Torsi (k4) Untuk Tampang Persegi ... 48 Tabel.III.5 : Nilai Konstanta Hubungan Antara Momen Torsi Dengan

DAFTAR GAMBAR

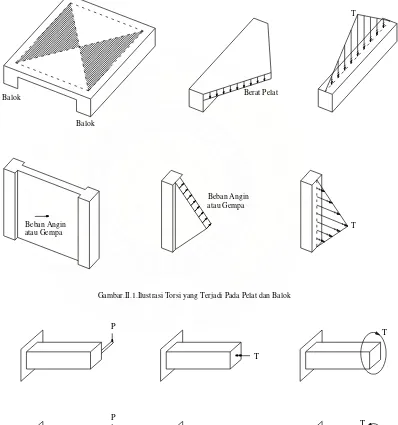
Gambar.II.1 : Ilustrasi Torsi yang Terjadi Pada Pelat dan Balok ... 9

Gambar.II.2 : Arah Kerja Torsi Sesuai Dengan Kaidah Tangan Kanan dan Panah Lengkung ... 9

Gambar.II.3 : Benda Tampang Sembarang yang Dibebani oleh Gaya-Gaya Luar ... 11

Gambar.II.4 : Komponen-Komponen Tegangan yang Bekerja Pada Potongan Kubus Kecil ... 12

Gambar.II.5 : Potongan Melintang Kubus yang Melalui Titik P ... 13

Gambar.II.6 : Komponen-Komponen Tegangan yang Bekerja Pada Potongan Kubus Kecil Dimana Gaya Luar Per Satuan Volume X, Y, Z Bekerja ... 14

Gambar.II.7 : Elemen Kecil Berdimensi dx dy dz ... 16

Gambar.II.8 : Perpindahan Titik-Titik P, A, dan B ... 17

Gambar.II.9 : Perubahan Bentuk Segi Empat Parelellogram ... 19

Gambar.II.10 : Analogi Selaput Sabun (Soap Film Analogy) ... 21

Gambar.II.11 : Titik Simpul dan Elemen ... 24

Gambar.II.12 : Derajat Kebebasan Pada Elemen Grid ... 25

Gambar.II.13 : Transformasi ke Sumbu Global ... 26

Gambar.II.14 : Elemen Torsi Dengan Tampang Sembarang ... 27

Gambar.II.15 : Potongan Melintang Suatu Elemen Torsi ... 29

Gambar.II.16 : Potongan Melintang Elemen Torsi ... 32

Gambar.III.1 : Tampang Persegi ... 36

Gambar.IV.1 : Ilustrasi Sistem Balok Bersilang ... 53

Gambar.IV.2 : Denah ... 53

Gambar.IV.3 : Beban Segitiga Pada Lantai ... 53

Gambar.IV.4 : Beban Lantai yang Dipikul Balok ... 54

BAB I

PENDAHULUAN

I.1. Latar Belakang Masalah

Selama ini masalah torsi sangat jarang dibahas dalam teknik sipil. Umumnya beban-beban yang dikenal dan diperhitungkan dalam struktur adalah berupa gaya aksial dan beban vertikal. Hal ini disebabkan karena pengaruh torsi ini memang sangat kecil dan dapat diabaikan bila bentuk bangunan simetri. Dan mengingat bentuk-bentuk bangunan lazimnya memang memiliki bentuk yang beraturan, maka pengaruh torsi ini menjadi kurang berpengaruh.

Namun, dengan berkembangnya konstruksi yang tidak lagi simetri, maka beban torsi pun mulai menentukan terhadap struktur sebuah bangunan. Beban torsi tidak dapat lagi diabaikan.

Walaupun jarang dibahas dalam kuliah perencanaan, namun sebenarnya torsi selalu terjadi pada komponen-komponen bangunan seperti balok dan kolom. Beban-beban dari pelat lantai dan balok anak akan menimbulkan suatu momen torsi tertentu pada balok. Sedangkan pada kolom, momen torsi akan terjadi jika ada gaya horizontal yang terjadi. Sebagai contoh gaya horizontal ini yaitu gaya gempa maupun gaya angin.

Dalam pembahasan tentang gempa juga, torsi merupakan suatu hal yang sangat berbahaya terhadap struktur bangunan. Dalam setiap perencanaan yang dianalisis dengan analisis dinamik, mode yang paling dihindari sebagai mode pertama dari suatu struktur adalah torsi. Jika hal ini sampai terjadi, maka bangunan tidak akan dapat bertahan.

Hal-hal di atas telah memberikan beberapa gambaran akan pentingnya gaya torsi untuk ikut diperhitungkan dalam suatu perencanaan struktur bangunan.

Bentuk pembahasan mengenai torsi yang paling sederhana yaitu pengaruh torsi pada tampang bulat. Pembahasan ini banyak kita jumpai dari beberapa literatur. Dan pembahasannya pun cukup sederhana. Berbeda dengan tampang bulat, pengaruh torsi pada tampang persegi panjang menjadi suatu permasalahan yang cukup kompleks untuk dibahas.

Namun, pada struktur-struktur bangunan, tentu saja tampang persegi panjang sering dijumpai terutama pada struktur bangunan beton bertulang, khususnya balok. Kolom berbentuk persegi panjang juga banyak dijumpai. Oleh karena itu, dalam tugas akhir ini, Penulis akan menjabarkan beberapa besaran yang berhubungan dengan torsi yang kemudian akan digunakan dalam perencanaan struktur beton bertulang yaitu tegangan torsi dan inersia torsi.

I.2. Permasalahan

Yang menjadi permasalahan yang akan dibahas dalam tugas akhir ini adalah bagaimana cara mendapatkan suatu fungsi torsi untuk tampang persegi. Fungsi torsi ini kemudian akan diperlukan untuk menghitung tegangan geser yang terjadi pada suatu tampang persegi dimana besarnya tegangan geser torsi adalah turunan pertama dari fungsi torsi terhadap panjang sisi persegi.

Fungsi torsi ini akan diturunkan dari suatu persamaan umum torsi dengan memasukkan kondisi-kondisi batas untuk bentuk persegi. Kemudian persamaan ini akan diselesaikan hingga diperoleh suatu fungsi torsi yang kemudian dapat digunakan untuk menghitung tegangan geser puntir maupun inersia torsi untuk tampang persegi.

I.3. Maksud dan Tujuan

Adapun maksud dan tujuan utama penulisan tugas akhir ini adalah untuk memperoleh tabel-tabel praktis yang dapat digunakan untuk perhitungan tegangan torsi dan inersia torsi pada tampang persegi panjang dengan perbandingan ukuran panjang (b) dan lebar (a) tampang yang bervariasi. Tabel-tabel yang dibuat dalam tugas akhir ini adalah tabel yang berisikan nilai-nilai konstanta yang diperlukan untuk memudahkan perhitungan besaran-besaran seperti tegangan torsi, momen torsi, inersia torsi, serta hubungan antara momen torsi dengan tegangan torsi.

Hubungan antara momen torsi dan tegangan torsi diperlukan karena pada umumnya melalui analisa struktur yang diperoleh terlebih dahulu adalah gaya-gaya dalam pada suatu komponen struktur dimana momen torsi termasuk salah satunya. Dari nilai momen yang diperoleh kemudian dengan bantuan tabel yang diperoleh dari tugas akhir ini, besarnya tegangan geser pada suatu tampang persegi dapat diperoleh dengan mudah.

Tugas akhir ini juga bertujuan untuk memberikan gambaran akan pentingnya analisis torsi pada suatu bangunan khususnya pada suatu elemen grid, contohnya sistem balok anak. Dari hasil-hasil analisis yang diperoleh, pada akhir tugas akhir ini akan diberikan sebuah contoh aplikasi analisis torsi pada suatu elemen grid dalam menghitung momen torsi yang terjadi serta bagaimana cara merencanakan tulangan untuk menahan momen torsi ini.

I.4. Pembatasan Masalah

Dalam tugas akhir ini akan dibahas mengenai analisis torsi pada tampang persegi dimana penurunan deformasi torsinya akan diturunkan dengan menggunakan bantuan tampang lingkaran, sedangkan untuk menentukan persamaan torsi didasarkan kepada Hukum Hooke dengan menggunakan bantuan Metode Semi-Invers Saint Venant dan penurunan fungsi torsinya didasarkan pada metode Prandtl (Soap Film Analogy).

tugas akhir ini. Sehingga pembahasan tentang struktur beton bertulang secara terperinci tidak termasuk di dalam tugas akhir ini.

Model yang digunakan untuk aplikasi dari hasil analisis torsi ini adalah model sistem balok bersilang dimana biasanya momen torsi yang terjadi cukup besar untuk diperhitungkan. Bahan yang digunakan adalah beton bertulang. Analisis struktur dilakukan dengan Finite Element Methode untuk elemen grid. Kontrol analisis struktur dengan menggunakan program SAP2000. Perencanaan tulangan untuk torsi didasarkan pada SNI-03-2847-2002.

I.5. Metodologi Pembahasan

Metode yang digunakan dalam penulisan tugas akhir ini adalah literatur yaitu dengan mengumpulkan data-data dan keterangan dari buku-buku yang berhubungan dengan pembahasan pada tugas akhir ini serta masukan-masukan dari dosen pembimbing. Untuk perhitungan tabel-tabel dilakukan dengan bantuan program Microsoft Excel 2007. Sedangkan untuk perhitungan gaya-gaya dalam yang terjadi pada komponen struktur dilakukan dengan metode Finite Element yang kemudian hasilnya akan dikontrol dengan bantuan program SAP2000.

Berikut ini adalah metodologi dalam penulisan Tugas Akhir ini : I. Pendahuluan

I.1. Latar Belakang Masalah I.2. Permasalahan

II. Tinjauan Pustaka

II.1. Dasar-Dasar Teori II.1.1. Pengantar Torsi II.1.2. Elastisitas II.1.3. Tegangan II.1.4. Regangan II.1.5. Hukum Hooke

II.1.6. Analogi Membrane Elastic oleh Prandtl (Soap Film Analogy) II.1.7. Metode Elemen Hingga Untuk Elemen Grid

II.2. Analisis Torsi Pada Tampang Sembarang II.2.1. Metode Semi-Invers Saint-Venant

II.2.2. Hubungan Antara Momen Torsi Dengan Fungsi Torsi II.3. Torsi Pada Beton Bertulang

III. Analisis Torsi Pada Tampang Persegi III.1. Fungsi Torsi

III.2. Tegangan Torsi III.3. Inersia Torsi

III.4. Hubungan Antara Momen Torsi Dengan Tegangan Torsi Maksimum IV. Cara Penggunaan Tabel

IV.1.Penggunaan Tabel III.1, Tabel.III.2, dan Tabel.III.3 Untuk Menghitung Besarnya Tegangan Geser Maksimum Pada Suatu Tampang Persegi IV.2.Penggunaan Tabel.III.4 Untuk Menghitung Besarnya Inersia Torsi Pada

IV.3.Penggunaan Tabel.III.5 Untuk Menghitung Besarnya Tegangan Geser Maksimum Arah zy Pada Suatu Tampang Persegi Jika Besarnya Momen Torsi yang Telah Diperoleh

V. Aplikasi Analisis Torsi Pada Tampang Persegi dan Pembahasan

V.1. Aplikasi Besaran Inersia Torsi Dalam Menghitung Gaya Dalam Pada Sistem Balok Bersilang dari Beton Bertulang

V.2. Aplikasi Besaran Tegangan Torsi Dalam Menghitung Tegangan Geser Maksimum yang Terjadi Pada Tampang Persegi

V.3. Pembahasan VI. Penutup

BAB II

TINJAUAN PUSTAKA

II.1. Dasar-Dasar Teori 1.1. Pengantar Torsi

Torsi adalah puntir yang terjadi pada batang lurus apabila batang tersebut dibebani momen yang cenderung menghasilkan rotasi terhadap sumbu longitudinal batang. Sebagai contoh dalam kehidupan sehari-hari yaitu jika seseorang memutar obeng, maka tangannya memberikan torsi ke obeng.

Demikian pula halnya dengan komponen struktur suatu bangunan. Jika diperhatikan lebih seksama, sebenarnya balok-balok pada bangunan mengalami torsi akibat beban-beban pada pelat. Demikian pula halnya dengan kolom. Namun torsi pada kolom kebanyakan diakibatkan oleh gaya-gaya yang arahnya horizontal seperti gaya angin ataupun gempa. Berikut ini beberapa ilustrasi yang memperlihatkan adanya torsi yang terjadi pada balok dan kolom.

Torsi timbul karena adanya gaya-gaya yang membentuk kopel yang cenderung memuntir batang terhadap sumbu longitudinalnya. Seperti diketahui dari statika, momen kopel merupakan hasil kali dari gaya dan jarak tegak lurus antara garis kerja gaya. Satuan untuk momen pada USCS adalah (lb-ft) dan (lb-in), sedangkan untuk satuan SI adalah (N.m).

yaitu dengan menggunakan tangan kanan, empat jemari selain jempol dilipat untuk menunjukkan momen sehingga jempol akan menunjuk ke arah vektor. Representasi momen yang lain adalah dengan menggunakan panah lengkung yang mempunyai arah torsi. Lihat Gambar.II.2.

Berat Pelat Balok

Balok

T

Gambar.II.1.Ilustrasi Torsi yang Terjadi Pada Pelat dan Balok Beban Angin

atau Gempa

Beban Angin atau Gempa

T

P

T

T

P

T

T

Momen yang menghasilkan puntir pada suatu batang disebut momen puntir atau momen torsi. Batang yang menyalurkan daya melalui rotasi disebut poris atau as (shaft). Dalam tugas akhir ini, shaft yang akan dibahas secara khusus adalah shaft yang berbentuk persegi yang dalam bidang teknik struktur bangunan banyak dijumpai yaitu pada balok dan kolom struktur beton bertulang.

1.2. Elastisitas

Elastisitas ialah sifat suatu bahan apabila gaya luar mengakibatkan perubahan bentuk (deformation) tidak melebihi batas tertentu, maka perubahan bentuk akan hilang setelah gaya dilepas. Hampir semua bahan teknik memiliki sifat elastisitas ini.

Dalam pembahasan torsi dalam tugas akhir ini, bahan-bahan akan dianggap bersifat elastis sempurna yaitu benda akan kembali seperti semula secara utuh setelah gaya yang bekerja padanya dilepas.

1.3. Tegangan

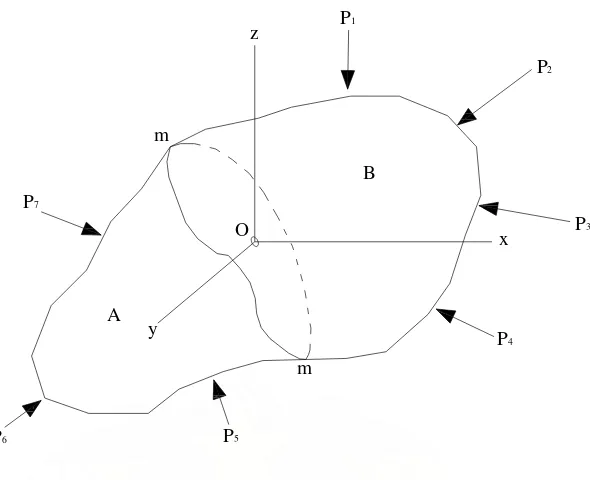
Tegangan didefinisikan sebagai intensitas gaya yang bekerja pada tiap satuan luas bahan. Untuk menjelaskan ini, maka akan ditinjau sebuah benda yang dalam keadaan setimbang seperti terlihat pada Gambar.II.3. Akibat kerja gaya luar

P1, P2, P3, P4, P5, P6, dan P7, maka akan terjadi gaya dalam di antara benda. Untuk

Kemudian tinjaulah salah satu bagian ini, misalnya A. Bagian ini dapat dinyatakan dalam keadaan setimbang akibat gaya luar P1, P2, P3, P4, P5, P6, P7 dan

gaya dalam terbagi di sepanjang penampang mm yang merupakan kerja bahan. Oleh karena intensitas distribusi ini, tegangan dapat diperoleh dengan membagi gaya tarik total P dengan luas potongan penampang A.

Untuk memperoleh besar gaya yang bekerja pada luasan kecil δ_{A, misalnya}

dari potongan penampang mm pada titik O, dapat diamati bahwa gaya yang bekerja pada elemen luas ini diakibatkan oleh kerja bahan bagian B terhadap bahan bagian A

yang dapat diubah menjadi sebuah resultante δ_{P. Apabila tekanan terus diberikan}

pada luas elemen δ_{A, harga batas} δ_P/δ_{A akan menghasilkan besar tegangan yang}

bekerja pada potongan penampang mm pada titik O. arah batas resultante δ_{P adalah}

arah tegangan.

z

x

y

P1

P2

P3

P4

P5 P6

P7

Gambar.II.3.Benda Tampang Sembarang yang Dibebani oleh Gaya-Gaya Luar m

m

O

B

Umumnya, arah tegangan ini miring terhadap luas δ_{A tempat gaya bekerja}

sehingga dapat diuraikan menjadi dua komponen tegangan yaitu tegangan normal

yang tegak lurus terhadap luas dan tegangan geser yang bekerja pada bidang luas δ_A.

Tegangan normal dinotasikan dengan huruf σ _{dan tegangan geser dengan}

huruf τ_{. Untuk menunjukkan arah bidang dimana tegangan tersebut bekerja,}

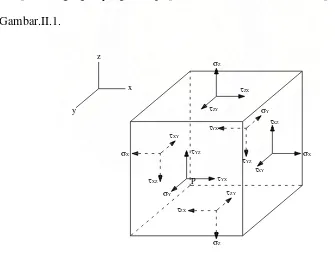
digunakan subskrip terhadap huruf-huruf ini. Tegangan normal menggunakan sebuah subskrip yang menunjukkan arah tegangan yang sejajar terbadap sumbu koordinat tersebut, sedangkan tegangan geser menggunakan dua buah subskrip dimana huruf pertama menunjukkan arah normal terhadap bidang yang ditinjau dan huruf kedua menunjukkan arah komponen tegangan. Gambar.II.4 menunjukkan arah komponen-komponen tegangan yang bekerja pada suatu elemen kubus kecil pada titik O pada Gambar.II.1.

Untuk menjelaskan tegangan yang bekerja pada keenam sisi elemen ini diperlukan tiga simbol σ_x, σ_y, σ_{z untuk tegangan normal dan enam simbol} τ_xy, τ_yx, τ_xz,

Gambar.II.4.Komponen-Komponen Tegangan yang Bekerja Pada Potongan Kubus Kecil z

x y

σZ

τZX

τZY

τYZ

σX

τXY τYX

τXZ σY

σY τYZ

τYX τXY

σX

τXZ

τZY

τZX

σZ

τ_zx, τ_yz, τ_{zy untuk tegangan geser. Dengan meninjau kesetimbangan elemen secara}

sederhana, maka jumlah simbol tegangan geser dapat dikurangi menjadi tiga.

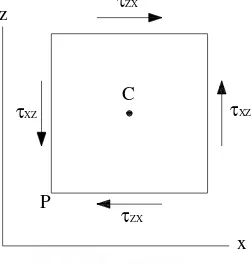
Apabila momen gaya yang bekerja pada elemen terhadap garis yang melalui titik tengah C dan sejajar sumbu x, maka hanya tegangan permukaan yang diperlihatkan pada Gambar.II.5 yang perlu ditinjau. Gaya benda, seperti berat elemen, dapat diabaikan karena semakin kecil ukuran elemen, maka gaya benda yang bekerja padanya berkurang sebesar ukuran linier pangkat tiga. Sedangkan gaya permukaan berkurang sebesar ukuran linier kuadrat. Oleh karena itu, untuk elemen yang sangat kecil, besar gaya benda sangat kecil jika dibandingkan dengan gaya permukaan sehingga dapat dihilangkan ketika menghitung momen.

Dengan cara yang sama, orde momen akibat ketidak-merataan distribusi gaya normal lebih tinggi dibandingkan dengan orde momen akibat gaya geser dan menjadi nol dalam limit. Juga gaya pada masing-masing sisi dapat ditinjau sebagai luas sisi kali tegangan di tengah. Jika ukuran elemen kecil pada Gambar.II.5 adalah

dx, dy, dz, maka momen gaya terhadap P, maka persamaan kesetimbangan elemen ini adalah :

τ_{xzdx dy dz =} τ_{zxdx dy dz (II.1)}

z

x C

P

τZX

τXZ

τZX

τXZ

Dua persamaan lain dapat diperoleh dengan cara yang sama sehingga didapatkan :

τ_{xy =} τ_yx τ_{zx =} τ_xz τ_{zy =} τ_{yz (II.2)}

Dengan demikian enam besaran σ_x, σ_y, σ_z, τ_{xy =} τ_yx, τ_{zx =} τ_xz, τ_{zy =} τ_{yz cukup}

untuk menjelaskan tegangan yang bekerja pada koordinat bidang melalui sebuah titik. Besaran-besaran ini disebut komponen tegangan pada suatu titik.

Jika kubus pada Gambar II.5 diberikan suatu komponen gaya per satuan volume sebesar X, Y, Z pada masing-masing sumbu x, y, dan z maka gambar komponen tegangan dalam Gambar.II.5 akan menjadi seperti pada Gambar.II.6 di bawah ini dan persamaan kesetimbangan akan dapat diperoleh dengan menjumlahkan semua gaya pada elemen dalam arah x yaitu :

[(σ_{x +} σ_{x) –} σ_{x] y z + [(}τ_{yx +} τ_{yx) –} τ_{yx] x z + [(}τ_{zx +} τ_{zx) –} τ_{zx] x y + X x y z= 0}

[(σ_{y +} σ_{y) –} σ_{y] x z + [(}τ_{xy +} τ_{xy) –} τ_{xy] y z + [(}τ_{zy +} τ_{zy) –} τ_{zy] x y + Y x y z= 0}

[(σ_{z +} σ_{z) –} σ_{z] x y + [(}τ_{xz +} τ_{xz) –} τ_{xz] y z + [(}τ_{yz +} τ_{yz) –} τ_{yz] x z + Z x y z= 0}

Gambar.II.6.Komponen-Komponen Tegangan yang Bekerja Pada Potongan Kubus Kecil Dimana Gaya Luar Per Satuan Volume X, Y, Z Bekerja

z

x

y

σZ+ σZ

τZX + τZX

τYZ

τYX

σY

τXY

σX

τXZ

τZY

τZX

σZ

P τZY + τZY

σY+ σY

τYZ + τYZ

τYX + τYX

σX+ σX

τXZ + τXZ

Sesudah dibagi dengan x, y, z, dan seterusnya hingga batas penyusutan elemen hingga titik x, y, z maka akan didapatkan :

+ + + = 0

+ + + = 0 (II.3)

+ + + = 0

Persamaan (II.3) ini harus dipenuhi di semua titik di seluruh volume benda. Tegangan berubah di seluruh volume benda, dan apabila sampai pada permukaan, tegangan-tegangan ini harus sedemikian rupa sehingga setimbang dengan gaya luar yang bekerja pada permukaan benda.

1.4. Regangan

Regangan didefinisikan sebagai suatu perbandingan antara perubahan dimensi suatu bahan dengan dimensi awalnya. Karena merupakan rasio antara dua panjang, maka regangan ini merupakan besaran tak berdimensi, artinya regangan tidak mempunyai satuan. Dengan demikian, regangan dinyatakan hanya dengan suatu bilangan, tidak bergantung pada sistem satuan apapun. Harga numerik dari regangan biasanya sangat kecil karena batang yang terbuat dari bahan struktural hanya mengalami perubahan panjang yang kecil apabila dibebani.

Pada pembahasan ini yang ditinjau hanya perubahan bentuk yang kecil yang biasa terjadi pada struktur teknik. Perpindahan kecil pertikel yang berubah bentuk ini diuraikan ke dalam komponen u, v, w berturut-turut sejajar dengan sumbu koordinat. Besar komponen ini dianggap sangat kecil dan bervariasi di seluruh volume benda.

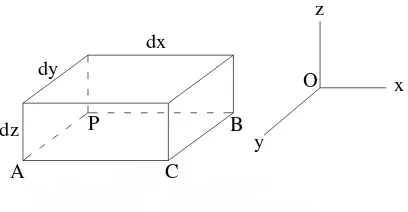
[image:31.595.223.427.199.305.2]

Tinjau elemen kecil dx dy dz dari sebuah benda elastis seperti terlihat pada Gambar.II.7. Apabila benda mengalami perubahan bentuk dan u, v, w merupakan komponen perpindahan titik P, perpindahan titik di dekatnya , A, dalam arah x pada sumbu x adalah orde pertama dalam dx, yaitu u + ( u/ x) dx akibat pertambahan fungsi u sebesar ( u/ x) dx sesuai dengan pertambahan panjang elemen PA akibat perubahan bentuk adalah ( u/ x) dx. Sedangkan satuan perpanjangan (unit elongation) pada titik P dalam arah x adalah ( u/ x). Dengan cara yang sama, maka diperoleh satuan perpanjangan dalam arah y dan z adalah ( v/ y) dan ( w/ z).

z

x

y O

dz

dx dy

A C

B P

[image:32.595.249.398.88.226.2]

Sekarang tinjaulah pelentingan sudut antara elemen PA dan PB dalam Gambar.II.8. Apabila u dan v adalah perpindahan titik P dalam arah x dan y, perpindahan titik A dalam arah y dan titik B dalam arah x berturut-turut adalah

v + ( v/ x) dx dan u + ( u/ y) dy. Akibat perpindahan ini, maka P’A’ merupakan arah baru elemen PA yang letaknya miring terhadap arah awal dengan sudut kecil yang ditunjukkan pada gambar, yaitu sama dengan ( v/ x). Dengan cara yang sama arah P’B’ miring terhadap PB dengan sudut kecil ( u/ y). Dari sini dapat dilihat bahwa sudut awal APB yaitu sudut antara kedua elemen PA dan PB berkurang sebesar ( v/ x) + ( u/ y). Sudut ini adalah regangan geser (shearing strain) antara bidang xz dan yz. Regangan geser antara bidang xy dan xz dan bidang yx dan yz dapat diperoleh dengan cara yang sama.

Selanjutnya kita menggunakan huruf Є_{untuk satuan perpanjangan dan huruf}

γ untuk regangan geser. Untuk menunjukkan arah regangan digunakan subskrip yang sama terhadap huruf ini sama seperti untuk komponen tegangan. Kemudian diperoleh dari pembahasan di atas beberapa besaran berikut :

O

y

x

dx

dy

v u

P'

A'

B'

v v + x dx

u u + y dy

B

A P

∈ = ∈ = ∈ =

= = + = = + = = + (II.4)

Keenam besaran ini disebut sebagai komponen regangan geser.

1.5. Hukum Hooke

Hubungan linier antara komponen tegangan dan komponen regangan umumnya dikenal sebagai hukum Hooke. Satuan perpanjangan elemen hingga batas proporsional diberikan oleh

∈ = !" (II.5)

dimana E adalah modulus elastisitas dalam tarik (modulus of elasticity in tension). Bahan yang digunakan di dalam struktur biasanya memiliki modulus yang sangat besar dibandingkan dengan tegangan izin, dan besarnya perpanjangan sangat kecil. Perpanjangan elemen dalam arah x ini akan diikuti dengan pengecilan pada komponen melintang yaitu

∈ = − !_{" ∈ = − !"} (II.6)

dimana adalah suatu konstanta yang disebut dengan ratio Poisson (Poisson’s Ratio). Untuk sebagian besar bahan, ratio poisson dapat diambil sama dengan 0,25. Untuk baja struktur biasanya diambil sama dengan 0,3.

Apabila elemen di atas mengalami kerja tegangan normal σ_x, σ_y, σ_{z secara}

serempak, terbagi rata di sepanjang sisinya, komponen resultante regangan dapat diperoleh dari persamaan (II.5) dan (II.6) yaitu :

∈ = 1"%! − &! + ! '(

∈ = 1"%! − )! + ! *(

(II.7)

Pada persamaan (II.7), hubungan antara perpanjangan dan tegangan sepenuhnya didefinisikan oleh konstanta fisik yaitu E dan . Konstanta yang sama dapat juga digunakan untuk mendefinisikan hubungan antara regangan geser dan tegangan geser.

Tinjaulah kasus khusus yaitu perubahan bentuk segi empat paralelogram di mana σ_{z =} σ_, σ_{y = –}σ _{, dan} σ_{x = 0. Potonglah sebuah elemen abcd dengan bidang yang}

sejajar dengan sumbu x dan terletak 45˚ terhadap sumbu y dan z (Gambar.II.9). Dengan menjumlah gaya sepanjang dan tegak lurus bc, bahwa tegangan normal pada sisi elemen ini nol dan tegangan geser pada sisi adalah :

τ

_{= ½ (}σ_{z –} σ_{y) =} σ _(II.8)

Kondisi tegangan seperti itu disebut geser murni (pure shear). Pertambahan panjang elemen tegak Ob sama dengan berkurangnya panjang elemen mendatar Oa dan Oc, dan dengan mengabaikan besaran kecil dari orde kedua, kita bisa menyimpulkan bahwa panjang elemen ab dan bc tidak berubah selama terjadinya perubahan bentuk. Sudut antara sisi ab dan bc berubah dan besar regangan geser yang bersangkutan γ

bisa diperoleh dari segi tiga Obc. Sedudah perbuahan bentuk akan didapatkan : b

y z

d a 45° o c

b

c o

σ

σ τ τ

τ τ

[image:34.595.153.453.200.424.2]

τ

+,

+- = tan 124 −25 =1 + 61 + 6

Untuk γ yang kecil, tan (γ/2) ≈γ/2, maka :

+,

+- = tan 124 −25 =_{1 + tan 24 tan}tan 24 − tan2₂=1 − 2_{1 + 2}=1 + 61 + 6

Maka diperoleh :

6 = − 2 dan 6 = 2

Sedangkan jika nilai-nilai σ_{z =} σ_, σ_{y = –}σ _{, dan} σ_{x = 0 disubstitusikan ke dalam}

persamaan (II.7) maka akan diperoleh :

∈ = 1")−! − !* = −&1+" '!= − 2

∈ = 1"7! − )−!*8 =&1+"'!= 2

Maka diperoleh hubungan antara regangan dengan regangan geser :

∈ = 2

(II.9)

Hubungan antara regangan dan tegangan geser didefinisikan oleh konstanta E dan v

yaitu :

= 2&1+_" '!= 2&1+_" '9 (II.10)

Jika digunakan notasi :

: =_2&1+" _' (II.11)

Maka persamaan (II.10) akan menjadi :

= 9: (II.12)

Apabila tegangan geser bekerja ke semua sisi elemen, seperti terlihat pada Gambar.II.5, pelentingan sudut antara dua sisi yang berpotongan hanya tergantung kepada komponen tegangan geser yang bersangkutan dan diperoleh :

= 9: = 9:

= 9:

1.6. Analogi Membrane Elastic oleh Prandtl (Soap Film Analogy)

Untuk pembahasan analogi membran ini, potonglah suatu bukaan pada potongan melintang dari elemen yang mengalami torsi untuk diselidiki. Anggaplah bukaan ini ditutupi oleh sejenis membran elastis yang homogen, seperti selaput sabun, dan kerjakan suatu tekanan pada salah satu sisi membran.

Kemudian tinjaulah suatu elemen membran elastis ABCD dengan dimensi

dx dy seperti ditunjukkan pada Gambar.II.10. Dengan menggunakan z sebagai besaran perpindahan lateral dari membran elastis, p adalah tekanan lateral dalam

y

x O

A B C D

dx dy

z

x O

S

S _α α

+ x dx

[image:36.595.155.441.339.594.2]

α

Gambar.II.10.Analogi Selaput Sabun (Soap Film Analogy)

gaya per satuan luas, dan S sebagai tegangan inisial dalam gaya per satuan panjang, maka gaya vertikal murni yang diakibatkan oleh tegangan S yang bekerja sepanjang sisi AD dan BC dari membran (dengan mengasumsikan perpindahan yang terjadi adalah sangat kecil sehingga nilai sinα≈ tanα) berturut-turut adalah

−; < sin ? ≈ −; < tan ? = −; <

; < sin A? + ?< B ≈ ; < tan A? + ?< B = ; < A + < B

Dengan cara yang sama akan diperoleh gaya vertikal murni yang diakibatkan oleh tegangan S yang bekerja sepanjang sisi AB dan DC berturut-turut adalah

−; <

; < A + < B

Jika keempat gaya vertikal di atas dijumlahkan maka akan diperoleh persamaan membran untuk elemen dx dy adalah sebagai berikut

−; < + ; < A + < B − ; < + ; < A + < B + C < < = 0

; < A < B + ; < A < B = −C < <

; D_D< < + ; D_D< < = −C < <

E E +

E

E = −F_G (II.13)

1.7. Metode Elemen Hingga Untuk Elemen Grid

Metode elemen hingga merupakan salah satu metode yang digunakan untuk menghitung gaya-gaya dalam yang terjadi dalam suatu komponen struktur. Metode elemen hingga juga dikenal sebagai metode kekakuan ataupun displacement methode

karena yang didapat terlebih dahulu dari perhitungan adalah perpindahan baru kemudian gaya batang dicari.

Dalam hubungannya dengan tugas akhir ini, metode elemen hingga ini digunakan untuk menganalisis atau menghitung besarnya momen torsi yang terjadi dalam komponen struktur. Untuk itu, metode elemen hingga yang digunakan adalah metode elemen hingga untuk elemen grid dimana gaya yang bekerja pada struktur yang diperhitungkan hanya terbatas pada gaya vertikal, momen lentur dan momen torsi.

Persamaan umum untuk metode elemen hingga ini adalah : HIJ = 7K8H<J − HILMNJ

(II.14)

dimana : {f} = Matriks gaya-gaya batang ( kg ) [k] = Matriks kekakuan struktur ( N/m2 ) {d} = Matriks perpindahan ( m dan rad )

{fred} = Matriks gaya-gaya pada titik simpul akibat beban merata

Derajat kebebasan adalah jumlah komponen perpindahan yang dapat terjadi pada kedua simpul yang ada pada suatu elemen. Jumlah derajat kebebasan berbeda-beda untuk tiap jenis struktur. Misalnya, untuk elemen rangka, jumlah derajat kebebasannya adalah dua yaitu masing-masing satu perpindahan dalam arah sumbu batang ( biasanya disebut sebagai sumbu 1 ) pada titik simpul (1) dan (2).

Dari jumlah derajat kebebasan yang ada, suatu matriks kekakuan untuk suatu jenis struktur dapat ditentukan. Masing-masing jenis struktur memiliki suatu matriks kekakuan tersendiri dimana matriks kekakuan untuk elemen rangka berbeda dengan matriks kekakuan untuk elemen frame dan lain-lainnya. Begitu pula halnya dengan matriks kekakuan untuk elemen grid. Matriks kekakuan dari elemen grid dapat diperoleh dengan menggabungkan matriks kekakuan dari elemen batang ( memiliki 4 derajat kebebasan ) dengan matriks kekakuan untuk elemen torsi murni.

Kekakuan dalam suatu struktur terbagi dalam dua jenis yaitu kekakuan lokal dan kekakuan global. Kekakuan lokal adalah kekakuan elemen yang mengacu arah sumbu masing-masing elemen sedangkan kekakuan global adalah kekakuan elemen yang mengacu pada sistem koordinat global yaitu sistem koordinat kartesian (XYZ). Jika dalam suatu struktur terdapat lebih dari satu batang dengan arah sumbu lokal yang berbeda, maka maka kekakuan lokal dari tiap elemen harus diubah menjadi kekakuan global agar matriks kekakuan dari semua elemen yang ada dapat digabungkan.

Gambar.II.11.Titik Simpul dan Elemen

Untuk elemen grid, seperti yang telah disebutkan di atas, kekakuan lokalnya merupakan gabungan dari kekakuan lokal untuk elemen batang dengan kekakuan lokal untuk elemen torsi murni. Berikut ini adalah matriks kekakuan yang disebutkan di atas :

• Matriks kekakuan lokal untuk elemen batang (Frame Element)

7K8 ="OPQR 12 6P −12 6P 6P 4PD −6P 2PD −12 −6P 12 −6P 6P 2PD −6P 4PD T

• Matriks kekakuan lokal untuk elemen torsi murni 7K8 =:U_{P V−1 1 W}1 −1

• Matrik kekakuan lokal untuk elemen grid

7K8 = X Y Y Y Y Y Y Y Y Y Y Y

Z12"O_PQ 0 6"O_PD

0 :U_P 0 6"O

PD 0 4"O_P

−12"O_PQ 0 6"O_PD

0 −:U_P 0

−6"O_PD 0 4"O_P −12"O_PQ 0 −6"O_PD

0 −:U_P 0

6"O

PD 0 4"O_P

12"O

PQ 0 −6"O_PD

0 :U_P 0 −6"O_PD 0 4"O_{P [}\

\ \ \ \ \ \ \ \ \ \ ]

Kekakuan lokal dari semua jenis struktur dapat diubah menjadi kekakuan global dengan menggunakan persamaan :

%K^( = 7_87K87_8`a

ΕΙ GJ Sy1

Μz1

Mx1

Sy2

Μz2

Mx2

[image:40.595.115.456.321.636.2]

L

dimana [T] merupakan matriks transformasi yang berbeda-beda untuk jenis struktur tertentu dan [T]-1 merupakan invers dari matriks transformasi.

Matriks transformasi untuk elemen grid dapat disusun dengan mengacu pada Gambar.II.13 sehingga diperoleh :

7_8 = X Y Y Y Y Z1₀

0 0 0 0 0 cos ? sin ? 0 0 0 0 − sin ?

cos ? 0 0 0 0 0 0 1 0 0 0 0 0 0 cos ? sin ? 0 0 0 0 − sin ?

cos ? [\ \ \ \ ]

7_8`a₌

X Y Y Y Y Z1₀

0 0 0 0 0 cos ? − sin ?

0 0 0 0 sin ? cos ? 0 0 0 0 0 0 1 0 0 0 0 0 0 cos ? − sin ?

0 0 0 0 sin ? cos ?[\

\ \ \ ]

Setelah matriks kekakuan diperoleh maka gaya-gaya batang untuk elemen grid dapat dihitung dengan terlebih dahulu menghitung besarnya perpindahan yang terjadi pada titik-titik simpul dengan menggunakan persamaan (II.14) :

[image:41.595.141.503.188.592.2]

z X α My2 My1 Mx1 V2 Mx2 V1 1 2 y

HIJ = 7K8H<J − HILMNJ

d ee f ee g_iha

a

i _a hD

i _D i _Djee

k ee l = X Y Y Y Y Y Y Y Y Y Y Y

Z12"OPQ 0 6"OPD

0 :U_P 0 6"O

PD 0 4"O_P

−12"O_PQ 0 6"O_PD

0 −:U_P 0

−6"O_PD 0 4"O_P

−12"O_PQ 0 −6"O_PD

0 −:U_P 0

6"O

PD 0 4"O_P

12"O

PQ 0 −6"O_PD

0 :U_P 0 −6"O_PD 0 4"O_{P [}\

\ \ \ \ \ \ \ \ \ \ ] d e f e g_ma_a

na D

mD

nDje

k e l − d ee f ee g_iha LMN

a LMN

i _{a LMN} hD LMN

i _{D LMN} i _{D LMNj}ee

k ee l

(II.15)

Setelah nilai-nilai perpindahan diperoleh dari persamaan (II.15), maka gaya-gaya dalam untuk tiap elemen dapat dicari dengan menggunakan persamaan (II.14).

II.2. Analisis Torsi Pada Tampang Sembarang 2.1. Metode Semi-Invers Saint-Venant

Anggap suatu bahan yang menalami torsi dengan suatu potongan melintang seragam dari tampang sembarang seperti terlihat pada Gambar.II.14. Tegangan yang didistribusikan pada ujung-ujung yaitu τ_{zx dan} τ_{zy akan menghasilkan torsi sebesar T.}

y y x O z P P' β T z

[image:42.595.154.487.80.274.2]

Sebelum Berubah Bentuk Setelah Berubah Bentuk

pada umumnya, semua distribusi tegangan pada ujung potongan akan menghasilkan torsi.

Menurut Saint-Venant, distribusi tegangan pada potongan yang cukup jauh dari ujung bergantung hanya pada besar momen torsi dan tidak tergantung pada distribusi tegangan pada ujungnya. Oleh karena itu, untuk suatu element torsi panjang, distribusi tegangan pada ujung tidak akan mempengaruhi distribusi pada bagian makro dari elemen torsi.

Metode Saint-Venant dimulai dengan suatu perkiraan komponen perpindahan akibat torsi. Perkiraan ini didasarkan kepada perubahan geometri yang terjadi pada elemen torsi yang terdeformasi. Saint-Venant mengasumsikan tiap elemen torsi lurus dengan tampang tetap selalu memiliki suatu sumbu putar yang tegak lurus terhadap potongan melintangnya yang bertindak sebagai poros kaku pada pusatnya. Dalam hal ini, poros diambil sejajar dengan sumbu z.

Tinjau suatu titik P dengan koordinat (x, y, z) dari pusat O sebelum mengalami deformasi. Setelah mengalami deformasi akibat torsi, P bergerak ke P’. P

Dengan mengacu pada Gambar.II.15, diperoleh : = o_{− = +p7cos)? + m* − cos ?8}

= +p7cos ? cos m − sin ? sin m − cos ?8 = +p cos ? )cos m − 1* − +p sin ? sin m

= )cos m − 1* − sin m

dan

= o_{− = +p7sin)? + m* − sin ?8}

= +p7sin ? cos m + cos ? sin m − sin ?8 = +p cos ? sin m + +p sin ? )cos m − 1*

= sin m + )cos m − 1*

Untuk perpindahan yang sangat kecil, akan diperoleh nilai-nilai sinβ≈β dan cosβ≈ 1, maka :

u = -yβ = -y θz v = xβ = x θz

Sedangkan untuk komponen w diambil :

w = θψ(x,y) dimana ψ(x,y) adalah fungsi warping.

Setelah komponen perpindahan ini diperoleh, maka kita akan mensubstitusikan nilai-nilai u, v, dan w ini ke dalam persamaan (II.4) dan diperoleh :

P'(x',y') P(x,y)

x

y y'

x'

β α

[image:44.595.209.358.88.243.2]

r

Gambar.II.15.Potongan Melintang Suatu Elemen Torsi x

∈ = = &− '= 0

∈ = = & '= 0

∈ = = % & , '(= 0

= = + = &− '+ & '= − + = 0

= = + = % & , '(+ &− '= r & , '− s

= = + = % & , '(+ & '= r & , '+ s (II.16)

Tinjau kembali persamaan kesetimbangan. Untuk komponen yang mengalami torsi murni, σ_{x = 0,} σ_{y = 0,} σ_{z = 0,} τ_{xy = 0, X = 0, Y = 0, Z = 0 sehingga}

dari persamaan kesetimbangan didapatkan :

= 0 (II.17.a)

= 0 (II.17.b)

+ = 0 (II.17.c)

Persamaan (II.17.a) dan (II.17.b) menunjukkan bahwa τ_{zx dan} τ_{zy tidak}

tergantung pada z. Dan komponen tegangan harus memenuhi persamaan (II.17.c). Oleh karena itu diambil persamaan tegangan geser ini menjadi :

9 = 9 = − (II.18)

Kemudian kedua persamaan di atas disubstitusikan ke persamaan (II.17.c) :

1

t

5

−

1

t

5

= 0

Tinjau kembali persamaan (II.16). Jika masing-masing γzx dan γzy didiferensi parsial kan terhadap y dan x, maka akan diperoleh :

u

= v

V

w) , *−

W

u = v

V

w) , *+

W

u

=

V

Ew) , *− 1

W

(II.19.a) u =

V

E_{w) , *}

+ 1

W

(II.19.b)

Jika persamaan (II.19.a) dengan (II.19.b), maka akan diperoleh : u

− u = −2 (II.20)

Substitusikan hubungan antara regangan geser dengan tegangan geser pada persamaan (II.14) ke dalam persamaan (II.20) maka akan diperoleh :

1

_x

5

−

1

_x

5

= −2

− = −2: (II.21)

Substitusikan persamaan (II.18) ke dalam persamaan (II.21) untuk mendapatkan suatu persamaan yang kemudian akan kita kenal sebagai persamaan torsi :

1

t

5

−

1

t

5

= −2:

E_t E −

E_t

E = −2: (II.22)

Pada bab berikutnya, persamaan (II.22) ini akan digunakan untuk menurunkan fungsi torsi untuk tampang persegi bantuan persamaan analogi membran Prandtl yang telah diturunkan sebelumnya.

ini harus berarah tegak lurus terhadap garis normalnya. Kedua komponen tegangan geser τ_{zx dan} τ_{zy yang bekerja pada potongan melintang dengan sisi-sisi dx, dy, dan}

ds dapat dinyatakan dengan :

τ_{zx =} τ _sinα τ_{zy =} τ _cosα

y

x O

R

S

dy dx

α

s

n ds

α

ds ds

ds α

τ τZY

τZX

y

x O

R S

dy y B

[image:47.595.137.497.166.703.2]

A

Dengan mengacu pada Gambar.II.16

sin ? = <<y cos ? = <<y (II.23)

Karena komponen tegangan geser pada arah n pada gambar pada keliling elemen harus bernilai nol, maka proyeksi τ_{zx dan} τ_{zy dalam arah normal adalah :}

τ_{zx cosα -} τ_{zy sinα = 0 (II.24)}

Substitusikan persamaan (II.18) dan (II.23) ke dalam persamaan (II.24) : t N

Nz + t N

Nz = Nt

Nz = 0

Dari penyelesaian ini menunjukkan bahwa nilai konstan di sepanjang keliling S. Karena tegangan merupakan turunan partial dari , maka nilai konstan ini dapat dianggap nol.

Distribusi τ_{zx dan} τ_{zy pada potongan melintang yang dibahas harus}

memenuhi ketiga persamaan berikut :

∑ | = } 9 < < = } t< < = 0 (II.25.a)

∑ | = } 9 < < = } t< < = 0 (II.25.b)

∑ i = _ = }& 9 − 9 ' < < = − } 1 t+ t5 < < (II.25.c)

2.2. Hubungan Antara Momen Torsi Dengan Fungsi Torsi

Dengan menyelesaikan persamaan (II.25.c), maka akan diperoleh hubungan antara momen torsi dengan fungsi torsi. Ambillah salah satu komponen integral dari persamaan (II.25.c). Karena fungsi tegangan tidak bervariasi dalam arah y untuk sebuah garis setebal dy seperti tampak pada Gambar.II.16, turunan parsial dapat digantikan dengan suatu turunan total sehingga diperoleh :

− ~ < < = −< • <_{< < = −< •}t)€*

t)•* < = −< ‚ |•

€_{− •} „

…

Mengingat nilai pada tepi-tepi elemen (A) = (B) = 0, maka diperoleh :

− ~ < < = ~ < <

Langkah yang sama dilakukan untuk komponen lain dari integaral pada persamaan (II.25.c) sehingga diperoleh :

− ~ < < = ~ < <

Dengan menjumlahkan kedua komponen ini, maka diperoleh hubungan antara momen torsi dengan fungsi torsi yaitu :

_ = − V‡ t< < + ‡ t< < W = 2 ‡ < < (II.24)

II.3. Torsi Pada Beton Bertulang

Pada struktur bangunan, terdapat komponen-komponen struktur yang mengalami gaya puntir atau torsi dan seringkali timbul bersamaan dengan lentur dan geser. Contoh yang paling mudah adalah balok anak. Balok induk terangkai sebagai satu kesatuan rangka monolit dengan balok anak. Sebagai akibat dari sifat kekakuannya, akan timbul momen di tempat dukungan balok anak pada balok induk ini. Momen ini akan mengakibatkan gaya puntir terhadap balok induk.

Akibat dari gaya torsi yang bekerja pada batang berpenampang bulat, permukaan rata penampang transversal akan tetap rata setelah terjadinya puntir. Sedangkan akibat pada komponen struktur yang berpenampang bukan bulat, akan timbul mekanisme gaya dan perilaku kompleks serta rumit, di mana penampang akan memilin dan melipat pada waktu terpuntir.

terjadi pada titik tengah dari sisi yang panjang dan arah kerjanya sejajar dengan sisi tersebut.

Gaya geser torsi akan timbul di permukaan batang terpuntir dan cenderung menyebabkan terjadinya retak tarik diagonal sama seperti yang diakibatkan oleh gaya geser lentur, akan tetapi gaya geser torsi akan bekerja pada arah yang berlawanan untuk sisi penampang yang berhadapan. Karena pada umumnya gaya geser dan torsi muncul secara bersamaan atau bahkan berinteraksi satu sama lain, tinjauan efek gaya tarik diagonal pada satu sisi permukaan penampang batang merupakan penjumlahan dari keduanya.

Apabila kuat tarik beton terlampaui, maka akan dapat dilihat bahwa pada permukaan terjadi retak beton yang kurang lebih membentuk sudut 45˚ terhadap sumbu batang komponen struktur tersebut. Dengan demikian, diperlukan batang tulangan baja untuk dipasang melintang terhadap arah retakan sedemikian sehingga mengahalangi keruntuhan lebih lanjut. Tulangan torsi pada balok umumnya dipasang pada arah memanjang balok dan letaknya disebar merata di sekeliling balok terpuntir.

BAB III

TORSI PADA TAMPANG PERSEGI

III.1.Fungsi Torsi

Fungsi torsi untuk tampang persegi akan diturunkan dengan menggunakan bantuan analogi selaput yang telah dijelaskan dalam BAB II sebelumnya. Tinjau kembali persamaan (II.13) dan (II.20) yang telah dibahan pada BAB II serta kondisi batas pada tepian. Jika kondisi tepi dari z dan φ dibandingkan, maka dapat disimpulkan bahwa kedua persamaan ini identik. Oleh karena itu, lendutan selaput z

dapat disetarakan dengan harga fungsi torsi φ dengan menukarkan besaran –p/s pada persamaan (II.13) dengan besaran 2Gθ pada persamaan (II.20).

Oleh karena itu, maka harga fungsi φ dapat diperoleh dengan menurunkan fungsi z dari persamaan (II.13).

Penurunan Fungsi Lendutan Selaput (z)

• Persamaan lendutan selaput :

E E +

E

E = −F_G (III.1)

• Kondisi batas pada tepi selaput : z = 0

[image:51.595.268.363.626.757.2]

• Geometri selaput yang dibahas adalah bentuk persegi seperti terlihat pada Gambar.III.1

b 2 _

b 2 _

2 2

O x

• Panjang b > a

• Dari kondisi simetri terhadap sumbu y dan kondisi batas pada sisi segiempat

x = ±a/2, maka persamaan (II.13) dapat dipenuhi dengan mengambil nilai z dalam bentuk deret :

= ˆ -‰cosŠ2_‹ ‰ Œ

‰•a,Q,Ž

(III.2)

dimana : bn = koefisien konstanta

Yn = fungsi y yang tidak tergantung pada x

• Pada persamaan (III.1), konstanta di sebelah kanan bisa dinyatakan untuk

–a < x < a dengan deret Fourier :

−C_{; = − ˆ} C_{;Š2 )−1*}4 )‰`a*/D_cosŠ2

‹

Œ

‰•a,Q,Ž

(III.3)

• Turunkan persamaan (III.2) terdapat x sehingga diperoleh : = ˆ -‰cosŠ2_‹ ‰

Œ

‰•a,Q,Ž

= ˆ -‰ Š2_{‹ sin}Š2_‹ ‰ Œ

‰•a,Q,Ž

D

D= − ˆ -‰ 1Š2_{‹ 5} D

cosŠ2_‹ ‰ Œ

‰•a,Q,Ž

(III.4)

• Turunkan persamaan (III.2) terdapat y sehingga diperoleh : = ˆ -‰cosŠ2_‹ ‰

Œ

‰•a,Q,Ž

= ˆ -‰cosŠ2_{‹ ′}‰ Œ

D

D= ˆ -‰cosŠ2_{‹ ′′}‰ Œ

‰•a,Q,Ž

(III.5)

• Subsitusikan persamaan (III.3), (III.4), dan (III.5) ke dalam persamaan (III.1) sehingga diperoleh :

D D+

D D= −C_;

− ˆ -‰ 1Š2_{‹ 5} D

cosŠ2_‹ ‰ Œ

‰•a,Q,Ž

+ ˆ -‰cosŠ2_{‹ ′′}‰ Œ

‰•a,Q,Ž

= − ˆ C_{;Š2 )−1*}4 )‰`a*/D_cosŠ2

‹

Œ

‰•a,Q,Ž

ˆ -‰cosŠ2_‹ Œ

‰•a,Q,Ž

r ′′‰− 1Š2_{‹ 5} D

‰s = −C_{; ˆ Š2 )−1*}4 )‰`a*/DcosŠ2_‹ Œ

‰•a,Q,Ž

′′‰− 1Š2_{‹ 5} D

‰= −C_{;Š 2 -}4 ‰)−1*

)‰`a*/D

(III.6)

• Persamaan (III.6) merupakan persamaan diferensial berordo dua.

• Untuk memperoleh fungsi komplementernya, persamaan pada ruas kiri dipecahkan dengan menganggap persamaan (III.6) sebagai :

‘D_{− 1}Š2

‹ 5

D

= 0

‘D _{= 1}Š2

‹ 5

D

‘ = ± 1Š2_{‹ 5}

Maka fungsi komplementer diperoleh :

‰a= “ cosh ‘ + • sinh ‘

‰a= “ coshŠ2_{‹ + • sinh}Š2_‹

(III.7)

• Untuk memperoleh integral khususnya, misalkan persamaan pada ruas kanan sebagai :

Substitusikan nilai ini ke dalam persamaan (III.6) : ′′‰− 1Š2_{‹ 5}

D

‰= −C_{;Š 2 -}4 ‰)−1*

)‰`a*/D

0 − 1Š2_{‹ 5}D, = −C_{;Š 2 -}4

‰)−1* )‰`a*/D

, =C_;ŠQ4 ‹ _2QD

-‰)−1* )‰`a*/D

Maka fungsi komplementer diperoleh :

‰D=C_; 4 ‹ D

ŠQ ₂Q _-‰)−1*)‰`a*/D

(III.8)

• Maka diperleh :

‰= ‰a+ ‰D

‰= “ coshŠ2_{‹ + • sinh}Š2_{‹ +}C_; 4 ‹ D

ŠQ ₂Q _-‰)−1*)‰`a*/D

(III.9)

• Karena lendutan permukaan selaput simetri terhadap sumbu x sedangkan grafik sinus hiperbolik tidak simetri terhadap sumbu x, maka konstanta integrasi B harus nol.

• Konstanta integrasi A dapat ditetapkan dari kondisi batas bahwa lendutan selaput adalah nol untuk y = ±b/2, sehingga :

‰= “ coshŠ2-_{2‹ +}C_; 4 ‹ D

ŠQ ₂Q _-‰)−1*)‰`a*/D= 0

“ coshŠ2-_{2‹ = −}C_;ŠQ4 ‹ _2QD

-‰)−1* )‰`a*/D

“ = − C ; 4 ‹

D

ŠQ ₂Q _-‰)−1*)‰`a*/D

• Substitusikan nilai B yang diperoleh ke dalam persamaan (III.9), maka akan diperoleh :

‰= −

C ; 4 ‹

D

ŠQ ₂Q _-‰)−1*)‰`a*/D

cosh Š2_2‹ cosh Š2

‹ +C; 4 ‹

D

ŠQ ₂Q _-‰)−1*)‰`a*/D

‰= −C_; 4 ‹ D

ŠQ ₂Q _-‰)−1*)‰`a*/D _{cosh)Š2-/2‹* +}cosh)Š2 /‹* C_; 4 ‹ D

ŠQ ₂Q _-‰)−1*)‰`a*/D

‰=C_; 4 ‹ D

ŠQ ₂Q _-‰)−1* )‰`a*

D —1 − cosh 1Š2‹ 5

cosh 1Š2-_{2‹ 5}˜

(III.10)

• Substitusikan persamaan (III.10) ke dalam persamaan (III.2) sehingga diperoleh :

= ˆ -‰cosŠ2_‹ C_; 4 ‹ D

ŠQ ₂Q _-‰)−1* )‰`a*

D —1 − cosh 1Š2‹ 5

cosh 1Š2-_{2‹ 5}˜

Œ

‰•a,Q,Ž

=C_; 4 ‹_2QD ˆ _Š1_Q )−1*)‰`a*D —1 − cosh 1Š2‹ 5

cosh 1Š2-_{2‹ 5}˜ cos Š2

‹

Œ

‰•a,Q,Ž

(III.11)

• Dengan menukarkan nilai p/s dengan 2Gθ, maka akan diperoleh fungsi torsi :

= 8: ‹_2Q D ˆ _Š1_Q )−1*)‰`a*D —1 − cosh 1Š2‹ 5

cosh 1Š2-_{2‹ 5}˜ cos Š2

‹

Œ

‰•a,Q,Ž

(III.12)

III.2.Tegangan Torsi

Menentukan Tegangan

• Tegangan torsi τ_zy

9 = −

9 =

9

• Tegangan torsi τ_zy

9 š›

9 š›

gangan Geser Maksimum Akibat Torsi Arah zy (τ_zy

merupakan turunan pertama dari fungsi torsi t

—8: ‹_2Q D ˆ _Š1_Q )#1*)‰`a*D œ1 # cosh 1Š2‹

cosh 1Š2-_2‹

Œ

‰•a,Q,Ž

8: ‹D

2Q ˆ _Š1Q )#1* )‰`a*

D Š2

‹ œ1 # cosh 1Š2‹ 5_cosh 1Š2-2‹ 5

• sin

Œ

‰•a,Q,Ž

8: ‹

2D ˆ _Š1D )#1* )‰`a*

D œ1 # cosh 1Š2‹ 5

cosh 1Š2-_{2‹ 5}• sin

Œ

‰•a,Q,Ž

mencapai nilai maksimum untuk nilai x = a/2

š› 8: ‹₂D ˆ _Š1D )#1* )‰`a*

D œ1 # 1

cosh 1Š2-_{2‹ 5}•

Œ

‰•a,Q,Ž

š› 8: ‹₂D ˆ _Š1D )#1* )‰`a*

D œ1 # 1

cosh 1Š2-_{2‹ 5}• )#

Œ

‰•a,Q,Ž

9 š› 8: ‹_2D ˆ _Š1_Dœ1 # 1

cosh 1Š2-_{2‹ 5}•

Œ

‰•a,Q,Ž

9 š› : ‹ —₂8_D ˆ _Š1_Dœ1 # 1

cosh 1Š2-_{2‹ 5}•

Œ

‰•a,Q,Ž

˜

zy)

si terhadap x Š2 5

Š2-5• cosŠ2‹ ˜

5 5• sin

Š2 ‹

• sinŠ2_‹

(III.13)

2 dan y = 0

5• sin Š2

2

5• )#1*

)‰`a* D

•

9 š› Ka: ‹

(III.14)

dimana :

Ka ₂8D ˆ _Š1Dœ1 # 1

cosh 1Š2-_{2‹ 5}•

Œ

‰•a,Q,Ž

Agar nilai deret dapat mendekati dengan cepat, maka persamaan untuk menentukan nilai k1 di atas disederhanakan menjadi :

Ka ₂8_D ˆ _Š1_D# 1

ŠD_cosh

1Š2-2‹ 5

Œ

‰•a,Q,Ž

Diketahui bahwa :

ˆ _Š1_D

Œ

‰•a,Q,Ž

1

1D+₃1D+₅1D+ ⋯ +_∞1D 2 D

8

Maka nilai k1 dapat dinyatakan dengan :

Ka 1 # ₂8_D ˆ 1

ŠD_cosh

1Š2-2‹ 5

Œ

‰•a,Q,Ž

Kemudian nilai k1 dihitung untuk berbagai variasi nilai b/a.

Untuk nilai b/a = 1, maka :

Ka 1 # ₂8D¢0.399¥¦§ ‰•a

+ 0.002¥¦§‰•Q + 0.000¥¦§‰•Ž +. . . + 0¨‰•Œ© 1 #₂8_D)0.401* 1 # 0.325 0.675

Untuk nilai b/a = 2, maka :

Ka 1 # ₂8D¢0.086¥¦§ ‰•a

+ 0.000¥¦§‰•Q + 0.000¥¦§‰•Ž +. . . + 0¨‰•Œ© 1 #₂8_D)0.086* 1 # 0.070 0.930

Untuk nilai b/a = 5, maka :

Ka 1 # ₂8D¢0.001¥¦§ ‰•a

+ 0.000¥¦§‰•Q + 0.000¥¦§‰•Ž +. . . + 0¨‰•Œ© 1 #₂8_D)0.001* 1 # 0.001 0.999

[image:58.595.132.531.130.365.2]

• Nilai k1 yang telah dihitung dapat dilihat pada Tabel.III.1

Tabel.III.1. Nilai Konstanta Tegangan Maksimum Arah zy (k1)

Untuk Tampang Persegi

b/a k1

1.0 0.675 1.1 0.720 1.2 0.759 1.3 0.793 1.4 0.822 1.5 0.848 1.6 0.869 1.7 0.888 1.8 0.904 1.9 0.918 2.0 0.930 2.1 0.940 2.2 0.949 2.3 0.956 2.4 0.963

b/a k1

2.5 0.968 2.6 0.973 2.7 0.977 2.8 0.980 2.9 0.983 3.0 0.985 3.1 0.988 3.2 0.989 3.3 0.991 3.4 0.992 3.5 0.993 3.6 0.994 3.7 0.995 3.8 0.996 3.9 0.996

b/a k1

4.0 0.997 4.5 0.999 5.0 0.999 5.5 1.000 6.0 1.000 6.5 1.000 7.0 1.000 7.5 1.000 8.0 1.000 8.5 1.000 9.0 1.000 9.5 1.000 10.0 1.000

∞ 1.000

Menentukan Tegangan Geser Maksimum Akibat Torsi Arah zx (τ_zx)

• Tegangan torsi τ_{zx merupakan turunan pertama dari fungsi torsi terhadap y}

9 = = —8: ‹_2Q D ˆ _Š1_Q )#1*)‰`a*D œ1 # cosh 1Š2‹ 5

cosh 1Š2-_{2‹ 5}•

Œ

‰•a,Q,Ž

cosŠ2_{‹ ˜}

9 8: ‹_2Q D ˆ _Š1_Q )#1*)‰`a*D Š2

‹ œ# _{cosh 1Š2-}sinh 1Š2‹ 5 2‹ 5

• cosŠ2_‹

Œ

‰•a,Q,Ž

9 8: ‹_2D ˆ _Š1_D )#1*)‰`a*D œ# sinh 1Š2‹ 5

cosh 1Š2-_{2‹ 5}• cos Š2

‹

Œ

‰•a,Q,Ž

(III.15)

• Tegangan torsi τ_{zy mencapai nilai maksimum untuk nilai x = 0 dan y = -}b_/2

9 š› 8: ‹