340 MatheMatics teacher | Vol. 101, No. 5 • December 2007/January 2008
T
he National Council of Teachers ofMathematics (2000) recommends that students at all grade levels be provided with instructional programs that enable them to “create and use representations to organize, record, and communicate mathematical ideas; select, apply, and translate among mathemati-cal representations to solve problems; and use rep-resentations to model and interpret physical, social, and mathematical phenomena” (p. 67). This article describes a particular classroom activity used to high-light the significance of mathematical representations.
As mathematics teacher educators, we pose the question: How can we support teachers in thinking about the significance of representations in math-ematics? In our teacher education courses, we do so through cyclic processes of solving, studying, dis-cussing, and reflecting on nonroutine mathematics problems, with a focus on different kinds of strategies and representations. This article shares two of these nonroutine mathematical problems, describes four solutions proposed by a class of beginning teachers, and concludes with a discussion that focuses on class-room implications.
THE MATHEMATICAL TASKS
The September 2006 issue of Mathematics Teacher
contains a letter to the editor by Mark Engerman
Laurie h. rubel and Betina a. Zolkower
On Blocks,
Stairs, and
Beyond
On Blocks,
Stairs, and
Beyond
(2006) that describes a stair climbing problem and its connection to the Fibonacci sequence as well as to Pascal’s triangle. We present a version of this same stair climbing problem along with an associ-ated blocks problem (Leikin and Winicki-Landman 2001), with the goal of describing how a compara-tive study of these two problems can motivate learning about the significance of representations. We suggest that readers try to solve each of the fol-lowing problems before reading further.
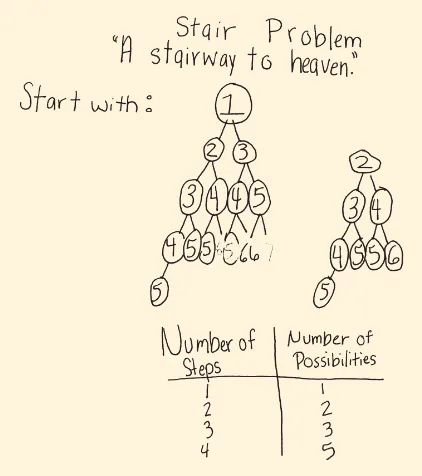
Staircase Problem: Suppose that a staircase com-prises ten steps and that you can climb the stairs one or two steps at a time. In how many different ways can you climb these ten steps?
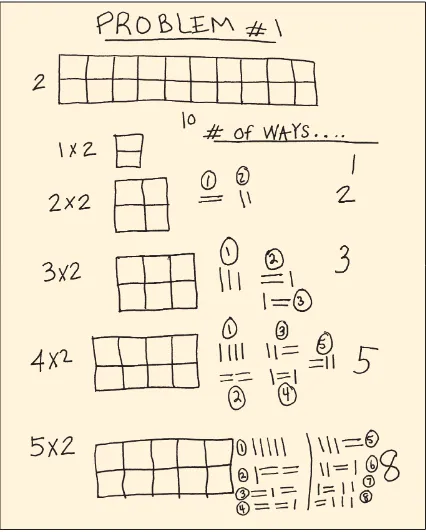
Blocks Problem: You have a 2-by-10 rectangular frame [as shown in figure 1] as well as ten rectangular blocks, each having the dimensions 2 by 1. Your task is to fill the frame with the ten blocks so that no blocks overlap and the frame is entirely filled. In how many different ways can you arrange the ten blocks?
Following is an account of an experience from Rubel’s teacher education course for middle and high school mathematics teachers. These two problems were posted on the chalkboard as participants arrived at the session. Students were asked to form groups, and each group had to choose one of the problems to solve. Many participants immediately expressed a strong preference for one problem or the other. (Readers might want to notice whether they expe-rienced this as well.) Each group then spent about forty minutes working on their selected problem and preparing a poster that summarized their work. The instructor circulated around the room, paying careful attention to each group’s emergent strategies. The groups then reconvened as a whole class for the pre-sentation and discussion of solutions.
The first group of participants selected to pres-ent their work on the Staircase problem and begin the whole-class conversation was chosen because they had adopted an inductive strategy. They found the number of ways to climb a staircase comprised of one stair, two stairs, and three stairs and then extended these findings to find the number of ways to climb a staircase comprising ten stairs. They made a clear drawing that depicted how they arrived at their combinatorial expressions for the latter case (see fig. 2).
This group presented its specific findings for climbing ten stairs as an organized list:
1. One could climb the stairs by taking a total of ten steps, all single steps.
2. One could climb the stairs by taking a total of nine steps (a combination of eight single steps
and one double step). This can be done in 9 ways (9C8).
3. One could climb the stars by taking a total of eight steps (a combination of six single steps and two double steps). This can be done in 28 ways (8C6).
4. One could climb the stairs by taking a total of seven steps (a combination of four single steps and three double steps). This can be done in 35 ways (7C4).
5. One could climb the stairs by taking a total of six steps (a combination of two single steps and four double steps). This can be done in 15 ways (6C2).
6. One could climb the stairs taking a total of five steps (all double steps). In sum, there are 89 ways to climb the staircase.
Fig. 1 the Blocks problem
2 units
10 units
Ten of these 1 × 2 rectangles need to be arranged in the 10 × 2 frame above.
When the first group stated this answer, a ripple of curiosity and intrigue spread across the class-room. Although other groups that tried the Stair-case problem might have been relieved to have a matching answer, those that worked on the Blocks problem seemed quite surprised to find that this answer matched their answer as well.
The next group of participants selected to pres-ent their solution had worked on the Blocks prob-lem. They too displayed their results as a vertical list (see fig. 3):
1. There is 1 way to arrange all the blocks vertically. 2. We could use eight vertical blocks and one pair of
horizontal blocks. This can be done in 9 ways (9C8).
3. We could use six vertical blocks and two pairs of horizontal blocks. This can be done in 28 ways (8C6).
4. We could use four vertical blocks and three pairs of horizontal blocks. This can be done in 35 ways (7C4).
5. We could also arrange the blocks by taking a combination of two vertical blocks and four pairs of horizontal blocks. This can be done in 15 ways (6C2).
6. Finally, there is 1 way to arrange all the blocks horizontally.
As before, the total is 89 possible arrangements.
At this point, looking at the first two groups’ solu-tions side by side, the class could see that the two lists of combinations corresponded directly. The
class then was invited to consider why the two lists corresponded. After a few moments, a participant explained that taking a single step in the Staircase problem corresponds to placing a vertical block in the Blocks problem. Similarly, a double step in the Staircase problem corresponds to a pair of horizontal blocks in the Blocks problem. At this point, many participants seemed surprised by the isomorphism between the two problems, especially given that most of them had gravitated strongly toward one problem or the other. But before opening a discussion about the implications of their preferences, the instructor directed everyone’s attention to the other groups’ solutions. Although the first two solutions provided correct answers to the two problems and aptly dem-onstrate the isomorphism between them, they do not address the significance of the solution 89.
A third group, which had worked on the Blocks problem, used an approach that differed from the previous group’s use of the combinations model to count all the possible arrangements. This group of participants used an inductive strategy as well. They experimented with a 1-by-2 frame, a 2-by-2 frame, a 3-by-2 fame, a 4-by-2 frame, and a 5-by-2 frame. They noted that counting the ways to arrange the blocks in each case resulted in a recur-sive rule resembling the Fibonacci sequence. They then extended the sequence of these numbers to arrive at 89 ways for the 10 × 2 frame (see fig. 4).
At this point in the sequencing of presentations, the participants showed high interest in the two prob-lems’ parallelism and their connection to the Fibonacci
Fig. 3 a vertical list display of the solution to the Blocks problem
sequence. The fourth group selected to present its solu-tion strategy began by considering the opsolu-tions at each stage of climbing the stairs. Participants in this group represented these options in a tree diagram, which they called “A Stairway to Heaven” (see fig. 5). Begin-ning at the first stair, one can step to either the second or the third stair, as shown in the first level of the dia-gram. However, the participants had difficulty using the tree diagram in this way to continue counting the number of possible paths up to the tenth stair. So they opted to consider the staircase in reverse, a process they represented in a diagram titled “From Heaven Back” (see fig. 6).
In this reverse representation, the group began at the tenth stair and noted that there was only one way to arrive at it directly from the ninth stair. Going down one level, one could reach the eighth stair in two ways, either by making a double step or by passing through the ninth stair. Going back another level, one could arrive from the seventh stair by going through the eighth stair and using those two previously counted ways or by going through the ninth stair and using that one way. In other words, to find the number of ways to get to the top of the staircase from the seventh stair, one can add the number of ways from the eighth stair to the number of ways from the ninth stair. Just to make the point clear, one can continue in this fashion and go back an additional level to the sixth stair. From here, one can either go to the sev-enth step and use one of those three ways or go to the eighth step and use one of the two paths from there. The fourth group continued this diagram back to the bottom of the staircase, showing that the 89 ways to climb the staircase are derived from
the 55 ways one can proceed from the first stair added to the 34 ways one can proceed from the sec-ond stair. This last representation has a double sig-nificance: It not only serves as a tool for solving the problem at hand but also reveals, quite suggestively, the reason why the answer lies in a recursive rule resembling the Fibonacci sequence.
IMPLICATIONS FOR TEACHING
Representation entails more than a direct or literal translation of a problematic situation into a mathe-matical model such as a formula or a diagram. When engaging in representing, problem solvers imagine a visual story—one that is not always or necessarily implied in the problem formulation. They impose that story on the problem, and, acting on this rep-resentation, they derive from it the sought solution (Arcavi 2003). In the lesson described here, the four solution methods resulted from the unique way in which each participant situated himself or herself within the mathematical tasks at hand and then schematized or abbreviated the counting processes needed for reaching a solution.
At the end of the lesson, the groups were asked to consider the similarities as well as the differ-ences between the two tasks. The Staircase and Blocks problems share three important similarities. First, both involve an iterative process—that is, one arranges one or two blocks at a time or climbs one or two steps at a time. Second, both tasks also suggest an inductive solution method, in which one proceeds by increasing the size of the outer rectangular frame
Fig. 5 a tree diagram solution to the staircase problem
respect to their problem-solving strategies and rep-resentations. Participants also noted that the col-laborative experience of solving these two problems in a variety of ways was a model for using these or other nonroutine problems in a school classroom.
Although this particular lesson was conducted as professional development for beginning teach-ers, the two tasks are appropriate for a wide range of classroom implementation. Some readers might find it productive to try the lesson as described here. Others might want to adapt it by posing the tasks in separate, consecutive lessons or spread over time during a school year. And others might now be interested in investigating other sets of isomorphic problems, with a specific focus on identifying how the specific features of each problem may motivate different kinds of mathematical representations.
REFERENCES
Arcavi, Avraham. “The Role of Visual Presentations in the Learning of Mathematics.” Educational Stud-ies in Mathematics 52 (2003): 215–41.
Engerman, Mark. “Climbing Stairs with Fibonacci and Pascal.” Mathematics Teacher 100, no. 2 (Septem-ber 2006): 89–90.
Leikin, R., and G. Winicki-Landman. “Defining as a Vehicle for Professional Development of Secondary School Mathematics Teachers.” Mathematics Edu-cation Research Journal 3 (2001): 62–73.
National Council of Teachers of Mathematics (NCTM). Principles and Standards for School Mathematics. Res-ton, VA: NCTM, 2000. ∞
Laurie rubeL, Lrubel@brooklyn. cuny.edu, is an assistant professor at brooklyn College of the City univer-sity of New York, brooklyn, NY 11210. She enjoys working with and learning from New York City teachers. betiNa ZoLkower, betinaZ@brooklyn.cuny. edu, also is an assistant professor at brooklyn College of the City university of New York. She is interested in how mathematics teach-ers working in urban heterogeneous classrooms orchestrate whole-classroom interaction within the context of nonroutine problem solving.
or the total number of steps, always making use of the previous result. Third, both tasks call for the use of a combinations model. One could imagine posing either task to students as a way to introduce or prac-tice combinatorial thinking or as a means of teaching specific problem-solving strategies, such as focusing on smaller cases, making organized lists, searching for patterns, or working backward.
Yet there are also important differences between the two tasks. The Blocks problem calls for arrang-ing objects within the constraints of a fixed space and thus entails a static situation. The Staircase problem, on the other hand, calls for a climbing
process that unfolds over time and thus involves a dynamic situation. Even though the two prob-lems are mathematically isomorphic, attending to these differences is crucial because these features of the tasks make each problem more imaginable, accessible, suggest a variety of rep-resentations strengthen teachers’ ability to guide students toward develop-ing representations as well as toward a disposition to build on and use such representations while solving or formulat-ing problems. The juxtaposition of these two tasks allowed for an engaging and productive problem-solving experience focusing on the relationship between the choices of representations and the characteristics of the tasks. In addition to learn-ing more about the significance of representations, the participants, through the activity of comparing and contrasting those representations, came to a deeper understanding of the mathematics embed-ded therein.
After sharing and discussing alternative solu-tion strategies and representasolu-tions, participants considered potential classroom implications of this problem-solving experience. One immediate obser-vation was the significance of the sequencing of the presentations of solutions. Participants noted the strategic manner in which the instructor made on-the-spot decisions regarding the sequencing of group presentations. This observation prompted discussion about the importance of monitoring groups as they work on a task, specifically with