TINJAUAN PUSTAKA
2.1 Model Aliran Dua-Fase Nonekulibrium pada Media Berpori
Penelitian ini merupakan kajian ulang terhadap penelitian yang telah dilakukan oleh
Juanes (2008), dalam tulisannya yang berjudulNonequilibrium effects in models of three-phase flow in porous media. Pada tulisan tersebut dilakukan simulasi wa-terfloodingdengan melakukan pendekatan diskritisasi menggunakancell-centered finite volumeyaitu solusi disimpan pada pusat setiap grid yang dibentuk, sedangkan pada skripsi ini, penulis melakukan diskritisasi dengan menggunakanvertex cente-red finite volumeyaitu solusi yang disimpan pada simpul (vertex) dari mesh dimana setiap vertexiharus dibangun cell (Praveen, 2013).
Juanes menyatakan bahwa model aliran dua fase dengan efek
nonekuilibri-um pada media berpori telah diajukan sebelnonekuilibri-umnya oleh Barenblatt dengan bebas
kapilaritas. Kemudian dipasangkan dengan model Buckley-Leverett dengan bebas
kapilaritas dimana fluks merupakaan fungsi saturasi efektif yang direpresentasikan
dengan persamaan
∂tS+∂xvf(σ) = 0 (2.1)
dan persamaan evolusi
σ−S =τ ∂tS (2.2)
Sistem ini harus dilengkapi denngan kondisi batas fluks pada batas kirix= 0dalam bentukf(σ) = ¯f(t). Selain itu juga diberikan kondisi awal padat= 0dalam bentuk
S =S0(x)
σ0+τ ∂xf(σ0) = S0(x)
(2.3)
dimanaSadalah saturasi aktual (saturasi saat ini) danτ adalah saturasi efektif (sa-turasi yang akan datang).
Persamaan Buckley-Leverett merupakan persamaan transportasi pada fluida
Sedangkan model Barenblatt menggambarkan dua fase aliran pada media berpori
dengan efek dinamik (nonekuilibrium) pada relatif permeabilitas. Pada kasus ini,
water flooding yang ditunjukkan oleh persamaan (2.1) yang dipasangkan dengan persamaan (2.2) akan diselesaikan melalui analisis numerik, yang akan dijelaskan
pada Bab selanjutnya
2.2 Deret Taylor
Biasanya metode numerik diturunkan berdasarkan hampiran fungsi terhadap bentuk
polinomial sehingga fungsi akan menjadi lebih sederhana. Deret Taylor dapat
digu-nakan pada hampir setiap pendekatan numerik yang didefinisikan sebagai berikut
Definisi
Andaikan terdapat f dan semua turunannya f′ , f′′
2.3 Metode Iterasi Newton Pada Sistem Aljabar
Metode iterasi Newton merupakan suatu metode yang berfungsi untuk mencari
ni-lai akar dari suatu persamaan, yaitu mencarir ∈ Ryang memenuhi f(r) = 0. Pe-nurunan metode ini dapat diperoleh dari deret Taylor yang direpresentasikan oleh
persamaan (2.5). Untukn= 1, persamaan (2.5) menjadi
dimana f′′(tx)
2! h
2 merupakan galat. Jika dimisalkan x+h merupakan pendekatan
untukr, maka dengan mengabaikan galat tersebut diperoleh
0 =f(x) +f′
yang diharapkan limn→∞xn = r. Penurunan diatas dapat dipakai untuk menda-patkan metode iterasi yang mencari r ∈ Rn yang memenuhi F(r) = 0, dimana
F :Rn →Rn. Dalam hal ini,
0=F(x)+F′(x)h
dimanaF′(x)merupakan matrix Jacobian dengan ordon×n
F′(x)=
Sehingga dapat ditunjukkan bahwa
h=−[F′ (x)]−1
F(x).
Jika terdapat nilai dugax0maka secara umum metode iterasi Newton untuk system
aljabar dapat ditulis sebagai berikut
xn+1 =xn−[F ′
(xn)] −1
F(xn)
2.4 Integrasi Numerik
Integral merupakan suatu pokok pembahasan mendasar yang berfungsi untuk
men-cari luas suatu daerah kurva f(x). Dalam kalkulus, dipelajari bahwa integral da-pat diselesaikan secara analitik pada persamaan yang sederhana. Namun pada
diselesaikan dengan cara analitik. Oleh karena itu, diperlukan suatu metode
nume-rik dimana penyelesaian integrasi dapat diselesaikan dengan bantuan perhitungan
komputer (integrasi numerik) dengan batas integral tertentu yang direpresentasikan
oleh
I = Z b
a
f(x)dx.
Rinaldi Munir (2003) dalam bukunyaIntegrasi Numerikmenjelaskan bahwa terdapat 3 cara dalam melakukan pendekatan dalam menurunkan rumus integrasi
numerik yaitu metode pias, metodeNewton-Codes danKuadratur Gauss. Penulis akan membatasi pembahasan hanya pada integrasi numerik dengan metode pias.
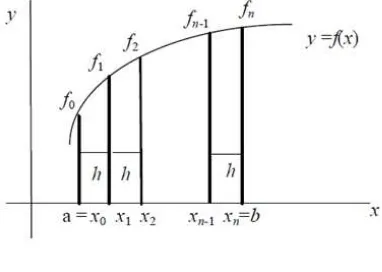
Perhatikan Gambar 2.1, andaikan[a, b] merupakan interval pada luas kurva f(x), maka dibentuk n partisi sepanjang interval [a, b], dimana lebar setiap pias
adalah
h= b−a n .
Dengan demikian, titik pias dinyatakanxi =a+ihdimanai= 0,1, ..., n
Gambar 2.1: Metode Pias
Terdapat beberapa metode yang dapat dikembangkan pada metode ini yaitu
aturan titik tengah (mid point rule), aturan titik kanan (rigth end point rule), aturan
2.4.1 Aturan Trapesium
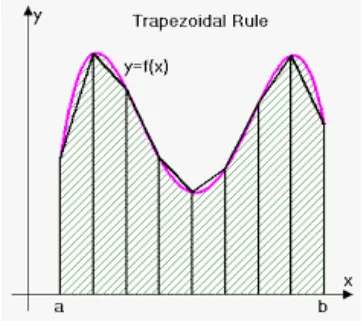
Pada pendekatan trapesium dapat digunakan rumus luas trapesium pada setiap
pi-as. Perhatikan Gambar 2.2. Secara umum, luas dibawah kurva pada pias(xi, xi+1
Gambar 2.2: Trapezoidal
didekati oleh
Z xi+1
xi
f(x)dx≈f(xi) +f(xi+1)h 2
dimanai= 0,1,2, ..., n−1. Dengan demikian,
Z b a
f(x)dx≈
n−1 X
i=0
f(xi) +f(xi+1)
h 2.
2.4.2 Aturan Titik Tengah
Luas daerah pias dapat digambarkan sebagai luas persegi panjang dimanahsebagai lebar danf(xi+1
2)sebagai panjang yang dapat ditunjukkan oleh Gambar 2.3, Secara
umum, pendekatan ini dapat ditulis sebagai
Z xi+1
xi
f(x)dx≈f(xi+1+xi 2 )h
dimanai= 0,1,2, ..., n−1, sehingga
Z b a
f(x)dx≈
n−1 X
i=0
f(xi+1+xi 2 )h.
2.4.3 Aturan Titik Kanan
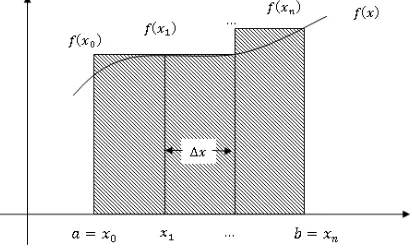
Pada pendekatan aturan titik kanan dapat dianggaphsebagai lebar pias danf(xi+1)
sebagai panjang. perhatikan Gambar 2.4, Secara umum, pendekatan ini dapat ditulis
Gambar 2.4: Aturan Titik Kanan
sebagai
Z xi+1
xi
f(x)dx≈f(xi+1)h,
dimanai= 0,1,2, ..., n−1, sehingga
Z b a
f(x)dx≈
n−1 X
i=0
f(xi+1)h.
2.4.4 Aturan Titik Kiri
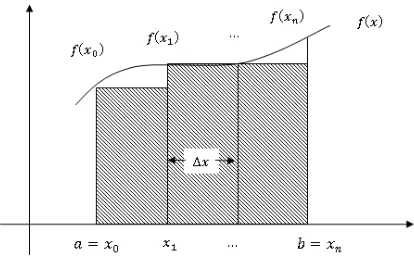
Pada pendekatan aturan titik kiri dapat dianggap h sebagai lebar pias dan f(xi) sebagai panjang. perhatikan Gambar 2.5, Secara umum dapat ditulis sebagai
Z xi+1
xi
f(x)dx≈f(xi)h,
dimanai= 0,1,2, ..., n−1, sehingga
Z b a
f(x)dx≈
n−1 X
i=0
Gambar 2.5: Aturan Titik Kiri
2.5 Galat
Penyelesaian numerik akan selalu memiliki nilai galat, karena metode numerik
me-rupakan suatu pendekatan terhadap nilai eksak. Jika nilai galat mendekati nol,
ma-ka penyelesaian numerik ama-kan mendema-kati nilai eksak. Hal itu ama-kan terjadi jima-ka jarak
pias (∆xdan∆t) diperkecil, namun perhitungan yang dilakukan akan semakin ba-nyak. Kita tahu bahwa nilai eksak merupakan jumlahan dari nilai hampiran dan
galat, yang berarti galat adalah selisih antara nilai eksak dan hampiran yang
dinya-takan oleh
ε=r−x
dimanaxadalah nilai hampiran danradalah nilai eksak.
Besar galat tidak memperhatikan nilai positif atau negatif, sehingga ditulis
dalam harga mutlak yang ditunjukkan oleh
|ε|=|r−x|.
Untuk mengetahui sebarapa besar pengaruh nilai galat terhadap nilai eksak, maka
nilai galat dapat dinormalkan terhadap nilai eksak yang disebut dengan galat relatif
yang representasikan oleh
εR = r−x
x .
Rinaldi Munir (2003) dalam bukunya Integrasi Numerik juga menjelaskan tentang galat dari iterasi Newton dan integrasi numerik dengan pendekatan aturan
2.5.1 Galat Iterasi Newton
Dalam menentukan nilai akar, iterasi Newton merupakan salah satu metode yang
sering digunakan karena konvergensinya lebih cepat (jika nilai iterasi konvergen)
dari pada metode yang lain. Pada kasus tertentu, metode Newton bisa bersifat
di-vergen sehingga tidak selamanya metode Newton dapat digunakan untuk mencari
nilai suatu akar. Metode ini dikatakan konvergen jika
(x)6= 0. Adapun pada orde konvergensi dinyatakan
εr+1 = f ′′
(xr)ε2r 2f′(x
r)
denganxr merupakan nilai hampiran terhadap akar. Dalam perhitungan menggu-nakan komputer, perlu bagi kita untuk membatasi jumlah perhitungan agar
kom-puter dapat menghentikan perhitungan. Sehingga dapat ditentukan bahwa iterasi
akan berhenti pada saat |xn+1 − xn| < ε adapun untuk menghitung galat relatif dinyatakan oleh
|xn+1−xn|
|xn+1|
< δ
dimanaε, δmerupakan toleransi galat yang diinginkan. Adapun pada sistem aljabar, galat dapat direpresentasikanεi =r−x(i)dan norm Euclidean galat adalah
kǫi k=
2.5.2 Galat Aturan Trapesium
Integrasi numerik menggunakan pendekatan trapesium memiliki galat yang
ditun-jukkan sebagai berikut
G=
Andaikan terdapat dua titik yaitux0 = 0danh = x, dengan menggunakan deret
sehingga
jadi, nilai eksak diperoleh
Z h
0
f(x)dx= h
2(f(x0) +f(x1)) +O(h
3)
Uraian diatas, merupakan galat trapesium untuk batas interval [0, h] dengan satu pias. Adapun untuk jumlah pias lebih dari satu (n > 1), dapat diperoleh galat total
sebagai berikut
n . Sehingga
Dapat disimpulkan bahwa galat total dari pendekatan trapesium berbanding lurus
dengan kuadrat lebar pias (h). semakin kecil lebar pias, maka ukuran galat akan
semakin kecil.
2.5.3 Galat Aturan Titik Tengah
Pendekatan titik tengah diperoleh galat untuk satu pias
G= Z h
0
f(x)dx−hf(x1 2)
Dengan metode yang sama pada aturan trapesium diperoleh
Gtotal =− h3 24(f
′′
(x0) +f′′(x1) +f′′(x2) +...f′′(xn−1))
Adapun untuk beberapa pias, diperoleh
Gtotal = h3
24 n−1 X
i=0
f′′ i (x)
= h
2
24
(b−a) n nf
′′ i(x) = (b−a)h
2
24f ′′ i(x)
≈O(h2)
dari uraian diatas dapat disimpulkan bahwa galat yang dihasilkan pada pendekatan
aturan titik tengah dua kali lebih kecil dari pada aturan trapesium, sehingga
die-tahui bahwa metode in lebih efisien dari aturan trapesium. Adapun galat untuk
pendekatan aturan titik kanan dan titik kiri telah dijelaskan oleh Jiwen He (2008)
yang iuraikan sebagai berikut
2.5.4 Galat Aturan Titik Kanan
Telah dijelaskan pendekatan integrasi numerik pada aturan titik kanan pada
pem-bahasan sebelumnya, maka untuk galat yang dihasilkan dapat ditunjukkan sebagai
berikut
G= Z h
0
dimanai= 0,1, ..., n−1. Sehingga diperoleh galat untuk satu pias
G= h
2
2 f ′
(x1)
Adapun pias sebanyak n diperoleh
Gtotal = 1
2(b−a)f ′
(xi)
≈O(h)
2.5.5 Galat Aturan Titik Kiri
Dapat ditunjukkan galat dari aturan titik kiri sebagai berikut
G= Z h
0
f(x)dx−hf(xi)
dimanai= 0,1, ..., nsehingga diperoleh galat untuk satu pias
G= h
2
2 f ′
(x0)
Adapun pias sebanyak n diperoleh
Gtotal = 1
2(b−a)f ′
(xi)
≈O(h)
Dapat dilihat bahwa pendekatan aturan titik kanan dan aturan titik kiri
me-miliki besar galat yang sama, namun berbeda pada pendekatan trapesium dan titik
tengah. Diketahui bahwa pendekatan yang memiliki galat yang paling kecil diantara
keempat pendekatan diatas adalah aturan titik tengah. Sehingga dapat disimpulkan
bahwa pendekatan aturan titik tengah yang memiliki efisiensi yang cukup cepat dari
jumlah diskritisasi yang dilakukan. Namun ada beberapa kondisi yang
menyebabk-an pendekatmenyebabk-an ymenyebabk-ang dilakukmenyebabk-an harus disesuaikmenyebabk-an dengmenyebabk-an permasalahmenyebabk-an ymenyebabk-ang sedmenyebabk-ang
dijalankan. Oleh karenanya perlu bagi kita untuk mempelajari lebih mendalam
ten-tang pendekatan numerik.
Contoh
x2−y2 =y,x2+y2 =xdenganinisial guessx0 = 0.8dany0 = 0.4.
maka solusi pada iterasi pertama yaitu:
Perhitungan dapat dilakukan dengan menggunakan MATLAB dimana code dapat
dilihat pada lampiran 1. Jika dilakukan iterasi sebanyak 5 kali, maka akan didapat
hasil yang ditunjukkan oleh tabel berikut
i xi yi error
0 0.8 0.4
-1 0.772881355932203 0.420338983050847 0.033898305084746 2 0.771845967451467 0.419644283432102 0.001246850779495 3 0.771844506348887 0.419643377608757 1.719109270156545e-006 4 0.771844506346038 0.419643377607081 3.304913436759251e-012 5 0.771844506346038 0.419643377607081 0
Dari penyelesaian diatas dapat kita ketahui bahwa pada iterasi ke-5 nilai galat telah
mencapai 0, sehingga diketahui nilai akar dari x = 0.771844506346038dan y = 0.419643377607081
2.6 Solusi Numerik pada Persamaan Diferensial Partial
Shaw (1992) menjelaskan bahwa persamaan yang mengatur pergerakan fluida
ada-lah persamaaan diferensial parsial. Persamaan ini terdiri dari kombinasi variable
aliran seperti kecepatan, tekanan dan turunan dari variabel tersebut. Komputer tidak
dapat menghasilkan solusi persamaan diferensial secara langsung karena komputer
komputer diprogram untuk melakukan perhitungan operasi sederhana seperti
pen-jumlahan, pengurangan, perkalian, pembagian, dan perulangan.
Oleh karena itu persamaan diferensial harus ditransformasikan kedalam
per-samaan yang hanya terdiri dari bilangan, kombinasi dari bilangan tersebut dapat
digambarkan oleh operasi yang sederhana. Untuk melakukan transformasi pada
persamaan tersebut maka dapat dilakukan suatu cara yang disebut diskritisasi
ya-itu setiap suku dalam persamaan diferensial harus diterjemahkan kedalam sebuah
bentuk numerik yang dapat diprogram oleh komputer untuk dihitung. Berbagai
tek-nik dapat dilakukan diantaranya metode beda hingga, metode elemen hingga, dan
metode volume hingga.
Metode beda hingga merupakan suatu teknik yang didasari pada deret Taylor
yang menggambarkan turunan dari variabel sebagai selisih antara nilai-nilai dari
va-riabel dari berbagai titik dalam ruang dan waktu. Teknik kedua yaitu metode elemen
hingga, dalam metode ini domain dari persamaan diferensial parsial yang berlaku
dibagi menjadi sejumlah elemen berhingga. Namun pada metode ini, proses
diskri-tisasi yang dilakukan lebih sulit dibandingkan dengan metode beda hingga. Teknik
yang ketiga adalah metode volume hingga, teknik ini cukup popular digunakan
un-tuk persoalan komputasi fluida dinamik.
Menurut Apsley (2005) metode volume hingga sesuai diterapkan pada
ma-salah aliran fluida dan aerodinamika. Pada metode volume hingga harus diketahui
domainnya dengan jelas, dari domain tersebut dibagi menjadi grid-grid baik
ters-truktur maupun tidak (unstrustured), pada masing-masing grid memenuhi
persama-an matematika ypersama-ang terbentuk.
Oleh referensi diatas, maka dapat diputuskan bahwa metode yang tepat
un-tuk menyelesaikan permasalahan ini adalah dengan menggunakan metode volume
hingga. Karena telah dijelaskan sebelumnya bahwawaterfloodingmeruapakan su-atu permasalahan aliran fluida pada media berpori. Oleh karena itu, maka metode
2.6.1 Metode Volume Hingga
Metode Volume Hingga (MVH) merupakan salah satu teknik diskritisasi pada
per-samaan diferensial parsial, dan biasanya diimplementasikan pada hukum
konser-vasi. Pada dasarnya metode ini mengatur persamaan diferensial agar dikonversi
kedalam bentuk numerik yaitu dengan membagi domainΩmenjadi himpunan dari
volume berhingga yang saling lepas. Domain yang dipartisi sebanyakiyang disebut grid atau mesh.
Tulus, Ariffin, Abdullah dan Norhamidi (2005) telah melakukan
peneliti-an mengenai aplikasi Computational Fluid Dinamic(CFD) dengan menggunakan metode volume hingga dalam tulisannya yang berjudulNumerical Simulation of In-Cylinder Gas Dynamic of Two-Stroke Linear Engines using Finite Volume Method.
Thomas J.W (2013) dalam bukunyaNumerical Partial Differential Equation Conservation Law and Elliptic Equation mengemukakan suatu formulasi umum dari hukum konservasi berikut
∂u ∂t +
∂f(u)
∂x = 0 inR×(0, T)
persamaan tersebut dapat diselesaikan dengan menggunaka metode volume hingga,
dimana akan dicari solusiU(xi, tn)atau dapat dinotasikan sebagaiUinyang kemu-dian dibentuk suatu grid terhadap domain xdan waktut. Andaikan terdapat suatu interval [a, b], maka untuk mencari solusinya dapat dipartisi sebanyak n, dimana n ∈N, sehingga∆x= (b−a)
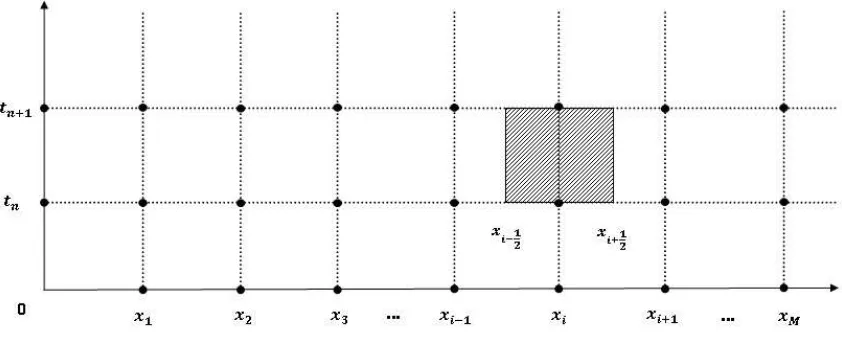
n . Maka untukxi =a+i∆xdan kemudian terdapat∆t sehinggatn =n∆t. Dalam hal ini, dibentukcontrol volumepada diskritisasi yaitu suatu bidang dengan batasxyaituxi−1
2 danxi+ 1
2 sedangkan batas terhadaptyaitu
tn−1 dantnyang dapat ditunjukkan oleh Gambar 2.6 sehingga dapat direpresenta-sikan oleh
Z xi+ 1
2
xi −12
Z tn tn−1
∂u ∂t +
∂f(u) ∂x
dtdx= 0
hal diatas akan sama dengan
Z xi+ 12
xi −12
Z tn tn−1
∂u
∂tdtdx+ Z xi+ 12
xi −12
Z tn tn−1
∂f(u)
Gambar 2.6: Control Volume
pada suku pertama integralkan terhadap batast, pada suku kedua integralkan terha-dap batasxsehingga diperoleh
Z xi+ 1
2
xi −12
u(x, tn)−u(x, tn−1)
dx+ Z tn
tn−1
f(u(xi+1
2, t))−f(u(xi− 1 2, t))
dt = 0
dengan mengaplikasikan pendekatanmid pointdapat ditunjukkan bahwa Z xi+ 1
2
xi −12
u(x, tn)−u(x, tn−1)
dx≈u(xi, tn)∆xi−u(xi, tn−1)∆xi
sedangkan pada fungsi flux dilakukan pendekatanleft pointdapat diperlihatkan bah-wa
Z tn tn−1
f(u(xi+1
2, t))−f(u(xi− 1 2, t))
dt≈f(u(xi+1
2, tn−1))∆ti
−f(u(xi−1
2, tn−1))∆ti
sehingga diperoleh
u(xi, tn)∆xi−u(xi, tn−1)∆xi+f(u(xi+1
2, tn−1))∆ti
−f(u(xi−1
2, tn−1))∆ti+Galat1 = 0.
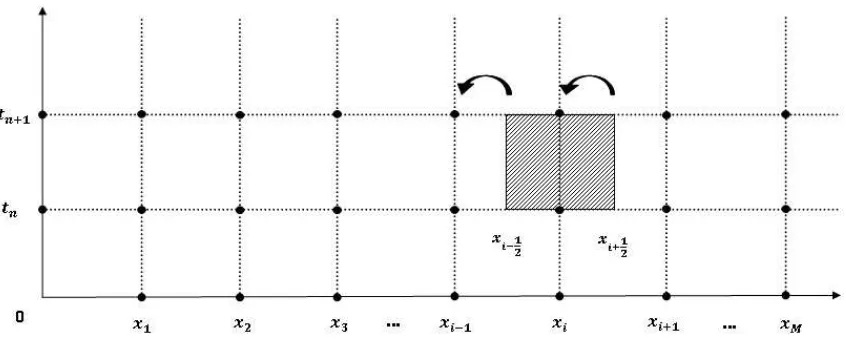
Lakukan pendekatan upwind yang diilustrasikan oleh Gambar 2.7, dimana
pende-katan upwind dapat direpresentasikan oleh
f(u(xi+1
2, tn−1))≈f(u(xi, tn−1))
f(u(xi−1
Gambar 2.7: Upwinding
Seperti yang telah disebutkan sebelumnya, terdapat galat pada setiap pendekatan
numerik sehingga
u(xi, tn)∆xi−u(xi, tn−1)∆xi+f(u(xi, tn−1))∆ti
−f(u(xi−1, tn−1))∆ti+Galat1+Galat2 = 0
(2.6)
dengan Galat1= galat integrasi numerik dan Galat2=galat upwinding. Dalam hal
ini∆xi dan∆ti merupakan pias yang dapat ditentukan besarnya, jika∆xi dan∆ti menuju nol, maka galatnya pun akan menuju nol sehingga solusi numerik akan
mendekati solusi eksak. Oleh karenanya dapat kita lakukan pendekatanu(xi, tn)≈ U(xi, tn)sehingga persamaan (2.6) dapat ditulis
U(xi, tn)∆xi−U(xi, tn−1)∆xi+f(U(xi, tn−1))∆ti
−f(U(xi−1, tn−1))∆ti = 0
jadi,
U(xi, tn) =U(xi, tn−1)− ∆ti ∆xi
f(U(xi, tn−1))−f(U(xi−1, tn−1))
(2.7)
Contoh
Terdapat suatu persamaan yang direpresentasikan oleh persamaan berikut
∂u ∂t +
1 2
∂u2
∂x = 0 inR×(0, T) (2.8)
dengan kondisi batas u(x,0) = 1−x2, tentukan solusi numerik dari persamaan
Penyelesaian
Persamaan (2.8) merupakan persamaan transport yang dikenal dengan sebutan
per-samaan Burger inviscid yang merupakan bentuk sederhana dari perper-samaan
diferen-sial pardiferen-sial nonlinier. Persamaaan Burger terkenal dengan solusinya berupa
gelom-bang kejut dan merupakan bentuk khusus dari model Buckley-Leverett.
Permasalahan ini dapat diselesaikan oleh beberapa metode, namun dalam
hal tulisan ini penulis akan menyelesaikan persamaan tersebut dengan
menggu-nakan metode volume hingga yang telah dijelaskan sebelumnya dengan melakukan
langkah-langkah yang dijelaskan sebelumnya yaitu dengan melakukan integrasi
se-perti persamaan (2.6.1)
Z xi+ 1
pada suku pertama integralkan terhadaptdan pada suku kedua integralkan terhadap x
pada suku pertama digunakan pendekatanmid pointdan pada suku kedua digunakan pendekatanleft pointsehingga diperoleh
u(xi, tn)∆xi−u(xi, tn−1)∆xi+
dengan menggunakan upwinding diperoleh
∆xi[u(xi, tn)−u(xi, tn−1)] + 1 2∆ti[u
2(x
i, tn−1)−u2(xi−1, tn−1)] = 0
dengan melakukan perhitungan al-jabar diperoleh
u(xi, tn) = u(xi, tn−1)− ∆ti 2∆xi[u
2(x
i, tn−1)−u2(xi−1, tn−1)]
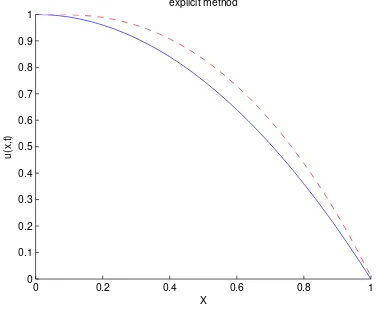
Solusi numerik diatas dapat direpresentasikan oleh Gambar 2.8 yang
dipe-roleh melalui perhitungan menggunakan MATLAB dengan code yang tertera pada
Lampiran 2. Gambar tersebut menunjukkan bahwa terdapat dua grafik dimana
persamaan (2.8) dapat diselesaikan secara numerik dengan menggunakan metode
volume hingga yang menjadi rujukan pada penelitian ini.
0 0.2 0.4 0.6 0.8 1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
explicit method
X
u(x,t)