1.
Limit dan kecil tak terhingga
Artikel utama untuk bagian ini adalah: LimitDefinisi limit: kita katakan bahwa limit f(x) ketika x mendekati titik p adalah L apabila untuk setiap bilangan ε > 0 apapun, terdapat bilangan δ > 0, sedemikian rupanya:
Kalkulus pada umumnya dikembangkan dengan memanipulasi sejumlah kuantitas yang sangat kecil. Objek ini, yang dapat diperlakukan sebagai angka, adalah sangat kecil. Sebuah bilangan dx yang kecilnya tak terhingga dapat lebih besar daripada 0, namun lebih kecil daripada bilangan apapun pada deret 1, ½, ⅓, ... dan bilangan real positif apapun. Setiap perkalian dengan kecil tak terhingga (infinitesimal) tetaplah kecil tak terhingga, dengan kata lain kecil tak terhingga tidak memenuhi properti Archimedes. Dari sudut pandang ini, kalkulus adalah sekumpulan teknik untuk memanipulasi kecil tak terhingga.
Pada abad ke-19, konsep kecil tak terhingga ini ditinggalkan karena tidak cukup cermat, sebaliknya ia digantikan oleh konsep limit. Limit menjelaskan nilai suatu fungsi pada nilai input tertentu dengan hasil dari nilai input terdekat. Dari sudut pandang ini, kalkulus adalah sekumpulan teknik memanipulasi limit-limit tertentu. Secara cermat, definisi limit suatu fungsi adalah:
Diberikan fungsi f(x) yang terdefinisikan pada interval di sekitar p, terkecuali mungkin pada p itu sendiri. Kita mengatakan bahwa limit f(x) ketika x mendekati p adalah L, dan menuliskan:
2. Turunan
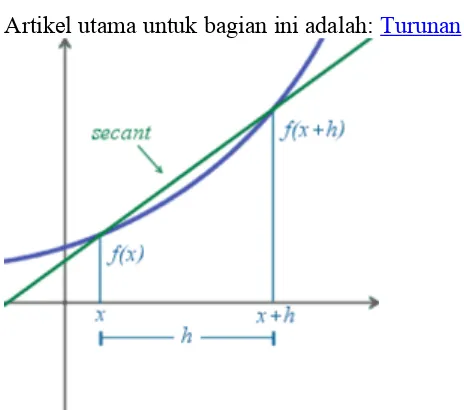
Artikel utama untuk bagian ini adalah: Turunan
Grafik fungsi turunan.
Turunan dari suatu fungsi mewakili perubahan yang sangat kecil dari fungsi tersebut terhadap variabelnya. Proses menemukan turunan dari suatu fungsi disebut sebagai pendiferensialan ataupun diferensiasi.
Secara matematis, turunan fungsi ƒ(x) terhadap variabel x adalah ƒ′ yang nilainya pada titik x adalah:
,
dengan syarat limit tersebut eksis. Jika ƒ′ eksis pada titik x tertentu, kita katakan bahwa ƒ terdiferensialkan (memiliki turunan) pada x, dan jika ƒ′ eksis di setiap titik pada domain ƒ, kita sebut ƒ terdiferensialkan.
Garis singgung pada (x, f(x)). Turunan f'(x) sebuah kurva pada sebuah titik adalah kemiringan dari garis singgung yang menyinggung kurva pada titik tersebut.
Perhatikan bahwa ekspresi pada definisi turunan di atas merupakan gradien dari garis sekan yang melewati titik (x,ƒ(x)) dan (x+h,ƒ(x)) pada kurva ƒ(x). Apabila kita mengambil limit h mendekati 0, maka kita akan mendapatkan kemiringan dari garis singgung yang menyinggung kurva ƒ(x) pada titik x. Hal ini berarti pula garis singgung suatu kurva merupakan limit dari garis sekan, demikian pulanya turunan dari suatu fungsi ƒ(x) merupakan gradien dari fungsi tersebut.
Sebagai contoh, untuk menemukan gradien dari fungsi f(x) = x2 pada titik (3,9):
Garis singgung sebagai limit dari garis sekan. Turunan dari kurva f(x) di suatu titik adalah kemiringan dari garis singgung yang menyinggung kurva pada titik tersebut. Kemiringan ini ditentukan dengan memakai nilai limit dari kemiringan garis sekan.
3. Notasi pendiferensialan
Terdapat berbagai macam notasi matematika yang dapat digunakan digunakan untuk menyatakan turunan, meliputi notasi Leibniz, notasi Lagrange, notasi Newton, dan notasi Euler.
Notasi Leibniz diperkenalkan oleh Gottfried Leibniz dan merupakan salah satu notasi
yang paling awal digunakan. Ia sering digunakan terutama ketika hubungan antar y = ƒ(x) dipandang sebagai hubungan fungsional antara variabel bebas dengan variabel terikat. Turunan dari fungsi tersebut terhadap x ditulis sebagai:
ataupun
Notasi Lagrange diperkenalkan oleh Joseph Louis Lagrange dan merupakan notasi yang
paling sering digunakan. Dalam notasi ini, turunan fungsi ƒ(x) ditulis sebagai ƒ′(x) ataupun hanya ƒ′.
Notasi Newton, juga disebut sebagai notasi titik, menempatkan titik di atas fungsi untuk
menandakan turunan. Apabila y = ƒ(t), maka mewakili turunan y terhadap t. Notasi ini hampir secara eksklusif digunakan untuk melambangkan turunan terhadap waktu. Notasi ini sering terlihat dalam bidang fisika dan bidang matematika yang berhubungan dengan fisika.
Notasi Euler menggunakan operator diferensial D yang diterapkan pada fungsi ƒ untuk
atau .
Notasi Euler ini sering digunakan dalam menyelesaikan persamaan diferensial linear.
Notasi Leibniz Notasi Lagrange Notasi Newton Notasi Euler
Turunan ƒ(x) terhadap
x ƒ′(x) dengan y = ƒ(x)
4. Integral
Artikel utama untuk bagian ini adalah: Integral
Integral dapat dianggap sebagai perhitungan luas daerah di bawah kurva ƒ(x), antara dua titik a dan b.
Integral merupakan suatu objek matematika yang dapat diinterpretasikan sebagai luas wilayah ataupun generalisasi suatu wilayah. Proses menemukan integral suatu fungsi disebut sebagai pengintegralan ataupun integrasi. Integral dibagi menjadi dua, yaitu: integral tertentu dan integral tak tentu. Notasi matematika yang digunakan untuk
menyatakan integral adalah , seperti huruf S yang memanjang (S singkatan dari "Sum"
yang berarti penjumlahan).
Integral tertentu
Diberikan suatu fungsi ƒ bervariabel real x dan interval antara [a, b] pada garis real,
integral tertentu:
Pada notasi integral di atas: a adalah batas bawah dan b adalah batas atas yang menentukan domain pengintegralan, ƒ adalah integran yang akan dievaluasi terhadap x
pada interval [a,b], dan dx adalah variabel pengintegralan.
Seiring dengan semakin banyaknya subinterval dan semakin sempitnya lebar subinterval yang diambil, luas keseluruhan batangan akan semakin mendekati luas daerah di bawah kurva.
Terdapat berbagai jenis pendefinisian formal integral tertentu, namun yang paling umumnya digunakan adalah definisi integral Riemann. Integral Rieman didefinisikan sebagai limit dari penjumlahan Riemann. Misalkanlah kita hendak mencari luas daerah yang dibatasi oleh fungsi ƒ pada interval tertutup [a,b]. Dalam mencari luas daerah tersebut, interval [a,b] dapat kita bagi menjadi banyak subinterval yang lebarnya tidak perlu sama, dan kita memilih sejumlah n-1 titik {x1, x2, x3,..., xn - 1} antara a dengan b
sehingga memenuhi hubungan:
Himpunan tersebut kita sebut sebagai partisi [a,b], yang membagi [a,b] menjadi sejumlah n subinterval
. Lebar subinterval pertama [x0,x1] kita nyatakan
sebagai Δx1, demikian pula lebar subinterval ke-i kita nyatakan sebagai Δxi = xi - xi - 1.
Pada tiap-tiap subinterval inilah kita pilih suatu titik sembarang dan pada subinterval ke-i
tersebut kita memilih titik sembarang ti. Maka pada tiap-tiap subinterval akan terdapat
batangan persegi panjang yang lebarnya sebesar Δx dan tingginya berawal dari sumbu x
sampai menyentuh titik (ti, ƒ(ti)) pada kurva. Apabila kita menghitung luas tiap-tiap
batangan tersebut dengan mengalikan ƒ(ti)· Δxi dan menjumlahkan keseluruhan luas
daerah batangan tersebut, kita akan dapatkan:
Penjumlahan Sp disebut sebagai penjumlahan Riemann untuk ƒ pada interval [a,b].
Secara cermat, definisi integral tertentu sebagai limit dari penjumlahan Riemann adalah:
Diberikan ƒ(x) sebagai fungsi yang terdefinisikan pada interval tertutup [a,b]. Kita katakan bahwa bilangan I adalah integral tertentu ƒ di sepanjang [a,b] dan bahwa I
adalah limit dari penjumlahan Riemann apabila kondisi berikut dipenuhi: Untuk setiap bilangan ε > 0 apapun terdapat sebuah bilangan δ > 0 yang berkorespondensi dengannya sedemikian rupanya untuk setiap partisi di sepanjang [a,b] dengan dan pilihan ti apapun pada [xk - 1, ti], kita dapatkan
Secara matematis dapat kita tuliskan:
Apabila tiap-tiap partisi mempunyai sejumlah n subinterval yang sama, maka lebar Δx = (b-a)/n, sehingga persamaan di atas dapat pula kita tulis sebagai:
Limit ini selalu diambil ketika norma partisi mendekati nol dan jumlah subinterval yang ada mendekati tak terhingga banyaknya.
Contoh
Sebagai contohnya, apabila kita hendak menghitung integral tertentu , yakni mencari luas daerah A dibawah kurva y=x pada interval [0,b], b>0, maka perhitungan
Pemilihan partisi ataupun titik ti secara sembarang akan menghasilkan nilai yang sama sepanjang norma partisi tersebut mendekati nol. Apabila kita memilih partisi P membagi-bagi interval [0,b] menjadi n subinterval yang berlebar sama Δx = (b - 0)/n = b/n dan titik
t'i yang dipilih adalah titik akhir kiri setiap subinterval, partisi yang kita dapatkan adalah:
dan , sehingga:
Seiring dengan n mendekati tak terhingga dan norma partisi mendekati 0, maka didapatkan:
Dalam prakteknya, penerapan definisi integral tertentu dalam mencari nilai integral tertentu tersebut jarang sekali digunakan karena tidak praktis. Teorema dasar kalkulus (lihat bagian bawah) memberikan cara yang lebih praktis dalam mencari nilai integral tertentu.
Integral tak tentu
bawah) menyatakan bahwa integral tertentu sebuah fungsi kontinu dapat dihitung dengan mudah apabila kita dapat mencari antiturunan/antiderivatif fungsi tersebut.
Keseluruhan himpunan antiturunan/antiderivatif sebuah fungsi ƒ adalah integral tak
tentu ataupun primitif dari ƒ terhadap x dan dituliskan secara matematis sebagai:
di mana
Ekspresi F(x) + C adalah antiderivatif umumƒ dan C adalah konstanta sembarang.
Misalkan terdapat sebuah fungsi f(x) = x2, maka integral tak tentu ataupun antiturunan
dari fungsi tersebut adalah:
Perhatikan bahwa integral tertentu berbeda dengan integral tak tentu. Integral tertentu
dalam bentuk adalah sebuah bilangan, manakala integral tak tentu :