Di bidang komputer, citra merupakan salah satu komponen dari multimedia yang berperan penting sebagai bentuk inforasi visual. Dengan perkembangan teknologi in-formasi masa sekarang ini, kebanyakan inin-formasi disampaikan dalam bentuk gambar (citra), berbanding dalam bentuk teks. Pada sisi lain, pengolahan citra juga tidak kalah pentingnya dengan beberapa tujuan, di antaranya untuk kepentingan kerahasi-aan informasi, perbaikan mutu citra, dan juga untuk keperluan variasi citra sebagai visual seni.
2.1 Citra digital
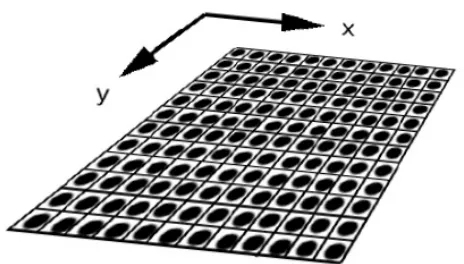
Secara sederhana, citra adalah gambar pada bidang dua dimensional. McAndrew (2004) menyatakan, citra merupakan sebuah gambar yang merepresentasikan sesu-atu benda. Ia bisa saja merupakan sebuah gambar seseorang, kumpulan orang-orang ataupun hewan, atau suatu adegan di luar, atau suatu microphotograph dari suatu komponen elektronik, atau hasil dari pencitraan medis. Sebuah citra juga dapat di-pandang sebagai sebuah array, atau matriks, piksel persegi (elemen gambar) yang diatur dalam kolom dan baris. Gambar 2.1 dan Gambar 2.2 masing-masing me-nunjukkan array dari piksel dalam baris dan kolom dan dalam koordinat (x, y). Se-mentara apabila dipandang dari sisi matematis, citra merupakan fungsi yang kontinu dari kumpulan intensitas cahaya pada bidang dua dimensional.
Gambar 2.1 : Array dari piksel keabuan dalam baris dan kolom Sumber: (ESA, 2012)
Petrou dan Bosdogianni (1999) menyatakan, bahwa array yang menggambarkan
Gambar 2.2 : Array dari piksel dalam koordinat (x, y) Sumber: (ESA, 2012)
suatu citra dapat merupakan formulasi berikut.
f(x, y) =
Dalam (8-bit) citra skala abu-abu setiap elemen memiliki intensitas yang dite-tapkan berkisar dari 0 sampai 255, seperti terlihat pada Gambar 2.3 . Sebuah citra skala abu-abu adalah apa yang biasanya disebut orang citra hitam dan putih, tapi nama tersebut menekankan bahwa gambar tersebut juga akan mencakup banyak nu-ansa abu-abu. Suatu citra dengan warna yang benar mempunyai 24 bit kedalaman warna = 8×8×8bits= 256×256×256 warna∼16 juta warna. Gambar 2.4 menun-jukkan contoh citra dengan warna benar. Beberapa gambar skala abu-abu memiliki lebih jumlah keabuan, misalnya 16 bit = 65536 jumlah keabuan. Pada prinsipnya tiga citra skala abu-abu dapat dikombinasikan untuk membentuk sebuah gambar dengan 281.474.976.710.656 jumlah keabuan.
Terdapat dua kelompok umum dari citra, yaitu grafik vektor dan bitmaps (pixel-based atau citra). Beberapa format file yang paling umum adalah:
Gambar 2.3 : Array dari piksel dengan nilai antara 0 (hitam) - 255 (putih) Sumber: (ESA, 2012)
2) JPEG suatu format bitmap yang sangat efisien (yaitu banyak informasi per-byte) terkompres destruktif 24 bit (16 juta warna). Cukup luas digunakan, khususnya untuk web dan internet (dengan bandwidth terbatas).
3) TIFF format bitmap standard 24 bit publikasi. Pengkompresan non-destruktif, misalnya dengan kompresi Lempel-Ziv-Welch (LZW).
4) PS Postscript, suatu format vektor standard. Format ini mempunyai banyak sub-standards dan dapat menjadi sulit memindahkan ke flatform dan sistem operasi yang berbeda.
5) PSD suatu format yang disarankan Photoshop yang menjaga semua informasi di dalam citra yang memuat semua lapisan.
Pembuatan sebuah citra dapat dipandang sebagai sebuah proses berikut. Sum-ber cahaya menerangi sebuah objek tertentu. Kemudian objek tersebut akan meman-tulkan kembali sebagian dari berkas cahaya tersebut, yang kemudian ditangkap oleh alat optik sebagai sebuah gambar. Sebagai contoh, Gambar 2.5 menunjukkan citra bunga hasil pemotretan.
Gambar 2.5 : Citra bunga
Ditinjau dari sudut pandang matematis, citra merupakan fungsi menerus (con-tinue) dari intensitas cahaya pada bidang dwimatra. Sumber cahaya menerangi objek, objek memantulkan kembali sebagian dari berkas cahaya tersebut. Pantulan cahaya ini ditangkap oleh oleh alat-alat optik, misalnya mata pada manusia, kamera, pe-mindai (scanner), dan sebagainya, sehingga bayangan objek yang disebut citra terse-but terekam. Citra sebagai keluaran dari suatu sistem perekaman data dapat bersifat (Murni, 1992):
1. optik berupa foto,
2. analog berupa sinyal video seperti gambar pada monitor televisi,
3. digital yang dapat langsung disimpan pada suatu pita magnetik.
citra biner berukuran 512×512, jumlah bit yang digunakan adalah 512×512×1 = 262.144 = 32768 bytes. Pada sisi lain, suatu citra keabuanmembutuhkan ukuran yang sama, yaitu 512×512×1 = 262.144 bytes. Sementara untuk citra warna setiap piksel dikaitkan dengan 3 bytes informasi warna. Suatu citra berukuran 512×512 membutuhkan 512×512×3 = 786.432 bytes. 2.1.2 Ruang Warna
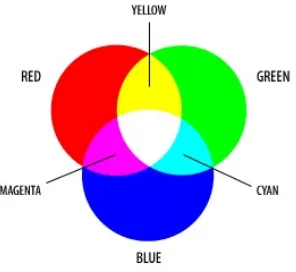
Untuk komunikasi sains, dua ruang warna utama adalah RGB dan CMYK. Model warna RGB berkaitan sangat erat dengan cara kita memandang warna de-ngan r, g dan b reseptor di retina mata. RGB menggunakan jumlahan pencampuran warna dan merupakan model warna dasar yang digunakan dalam televisi atau media lainnya yang memproyeksikan warna dengan cahaya. Ini adalah model warna dasar yang digunakan dalam komputer dan untuk grafik web, tetapi tidak dapat digunakan untuk produksi cetak. Warnawarna sekunder RGB cyan, magenta, dan kuning -yang dibentuk dengan mencampur dua warna primer (merah, hijau atau biru) dan mengecualikan warna ketiga. Merah dan hijau menggabungkan untuk membuat kun-ing, hijau dan biru untuk membuat cyan, dan biru dan merah membentuk magenta. Kombinasi merah, hijau, dan biru dalam intensitas penuh membuat putih, seperti terlihat pada Gambar 2.6 . Sebuah citra dalam gabungan warna RGB dapat direp-resentasikan kepada tiga matriks yang masing-masing mewakili R, G dan B, seperti pada Gambar 2.7 .
Gambar 2.6 : Model penjumlahan dari RGB
2.2 Sistem Pengolahan Citra
Gambar 2.7 : Matriks representasi citra dalam RGB Sumber: (McAndrew, 2004)
Gambar 2.8 : Model sistem pengolahan citra
2.2.1 Definisi Pengolahan Citra
Agar citra yang mengalami gangguan mudah diinterpretasi (baik oleh manusia maupun mesin), maka citra tersebut perlu dimanipulasi menjadi citra lain yang kualitasnya lebih baik. Bidang studi yang menyangkut hal ini adalah pengolahan citra (image pro-cessing). Pengolahan citra adalah pemrosesan citra, khususnya dengan menggunakan komputer, menjadi citra yang kualitasnya lebih baik.
Pengolahan Citra bertujuan memperbaiki kualitas citra agar mudah diinterpre-tasi oleh manusia atau mesin (dalam hal ini komputer). Teknik-teknik pengolahan citra mentransformasikan citra menjadi citra lain. Jadi, masukannya adalah citra dan keluarannya juga citra, namun citra keluaran mempunyai kualitas lebih baik daripada citra masukan. Termasuk ke dalam bidang ini juga adalah pemampatan citra (im-age compression). Pemrosesan citra mencakup pengubahan alamiah suatu citra yang terkait dengan salah satu yang berikut:
1) Memperbaiki informasi berbasis gambarnya untuk tujuan interpretasi manusia,
2) Mengubah citra sehingga lebih sesuai untuk persepsi mesin otonom.
Manusia menyukai citra yang tajam, bersih dan rinci, sementara mesin citranya yang sederhana dan rapi (McAndrew, 2004).
Citra ✲ Pengolahan Citra ✲ Citra
Gambar 2.9 : Proses dalam pengolahan citra
2.2.2 Operasi Pengolahan Citra
Umumnya, operasi-operasi pada pengolahan citra diterapkan pada citra bila (Jain, 1989):
1. Perbaikan atau memodifikasi citra perlu dilakukan untuk meningkatkan kualitas penampakan atau untuk menonjolkan beberapa aspek informasi yang terkan-dung di dalam citra. Jenis operasi ini bertujuan untuk memperbaiki kualitas citra dengan cara memanipulasi parameter-parameter citra. Dengan operasi ini, ciri-ciri khusus yang terdapat di dalam citra lebih ditonjolkan. Beberapa operasi perbaikan citra antara lain: perbaikan kontras gelap/terang, perbaikan tepian objek (edge enhancement), penajaman (sharpening), pemberian warna semu (pseudocoloring), penapisan derau (noise filtering).
2. Pemugaran citra (image restoration). Operasi ini bertujuan menghilangkan/ meminimumkan cacat pada citra. Tujuan pemugaran citra hampir sama dengan operasi perbaikan citra. Bedanya, pada pemugaran citra penyebab degradasi gambar diketahui. Contoh-contoh operasi pemugaran citra, yaitu: penghilangan kesamaran (deblurring), dan penghilangan derau (noise).
3. Pemampatan citra (image compression). Jenis operasi ini dilakukan agar citra dapat direpresentasikan dalam bentuk yang lebih kompak sehingga memerlukan memori yang lebih sedikit. Hal penting yang harus diperhatikan dalam pemam-patan adalah citra yang telah dimampatkan harus tetap mempunyai kualitas gambar yang bagus.
5. Analisis citra (image analysis). Jenis operasi ini bertujuan menghitung besaran kuantitatif dari citra untuk menghasilkan deskripsinya. Teknik analisis citra mengekstraksi ciri-ciri tertentu yang membantu dalam identifikasi objek. Proses segmentasi kadangkala diperlukan untuk melokalisasi objek yang diinginkan dari sekalilingnya.
6. Rekonstrusi citra (image reconstruction). Jenis operasi ini bertujuan untuk membentuk ulang objek dari beberapa citra hasil proyeksi. Operasi rekonstruksi citra banyak digunakan dalam bidang medis.
Menurut Petrou dan Bosdogianni (1999), operator didefinisikan dalam bentuk fungsi penyebaran titik. Fungsi penyebaran titik merupakan operator yang diperoleh ketika operator dikenakan kepada suatu titik sumber, yaitu
O[sumber titik] = fungsi penyebaran titik, (2.1)
atau
O[δ(x−α, y−β)] =h(x, α, y, β). (2.2) denganδ(x−α, y−β) adalah sumber titik dari kecerahan 1 yang berpusat pada titik (α, β). Jika operator pada Persamaan 2.2 adalah linear, yaitu ika sumber titik adalah a kali kecerahan, maka hasilnya akan a kali lebih besar, yaitu
O[aδ(x−α, y−β)] =ah(x, α, y, β). (2.3)
2.2.3 Pembagian permukaan
Tempelan ini dapat dibagi ke dalam empat sub-tempelan, yang dapat dibangkitkan dari 16 titik sub-kendali yang tunggal. Di sini difokuskan pada skema subdivisi hanya untuk satu dari empat (sub tempelan yang sesuai dengan 0≤u, v ≤ 1
2), sebagaimana yang lainnya secara simetri. Gambar berikut mengilustrasikan 16 titik yang dihasilkan oleh sub pembagian ke dalam empat sub tempelan. Kenneth (2000) telah menurunkan rumusan transformasi terkait dengan ini, seperti berikut.
dimanaP′
2.3 Formulasi B-spline kuadratik
Andaikan terdapat suatu fungsi dengan dua variabel bebas yang dinyatakan dalam bentuk tabulasi sejumlah berhingga titik, yang akan diinterpolasi untuk semua vari-abelnya. Interpolasi dua-dimensi adalah masalah interpolasi dalam array nilai tabular dua-dimensi. Nilai fungsif(a1,i, a2,j) diketahui untuki= 1,· · · , n1 danj = 1,· · · , n2, dan akan dicari nilai f(x1, x2) pada suatu titik sembarang (x1, x2) di dalam daerah yang ditutupi oleh tabel. Jika titik-titik tabular diplot pada suatu bidang, maka akan terbentuk verteks-verteks grid segi empat.
Suatu spline adalah sebuah suku banyak berorderkpotong demi potong (paling tinggi derajatk−1) yang didefinisikan pada interval [a, b]; a=x0 < x1,· · · , < xN−1 dengan h = xi+1 −xi, i = 0,· · · , N −1. Spline u(x) biasanya dideskripsikan di dalam representasi B-spline sebagai u(x) = PN
i=1αiβik(x) dengan βik adalah fungsi spline khusus berorder k yang disebut B-spline, yang mempunyai sifat khusus yang mempunyai pendukung kompak (Fletcher, 1988).
2.3.1 Persamaan matriks untuk permukaan spline bikuadratik
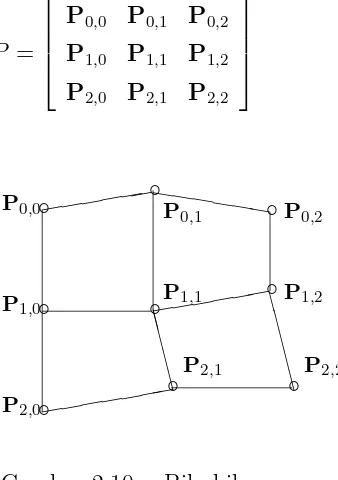
2.10 . Permukaan tersebut dapat dipandang sebagai B-spline seragam bikuadratik P(u, v) yang didefinisikan oleh array 3×3 dari titik-titik kendali seperti pada per-samaan 3.2.
Gambar 2.10 : Bikubik
Dalam bentuk matriks, persamaan 3.3 berikut dapat digunakan, yaitu
P(u, v) = h 1 u u2 iM P MT
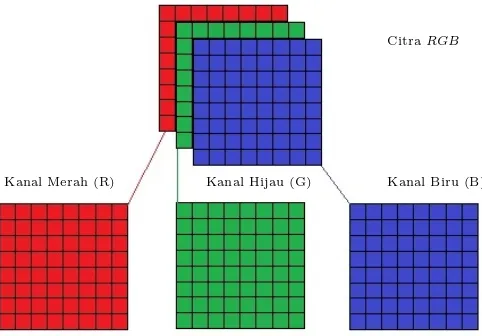
terhadap warnadibangkitkan dengan memadukan tiga kanal fundamental monokrom yang direkonstruksi menggunakan algoritmayang diperhatikan ke dalam sebuah citra.
CitraRGB
Kanal Merah (R) Kanal Hijau (G) Kanal Biru (B)
Gambar 2.11 : Citra RGB dengan kanal Merah, Hijau dan Biru Sumber: (Vuong, 2011)
Pixel Input
Pixel Input
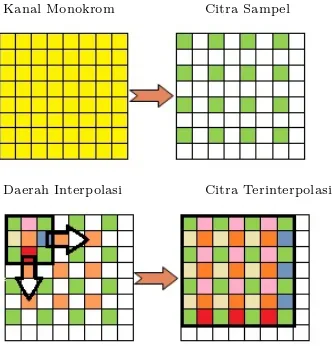
Kanal Monokrom Citra Sampel
Daerah Interpolasi Citra Terinterpolasi
Gambar 2.13 : Langkah-langkah interpolasi
2.5 Spline
Suatu spline dapat digunakan untuk menanggulangi masalah yang muncul ketika su-atu taksiran dilakukan menggunakan polinomial berderajat tinggi yang diakibatkan oleh banyaknya titik data yang diberikan (Yang et al., 2005). Spline digambarkan se-bagai pelat lentur tipis yang dilekatkan pada setiap titik-titik data yang digambarkan sebagai pin. Dengan lekatnya pelat tersebut pada setiap pin yang diberikan, dapat diasumsikan bahwa kedudukan bagian pelat pada setiap pin adalah sama dengan ke-dudukan pin. Dengan asumsi bahwa pelat tidak patah pada setiap posisi pin, maka kemiringan dari suatu bagian pelat dan bagian lain di setiap posisi pin adalah sama. Selain itu juga lengkungan mereka di setiap posisi pin adalah sama. Gambar 2.14 mengilustrasikan mekanisme ini.
Gambar 2.14 : Mekanisme Model Spline Sumber: (Vuong, 2011)
mem-punyai sebanyakn−1 kurva, yaituf1,2(x), f2,3(x),· · · , fn−1,n(x) yang masing-masing bentuk kuadratik dengan koefisien-koefisien yang tidak sama.
Gambar 2.15 : Spline kuadratik di setiap sub interval Sumber: (Vuong, 2011)
2.6 Spline hirarki
Satu-satunya persyaratan filosofis yang mencirikan pendekatan hirarkis adalah sifat daya halus dari fungsi basis yang mendasari yang didefinisikan pada ruang pendekatan bersarang. Kontrol lokal penghalusan ini dicapai melalui prosedur adaptif yang secara eksklusif didasarkan pada perbaikan. Voung et al. (2011) dalam karyanya memper-timbangkan ruang B-spline hirarki, tetapi keluarga fungsi dasar yang lain yang me-nunjukkan sifat analog dan juga memungkinkan penghalusan adaptif juga dapat di-gunakan untuk menentukan hirarki spline yang cocok untuk analisis. Voung juga me-nunjukkan bagaimana membangun sebuah polinomial basis tak-negatif potong demi potong yang disusun dari yang didukung secara lokal yang juga dapat dimodifikasi untuk membentuk partisi dari unit. Selain itu, telah diuraikan bahwa pembangunan hirarkis spline basis langsung mengakibatkan sifat bersarang dari hirarki ruang yang sesuai.
2.6.1 Ruang B-Spline produk tensor
Suatu ruang B-spline produk tensorBdidefinisikan dengan menentukan derajat poli-nomial (p, q) dan vektor simpul horizontal dan vertikal
U ={u0 ≤u1 ≤ · · · ≤un+p+1}, V ={v0 ≤v1 ≤ · · · ≤vm+q+1}, yang memuat nilai real parametrik tak negatif sedemikian sehingga
0≤µ(U, u)≤p+ 1, dan 0≤µ(V, v)≤q+ 1
B direntang oleh produk tensor B-spline
Sembarang fungsi B-spline f(u, v)∈ B dapat digambarkan sebagai
f(u, v) =
2.6.2 Ruang dan domain tersarang
Perhatikan barisan berhingga dari N ruang B-spline bivariat (B)l=0,···,N−1 yang di-anggap tersarang,
B0
⊂ B1
⊂ · · · ⊂ BN−1 ,
bersama dengan barisan berhinggaN himpunan buka terbatas (Ωl)
l=0,···,N−1 dengan ΩN−1
⊆ΩN−2
⊆ · · · ⊆Ω0 =∅,
yang mendefinisikan domain tersarang untuk hiraiki spline, seperti terlihat pada Gam-bar 2.16 .
2.6.3 B-spline basis hirarkis
Perhatikan support dari setiap fungsif yang dibatasi pada domain Ω0
dengan men-definisikan
supp f ={(x, y) :f(x, y)6= 0∧(x, y)∈Ω0
}.
Basis K dari ruang spline hirarkis secara rekursif dibentuk seperti berikut.
(i) Inisialisasi: K0
={τ ∈ N0
Gambar 2.16 : Domain tersarang untuk hirarki spline Sumber: (Vuong, 2011)
(ii) Konstruksi Kl+1
dari Kl: secara rekursif.
Kl+1 =KAl+1∪KBl+1, l= 0,· · ·, N −2, dengan
Kl+1
A ={τ ∈K l
: supp τ *Ωl+1
}
dan
KBl+1 ={τ ∈ Nl+1
: supp τ ⊆Ωl+1
}
(iii) K=KN−1 .
Gambar 2.17 menunjukkan langkah inisialisasi semua fungsi basis dari basis B-spline dasarN yang supportnya memotong Ω0
, sementara di dalam langkah rekursif, pertama diperhatikanKAl+1, dan ditambahkan semua fungsi basisτ dari level sebelum-nya yang supportsebelum-nya tidak keseluruhansebelum-nya termuat di dalam Ωl+1
. Kemudian Ωl+1 ditutupi oleh fungsi basis yang telah halus dalamNl+1
yang termuat di dalam KBl+1.
2.7 Penghalusan Hirarki Adaptif
(a) Langkah 0 (b) Langkah 1 (c) Langkah 2
Gambar 2.17 : Pemilihan fungsi basis dengan prosedur iterasi
1. Domain parameter adalah suatu domain empat persegi atau tanpa mengurangi keumuman merupakan bujur sangkar satuan,
Ω0
= [0,1]2
. (2.9)
2. Batas daerah yang dihaluskan selalu dicocokkan dengan garis simpul dariBl−1
3. Derajat (p, q) tidak berubah selama penghalusan hiraiki.
2.8 Matlab untuk pengolahan citra
Matlab merupakan satu perangkat lunak yang di dalamnya pengguna dapat menuliskan program sesuai keperluannya. Kemampuan Matlab dalam menghitung persoalan nu-merik telah dinyatakan baik oleh penggunanya. Dengan perkembangan kemampuan Matlab, software ini juga banyak digunakan untuk pengolahan citra. Cukup banyak fungsi-fungsi yang telah disediakan di dalam software ini.
2.8.1 Jenis data dan konversi
Elemen-elemen di dalam matriks Matlab bisa mempunyai jenis data yang berbeda. Tabel 2.1 merupakan jenis data yang paling umum.
Tabel 2.1 : Jenis Data dalam Matlab
Jenis Data Deskripsi Range
int8 8-bit integer -128 - 127
uint8 8-bit unsigned integer 0 - 255
int16 16-bit integer -32768 - 32768
Meskipun variabel a dan b memiliki nilai numerik yang sama, mereka adalah tipe data
berbeda-beda. Satu pertimbangan penting adalah bahwa operasi aritmatika tidak diizinkan
dengan tipe data int8, int16, uint8 dan uint16.
Sebuah citra keabuan dapat terdiri dari piksel yang nilainya adalah tipe data uint8.
Citra-citra ini karenanya cukup efisien dalam hal ruang penyimpanan, karena setiap
pik-sel hanya membutuhkan satu byte. Namun, operasi aritmatika tidak diizinkan pada tipe
data citra uint8 dan harus dikonversi ke double sebelum aritmatika dicoba. Tabel 2.2
menunjujkan konversi jenis data yang dapat digunakan.
Tabel 2.2 : Konversi citra dalam Matlab
Fungsi PEnggunaan Format
ind2gray Indexed to Greyscale y=ind2gray(x,map); gray2ind Greyscale to indexed [y,map]=gray2ind(x); rgb2gray RGB to greyscale y=rgb2gray(x); gray2rgb Greyscale to RGB y=gray2rgb(x); rgb2ind RGB to indexed [y,map]=rgb2ind; ind2rgb Indexed to RGB y=ind2rgb(x,map);
2.8.2 Perintah di Matlab untuk pengelolaan citra
Di dalam pengelolaan citra perlu beberapa perintah Matlab, seperti misalnya pembacaan
citra, menampilkan citra, dan menyimpan citra. Citra dibaca dalam lingkungan Matlab
menggunakan fungsi imread dengan sintaks seperti berikut
imread(’namafile’)
Parameter nama file adalah string yang berisi nama lengkap file dari file citra
(terma-suk ekstensi dari file juga harus disertakan). Berikut adalah contoh perintah imread dalam
Matlab.
>> i = imread(’bungamawar.jpg’);
Perintah di atas merupakan pembacaan file dengan nama bungamawar dan berekstensi jpg,
dan kemudian disimpan ke dalam variabel i dengan jenis matriks.
Citra ditampilkan di desktop Matlab dengan menggunakan fungsi imshow, yang
mem-punyai sintaks seperti berikut.
dengan f adalah array citra dan G adalah jumlah level intensitas yang digunakan untuk
menampilkannya. JikaGdiabaikan, maka akan digunakan intensitas default, yaitu 256.
Menyimpan citra ke dalam temat penyimpanan digunakan perintah imwrite, yang
sintaks dasarnya sepaerti berikut:
imwrite(f, ’namafile’)