artikel Nury Ardillah
Teks penuh
Gambar
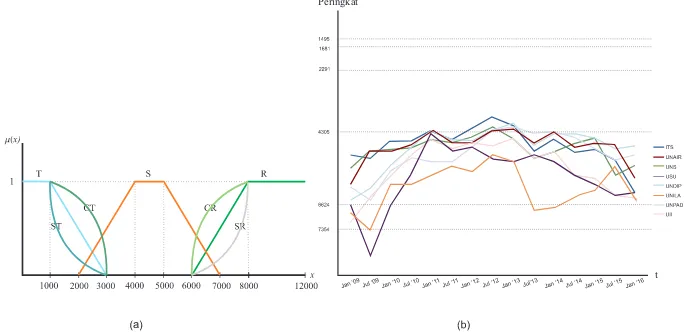
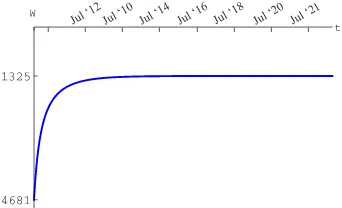
Dokumen terkait
Sistim fermentasi cair dapatdilakukan dengan 3 cara yaitu fermentasi tertutup (batch prosess), fermentasi kontiniu dan fermentasi tetutup dengan penambahan substrat pada selang
Bahwa Dalam rangka pelaksanaan Undang-Undang Nomor 32 Tahun 2004 tentang Pemerintahan Daerah sebagaimana telah diubah dua kali, terakhir dengan Undang-Undang Nomor
Berdasarkan struktur cerita pada kedua cerita rakyat yang diteliti tersebut, penelitian ini bisa memperoleh struktur wacana yang dapat dirangkum dalam beberapa
Adalah percikan las yang terlalu banyak.. Pastikan peralatan dan perlengkapan pengelasan sudah siap semua. Nyalakan generator las, dan atur amperenya sesuai dengan bahan yang
Dalam kegiatan Bimbingan, Modul Bimbel dipakai ketika Soal-soal dari Buku sekolah sudah Dalam kegiatan Bimbingan, Modul Bimbel dipakai ketika Soal-soal dari Buku
Tujuan uji tekan adalah untuk mengukur kuat tekan uniaksial sebuah Tujuan uji tekan adalah untuk mengukur kuat tekan uniaksial sebuah conto batuan dlam geometri
Sesuai dengan rumusan masalah di atas, maka tujuan penelitian ini adalah untuk mengetahui Pengaruh Model Pembelajaran Jigsaw Terhadap Motivasi Belajar Siswa Kelas
Hasil yang didapatkan setelah diimplementasikannya metode SLC dalam pembelajaran adalah literasi sains siswa untuk keseluruhan aspeknya meningkat dengan indeks gain