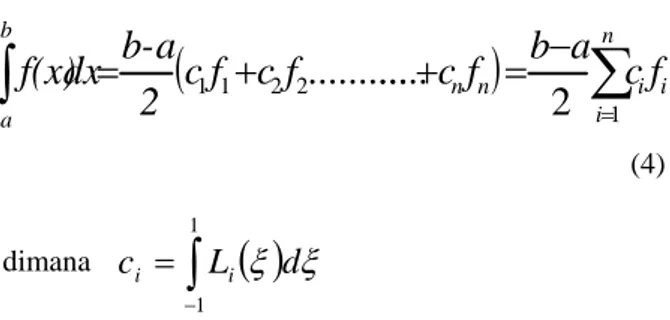Vol. 17 No. 1 April 2010 Abstrak
Paper ini mempresentasikan penyelesaian pesamaan vibrasi secara numeris dengan menggunakan integrasi numeris metoda Newton-Cote. Eksekusi model selama sepuluh kali period gelombang memberikan solusi yang sangat stabil.
Kata-kata Kunci: Polinomial lagrange, integrasi numeris. Abstract
This paper presents a numerical method for solving vibration equation using Newton-Cote’s numerical integra-tion. Model execution during ten times of vibration period gives a very stabile soluintegra-tion.
Keywords: Lagrangian polynomial, numerical integration.
Catatan Teknik (Technical Notes)
Penyelesaian Persamaan Vibrasi dengan Integrasi Newton-Cote
Syawaluddin Hutahaean
Kelompok Keahlian Teknik Kelautan, Fakultas Teknik Sipil dan Lingkungan, Institut Teknologi Bandung, Jl. Ganesha No. 10 Bandung 40132, E-mail: [email protected]
Jurnal Teoretis dan Terapan Bidang Rekayasa Sipil Jurnal Teoretis dan Terapan Bidang Rekayasa Sipil
1. Pendahuluan
Penyelesaian persamaan vibrasi dengan metoda integrasi telah lama dikenal, yaitu antara lain metoda Wilson-q dan Newmark-b, (Bathe, 1982). Penyele-saian diferensial waktu orde satu dengan metoda inte-grasi juga telah banyak digunakan, yaitu dikerjakan pada penyelesaian persamaan gelombang nonlinier dari Boussinesq, Liu (1999), (Meftah, 2004). (Hutahaean, 2005, 2007a, 2007b, 2008) menyelesai-kan persamaan gelombang panjang Airy dengan metoda integrasi dengan menggunakan integrasi numeris dari Newton-Cote.
Pada penelitian ini dikerjakan integrasi numeris dari Newton-Cote pada persamaan vibrasi yang meru-pakan diferensial waktu orde 2.
2.
PolinomialLagrange
Pendekatan fungsi f(x) dengan polinomial Lagrange adalah, Arden (1970),
dimana
Li(x) = polinomial Lagrange pada titik i
fi = harga fungsi pada titik i n = jumlah titik polinomial
Bentuk umum polinomial Lagrange adalah, Arden (1970), f (x) = i n i i
(x)
f
L
∑
=1 (1)Apabila pada suatu domain 0 < x < L didekati dengan 3 titik polinomial Gambar 1, maka bentuk pendekatannya adalah pada x = x1, L1 (x1) = 1, L2 (x1) = 0, L3 (x1) = 0, maka f(x1) = L1 (x1) f1 + L2 (x1) f2 + L3 (x1) f3 = f1
(
)(
)(
)
(
)
(
i)(
i)(
i)
(
i n)
n ix
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
L
−
−
−
−
−
−
−
−
=
....
...
...
...
...
...
)
(
3 2 1 3 2 1(
)
(
)
∏
=−
−
=
n j i j j ix
x
x
x
x
L
1)
(
,j
≠
i
atau: 1 2 3Gambar 1. Pendekatan dengan 3 titik polinomial
3 3 2 2 1 1
(
)
(
)
(
)
)
(
x
L
x
f
L
x
f
L
x
f
f
=
+
+
(
)(
)
(
1 2)(
1 3)
3 2x
-x
x
-x
x
-x
x
-x
x
L
1(
)
=
dimana:(
)(
)
(
2 1)(
2 3)
3 1x
-x
x
-x
x
-x
x
-x
x
L
2(
)
=
(
)(
)
(
3 1)(
3 2)
2 1x
-x
x
-x
x
-x
x
-x
x
L
3(
)
=
pada x = x2, L1 (x2) = 1, L2 (x2) = 0, L3 (x2) = 0, maka
f(x2) = L1 (x2) f1 + L2 (x2) f2 + L3 (x2) f3 = f2 pada x = x3, L1 (x3) = 1, L2 (x3) = 0, L3 (x3) = 0, maka
f(x3) = L1 (x3) f1 + L2 (x3) f2 + L3 (x3) f3 = f3
Jadi pendekatan fungsi dengan polinomial Lagrange adalah exact pada titik-titik polinomial dimana
f(x1) = f1, f(x2) = f2, f(x3) = f3
Pendekatan fungsi f(x) dengan polinomial Lagrange dapat saja dilakukan pendekatan langsung yaitu pada seluruh domain langsung digunakan n titik polinomial. Tetapi pendekatan seperti ini akan terbentuk polino-mial dengan pangkat tinggi pada x yaitu xn-1, dimana semakin besar n, akan semakin besar derajat polinomi-alnya dan sering terjadi malah mengurangi ketelitian.
Metoda pendekatan yang termudah adalah dengan membagi-bagi daerah perhitungan dalam sejumlah sub -domain, selanjutnya pendekatan polinomial dilakukan pada masing-masing sub-domain.
Untuk domain
yang dibagi dalam 3 sub domain dan pada sub domain digunakan 3 titik polinomial,
a. domain perhitungan
b. pembagian domain dalam sejumlah sub-domain
c. pendekatan dilakukan pada sub-domain dengan sejumlah titikpolinomial
Gambar 2. Pendekatan polinomial dengan sub-domain 1 2 3 4 5 6 7 1 2 3 Pada sub-domain 1 f(x) = L1(x) f1 + L2(x) f2 + L3(x) f3 L1(x) =
(
)(
)
(
1 2)(
1 3)
3 2x
-x
x
-x
x
-x
x
-x
L2(x) =(
)(
)
(
2 1)(
2 3)
3 1x
-x
x
-x
x
-x
x
-x
L3(x) =(
)(
)
(
3 1)(
3 2)
2 1x
-x
x
-x
x
-x
x
-x
Pada sub-domain 2 f(x) = L1(x) f3 + L2(x) f4 + L3(x) f5 L1(x) =(
)(
)
(
3 4)(
3 5)
5 4x
-x
x
-x
x
-x
x
-x
Untuk selanjutnya, yang dimaksudkan dengan pendekatan polinomial Lagrange adalah pendekatan pada sub-domain.
3.
Integrasi Numeris dengan Metoda
Newton-Cote
Dengan menggunakan polinomial Lagrange dapat dengan mudah dilakukan integrasi suatu fungsi, yaitu
Untuk pendekatan 3 titik polinomial
mengingat Li (x) adalah suatu polinomial, maka integrasi dapat dengan mudah dilakukan.
3.1 Koefisien integrasi
Pada Persamaan (3) terlihat bahwa dengan interval integrasi yang konstan, maka didapat hasil integrasi Li
(x) yang konstan juga. Jadi untuk harga a dan b yang tetap, maka bila
L2(x) =
(
)(
)
(
4 3)(
4 5)
5 3x
-x
x
-x
x
-x
x
-x
L3(x) =(
)(
)
(
5 3)(
5 4)
4 3x
-x
x
-x
x
-x
x
-x
Pada sub-domain 3 7 3 6 2 5 1(
)
(
)
(
)
)
(
x
L
x
f
L
x
f
L
x
f
f
=
+
+
(
)(
)
(
5 6)(
5 7)
7 6x
-x
x
-x
x
-x
x
-x
x
L
1(
)
=
(
)(
)
(
x
-
x
)(
x
-
x7
)
x
-x
x
-x
x
L
6 5 6 7 5=
)
(
2(
)(
)
(
7 5)(
7 6)
6 5x
-x
x
-x
x
-x
x
-x
x
L
3(
)
=
∑
==
n 1 i i i(x)
f
L
(x)
f
(2)∑ ∫
∫
=
=n 1 i i i b adx
f
(x)
L
dx
(x)
f
3 b a 3 2 b a 2 1 b a 1 b a f dx (x) L f dx (x) L f dx (x) L dx (x) f∫
∫
∫
∫
= + + (3) 1 b a 1(x)
dx
c
L
=
∫
2 b a 2(x)
dx
c
L
=
∫
, 3 b a 3(x)
dx
c
L
=
∫
dan 3 3 2 2 1 1 b a 1(x)
dx
c
f
c
f
c
f
L
=
+
+
∫
makaVol. 17 No. 1 April 2010
c1, c2 dan c3 disebut dengan koefisien integrasi.
Telah diketahui bahwa suatu fungsi f(x) pada domain
a ≤ x ≤ b untuk setiap harga a dan b, dapat ditransformasikan menjadi suatu fungsi g(ξ) pada domain -1 ≤ ξ ≤ 1. Jadi bila didapatkan harga-harga koefisien integrasi pada domain ξ, maka integrasi akan dapat dilakukan dengan menggunakan koefisien integrasi tersebut tanpa harus melakukan integrasi polinomial Lagrange lagi, dimana metoda integrasi ini disebut dengan.metoda Newton-Cote.
Untuk x yang konstan, fungsi transformasi dari x ke
ξ dapat digunakan persamaan transformasi yang sederhana, yaitu
x = p + q
Pada = -1, x = a ; dan pada = 1, x = b, sehing-ga diperoleh dua persamaan yaitu
a = - p + q b = p + q
Dengan persamaan transformasi tersebut, maka Dari ke 2 persamaan tersebut diperoleh q =
2
b
a
+
dan p= 2 a b−sehingga persamaan transformasi menjadi
x =
2
a
b
−
+2
b
a
+
ξ
d
dx
2
a
b
−
= dx =2
a
b
−
dξ
ξ
d
2
a
-b
)
g(
dx
f(x)
1 1 -b a∫
∫
=
dengan i i n 1 ig
)
(
L
)
g(
ξ
∑
ξ
==
, dimanag
i=
f
i( )
∑ ∫
( )
∫∑
= − =⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
n i i i 1 1 -i n i iL
f
d
a
b
d
g
L
2
a
-b
1 1 1 12
ξ
ξ
ξ
ξ
dx
f(x)
b a∫
Integrasi menjadi, =dx
f(x)
b a∫
=( )
( )
( )
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∫
∫
∫
− − − n nd
f
L
f
d
L
f
d
L
2
a
-b
1 1 2 1 1 2 1 1 1 1ξ
ξ
ξ
ξ
...
..
ξ
ξ
yang berharga konstan mengingat integrasi selalu dilakukan pada domain -1 ≤ξ ≤ 1. Jadi bila diperoleh harga-harga ci, integrasi akan dapat dilakukan setiap saat dengan menggunakan Persamaan (4) tanpa harus mengintegrasikan polynomial Lagrange lagi.
Pada bagian berikut akan dihitung koefisien integrasi untuk sejumlah konfigurasi titik integrasi dengan men-gintegrasikan polynomial Lagrange.
Integrasi dengan 3 titik polinomial
Pada skema ini interval garis a-b dibagi dalam 2 inter-val, yaitu seperti terlihat pada Gambar (3). Untuk pendekatan dengan 3 titik polinomial, maka
Dengan 3 titik polinomial atau titik integrasi tersebut dimana ξ1 = -1, ξ2= 0, ξ3= 1, polinomial Lagrange akan berbentuk
(
)
∑
∫
=−
=
+
+
=
n i i i n n b af
c
a
b
f
c
f
c
f
c
2
a
-b
dx
f(x)
1 2 2 1 12
...
...
(4) dimanac
i∫
L
i( )
ξ
d
ξ
−=
1 1⎜⎜
⎝
⎛
+
=
∫
∫
∫
2 1 1 -2 1 1 1 -1 b af
d
)
(
L
f
d
)
(
L
2
a
-b
dx
(x)
f
ξ
ξ
ξ
ξ
⎟⎟
⎠
⎞
+
∫
3 1 1 -3(
)
d
f
L
ξ
ξ
a b x ‐1 1ξ
2 b a− 0ξ
1ξ
2ξ
3Gambar 3. Integrasi dengan 3 titik polinomial
( ) (
(
)(
)(
)
)
(
1
)
2
1
3 1 2 1 3 2 1=
−
−
−
−
−
−
=
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
L
( ) (
(
)(
)(
)
)
(
2)
3 2 1 2 3 1 2ξ
ξ
ξ
ξ
1
ξ
ξ
ξ
ξ
ξ
ξ
=
−
−
−
−
−
=
L
( ) (
(
)(
)(
)
)
(
1
)
2
1
2 3 1 3 2 1 3−
−
=
+
−
−
=
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
L
Dengan demikian diperoleh koefisien integrasi yaitu
Integrasi dengan 4 titik polinomial
Pada skema ini interval garis a - b dibagi dalam 3 interval, yaitu
Dengan 4 titik polinomial ini, maka polinomial Lagrange berbentuk
Dengan memasukkan harga-harga ξ1 s/d ξ4 seperti pada Gambar (4) dan dengan mengintegrasikan dari
–1 dan ke 1, maka diperoleh
Koefisien integrasi, untuk berbagai titik integrasi dengan persamaan integrasi
ξ
ξ
)
d
(
L
c
1 1 -1∫
=
1(
)
∫
−=
−
−
=
1 13
1
1
2
1
ξ
ξ
ξ
d
(
)
∫
∫
−=
−
=
=
1 1 2 23
4
1
ξ
ξ
ξ
ξ
)
d
d
(
L
c
1 1 -2(
)
∫
∫
−=
+
=
=
1 1 33
1
1
2
1
ξ
ξ
ξ
ξ
ξ
)
d
d
(
L
c
1 1 -3 ‐1 1ξ
2
1
−
2
1
Gambar 4. Integrasi dengan 4 titik polinomial
( ) (
)(
)(
)
(
1 2)(
1 3)(
1 4)
4 3 2-L
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
=
1( )
(
)(
)(
)
(
2 1)(
2 3)(
2 4)
4 3 1-L
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
=
2( )
(
)(
)(
)
(
3 1)(
3 2)(
3 4)
4 2 1-L
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
=
3( )
(
)(
)(
)
(
4 1)(
4 2)(
4 3)
3 2 1-L
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
=
425
.
0
1=
∫
L
(
ξ
)
d
ξ
=
c
1 1 -175
.
0
2=
∫
L
(
ξ
)
d
ξ
=
c
1 1 -2 ;75
.
0
3=
∫
L
(
ξ
)
d
ξ
=
c
1 1 -3 ;25
.
0
4=
∫
L
(
ξ
)
d
ξ
=
c
1 1 -4∫
b af(x)
dx = i n 1 i if
c
2
a
-b
∑
=, adalah seperti pada tabel
berikut.
a. dengan 3 titik integrasi
b. dengan 4 titik integrasi
Dari kedua hasil perhitungan tersebut terlihat bahwa semakin banyak titik integrasi, semakin baik keteli-tian. Hal ini dikarenakan semakin banyak titik inte-grasi semakin kecil dx.
Tabel 1. Koefisien integrasi ci pada persamaan
∫
b af(x)
dx = i n 1 i if
c
2
a
-b
∑
=∫
2 0sin
πxdx
Contoh : akan dihitung( )
x
x
f
=
sin
dalam hal ini ,
a
=
0
2
π
=
b
dan0
1=
x
;f
1=
0
;4
2π
=
x
2
2
1
2=
f
;2
3π
=
x
f
3=
1
00228 . 1 1 3 1 2 2 1 3 4 0 3 1 2 0 2 sin 2 0 = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + − =∫
xdx x x x π πDimana hasil eksak
∫
=
2 0
1
sin
πxdx
0
1=
x
;f
1=
0
;6
2π
=
x
f
2=
0
.
5
;3
3π
=
x
f
3=
0
.
866025
;2
4π
=
x
f
4=
1
.
0
(
0
.
25
0
0
.
75
0
.
5
2
0
2
sin
2 0+
−
=
∫
xdx
x
x
π
π)
1
.
001005
1
25
.
0
866025
.
0
75
.
0
+
=
+
x
x
n c1 c2 c3 c4 c5 c6 c7 2 1.000000 1.000000 3 1/3 4/3 1/3 4 0.250000 0.750000 0.750000 0.250000 5 0.155556 0.711111 0.266667 0.711111 0.155556 6 0.131944 0.520833 0.347222 0.347222 0.520833 0.131944 7 0.097619 0.514286 0.064286 0.647619 0.064286 0.514286 0.097619Vol. 17 No. 1 April 2010
4. Penyelesaian Persamaan Vibrasi
Persamaan vibrasi untuk satu derajad kebebasan, Bathe (1982), adalah,
dimana
u = simpangan (Gambar 5)
m = masa
c = koefisien redaman (damping)
k = koefisien kekakuan
f(t) = gaya luar yang bekerja pada system
Persamaan tersebut akan diselesaikan dengan metoda integrasi dari Newton-Cote, dengan 4 titik integrasi. Persamaan (5) dapat ditulis dalam bentuk lain, yaitu
Persamaan terakhir, dikalikan dengan dt dan diintegrasikan dari t-2 t ke t+ t,
Suku ke 1 dan ke 2 ruas kiri persamaan diselesaikan secara analitik, sedangkan suku ke 3 diselesaikan secara numeris.
f(t)
u
k
dt
du
c
dt
u
d
m
2 2=
+
+
(5) f(t) uGambar 5. Sistem SDOF
Dalam hal ini
a
=
t
−
2
δ
t
,b
=
t
+
δ
t
,
(
) (
)
2
3
2
2
2
t
t
t
t
t
a
b
δ
δ
δ
=
−
−
+
=
−
(
)
2
k
t
3
u
-u
c
dt
du
-dt
du
m
t t t 2t t 2 t t tδ
δ δ δ δ+
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
+ − − +(
t 2t t t tu
0.75
u
0.75
u
0.25
−δ+
−δ+
Persamaan dikalikan dengan t dan dikelompokkan suku-suku yang mengandung u dengan referens waktu yang sama.
Persamaan terakhir dapat ditulis ringkas
kef ut+ t = fef
)
k
f(t)
dt
u
0.25
t t t 2 t t t∫
+ − +=
+
δ δ δ (6) t tdt
du
+δ⎟
⎠
⎞
⎜
⎝
⎛
diselesaikan dengan metoda selisih hingga dengan skema diferensial ke belakang, yaitu t tdt
du
+δ⎟
⎠
⎞
⎜
⎝
⎛
=t
2
u
3
u
4
-u
t t t t tδ
δ δ + −+
Substitusi persamaan untuk
t t
dt
du
+δ⎟
⎠
⎞
⎜
⎝
⎛
ke Persamaan (6) dan t 2 tdt
du
−δ⎟
⎠
⎞
⎜
⎝
⎛
dipindahkan ke ruas kanan(
)
2
k
t
3
u
-u
c
t
2
u
3
4u
-u
m
t t t 2t t t t t tδ
δ
δ δ δ δ+
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−+
+ + −(
t 2t t t tu
0.75
u
0.75
u
0.25
−δ+
−δ+
)
f(t)
dt
dt
du
m
u
0.25
t t t 2 t t 2 t t t∫
+ − − +⎟
+
⎠
⎞
⎜
⎝
⎛
=
+
δ δ δ δ t 2 t t 2u
2
k
t
2.25
2m
-u
2
k
t
0.75
c
t
2
m
3
δ
δ
+δδ
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
t t 2 tu
2
k
t
2.25
2
m
δ
−δ⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
t t 2u
2
k
t
0.75
c
t
-
δ
δ
⎟⎟
−2δ⎠
⎞
⎜⎜
⎝
⎛
+
+
= t mdt
f(t)
t
dt
du
t t t 2 t t 2 t∫
+ − −+
⎟
⎠
⎞
⎜
⎝
⎛
δ δ δδ
kef =2
k
t
0.75
c
t
2
m
3
+
δ
+
δ
2 (7)( )
∫
+ − − −⎟
+
⎠
⎞
⎜
⎝
⎛
+
−
−
=
t t t t t t t t t eft
f
t
dt
dt
du
tm
u
a
u
a
f
δ δ δ δδ
δ
2 2 2 1 (8) 2 2 2 2tergantung dari bentuknya. Dalam hal f(t) merupakan fungsi yang diketahui bentuknya, maka misal f(t) =
Asin ωt, maka dapat diselesaikan secara analitik. Sedangkan bila f(t) berupa data series, maka integrasi dilakukan secara numerik.
Contoh :
Model dieksekusi dengan data :
Perhitungan dilakukan dengan δt = 0.07 dt. Hasil eksekusi adalah disajikan pada gambar grafik simpangan u terhadap waktu t, seperti pada Gambar (4.2).
2
k
t
2.25
m
2δ
+
−
2
a1 = (9)2
k
t
2.25
2
m
+
δ
2 a2 = (10) a3 =⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
2
k
t
0.75
c
t
-2
δ
δ
(11) t 2tdt
du
−δ⎟
⎠
⎞
⎜
⎝
⎛
=t
2
u
-u
t t t 3tδ
δ δ − −dt
f(t)
t t t 2 t∫
+ − δ δ m = 2.0, c = 11.5, k = 30.0,⎟
⎠
⎞
⎜
⎝
⎛
=
t
t
f
1
.
2
2
sin
0
.
2
)
(
π
-0.1 -0.08 -0.06 -0.04 -0.02 0 0.02 0.04 0.06 0.08 0.1 1.00 3.00 5.00 7.00 9.00 11.00 13.00 15.00 17.00 19.00 21.00 waktu t (detik) si m p a nga n u ( m )Gambar 6. Grafik simpangan (u) terhadap waktu (t), hasil model
5. Kesimpulan
1. Seperti terlihat pada Gambar 6, eksekusi model pada jangka waktu 10x perioda eksitasi solusi model adalah stabil.
2. Adapun ketelitian dari metoda ini adalah ditentu-kan oleh ketelitian dari metoda integrasi dari Newton-Cote, dimana pada contoh integrasi fungsi sinusoidal metoda memberikan hasil yang baik. Hutahaean, (2005, 2007a, 2007b, 2008), meng-gunakan metoda integrasi dari Newton-Cote pada pemodelan transformasi gelombang, yang juga memberikan hasil yang baik.
3. Ketelitian berikutnya adalah ditentukan oleh metoda selisih hingga yang digunakan, dimana pada penelitian ini digunakan ketelitian metoda selisih hingga dengan tingkat ketelitian O(d)2 baik pada skema central-difference maupun pada back-ward-difference.
4. Secara umum metoda yang dikembangkan cukup mempunyai prospek yang baik, baik untuk diteliti lebih lanjut maupun untuk diaplikasikan pada suatu analisis vibrasi.
Daftar Pustaka
Arden, B.W. and Astill, K.N., 1970, Numerical
Algo-rithm: Origins and Applications.
Addison-Wesley Publishing Company, Inc.
Li, Y. S., Liu, S.-X., Yu, Y.-X., and Lai, G.-Z., 1999, Numerical modeling of Boussinesq equations by finite element method Journal Coastal Engineering, Elsevier.
Vol. 17 No. 1 April 2010
Meftah, Sorgent, P., and Gami P., 2004,Linear analy-sis of a new type of extended Boussinesq model. Coastal Engineering.
Hutahaean, S., 2005, Model Difraksi dengan Persamaan Gelombang Airy yang Disempur-nakan, Thesis S3, Departemen Teknik Sipil, ITB.
Hutahaean, S., 2007a, Pemodelan Dinamika Gelom-bang dengan Mengerjakan Persamaan Kekekalan Energi, Jurnal Teknik Sipil, Volume 14, No. 1, Fakultas Teknik Sipil dan Lingkun-gan, ITB.
Hutahaean, S., 2007b, Model Refraksi Gelombang dengan Menggunakan Persamaan Gelombang Nonlinier, Jurnal Infrastruktur dan Lingkungan Binaan, Volume III, No. 2, Fakultas Teknik Sipil dan Lingkungan, ITB.
Hutahaean, S., 2008, Momentum Equilibrium Appli-cation in Airy’s Long Wave Equation, Jurnal Infratsruktur dan Lingkungan Binaan, Volume IV, No.1, Fakultas Teknik Sipil dan Lingkungan, ITB, Volume 15 No.1, 2008..