i
PELABELAN TOTAL TAK AJAIB SISI KUAT
PADA GRAF MULTISIKEL (
mCp
)
Skripsi
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Program Studi Pendidikan Matematika pada Fakultas Keguruan dan Ilmu Pendidikan
Oleh:
Ryan Sanjaya
091414066
PROGRAM STUDI PENDIDIKAN MATEMATIKA
JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS SANATA DHARMA
YOGYAKARTA
HALAMAN PERSEMBAHAN
Whatever you do, work at it with all your heart, as though
you were working for the Lord and not for men.
-Colossians 3 : 23-
vii
ABSTRAK
Ryan Sanjaya, 2013. Pelabelan Total Tak Ajaib Sisi Kuat pada Graf Multisikel
(𝒎𝑪𝒑). Program Studi Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma, Yogyakarta.
Suatu graf dikatakan memiliki pelabelan total tak ajaib sisi kuat jika 𝑉(𝐺)∪ 𝐸(𝐺) dipetakan secara bijektif ke bilangan bulat positif {1, 2, 3,…,𝑝+𝑞} dimana 𝑝= 𝐸(𝐺) , dan 𝑞= 𝑉(𝐺) , dengan jumlah label masing-masing sisi dengan kedua titik ujungnya membentuk sebuah barisan aritmetika naik dengan suku pertama 𝑎 dan beda 𝑑 maka pelabelannya disebut pelabelan total tak ajaib sisi (𝑎,𝑑). Suatu pelabelan dikatakan kuat jika label titiknya merupakan bilangan bulat positif {1, 2, 3,…,𝑝}, 𝑝= 𝑣(𝐺) .
Penelitian ini menyelidiki pelabelan total tak ajaib sisi kuat pada gabungan beberapa graf yang memiliki jumlah titik dan sisi yang sama yaitu graf multisikel(𝑚𝐶𝑝), 𝑚 ≥1; 𝑝 ≥3. Tujuan dari penelitian ini adalah meninjau apakah graf multisikel memenuhi super 𝑎,𝑑 edge antimagic total labeling, menentukan barisan aritmetika yang terbentuk, yakni suku pertama a dan beda d
dari super 𝑎,𝑑 edge antimagic total labeling, serta menentukan pola pelabelannya. Penelitian ini mengkaji beberapa buku, jurnal, dan hasil penelitian sebelumnya untuk mendapatkan teori-teori yang mendukung.
ABSTRACT
Ryan Sanjaya, 2013. Super Edge Antimagic Total Labeling on The Multicycle Graph 𝒎𝑪𝒑 . Mathematics Education Study Program. Mathematics and Science Education Department, Faculty of Teachers Training and Education, Sanata Dharma University, Yogyakarta.
A graph has an edge antimagic total labeling if 𝑉(𝐺)∪ 𝐸(𝐺) is mapped one to one to the positive integers {1, 2, 3,…,𝑝+𝑞} where𝑝= 𝐸(𝐺) , and 𝑞= 𝑉(𝐺) , with the sum of label of each edges incident to each vertex are distinct and obtain a line of increase arithemetic with the first rate is 𝑎 and the difference is 𝑑, so this labeling can be called (𝑎,𝑑) edge antimagic total labeling. A labeling is called super if the vertex labels are positive integers {1, 2, 3,…,𝑝},𝑝 = 𝑉(𝐺) .
This research observed the super edge antimagic total labeling on a graph that obtained from several cycle graph with the sum of edges and vertices of each cycle graph are same. The purpose of this research is to observe how far a multicycle graph 𝑚𝐶𝑝 ,𝑚 ≥1;𝑝 ≥3 imply (𝑎,𝑑) super edge antimagic total labeling, and to investigate how the sequences are, those are the first tribal and the different tribal of (𝑎,𝑑) super edge antimagic total labeling, and to find the labeling patterns.This research examined several books, journals, and the result of previous researchs to obtain the supporting theories.
The result of analysis obtained that the multicycle graph 𝑚𝐶𝑝 ,𝑚 ≥1 and
ix
KATA PENGANTAR
Puji dan syukur ke hadirat Tuhan Yang Maha Kuasa atas segala kasih, rahmat dan berkat-Nya sehingga penulis dapat menyelesaikan skripsi dengan judul
”Pelabelan Total Tak Ajaib Sisi Kuat pada Graf Multisikel (𝑚𝐶𝑝)” ini. Skripsi ini
diajukan untuk memenuhi salah satu syarat memperoleh gelar sarjana pendidikan pada Program Studi Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma, Yogyakarta.
Skripsi ini dapat tersusun berkat bimbingan dan bantuan serta dukungan dari berbagai pihak. Oleh karena itu, pada kesempatan kali ini penulis menyampaikan terima kasih kepada:
1. Bapak Dominikus Arif Budi Prasetyo, S.Si, M.Si. selaku Dosen Pembimbing Akademik sekaligus dosen pembimbing skripsi atas dukungan dan bimbingan selama studi terlebih selama penulis menyusun skripsi ini.
2. Bapak Rohandi, Ph.D selaku Dekan Fakultas Keguruan dan Ilmu Pendidikan Universitas Sanata Dharma.
3. Bapak Drs. A. Atmadi, M.Si. selaku Ketua Jurusan Pendidikan dan Ilmu Pengetahuan Alam, FKIP, Universitas Sanata Dharma.
4. Bapak Dr. M. Andy Rudhito, S.pd. selaku Kaprodi Pendidikan Matematika. 5. Ibu Ch. Enny Murwaningtyas, S.Si, M.Si. dan Ibu Veronika Fitri Rianasari,
6. Seluruh Dosen Program Studi Pendidikan Matematika yang telah banyak memberikan ilmu pengetahuan dan bekal keterampilan.
7. Segenap Staf Sekretariat JPMIPA yang telah membantu dalam hal administrasi kampus selama penulis belajar di sini.
8. Kedua orang tua penulis, Bapak Liu Kim Chiung dan Ibu Shinta Lie Jun, Adik Lius Alfredo dan Jonathan Prawira, Kakak Selly Fortuna dan Vivi Fransiska, Paman Doddy Lung dan Bibi Ana, serta Nenek Can Miaw Chu yang telah memberikan dukungan dan doa.
9. Teman-teman Fire Community, komsel “Areaqu”, PMK Oikumene USD dan
“Domby Kid’s Hope” yang selalu memberi semangat dan mengingatkan
untuk selalu melibatkan Tuhan dalam setiap langkahku.
10. Teman-teman Program Studi Pendidikan Matematika Angkatan 2009, khususnya Yasi, Ayu, Iin, Chintya, Hendra, Retha, Dhinta, Dian, Ririn, Rinda, Putri, Awang, yang telah berbagi hari-hari menyenangkan serta semangat dan dukungan untuk terus maju.
11. Dea, Gloria, Willy, Wuri, Kak Yael yang selalu mendukung dan menyemangati.
12. Semua pihak yang tidak dapat disebutkan satu per satu, terima kasih atas bantuan dan saran yang berguna selama penulisan skripsi ini.
Akhir kata, penulis berharap kiranya skripsi ini dapat bermanfaat bagi para pembaca.
xi
DAFTAR ISI
Halaman
HALAMAN JUDUL ... i
HALAMAN PERSETUJUAN PEMBIMBING ... ii
LEMBAR PENGESAHAN ... iii
LEMBAR PERSEMBAHAN ... iv
PERNYATAAN KEASLIAN KARYA ... v
PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH ... vi
ABSTRAK ... vii
ABSTRACT ... viii
KATA PENGANTAR ... ix
DAFTAR ISI ... xi
DAFTAR GAMBAR ... xiii
DAFTAR TABEL ... xv
DAFTAR NOTASI ... xvii
BAB I PENDAHULUAN ... 1
1.1. Latar Belakang ... 1
1.2. Rumusan Masalah ... 7
1.3. Batasan Masalah ... 8
1.4. Tujuan dan Manfaat Penelitian ... 8
1.5. Metodologi Penelitian ... 9
BAB II KAJIAN PUSTAKA DAN LANDASAN TEORI ... 11
2.1. Teori Graf ... 11
2.2. Pelabelan Graf ... 22
2.3. Pelabelan pada Graf Sikel (Cycle Graph) dan Graf Multisikel (Multycycle Graph) ... 26
BAB III HASIL PENELITIAN DAN PEMBAHASAN ... 29
3.1. Perhitungan Dasar Pelabelan Total Tak Ajaib Sisi ... 29
3.2. Pelabelan Total Tak Ajaib Sisi pada Graf Multisikel ( 𝑚𝐶𝑝) ... 30
3.3. (𝑎, 1) 𝑆𝐸𝐴𝑇𝐿 pada Graf Multisikel (𝑚𝐶𝑝) ... 35
3.4. (𝑎, 2) 𝑆𝐸𝐴𝑇𝐿 pada Graf Multisikel (𝑚𝐶𝑝) ... 55
BAB IV PENUTUP ... 86
4.1. Kesimpulan ... 86
4.2. Saran ... 90
xiii
DAFTAR GAMBAR
Halaman
Gambar 1.1 Jembatan Königsberg dan Grafnya ... 1
Gambar 1.2 Struktur Sebuah Organisasi ... 3
Gambar 1.3 Rute Jalan dari Satu Tempat ke Tempat Lain ... 3
Gambar 1.4 Persegi Ajaib 4x4 ... 4
Gambar 1.5 Contoh Pelabelan ... 6
Gambar 2.1 Graf dan Bukan Graf ... 12
Gambar 2.2 Graf 𝐺1 ... 12
Gambar 2.3 Graf 𝐺2 ... 13
Gambar 2.4 Graf 𝐺3 ... 13
Gambar 2.5 Graf 𝐺4 ... 14
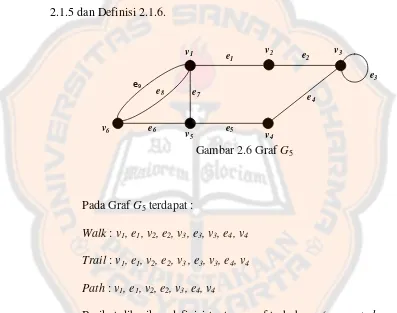
Gambar 2.6 Graf 𝐺5 ... 15
Gambar 2.7 Graf 𝐺6 dan 𝐺7 ... 16
Gambar 2.8 Graf 𝐺8, 𝐺9, dan 𝐺10 ... 17
Gambar 2.9 Graf 𝐺11dan 𝐺12 ... 18
Gambar 2.10 Graf Lengkap ... 19
Gambar 2.11 Graf Sikel ... 20
Gambar 2.12 Graf Roda ... 20
Gambar 2.13 Graf Teratur dengan 𝑟= 3 ... 21
Gambar 2.14 𝐾4Graf Planar ... 22
Gambar 2.16 Graf 𝐺13 ... 24
Gambar 2.17 Graf 𝐺14 ... 25
Gambar 2.18 Pelabelan Total TakAjaib Sisi pada 𝐶3 ... 26
Gambar 2.19 2𝐶3 ... 27
Gambar 2.20 Pelabelan Total Tak Ajaib Sisi pada Graf Multisikel (2𝐶3) ... 27
Gambar 3.1 Ilustrasi Pelabelan Graf Multisikel ((𝑚𝐶𝑝) ... 30
Gambar 3.2 Contoh Graf Multisikel (2𝐶3) ... 30
Gambar 3.3 Contoh Pelabelan Total Tak Ajaib Sisi pada 2𝐶3 ... 33
Gambar 3.4 (18,1) SEATL pada Graf Multisikel (2𝐶4) ... 35
Gambar 3.5 (20,1) SEATL pada Graf Multisikel (3𝐶3) ... 35
Gambar 3.6 (22,1) SEATLpada 2C5 ... 49
Gambar 3.7 (26,1) SEATL pada 2C6 ... 50
Gambar 3.8 (20,1) SEATL pada 3C3 ... 52
Gambar 3.9 (26,1) SEATL pada 3C4 ... 53
Gambar 3.10 Pelabelan Graf Multisikel (3C3) ... 55
Gambar 3.11 Pelabelan Graf Multisikel (3C7) ... 56
Gambar 3.12 (16,2) SEATL pada 3𝐶3 ... 73
Gambar 3.13 (43,2) SEATL pada 3𝐶9 ... 75
xv
DAFTAR TABEL
DAFTAR NOTASI
𝑉(𝐺) himpunan titik di 𝐺 𝐸(𝐺) himpunan sisi di 𝐺
𝑉(𝐺) order (banyak titik) dari 𝐺 𝐸(𝐺) size (banyak sisi) dari 𝐺 𝑣𝑖 titik ke-𝑖
𝑒𝑖,𝑗 sisi yang menghubungkan titi ke-𝑖 dan titik ke-𝑗 𝑆𝑣 jumlah semua label titik
𝑆𝑒 jumlah semua label sisi
𝑆𝑤 jumlah semua bobot sisi
𝑓(𝑣𝑖) label titik 𝑣𝑖 𝑓 𝑒𝑖,𝑗 label sisi 𝑒𝑖,𝑗
𝑤𝑡 𝑒 bobot masing-masing sisi 𝑒
𝐶𝑛 graf sikel berorder 𝑛
𝑚𝐶𝑝 graf multisikel
∪ gabungan himpunan
1
BAB I
PENDAHULUAN
1.1Latar Belakang
Graf merupakan salah satu cabang matematika yang saat ini sedang berkembang. Teori graf diperkenalkan oleh Leonard Euler pada tahun 1736. Bermula ketika pada saat itu masyarakat kota Königsberg di Prusia Timur ingin melintasi kota yang memiliki dua pulau dan tujuh jembatan, dengan menyeberangi ketujuh jembatan itu tanpa menyeberangi satu jembatan sebanyak dua kali.
Gambar 1.1 Jembatan Königsberg dan grafnya
Masyarakat Königsberg kemudian menanyakan hal ini kepada Leonard Euler yang merupakan seorang ahli matematika Swiss terkenal saat itu. Kemudian Euler membuktikan pada tahun 1736 bahwa hal ini mustahil untuk dilakukan.
Pembuktian yang dilakukan oleh Euler dilakukan dengan cara merepresentasikan kedua pulau dan kedua sisi sungai dengan titik-titik dan
A
B C
jembatan dengan sisi / kurva, seperti pada Gambar 1.1. Representasi jembatan Königsberg ke dalam titik-titik dan sisi-sisi yang dilakukan oleh Euler inilah yang kemudian dikenal sebagai teori graf .
Teori graf merupakan pokok bahasan yang sudah ada sejak lama namun memiliki banyak terapan sampai saat ini. Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Representasi visual dari graf adalah dengan menyatakan objek sebagai titik, atau bulatan, sedangkan hubungan antara objek dinyatakan dengan garis.
Aplikasi dari teori graf sangat luas dan dipakai dalam berbagai disiplin ilmu maupun kehidupan sehari-hari. Dalam ilmu sosiologi salah satunya, penerapan graf dalam bidang ilmu ini telah memberikan manfaat bagi kita, baik secara kita sadari maupun tidak. Graf dalam masyarakat sekarang ini banyak digunakan untuk menggambarkan struktur hubungan orang yang satu dengan yang lain, baik itu dalam keluarga, maupun dalam lingkungan. Sebagai contoh yang hampir setiap hari kita temui yaitu jaringan pertemanan
Beberapa contoh graf yang sering dijumpai dalam kehidupan sehari-hari antara lain: struktur organisasi, bagan alir pengambilan mata kuliah, peta, rangkaian listrik, dan lain-lain. Di bawah ini diberikan beberapa contoh dalam kehidupan sehari-hari yang bisa divisualisasikan ke dalam bentuk graf.
Gambar 1.2 Struktur Sebuah Organisasi
Gambar 1.3 Rute Jalan dari Satu Temapt ke Tempat Lain
Dalam hal ini, graf yang dipakai adalah graf terbatas (finite graph), sederhana dan tidak berarah (undirected graph). Selanjutnya untuk menyebutkan graf sederhana dan tidak berarah cukup dengan menyebutkan graf saja. Istilah graf yang lain akan tetap disebutkan jika diperlukan.
Salah satu bagian dari graf adalah pelabelan graf (graph labeling). Graf G merupakan gabungan himpunan tak kosong dan titik-titik (vertices)
Dewan penasehat
Divisi 1 Divisi 2 Divisi 3 Divisi 4
𝑉= 𝑉(𝐺) dan himpunan sisi-sisi (edges) 𝐸 =𝐸(𝐺) dengan jumlah vertex |V| = p dan jumlah edge |E| = q. Suatu pelabelan graf memetakan setiap elemen dari graf tersebut yaitu titik (vertex) atau sisi (edge) atau keduanya ke himpunan bilangan, biasanya bilangan bulat positif. Jika yang dilabeli hanya titik, disebut pelabelan titik (vertex labeling), jika sisi maka disebut pelabelan sisi (edge labeling), atau keduanya disebut pelabelan total (total labeling). Dalam penelitian ini domain yang dipakai adalah titik dan sisi, sehingga disebut pelabelan total (total labeling).
Dalam pelabelan graf diperkenalkan juga pelabelan ajaib dan pelabelan tak ajaib. Ide awal pelabelan ajaib adalah generalisasi dari persegi ajaib. Penelitian ini pertama kali dilakukan oleh Kotzig dan Rosa (1970). Persegi ajaib (magic square) adalah suatu persegi dengan ukuran n x n petak dimana setiap baris, kolom dan diagonal memiliki jumlah yang sama. Persegi ajaib sudah dikenal oleh matematikawan Cina sejak 650 Sebelum Masehi. Ada kemungkinan dikenal oleh matematikawan Arab sejak abad ke-7. Berawal dari pembuatan persegi ajaib inilah muncul ide untuk menggunakannya pada graf yaitu yang disebut pelabelan ajaib (magic labeling).
Pelabelan ajaib merupakan pemetaan satu-satu pada himpunan bilangan bulat berurutan mulai dari 1 yang memenuhi sifat jumlahannya tetap.
Gambar 1.5 di atas merupakan salah satu contoh persegi ajaib dengan ukuran 4 x 4. Pemberian angka pada persegi ajaib 4 x 4 dimulai dari 1 sampai 16. Jumlah dari setiap baris, kolom, dan diagonalnya adalah 34.
Konsep tentang graf tak ajaib (antimagic graph) diperkenalkan oleh Hartsfield dan Ringel (1990). Mereka menuliskan bahwa pelabelan tak ajaib
merupakan pelabelan sisi dari suatu graf dengan bilangan bulat {1, 2, …, q}
sedemikian hingga bobot setiap titiknya berbeda. Selanjutnya Bodendiek dan Walther (1993) mendefinisikan konsep (a,d) antimagic labeling sebagai suatu pelabelan sisi dengan bobot titik-titiknya membentuk suatu barisan aritmetika dengan suku pertama a dan beda d.
Penelitian yang dilakuan Arif (2008) pada salah satu bagiannya telah membahas mengenai pelabelan total tak-ajaib titik pada gabungan beberapa sikel atau yang disebut graf multisikel. Arif (2012) juga telah menunjukkan keberlakuan pelabelan total tak ajaib titik kuat pada graf multisikel Sedangkan dalam penelitian ini akan membahas pelabelan total tak ajaib sisi kuat (super edge antimagic total labeling) pada graf multisikel.
p + q }. Dengan kata lain, label titik-titiknya merupakan bilangan-bilangan yang lebih kecil daripada bilangan untuk label sisi-sisinya.
Sebagai contoh diberikan ilustrasi pada gambar berikut, yaitu pelabelan total tak ajaib sisi (a,d) dan pelabelan total tak ajaib sisi kuat (a,d)pada cycle.
(a) (b)
Gambar 1.5 (a) Pelabelan Total Tak Ajaib Sisi Kuat (7,2)pada C3 dan (b). Pelabelan Total Tak Ajaib Sisi (10,2) pada C4 (b)
Pelabelan (a) pada gambar 1.5 adalah pelabelan kuat karena bilangan-bilangan pada label titik-titiknya lebih kecil daripada bilangan-bilangan-bilangan-bilangan pada label sisi-sisinya serta membentuk barisan aritmetika naik dengan suku pertama 7 dan beda 2. Sedangkan pelabelan (b) bukan merupakan pelabelan kuat, terlihat dari adanya bilangan pada label titik yang lebih besar daripada bilangan pada label sisinya.
Martin Baca, dkk. (2003) telah mengkaji beberapa kasus mengenai
Super (a,d) Edge Antimagic Total Labeling atau (a,d) SEATL. Mereka telah menunjukkan keberlakuan SEATL untuk lintasan (path), Petersen graph, sikel ganjil dan beberapa bentuk perluasan lainnya. Selain itu, peneliti yang sama juga menunjukkan beberapa bentuk graf yang bukan SEATL.
1 3
6 4
5 1 7
2 6
8
Berdasaran hasil dari peneliti-peneliti sebelumnya, penulis ingin mengembangkan hasil yang sudah ditunjukkan Martin Baca, dkk. (2003) yakni menyelidiki keberlakuan (a,d) SEATL pada graf multisikel. Untuk selanjutnya akan digunakan istilah (a,d) SEATL untuk menyebutkan pelabelan total tak ajaib sisi kuat (a,d).
1.2Rumusan Masalah
Semua (a,d) SEATL dilakukan dengan memberikan label pada p titik dan q sisi dengan bilangan {1, 2, …, p+q} dan bobot setiap sisinya berbeda serta membentuk barisan aritmetika naik dengan suku pertama a dan beda d. Pelabelan titik-titik dan sisi-sisi pada graf tersebut juga harus diperhatikan, yakni label untuk titik-titiknya adalah {1, 2, 3, …, p} dan label sisi-sisinya adalah {p + 1, p + 2, …, p + q}. Dengan kata lain, label titik-titiknya merupakan bilangan-bilangan yang lebih kecil daripada bilangan untuk label sisi-sisinya.
Dalam penelitian ini akan dirumuskan masalah sebagai berikut.
1. Sejauh mana graf multisikel (mCp) dengan p ≥ 3 dan m≥ 1 memenuhi (a,d) SEATL ?
2. Bagaimana perumusan pola pelabelan yang berlaku umum untuk graf multisikel (mCp) yang memenuhi (a,d) SEATL ?
1.3Batasan Masalah
Untuk (𝑎,𝑑) SEATL pada graf multisikel (𝑚𝐶𝑝) untuk 𝑑 = 1, tidak ada batasan untuk 𝑚 dan 𝑝. Itu artinya pola pelabelan berlaku untuk semua 𝑚 dan 𝑝, dengan 𝑚 ≥1 dan 𝑝 ≥3. Sedangkan untuk (a,d) SEATL dengan 𝑑 = 2, peneliti membatasi hanya untuk m = 3 karena peneliti belum menemukan keberlakuan pola pelabelan secara umum untuk m yang lain sehingga pada penelitian ini, graf multisikel yang akan ditunjukkan keberlakuan (a,d) SEATL
untuk d = 2 adalah 3Cp dengan 𝑝 ≥3 dan p ganjil.
1.4Tujuan dan Manfaat Penelitian
Tujuan penelitian ini adalah :
1. Meninjau graf multisikel (mCP) yang memenuhi (a,d) SEATL.
2. Menentukan rumus pola pelabelan yang berlaku umum untuk graf multisikel yang memenuhi (a,d) SEATL.
3. Menentukan bentuk barisan, yakni suku pertama a dan beda d dari (a,d) SEATL pada graf multisikel yang memenuhi (a,d) SEATL.
Manfaat dari penelitian ini adalah menambah wawasan tentang (a,d)
1.5Metodologi Penelitian
Penelitian ini adalah penelitian pustaka (Library Research). Penelitian ini dilakukan dengan beberapa langkah kerja yang menjadi pedoman untuk mencapai tujuan penelitian.
1. Langkah yang pertama adalah melakukan kajian terhadap buku-buku teori graf dan jurnal ataupun makalah yang memuat topik tentang pelabelan pada graf dan sifat (a,d) SEATL pada graf multisikel (mCp). 2. Langkah kedua adalah meninjau keberlakuan (a,d) SEATL pada graf
multisikel, mulai dari p ≥ 3 dan m ≥ 1, yaitu 2C3, 3C3, 2C4, 3C4 dan seterusnya.
3. Langkah ketiga adalah menentukan syarat 𝑑dan batas-batas 𝑎 yang memenuhi 𝑎,𝑑 𝑆𝐸𝐴𝑇𝐿.
4. Langkah keempat adalah menentukan rumusan pelabelan untuk titik dan sisi dari graf multisikel yang memenuhi (a,d) SEATL. Pada bagian ini, peneliti juga akan membuktikan bahwa rumus pelabelan berlaku secara umum dengan menggunakan induksi matematika.
1.6Sistematika Penulisan
Untuk mempermudah penulis sekaligus pembaca dalam mengkaji skripsi ini, maka sistematika penulisannya dibagi menjadi empat bagian yaitu : BAB I : PENDAHULUAN
Pada bab ini dijelaskan tentang latar belakang, rumusan masalah, tujuan dan manfaat penulisan, dan sistematika penulisan.
BAB II : LANDASAN TEORI
Pada bab ini dijelaskan tentang teori dasar graf, beberapa istilah dalam graf, jenis-jenis graf, pelabelan pada graf sikel, dan graf multisikel.
BAB III : PEMBAHASAN
Pada bab ini dijelaskan tentang pembahasan mengenai SEATL pada graf multisikel (mCp), perhitungan dasar (basic counting) untuk menentukan batasan suku pertama a dan beda d dari (a,d) SEATL pada graf multisikel (mCp).
BAB IV : PENUTUP
11
BAB II
KAJIAN PUSTAKA DAN LANDASAN TEORI
2.1Teori Graf
Dalam mempelajari graf terdapat beberapa teori dasar untuk mendukung pembuktian dan mempermudah pemahaman. Beberapa teori dasar meliputi pengertian graf, beberapa istilah dalam graf, jenis-jenis graf, dan pelabelan graf. Berikut ini disajikan pengertian graf :
1. Pengertian Graf :
Graf tak bearah G, yang selanjutnya hanya disebut dengan graf G
didefinisikan sebagai himpunan pasangan teurut 𝐺 = (𝑉,𝐸)dengan 𝑉 adalah himpunan berhingga titik-titik (vertex-vertex) yang tidak kosong
v v1, ,2 ,vp
dan 𝐸 adalah himpunan edge sehingga 𝑢𝑣= 𝑣𝑢𝜖𝐸 untuk𝑢,𝑣
v v1, ,2 ,vp
. Selanjutnya anggota 𝑉 disebut titik dan anggota 𝐸disebut sisi.
Banyaknya titik dari graf G disebut order graf G dan dinotasikan dengan 𝑉 = 𝑝 dan banyaknya sisi dari graf G disebut ukuran (size) dari
Contoh graf dan yang bukan graf:
(a) Graf (b) Bukan graf
Gambar 2.1 Graf dan Bukan Graf
Gambar 2.1 (a) di atas merupakan contoh graf dengan 𝑉 = 4, dan 𝐸 = 4, sedangkan gambar (b) bukan graf karena 𝑉 = 0, sehingga tidak
memenuhi definisi.
2. Beberapa istilah dalam Graf
Dalam mempelajari tentang graf terdapat beberapa istilah yang berkaitan dengan graf. Berikut ini diberikan definisi tentang adjacent, incident, derajat verteks, gelang (loop), serta sisi ganda.
Definisi 2.1.1 (Suryadi, 1996)
Misal pada graf G terdapat dua titik vi dan vj, dua buah titik pada G dikatakan berdampingan (adjacent) bila terdapat sisi yang menghubungkan kedua titik tersebut. Dapat ditulis dengan notasi e = (vi,
vj)
E (G) dimana vi≠ vj.Gambar 2.2 Graf G1
v3
v2
v1
Pada Gambar 2.4, derajat (degree) titik v1 adalah tiga, karena ada tiga sisi yang bersisian dengan titik v1. Sedangkan derajat v2 adalah dua. Untuk titik v5, derajatnya adalah nol sehingga disebut titik terisolasi (isolated vertex). Sisi e1 disebut sebagai gelang (loop) karena titik-titik di ujung-ujungnya adalah sama yaitu v4.
Definisi 2.1.4 (Wiitala, 1987)
Misal terdapat beberapa sisi berbeda pada graf yang menghubungkan pasangan titik yang sama, maka graf yang demikian dapat dikatakan mempunyai sisi ganda (multiple edge).
Gambar 2.5 Graf G4
Pada Gambar 2.5, Graf G4 memuat sisi ganda yaitu sisi e1 dan e2 karena menghubungkan dua titik yang sama yaitu v1 dan v2.
Berikut ini akan diberikan definisi tentang walk, trail, dan path.
Definisi 2.1.5 (West, 2009)
Suatu walk pada sebuah graf adalah suatu urutan yang terdiri atas titik-titik dan sisi-sisi bergantian, dimana setiap sisi bersisian dengan titik terdekat, dengan diawali dan diakhiri pada suatu titik.
v1
e1
e2
e3 e4
e5
e6 v2
v3
Definisi 2.1.6 (West, 2009)
Suatu walk yang setiap sisinya berbeda disebut trail. Suatu trail
yang setiap titiknya berbeda disebut lintasan (path). Panjang lintasan adalah banyaknya sisi dalam lintasan tersebut.
Di bawah ini akan diberikan contoh untuk memperjelas Definisi
Berikut diberikan definisi tentang graf terhubung (connected graph) dan graf tak terhubung (disconnected graph).
Definisi 2.1.7 (Wiitala, 1987)
Suatu graf G dikatakan graf terhubung jika untuk setiap pasang titik
vidan titik vj, vi ≠ vj, di dalam himpunan V terdapat lintasan dari vi ke vj. Jika tidak, maka graf G disebut graf tak terhubung (connected graph).
Di bawah ini diberikan contoh untuk memperjelas Definisi 2.1.7.
Contoh :
Gambar 2.7 Graf G6 dan G7
Graf G6 pada Gambar 2.7 merupaan graf tak terhubung karena tidak terdapat sisi yang menghubungkan titik v5 dengan titik v1, v2, v3, v4, sedangkan graf G7 merupakan graf terhubung karena setiap titik terhubung oleh suatu sisi.
3. Jenis-jenis Graf
Berdasarkan sifatnya graf dapat dikelompokkan menjadi beberapa jenis bergantung pada sudut pandang pengelompokannya. Pengelompokan graf dapat dipandang berdasarkan ada tidaknya sisi ganda, berdasarkan banyak titik,atau berdasarkan orientasi arah pada sisi.
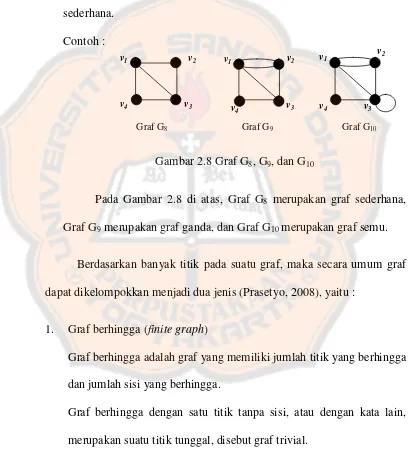
Berdasarkan ada tidaknya gelang atau sisi ganda pada suatu graf, maka graf dikelompokkan menjadi dua jenis (Prasetyo, 2008), yaitu : 1. Graf sederhana (simple graph)
Graf sederhana adalah graf yang tidak mengandung gelang maupun sisi-ganda.
2. Graf tak sederhana (unsimple graph)
(multigraph) dan graf semu (pseudograph). Graf ganda adalah graf Graf G9 merupakan graf ganda, dan Graf G10 merupakan graf semu.
Berdasarkan banyak titik pada suatu graf, maka secara umum graf dapat dikelompokkan menjadi dua jenis (Prasetyo, 2008), yaitu :
1. Graf berhingga (finite graph)
Graf berhingga adalah graf yang memiliki jumlah titik yang berhingga dan jumlah sisi yang berhingga.
Graf berhingga dengan satu titik tanpa sisi, atau dengan kata lain, merupakan suatu titik tunggal, disebut graf trivial.
2. Graf tak-berhingga (infinite graph)
Berdasarkan orientasi arah pada sisi (edge), maka secara umum graf dapat dikelompokkan menjadi dua jenis (Prasetyo, 2008) , yaitu :
1. Graf tak berarah (undirected graph)
Graf tak berarah adalah graf yang sisinya tidak mempunyai orientasi arah. Pada graf tak berarah, urutan pasangan titik yang dihubungkan oleh sisi tidak diperhatikan. Jadi (vj, vk) = (vk, vj) adalah sisi yang sama. 2. Graf berarah (directed graph)
Graf berarah adalah graf yang setiap sisinya diberikan orientasi arah. Pada graf bearah (vj, vk) dan (vk, vj) menyatakan dua sisi yang berbeda, dengan kata lain (𝑣𝑗,𝑣𝑘) ≠(𝑣𝑘,𝑣𝑗). Untuk sisi (𝑣𝑗,𝑣𝑘)titik vj dinamakan titik asal (initial vertex) dan titik vk dinamakan titik terminal (terminal vertex).
Di bawah ini diberikan contoh untuk graf tak berarah dan graf berarah.
Contoh :
Gambar 2.9 Graf G11 dan G12
Pada gambar 2.9 di atas, Graf G11 merupakan graf tak berarah. Sedangkan Graf G12 merupakan graf berarah.
v3
v2
v1
v4
v3
v2
v1
v4
Terdapat beberapa jenis graf sederhana khusus. Berikut ini didefinisikan beberapa graf khusus (Prasetyo, 2008):
1. Graf lengkap (Complete Graph)
Graf lengkap merupakan graf sederhana yang setiap titiknya terhubung langsung (oleh satu sisi) ke semua titik lainnya. Dengan kata lain, setiap titiknya bertetangga. Graf lengkap dengan n buah titik dilambangkan dengan Kn. Banyak sisi pada sebuah graf lengkap yang terdiri dari n buah titik adalah 1
2𝑛(𝑛 −1) sisi.
Di bawah ini diberikan beberapa contoh graf lengkap. Contoh :
Gambar 2.10 Graf Lengkap
Pada Gambar 2.10 di atas, gambar graf berturut-turut dari kiri adalah graf lengkap dengan n = 1, 2, 3, 4, 5, dan 6. Dituliskan K1, K2,
K3, K4, K5, dan K6. 2. Graf sikel ( cycle graph )
Graf sikel merupakan graf sederhana yang setiap titiknya mempunya dua sisi yang insiden (bersisian). Graf sikel dengan p titik dilambangkan dengan Cp.
Gambar 2.11 Graf sikel
Pada gambar 2.7 berturut-turut dari kiri adalah graf sikel dengan p = 3, 4, 5, dan 6. Dilambangkan dengan C3, C4, C5, dan
C6.
3. Graf Roda (Wheels Graph)
Graf roda merupakan graf yang diperoleh dengan cara menambahkan satu titik pada graf sikel CP, dan menghubungkan titik baru tersebut dengan semua titik pada graf sikel tersebut.
Di bawah ini diberikan beberapa contoh graf roda. Contoh :
Gambar 2.12 Graf Roda
Pada gambar 2.8 berturut-turut dari kiri adalah graf roda yang terbentuk dari graf sikel dengan p = 3,4,5, dan 6. Dituliskan dengan
W3, W4, W5, dan W6.
Graf teratur merupakan graf yang setiap titiknya mempunyai derajat yang sama. Apabila derajat setiap titik pada graf teratur adalah
r, maka graf tersebut dinamakan graf teratur berderajat r. Banyak sisi pada graf teratur dengan n titik adalah 2nr sisi.
Di bawah ini diberikan salah satu contoh graf teratur. Contoh :
Gambar 2.13 Graf Teratur dengan r = 3 5. Graf Planar (Planar Graph) dan Graf Bidang (Plane Graph)
Suatu graf disebut graf planar jika graf tersebut dapat digambarkan pada bidang datar sedemikian sehingga tidak ada sisi-sisinya yang berpotongan kecuali di titik dimana keduanya bersisian.
Dibawah ini diberikan beberapa contoh graf planar dan graf bidang.
Contoh :
- Semua graf sikel merupakan graf planar
Tetapi graf lengkap Kn untuk n ≥ 5 merupakan graf tak-planar. Graf planar yang digambarkan dengan sisi-sisi yang tidak saling berpotongan dinamakan graf bidang.
Gambar 2.14 K4 adalah graf planar
Gambar 2.15 K5 bukan graf planar
Pada Gambar 2.15, K5 bukan graf planar karena terdapat sisi yang berpotongan pada titik yang tidak bersisian.
2.2Pelabelan Graf (Graph Labeling)
Dalam mengevaluasi graf terdapat bobot yang akan dihitung. Bobot adalah jumlahan dari label-label pada setiap elemen graf. Pada pelabelan graf terdapat dua jenis pelabelan menurut jumlah dari setiap bobotnya yaitu pelabelan ajaib (magic labeling) dan pelabelan tak ajaib (antimagic labeling). Pelabelan ajaib adalah suatu pelabelan yang jumlah setiap bobotnya sama / konstan, sedangkan pelabelan tak ajaib adalah suatu pelabelan yang jumlah setiap bobotnya berbeda. Pada penelitian ini akan digunakan pelabelan total tak ajaib sisi dalam pengkajian masalah yaitu pelabelan pada graf multisikel. Graf multisikel di sini merupakan gabungan beberapa sikel identik yang tidak terhubung.
Berikut ini diberikan beberapa definisi tentang pelabelan.
Definisi 2.2.1 (Baca, dkk., 2003)
Suatu pemetaan bijektif 𝑓 ∶ 𝑉 𝐺 ∪𝐸 𝐺 {1, 2, 3, … , p + q }
disebut pelabelan total tak ajaib sisi dari graf G (𝑝,𝑞) jika bobot dari sisi 𝑤𝑓 𝑢𝑣 = 𝑓 𝑢 + 𝑓 𝑢𝑣 + 𝑓(𝑣) , untuk setiap 𝑢𝑣𝜖𝐸 𝐺 .
Jika bobot-bobot sisi pada pelabelan total tak ajaib sisi membentuk suatu barisan aritmetika naik dengan suku pertama a dan beda d maka pelabelannya disebut pelabelan total tak-ajaib sisi (𝑎,𝑑).
Gambar 2.16 Graf G13
Dari Gambar 2.16, bobot sisi terkecil adalah sisi dengan label 2, yaitu 5 + 2 + 4 = 11, kemudian dilanjutkan dengan sisi berlabel 1, yaitu 5 + 1 + 6 = 12, dan sisi berlabel 3, yaitu 6 + 3 + 4 = 13. Terlihat bahwa bobot sisi-sisinya membentuk suatu barisan aritmetika naik dengan suku pertama 11, dan beda 1, sehingga menurut Definisi 2.2.1 maka pelabelan pada Gambar 2.16 disebut pelabelan total tak ajaib sisi (11,1) pada Graf G13.
Definisi 2.2.2 (Baca, dkk., 2003)
Suatu pemetaan bijektif 𝑓 ∶ 𝑉 𝐺 ∪𝐸 𝐺 {1, 2, 3, … , p + q }
disebut pelabelan toal tak-ajaib sisi (𝑎,𝑑) dari graf G 𝑝,𝑞 jika bobot dari sisi-sisinya membentuk suatu barisan aritmetika naik dengan suku pertama a dan beda d.
𝑊 = 𝑤𝑓 𝑢𝑣 𝑢𝑣𝜖𝐸} = {𝑎,𝑎+𝑑,𝑎+ 2𝑑,…,𝑎+ 𝑝 −1 𝑑}
Sebagai contoh, kita ambil contoh Graf G13 pada Gambar 2.16. maka bobot dari sisi-sisinya membentuk suatu barisan aritmetika naik dengan suku pertama 11 dan beda 1.
1
2 3
4
Definisi 2.2.3 (Baca, dkk., 2003)
Suatu pelabelan dikatakan „kuat‟ jika label titik-titik pada graf tersebut adalah 1, 2, 3,…, 𝑉(𝐺) dan label sisi-sisinya adalah 𝑉(𝐺) + 1, 𝑉(𝐺)+ 2, …, 𝑉(𝐺)+𝐸(𝐺) dengan 𝑉(𝐺) adalah banyaknya titik pada graf tersebut dan 𝐸(𝐺) adalah banyaknya sisi pada graf tersebut. Dengan kata lain, label titik-titiknya merupakan bilangan-bilangan yang lebih kecil daripada bilangan untuk label sisi-sisinya.
Contoh :
Gambar 2.17 Graf G14
Pada Gambar 2.17, 𝑉(𝐺) = 3. Label titik-titiknya adalah 1, 2, 3 dan label sisi-sisinya adalah {4, 5, 6} sehingga berdasarkan
Definisi 2.2.3 maka pelabelan ini dikatakan sebagai pelabelan kuat. Karena membentuk barisan aritmetika dengan suku pertama 8 dan beda 1, maka disebut pelabelan total tak ajaib sisi kuat (8,1) pada Graf G14.
1 2
3
4 5
2.3Pelabelan pada graf sikel (cycle graph) dan graf multisikel ( multicycle
graph )
Graf sikel merupakan graf sederhana yang setiap titiknya berderajat dua, atau graf dengan lintasan tertutup. Graf sikel dengan p titik dilambangkan dengan 𝐶𝑝.
Baca, dkk.(2003) telah menunjukkan keberlakuan pelabelan total tak ajaib sisi (𝑎,𝑑) pada graf sikel. Hasil penelitian yang dilakukan oleh Baca, dkk. salah satunya adalah setiap sikel ganjil, 𝐶𝑝 dengan 𝑝 ≥ 3 terdapat pelabelan total tak ajaib sisi (2𝑝+ 2, 1) (Baca, dkk., 2003). Ilustrasi hasil penelitian dari Baca, dkk. adalah sebagai berikut :
Gambar 2.18 Pelabelan total tak ajaib sisi pada C3
Gambar 2.18 di atas merupakan contoh pelabelan total tak-ajaib sisi pada C3. Bobot terkecil dari sisinya adalah 1 + 4 + 3 = 8 yaitu bobot pada sisi dengan label 4. Bobot dari dua titik lain adalah 5 + 2 + 3 = 10 yaitu bobot pada sisi dengan label 2 dan 5 + 6 + 1 = 12 yaitu bobot pada sisi dengan label 6. Karena bobot terkecil titik adalah 8 dan beda dari bobot
1
2
3
4 5
sisi yang lain adalah 2, maka contoh pada Gambar 2.18 disebut pelabelan total tak-ajaib sisi ( 8, 2 ) pada C3.
Graf multisikel merupakan gabungan beberapa graf sikel Cp yang tidak terhubung. Gabungan sikel yang dimaksud adalah sikel-sikel yang mempunyai banyak titik dan sisi yang sama. Graf multisikel yang terdiri dari sejumlah 𝑚 graf sikel ( Cp ) dilambangkan dengan ( mCp ) dengan banyak titik 𝑚𝑝 buah titik dan 𝑚𝑝 buah sisi (Arif, 2008).
Berikut diberikan contoh graf multisikel ( mCp ).
Gambar 2.19 2C3
Gambar 2.19 merupakan contoh graf multisikel 2C3 karena banyaknya graf sikel C3 adalah 2. Graf multisikel (2C3 ) memiliki 6 buah titik dan 6 buah sisi. Contoh pelabelannya sebagai berikut.
Gambar 2.20 Pelabelan pada graf multisikel (2C3)
29
BAB III
HASIL PENELITIAN DAN PEMBAHASAN
Hasil dari penelitian ini dibagi menjadi empat bagian, yaitu perhitungan dasar tentang pelabelan total tak ajaib sisi, pelabelan total tak ajaib sisi pada graf multisikel (𝑚𝐶𝑝) untuk 𝑝 ≥3, dan 𝑚 ≥1, 𝑎, 1 𝑆𝐸𝐴𝑇𝐿 graf multisikel (𝑚𝐶𝑝), dan 𝑎, 2 𝑆𝐸𝐴𝑇𝐿 graf multisikel (3𝐶𝑝)
3.1Perhitungan Dasar Pelabelan Total Tak Ajaib Sisi
Pelabelan total tak ajaib sisi merupakan pemetaan bijektif dari setiap titik dan sisi ke bilangan bulat positif mulai dari satu sampai dengan jumlah total titik dan sisi 𝑓 ∶ 𝑉 𝐺 ∪ 𝐸 𝐺 → 1, 2, 3,…,𝑝+𝑞 dimana 𝑝 adalah jumlah titik dan 𝑞 adalah jumlah sisi (Baca, dkk., 2003).
Pada pelabelan total tak ajaib sisi, setiap label sisi dihitung sekali dan label titik dihitung dua kali, akibatnya :
𝑆𝑤 = 𝑆𝑒 + 2𝑆𝑣
Dimana 𝑆𝑤 adalah jumlah semua bobot sisi, 𝑆𝑣 adalah jumlah semua label titik, dan 𝑆𝑒adalah jumlah semua label sisi (Baca, dkk., 2003).
Bobot setiap sisi dihitung dengan cara menjumlahkan label dari sisi tersebut dengan label pada titik-titik ujung dari sisi tersebut. Bobot dari setiap sisi dilambangkan dengan 𝑊𝑓(𝐸𝑖).
𝑓 𝑥𝑖 + 𝑓 𝑥𝑖 𝑥𝑖+1 + 𝑓 (𝑥𝑖+1 ) 𝑖 = 1, 2,…,𝑛 −1 𝑓 𝑥𝑛 + 𝑓 𝑥𝑛 𝑥1 + 𝑓 (𝑥1 ) 𝑖 =𝑛
3.2Pelabelan Total Tak Ajaib Sisi pada Graf Multisikel (mCp)
Graf multisikel merupakan gabungan beberapa graf sikel 𝐶𝑝 yang tidak terhubung. Gabungan sikel yang dimaksud adalah sikel-sikel yang mempunyai banyak titik dan sisi yang sama. Graf multisikel yang terdiri dari sejumlah 𝑚 graf sikel (𝐶𝑝) dilambangkan dengan (𝑚𝐶𝑝) dengan banyak titik 𝑚𝑝 buah titik dan 𝑚𝑝 buah sisi.
Berikut diberikan contoh ilustrasi pelabelan pada graf multisikel (𝑚𝐶𝑝).
Gambar 3.1 Ilustrasi pelabelan Graf Multisikel (𝑚𝐶𝑝)
Gambar 3.2 Contoh Graf Multisikel (2𝐶3)
Pada graf multisikel (𝑚𝐶𝑝) memiliki 𝑚𝑝 buah titik dan 𝑚𝑝 buah sisi, karena setiap sikel mempunyai 𝑝 buah titik dan 𝑝 buah sisi. Banyak total dari
v13
v23
v
11v12
v21
v
22...
v1,1 v1,2
v1,p-1
v2,1 v2,2
vm,1 vm,2
Graf ke-1 Graf ke-2
Graf ke-m
titik dan sisinya adalah 2𝑚𝑝. Berdasarkan Definisi 2.2.2, diperoleh pemetaan 𝑓 ∶ 𝑉 𝐺 ∪ 𝐸 𝐺 → 1, 2, 3,…, 2𝑚𝑝 . Berdasarkan Definisi 2.2.2, bobot sisi-sisi pada 𝑚𝐶𝑝 adalah jumlahan dari label sisi dan titik-titik ujung dari sisi tersebut. Akibatnya jika semua bobot sisi-sisinya dijumlahkan akan diperoleh :
𝑆𝑤 = 𝑆𝑒 + 2𝑆𝑣
1
Dari perhitungan dasar ini, diperoleh hasil :
Teorema 3.1. Setiap graf multisikel (𝑚𝐶𝑝) mempunyai pelabelan total tak ajaib sisi 𝑎,𝑑 dengan 𝑎 ≥ 𝑚𝑝+ 4 dan 𝑑 ≤3 untuk semua 𝑚 ≥1 dan 𝑝 ≥3.
Bukti :
Bobot sisi graf sikel 𝑤𝑓 𝑥𝑦 = 𝑓 𝑥 +𝑓 𝑥𝑦 +𝑓(𝑦)karena setiap sisi terdapat dua titik yaitu titik-titik di ujung-ujungnya.
Ambil nilai 𝑎terkecil yaitu 1 + 𝑚𝑝+ 1 + 2 =𝑚𝑝+ 4. Bobot sisi yang paling besar adalah
Di bawah ini diberikan contoh pelabelan total tak ajaib sisi pada graf multisikel (2𝐶3)
Gambar 3.3 Contoh Pelabelan Total Tak Ajaib Sisi pada (2𝐶3) Graf pada Gambar 3.3 di atas adalah graf multisikel dengan 𝑚= 3 dan 𝑝= 3, sehingga dapat dilakukan pelabelan total tak ajaib sisi pada graf
tersebut. Bobot sisi 𝑤𝑓 𝑥 =𝑓 𝑥 +𝑓 𝑥𝑦 +𝑓 𝑦 , dengan bobot terkecil yaitu 1 + 8 + 5 = 14≥10 dan 𝑑 = 2≤ 3 , sehingga pelabelan di atas dapat dikatakan sebagai pelabelan total tak ajaib sisi (14,2) pada 2𝐶3. Jadi Setiap graf multisikel (𝑚𝐶𝑝) mempunyai pelabelan total tak ajaib sisi (𝑎,𝑑) dengan 𝑎 ≥ 𝑚𝑝+ 4 dan 𝑑 ≤3 untuk semua 𝑚 ≥1 dan 𝑝 ≥3.
Selanjutnya dicari batas atas dari 𝑎 sehingga graf multisikel dapat diberi label. Karena 𝑎 ≥ 𝑚𝑝+ 4 maka nilai 𝑎 bergantung pada banyaknya sikel dan titik serta sisi pada sikel tersebut dan 𝑑 ≤3 maka nilai 𝑑 yang memungkinkan adalah 𝑑 = 1, 2, dan 3. Selanjutnya akan ditentukan nilai 𝑎 dan 𝑑 yang mungkin.
(i) Untuk 𝑑 = 1
Bobot sisi yang paling besar adalah
𝑎+ 𝑚𝑝 −1 𝑑 ≤2𝑚𝑝+𝑚𝑝+ (𝑚𝑝 −1)
5 11
1 3 7 9
2 4
6
8 10
Dari 𝑑 = 1, diperoleh
𝑎+ 𝑚𝑝 −1 ≤2𝑚𝑝+𝑚𝑝+ (𝑚𝑝 −1)
𝑎+𝑚𝑝 −1≤2𝑚𝑝+𝑚𝑝+𝑚𝑝 −1 𝑎 ≤3𝑚𝑝
Jadi untuk 𝑑 = 1, nilai batasan 𝑎 adalah 𝑚𝑝+ 4 ≤ 𝑎 ≤3𝑚𝑝 (ii) Untuk 𝑑 = 2
Bobot sisi yang paling besar adalah
𝑎+ 𝑚𝑝 −1 𝑑 ≤2𝑚𝑝+𝑚𝑝+ (𝑚𝑝 −1)
Dari 𝑑 = 2, diperoleh
𝑎+ 𝑚𝑝 −1 2≤2𝑚𝑝+𝑚𝑝+ (𝑚𝑝 −1) 𝑎+ 2𝑚𝑝 −2≤2𝑚𝑝+𝑚𝑝+𝑚𝑝 −1
𝑎 ≤2𝑚𝑝+ 1
Nilai batasan 𝑎 adalah 𝑚𝑝+ 4 ≤ 𝑎 ≤2𝑚𝑝+ 1 (iii) Untuk 𝑑 = 3
Bobot sisi yang paling besar adalah
𝑎+ 𝑚𝑝 −1 𝑑 ≤2𝑚𝑝+𝑚𝑝+ (𝑚𝑝 −1)
Dari 𝑑 = 3, diperoleh
𝑎+ 𝑚𝑝 −1 3≤2𝑚𝑝+𝑚𝑝+ (𝑚𝑝 −1) 𝑎+ 3𝑚𝑝 −3≤2𝑚𝑝+𝑚𝑝+𝑚𝑝 −1
𝑎 ≤ 𝑚𝑝+ 2
𝑚= 1 dan 𝑝= 3, diperoleh 𝑎 = 5, sedangkan pada Teorema 4.1
Akan diperlihatkan beberapa contoh gambar graf multisikel yang telah dilabeli dengan (𝑎, 1)SEATL.
Gambar 3.4 (18,1) SEATL pada Graf Multisikel (2𝐶4)
Gambar 3.5 (20,1) SEATL pada Graf Multisikel (3𝐶3)
Dari contoh pelabelan beberapa graf multisikel pada Gambar 3.4 dan Gambar 3.5, diambil salah satu pola pelabelan yang memenuhi 𝑎,𝑑 SEATL pada graf multisikel. Pelabelan dilakukan dengan menggunakan rumus sebagai berikut.
Konstruksi graf multisikel (𝑚𝐶𝑝) dengan label titik sebagai berikut : 𝑓 𝑣𝑖𝑗 =𝑝 𝑖 −1 +𝑗 ;𝑖 = 1, 2,…,𝑚; 𝑗 = 1, 2,…,𝑝 (Rumus 3.3.1)
Sedangkan label dari sisi adalah sebagai berikut : 𝑖= 1, 2,…,𝑚
𝑓 𝑣𝑖𝑗,𝑣𝑖𝑗+1 = 2𝑚 − 𝑖+ 1 𝑝 − 𝑗+ 1 ;𝑗= 1, 2,…,𝑝 −1
𝑓 𝑣𝑖𝑗,𝑣𝑖𝑗+1 = 2𝑚 − 𝑖 𝑝+ 1 ;𝑗= 𝑝 (Rumus 3.3.2)
Pelabelan titik –titik dari graf multisikel (𝑚𝐶𝑝) adalah sebagai berikut. Untuk 𝑖= 1,
𝑓(𝑣1,1) =𝑝 𝑖 −1 + 1 =𝑝 1−1 + 1 = 1
𝑓(𝑣1,2) =𝑝 1−1 + 2 = 2
…
𝑓(𝑣1,𝑝−1) =𝑝 1−1 +𝑝 −1 =𝑝 −1
𝑓(𝑣1,𝑝) =𝑝 1−1 +𝑝 =𝑝
Untuk 𝑖= 2,
𝑓(𝑣2,1) =𝑝 2−1 + 1 =𝑝+ 1
𝑓(𝑣2,2) =𝑝 2−1 + 2 =𝑝+ 2
…
𝑓(𝑣2,𝑝−1) =𝑝 2−1 +𝑝 −1 = 2𝑝 −1
𝑓(𝑣2,𝑝) =𝑝 2−1 +𝑝= 2𝑝
𝑓(𝑣𝑚,1) =𝑝 𝑚 −1 + 1 =𝑚𝑝 − 𝑝+ 1 𝑓(𝑣𝑚,2) =𝑝 𝑚 −1 + 2 =𝑚𝑝 − 𝑝+ 2
…
𝑓(𝑣𝑚,𝑝−1) =𝑝 𝑚 −1 +𝑝 −1 = 𝑚𝑝 −1
𝑓(𝑣𝑚,𝑝) =𝑝 𝑚 −1 +𝑝= 𝑚𝑝
Sedangkan untuk pelabelan sisi-sisinya adalah sebagai berikut. Untuk 𝑖= 1,
𝑓(𝑒1,1) =𝑓 𝑣1,1𝑣1,2 = 2𝑚 − 𝑖+ 1 𝑝 − 𝑗+ 1
= 2𝑚 −1 + 1 𝑝 −1 + 1
= 2𝑚𝑝
𝑓(𝑒1,2) =𝑓 𝑣1,2𝑣1,3 = 2𝑚 −1 + 1 𝑝 −2 + 1 = 2𝑚𝑝 −1
…
𝑓(𝑒1,𝑝−1) =𝑓 𝑣1,𝑝−1𝑣1,𝑝 = 2𝑚 −1 + 1 𝑝 − 𝑝 −1 + 1
= 2𝑚𝑝 − 𝑝+ 2 𝑓(𝑒1,𝑝) =𝑓 𝑣1,1𝑣1,𝑝 = 2𝑚 −1 𝑝+ 1
Untuk 𝑖= 2,
𝑓(𝑒2,1) =𝑓 𝑣2,1𝑣2,2 = 2𝑚 − 𝑖+ 1 𝑝 − 𝑗+ 1
= 2𝑚 −2 + 1 𝑝 −1 + 1 = (2𝑚 −1)𝑝
…
𝑓(𝑒2,𝑝−1) =𝑓 𝑣2,𝑝−1𝑣2,𝑝 = 2𝑚 −2 + 1 𝑝 − 𝑝 −1 + 1
= (2𝑚 −2)𝑝+ 2 𝑓(𝑒2,𝑝) =𝑓 𝑣2,1𝑣2,𝑝 = 2𝑚 −2 𝑝+ 1
Untuk 𝑖=𝑚,
𝑓(𝑒𝑚,1) =𝑓 𝑣𝑚,1𝑣𝑚,2 = 2𝑚 − 𝑚+ 1 𝑝 − 𝑗+ 1
= 2𝑚 − 𝑚+ 1 𝑝 −1 + 1 = (𝑚+ 1)𝑝
𝑓(𝑒𝑚,2) =𝑓 𝑣𝑚,2𝑣𝑚,3 = 2𝑚 − 𝑚+ 1 𝑝 −2 + 1 = (𝑚+ 1)𝑝 −1
…
𝑓(𝑒𝑚,𝑝−1) =𝑓 𝑣𝑚,𝑝−1𝑣𝑚,𝑝 = 2𝑚 − 𝑚+ 1 𝑝 − 𝑝 −1 + 1
=𝑚𝑝+ 2
𝑓(𝑒𝑚,𝑝) =𝑓 𝑣𝑚,1𝑣𝑚,𝑝 = 2𝑚 − 𝑚 𝑝+ 1 =𝑚𝑝+ 1
Pembuktian I
Akan dibuktikan bahwa konstruksi pelabelan (Rumus 3.3.1 dan Rumus 3.3.2) berlaku untuk semua 𝑚.
Jadi akan dibuktikan keberlakuan rumus untuk 𝑖= 1, 2,…,𝑚,𝑚+ 1 dan 𝑗 = 1, 2,…,𝑝
Bukti :
Pelabelan titik : Untuk 𝑖= 1,
𝑓(𝑣1,1) =𝑝 1−1 + 1 = 1
𝑓(𝑣1,2) =𝑝 1−1 + 2 = 2
…
𝑓(𝑣1,𝑝−1) =𝑝 1−1 +𝑝 −1 =𝑝 −1
𝑓(𝑣1,𝑝) =𝑝 1−1 +𝑝 =𝑝
Untuk 𝑖= 2,
𝑓(𝑣2,1) =𝑝 2−1 + 1 =𝑝+ 1
𝑓(𝑣2,2) =𝑝 2−1 + 2 =𝑝+ 2
…
𝑓(𝑣2,𝑝−1) =𝑝 2−1 +𝑝 −1 = 2𝑝 −1
𝑓(𝑣2,𝑝) =𝑝 2−1 +𝑝= 2𝑝
Untuk 𝑖=𝑚,
𝑓(𝑣𝑚,2) =𝑝 𝑚 −1 + 2 =𝑚𝑝 − 𝑝+ 2
…
𝑓(𝑣𝑚,𝑝−1) =𝑝 𝑚 −1 +𝑝 −1 = 𝑚𝑝 −1
𝑓(𝑣𝑚,𝑝) =𝑝 𝑚 −1 +𝑝= 𝑚𝑝
Untuk 𝑖=𝑚+ 1
𝑓(𝑣𝑚+1,1) =𝑝 𝑚+ 1−1 + 1 =𝑚𝑝+ 1 𝑓(𝑣𝑚+1,2) =𝑝 𝑚+ 1−1 + 2 =𝑚𝑝+ 2
…
𝑓(𝑣𝑚+1,𝑝−1) =𝑝 𝑚+ 1−1 +𝑝 −1 =𝑚𝑝+𝑝 −1
𝑓(𝑣𝑚+1,𝑝) =𝑝 𝑚+ 1−1 +𝑝= 𝑚𝑝+𝑝
Sedangkan pelabelan sisi-sisinya adalah Untuk 𝑖= 1,
𝑓(𝑒1,1) =𝑓 𝑣1,1𝑣1,2 = 2(𝑚+ 1)− 𝑖+ 1 𝑝 − 𝑗+ 1
= 2 𝑚+ 1 −1 + 1 𝑝 −1 + 1
= 2𝑚+ 2 𝑝
= 2 𝑚+ 1 𝑝
𝑓(𝑒1,2) =𝑓 𝑣1,2𝑣1,3 = 2(𝑚+ 1)−1 + 1 𝑝 −2 + 1
= 2𝑚+ 2 𝑝 −1
…
𝑓(𝑒1,𝑝−1) =𝑓 𝑣1,𝑝−1𝑣1,𝑝 = 2(𝑚+ 1)−1 + 1 𝑝 − 𝑝 −1 + 1
= 2𝑚𝑝+𝑝+ 2 𝑓(𝑒1,𝑝) =𝑓 𝑣1,1𝑣1,𝑝 = 2 𝑚+ 1 −1 𝑝+ 1
= 2𝑚+ 1 𝑝+ 1 = 2𝑚𝑝+𝑝+ 1
Untuk 𝑖= 2
𝑓(𝑒2,1) =𝑓 𝑣2,1𝑣2,2 = 2(𝑚+ 1)−2 + 1 𝑝 − 𝑗+ 1
= 2𝑚+ 1 𝑝 −1 + 1
= 2𝑚𝑝+𝑝
𝑓(𝑒2,2) =𝑓 𝑣2,2𝑣2,3 = 2(𝑚+ 1)−2 + 1 𝑝 −2 + 1
= 2𝑚+ 1 𝑝 −1
= 2𝑚𝑝+𝑝 −1
…
𝑓(𝑒2,𝑝−1) =𝑓 𝑣2,𝑝−1𝑣2,𝑝 = 2(𝑚+ 1)−2 + 1 𝑝 − 𝑝 −1 + 1
= 2𝑚+ 1 𝑝 − 𝑝+ 2 = 2𝑚𝑝+ 2
𝑓(𝑒2,𝑝) =𝑓 𝑣2,1𝑣2,𝑝 = 2 𝑚+ 1 −2 𝑝+ 1
= 2𝑚 𝑝+ 1 = 2𝑚𝑝+ 1
Untuk 𝑖 =𝑚,
𝑓(𝑒𝑚,1) =𝑓 𝑣𝑚,1𝑣𝑚,2 = 2(𝑚+ 1)− 𝑖+ 1 𝑝 − 𝑗+ 1
=𝑚𝑝+ 3𝑝
𝑓(𝑒𝑚,2) =𝑓 𝑣𝑚,2𝑣𝑚,3 = 2(𝑚+ 1)− 𝑚+ 1 𝑝 −2 + 1
=𝑚𝑝+ 3𝑝 −1
…
𝑓(𝑒𝑚,𝑝−1) =𝑓 𝑣𝑚,𝑝−1𝑣𝑚,𝑝 = 2(𝑚+ 1)− 𝑚+ 1 𝑝 − 𝑝 −1 + 1
= 2𝑚+ 3− 𝑚 𝑝 − 𝑝+ 2
=𝑚𝑝+ 2𝑝+ 2
𝑓(𝑒𝑚,𝑝) =𝑓 𝑣𝑚,1𝑣𝑚,𝑝 = 2 𝑚+ 1 − 𝑚 𝑝+ 1
= 2𝑚+ 2− 𝑚 𝑝+ 1 =𝑚𝑝+ 2𝑝+ 1 Untuk 𝑖=𝑚+ 1,
𝑓(𝑒𝑚+1,1) =𝑓 𝑣𝑚+1,1𝑣𝑚+1,2 = 2𝑚 − 𝑖+ 1 𝑝 − 𝑗+ 1
= 2 𝑚+ 1 − 𝑚 −1 + 1 𝑝 −1 + 1 = 2𝑚+ 2− 𝑚 𝑝
=𝑚𝑝+ 2𝑝
𝑓(𝑒𝑚+1,2) =𝑓 𝑣𝑚+1,2𝑣𝑚+1,3 = 2(𝑚+ 1)− 𝑚 −1 + 1 𝑝 −2 + 1
=𝑚𝑝+ 2𝑝 −1
…
𝑓 𝑒𝑚+1,𝑝−1 = 𝑓 𝑣𝑚+1,𝑝−1𝑣𝑚+1,𝑝 = 2 𝑚+ 1 − 𝑚 𝑝 − 𝑝+ 2
= 2𝑚+ 2− 𝑚 𝑝 − 𝑝+ 2
=𝑚𝑝+𝑝+ 2
= 2𝑚+ 2− 𝑚 −1 𝑝+ 1
=𝑚𝑝+𝑝+ 1
Dari konstruksi pelabelan di atas, label untuk titik merupakan bilangan bulat positif 1, 2, 3,…,𝑚𝑝+𝑝 dan label untuk sisi merupakan bilangan bulat positif 𝑚𝑝+𝑝+ 1,𝑚𝑝+𝑝+ 2,…, 2 𝑚+ 1 𝑝 . Hal ini sesuai dengan syarat pelabelan kuat yaitu bilangan yang merupakan label titik-titiknya lebih kecil daripada label sisi-sisinya. Itu artinya konstruksi pelabelan yang diberikan berlaku untuk semua 𝑚. □
Pembuktian II :
Akan dibuktikan bahwa konstruksi pelabelan juga berlaku untuk semua 𝑝. Jadi akan dibuktikan keberlakuan rumus tersebut untuk 𝑖= 1, 2,…,𝑚 dan 𝑗 = 1, 2,…,𝑝 −1,𝑝,𝑝+ 1.
Pelabelan titik-titiknya sebagai berikut. Untuk 𝑖= 1,
𝑓(𝑣1,1) = (𝑝+ 1) 1−1 + 1 = 1
𝑓(𝑣1,2) = (𝑝+ 1) 1−1 + 2 = 2
…
𝑓(𝑣1,𝑝−1) = (𝑝+ 1) 1−1 +𝑝 −1 = 𝑝 −1
𝑓(𝑣1,𝑝) = (𝑝+ 1) 1−1 +𝑝= 𝑝
𝑓(𝑣1,𝑝+1) = 𝑝+ 1 1−1 +𝑝+ 1 =𝑝+ 1
𝑓(𝑣2,1) = 𝑝+ 1 2−1 + 1 =𝑝+ 2
𝑓(𝑣2,2) = 𝑝+ 1 2−1 + 2 =𝑝+ 3
…
𝑓(𝑣2,𝑝−1) = (𝑝+ 1) 2−1 +𝑝 −1 = 2𝑝 𝑓(𝑣2,𝑝) = 𝑝+ 1 2−1 +𝑝 = 2𝑝+ 1
𝑓(𝑣2,𝑝+1) = 𝑝+ 1 2−1 +𝑝+ 1 = 2𝑝+ 2
Untuk 𝑖=𝑚 −1,
𝑓(𝑣𝑚−1,1) = 𝑝+ 1 𝑚 −1−1 + 1 = 𝑝+ 1 𝑚 −2 + 1 𝑓(𝑣𝑚−1,2) = 𝑝+ 1 𝑚 −1−1 + 2 = 𝑝+ 1 𝑚 −2 + 2
…
𝑓(𝑣𝑚−1,𝑝−1) = 𝑝+ 1 𝑚 −2 +𝑝 −1 = 𝑝+ 1 𝑚 −2 +𝑝 −1
𝑓(𝑣𝑚−1,𝑝) = 𝑝+ 1 𝑚 −1−1 +𝑝 = 𝑝+ 1 𝑚 −2 +𝑝
𝑓(𝑣𝑚−1,𝑝+1) = 𝑝+ 1 𝑚 −2 +𝑝+ 1 = 𝑝+ 1 𝑚 −2 +𝑝+ 1
Untuk 𝑖=𝑚,
𝑓(𝑣𝑚,1) = 𝑝+ 1 𝑚 −1 + 1 =𝑚𝑝 − 𝑝+𝑚
𝑓(𝑣𝑚,2) = 𝑝+ 1 𝑚 −1 + 2 =𝑚𝑝 − 𝑝+𝑚+ 1
…
𝑓(𝑣𝑚,𝑝−1) = 𝑝+ 1 𝑚 −1 +𝑝 −1 =𝑚𝑝+𝑚 −2
𝑓(𝑣𝑚,𝑝) = 𝑝+ 1 𝑚 −1 +𝑝=𝑚𝑝+𝑚 −1
Sedangkan untuk pelabelan sisi-sisinya adalah Untuk 𝑖= 1,
𝑓(𝑒1,1) =𝑓 𝑣1,1𝑣1,2 = 2𝑚 − 𝑖+ 1 (𝑝+ 1)− 𝑗+ 1
= 2𝑚 −1 + 1 (𝑝+ 1)−1 + 1
= 2𝑚(𝑝+ 1)
𝑓(𝑒1,2) =𝑓 𝑣1,2𝑣1,3 = 2𝑚 −1 + 1 (𝑝+ 1)−2 + 1
= 2𝑚(𝑝+ 1)−1
…
𝑓(𝑒1,𝑝−1) =𝑓 𝑣1,𝑝−1𝑣1,𝑝 = 2𝑚 −1 + 1 (𝑝+ 1)− 𝑝 −1 + 1
= 2𝑚(𝑝+ 1)− 𝑝+ 2
𝑓(𝑒1,𝑝) =𝑓 𝑣1,𝑝𝑣1,𝑝+1 = 2𝑚 −1 + 1 𝑝+ 1 − 𝑝+ 1
= 2𝑚 𝑝+ 1 − 𝑝+ 1 𝑓(𝑒1,𝑝+1) =𝑓 𝑣1,1𝑣1,𝑝+1 = 2𝑚 −1 𝑝+ 1 + 1
Untuk 𝑖= 2,
𝑓(𝑒2,1) =𝑓 𝑣2,1𝑣2,2 = 2𝑚 − 𝑖+ 1 (𝑝+ 1)− 𝑗+ 1
= 2𝑚 −2 + 1 (𝑝+ 1)−1 + 1
= 2𝑚 −1 𝑝+ 1 𝑓(𝑒2,2) =𝑓 𝑣2,2𝑣2,3 = 2𝑚 −1 𝑝+ 1 −1
= (2𝑚 −1)(𝑝+ 1)−1
…
= 2𝑚 −1 𝑝+ 1 − 𝑝+ 2 𝑓(𝑒2,𝑝) =𝑓 𝑣2,𝑝𝑣2,𝑝+1 = 2𝑚 −2 + 1 𝑝+ 1 − 𝑝+ 1
= (2𝑚 −1) 𝑝+ 1 − 𝑝+ 1 𝑓(𝑒2,𝑝+1) =𝑓 𝑣2,1𝑣2,𝑝+1 = 2𝑚 −2 𝑝+ 1 + 1
Untuk 𝑖=𝑚-1,
𝑓(𝑒𝑚−1,1) =𝑓 𝑣𝑚−1,1𝑣𝑚−1,2 = 2𝑚 − 𝑖+ 1 (𝑝+ 1)− 𝑗+ 1
= 2𝑚 − 𝑚+ 1 + 1 (𝑝+ 1)−1 + 1
= (𝑚+ 2)(𝑝+ 1)
𝑓(𝑒𝑚−1,2) =𝑓 𝑣𝑚−1,2𝑣𝑚−1,3 = 2𝑚 − 𝑚+ 1 + 1 𝑝+ 1 −2 + 1
= (𝑚+ 2)(𝑝+ 1)−1
…
𝑓(𝑒𝑚−1,𝑝−1) =𝑓 𝑣𝑚−1,𝑝−1𝑣𝑚−1,𝑝 = 2𝑚 − 𝑚+ 2 𝑝+ 1 − 𝑝+ 2
= (𝑚+ 2)(𝑝+ 1)− 𝑝+ 2 𝑓(𝑒𝑚−1,𝑝) =𝑓 𝑣𝑚−1,𝑝𝑣𝑚−1,𝑝+1 = 2𝑚 − 𝑚+ 2 𝑝+ 1 − 𝑝+ 1
= (𝑚+ 2) 𝑝+ 1 − 𝑝+ 1 𝑓(𝑒𝑚−1,𝑝+1) =𝑓 𝑣𝑚−1,1𝑣𝑚−1,𝑝+1 = 2𝑚 − 𝑚+ 1 𝑝+ 1 + 1
= 𝑚+ 1 𝑝+ 1 + 1
Untuk 𝑖=𝑚,
𝑓(𝑒𝑚,1) =𝑓 𝑣𝑚,1𝑣𝑚,2 = 2𝑚 − 𝑖+ 1 (𝑝+ 1)− 𝑗+ 1
= (𝑚+ 1)(𝑝+ 1)
𝑓(𝑒𝑚,2) =𝑓 𝑣𝑚,2𝑣𝑚,3 = 2𝑚 − 𝑚+ 1 𝑝+ 1 −2 + 1
= (𝑚+ 1)(𝑝+ 1)−1
…
𝑓(𝑒𝑚,𝑝−1) =𝑓 𝑣𝑚,𝑝−1𝑣𝑚,𝑝 = 2𝑚 − 𝑚+ 1 (𝑝+ 1)− 𝑝 −1 + 1
= (𝑚+ 1)(𝑝+ 1)− 𝑝+ 2
=𝑚 𝑝+ 1 + 3
𝑓(𝑒𝑚,𝑝) =𝑓 𝑣𝑚,𝑝𝑣𝑚,𝑝+1 = 2𝑚 − 𝑚+ 1 𝑝+ 1 − 𝑝+ 1
= 𝑚+ 1 𝑝+ 1 − 𝑝+ 1
= 𝑚𝑝+𝑚+ 2 =𝑚 𝑝+ 1 + 2
𝑓(𝑒𝑚,𝑝+1) =𝑓 𝑣𝑚,1𝑣𝑚,𝑝+1 = 2𝑚 − 𝑚 𝑝+ 1 + 1
=𝑚 𝑝+ 1 + 1
Dari konstruksi pelabelan di atas, terlihat bahwa label untuk titik merupakan bilangan bulat positif 1, 2, 3,…,𝑚 𝑝+ 1 dan label untuk sisi merupakan bilangan bulat positif 𝑚(𝑝+ 1) + 1,𝑚(𝑝+ 1) + 2, …, 2𝑚(𝑝+1). Hal ini juga sesuai dengan syarat pelabelan kuat yaitu
bilangan yang merupakan label titik-titiknya lebih kecil daripada label sisi-sisinya. Itu artinya konstruksi pelabelan yang diberikan berlaku untuk
semua 𝑝. □
Dari Pembuktian I dan Pembuktian II, maka terbukti rumus pelabelan berlaku untuk semua 𝑚 dan 𝑝.
Teorema 3.2 syarat pelabelan kuat berdasarkan Definisi 2.2.3, akibatnya Persamaan (3.2) juga berlaku dalam hal ini.
Contoh 1 :
Gambar 3.6 (22,1) SEATL pada 2C5
- Bobot sisi dengan label 16 adalah 16 + 1+ 5 = 22
Dari hasil perhitungan diperoleh bahwa bobot sisi-sisinya membentuk barisan
aritmetika naik dari 22, 23, 24, 25, …, 31 dengan suku pertama 22 dan beda 1.
Oleh karena itu Gambar 3.6 disebut (22,1) SEATLpada 2C5 Contoh 2 :
Gambar 3.7 (26,1) SEATL pada 2C6
- Bobot sisi dengan label 17 adalah 17 + 8+ 9 = 34
- Bobot sisi dengan label 16 adalah 16 + 9+ 10 = 35
- Bobot sisi dengan label 15 adalah 15 + 10+ 11 = 36
- Bobot sisi dengan label 14 adalah 14 + 11+ 12 = 37
Dari hasil perhitungan diperoleh bahwa bobot sisi-sisinya membentuk barisan
aritmetika naik dari 26, 27, 28, 29, …, 37 dengan suku pertama 26 dan beda 1. Jadi Gambar 3.7 disebut (26,1) SEATLpada 2C6
Contoh 3:
Gambar 3.8 (20,1) SEATL pada 3C3
f (v2,2v2,3) = (6-2+1)3 - 2+ 1 = 14
f (v2,1v2,3) = (6-2)3 + 1 = 13
f (v3,1v3,2) = (6-3+1)3 - 1+ 1 = 12
f (v3,2v3,3) = (6-3+1)3 - 2+ 1 = 11
f (v3,1v3,3) = (6-3)3 + 1 = 10
Pada Gambar 3.8 bobot terkecil dari sisinya adalah sisi dengan label 16, yaitu 16 + 1 + 3 = 20. Perhitungan bobot sisi :
Langkah pelabelan untuk contoh pada Gambar 3.9 adalah sebagai berikut :
- Bobot sisi dengan label 21adalah 21 + 1+ 4 = 26
Dari hasil perhitungan diperoleh bahwa bobot sisi-sisinya membentuk barisan aritmetika naik dari 26, 27, 28, 29, …, 37 dengan suku pertama 26 dan beda 1. Jadi Gambar 3.9 disebut (26,1) SEATL pada 3C4.
3.4 𝒂,𝟐 𝑺𝑬𝑨𝑻𝑳 pada Graf Multisikel (𝟑𝑪𝒑)
Berikut ini akan diberikan beberapa contoh graf multisikel (3𝐶𝑝) yang telah dilabeli untuk 𝑑 = 2.
Gambar 3.10 Pelabelan Graf multisikel (3𝐶3)
Gambar 3.11 Pelabelan Graf Multisikel (3𝐶7)
Tabel 3.1 Tabel Pola Pelabelan titik (vertex) pada 3𝐶𝑝
Tabel 3.2 Pola pelabelan sisi pada graf multisikel 3𝐶𝑝
Dari Tabel 3.1 dan Tabel 3.2 di atas, 𝑎,𝑑 𝑆𝐸𝐴𝑇𝐿 dengan 𝑑 = 2 pada graf multisikel (3𝐶𝑝) dapat dibagi dalam beberapa pola pelabelan yaitu untuk 𝑝= 6𝑘+ 1,𝑝 = 6𝑘 −1, dan 𝑝= 6𝑘 −3,dengan 𝑘 = 1,2,3,…dengan rumus sebagai berikut.
Konstruksi pelabelan untuk titik sebagai berikut : 1. Untuk 𝑝= 6𝑘+ 1, 𝑘= 1,2,3,…
Untuk 𝑗 = 1;𝑖= 1,2,3 𝑓 (𝑣𝑖𝑗) = 𝑖
Untuk𝑗 = 2
𝑓 𝑣𝑖𝑗 = 3𝑝+132 −2𝑖 ;𝑖= 1, 2
𝑓 𝑣𝑖𝑗 = 3𝑝2+7 ;𝑖= 3
Untuk𝑗 = 3, 4, 5,…, 𝑝 −2 ; 𝑖 = 1, 2, 3
𝑓(𝑣𝑖,𝑗−2)𝑚𝑜𝑑 3 = 0→ 𝑓 (𝑣𝑖𝑗) = 𝑓(𝑣𝑖,𝑗 −2) + 1 𝑓(𝑣𝑖,𝑗−2)𝑚𝑜𝑑 3≠0→ 𝑓 (𝑣𝑖𝑗) = 𝑓(𝑣𝑖,𝑗 −2) + 4
Untuk𝑗 = 𝑝 −1
𝑓 (𝑣𝑖,𝑝−1) = 3𝑝+ 𝑖 −2 ;𝑖= 1, 2
𝑓 𝑣𝑖,𝑝−1 = 3𝑝 −2 ;𝑖= 3
Untuk𝑗 = 𝑝;𝑖= 1, 2, 3 𝑓 (𝑣𝑖,𝑝) = 3𝑝+7
2 −2𝑖 ;𝑖= 1, 2
𝑓 𝑣𝑖,𝑝 = 3𝑝+1
2 ;𝑖= 3
𝑓 (𝑣𝑖𝑗) = 𝑖 ;𝑖 = 1, 2, 3 Untuk𝑗 = 2
𝑓 𝑣𝑖𝑗 = 3𝑝+132 −2𝑖 ;𝑖= 1, 2
𝑓 𝑣𝑖𝑗 = 3𝑝2+7 ;𝑖= 3
Untuk𝑗 = 3, 4, 5,…, 𝑝 −2 ; 𝑖 = 1, 2, 3
𝑓(𝑣𝑖,𝑗−2)𝑚𝑜𝑑 3 = 0→ 𝑓 (𝑣𝑖𝑗) = 𝑓(𝑣𝑖,𝑗 −2) + 1 𝑓(𝑣𝑖,𝑗−2)𝑚𝑜𝑑 3≠0→ 𝑓 (𝑣𝑖𝑗) = 𝑓(𝑣𝑖,𝑗 −2) + 4
Untuk𝑗 = 𝑝 −1;𝑖= 1, 2, 3 𝑓 (𝑣𝑖,𝑝−1) = 3𝑝+ 𝑖 −3
Untuk𝑗 = 𝑝 𝑓 𝑣𝑖,𝑝 =
3𝑝+3
2 ;𝑖= 1
𝑓 𝑣𝑖,𝑝 = 3𝑝−5
2 +𝑖 ;𝑖= 2, 3
3. Untuk 𝑝= 6𝑘 −3, 𝑘= 1,2,3,… Untuk 𝑗 = 1
𝑓 (𝑣𝑖𝑗) = 𝑖 ;𝑖 = 1, 2, 3
Untuk𝑗 = 2
𝑓 𝑣𝑖𝑗 = 3𝑝+132 −2𝑖 ;𝑖= 1, 2
𝑓 𝑣𝑖𝑗 = 3𝑝2+7 ;𝑖= 3
Untuk𝑗 = 3, 4, 5,…, 𝑝 −2 ; 𝑖 = 1, 2, 3
Untuk𝑗 = 𝑝 −1;𝑖= 1, 2, 3
𝑓 𝑣𝑖,𝑝−1 = 3𝑝 ;𝑖= 1
𝑓 𝑣𝑖,𝑝−1 = 3𝑝+ 𝑖 −4 ;𝑖= 2, 3
Untuk𝑗 = 𝑝 𝑓 𝑣𝑖,𝑝 =
3𝑝−1
2 +𝑖 ;𝑖= 1,2
𝑓 𝑣𝑖,𝑝 = 3𝑝−1
2 ;𝑖= 3
(Rumus 3.4.1) Konstruksi pelabelan sisi sebagai berikut:
1. Untuk 𝑝= 6𝑘+ 1, 𝑘= 1,2,3,… Untuk 𝑗 = 1
𝑓 𝑣𝑖,𝑗𝑣𝑖,𝑗+1 = 3𝑝+ 6− 𝑖 ; 𝑖= 1,2
𝑓 𝑣𝑖,𝑗𝑣𝑖,𝑗+1 = 3𝑝+ 6 ; 𝑖= 3
Untuk 𝑗 = 2, 3, 4,…,𝑝 −2;𝑖= 1, 2, 3,
𝑓 (𝑣𝑖,𝑗𝑣𝑖,𝑗+1) 𝑚𝑜𝑑 3 = 0→ 𝑓 (𝑣𝑖,𝑗+1𝑣𝑖,𝑗+2) = 𝑓(𝑣𝑖,𝑗𝑣𝑖,𝑗+1) + 1
𝑓 (𝑣𝑖,𝑗𝑣𝑖,𝑗+1) 𝑚𝑜𝑑 3≠0→ 𝑓 (𝑣𝑖,𝑗+1𝑣𝑖,𝑗+2) = 𝑓(𝑣𝑖,𝑗𝑣𝑖,𝑗+1) + 4
Untuk 𝑗 =𝑝 −1; 𝑖= 1,2,3 𝑓 (𝑣𝑖,𝑝−1𝑣𝑖,𝑝) = 6𝑝 − 𝑖+ 1
Untuk 𝑗 =𝑝; 𝑖 = 1,2,3 𝑓 (𝑣𝑖,1𝑣𝑖,𝑝) = 3𝑝+ 𝑖
+3
2. Untuk 𝑝= 6𝑘 −1, 𝑘= 1,2,3,… Untuk 𝑗 = 1
𝑓 𝑣𝑖,𝑗𝑣𝑖,𝑗+1 = 3𝑝+ 6− 𝑖 ; 𝑖= 1,2
𝑓 𝑣𝑖,𝑗𝑣𝑖,𝑗+1 = 3𝑝+ 6 ; 𝑖= 3
Untuk 𝑗 = 2, 3, 4,…,𝑝 −2;𝑖= 1, 2, 3,
𝑓 (𝑣𝑖,𝑗𝑣𝑖,𝑗+1) 𝑚𝑜𝑑 3 = 0→ 𝑓 (𝑣𝑖,𝑗+1𝑣𝑖,𝑗+2) = 𝑓(𝑣𝑖,𝑗𝑣𝑖,𝑗+1) + 1
𝑓 (𝑣𝑖,𝑗𝑣𝑖,𝑗+1) 𝑚𝑜𝑑 3≠ 0→ 𝑓 (𝑣𝑖,𝑗+1𝑣𝑖,𝑗+2) = 𝑓(𝑣𝑖,𝑗𝑣𝑖,𝑗+1) + 4
Untuk 𝑗= 𝑝 −1
𝑓 (𝑣𝑖,𝑝−1𝑣𝑖,𝑝) = 6𝑝 − 𝑖 𝑖 = 1,2
𝑓 (𝑣𝑖,𝑝−1𝑣𝑖,𝑝) = 6𝑝 𝑖 = 3
Untuk 𝑗 =𝑝; 𝑖 = 1,2,3 𝑓 (𝑣𝑖,1𝑣𝑖,𝑝) = 3𝑝+ 𝑖+3
2 ; 𝑖 = 1,3 𝑓 (𝑣𝑖,1𝑣𝑖,𝑝) = 3𝑝+ 1 ; 𝑖= 2
3. Untuk 𝑝= 6𝑘 −3, 𝑘= 1,2,3,… Untuk 𝑗 = 1
𝑓 𝑣𝑖,𝑗𝑣𝑖,𝑗+1 = 3𝑝+ 6− 𝑖 ; 𝑖= 1,2
𝑓 𝑣𝑖,𝑗𝑣𝑖,𝑗+1 = 3𝑝+ 6 ; 𝑖= 3
Untuk 𝑗 = 2, 3, 4,…,𝑝 −2;𝑖= 1, 2, 3,
𝑓 (𝑣𝑖,𝑗𝑣𝑖,𝑗+1) 𝑚𝑜𝑑 3 = 0→ 𝑓 (𝑣𝑖,𝑗+1𝑣𝑖,𝑗+2) = 𝑓(𝑣𝑖,𝑗𝑣𝑖,𝑗+1) + 1
𝑓 (𝑣𝑖,𝑗𝑣𝑖,𝑗+1) 𝑚𝑜𝑑 3≠ 0→ 𝑓 (𝑣𝑖,𝑗+1𝑣𝑖,𝑗+2) = 𝑓(𝑣𝑖,𝑗𝑣𝑖,𝑗+1) + 4
Untuk 𝑗= 𝑝 −1; 𝑖 = 1,2,3
Untuk 𝑗 =𝑝; 𝑖 = 1,2,3 Berikut ini akan ditunjukkan bahwa rumus pelabelan di atas berlaku untuk semua 𝑝= 2𝑛+ 1 untuk 𝑛 = 1, 2, 3,….
𝑓 𝑣𝑖𝑗 =
Sedangkan untuk pelabelan sisi-sisinya adalah sebagai berikut. Untuk 𝑖= 1,
𝑛= 1 benar, maka akan dibuktikan bahwa rumus pelabelan juga
berlaku untuk 𝑝= 2𝑛+ 1 untuk n yang lain, yaitu 𝑛 = 2, 3, 4,… Bukti :
Anggap 𝑛 =𝑐 benar, artinya rumus berlaku pada graf multisikel (3𝐶𝑝) dengan 𝑝 = 2𝑐+ 1. Ambil salah satu pola pelabelan dari tiga pola pelabelan yang telah ditentukan, misal pola pelabelan untuk 𝑝= 6𝑘+ 1, 𝑘= 1,2,3,…maka pelabelannya adalah sebagai berikut.