ANALISIS PERBANDINGAN SIFAT ALIRAN PADA MODEL 2D
AXISYMMETRIC DENGAN MODEL 3D DENGAN METODE
NUMERIK
J. Hendrarsakti1,2 , A.D Prakoso1, D. Montreano2
1Fakultas Teknik Mesin dan Dirgantara, Institut Teknologi Bandung Jalan Ganesha 10, Bandung 40132
2Fakultas Teknik, Universitas Pembangunan Nasional “Veteran” Jakarta Jalan RS Fatmawati No. 1, Jakarta
Email: [email protected]
Abstract
Many previous studies of ejector have been conducted to understand and maximize the ejector performance. The study can be in form of experiments, analytical, and numerical simulation. The numerical simulation looks for the most effective and efficient effort and time in modeling flow process inside the ejector. Model simplification becomes one of solution in conducting simulation effectively. Three dimensional models in general are applied to an ejector that would be analyzed. These models can be compared to the simpler model, namely axisymmetric 2D model. The current study investigated the comparison between 3D and 2D models using numerical solution. Three types of ejectors from different application were used as the objects of the study. The analysis was conducted by comparing the qualitative and quantitative results. The results show that qualitatively the 2D axisymmetric model has good comparison to the 3D model. Quantitatively, 2D axisymmetric model has good similarity to 3D model for ejector performance parameters, such as entrainment ratio and Mach number with biggest difference of 5.7%. However, the velocity and pressure distribution have bigger discrepancies at both axial and radial directions at the area with extreme change, such as at throat nozzle. It can be concluded that the 2D axisymmetric model can be used as substitution of 3D model when the objective is only to obtain ejector performance and qualitative study.
Keywords : Ejector, CFD, 2D axisymmetric, 3D simulation
PENDAHULUAN
Ejektor telah diperkenalkan dalam dunia
engineering di awal abad ke-20. Ejektor menjadi peralatan mekanikal yang cukup banyak diaplikasikan di dunia industri. Pada dunia pembangkit, ejektor digunakan untuk menvakumkan kondenser agar kinerja turbin dapat maksimal. Selain itu, ejektor juga banyak digunakan untuk mengevakuasi atau memisahkan gas-gas yang tidak digunakan pada berbagai macam industri, seperti industri minyak dan gas, petrokimia, dan lain-lain. Ejektor banyak digunakan karena konstruksi yang sederhana dan perawatan yang mudah.
Penelitian mengenai mekanisme kerja ejektor telah dimulai sejak tahun 1950. Keenan dan Neuman menjadi orang pertama yang menampilkan analisis analitik dan eksperimen mengenai mekanisme kerja ejektor. Model tekanan konstan dan luas area konstan yang diperkenalkan Keenan dan Neuman, menurut Liao [1] menjadi dasar teori pemodelan dan analisis ejektor sejak saat itu. Penelitian tentang ejektor masih terus dilakukan hingga saat ini untuk memahami dan memaksimalkan kinerja ejektor.
Dalam penelitian era dewasa ini, metode numerik dengan bantuan perangkat lunak komputer sangat digemari. Penelitian dengan bantuan komputer atau yang sering disebut pemodelan juga tidak sedikit menghabiskan waktu dan usaha dalam pengerjaannya. Oleh karena itu, peneliti dituntut untuk melakukan usaha seefektif mungkin. Liao [1] memodelkan ejektor dengan model 2D
axisymmetric dan hasil yang didapatkan memiliki kesamaan yang baik dengan hasil eksperimen. Dari model tersebut, terdapat peluang dalam penyederhanaan model yang nantinya akan mengefektifkan kerja penelitian. Hal ini yang melatarbelakangi penelitian ini.
Gambaran umum tentang ejector
dioperasikan dengan compressible fluid, sering disebut sebagai injector.
Secara umum, bagian-bagian ejektor ditampilkan pada Gambar 1.
Gambar 1. Bagian-bagian ejektor
Fluida kerja bertekanan tinggi masuk dan diekspansikan melalui sebuah nozel. Di dalam nozel, energi tekanan motive fluid diubah menjadi energi kinetik sehingga motive fluid mengalami percepatan dan tekanannya menjadi lebih rendah pada saat keluar dari nozel. Kondisi ini mengakibatkan fluida isap terisap ke dalam ruang pencampur dan diffuser, energi kinetik fluida campuran (motive fluid dan suction fluid) diubah kembali menjadi energi tekanan. Pada saat keluar difuser, tekanan fluida campuran sama dengan tekanan keluaran.
Pemodelan dan Simulasi
Pemodelan ini dilakukan pada tiga ejektor sebagai sample, yaitu ejektor PLTP X, ejektor Korting, dan ejektor Jerguson. Ejektor PLTP X merupakan jenis gas jet ejektor. Ejektor ini bertujuan untuk menarik NCG (Non condensable gas) yang ada pada condenser yang terdapat pada Pembangkit Listrik Panas Bumi. NCG ini menyebabkan tekanan condenser naik, hal ini bertentangan dengan tujuan adanya condenser yang bertekanan vakum agar performa turbin maksimal. Sedangkan ejektor korting dan ejektor Jerguson merupakan jenis water jet ejektor. Ejektor korting dan ejektor Jerguson merupakan ejektor dari perusahaan manufaktur yang berfungsi menarik gas pada suatu tanki atau pada instalasi pipa untuk tujuan penvakuman.
(a)
(b)
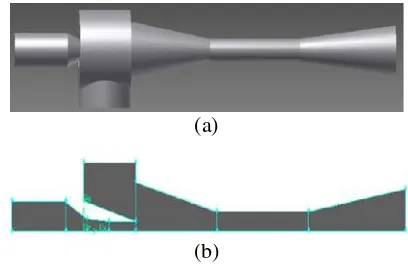
Gambar 2. Contoh 3D (a) dan 2D model (b) untuk ejector jenis Jerguson
Dalam melakukan pemodelan dan simulasi aliran, Pembuatan model 2D dan 3D dimana contoh diberikan pada Gambar 2. Tipe kondisi batas yang dipilih pada pemodelan ini ditampikan pada Tabel 1.
Tabel 1 Tipe kondisi batas
Jenis Ejector PLTP X Korting Jerguson
Motive Inlet Pressure inlet
Pressure
inlet
Pressure
inlet
Suction Inlet Mass flow inlet
Pressure
inlet
Pressure
inlet
Outlet Pressure outlet Pressure inlet Pressure inlet
Nozzle Outlet Interior Interior Interior
Interior Interior Interior Interior
Dinding Wall Wall Wall
Kondisi batas untuk model 2D axysimmetric
terdapat penambahan pada sumbu dengan tipe
boundary conditions axis sebagai fungsi
percermnan.
Validasi Hasil Simulasi
Validasi dilakukan dengan dua metode, yang pertama uji grid independence dan yang kedua adalah Perbandingan dengan metode empiris.
• Uji Grid Independence
Validasi hasil simulasi yang pertama dilakukan adalah dengan uji Grid Independence.
Uji Grid Independence dilakukan dengan
mengubah ukuran grid dan dilihat perbedaan parameter hasil simulasinya. Hal ini dilakukan dengan terlebih dahulu menetapkan parameter apa yang hendak dijadikan parameter acuan untuk melihat perubahannya terhadap penambahan jumlah grid. Parameter yang dipilih adalah parameter performansi ejektor, yaitu rasio entrainment dan Mach number maksimum untuk diobservasi perubahannya terhadap penambahan jumlah grid. Jika seiring bertambahnya jumlah cell, perubahan parameter tersebut tidak berubah secara signifikan maka nominal jumlah cell optimal telah ditemukan.
Uji konvergensi dilakukan pada semua ejektor pada penelitian ini dan nilai error
sampai mencapai konvergen. Dari hasil Uji Grid independence, didapatkan error terbesar pada ejektor Korting 7,7%, dari referensi [3], eror sebesar 8% masih dapat diterima.
• Perbandingan dengan Pendekatan
Empiris
Perbandingan dengan pendekatan empiris dilakukan pada pengukuran rasio entrainment
ejektor PLTP X. Pendekatan ini tidak dilakukan kepada ejektor Korting dan Jerguson karena tidak ditemukan teori untuk menghitung rasio entrainment kedua ejektor tersebut. Pendekatan empiris untuk mencari rasio entrainment pada ejektor PLTP X menggunakan metode Freeston. Metode ini banyak digunakan oleh orang lapangan di dunia industri pembangkit panas bumi [16].
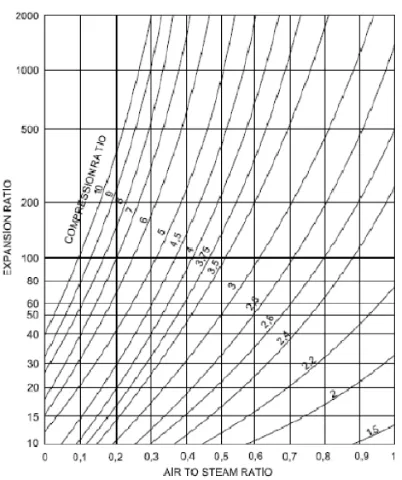
Perhitungan dilakukan dengan menggunakan Gambar 3 yang berupa grafik hubungan antara ATSR (Air to Steam Ratio), expansion ratio, dan
compression ratio. ATSR yang dimaksud Freeston adalah rasio entrainment pada ejektor. Dari data ejektor PLTP X, didapatkan compression ratio dan expansion ratio pada perhitungan berikut.
• Model 2D axisymmetric
Expansion ratio (ER) = 𝑃𝑃𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑖𝑖𝑖𝑖𝑚𝑚𝑚𝑚
𝑃𝑃𝑠𝑠𝑠𝑠𝑠𝑠𝑚𝑚𝑚𝑚𝑚𝑚𝑖𝑖 = 6,3
0,059 = 102,44
Compression ratio (CR)= 𝑃𝑃𝑚𝑚𝑠𝑠𝑚𝑚𝑖𝑖𝑚𝑚𝑚𝑚
𝑃𝑃𝑠𝑠𝑠𝑠𝑠𝑠𝑚𝑚𝑚𝑚𝑚𝑚𝑖𝑖 = 0,31
0,059 = 5,25
Dari membaca grafik pada Gambar 3, didapat ATSR untuk model 2D sebesar 0,3.
• Model 3D
Expansion ratio (ER) = 𝑃𝑃𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑖𝑖𝑖𝑖𝑚𝑚𝑚𝑚
𝑃𝑃𝑠𝑠𝑠𝑠𝑠𝑠𝑚𝑚𝑚𝑚𝑚𝑚𝑖𝑖 = 6,3
0,0615 =
106,78
Compression ratio (CR)= 𝑃𝑃𝑚𝑚𝑠𝑠𝑚𝑚𝑖𝑖𝑚𝑚𝑚𝑚
𝑃𝑃𝑠𝑠𝑠𝑠𝑠𝑠𝑚𝑚𝑚𝑚𝑚𝑚𝑖𝑖 = 0,31
0,059 = 5,25
Dari membaca grafik pada Gambar 3, maka ATSR untuk model 3D adalah 0,3
Gambar 3 Metode Freeston [3]
Dengan Error yang didapatan sebesar 3,38% maksimal, dapat dinyatakan bahwa hasil simulasi sudah valid.
PEMBAHASAN
Dalam menganalisis kebutuhan model 3D untuk sifat aliran ejektor, dilakukan analisis perbandingan hasil simulasi aliran ejektor dengan model yang lebih sederhana. Model yang lebih sederhana dipilih model 2D axisymmetric. Model
2D axisymmetric merupakan model 2D yang
mempunyai sumbu simetri sehingga pembuatannya hanya dilakukan pada salah satu bagian simetrinya. Model ini relatif lebih sederhana dan cepat pengerjaannya.
Perbandingan model 2D axisymmetric
Tabel 2 Perbandingan hasil 2D dan 3D Ejektor korting 1,443
- Percent
difference (%) 5,722 Ejektor
Jerguson 0,0059
Percent
difference (%) 0,793
Dari Tabel 2, terlihat bahwa model 3D memiliki waktu iterasi yang lebih lama dibanding model 2D axisymmetric. Dengan jumlah elemen 4 kali lebih besar, model 3D memiliki rata-rata perbedaan waktu 5-8 kali lebih lama dibanding model 2D axisymmetric. Selain itu juga dibandingkan tingkat kesulitan dalam pemodelan dan simulasi kedua model. Untuk model 2D
axisymmetric secara subjektif diberikan nilai 2 dan untuk model 3D diberikan nilai 5 untuk skala tingkat kesulitan 1÷5. Secara keseluruhan model 2D axisymmetric relatif lebih mudah dan cepat, baik dalam membuat geometri maupun dalam iterasinya. Model 3D memiliki bentuk yang lebih kompleks dibanding 2D axisymmetric, sehingga relatif lebih sulit terutama pada saat iterasi menuju konvergensinya.
Perbandingan lain dilakukan dengan analisis secara kuantitatif. Analisis kuantitatif adalah analisis yang dilakukan dengan membandingkan hasil yang berupa angka/nilai.
Analisis kuantitatif dilakukan pada 4 parameter, antara lain:
1. Distribusi kecepatan dan tekanan aliran sepanjang sumbu X/centerline pada model 3D dengan model 2D axisymmetricnya. Dari beberapa titik pada grafik, akan dicari perbedaannya (difference), sehingga akan terlihat titik yang memiliki perbedaan cukup mencolok.
2. Distribusi kecepatan arah radial (sumbu Y) pada beberapa titik ekstrim seperti daerah throat nozzle, outletnozzle dan mixing chambers.
3. Perbandingan perhitungan terhadap beberapa performansi ejektor, seperti rasio entrainment, dan bilangan Mach maksimum.
4. Analisis hubungan sifat aliran ejektor dengan fungsi dan bentuk ejektor
Perbedaan antara model 2D axisymmetric dengan model 3D dihitung dalam bentuk percent difference.
Percent difference (PD) = |nilai2D−nilai3𝐷𝐷|
0,5(nilai2D+nilai3D)
• Analisis Kuantitatif terhadap Distribusi
Kecepatan dan tekanan sepanjang sumbu X Ejektor PLTP X
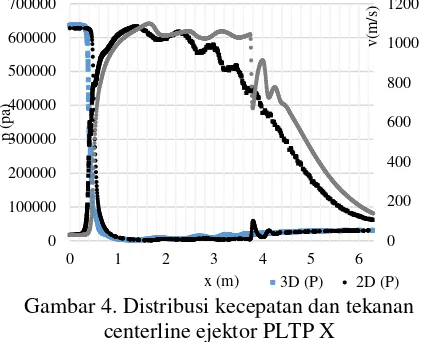
Distribusi kecepatan sepanjang sumbu X ditampilkan pada Gambar 4. Terlihat bahwa grafik dengan warna abu-abu untuk model 2D dan hitam untuk model 3D.
Gambar 4. Distribusi kecepatan dan tekanan centerline ejektor PLTP X
Dari Gambar 4, dapat diamati bahwa perbedaan kecepatan terbesar terjadi pada rentang nilai x = 0.5 sampai dengan x = 1 dan nilai x = 3 sampai dengan x = 6. Rentang tersebut merupakan daerah pada nozzle setelah melewati throat nozle
dan sisi masuk mixing chamber sampai dengan
diffuser.
Untuk distribusi kecepatannya, perbedaan terbesar hanya terjadi pada daearh nozel, hal ini juga ditunjukkan oleh distibusi kecepatannya.
Percent difference paling tinggi untuk kecepatan terdapat pada x = 404 mm dan x = 3790, yaitu sebesar 162,8% % dan 14,42%. Lokasi tersebut terletak pada nozzle dan mixing chamber. Pada daerah tersebut, aliran melalui luas area yang lebih kecil, fenomena ini sering disebut throat. Perbedaan tersebut terjadi karena pada model 2D
axisymmetric, dinding yang melingkupi aliran
• Analisis Kuantitatif terhadap Distribusi Kecepatan dan tekanan sepanjang sumbu X Ejektor Korting dan Jerguson
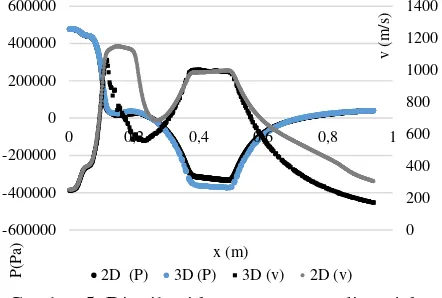
Dari Gambar 5 dan 6, terlihat bahwa perbedaan hasil simulasi model 2D axisymmetric dengan model 3D pada ejektor Korting dan Jerguson berada pada rentang daerah yang sama seperti ejektor PLTP X, yaitu pada daerah dengan perubahan ekstrim.
Gambar 5. Distribusi kecepatan centerline ejektor Korting
Gambar 6. Distribusi kecepatan centerline ejektor Jerguson
• Analisis Kuantitatif terhadap Distribusi
Kecepatan Radial Ejektor PLTP X,
Distribusi kecepatan radial ketiga ejektor ditampilkan pada Gambar 7- 9.
Gambar 7. Distribusi kecepatan radial throat nozzle ejektor PLTP X
Gambar 8. Distribusi kecepatan radial outlet nozzle ejektor PLTP X
Gambar 9. Distribusi kecepatan radial mixing chamber ejektor PLTP X
Ketiga grafik tersebut menunjukkan hubungan antara model 2D axisymmetric dengan model 3D pada distribusi kecepatan radialnya. Pada daerah throat, kecepatan radial model 3D lebih besar dibanding model 2D axisymmetric. Daerah outlet nozel, kedua model menunjukkan kesamaan yang sangat baik, sedangkan pada daerah mixing chamber model 2D axisymmetric
kecepatan aliran radialnya lebih besar nilainya dibanding model 3D.
Hubungan antara kedua model pada parameter kecepatan arah radial menunjukkan hal yang sama dengan parameter pada sumbu X/centerline, yaitu pada daerah dengan perubahan nilai kecepatan yang ekstrim, perbedaan yang terjadi cenderung besar. Hal ini dibuktikan dengan kecepatan arah radial pada daerah throat dan
mixing chamber memiliki perbedaan yang cukup signifikan, berbeda dengan daerah outlet nozel yang memiliki kesamaan yang baik.
• Analisis terhadap Parameter Performansi
Ejektor
Analisis kuantitatif pada performansi ejektor dilakukan dengan melihat nilai rasio entrainment, rasio tekanan, dan bilangan Mach hasil simulasi
0
-0,16 0,04 0,24 0,44 0,64
ketiga ejektor. Sebelum melakukan perbandingan, dilakukan perhitungan bilangan Mach pada ketiga ejektor. Dari data ketiga ejektor, fluida kompresibel untuk ejektor PLTP X dan fluida inkompresibel untuk ejektor Korting dan Jerguson. Persamaan unutk menghitung kedua jenis fluida tersebut berbeda. Untuk ejektor PLTP X dengan fluida seperti gas yang dianggap sebagai gas ideal, bilangan Mach dihitung berdasarkan Persamaan 1.
M =v
c (1)
dimana M adalah bilangan Mach, v adalah kecepatan, dan c adalah kecepatan suara
c = √kRT (2)
dimana k adalah rasio koefisien panas, R adalah konstanta gas, dan T adalah temperatur
Temperatur pada ejektor PLTP X ditentukan sebesar 108°C dengan alasan temperatur tersebut
merupakan temperatur keluaran dari ejektor. Kecepatan suara (c) didapatkan dengan melihat tabel sifat udara pada berdasarkan Persamaan 2 Didapatkan kecepatan suara sekitar 387 m/s.
Untuk fluida seperti air, yang digunakan sebagai motive fluid pada ejektor Korting dan Jerguson, bilangan Mach dihitung berasarkan Persamaan 1, tetapi dengan persamaan kecepatan suara yang berbeda, persamaan kecepatan suara ditampilkan pada Persamaan 3.
𝑐𝑐= Ev
ρ (3)
dimana EV adalah energy, dan ρ adalah massa jenis
Kecepatan suara (c) untuk fluida air didapatkan dengan melihat tabel sifat udara pada Lampiran B berdasarkan Persamaan 4. Kecepatan suara didapat sebesar 1507 m/s pada T = 30°C. Nilai performansi ketiga ejektor ditampilkan pada Tabel 3.
Pada ejektor Korting dan Jerguson tidak ditampilkan rasio kompresi karena rasio kompresi kedua ejektor sudah diperoleh dari data awal. Perbandingan performansi ejektor model 2D
axisymmetric denagan model 3D pada ketiga ejektor menunjukkan kesamaan yang baik dengan percent difference terbesar 7.5 %, yaitu pada rasio entrainment ejektor Korting. Perbandingan ini
merujuk pada penelitian Liao [1] yang menyatakan bahwa perbedaan sekitar 10% masih dianggap baik.
• Analisis Hubungan Sifat Aliran Ejektor
dengan Fungsi dan Bentuk Ejektor
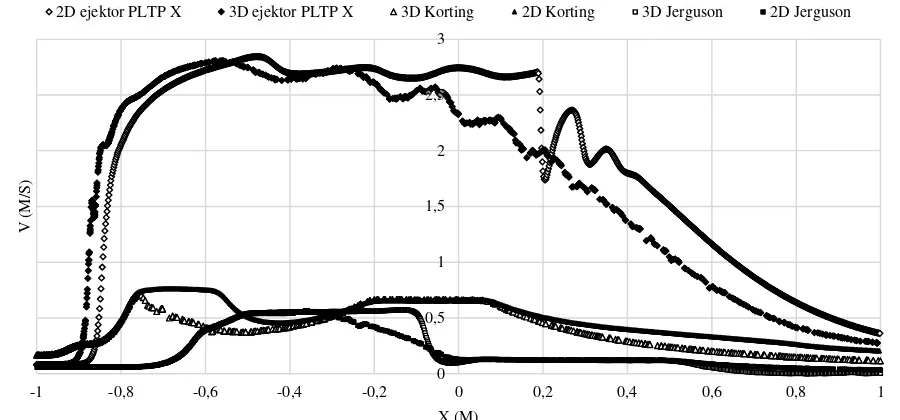
Untuk menganalisis hubungan ini, dibuat plot grafik pada Gambar 10 yang memuat ketiga ejektor. Ketiga ejektor memiliki panjang yang berbeda-beda, ejektor PLTP X memiliki panjang total 6,3 m, ejektor Korting 0.94 m, dan ejektor Jerguson 0.6 m. Plot grafik dibuat dengan terlebih dahulu menseragamkan sumbux dengan cara melakukan non-dimensional analisis dimana. disimbolkan Gambar 10 Distribusi kecepatan centerline ketiga ejektor
0 0,5 1 1,5 2 2,5 3
-1 -0,8 -0,6 -0,4 -0,2 0 0,2 0,4 0,6 0,8 1
V
(
M/S
)
X (M)
dengan x ̽ , dimana x ̽ = x/𝑥𝑥𝑚𝑚𝑚𝑚𝑚𝑚., x = panjang ejektor
sepanjang sumbu X, dan 𝑥𝑥𝑚𝑚𝑚𝑚𝑚𝑚= panjang maksimum ejektor pada sumbu X
Titik 0 pada Gambar 10 tersebut terletak di tengah daerah mixing chamber untuk ejektor PLTP X dan ejektor Korting, sedangkan untuk ejektor Jerguson, titik 0 terletak di sisi masuk daerah mixing chamber. Posisi nozel pada ejektor PLTP X terletak pada rentang axis -1÷-0,6, ejektor Korting pada rentang axis -1−-0,75, dan ejektor Jerguson pada rentang -1−-0,3. Parameter yang dianalisis adalah distribusi bilangan Mach sepanjang sumbu X/centerline. Distribusi bilangan Mach ketiga ejektor ditampilkan pada Gambar 10.
Dari Gambar 10, diketahui bahwa distribusi bilangan Mach secara keseluruhan sama, yaitu mengalami kenaikan ketika aliran memasuki nozzle, dan mulai turun ketika keluar dari nozzle. Namun pada ejektor PLTP X, penurunan yang terjadi tidak setajam kedua ejektor lainnya. Hal ini terjadi karena bentuk nozzle dari ejektor PLTP X.
Bentuk nozzle PLTP X berbeda dengan kedua ejektor lainnya, yaitu berbentuk konvergen-divergen. Bentuk tersebut jika dilalui aliran supersonic (M>1) seperti pada ejektor PLTP X, maka bentuk divergen akan mempertahankan kecepatan tingginya, tidak mengalami penurunan secara drastis. Dengan kata lain bahwa kenaikan luas penampang akan mengakibatkan kenaikan kecepatan juga, bukan sebaliknya. Kejadian sebaliknya terjadi pada aliran dengan kecepatan subsonik yang dialami ejektor Korting dan Jerguson. Hal ini dapat dibuktikan dengan Persamaan 4 dan 5.
𝑑𝑑𝑃𝑃
ρ = −𝑑𝑑(
𝑚𝑚2
𝑑𝑑) (4) 𝑑𝑑𝑑𝑑
A = −
𝑑𝑑𝑚𝑚
𝑚𝑚 (1− 𝑀𝑀2) (5)
Jika ditinjau Persamaan 4, alirannya subsonic (M < 1), maka tanda nilai perubahan luas penampang berbeda dengan perubahan kecepatannya, dengan kata lain jika luas penampang meningkat, maka kecepatannya akan turun. Dari Persamaan 5, diketahui jika kecepatannya turun, maka tekanannya akan naik. Berbeda jika alirannya supersonic (M > 1), Persamaan 5 menunjukkan bahwa perubahan kecepatan akan bernilai positif, sama tanda dengan perubahan luas penampangnya. Dengan kata lain jika luas penampang meningkat, maka kecepatannya pun akan meningkat.
Fenomena itu yang ditunjukkan pada ejektor PLTP X, kecepatan aliran tidak turun tajam ketika keluar nozzle seperti ejektor lainnya. Kecepatan dipertahankan tetap pada supersonik agar debit fluida sekunder yang ditarik besar.
SIMPULAN
1. Hasil simulasi aliran model 2D axisymmetric
memiliki kesamaan yang sangat baik secara kualitatif terhadap model 3D. Secara kuantitatif, menunjukkan hasil yang sangat baik juga pada parameter performansi ejektor dengan perbedaan terbesar 5,7%. Namun, model 2D axisymmetric tidak dapat menunjukkan kesamaan yang baik pada distribusi kecepatan dan tekanan baik pada
centerline maupun arah radialnya terutama ketika melalui daerah yang ekstrim, seperti daerah throat.
2. Dalam pemodelan dan simulasi aliran pada ejektor, model 3D tidak dibutuhkan dalam penelitian jika tujuan simulasi hanya ingin mendapatkan nilai performansi ejektor, cukup menggunakan model 2D axisymmetric.
Saran
1. Dalam pemodelan ejektor selanjutnya, perlu diketahui terlebih dahulu parameter apa yang akan diteliti. Jika yang diteliti performansi dan studi kualitatif, cukup dilakukan model 2D
axisymmetric saja.
2. Untuk mendapatkan kesamaan yang lebih baik dari model 2D axisymmetric ejektor, kedalaman (sumbu Z) pada nilai referensinya diperkecil.
3. Perlu dilakukan analisis dengan metode lain agar hasil pada penelitian ini lebih meyakinkan.
DAFTAR PUSTAKA
1. Chaqing Liao, Gas ejector modeling, Dissertation, Nuclear engineering, Texas A&M University, 2008.
2. Maqsood Asim, A Study of Subsonic Air-Air
Ejectors with Short Bent Mixing Tubes,
Dissertation, Universitas Queen’s, 2008. 3. Freeston, D. H. Modul Ajar Geothermal,