A. Interpolasi Linier - PERSAMAAN

b. orde 1 yang menghubungkan 3 titik a. orde 1 yang menghubungkan 2 titik

c. Orde 3 menghubungkan 4 titik

X f(x1)

f(x2)

f(x0)

X0 X X1

f(x)

A

C

B D

E

PERSAMAAN INTERPOLASI

Dalam mengestimasi suatu data-data yang ada, diperlukan suatu metode untuk penyelesaiannya yaitu interpolasi.

Metode interpolasi yang paling banyak digunakan adalah interpolasi polinomial, dengan bentuk: F(x) = a0 + a1x + a2x2 + ….. + anxn

Pada polinomial berderajat satu, maka diperoleh bentuk interpolasi linier.

A. Interpolasi Linier

 Bentuk yang paling sederhana adalah dengan menghubungkan dua titik data dengan garis lurus interpolasi linier

 Diketahui nilai suatu fungsi di titik x0 dan x1 yaitu fungsi f(x0) dan f(x1), dengan metode interpolasi linier akan dicari fungsi dititik x, f(x)

BC

AB

=

DE

AD

f

₁

(

x

)−

f

(

x

₀

)

x

−

x

₀

=

f

(

x

₁

)−

f

(

x

₀

)

x

₁

−

x

₀

f

₁

(

x

)=

f

(

x

₀

)+

f

(

x

x

1

)−

f

(

x

0

)

1

−

x

0

(

x

−

x

0

)

 Persamaan yang didapat adalah persamaan interpolasi linier (interpolasi polinomial orde satu)

Contoh:

Dicari nilai ln 2 dengan metode interpolasi linier berdasarkan data ln 1 = 0 dan ln 6 = 1,7917595

Penyelesaian:

Interpolasi linier dari: x0 = 1 f(x0) = 0

x1 = 6 f(x1) = 1,7917595

x = 2 f1(x) = ?

f

1

(

2

)=

0

+

1

,7917595

6

−

0

−

1

(

2

−

1

)=

0

,3583519

Nilai eksak dari ln 2 = 0,69314718

Besar kesalahan:

e

t

=|

0

,

69314718

−

0

,

3583519

0

,

69314718

|

x

100%

=

48

,

3%

B. Interpolasi Kuadrat

 Kesalahan yang terjadi pada contoh di atas, karena kurva dari fungsi didekati dengan garis lurus.

 Untuk mengurangi kesalahan tersebut, perkiraan dilakukan dengan menggunakan garis lengkung.

 Polinomial orde dua menghubungkan tiga titik data, persamaan dapat ditulis dalam bentuk:

f2(x) = b0 + b1(x-x0) + b2(x-x0) (x-x1) ……….………...……. (1)  Persamaan di atas identik dengan persamaan:

f2(x) = a0 + a1x + a2x2

dengan: a0 = b0 - b1x0 + b2x0x1 a1 = b1 - b2x0 - b2x0x1 a2 = b2

didapat b0 = f(x0) ……… (2)  Koefisien b1, masukkan nilai x = x1 pada persamaan (1)

didapat

b

1

=

f

(

x

1

)−

f

(

x

0

)

x

₁

−

x

0 _{…...……… (3)}

 Koefisien b2, substitusi persamaan (2) dan (3) dan x = x2 pada persamaan (1)

Didapat

b

2

=

f

(

x

₂

)−

f

(

x

₁

)

x

2

−

x

1

−

f

(

x

₁

)−

f

(

x

₀

)

x

1

−

x

0

x

₂

−

x

₀

Contoh:

Dicari nilai ln 2 atau f(2) dengan metode interpolasi kuadrat berdasarkan data:

x0 = 1 f(x0) = 0

x1 = 4 f(x1) = 1,3862944 x2 = 6 f(x2) = 1,79177595 Penyelesaian:

· Koefisien b0 = f(x0) = 0

· Koefisien

b

1

=

f

(

x

1

)−

f

(

x

0

)

x

1

−

x

0

=

1

,

3862944

−

0

4

−

1

=

0

,

46209813

· Koefisien b2

b

2

=

f

(

x

₂

)−

f

(

x

₁

)

x

₂

−

x

₁

−

f

(

x

₁

)−

f

(

x

₀

)

x

₁

−

x

₀

x

₂

−

x

₀

=

1

,

7917595

−

1

,

3862944

6

−

1

−

1

,

3862944

−

0

4

−

1

6

−

1

=−

0

,

051873

Nilai-nilai tersebut disubstitusikan ke persamaan (1),

diperoleh: f2(x) = 0 + 0,4629813(x-1) – 0,051873(x-1)(x-4), sehingga untuk x = 2 → f2(2) = 0,56584436

Nilai eksak dari ln 2 = 0,69314718

Besar kesalahan:

e

t

=|

0

,

69314718

−

0

,

56584436

0

,

69314718

|

x

100%

=

18

,

4%

C. Bentuk Umum Interpolasi Polinomial Newton  Bentuk umum polinomial orde n adalah

 Dengan menggunakan titik-titik data tersebut, persamaan berikut digunakan untuk mengevaluasi koefisien b0, b1, ….., bn

b₀=f(x0)

b1=f[x1, x0]=

f(x₁)−f(x₀) x₁−x₀

b₂=f_[x2, x1,x0]=

f_[x₂,x_1]−f_[x₁, x_0] x2−x0

b_n=f_[xn,xn−1,...,x1,x0]=

f_[x_n, x_n−1,...,x_1]−f_[x_n−1,x_n−2,..., x_0] x_n−x₀

 Definisi fungsi berkurung ([………..]) adalah pembagian beda hingga

 Persamaan di atas adalah berurutan, artinya pembagian beda hingga lebih tinggi terdiri dari pembagian beda hingga yang lebih rendah, seperti terlihat pada tabel berikut:

i xi f(xi) Pertama Kedua ketiga

0 1 2 3

x0 x1 x2 x3

f(x0) f(x1) f(x2) f(x3)

f[x1,x0] f[x2,x1] f[x3,x2]

f[x2,x1,x0] f[x3,x2,x1]

f[x3,x2,x1,x0]

Contoh

Dicari nilai ln 2 atau f(2) dengan metode interpolasi polinomial order tiga berdasarkan data

x0 = 1 f(x0) = 0

x1 = 4 f(x1) = 1,3862944

x2 = 6 f(x2) = 1,7917595

x3 = 5 f(x3) = 1,6094379

Penyelesaian

 Persamaan polinomial order tiga diperoleh dengan memasukkan nilai n = 3 ke dalam persamaan umum polinomial, sehingga:

f3(x)=b0+b1(x−x0)+b2(x−x0)(x−x1)+b3(x−x0)(x−x1))(x−x2)

 Pembagian beda hingga pertama dihitung dengan persamaan:

f[x1,x0]=

f(x1)−f(x0)

x1−x0 =

1,3862944−0

4−1 =0,46209813

f[x2,x1]=

f(x₂₎−f(x₁)

x2−x1 =

1,7917595−1,3862944

6−4 =0,2027326

f_[x3,x2]=

f(x3)−f(x2)

x3−x2 =

1,6094379−1,7917595

 Pembagian beda hingga kedua dihitung dengan persamaan:

f

[

x2,x1, x0

]

=

f

[

x2, x1

]

−f

[

x1, x0

]

x2−x0 =

0,2027326−0,46209813

6−1 =−0,051873116

f

[

x3,x2,x1

]

=

f

[

x3, x2

]

−f

[

x2, x1

]

x3−x1 =

0,1823216−0,2027326

5−4 =−0,020410950

 Pembagian beda hingga ketiga dihitung dengan persamaan:

f[x3,x2,x1, x0]=

f[x3,x2, x1]−f[x2, x1,x0] x₃−x₁ =

−0,02041095−(−0,05187312

5−1 =0,0078655415 _H

asil dari f[x1,x0] = b1, f[x2,x1,x0] = b2 f[x3,x2,x1,x0] = b3 dan f(x0) = b0 dan f(x0) = b0

b

1

=

0

_;

b

1

=

0

,

46209813

_;

b

2

=−

0

,

051873116

_;

b

3

=−

0

,

0078655415

x0 = 1 f(x0) = 0

x1 = 4 f(x1) = 1,3862944

x2 = 6 f(x2) = 1,7917595

x3 = 5 f(x3) = 1,6094379

 Maka persamaan polinomial order tiga diperoleh dengan memasukkan nilai n = 3 ke dalam persamaan umum polinomial

f3(x)=b0+b1(x−x0)+b2(x−x0)(x−x1)+b3(x−x0)(x−x1))(x−x2)

f3(x) = 0 + 0,46209813 (x-1) - 0,051873116 (x-1) (x-4) + 0,0078655415 (x-1) (x-4) (x-6)

 Dengan mensubstitusikan nilai x = 2, maka f3 (2) = 0,62876869

Nilai eksak dari ln 2 = 0,69314718

Besar kesalahan:

e

t

=|

0

,

69314718

−

0

,

62876869

0

,

69314718

|

x

100%

=

9,3%

D. Interpolasi Polinomial Lagrange

 Hampir sama dengan polinomial Newton tetapi tidak menggunakan bentuk pembagian beda hingga

 Interpolasi polinomial Lagrange dapat diturunkan dari persamaan Newton.  Bentuk polinomial Lagrange orde satu:

F1(x) = f(x0) + (x-x0) f[x1,x0] ……….. (D1)

Dengan

f

[

x

1

,x

0

]

=

f

(

x

1

)−

f

(

x

0

)

x

₁

−

x

₀

=

f

(

x

1

)

x

₁

−

x

₀

+

f

(

x

0

)

x

₀

−

x

_{1 ...………..(D2)}

f

₁

(

x

)=

f

(

x

₀

)+

x

x

−

x

0

1

−

x

0

f

(

x

1

)+

x

−

x

₀

x

₀

−

x

₁

f

(

x

0

)

Dengan mengelompokkan suku-suku di ruas kanan

f

₁

(

x

)=

x

x

−

x

1

0

−

x

1

f

(

x

0

)+

x

−

x

0

x

₁

−

x

0

f

(

x

1

)

Persamaan dikenal dengan interpolasi polinomial Lagrange order satu  Dengan prosedur di atas, untuk interpolasi order dua akan didapat

f

₂

(

x

)=

x

x

−

x

1

0

−

x

1

x

−

x

2

x

₀

−

x

₂

f

(

x

0

)+

x

−

x

0

x

₁

−

x

₀

x

−

x

2

x

₁

−

x

₂

f

(

x

1

)+

x

−

x

0

x

₂

−

x

₀

x

−

x

1

x

₂

−

x

₁

f

(

x

2

)

 Secara umum bentuk interpolasi polinomial Lagrange orde n adalah

¿

j

≠

1

¿¿¿

n

¿¿

dimana simbol п merupakan simbol perkalian (hasil kali dari)

 Dengan persamaan tersebut, dapat dihitung interpolasi lagrange orde yang lebih tinggi, misalnya untuk interpolasi lagrange orde 3, persamaan tersebut adalah :

f3(x)=

∑

i=1

3

Li(x)f(xi)

f3(x)=L0(x)f(x0)+L1(x)f(x1)+L2(x)f(x2)+L3(x)f(x3)

L

0

(

x

)=

x

−

x

1

x

0

−

x

1

x

−

x

2

x

0

−

x

2

x

−

x

3

x

0

−

x

3

L

1

(

x

)=

x

−

x

0

x

1

−

x

0

x

−

x

2

x

1

−

x

2

x

−

x

3

x

1

−

x

3

L

2

(

x

)=

x

−

x

0

x

2

−

x

0

x

−

x

1

x

2

−

x

1

x

−

x

3

x

2

−

x

3

L

3

(

x

)=

x

−

x

0

x

3

−

x

0

x

−

x

1

x

3

−

x

1

x

−

x

2

x

3

−

x

2

Sehingga bentuk interpolasi polinomial lagrange orde 3 adalah ;

f

₃

(

x

)=

x

x

−

x

1

0

−

x

1

x

−

x

2

x

0

−

x

2

x

−

x

3

x

0

−

x

3

f

(

x

0

)+

x

−

x

0

x

1

−

x

0

x

−

x

2

x

1

−

x

2

x

−

x

3

x

1

−

x

3

f

(

x

1

)

+

x

x

−

x

0

2

−

x

0

x

−

x

₁

x

2

−

x

1

x

−

x

₃

x

2

−

x

3

f

(

x

2

)+

x

−

x

₀

x

3

−

x

0

x

−

x

₁

x

3

−

x

1

x

−

x

₂

x

3

−

x

2

f

(

x

3

)

Dicari nilai ln 2 atau f(2) dengan menggunakan interpolasi lagrange order satu dan dua berdasar data

x0 = 1 f(x0) = 0

x1 = 4 f(x1) = 1,3862944

x2 = 6 f(x2) = 1,7917595

Penyelesaian

 Penyelesaian order satu, untuk x = 2

f₁(x)=x_x−x1

0−x1f(x0)+ x−x0

x1−x0f(x1)=

2−4

1−4(0)+

2−1

4−1(1,3862944)

f₁(x)=0,4620981

 Penyelesaian order dua, untuk x = 2

f₂(x)=x_x−x1 0−x1

x−x2

x0−x2f(x0)+

x−x0

x1−x0

x−x2

x1−x2 f(x1)+

x−x0

x2−x0

x−x1

x2−x1 f(x2)

f2(x)=2₁−₋4_{4 1}2−₋6₆(0)+2₄−₋1₁₄2−₋6₆(1,3862944)+₆2₋−1₁2₆−₋4₄(1,7917595)

f2(x)=0,56584437

D. Interpolasi Spline

Seperti telah dibahas dalam dua metode terdahulu, bahwa untuk n+1 data akan terdapat polinom interpolasi orde ke-n yang dapat dihasilkan untuk menginterpolasi nilai suatu fungsi di dalam selang titik data. Namun terkadang hal ini tidak memberikan kecocokan yang bagus (gambar). Pendekatan lainnya adalah dengan menerapkan polinom interpolasi yang lebih rendah pada sebagian titik data. Polinom demikian dikenal sebagai polinom interpolasi

Spline. Jika diantara dua titik data dibangun suatu polinom orde 3, maka kurva ini disebut

spline kubik (cubic spline).  Spline Linier

Hubungan paling sederhana yang dapat dibangun diantara dua titik data adalah hubungan linier. Spline orde satu untuk sekelompok titik data merupakan himpunan;

f(x)=f(x0)+m0(x−x0) x0≤x≤x1

f(x)=f(x1)+m1(x−x1) x1≤x≤x2 ...

f(x)=f(xn−1)+mn−1(x−xn−1) xn−1≤x≤xn

mi adalah kemiringan garis lurus yang menghubungkan titik-titik tersebut.

m_i=f(x_xi+1)−f(xi)

5

-2 4 3 2 1

-1

0 1 2

-1 -2

-3 3

5

-2 4 3 2 1

-1

0 1 2

-1 -2

-3 3

5

-2 4 3 2 1

-1

0 1 2

-1 -2

-3 3

5

-2 4 3 2 1

-1

0 1 2

-1 -2

-3 3

Perbandingan Polinom Interpolasi Newton / Lagrange vs Spline

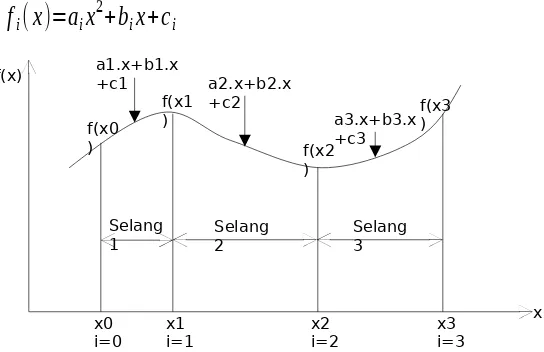
 Spline Kuadrat

Selang

2 Selang 3

Selang 1

x0

f(x1 )

f(x2 )

f(x3 ) f(x0

)

x1 x2 x3

i=0 i=1 i=2 i=3

x f(x) a1.x+b1.x_{+c1 a2.x+b2.x}

+c2

a3.x+b3.x +c3

f

_i

(

x

)=

a

_i

x

2

+

b

_i

x

+

c

_i

Gambar diatas menjelaskan proses penyusunan spline kuadrat, untuk n+1 (i=1,2,3,...) titik data maka akan terdapat n buah selang, dan akibatnya akan terdapat 3n buah konstanta, sehingga diperlukan 3n buah persamaan, yaitu:

1. Nilai-nilai fungsi harus sama pada titik-titik dalam

ai−1.x_i−12+bi−1.xi−1+ci−1=f(xi−1)

ai.x_i−12+bi.xi−1+ci=f(xi−1)

Untuk i = 2 hingga n, persamaan diatas memberikan n-1 kondisi, sehingga total ada 2n-2 kondisi.

2. Fungsi-fungsi pertama dan terakhir harus melalui titik ujung

a1.x₀2+b1.x0+c1=f(x0)

an.x_n2+bn.xn+cn=f(xn)

Persamaan diatas memberi 2 kondisi sehingga total ada 2n kondisi, 3. Turunan pertama pada titik-titik dalam harus sama

2

a

i−1

.

x

i−1

+

b

i−1

=

2

a

i

.

x

i−1

+

b

i

Untuk i = 2 hingga n, persamaan diatas memberikan n-1 kondisi, sehingga total ada 3n-1 kondisi.

4. Asumsikan turunan kedua adalah nol pada titik pertama, sehingga a1=0

Dengan demikian maka lengkaplah 3n buah kondisi yang diperlukan untuk menghitung 3n buah konstanta.

 Spline Kubik

Jika di antara dua titik dibangun suatu polinom orde tiga, maka hal ini disebut sebagai

spline kubik. Polinom orde ketiga itu dalam bentuk:

f

_i

(

x

)=

a

_i

.

x

3

+

b

_i

.

x

2

+

c

_i

.

x

+

d

_i

Jika terdapat n+1 data (i = 0, 1, 2, 3, ..., n) maka akan terdapat n buah selang dan terdapat 4n buah konstanta. Untuk itu diperlukan 4n buah kondisi, yang diperoleh dari:

2. Fungsi pertama dan terakhir melalui titik ujung (2 kondisi). 3. Turunan pertama pada simpul dalam harus sama (n-1 kondisi). 4. Turunan kedua pada simpul dalam harus sama (n-1 kondisi). 5. Turunan kedua pada titik ujung harus = nol (2 kondisi).

Persamaan spline kubik tiap selang titik data dapat diturunkan sebagai:

f_i(x)=f

''

(xi−1)

6(xi−xi−1)

.(xi−x)3+

f''(xi−1)

6(xi−xi−1)

.(xi−x)3+

[

f(xi−1)

xi−xi−1−

f''(xi−1)(xi−xi−1)

6

]

(xi−x)+

+

[

f_x(xi)

i−xi−1−

f''(xi)(xi−xi−1)

6

]

(xi−xi₋₁)

Pers amaan diatas mengandung turunan kedua di ujung tiap selang titik data yang tak diketahui, namun nilainya dapat dihitung dari persamaan:

(x_i−x_i

−1).f

''

(x_i−1)+2(xi+1−xi−1).f''(xi)+(xi+1−xi).f''(xi+1)

¿6

(xi+1−xi)

.

[

f(x_i+1)−f(x_i)

]

+6

(xi−xi−1)

.

[

f(x_i−1)−f(x_i)

]

Contoh:

Gunakan spline orde satu, dua dan tiga untuk menginterpolasi nilai fungsi pada x = 5 jika diketahui data-data:

x 3,0 4,5 7,0 9,0

f(x) 2,5 1,0 2,5 0,5

Spline orde satu:

f

₁

(

x

)=

2,5

+

1

4,5

−

2,5

−

3 .

(

x

−

3

)=−

x

+

5,5

f

₂

(

x

)=

1,0

+

7

2,5

−

−

4,5 .

1,0

(

x

−

4,5

)=

0,6.

x

−

1,7

f

3

(

x

)=

2,5

+

9

0,5

−

−

7

2,5

.

(

x

−

7

)=−

x

+

9,5

(

3,0≤

x

≤4,5

)

(

4,5

≤

x

≤7,0

)

(

7,0≤

x

≤9,0

)

sehingga f2(5)=0,6.(5)−1,7=1,3

Spline orde dua:

1. Nilai-nilai fungsi harus sama pada titik-titik dalam

ai−1.x_i−12+bi−1.xi−1+ci−1=f(xi−1) ai.x_i−12+bi.xi−1+ci=f(xi−1)

Untuk i = 2 hingga n, persamaan diatas memberikan n-1 kondisi, sehingga total ada 2n-2 kondisi.

20

,

25.

a

1

+

4,5.

b

1

+

c

1

=

1,0

20

,

25.

a

₂

+

4,5.

b

₂

+

c

₂

=

1,0

49.

a

2

+

7.

b

2

+

c

2

=

2,5

49.

a

₃

+

7.

b

₃

+

c

₃

=

2,5

2. Fungsi-fungsi pertama dan terakhir harus melalui titik ujung

a1.x₀2+b1.x0+c1=f(x0)

an.x_n2+bn.xn+cn=f(xn)

Persamaan diatas memberi 2 kondisi sehingga total ada 2n kondisi, Dari persamaan diatas diperoleh a.

9.

a

1

+

3.

b

1

+

c

1

=

2,5

81.

a

₃

+

9.

b

₃

+

c

₃

=

0,5

3. Turunan pertama pada titik-titik dalam harus sama

2

a

i−1

.

x

i−1

+

b

i−1

=

2

a

i

.

x

i−1

+

b

i

Untuk i = 2 hingga n, persamaan diatas memberikan n-1 kondisi, sehingga total ada 3n-1 kondisi.

Dari persamaan diatas memberikan:

9.

a

1

+

b

1

=

9.

a

2

+

b

2

14.

a

₂

+

b

₂

=

14.

a

₃

+

b

₃

4. Asumsikan turunan kedua adalah nol pada titik pertama, sehingga a1=0

Ditentukan bahwa a1=0. Persamaan-persamaan di atas kemudian disusun dalam bentuk matriks.

[

4,5 1,0

0

0 20

0

,

25 4,5 1,0

0

0

0

0

0

0

0

0

0

0 49

,

00 7,0 1,0

0

0

0

0

0

0

0

0 49

,

00

7

,

00 1,0

3,0 1,0

0

0

0

0

0

0

0

0

0

0

0 81

,

00

9

,

00 1,0

1,0 0

−

9,0

−

1,0 0

0

0

0

0

0 14

,

00 1,0

0

−

14

,

00

−

1

,

00 0

]

{

b1

c₁ a2

b2

c2

a3

b3

c3

}

=

{

1,0

1,0

2,5

2,5

2,5

0,5

0

0

}

Dengan metode-metode yang telah dibahas dalam penyelesaian Sistem Persamaan Linier (SPL), maka diperoleh:

a

₁

=

0

a

₂

=

0

,

64

a

₃

=−

1,6

b

₁

=−

1

b

₂

=−

6

,

76

b

₃

=

24

,

6

c

₁

=

5,5

c

₂

=

18

,

46

c

₃

=−

91

,

3

f1(x)=−x+5,5

f₂(x)=0,64.x2+6,76.x−18,46

f₃(x)=−1,6.x2+24,6.x−91,3

(3,0≤x≤4,5) (4,5≤x≤7,0) (7,0≤x≤9,0)

Dan nilai fungsi

f

2

(

5

)=

0

,

64.

(

5

)

2

+

6

,

76.

(

5

)+

18

,

46

=

0

,

66

Spline Kubik

f_i(x)=f

''

(xi−1)

6(xi−xi−1)

.(xi−x)3+

f''(xi−1)

6(xi−xi−1)

.(xi−x)3+

[

f(xi−1)

xi−xi−1−

f''(xi−1)(xi−xi−1)

6

]

(xi−x)+

+

[

f_x(xi)

i−xi−1− f''

(xi)(xi−xi−1)

6

]

(xi−xi₋₁)

Dari persamaan diatas dicari turunan kedua pada simpul-simpul dalam.

 Untuk simpul dalam pertama:

x

₀

=

3

x

₁

=

4,5

x

₂

=

7

f(x0)=2,5

f(x₁)=1

f(x2)=2,5

Substitusikanlah nilai-nilai ini ke persamaan berikut ini:

(xi−xi₋₁).f''(xi−1)+2(xi+1−xi−1).f

''

(xi)+(xi+1−xi).f

''

(xi+1)

¿6

(x_i+1−xi)

.

[

f(x_i+1)−f(x_i)

]

+6

(x_i−x_i−1)

.

[

f(x_i−1)−f(x_i)

]

Diperoleh:

(4,5−3).f''(3)+2(7−3).f''(4,5)+(7−4,5).f '(7)

=6

(7−4,5).(2,5−1)+ 6

(4,5−3).(2,5−1)

Dengan mengingat bahwa f''(3)=0 _{, maka diperoleh:}

8.f''(4,5)+2,5.f''(7)=9,6 _(i)

 Untuk simpul dalam kedua:

x

₁

=

4,5

x

₂

=

7

x

₃

=

9

f(x1)=1

f(x₂)=2,5

f(x3)=0,5

Substitusikanlah nilai-nilai ini ke persamaan berikut ini:

(xi−xi₋₁).f''(xi−1)+2(xi+1−xi−1).f''(xi)+(xi+1−xi).f''(xi+1)

¿6

(xi+1−xi)

.

[

f(x_i+1)−f(x_i)

]

+6

(xi−xi−1)

5 4 3 2 1

f(x)

0 1 2

Spline linier

4 5 _x

5 4 3 2 1

f(x)

0 1 2

Spline kuadrat

4 5 _x

Kubik Spline

Diperoleh:

(7−4,5).f''(4,5)+2(9−4,5).f''(7)+(9−7).f '(9)

=6

(9−7).(0,5−2,5)+ 6

(7−4,5).(1−2,5)

Dengan f''(9)=0

2,5.f''(4,5)+9.f''(7)=−9,6 _(ii)

Dari (i) dan (ii) diperoleh:

f''(4,5)=1,67909 _dan f''(7)=−1,53308

Nilai-nilai yang diperoleh kemudian disubstitusikan ke persamaan berikut untuk mendapatkan Spline Kubik bagi tiap selang:

fi(x)=

f''(xi−1)

6(xi−xi−1)

.(xi−x)3+

f''(xi−1)

6(xi−xi−1)

.(xi−x)3+

[

f(xi−1)

xi−xi−1−

f''(xi−1)(xi−xi−1)

6

]

(xi−x)+

+

[

f_x(xi)

i−xi−1− f''

(xi)(xi−xi−1)

6

]

(xi−xi₋₁)

f₁(x)=0,186566(x−3)3+1,666667(4,5−x)+0,246894(x−3)

f₂(x)=0,111939(7−x)3−0,102205(x−4,5)3−0.299621(7−x)+1,638783(x−4,5)

f₃(x)=−0,127757(9−x)3+1,761027(9−x)+0,25(x−7)

(3,0≤x≤4,5) (4,5≤x≤7,0) (7,0≤x≤9,0)

Dengan demikian untuk nilai fungsi x = 5 (pada selang kedua): f2(5)=0,111939(7−5)3+0,102205(5−4,5)−0,299621(7−5)+1,638783(5−4,5)