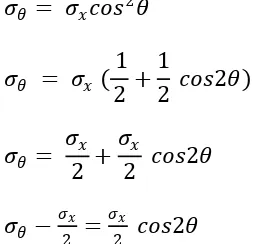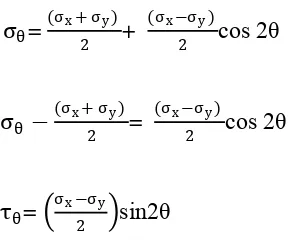BAB II
TINJAUAN PUSTAKA 2.1 Sistem Perpipaan
Pipa digunakan untuk mengalirkan fluida (zat cair atau gas) dari satu atau
beberapa titik ke satu titik atau beberapa titik lainnya. Sistem perpipaan (piping
sistem) terdiri dari gabungan pipa-pipa yang memiliki panjang total relatif pendek
dan digunakan untuk mengalirkan fluida dari suatu peralatan ke peralatan lainnya
yang beroperasi pada suatu plant. Sistem perpipaan dilengkapi dengan
komponen-komponen seperti katup, flens, belokan, percabangan, nozzle, reducer,
tumpuan, isolasi, dan lain-lain.
Dalam dunia industri, biasa dikenal beberapa istilah mengenai sistem
perpipaan seperti piping dan pipeline. Piping adalah sistem perpipaan di suatu
plant, sebagai fasilitas untuk mengantarkan fluida (cairan atau gas) antara satu
komponen ke komponen lainnya untuk melewati proses-proses tertentu. Piping ini
tidak akan keluar dari satu wilayah plant.Sedangkan Pipeline adalah sistem
perpipaan untuk mengantarkan fluida antara satu plant ke plant lainnya yang
biasanya melewati beberapa daerah.Ukuran panjang pipa biasanya memiliki
panjang lebih dari 1 km bergantung jarak antar plant.
Sistem perpipaan dapat ditemukan hampir pada semua jenis industri, dari
sistem pipa tunggal yang sederhana sampai sistem pipa bercabang yang sangat
kompleks. Contoh sistem perpipaan adalah, sistem distribusi air minum pada
tangki penyimpan, sistem distribusi udara pendingin pada suatu gedung, sistem
distribusi uap pada proses pengeringan dan lain sebagainya.
Sistem perpipaan meliputi semua komponen dari lokasi awal sampai
dengan lokasi tujuan antara lain, saringan (strainer), katup atau kran, sambungan,
nosel dan sebagainya. Untuk sistem perpipaan yang fluidanya liquid, umumnya
dari lokasi awal fluida, dipasang saringan untuk menyaring kotoran agar tidak
menyumbat aliran fuida. Saringan dilengkapi dengan katup searah ( foot valve)
yang fungsinya mencegah aliran kembali ke lokasi awal atau tandon. Sedangkan
sambungan dapat berupa sambungan penampang tetap, sambungan penampang
berubah, belokan (elbow) atau sambungan bentuk T (Tee).
2.2 Teori Tegangan
Pengetahuan mengenai sifat-sifat mekanik material sangat penting.Melalui
pengetahuan ini dapat diperkirakan tegangan-tegangan yang terjadi pada sistem
perpipaan.Dalam kode ditetapkan aturan-aturan agar pada sistem perpipaan tidak
terjadi tegangan yang berlebih sehingga dapat terhindar dari kegagalan.Secara
umum teori tegangan pada sistem perpipaan merupakan pengembangan dari teori
tegangan dalam mekanika.Oleh sebab itu, dapat digunakan dalam perhitungan dan
analisis tegangan pada sistem perpipaan.
2.2.1. Tegangan Satu Arah (Uniaxial)
Tegangan uniaxial adalah tegangan yang bekerja pada suatu benda dimana
benda merupakan tegangan tarik untuk keadaan normal ( tanpa terbentuk sudut ).
Untuk tegangan yang terdapat pada benda dengan sudut tertentu,maka akan
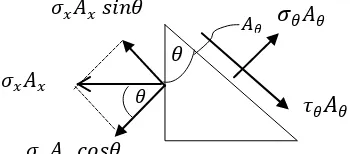
dihasilkan tagangan geser dan tegangan tarik dalam arah 𝜃𝜃.Keadaan tegangan ini pada aplikasi suatu batang lurus berpenampang A dengan gaya dan arah yang
ditunjukkan seperti gambar 2.1. Dianggap bahwa tegangan terbagi rata diseluruh
penampang yang tegak lurus dengan luasan pada benda, dimana gaya yang
bekerja terdapat pada koordinat sumbu x.
Gambar 2.1 Distribusi Tegangan Uniaxial
Akibat dari gaya-gaya yang bekerja pada benda, maka akan terbentuk
sudut potong pada benda sebesar 𝜃𝜃. Dimana dengan sudut tersebut akan diproyeksikan nilai tegangan – tegangan yang terjadi pada benda tersebut seperti
tegangan geser dan tarik dalam arah 𝜃𝜃. Kesetimbangan gaya dan tegangan dapat dilihat pada gambar 2.2.
Gambar 2.2 Distribusi Tegangan Uniaxial
Persamaan untuk distribusi tegangan pada gambar 2.2 dapat dilihat pada
persamaan dibawah ini.
A
S
I
ANALIS A DATA
F STA
𝜎𝜎=𝐹𝐹
dimana:
σ
= tegangan (N/𝑚𝑚2)P = gaya (N)
A = luas penampang (𝑚𝑚2)
Gambar 2.3 distribusi tegangan pada penampang sederhana
Gambar 2.4 Distribusi Tegangan Uniaxial terhadap sudut 𝜃𝜃
Pada gambar 2.3 terlihat beberapa tegangan yang terdapat pada benda
yang membentuk sudut 𝜃𝜃. Dengan menuliskan bentuk persamaan dari gambar tersebut kedalam kesetimbangan gaya maka akan diperoleh nilai tegangan tarik
dan tegangan geser.
Untuk persamaan tegangan tarik pada gambar 2.3 diperoleh dengan
menjumlahkan tegangan pada garis sumbu yang sama, dimana tegangan terhadap
sudut 𝜃𝜃 bekerja pada arah yang samadengan tegangan 𝜎𝜎𝑥𝑥𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃, dengan menggunakan kesetimbangan gaya akan diperoleh persamaan 2.1.
𝜃𝜃
P P
𝜃𝜃
𝜃𝜃
𝐴𝐴𝜃𝜃
𝜎𝜎𝑥𝑥𝐴𝐴𝑥𝑥
𝜎𝜎𝜃𝜃𝐴𝐴𝜃𝜃
𝜏𝜏𝜃𝜃𝐴𝐴𝜃𝜃
𝜎𝜎𝑥𝑥𝐴𝐴𝑥𝑥𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃
𝜎𝜎𝜃𝜃 𝐴𝐴𝜃𝜃 -𝜎𝜎𝑥𝑥𝐴𝐴𝑥𝑥 𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃 = 0 (2.1)
Untuk menentukan nilai 𝐴𝐴𝑥𝑥dapat diubah ke dalam bentuk A𝜃𝜃 dengan menggunakan persamaan 2.2 :
(𝐴𝐴 − 𝐵𝐵) =𝐴𝐴𝑥𝑥 = 𝐴𝐴𝜃𝜃 𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃
(𝐴𝐴 − 𝐶𝐶) =𝐴𝐴𝑦𝑦 = 𝐴𝐴𝜃𝜃 𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃 (2.2)
Dengan demikian nilai 𝐴𝐴𝑥𝑥 pada persamaan 2.2, dapat disubstitusikan kedalam persamaan 2.1 sehingga akan diperoleh persamaan tegangan tarik
𝜎𝜎𝜃𝜃yang bekerja terhadap sumbu 𝜃𝜃,dapat dilihat pada persamaan 2.3:
𝜎𝜎𝜃𝜃 𝐴𝐴𝜃𝜃-𝜎𝜎𝑥𝑥𝐴𝐴𝑥𝑥 𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃= 0
𝜎𝜎𝜃𝜃 𝐴𝐴𝜃𝜃 = 𝜎𝜎𝑥𝑥𝐴𝐴𝑥𝑥 𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃
𝜎𝜎𝜃𝜃 𝐴𝐴𝜃𝜃 = 𝜎𝜎𝑥𝑥(𝐴𝐴𝜃𝜃 𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃)𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃
𝜎𝜎𝜃𝜃 = 𝜎𝜎𝑥𝑥𝑐𝑐𝑐𝑐𝑐𝑐2𝜃𝜃 (2.3)
Pada saat kondisi 𝜃𝜃 = 0 , maka persamaan 2.3 akan berubah menjadi persamaan 2.4 :
𝜎𝜎𝜃𝜃 = 𝜎𝜎𝑥𝑥𝑐𝑐𝑐𝑐𝑐𝑐2𝜃𝜃
𝜎𝜎𝜃𝜃 = 𝜎𝜎𝑥𝑥(12)
𝜎𝜎𝜃𝜃 = 𝜎𝜎𝑥𝑥 (2.4)
𝐴𝐴𝑦𝑦
𝜃𝜃 𝐴𝐴𝜃𝜃
𝐴𝐴𝑥𝑥
𝐴𝐴 𝐵𝐵
Untuk persamaan tegangan geser pada gambar 2.3 diperoleh dengan
menjumlahkan semua tegangan pada garis sumbu yang sama, dimana tegangan
geser terhadap sudut 𝜃𝜃 bekerja pada arah yang sama dengan tegangan 𝜎𝜎𝑥𝑥𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃, dengan menggunakan kesetimbangan gaya akan diperoleh persamaan 2.5 :
𝜏𝜏𝜃𝜃𝐴𝐴𝜃𝜃 − 𝜎𝜎𝑥𝑥𝐴𝐴𝑥𝑥 𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃= 0
𝜏𝜏𝜃𝜃𝐴𝐴𝜃𝜃 = 𝜎𝜎𝑥𝑥𝐴𝐴𝑥𝑥 𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃
𝜏𝜏𝜃𝜃𝐴𝐴𝜃𝜃 = 𝜎𝜎𝑥𝑥𝐴𝐴𝜃𝜃 𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃
𝜏𝜏𝜃𝜃 =𝜎𝜎𝑥𝑥𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃 (2.5)
Melalui persamaan trigonometri diketahui bahwa :
𝑐𝑐𝑠𝑠𝑠𝑠2𝜃𝜃 = 2𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃
𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃= 1
2 𝑐𝑐𝑠𝑠𝑠𝑠2𝜃𝜃
Dengan merubah persamaan trigonometri diatas kedalam persamaan
trigonometri pada persamaan tegangan geser maka akan dihasilkan persamaan
akhir untuk tegangan geser, yaitu pada persamaan 2.6 :
𝜏𝜏𝜃𝜃 = 𝜎𝜎𝑥𝑥𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃
𝜏𝜏𝜃𝜃 = 𝜎𝜎𝑥𝑥12𝑐𝑐𝑠𝑠𝑠𝑠2𝜃𝜃 (2.6)
Pada saat kondisi 𝜃𝜃 = 0 dan 𝜃𝜃 = 45𝑐𝑐 , akan diperoleh tegangan geser:
𝜃𝜃 = 0 𝜃𝜃 = 45𝑐𝑐
𝜏𝜏𝜃𝜃 = 𝜎𝜎𝑥𝑥12𝑐𝑐𝑠𝑠𝑠𝑠2(0) 𝜏𝜏𝜃𝜃 = 𝜎𝜎𝑥𝑥12𝑐𝑐𝑠𝑠𝑠𝑠2(45°)
Tegangan tarik maksimum adalah nilai tegangan pada batas tertinggi yang
dapat diterima oleh benda yang mengalami gaya tarik pada luasan .Tegangan
tarik maksimum merupakan batas pada benda untuk berubah bentuk ketika
diberikan pembebanan secara terus menerus sehingga melewati batas nilai
tegangan maksimum.Nilai dari tegangan ini dapat dihitung melalui perhitungan
secara matimatik pada lingkaran mohr pada gambar 2.4.
Syarat untuk memperoleh tegangan tarik maksimum adalah :
Syarat 𝜕𝜕𝜎𝜎𝜃𝜃
𝜕𝜕𝜃𝜃 = 0
𝑑𝑑(𝜎𝜎2𝑥𝑥+ 𝜎𝜎2𝑥𝑥 𝑐𝑐𝑐𝑐𝑐𝑐2𝜃𝜃)
𝑑𝑑𝜃𝜃 = 0
0 + −2 �𝜎𝜎𝑥𝑥
2 𝑐𝑐𝑠𝑠𝑠𝑠2𝜃𝜃� = 0 −2�𝜎𝜎𝑥𝑥
2 𝑐𝑐𝑠𝑠𝑠𝑠2𝜃𝜃� = 0 𝑐𝑐𝑠𝑠𝑠𝑠2𝜃𝜃 = 0
−𝜎𝜎𝑥𝑥 = 0
2𝜃𝜃= 𝑐𝑐𝑠𝑠𝑠𝑠−10
𝜃𝜃 = 1 2 (𝑐𝑐𝑠𝑠𝑠𝑠
−10)
𝜃𝜃 = 0, 90, 180
𝜃𝜃 = 0,𝜋𝜋 2,𝜋𝜋
𝜎𝜎𝜃𝜃 = 𝜎𝜎2𝑥𝑥 + 𝜎𝜎2𝑥𝑥 𝑐𝑐𝑐𝑐𝑐𝑐2𝜃𝜃
𝜎𝜎𝜃𝜃 = 𝜎𝜎2𝑥𝑥+ 𝜎𝜎2𝑥𝑥 (1) = 𝜎𝜎𝑥𝑥
𝜎𝜎𝜃𝜃𝑚𝑚𝜃𝜃𝑥𝑥 = 𝜎𝜎𝑥𝑥 ( 2.7)
Tegangan geser maksimum adalah tegangan yang paling besar diterima
benda ketika diberikan gaya F pada arah 𝜃𝜃. Dengan demikian tegangan geser maksimum merupakan batas dari tegangan yang dapat diterima oleh benda yang
jika diberikan gaya yang lebih besar maka akan terjadi perubahan bentuk pada
benda.
Syarat untuk terjadinya tegangan geser maksimum adalah :
𝜕𝜕𝜏𝜏𝜃𝜃
Sehingga dengan memasukkan besaran sudut yang menghasilkan tegangan
geser maksimum akan diperoleh nilai maksimum dari tegangan geser yaitu pada
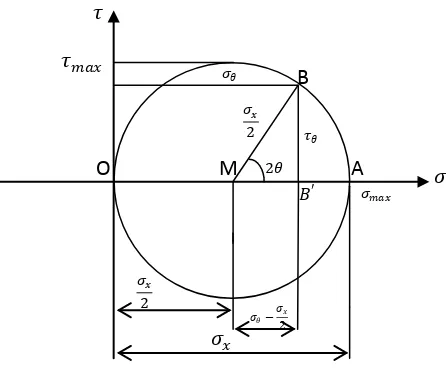
2.2.1.1 Lingkaran Mohruntuk Tegangan Uniaxial
Persamaan lingkaran mohr untuk tegangan uniaxial diperoleh dengan
menjumlahkan kuadrat dari tiap –tiap tegangan geser dan tegangan tarik pada arah
𝜃𝜃 yang merupakan bentuk dari persamaan dasar lingkaran. Persamaan yang
dibentuk akan menjadi persamaan lingkaran mohr untuk tegangan uniaxial,
merupakan bentuk perwakilan dari besaran besaran nilai tegangan kedalam bentuk
gambar. Penyederhanaan persamaan untuk lingkaran mohr dapat dilakukan
dengan menggunakan persamaan trigonometri dalam aturan kosinus sebagai
berikut.
cos 2𝜃𝜃 = 𝑐𝑐𝑐𝑐𝑐𝑐2𝜃𝜃 − 𝑐𝑐𝑠𝑠𝑠𝑠2𝜃𝜃
Cos 2𝜃𝜃 = 𝑐𝑐𝑐𝑐𝑐𝑐2𝜃𝜃 −(1− 𝑐𝑐𝑐𝑐𝑐𝑐2𝜃𝜃) cos 2𝜃𝜃 = 2𝑐𝑐𝑐𝑐𝑐𝑐2𝜃𝜃 − 1
2cos 2𝜃𝜃 = 1 +𝑐𝑐𝑐𝑐𝑐𝑐2𝜃𝜃
cos2𝜃𝜃= 1 2 +
1
2 𝑐𝑐𝑐𝑐𝑐𝑐2𝜃𝜃
Persamaan untuk tegangan tarik pada arah 𝜃𝜃 dengan menggunakan penyederhanaan aturan kosinus.
𝜎𝜎𝜃𝜃 = 𝜎𝜎𝑥𝑥𝑐𝑐𝑐𝑐𝑐𝑐2𝜃𝜃
𝜎𝜎𝜃𝜃 = 𝜎𝜎𝑥𝑥 (
1 2 +
1
2 𝑐𝑐𝑐𝑐𝑐𝑐2𝜃𝜃) 𝜎𝜎𝜃𝜃 = 𝜎𝜎2𝑥𝑥 +𝜎𝜎2𝑥𝑥 𝑐𝑐𝑐𝑐𝑐𝑐2𝜃𝜃
Persamaan untuk tegangan geser pada permukaan 𝜃𝜃 yaitu :
Pada penjumlahan eliminasi yang sama sehingga akan menghasilkan
persamaan lingkaran mohr sebagai berikut:
(𝜎𝜎𝜃𝜃 −𝜎𝜎𝑥𝑥
Dengan demikian persamaan lingkaran mohr diperoleh pada persamaan 2.12:
(𝜎𝜎𝜃𝜃 −𝜎𝜎𝑥𝑥 2)
2 +𝜏𝜏
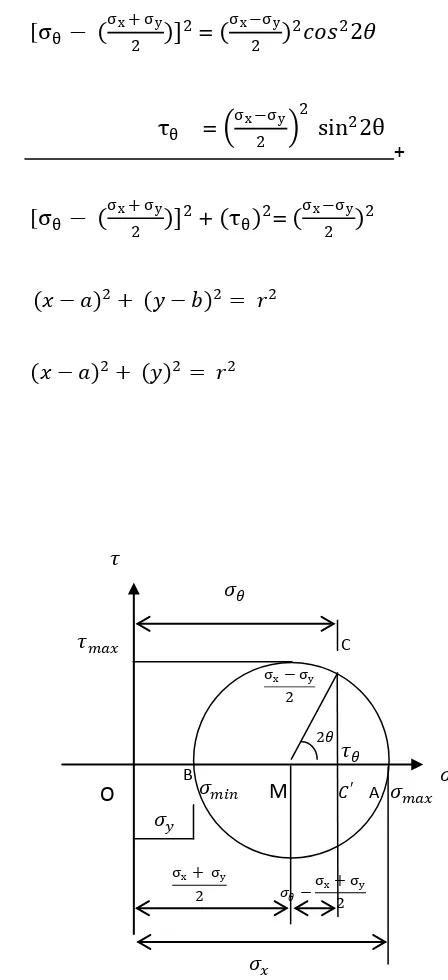
Gambar 2.5 Lingkaran Mohr Untuk Tegangan Uniaxial
Gambar 2.5 pada lingkaran mohr merupakan bentuk perhitungan tegangan
secarah menyeluruh, dimana dengan gambar tersebut akan dapat lebih mudah
untuk menentukan tegangan maksimum dan minimum yang dialami oleh benda
yang dapat dilihat melalui ilustrasi gambar. Pada lingkaran mohr untuk tegangan
uniaxial dapat dilihat bahwa nilai dari tegangan minimum adalah nol untuk
tegangan tarik.
A O
𝜏𝜏
𝜎𝜎
B
𝐵𝐵′
M
𝜎𝜎𝑥𝑥
2
𝜎𝜎𝜃𝜃−𝜎𝜎2𝑥𝑥
𝜎𝜎𝑥𝑥
2
2𝜃𝜃
𝜏𝜏𝜃𝜃
𝜎𝜎𝑚𝑚𝜃𝜃𝑥𝑥
𝜎𝜎𝜃𝜃
𝜎𝜎𝑥𝑥
x y
n
𝜃𝜃 𝜃𝜃
2.2.2. Tegangan Dua Arah (Biaxial)
Tegangan biaxial adalah tegangan yang bekerja pada suatu benda dimana
gaya yang berkerja terjadidalam dua arah. Tegangan dalam dua arah meliputi
tegangan terhadap sumbu x dan terhadap sumbu y.Tegangan yang dialami oleh
benda merupakan tegangan tarik untuk keadaan normal ( tanpa terbentuk sudut ).
Untuk tegangan yang terdapat pada benda dengan sudut tertentu,maka akan
dihasilkan tagangan geser dan tegangan tarik dalam arah 𝜃𝜃. sehingga dengan menggunakan kesetimbangan energi akan diperoleh persamaan persamaan untuk
tegangan geser dan tegangan tarik. Pada tegangan biaxial terdapat tiga tegangan
yang bekerja pada tiap garis yang sama yaitu tegangan pada sudut 𝜃𝜃, tegangan pada luasan sumbu y dan tegangan pada sumbu x yang diproyeksikan terhadap
satu garis yang sama.
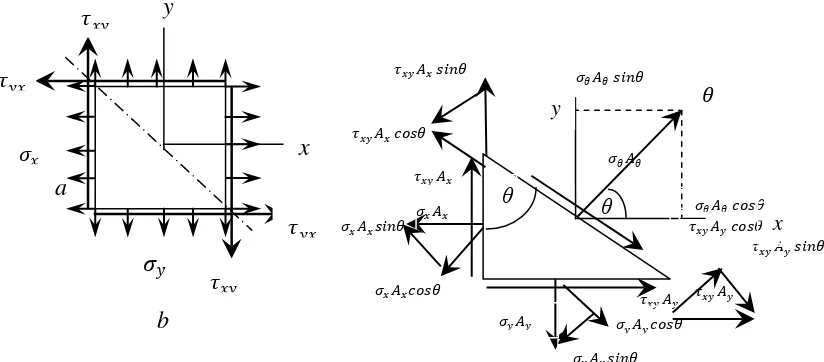
Gambar.2.6 tegangan biaksial
Dari gambar 2.6 akan diperoleh persamaan untuk tegangan tarik dan geser
dengan menggunakan kesetimbangan gaya pada satu sumbu garis yang
sama.Untuk persamaan tegangan tarik pada gambar 2.5 diperoleh dengan
menjumlahkan tegangan pada garis sumbu yang sama, dimana tegangan terhadap
sudut 𝜃𝜃 bekerja pada arah yang samadengan tegangan 𝜎𝜎𝑥𝑥𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃 dan 𝜎𝜎𝑥𝑥𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃 pada dua luasan yang berbeda dengan menggunakan kesetimbangan gaya akan
diperoleh persamaan 2.13.
𝜎𝜎𝜃𝜃𝐴𝐴𝜃𝜃−𝜎𝜎𝑥𝑥𝐴𝐴𝑥𝑥cos θ −𝜎𝜎𝑦𝑦𝐴𝐴𝑦𝑦 sin θ =0
𝜎𝜎𝜃𝜃𝐴𝐴𝜃𝜃 = 𝜎𝜎𝑥𝑥𝐴𝐴𝑥𝑥cos θ + 𝜎𝜎𝑦𝑦𝐴𝐴𝑦𝑦 sin θ
𝜎𝜎𝜃𝜃𝐴𝐴𝜃𝜃 = 𝜎𝜎𝑥𝑥(𝐴𝐴𝜃𝜃 cos θ) cos θ + 𝜎𝜎𝑦𝑦(𝐴𝐴𝜃𝜃 sin θ) sin θ
𝜎𝜎𝜃𝜃= 𝜎𝜎𝑥𝑥 cos2θ + 𝜎𝜎𝑦𝑦 sin2
𝜎𝜎𝜃𝜃= 1
2 (𝜎𝜎𝑥𝑥 + 𝜎𝜎𝑦𝑦) + 1
2 (𝜎𝜎𝑥𝑥− 𝜎𝜎𝑦𝑦) cos 2θ ( 2.13 )
θ
Jadi persamaan untuk menentukan tegangan maksimal pada tegangan dua arah
adalah :
𝝈𝝈𝜽𝜽= 𝟏𝟏𝟐𝟐 (𝝈𝝈𝒙𝒙 + 𝝈𝝈𝒚𝒚) + 𝟏𝟏𝟐𝟐 (𝝈𝝈𝒙𝒙− 𝝈𝝈𝒚𝒚) cos 2θ (2.14)
Untuk persamaan tegangan geser pada gambar 2.5 diperoleh dengan
menjumlahkan semua tegangan pada garis sumbu yang sama, dimana tegangan
geser terhadap sudut 𝜃𝜃 bekerja pada arah yang sama dengan tegangan 𝜎𝜎𝑥𝑥𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃 dan 𝜎𝜎𝑦𝑦 𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃pada dua gaya yang bekerja pada permukaan 𝜃𝜃 dengan menggunakan
𝜎𝜎𝑥𝑥𝐴𝐴𝑥𝑥 𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃 − 𝜏𝜏𝜃𝜃𝐴𝐴𝜃𝜃 − 𝜎𝜎𝑦𝑦𝐴𝐴𝑦𝑦 𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃 = 0
𝜏𝜏𝜃𝜃𝐴𝐴𝜃𝜃 =𝜎𝜎𝑥𝑥𝐴𝐴𝑥𝑥 𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃 − 𝜎𝜎𝑦𝑦𝐴𝐴𝑦𝑦 𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃
𝜏𝜏𝜃𝜃𝐴𝐴𝜃𝜃 =𝜎𝜎𝑥𝑥(𝐴𝐴𝜃𝜃 𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃)𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃 − 𝜎𝜎𝑦𝑦(𝐴𝐴𝜃𝜃 𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃) 𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃
𝜏𝜏𝜃𝜃 = 𝜎𝜎𝑥𝑥 𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃 − 𝜎𝜎𝑦𝑦𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃
𝝉𝝉𝜽𝜽= 𝟏𝟏𝟐𝟐 (𝝈𝝈𝒙𝒙− 𝝈𝝈𝒚𝒚)sin2θ (2.15)
Tegangan tarik maksimum adalah nilai tegangan pada batas tertinggi yang
dapat diterima oleh benda yang mengalami gaya tarik pada luasan .Tegangan
tarik maksimum merupakan batas pada benda untuk berubah bentuk ketika
diberikan pembebanan secara terus menerus sehingga melewati batas nilai
tegangan maksimum.Nilai dari tegangan ini dapat dihitung melalui perhitungan
secara matimatik pada lingkaran mohr pada gambar 2.6 diatas.
Syarat untuk mendapatkan tegangan tarik maksimum adalah :
𝜕𝜕𝜎𝜎𝜃𝜃
𝜕𝜕𝜃𝜃 = 0
𝜕𝜕[�σx + 2 σy�+ �σx− σy2 � cos2θ
𝜕𝜕𝜃𝜃 = 0
0 + −2�σx− σy
2 � sin2θ= 0 − (σx − σy) sin2θ= 0
sin2θ= 0
Tegangan tarik maksimum diperoleh dengan mensubsitusikan nilai sudut
yang mengakibatkan terbentuknya tegangan tarik maksimum untuk tegangan
biaxial.
Tegangan geser maksimum adalah tegangan yang paling besar diterima benda
ketika diberikan gaya F pada arah 𝜃𝜃. Dengan demikian tegangan geser maksimum merupakan batas dari tegangan yang dapat diterima oleh benda yang jika
diberikan gaya yang lebih besar maka akan terjadi perubahan bentuk pada benda.
Syarat untuk terjadinya tegangan geser maksimum adalah :
Dengan demikian akan diperoleh nilai dari tegangan geser maksimum dengan
memasukkan besaran dari nilai sudut yang menghasilkan tegangan maksimum.
Sehingga akan diperoleh tegangan geser maksimum untuk biaxial ditunjukkan
pada persamaan 2.17 :
τθ= �σx−σ2 y�sin2 (𝜋𝜋4)
τθ= �σx−σ2 y�sin 2 (45o)
τmax= �σx−σy
2 � ( 2.17)
2.2.2.1Lingkaran Mohr untuk Tegangan Biaxial
Persamaan lingkaran mohr untuk tegangan biaxial diperoleh dengan
menjumlahkan kuadrat dari tiap –tiap tegangan geser dan tegangan tarik pada arah
𝜃𝜃 yang merupakan bentuk dari persamaan dasar lingkaran. Persamaan yang
dibentuk akan menjadi persamaan lingkaran mohr untuk tegangan biaxial,
merupakan bentuk perwakilan dari besaran besaran nilai tegangan kedalam bentuk
gambar.
σθ= (σx+ 2σy) + (σx−σ2 y) cos 2θ
σθ−(σx+ 2σy) = (σx−σ2 y) cos 2θ
Sehingga dengan menjumlahkan kuadrat dari tiap persamaan tegangan akan
terbentuk persamaan lingkaran dasar dalam bentuk tegangan umum yang dapat
menentukan nilai maksimum dan nilai minimum tegangan geser dan tegangan
tarik.
Gambar 2.7 Lingkaran Mohr Untuk Tegangan Biaxial
𝜏𝜏𝜃𝜃𝐴𝐴𝜃𝜃
Gambar 2.7 pada lingkaran mohr merupakan bentuk perhitungan tegangan
secarah menyeluruh, dimana dengan gambar tersebut akan dapat lebih mudah
untuk menentukan tegangan maksimum dan minimum yang dialami oleh benda
yang dapat dilihat melalui ilustrasi gambar. Pada lingkaran mohr untuk tegangan
uniaxial dapat dilihat bahwa nilai dari tegangan minimum adalah nol untuk
tegangan tarik.
2.2.3 Tegangan Utama (Principal Stress)
Tegangan maksimum atau minimum pada suatu batang dapat
digambarkan pada sebuah elemen yang mendapat beban. Dimana penjabaran
tegangan yang terjadi dapat diuraikan, sehingga nantinya mendapatkan persamaan
minimum dan maksimum untuk mencari nilai suatu tegangan. Titik centroid
pada benda akan menjabarkan tegangan-tegangan yang terjadi, sehingga untuk
mendapatkan persamaan akan lebih mudah.
Gambar.2.8 tegangan utama
Tegangan tarik utama adalah tegangan yang dibentuk dari gaya tarik utama
pada tiap – tiap sumbu yaitu tegangan tarik pada sumbu x dan tegangan tarik
terhadap sumbu y, dimana persamaan untuk tegangan tarik utama diperoleh
dengan menjumlahkan tiap tegangan pada satu sumbu yang sama dan segaris.
Tegangan tarik pada luasan θ terletak pada satu garis dengan tegangan 𝜎𝜎𝑥𝑥cos θ dan σysin θ. Dengan penjumlahan secara vektor maka akan diperoleh persamaan
untuk tegangan tarik utama yang terlihat pada persamaan 2.18 berikut :
σθAθ = σx Axcos θ + σy Ay sin θ- 2 τ
σθAθ= σ
xy Aθcos θ sin θ
x (Aθcos θ) cos θ+ σy (Aθsin θ)sin θ - 2 τ
σθ = σ
xy Aθcos θ sin θ x cos2θ+ σy sin2θ- 2 τxy
𝛔𝛔𝛉𝛉 = (𝛔𝛔𝐱𝐱+ 𝟐𝟐𝛔𝛔𝐲𝐲)+(𝛔𝛔𝐱𝐱−𝟐𝟐𝛔𝛔𝐲𝐲) cos 2θ - 2 τ
cos θ sin θ
xy sin 2θ ( 2.18)
Tegangan geser utama adalah tegangan yang dibentuk dari gaya geser utama
pada tiap – tiap sumbu yaitu tegangan geser pada sumbu x dan tegangan geser
terhadap sumbu y, dimana persamaan untuk tegangan geser utama diperoleh
dengan menjumlahkan tiap tegangan pada satu sumbu yang sama dan segaris.
Tegangan geser θ yang terletak pada satu garis dengan tegangan 𝜎𝜎𝑥𝑥sin θ dan σycos
θ. Dengan penjumlahan secara vektor maka akan diperoleh persamaan untuk
tegangan geser utama yang terlihat pada persamaan 2.19(Lit.Timosenko hal 75).
𝜏𝜏𝜃𝜃𝐴𝐴𝜃𝜃 +𝜎𝜎𝑦𝑦𝐴𝐴𝑦𝑦𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃+𝜏𝜏𝑥𝑥𝑦𝑦𝐴𝐴𝑦𝑦𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃 − 𝜎𝜎𝑥𝑥𝐴𝐴𝑥𝑥𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃 − 𝜏𝜏𝑥𝑥𝑦𝑦𝐴𝐴𝑥𝑥𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃 = 0
𝜏𝜏𝜃𝜃𝐴𝐴𝜃𝜃 =𝜎𝜎𝑥𝑥𝐴𝐴𝑥𝑥𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃 − 𝜏𝜏𝑦𝑦𝐴𝐴𝑦𝑦𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃 − 𝜏𝜏𝑥𝑥𝑦𝑦𝐴𝐴𝑦𝑦𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃+𝜏𝜏𝑥𝑥𝑦𝑦𝐴𝐴𝑥𝑥𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃
𝜏𝜏𝜃𝜃𝐴𝐴𝜃𝜃 =𝜎𝜎𝑥𝑥(𝐴𝐴𝜃𝜃𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃)𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃 − 𝜎𝜎𝑦𝑦(𝐴𝐴𝜃𝜃𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃)𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃+𝜏𝜏𝑥𝑥𝑦𝑦(𝐴𝐴𝜃𝜃𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃)𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃 −
Tegangan tarik maksimum adalah nilai tegangan pada batas tertinggi yang
mampu diterima oleh beban. Tegangan tarik maksimum merupakan batas yang
diizinkan dalam pemberian gaya berupa pembebanan. Tagangan tarik maksimum
pada tegangan utama memiliki syarat dalam penentuan nilai sudut yang dibentuk.
Syarat untuk memperoleh tegangan tarik utama maksimum adalah :
𝑐𝑐𝑠𝑠𝑠𝑠2𝜃𝜃
Sehingga Tegangan Tarik Utama Maximum adalah :
𝜎𝜎𝑚𝑚𝜃𝜃𝑥𝑥 = �𝜎𝜎𝑥𝑥
Tegangan geser utama maksimumadalah batas nilai tegangan tertinggi yang
mampu diterima oleh benda pada pembentukan sudut tertentu, dimana nilai sudut
yang dibentuk dapat ditentukan dengan menentukan titik maksimum dari tegangan
geser utama.Syarat untuk menentukan tegangan geser utama maksimum
mempengaruhi besarnya pembebana yang mampu diterima oleh benda.
Syarat untuk memperoleh tegangan geser utama maksimum adalah :
𝜕𝜕𝜏𝜏𝜃𝜃
𝜕𝜕𝜃𝜃 = 0
𝜕𝜕 ��𝜎𝜎𝑥𝑥− 𝜎𝜎2 𝑦𝑦� 𝑐𝑐𝑠𝑠𝑠𝑠2𝜃𝜃+𝜏𝜏𝑥𝑥𝑦𝑦𝑐𝑐𝑐𝑐𝑐𝑐2𝜃𝜃�
𝜕𝜕 �𝜎𝜎𝑥𝑥 − 𝜎𝜎2 𝑦𝑦� 𝑐𝑐𝑐𝑐𝑐𝑐2𝜃𝜃+𝜏𝜏𝑥𝑥𝑦𝑦(−2𝑐𝑐𝑠𝑠𝑠𝑠2𝜃𝜃) = 0
Sehingga Tegangan Geser Maximum Utama adalah :
2.2.3.1. LingkaranMohr Tegangan Utama
Lingkaran mohr untuk tegangan utama dibentuk dari persamaan dasar dari
lingkaran dengan menjumlahkan persamaan pada tegangan tarik utama dan
tegangan geser utama.Persamaan yang diperoleh merupakan dasar untuk
membentuk lingkaran.Tegangan maksimum dan minimum dapat dihitung melalui
perhitungan untuk titik terjauh pada lingkaran sepanjang sumbu x dan tegangan
tarik utama minimum dapat dihitung melalui penentuan titik terdekat pada sumbu
x. Persamaan – persamaan tersebut dapat dilihat pada lingkaran mohr pada
gambar 2.9.
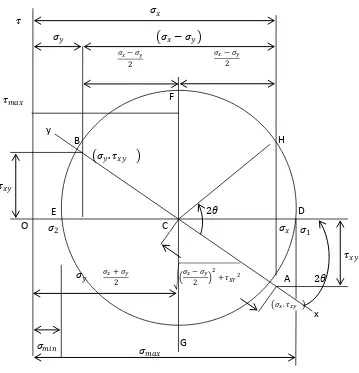
Gambar 2.9 Lingkaran Mohr Untuk Tegangan Utama
Dengan demikian nilai – nilai tegangan yang dapat diperhitungkan pada
pembebana yang diberikan dapat dilihat berdasarkan gambar yang dilukis
berdasarkan perhitungan dari nilai – nilai tegangan tarik dan geser pada sudut
pembentuk.Diagram mohr merupakan bentuk dari semua tegangan yang
mempengaruhi benda yang dapat dilihat melalui gambar.
2.3. Sistem Penumpu
Pipe support adalah salah satu bagian yang penting dalam sistem perpipaan
atau di suatu plant.Sistem penumpu berfungsi untuk menahan dan
mengkondisikan suatu sistem perpipaan sehingga aman sampai waktu yang telah
ditentukan, bahkan diharapkan berfungsi selama pipa masih digunakan.
2.3.1. Momen Lentur (Bending Momen)
Jadi momen lentur merupakan kebalikan (arah) dari tahanan momen
dengan besaran yang sama. Momen lentur juga dinotasikan dengan M. Momen
lentur lebih lazim digunakan daripada tahanan momen dalam perhitungan karena
momen ini dapat dinyatakan secara langsung dari beban atau gaya-gaya
eksternalnya.
2.3.2. Gaya geser
Gaya geser adalah berlawanan arah dengan tahanan geser tetapi besarnya
sama. Biasanya dinyatakan dengan V. Dalam perhitungan, gaya geser lebih sering
2.3.3. Gaya dan Momen pada tumpuan
Ketika pipa dibebani dengan gaya atau momen, tegangan internal terjadi
pada batang. Secara umum, terjadi tegangan normal dan tegangan geser.Untuk
menentukan besarnya tegangan-tegangan ini pada suatu bagian atau titik
tersebut.Untuk menentukan besarnya resultan pada tumpuan dapat menggunakan
persamaan-persamaan kesetimbangan.
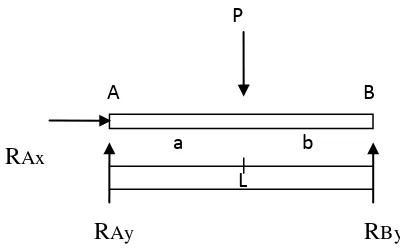
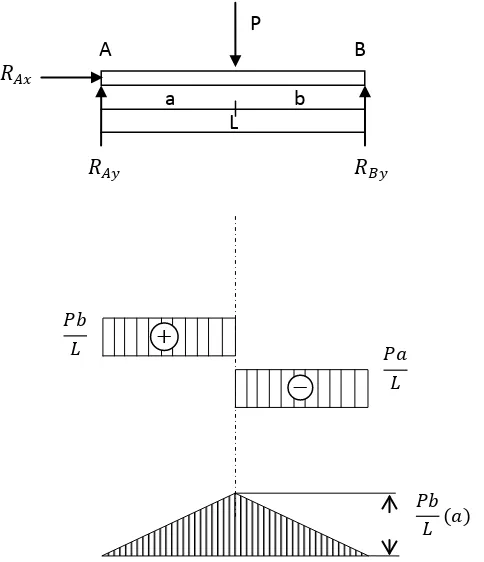
Berikut ini adalah contoh analisa 1 dimensi arah x untuk menentukan arah
gaya dan momen pada sebuah pipa yang ditumpu.
RAx
RAy RBy
Gambar 2.10 Free Body Diagram kesetimbangan gaya dan momen
Dari diagram benda bebas diatas akan didapatgaya–gaya reaksi yang
bekerja pada tiap tumpuan yangterlihat pada persamaan dari gambar 2.10 :
A B
L
a b
∑𝑀𝑀𝐴𝐴 = 0
𝑃𝑃𝜃𝜃 − 𝑅𝑅𝐵𝐵𝑦𝑦(𝐿𝐿) = 0
𝑅𝑅𝐵𝐵𝑦𝑦 (𝐿𝐿) = 𝑃𝑃𝜃𝜃
𝑅𝑅𝐵𝐵𝑦𝑦
=
𝑃𝑃𝜃𝜃𝐿𝐿∑𝐹𝐹𝑦𝑦 = 0
𝑅𝑅𝐴𝐴𝑦𝑦 + 𝑅𝑅𝐵𝐵𝑦𝑦− 𝑃𝑃 = 0
𝑅𝑅𝐴𝐴𝑦𝑦 =𝑃𝑃 − 𝑅𝑅𝐵𝐵𝑦𝑦
𝑅𝑅𝐴𝐴𝑦𝑦 =𝑃𝑃 −
𝑃𝑃𝜃𝜃
𝐿𝐿
𝑅𝑅𝐴𝐴𝑦𝑦
=
𝑃𝑃𝑏𝑏
𝐿𝐿
Persamaan momen untuk batasan0 ≤ 𝑥𝑥 ≤ 𝜃𝜃
𝑅𝑅𝐴𝐴𝑥𝑥
𝑅𝑅𝐴𝐴𝑦𝑦
∑𝑀𝑀 = 0
𝑀𝑀𝑥𝑥 − 𝑅𝑅𝐴𝐴𝑦𝑦(𝑥𝑥) = 0
𝑀𝑀𝑥𝑥 = 𝑅𝑅𝐴𝐴𝑦𝑦(𝑥𝑥)
𝑀𝑀𝑥𝑥 = 𝑃𝑃𝑏𝑏𝐿𝐿 (𝑥𝑥) v
Mx
Untuk nilai x = 0
𝑀𝑀0 = 0
Untuk nilai x = a
𝑀𝑀𝜃𝜃 = 𝑃𝑃𝑏𝑏𝐿𝐿𝜃𝜃
Dan untuk persamaan gaya geser diperoleh :
∑𝐹𝐹𝑦𝑦 = 0
𝑅𝑅𝐴𝐴𝑦𝑦 − 𝑉𝑉𝑥𝑥 = 0
𝑉𝑉𝑥𝑥 =𝑅𝑅𝐴𝐴𝑦𝑦
𝑉𝑉𝑥𝑥 =𝑃𝑃𝑏𝑏𝐿𝐿
Untuk nilai x = 0
𝑉𝑉0 = 𝑃𝑃𝑏𝑏
𝐿𝐿
Untuk nilai x = a
𝑉𝑉𝜃𝜃 = 𝑃𝑃𝐿𝐿𝑏𝑏
Sedangkan persamaan momen untuk batasan 𝜃𝜃 ≤ 𝑥𝑥 ≤ 𝐿𝐿
x
M
a v
𝑅𝑅𝐴𝐴𝑋𝑋
𝑅𝑅𝐴𝐴𝑋𝑋
Nx P
∑𝑀𝑀𝐴𝐴 = 0
𝑀𝑀𝑥𝑥 +𝑃𝑃(𝑥𝑥 − 𝜃𝜃)− 𝑅𝑅𝐴𝐴𝑦𝑦(𝑥𝑥) = 0
𝑀𝑀𝑥𝑥 = 𝑅𝑅𝐴𝐴𝑦𝑦(𝑥𝑥)− 𝑃𝑃(𝑥𝑥 − 𝜃𝜃)
𝑀𝑀𝑥𝑥 =
𝑃𝑃𝑏𝑏
𝐿𝐿
(𝑥𝑥)− 𝑃𝑃(𝑥𝑥 − 𝜃𝜃)Untuk nilai x = a
𝑀𝑀𝜃𝜃 =𝑃𝑃𝑏𝑏𝐿𝐿𝜃𝜃
Untuk nilai x = l
𝑀𝑀𝑙𝑙 = 0
Dan untuk persamaan gaya geser diperoleh :
∑𝐹𝐹𝑦𝑦 = 0
𝑅𝑅𝐴𝐴𝑦𝑦 − 𝑃𝑃 − 𝑉𝑉𝑥𝑥 = 0
𝑉𝑉𝑥𝑥 =𝑅𝑅𝐴𝐴𝑦𝑦 − 𝑃𝑃
𝑉𝑉𝑥𝑥 =
𝑃𝑃𝑏𝑏
𝐿𝐿
− 𝑃𝑃Untuk nilai x = a
𝑉𝑉𝜃𝜃 =
𝑃𝑃𝑏𝑏
𝐿𝐿
− 𝑃𝑃Untuk nilai x = l
𝑉𝑉𝑙𝑙 =
𝑃𝑃𝑏𝑏
𝐿𝐿 − 𝑃𝑃
𝑉𝑉𝑙𝑙 =−
𝑃𝑃𝜃𝜃
𝐿𝐿
Dari hasil penurunan persamaan diatas untuk momen dan gaya geser akan
didapat bentuk diagram untuk masing-masing persamaan momen dan gaya geser
dimana gambar yang dihasilkan berdasarkan bentuk dari diagram benda bebas
pada gambar 2.11 :
Gambar 2.11 Diagram gaya geser dan momen lentur
A B
L
a b
𝑅𝑅𝐴𝐴𝑥𝑥
𝑅𝑅𝐴𝐴𝑦𝑦 𝑅𝑅𝐵𝐵𝑦𝑦
P
𝑃𝑃𝑏𝑏
𝐿𝐿 𝑃𝑃𝜃𝜃
𝐿𝐿
−
+
2.4 Klasifikasi Tegangan
Tegangan yang tejadi dalam sistem perpipaan dapat dikelompokkan ke
dalam dua kategori, yakni Tegangan Normal (Normal Stress) dan Tegangan Geser
(Shear Stress). Tegangan normal terdiri dari tiga komponen tegangan, yang
masing-masing adalah:
1. Tegangan Longitudinal (Longitudinal Stress), yaitu tegangan yang searah
panjang pipa.
2. Tegangan Tangensial atau Tegangan Keliling (Circumferential Stres
satau Hoop Stress), yaitu tegangan yang searah garis singgung
penampang pipa.
3. Tegangan Radial (Radial Stress), yaitu tegangan searah jari-jari
penampang pipa.
Tegangan Geser terdiri dari dua komponen tegangan, yang masing-masing adalah:
1. Tegangan Geser (Shear Stress), yaitu tegangan akibat adanya gaya yang
berimpit atau terletak pada luas permukaan pipa.
2. Tegangan Puntir atau Tegangan Torsi (Torsional Stress), yaitu tegangan
yang terjadi akibat momen puntir pada pipa.
2.4.1 Tegangan Longitudinal ( Longitudinal Stress)
Tegangan Longitudinal merupakan jumlah dari Tegangan Aksial (Axial
Stress), Tegangan Lentur (Bending Stress) dan Tegangan Tekanan Dalam
(Internal Pressure Stress). Mengenai ketiga tegangan ini dapat diuraikan berikut
2.4.1.1 Tegangan Aksial
Tegangan aksial adalah tegangan yang ditimbulkan oleh gaya F
axyang
bekerjasearah dengan sumbu pipa, dan dapat diperlihatkan seperti gambar 2.12:
Gambar 2.12Tegangan Aksial
σ
Dimana :
ax = 𝐹𝐹𝜃𝜃𝑥𝑥 𝐴𝐴𝑚𝑚
(2.20)
σ
axAm = luas penampang pipa =tegangan aksial
= 𝜋𝜋 4(do
2 – di2
do = diameter luar
)
di = diameter dalam
2.4.1.2Tegangan Lentur (Bending Stress)
Tegangan yang ditimbulkan oleh momen M yang bekerja diujung-ujung
benda. Dalam hal ini tegangan yang terjadi dapat berupa Tensile Bending.
Tegangan lentur maksimum terletak pada permukaan pipa dan nol pada sumbu
pipa, dapat ditunjukkan pada gambar 2.13:
Gambar 2.13.Bending Momen
𝜎𝜎
𝑏𝑏=
𝑀𝑀𝐼𝐼𝑥𝑥𝑐𝑐 (2.21)Tegangan maksimum terjadi pada dinding terluar dari pipa
𝜎𝜎
𝑏𝑏𝑚𝑚𝜃𝜃𝑥𝑥=
𝑀𝑀𝑥𝑥𝐼𝐼𝑅𝑅𝑐𝑐=
𝑀𝑀𝑍𝑍(2.22)
Dimana :
M = momen bending
c = jari-jari terluar pipa
I = Momen inersia penampang
I = 𝜋𝜋 64( do
4 – di4
Z = section modulus
= 𝐼𝐼
𝑅𝑅𝑐𝑐
2.4.2 Tegangan Geser
Berbeda dengan tegangan normal akibat gaya aksial, Tegangan geser
terjadi pada permukaan pipa dimana gaya yang bekerja terletak pada permukaan
pipa atau bekerja sejajar terhadap permukaan pipa. Tegangan geser terjadi
diakibatkan oleh gaya yang bekerja sejajar dengan permukaan pipa dan karena
adanya momen torsi yang terdapat pada pipa, momen torsi ini dapat berupa dua
gaya yang bekerja sejajar dengan arah yang berlawanan (momen kopel).
2.4.2.1 Akibat gaya geser (V)
Tegangan geser akibat gaya geser (V) dapat dihitung dengan
menggunakan persamaan 2.23:
τ
Dimana :
max
=
𝑉𝑉𝐴𝐴 (2.23)V = Gaya Geser
A = Luas penampang
Tegangan ini mempunyai nilai minimum di sumbu netral (di sumbu
simetri pipa) dan bernilai nol pada titik dimana tegangan lendut maksimum ( yaitu
pada permukaan luar dinding pipa). Karena hal ini dan juga karena besarnya
2.4.2.2Akibat momen puntir
Tegangan geser akibat momen puntir (Mt) dapat dihitung dengan
menggunakan persamaan 2.24 (Lit. Hibeller, Hal 143) :
τ
Dimana :
max
=
𝑴𝑴𝑡𝑡𝑥𝑥𝑟𝑟
𝐽𝐽 (2.24)
Mt = Momen Puntir
J = Momen Inersia Polar
Tegangan ini terjadi akibat adanya momen yang bekerja pada pipa yang
mengakibatkan adanya pergeseran sudut terhadap sumbu pipa, momen yang
bekerja dapat berupa momen ataupun gaya yang mengakibatkan terjadinya
puntiran.
2.4.3 Tegangan Torsi
Suatu bentangan bahan dengan luas permukaan tetapdikenai suatu puntiran
( twisting ) pada setiap ujungnya danpuntiran ini disebut juga dengan torsional,
dan bentangan bendatersebut dikatakan sebagai poros ( shaft ).Distribusi tegangan
bervariasi dari nol pada pusat poros sampai dengan maksimum pada sisi luar
Gambar 2.14. Distribusi Tegangan Geser
2.4.3.1Momen Inersia( Polar )
Untuk suatu batang bulat berlubang (pipa) dengan diameter luar Do dan
diameter dalam Di, momen kutub inersia (polar momen of inertia) penampang
melintang luasnya, biasanya dinotasikan dengan J (Lit.Hibbeler, hal 72).
Dimana :
J = 𝜋𝜋
32 (D0
4 – Di4)
Momen kutub inersia untuk batang bulat tanpa lubang (batang pejal) dapat
diperoleh dengan memberi nilai Di = 0. Kuantitas dari J merupakan sifat
matematis dari geometri penampang yang melintang yang muncul dalam kajian
tegangan pada batang atau poros bulat yang dikenai torsi.
2.4.3.2Regangan geser
Suatu garis membujur a-b digambarkan pada permukaan poros tanpa
beban.Setelah suatu momen punter T dikenakan pada poros, garis a-b bergerak
menjadi a-b’ seperti ditunjukkan pada gambar berikut.Sudut γ, yang diukur dalam
regangan geser pada permukaan poros. Definisi yang sama berlaku untuk setiap
titik pada batang poros tersebut, dapat ditunjukkan pada gambar 2.15:
Gambar 2.15. Regangan Geser
2.5 Persamaan Tegangan Pada Sistem Perpipaan
Persamaan tegangan pada sistem perpipaan merupakan persamaan yang
dapat diturunkan dari persamaan untuk tegangan 𝜎𝜎1,2 yang sesuai dengan aplikasi
tersebut. Pada dasarnya persamaan tegangan yang dihasilkan pada tiap kondisi
yang berbeda diperoleh dari persamaan untuk tegangan utama, yang membedakan
persamaan tegangan pada tiap-tiap kondisi itu adalah tegangan terhadap sumbu x
dan tegangan terhadap sumbu y. Pada kondisi bending tegangan terhadap sumbu x
tidak berlaku atau diabaikan dengan sudut pembentuk
𝜃𝜃
dengan nilai 90 derajat.Secara umum akan terlihat pada gambar 2.16.
Maka akan berlaku persamaan Tegangan Utama dengan ketentuan dimana
pada gambar diatas menunjukkan bahwa, arah tegangan terhadap sumbu x adalah
0, dan hanya ada tegangan yang bekerja terhadap sumbu y. Tegangan geser yang
terjadi pada gambar diatas adalah tegangan geser akibat gaya geser yang bekerja
searah dengan luas penampang pipa, secara umum dapat dilihat pada persamaan
dibawah ini (Lit. Timosenko hal 43 ).
𝜎𝜎1,2 = �
𝜎𝜎𝑥𝑥+𝜎𝜎𝑦𝑦
2 �±��
𝜎𝜎𝑥𝑥−𝜎𝜎𝑦𝑦
2 � 2
+𝜏𝜏𝑥𝑥𝑦𝑦2
Dimana 𝜎𝜎𝑦𝑦 dan 𝜏𝜏𝑥𝑥𝑦𝑦 pada kondisi lentur pada sistem penumpu akan berubah
menjadi persamaan yang sesuai dengan keadaan dari bentuk beam yang dalam hal
ini berbentuk pipa dimana tidak terjadi tegangan dalam arah sumbu x (𝜎𝜎𝑥𝑥=0).
𝜎𝜎𝑥𝑥 = 0( tidak ada tegangan terhadap sumbu x )
𝜎𝜎𝑦𝑦=𝑀𝑀𝐼𝐼𝑥𝑥 𝑐𝑐
𝜏𝜏𝑥𝑥𝑦𝑦= 𝑉𝑉𝐴𝐴
Dimana :
M= momen bending
C= jari-jari terluar pipa
I= Momen inersia penampang
V= Gaya Geser
2.6 Metode Elemen Hingga
Metode Elemen Hingga adalah salah satu dari metode numerik yang
memanfaatkan operasi matrix untuk menyelesaikan masalah-masalah fisik.
Metode ini dibangun sebagai metode numeric untuk analisa tegangan, tapi
sekarang pemakainanya telah meluas sebagai metode yang umum untuk banyak
permasalahan engineering kompleks dan ilmu-ilmu fisika.Mengandung banyak
perhitungan, pertumbuhannya berhubungan dekat dengan pengembangan
teknologi komputer.
Metode Elemen Hingga digunakan dengan membagi suatu benda menjadi
bebrapa bagian dan bagian-bagian tersebut disebut dengan mesh. Beberapa mesh
yang terbentuk dari suatu benda dan terdiri dari beberapa titik (node). Nilai dan
jumlah titik (node) ditentukan oleh jumlah mesh.
Gambar 2.15 Gambar Pembagian Mesh pada benda
n= m+1 (2.25)
dimana :
n= jumlah node
m= jumlah mesh
Mesh 1 Mesh 2 Mesh 3
Dengan demikian, pada persamaan 2.15 didapat bahwa jumlah titik (node)
pada pembagian elemen sama dengan jumlah mesh ditambah satu.
2.6.1 Node (U)
Node atau titik merupakan dasar dalam penghitungan tegangan. Dimana
perpindahan node akibat pemberian gaya yang berupa pembebanan pada benda
yang merupakan nilai dari pertambahan panjang atau perpindahan node (∆u).
Nilai dari perubahan panjang akan mempengaruhi nilai kekakuan dari pipa (k).
Semakin besar jarak perpindahan antar node pada suatu mesh akibat pembebanan
berupa gaya maka akan semakin besar tegangan yang diterima pada mesh dimana
node berada. Dimana nilai perpindahan node dirumuskan dengan persamaan 2.26
:
∆u = Ui+1 - Ui (2.26)
Dimana :
∆u : Perpindahan Node
Ui
U
: node urutan ke-i
2.6.2 Konstanta Kekakuan (K)
Nilai konstanta kekakuan dipengaruhi oleh nilai gaya dan perpindahan
node (∆u). Dimana jika semakin besar nilai perpindahan node pada pembebanan
yang sama maka akan menghasilkan nilai Konstanta Kekakuan (𝑘𝑘) yang lebih kecil, sebaliknya jika nilai perpindahan node kecil pada pembebanan yang sama
maka akan menghasilkan nilai Konstanta Kekakuan (k) yang lebih besar.
Nilai konstanta kekakuan pada Metode Elemen Hingga diperoleh dengan
meggunakan persamaan dari konstanta kekakuan pegas yang di tunjukkan pada
gambar (2.10 )
Gambar 2.16 Konstanta kekakuan pegas
Dimana nilai konstanta pegas yang diberikan pada persamaan (2.27)
𝐹𝐹 =𝑘𝑘∆𝑥𝑥 (2.27)
Dimana :
F : Gaya
k : Konstanta Pegas x
∆𝑥𝑥
F
∆x : Pertambahan Panjang
Untuk kondisi benda yang mengalami perubahan panjang atau
penambahan panjang akibat gaya yang dibebankan pada benda yang dibagi
menjadi beberapa elemen, defleksi atau lendutan yang terjadi mengakibatkan
benda mengalami perpanjangan searah sumbu pusat benda, sehingga pertambahan
panjang akibat pengaruh gaya ditentukan berdasarkan penurunan persamaan 2.27
𝜎𝜎= 𝐹𝐹
𝐴𝐴 Untuk persamaan tegangan
𝜀𝜀 =∆𝑥𝑥
𝑥𝑥 Untuk persamaan pertambahan panjang
Persamaan umum untuk menghubungkan nilai tegangan dan pertambahan
panjang dapat dilihat pada persamaan 2.28
𝜎𝜎 =𝐸𝐸𝜀𝜀 (2.28)
Dimana :
𝜎𝜎 : Tegangan
𝐸𝐸 : Modulus Elastisitas
𝜀𝜀 : Regangan
Sehingga dengan mensubtitusikan persamaan tegangan dan pertambahan
panjang kedalam persamaan 2.27 akan menghasilkan nilai konstanta kekakuan
secara umum yang ekuivalen dengan konstanta kekakuan pegas yang terlihat pada
𝐹𝐹
𝐴𝐴 =𝐸𝐸 ∆𝑥𝑥
𝐿𝐿
𝐹𝐹 =�𝐴𝐴𝐿𝐿𝐸𝐸� ∆𝑥𝑥 (2.29)
Dimana :
F : Gaya yang bekerja
A : Luas permukaan elemen
E : Modulus elastisitas Elemen
∆𝑥𝑥 : Pertambahan panjang
Persamaan 2.29 ekuivalen dengan persamaan 2.27 pada kondisi yang
sama, sehingga nilai konstanta kekakuan dapat diwakilkan dengan persamaan 𝑘𝑘 pada benda yang mengalami perpanjangan akibat lendutan oleh beban F yang
bekerja padanya. Persamaan untuk nilai 𝑘𝑘 diperoleh dengan mensubtitusikan persamaan 2.29 kedalam persamaan 2.27 sehingga akan diperoleh persamaan
kekakuan untuk Metode Elemen Hingga yang terlihat pada persamaan 2.30
𝐹𝐹 =𝑘𝑘∆𝑥𝑥 Persamaan untuk konstanta pegas
𝐹𝐹 =�𝐴𝐴𝐸𝐸
𝐿𝐿 � ∆𝑥𝑥 Persamaan untuk konstanta Metode Elemen
Hingga
�𝐴𝐴𝐿𝐿𝐸𝐸� ∆𝑥𝑥 = 𝑘𝑘∆𝑥𝑥
𝑘𝑘 =�𝐴𝐴𝐸𝐸
Dimana :
k :Nilai kekakuan elemen
A : Luas permukaan elemen
E : Modulus elastisitas Elemen
L : Panjang Elemen
Dengan demikian, persamaan 2.30 merupakan persamaan untuk konstanta
metode elemen hingga secara umum yang digunakan dengan mengasumsikan
keadaan yang sama dengan konstanta kekakuan pegas.
2.7 Matriks Kekakuan Akibat Pembebanan Axial
Untuk menghitung nilai perpindahan node (𝑢𝑢) diperlukan perhitungan matriks dengan menggunakan nilai matriks kekakuan dan matriks gaya. Matriks
kekakuan dan matriks gaya berisi nilai kekakuan dan gaya yang ada pada setiap
elemen. Perhitungan matriks perpindahan node (𝑢𝑢) dapat dilihat pada persamaan 2.31.
[𝑘𝑘][𝑢𝑢] = [𝐹𝐹]
Pada suatu benda yang terbagi dalam beberapa elemen, terdapat lebih dari
satu nilai kekakuan.Nilai-nilai kekakuan elemen yang berbeda tersebut disusun
dalam satu matriks global.
Pada suatu elemen terdapat gaya-gaya yang bekerja pada tiap node elemen
tersebut. Gaya-gaya tersebut terlihat pada gambar 2.17 (Lit Saeed Moaveni hal
:58)
Gambar 2.17 Perpindahan dan Gaya di suatu elemen
x
y Uix
Uiy
Uiy
Uix
Ujx Ujy
Ujy
Ujx
x
y Fix
Fiy
Fiy
Fix
Fjx Fjy
Fjy
Pada gambar 2.17 dapat diuraikan titik perpindahan serta gaya yang
bekerja yang terlihat pada persamaan
Persamaan untuk perpindahan
𝑈𝑈𝑠𝑠𝑋𝑋 = 𝑢𝑢𝑠𝑠𝑥𝑥 𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃 − 𝑢𝑢𝑠𝑠𝑦𝑦sin𝜃𝜃
𝑈𝑈𝑠𝑠𝑋𝑋 = 𝑢𝑢𝑠𝑠𝑥𝑥 𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃+ 𝑢𝑢𝑠𝑠𝑦𝑦𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃
𝑈𝑈𝑗𝑗𝑋𝑋 = 𝑢𝑢𝑗𝑗𝑥𝑥 𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃 − 𝑢𝑢𝑗𝑗𝑦𝑦 sin𝜃𝜃
𝑈𝑈𝑗𝑗𝑋𝑋 = 𝑢𝑢𝑗𝑗𝑥𝑥 𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃+𝑢𝑢𝑗𝑗𝑦𝑦 cos𝜃𝜃
Untuk menuliskan persamaan perpindahan ke dalam matriks maka dapat
dirumuskan sebagai (Lit Saeed Moaveni hal : 59)
{𝑈𝑈} = [𝑇𝑇]{𝑢𝑢}
gambar 2.17 .sedangkan [T] merupakan matriks transformasi yang
sama kita dapat menjabarkan gaya yang bekerja pada elemen seperti persamaan
2.32
𝐹𝐹𝑠𝑠𝑋𝑋 = 𝑢𝑢𝑠𝑠𝑥𝑥 𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃 − 𝑢𝑢𝑠𝑠𝑦𝑦 sin𝜃𝜃
𝐹𝐹𝑠𝑠𝑋𝑋 = 𝑓𝑓𝑠𝑠𝑥𝑥 𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃+ 𝑓𝑓𝑠𝑠𝑦𝑦𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃
𝐹𝐹𝑠𝑠𝑋𝑋 = 𝑢𝑢𝑠𝑠𝑥𝑥 𝑐𝑐𝑐𝑐𝑐𝑐𝜃𝜃 − 𝑢𝑢𝑠𝑠𝑦𝑦 sin𝜃𝜃
𝐹𝐹𝑗𝑗𝑋𝑋 = 𝑓𝑓𝑗𝑗𝑥𝑥 𝑐𝑐𝑠𝑠𝑠𝑠𝜃𝜃+𝑓𝑓𝑗𝑗𝑦𝑦 cos𝜃𝜃 (2.32)
Untuk menuliskan persamaan gaya yang bekerja ke dalam matriks maka
dapat dirumuskan sebagai
{𝐹𝐹} = [𝑇𝑇]{𝑓𝑓}
Dengan mensubtitusikan nilai {F} dan {u} kedalam persamaan 2.31 maka
didapat persamaan 2.33
[𝑇𝑇]−1{𝐹𝐹} = [𝐾𝐾][𝑇𝑇]−1{𝑢𝑢}
{𝐹𝐹} = [𝑇𝑇] [𝐾𝐾][𝑇𝑇]−1{𝑢𝑢} (2.33)
Dimana nilai [𝑇𝑇]−1 merupakan invers dari matriks [T] yang bernilai
[𝑇𝑇]−1 = �
cos𝜃𝜃 sin𝜃𝜃 −sin𝜃𝜃 cos𝜃𝜃
0 0
0 0
0 0
0 0
cos𝜃𝜃 sin𝜃𝜃 −sin𝜃𝜃 cos𝜃𝜃 �
Maka dengan mensubtitusikan persamaan 2.33 Dengan nilai-nilai yang
⎩
Sehingga bentuk matriks kekakuan global bisa dituliskan dalam matrik
[𝑘𝑘] =𝑘𝑘 �
Untuk elemen yang berdeformasi hanya dalam 1 dimensi saja maka hanya
diambil 1 titik diantara X atau Y sebagai matriks kekakuannya. Sudut 𝜃𝜃 pada matriks trigonometri menggambarkan posisi elemen terhadap sumbu X.
Jika suatu elemen berdeformasi terhadap sumbu X dengan nilai sudut 0o,
maka matriks kekakuan elemennya menjadi
[𝑘𝑘] =𝑘𝑘 �
Karena elemen hanya berdeformasi kearah sumbu X maka matriks pada
sumbu Y dihilangkan sehingga nilai matriks kekauan menjadi
Bentuk dasar matriks kekakuan pada elemen diuraikan seperti
persamaan-persamaan matriks
Persamaan matriks untuk elemen 1 (𝑘𝑘1)
[𝑘𝑘]1 = � 𝑘𝑘1 −𝑘𝑘1 −𝑘𝑘1 𝑘𝑘1 �
Posisi matriks pada matriks global
[𝑘𝑘](1𝐺𝐺) =�
Persamaan matriks untuk elemen 2 (𝑘𝑘2)
[𝑘𝑘2] =� 𝑘𝑘2 −𝑘𝑘2 −𝑘𝑘2 𝑘𝑘2�
Posisi matriks pada matriks global
[𝑘𝑘](2𝐺𝐺) = �
Persamaan matriks untuk elemen (𝑘𝑘3)
Posisi matriks pada matriks global
Persamaan matriks-matriks satuan dibentuk menjadi matriks global secara
umum yang berurutan berdasarkan letak node pada tiap elemen yang berbeda,
secara matematis elemen ini mengikuti kaidah ‘Lagrace’ dalam matematika
numerik.Untuk penjumlahan matriks satuan tiap masing-masing konstanta k
tiap-tiap elemen dijumlahkan berdasarkan asumsi keadaan node. Pada matriks satuan
k1 hanya memiliki matrik tunggal karena node 1 hanya berada pada 1 elemen,
untuk matriks pada node 2 terdapat 2 elemen yang berbeda pada tiap node
tersebut, sehingga pada node 2 terdapat 2 nilai konstanta yang bekerja yaitu k1 dan
k2. Untuk node 3 terdapat 2 konstanta k, yaitu k2dan k3.
konstanta yang terdapat pada tiap node akan dijumlahkan dan disusun berdasarkan
matriks global pada matematika numeric yang terlihat pada susunan matriks 2.34
[𝑘𝑘](𝐺𝐺) = [𝑘𝑘](1𝐺𝐺)+ [𝑘𝑘](2𝐺𝐺)+ [𝑘𝑘](3𝐺𝐺)
Susunan matriks diatas digunakan untuk pembagian benda menjadi tiga
elemen (tiga mesh) yang terdiri dari empat node. Dimana nilai kekakuan untuk
Cara penyusunan matriks seperti penyusunan matriks 2.34 dapat digunakan juga
bila suatu benda terbagi menjadi lebih dari 3 elemen.
2.7.1 Metode Elemen Hingga Untuk Pembebanan Aksial
Untuk menghitung nilai tegangan aksial menggunakan metode elemen
hingga, setelah mendapatkan nilai perpindahan (u), kita dapat menggunakan
rumus (Lit 4 hal: 10)
𝜎𝜎=𝐸𝐸 �𝑢𝑢𝑠𝑠+1− 𝑢𝑢𝑠𝑠 𝑙𝑙 �
Nilai 𝑢𝑢𝑠𝑠+1𝑑𝑑𝜃𝜃𝑠𝑠 𝑢𝑢𝑠𝑠 merupakan nilai perpindahan ada titik i dan seterusnya.
2.8 Matriks Kekakuan Untuk Pembebanan Lentur
Metode elemen hingga untuk defleksi merupakan perubahan bentuk benda
akibat adanya pembebanan yang membuat adanya lengkungan, lengkungan
menghasilkan perpindahan titik terluar pada benda, perpindahan titik ini
dinamakan dengan perpindahan node. Kedudukan titik sebelum terjadinya
defleksi dengan kedudukan titik setelah adanya defleksi disebut pertambahan
panjang elemen Un+1 – Un.
Analogi perpindahan node pada kasus defleksi, merupakan pendekatan
yang dilakukan untuk menghitung nilai perpindahan yang diakibatkan oleh
Gambar 2.18 Pembebanan Defleksi
Untuk menentukan nilai perpindahan dari benda yang mengalami defleksi
akan digunakan persamaan diferensial yang diperoleh dari persamaan momen,
secara matematis persamaan momen dapat diperoleh langkah-langkah berikut.
Menentukan gaya-gaya reaksi
� 𝑀𝑀𝐴𝐴 = 0
𝑀𝑀𝐴𝐴 =𝑃𝑃.𝐿𝐿= 0
𝑀𝑀𝐴𝐴 =𝑃𝑃.𝐿𝐿
� 𝐹𝐹𝑥𝑥 = 0
𝑅𝑅𝐴𝐴𝑥𝑥 = 0
� 𝐹𝐹𝑦𝑦 = 0
L
P
L
𝑅𝑅𝐴𝐴𝑋𝑋
𝑅𝑅𝐴𝐴𝑋𝑋
B
P
A
C M
v
𝑅𝑅𝐴𝐴𝑦𝑦 − 𝑃𝑃= 0
𝑅𝑅𝐴𝐴𝑦𝑦 =𝑃𝑃
𝑅𝑅𝐴𝐴 =𝑃𝑃
Menentukan persamaan kurva elastis
� 𝑀𝑀𝑐𝑐 = 0
𝑀𝑀𝐴𝐴 +𝑀𝑀 − 𝑅𝑅𝐴𝐴𝑥𝑥= 0
𝑀𝑀 =𝑅𝑅𝐴𝐴𝑥𝑥 − 𝑀𝑀𝐴𝐴
𝑀𝑀 = (𝑃𝑃.𝑥𝑥)−(𝑃𝑃.𝐿𝐿) (2.35)
Pada persamaan 2.35 diperoleh persamaan momen untuk benda yang
mengalami defleksi sehingga untuk mendapatkan nilai perpindahan dan
perubahan sudut akibat pembebanan pada benda yang mengalami defleksi nilai
momen pada persamaan 2.35 disubtitusikan dalam persamaan 2.36 yang
merupakan persamaan deferensial untuk perpindahan dengan batas sumbu y.
𝐸𝐸𝐼𝐼 𝑑𝑑𝑑𝑑𝑥𝑥2𝑦𝑦2 = 𝑀𝑀 =𝑃𝑃𝑥𝑥 − 𝑃𝑃𝐿𝐿 (2.36)
𝐸𝐸𝐼𝐼 𝑑𝑑𝑦𝑦𝑑𝑑𝑥𝑥 = 𝐸𝐸𝐼𝐼𝜃𝜃 =1 2 𝑃𝑃𝑥𝑥
2− 𝑃𝑃𝐿𝐿𝑥𝑥+𝑐𝑐1 (2.37)
x
𝑅𝑅𝐴𝐴𝑋𝑋 A
𝜃𝜃
Dengan menggunakan syarat batas
XA = 0 ;𝜃𝜃𝐴𝐴 = 0 ; YA
Defleksi maksimum terjadi pada titik B
XB= L
𝑦𝑦𝑚𝑚𝜃𝜃𝑘𝑘𝑐𝑐 = 𝑦𝑦𝑏𝑏 =6𝑃𝑃𝐸𝐸𝐼𝐼 (𝐿𝐿3−3𝐿𝐿3)
𝑦𝑦𝑏𝑏 = 6𝑃𝑃𝐸𝐸𝐼𝐼(−2𝐿𝐿3) = 𝑃𝑃𝐿𝐿
3
3𝐸𝐸𝐼𝐼
Slope pada titik B
XB
Untuk benda yang mengalami defleksi akibat adanya momen yang bekerja
di ujung benda, dimana pada titik tersebut merupakan titik maksimum terjadinya
perpindahan yang terlihat pada gambar 2.19. = L
𝜃𝜃𝐵𝐵 = �𝑑𝑑𝑦𝑦𝑑𝑑𝑥𝑥� 𝐵𝐵 =
𝑃𝑃 2𝐸𝐸𝐼𝐼 (𝐿𝐿
2−2𝐿𝐿2)
𝜃𝜃𝐵𝐵 = 2𝑃𝑃𝐸𝐸𝐼𝐼 (−𝐿𝐿2)
𝜃𝜃𝐵𝐵 = −𝑃𝑃𝐿𝐿
2
2𝐸𝐸𝐼𝐼
2.19 Pembebanan Defleksi Akibat Momen
L
C Mc
v
Untuk menentukan nilai perpindahan dari benda yang mengalami defleksi
akan digunakan persamaan diferensial yang diperoleh dari persamaan momen,
secara matematis persamaan momen dapat diperoleh langkah-langkah berikut.
Menentukan persamaan momen
� 𝑀𝑀𝐴𝐴 = 0
𝑀𝑀𝐴𝐴 − 𝑀𝑀= 0
𝑀𝑀𝐴𝐴 =𝑀𝑀
� 𝐹𝐹𝑥𝑥 = 0
𝑅𝑅𝐴𝐴𝑥𝑥 = 0
� 𝐹𝐹𝑦𝑦 = 0
𝑅𝑅𝜃𝜃𝑦𝑦 = 0
Persamaan diferensial kurva elastis (x < L)
L
𝑅𝑅𝐴𝐴𝑋𝑋
𝑅𝑅𝐴𝐴𝑋𝑋
MA M
x
A
� 𝑀𝑀 = 0
𝑀𝑀𝐴𝐴 +𝑀𝑀𝑐𝑐 = 0
𝑀𝑀𝑐𝑐 = −𝑀𝑀𝐴𝐴 = −𝑀𝑀 (2.39)
Pada persamaan 2.39 diperoleh persamaan momen untuk benda yang
mengalami defleksi akibat momen sehingga untuk mendapatkan nilai perpindahan
dan perubahan sudut akibat pembebanan pada benda yang mengalami defleksi
nilai momen pada persamaan2.39 disubtitusikan dalam persamaan 2.40 yang
merupakan persamaan deferensial untuk perpindahan dengan batas sumbu y.
𝐸𝐸𝐼𝐼𝑑𝑑𝑑𝑑𝑥𝑥2𝑦𝑦2 = −𝑀𝑀 (2.40)
𝐸𝐸𝐼𝐼𝑑𝑑𝑦𝑦𝑑𝑑𝑥𝑥 = 𝐸𝐸𝐼𝐼𝜃𝜃 = −𝑀𝑀𝑥𝑥+𝑐𝑐1 (2.41)
𝐸𝐸𝐼𝐼𝑦𝑦= −1 2𝑀𝑀𝑥𝑥
2+ 𝑐𝑐1𝑥𝑥+𝑐𝑐2 (2.42)
Dengan mengguakan syarat batas
𝑥𝑥= 0 ; 𝜃𝜃 = 0
Pada persamaan 2.41 diperoleh c1
Pada persamaan 2.42 diperoleh c = 0
𝑥𝑥= 0 ;𝑦𝑦 = 0
2
Dengan mensubtitusikan c
=0
1 = 0 dan c2 = 0 pada persamaan 2.41 dan 2.42
𝜃𝜃 =𝑑𝑑𝑦𝑦 𝑑𝑑𝑥𝑥=
−𝑀𝑀𝑥𝑥 𝐸𝐸𝐼𝐼
𝑦𝑦 =− 𝑀𝑀𝑥𝑥 2
2𝐸𝐸𝐼𝐼
Defleksi maksimum terjadi pada titik B, sehingga :
Xb = L
𝑦𝑦 =− 𝑀𝑀𝐿𝐿 2
2𝐸𝐸𝐼𝐼
𝑦𝑦𝑚𝑚𝜃𝜃𝑘𝑘𝑐𝑐 = 𝑦𝑦𝑏𝑏 = − 𝑀𝑀𝐿𝐿
2
2𝐸𝐸𝐼𝐼
Slope pada titik B
X = L
𝜃𝜃𝐵𝐵 = �𝑑𝑑𝑦𝑦𝑑𝑑𝑥𝑥� 𝐵𝐵 =
𝑀𝑀𝐿𝐿 𝐸𝐸𝐼𝐼
Dari persamaan defleksi akibat momen dan gaya diperoleh nilai
perpindahan node dan perpindahan sudut (slope) yang ditunjukkan pada
Perpindahan node dan sudut akibat gaya
𝑦𝑦 = 𝑃𝑃
6𝐸𝐸𝐼𝐼(−2𝐿𝐿
3) = 𝑃𝑃𝐿𝐿3
3𝐸𝐸𝐼𝐼 (2.43)
𝜃𝜃 = −𝑃𝑃𝐿𝐿2
2𝐸𝐸𝐼𝐼 (2.44)
Perpindahan node dan sudut akibat momen
𝑦𝑦 =− 𝑀𝑀𝐿𝐿2
2𝐸𝐸𝐼𝐼 (2.45)
𝜃𝜃 = 𝑀𝑀𝐿𝐿
𝐸𝐸𝐼𝐼 (2.46)
Pada gambar 2.20 digambarkan kondisi batang yang mengalami defleksi
dengan batas-batas tertentu. (Lit Y.C Pao hal:66)
Gambar 2.20 kondisi batas untuk menentukan nilai perpindahan
Setelah mendapatkan persamaan perpindahan node dan sudut akibat gaya
dan momen yang menyebabkan defleksi, dapat kita ambil dua kondisi sebagai
𝑦𝑦= 1
𝑃𝑃
𝑀𝑀1 𝐿𝐿
𝑥𝑥 𝜃𝜃= 0
y
𝑦𝑦= 0 𝑃𝑃
𝑦𝑦
𝑀𝑀1 𝐿𝐿
syarat untuk menentukan nilai perpindahan gaya dan sudut untuk mendapatkan
nilai kekakuan suatu bahan.
Pada kasus pertama seperti gambar 2.20 nilai dari y=1 dan 𝜃𝜃= 0. Untuk mencari kombinasi nilai
gaya (P) dan momen (M), maka didapat persamaan 2.41 dan 2.42
𝑦𝑦 = 𝑃𝑃𝐿𝐿3
Dengan mengeliminasi dan mensubtitusikan persamaan 2.41 dan 2.42
maka diperoleh persamaan 2.43
𝑃𝑃 = 12𝐸𝐸𝐼𝐼
𝐿𝐿3 𝑀𝑀 =
6𝐸𝐸𝐼𝐼
𝐿𝐿2 (2.43)
Pada kasus kedua seperti gambar 2.20 nilai dari y=0 dan 𝜃𝜃= 1. Untuk mencari kombinasi nilai
gaya (P) dan momen (M), maka didapat persamaan 2.44 dan 2.45
𝑦𝑦 =𝑃𝑃𝐿𝐿3
Dengan mengeliminasi dan mensubtitusikan persamaan 2.44 dan 2.45
maka diperoleh persamaan 2.46
𝑃𝑃 = 6𝐸𝐸𝐼𝐼
𝐿𝐿2 𝑀𝑀 =
4𝐸𝐸𝐼𝐼
Persamaan 2.43 dan 2.46 yang kita dapat merupakan persamaan nilai
kekakuan yang merupakan kombinasi dari gaya dan momen yang bekerja pada
benda yang mengalami defleksi. Jika disusun dalam bentuk matriks maka
persamaannya akan menjadi. (Lit Y.C Pao hal: 67)
𝑘𝑘11 = 𝑃𝑃= 12𝐸𝐸𝐼𝐼
𝐿𝐿3 𝑘𝑘12 = 𝑀𝑀=
6𝐸𝐸𝐼𝐼
𝐿𝐿2
𝑘𝑘13 = −𝑃𝑃=− 12𝐿𝐿𝐸𝐸𝐼𝐼3 𝑘𝑘14 =𝑀𝑀 = 4𝐿𝐿𝐸𝐸𝐼𝐼 (2.47)
Nilai konstanta kekakuan pada persamaan 2.47 diperoleh melalui
perhitungan nilai defleksi atau perpindahan batang akibat pembebanan dengan
arah yang tegak lurus dengan batang. Pembebanan yang mengakibatkan defleksi
terdiri dari beban momen yang terletak pada ujung batang dan beban akibat gaya
geser pada batang.
Gambar 2.21 Kondisi batang yang mengalami defleksi
Pada gambar 2.21, batang yang dikenai gaya dan momen pada ujung
batang sebelah kanan akan menghasilkan persamaan momen dan persamaan gaya
geser akibat pembebanan (dimana θ=0 dan δ=1) pada pembebanan batang dengan
arah titik perpindahan ke atas. Sedangkan pada arah pembebanan ke bawah pada
batang, syarat untuk perhitungan persamaan momen dan gaya geser adalah θ=1
dan δ=0. Sehingga diperoleh nilai kekakuan sebesar : (Lit Y.C Pao hal: 67)
𝐾𝐾21 =𝑉𝑉𝑝𝑝 =
Sehingga matriks kekakuan global dapat kita susun menjadi
[𝐾𝐾] =�
Dengan mensubtitusikan tiap-tiap nilai dari matriks kekakuan persegmen
[𝐾𝐾] =𝐸𝐸𝐼𝐼 𝐿𝐿3�
12 6𝐿𝐿 −12 6𝐿𝐿 6𝐿𝐿 4𝐿𝐿2 −6𝐿𝐿 2𝐿𝐿2 −12 −6𝐿𝐿 12 −6𝐿𝐿
6𝐿𝐿 2𝐿𝐿2 −6𝐿𝐿 4𝐿𝐿2 �
2.8.1 Metode Elemen Hingga Untuk Pembebanan Lentur
Untuk mendapatkan nilai tegangan dalam kasus pembebanan lentur
diperlukan perhitungan gaya-gaya reaksi maksimal untuk mendapatkan besarnya
nilai tegangan pada elemen. Gaya-gaya reaksi dalam Metode Elemen Hingga
dapat dicari dengan menggunakan persamaan matriks 2.48 (Lit Saeed Moaveni
Hal: 17)
{𝑅𝑅} = [𝐾𝐾]{𝑈𝑈}−{𝐹𝐹} (2.48)
Dimana matriks R merupakan matriks gaya-gaya reaksi yang terjadi pada
suatu elemen yang dikenai gaya. Gaya-gaya reaksi reaksi yang didapat juga
meliputi momen maksimum yang terjadi pada suatu elemen. Setelah momen
maksimum didapat, maka tegangan lentur maksimum dapat dihitung dengan
menggunakan rumus :
𝜎𝜎= 𝑀𝑀𝑐𝑐 𝐼𝐼
Dimana :
M = momen bending (Nm)
c = jari-jari terluar pipa (mm)