KONVERGENSI DAN STABILITAS SOLUSI PERSAMAAN LAPLACE PADA BATAS DIRICHLET. Lasker P. Sinaga. Abstract. terdapat y0

Lasker P. Sinaga Abstract

Persamaan laplace adalah salah satu bentuk persamaan differensial tipe eliptik yang dapat diselesaikan dengan metode pemisahan variabel. Metode pemisahan variabel membuat persamaan laplace menjadi dua persamaan differensial linear homogen orde dua yang memenuhi batas dirichlet pada persegi (rectangular). Solusi persamaan laplace adalah sebuah barisan yang konvergen dan stabil asimtot terhadap bidang keseimbangannya. Kata kunci : Laplace, Dirichlet, Konvergensi, Stabilitas

PENDAHULUAN

Kestabilan (stability) dan keseimbangan (equilibrium) diperkenalkan oleh matematikawan Rusia, A. M. Lyapunov. Jika solusi-solusi dari sebuah persamaan berada dekat dan selalu dekat terhadap solusi lainnya maka kondisi tersebut dikatakan stabil, sebaliknya disebut dengan tidak stabil. Andaikan persamaan

)

,

(

t

y

f

dt

dy

_

dengan kondisi awal 0

)

0

(

y

y



mempunyai solusi

y



y

(

t

,

y

₀

)

dimana y adalah fungsi kontinu pada interval tertutup

 

0

,

T

maka untuk





0

terdapat



y

₀ yang sangat kecil sehingga kurva

y



y

(

t

,

y

₀





y

₀

)

dimuat dalam sebuah bidang dengan lebar

2



disekitar solusi tersebut.

Permasalahan yang cukup menarik adalah bagaimana cara mengekspresikan penganalisisan konvergensi dan kestabilan dari solusi persamaan laplace pada batas dirichlet dengan bentuk: 0 ) , ( ) , ( ) , ( ₂ 2 2 2 2 _        y y x u x y x u y x u . ) , ( ) , (x y f x y u  pada 0xa, y0 0 ) , (x y 

Lasker P. Sinaga adalah Dosen Jurusan Matematika, Fakultas Matematika dan Ilmu METODE PENELITIAN

Penelitian ini dilakukan dengan cara studi literatur dengan berbagai dukungan definisi dan teorema.

PEMBAHASAN DAN HASIL Solusi Persamaan Laplace

Persamaan laplace diselesaikan dengan menggunakan metode pemisahan variabel. Andaikan u(x,y) sebagai solusi dari persamaan laplace dan

memisahnya atas perkalian dua fungsi dengan variabel bebas berbeda

) ( ) ( ) , (x y X x Y y u  sehingga: ) ( ) ( " ) , ( 2 2 y Y x X x y x u _   dan (₂, ) ( ) "( ) 2 y Y x X y y x u _   Persamaan laplace akan menjadi:

0 ) , ( ) , ( 2 2 2 2       y y x u x y x u  X"(x)Y(y)X(x)Y"(y)0  0 ) ( ) ( " ) ( ) ( " _{ } y Y y Y x X x X Misalkan    ) ( ) ( " ) ( ) ( " y Y y Y x X x X

, sedemikian diperoleh dua persamaan differensial homogen orde dua, X"(x)X(x)0 dan Y"(y)Y(y)0.

Kedua persamaan differensial biasa tersebut akan diselesaikan dengan memperhatikan problema nilai eigen



agar diperoleh solusi nontrivial serta memenuhi kondisi batas yang ditentukan. Yang dapat dilakukan adalah menunjukkan semua kemungkinan nilai



. Kasus 1. X"(x)X(x)0 _dengan 0 ) ( ) 0 (  X a  X

1. Pada



0 diperoleh solusi trivial sehingga



0 bukan nilai eigen dari masalah diatas.

2. Pada



0 diperoleh solusi trivial sehingga



0 bukan nilai eigen dari masalah diatas.

maka _X"(_x)_{ p}2_X(_x)_0 _sehingga

diperoleh solusi

px px

x

X( )₁cos ₁sin dengan

0 )

0

( ₁  X

danX(a)₁sinap0. Untuk

0 1



maka apn atau a n p  sehingga 2 2₂2 a n p   untuk nN. Dengan demikian, diperoleh barisan

solusi x a n x Xn 2 2 2 1sin ) (   untuk N n . Kasus 2. Y"(y)Y(y)0 dengan 0 ) ( ) 0 ( Y b  Y

Karena pada kasus 1 telah diperoleh nilai

eigen ₂ 2 2 2 a n p     , nN maka

kasus 2 dapat diselesaikan menjadi y a n y a n y Yn     cosh sinh ) (  2  2 dengan 0 sinh cosh ) (  ₂  ₂ b a n b a n b Y_n     sehingga             b a n b a n     sinh cosh 2 2 ) ( sinh sinh ) ( 2 _{b y} a n b a n y Yn                  .

Solusi persamaan menjadi

            _   b a n y b a n x a n k y Y x X y x u n n _   sinh ) ( sinh sin ) ( ) ( ) , (

dengan k



2



1_{.. Jadi, diperoleh solusi} yang sangat banyak tetapi belum memenuhi kondisi batas. Hal ini dapat dilakukan dengan menggunakan prinsip superposisi.



            _  b a n y b a n x a n k y x u _   sinh ) ( sinh sin ) , (

Dengan problema dirichlet, maka:



             b a n b a n x a n k x u    sinh sinh sin ) 0 , ( =



x a n ksin  =f(x) Misalkan x a n k x f_n( ) sin  maka xdx a n x f a k a n  sin ) ( 2 0



 . Dengan demikian

Lasker P. Sinaga adalah Dosen Jurusan Matematika, Fakultas Matematika dan Ilmu             _  b a n y b a n x a n k y x un _   sinh ) ( sinh sin ) , ( =           nb y b n nx k sinh ) ( sinh sin =





















      



nb y b n ny

e

e

e

nx

k

2 ) ( 2

1

1

sin

Konvergensi dan Stabilitas Solusi Persamaan Laplace

Dengan memisalkan b n y n n

e

e

k

v

  2

1

 





,

k



0

dan

1

sin

1







n



x

maka n n

u

x

y

v

v







(

,

)

atau n n

x

y

v

u





(

,

)

0

. Analisis berikutnya adalah menunjukkan kekonvergenan barisan tersebut dengan menunjukkan kekonvergenan

v

_n

(

x

,

y

)

terlebih dahulu.

Misalkan

P

n n

ke

ny    1



}

{

dan  nb n n

e

Q

2 1

1

}

{

  





sehingga n n n

_Q

P

v



. Kekonvergenan

v

_n

(

x

,

y

)

akan ditunjukkan dengan menunjukkan kekonvergenan dari

{

P

n

}

n1 dan

 1

}

{

Q

_{n n} berdasarkan definisi berikut.

Definisi 3.1Sebuah barisan

{

x

n

}

n1 konvergen ke limit xjika untuk setiap





0

terdapat bilangan bulat N,

n



N

sehingga

x

_n



x





.

Contoh 3.2 Jika

lim



lim





0

     ny n n n

P

ke

maka

{

P

n

}

n1 konvergen ke 0. Bukti:

Pilih untuk setiap





0

terdapat

n

₀



N

sedemikian

ke

ny 



0



ke

ny 





Karena

n



N

,

n



n

0 sehingga  ny

ke

 = _{ny }

e

k

< . Dan





k

e

ny

_



ny





ln

_

k

atau 

_

_

k

y

n



1

ln

Pilih





K

sedemikian

n



0

. Ambil

1



n

sehingga

k

e

k

y 



Dengan demikian

P

n n

Ke

ny    1



}

{

konvergen ke 0.

1

)

1

(

lim

lim







     n n n

Q

e

maka  1

}

{

Q

n n konvergen ke 1. Bukti:

Pilih untuk setiap





0

terdapat

n

₀



N

sedemikian



  

_

_

_

_

_



_e

2nb

₎

₁

_e

2nb

_e

2nb

1

(

Karena

n



N

,

n



n

0 sehingga



 

_

_

 nb nb

e

e

2 ₂

1

.







_

ln

_

1

2

1

b

n



Pilih





1

sedemikian

n



0

. Ambil

1



n

sehingga 2

_

₂

1

_

1

  b b

e

e

Dengan demikian

Q

n n

e

nb  2 1

1

}

{







 konvergen ke 1.

Teorema 3.4Jika

{

P

n

}

n1 konvergen ke Pdan 

1

}

{

Q

_{n n} konvergen ke Q, dengan

Q



0

dan

0



n

Q

untuk setiap n, maka  













1 n n n

Q

P

konvergen ke

Q

P

. Bukti:

Pilih





0

, terdapat sebuah bilangan positif bilangan Riel M dan sebuah bilangan bulat positif

N

₁, sedemikian

M

Q

_n



untuk setiap

n



N

1. Kemudian

0

1

'







Q

P

M





Terdapat sebuah bilangan positif

N

₂ sehingga, untuk

n



N

2,

P

n



P





'

dan

sebuah bilangan bulat positif

n



N

₃, sehingga

Q

_n



Q





'

. Misalkan

}

,

,

max{

N

₁

N

₂

N

₃

N



. Untuk

n



N

,

'







Q

Q

_n ,

P

_n



P





'

dan

Q

_n



M

. Jadi

Q

Q

P

Q

Q

P

Q

P

Q

P

n n n n n

_

_



₌

Q

Q

P

Q

PQ

PQ

Q

P

n n n







_

Q

Q

Q

Q

P

Q

P

P

n n n n



_



<

_

















Q

Q

P

Q

_{n n}

1

'







'

1

_





1



P





_

₌

_

_

Lasker P. Sinaga adalah Dosen Jurusan Matematika, Fakultas Matematika dan Ilmu Dengan demikian n n n

Q

P

v



konvergen ke 0.

Teorema 3.5 (The Ratio Test) Misalkan bahwa

v

_n



0

untuk

n



k

maka a.



v

n





jika

lim

1

1

_

   n n n

v

v

b.



v

n





jika

lim

1



1

   _n n n

v

v

Bukti: a. Jika

lim

_ 1



1

n n n

v

v

, terdapat bilangan r sehingga

0



r



1

dan

r

v

v

n n1

_

untuk n yang

semakin besar. Pernyataan ini dapat dituliskan sebagai n n n n

r

r

v

v

1 1  

_

. Karena



r

n





maka



v

n





b. Jika

lim

1



1

  _n n n

v

v

terdapat bilangan r sehingga

r



1

dan

r

v

v

n n1

_

untuk n yang

semakin besar. Pernyataan ini dapat dituliskan sebagai _n

n n n

r

r

v

v

1 1  

_

_. Karena



r

n





maka



v

n







Berdasarkan tes rasio diatas, kekonvergenan dari





_ 





b n y n n

e

e

k

v

  2

1

ditunjukkan dengan n n n

v

v

₁

lim

   =

)

1

)(

1

(

lim

2 ) 1 ( 2 ) 1 ( y n b n b n y n n

_ke

e

e

ke

           





=

_



















      n b b n y n

_e

e

e

 _ ) 1 ( 2 2

1

1

lim

=

e

 y

dan jika



v

n konvergen maka



u

n juga konvergen.

Bukti:

Misalkan

s

_n



u

₁



u

₂



...



u

_n dan

t

_n



v

₁



v

₂



...



v

_n, kemudian karena



v

n konvergen,

)

(

t

_n adalah terbatas. Misalkan

t

_n



t

, untuk setiap

n



N

,

t

t

v

v

v

u

u

u

s

_n



₁



₂



...



_n



₁



₂



...



_n



_n



sehingga

s

n juga terbatas. Karena (

s

n)

adalah barisan yang naik (increasing,

u

_n



0

), (

s

_n) menuju titik limit pada

n





, dan



u

n konvergen. 

Karena

0



u

_n

(

x

,

y

)



v

_n

(

x

,

y

)

dan comparison test maka



u

_n adalah konvergen.

Teorema 3.7 Misalkan



u

n adalah sebuah barisan bilangan riel. Jika



u

n konvergen

maka



u

n juga konvergen.

Bukti: Misalkan













0

0

0

n n n n

u

jika

u

jika

u

a

dan















0

0

0

n n n n

u

jika

u

u

jika

b

Kemudian untuk setiap

n



N

,

a

_n



0

,

0



n

b

dan

u

_n



a

_n



b

_n. Dengan demikian

0



a

_n



u

_n dan

0



b

_n



u

_n . Jadi, jika



u

n adalah konvergen maka

berdasarkan comparison test membuktikan bahwa



a

_n dan



b

_n adalah konvergen, sehingga



(

a

_n



b

_n

)

juga konvergen. _

Solusi u(x,y)



u_n(x,y)

dengan 0u_n(x,y) v_n(x,y) telah terbukti konvergen dan u~(x0,y)0

adalah bidang keseimbangan. Yang menjadi pertanyaan adalahapakah solusi nol u~(x₀,y)0 adalah stabil?

Lasker P. Sinaga adalah Dosen Jurusan Matematika, Fakultas Matematika dan Ilmu Definisi 3.8 Jika untuk setiap





0

terdapat



(



)

sehingga x₀ (),

     , ) ~( , ) (x₀ x₀ y u x₀ y

u untuk setiap

y



0

maka u~(x₀,y) disebut stabil.

Misalkan x₀ () dan berdasarkan teorema 3.4 diatas maka



  

_





















    nb y b n ny

e

e

ke

2 ) ( 2

1

1

sehingga: ) , ( ~ ) , (x₀ x₀ y u x₀ y u   =



_























 _    



nb y b n ny

e

e

e

x

x

n

k

2 ) ( 2 0 0

1

1

)

(

sin

<

_



















       nb y b n ny

e

e

ke

2 ) ( 2

1

1





Definisi 3.9 Penyelesaian u~(x₀,y) disebut stabil asimtot, jika stabil dan terdapat bilangan

0

0





sehingga x₀ ₀ dan lim( ( ₀ ₀, )~( ₀, ))0 

 u x x y u x y

y

Dengan definisi tersebut,

0

0

1

1

sin

lim

2 ) ( 2











































        



ny nb_nby y

_e

e

e

nx

k

.

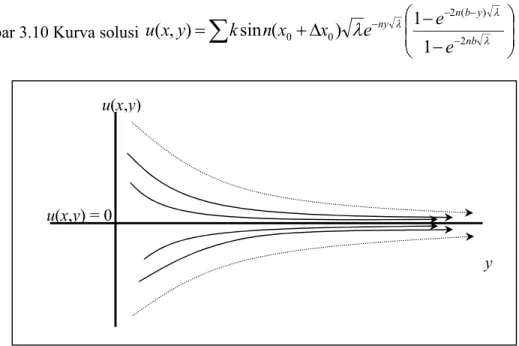
Dengan demikian, solusi persamaan laplace yang diperoleh adalah barisan solusi yang konvergen dan stabil

asimtotik terhadap bidang keseimbangan seperti ilustrasi pada gambar berikut.









1



e



Gambar 3.11 Sudut pandang dimensi dua kestabilan solusi persamaan laplace KESIMPULAN DAN SARAN

Berdasarkan penelitian tersebut, dapat diambil kesimpulan bahwa solusi persamaan laplace pada batas dirichlet dapat diperoleh dengan metode pemisahan variabel dengan nilai eigen positif. Solusi yang diperoleh adalah barisan solusi yang konvergen dan solusi nol adalah bidang keseimbangannya.

Solusi tersebut stabil asimtotik terhadap bidang keseimbangan.

Persamaan laplace adalah salah satu bentuk persamaan differensial elliptik. Penelitian ini dapat dilanjutkan ke bentuk persamaan-persamaan elliptik lainnya atau ke tipe persamaan parabolik ataupun hiperbolik.

DAFTAR PUSTAKA

Bartle R. G., 1976, The Element of Real Analysis, Jhon Wiley & Sons Inc. Canada.

Brown A. L. dan Page A., 1970, Element of Functional Analysis, Van Nostrand Reinhold Company, London.

Farlow S. J., 1982, Partial Differential Equations for Scientist and

Inc, Canada.

Gaughan D. E., 1987, Introduction to Analysis, Wadsworth Inc, Belmont, California, USA.

Gustafson K. E., 1987, Partial Differential Equations and Hilbert Space Methods, Jhon Wiley & Sons Inc. Canada.

John F., 1978, Partial Differential y

u(x,y)

Lasker P. Sinaga adalah Dosen Jurusan Matematika, Fakultas Matematika dan Ilmu York Inc, New York, USA.

Seydel R., 1994, Practical Bifurcation and Stability Analysis, -Verlag New York Inc, New York, USA.

Tikhonov N., Vasil’eva A. B., dan Sveshnikov A. B., 1985, Differential Equations, -Verlag New York Inc, New York, USA.